Functional Data Analysis for Dynamical System Identification of Behavioral Processes

Abstract

Efficient new technology has made it straightforward for behavioral scientists to collect anywhere from several dozen to several thousand dense, repeated measurements on one or more time-varying variables. These intensive longitudinal data (ILD) are ideal for examining complex change over time, but present new challenges that illustrate the need for more advanced analytic methods. For example, in ILD the temporal spacing of observations may be irregular, and individuals may be sampled at different times. Also, it is important to assess both how the outcome changes over time and the variation between participants' time-varying processes to make inferences about a particular intervention's effectiveness within the population of interest. The methods presented in this article integrate two innovative ILD analytic techniques: functional data analysis and dynamical systems modeling. An empirical application is presented using data from a smoking cessation clinical trial. Study participants provided 42 daily assessments of pre-quit and post-quit withdrawal symptoms. Regression splines were used to approximate smooth functions of craving and negative affect and to estimate the variables' derivatives for each participant. We then modeled the dynamics of nicotine craving using standard input-output dynamical systems models. These models provide a more detailed characterization of the post-quit craving process than do traditional longitudinal models, including information regarding the type, magnitude, and speed of the response to an input. The results, in conjunction with standard engineering control theory techniques, could potentially be used by tobacco researchers to develop a more effective smoking intervention.

Introduction

Longitudinal studies, which involve repeated observations over time with the same subjects, enable researchers to examine change over time. Traditional longitudinal data typically consist of relatively few observations per subject with long periods of time between observations. These data are ideal for examining long-term trends, but not the short-term changes that may occur on a smaller time scale. For example, observing participants' weekly nicotine craving levels during a smoking cessation study does not capture the daily (or even hourly) fluctuations in craving that an individual may experience during a quit attempt. Often, many more measurements are needed to study how the outcome evolves and reflects changes in treatment or other covariates throughout the duration of the study.

Recent advances in ecological momentary assessment (EMA) data collection strategies based on the use of personal digital assistants, smart phones, and the like are now enabling behavioral scientists to collect many repeated measurements of an individual's behavior and experiences in the real world (Stone & Shiffman, 1994). We will refer to these dense, comprehensive, and numerous repeated measurements of one or more time-varying variables as intensive longitudinal data (ILD; Walls & Schafer, 2006).

Many features set ILD apart from traditional longitudinal data, such as the high number of observations and the relatively short temporal spacing between observations in ILD. For example, McCarthy and colleagues (2008) studied smoking cessation by randomly assigning 403 participants to receive either bupropion or placebo, and asking the participants to provide assessments about their smoking behavior, affect, and withdrawal symptoms up to nine times each day for two weeks prior to and four weeks following the day they attempted to quit smoking. Each participant provided as many as 380 measurements of smoking behavior and withdrawal symptoms over a six-week period, with as few as 30 minutes in between measurements.

Rich ILD such as these present a new set of opportunities and challenges when it comes to statistical analysis. The opportunities stem from the ability to address a new set of questions about complex change in a particular behavior over time, as well as its determinants, correlates, and consequences. The challenges of ILD stem from the complex nature of the data. For example, the temporal spacing of observations may be irregular, and individuals may be sampled at different times. This often renders traditional time series methods inappropriate because these approaches require that each subject is measured at equal time intervals, and the same time intervals are used for all subjects. Another challenge is that the motivation for ILD collection is often to study complex nonlinear growth. In growth curve modeling and similar approaches that are commonly used for analysis of ILD in the behavioral sciences, the user must select a functional form (e.g., linear, quadratic) for change in the outcome. However, complex change, such as whether or not the process oscillates and how long it takes until the process settles, may not be represented well by these functional forms. This concern is especially relevant to the study of tobacco withdrawal, where evidence suggests that symptoms may be highly labile or volatile over relatively brief periods of time (McCarthy et al., 2006; Piasecki et al., 2003; Piper et al., 2011).

Functional data analysis (FDA) is an alternative to time series and growth curve analysis. This approach provides a way to fit several types of models, such as dynamical systems models and time-varying effect models, which are ideal for the statistical analysis of ILD. Ramsay and Dalzell (1991) introduced the term FDA in the statistics literature to represent the collection of statistical analyses available to study any data in the form of curves or functions of other variables. The basic premise behind FDA for longitudinal data is to use nonparametric smoothing to represent a set of discrete, repeated measures as a smooth function which is continuous and differentiable on some time interval. (We refer interested readers to Eubank, 1999, which offers an excellent technical introduction to nonparametric regression and spline smoothing.) FDA methods are ideal for ILD: the frequent and dense nature of ILD makes it plausible to assume the data represent smooth functions of time.

Dynamical Systems Models and System Identification in the Behavioral Sciences

Although originally developed for use in the physical sciences and engineering, dynamical systems models are increasingly being applied to ILD in the behavioral and social sciences (Boker & Graham, 1998; Boker & Ghisletta, 2001; Boker & Nesselroade, 2002; Bisconti, Bergeman, & Boker, 2004; Boker & Laurenceau, 2006; Rivera, Pew, & Collins, 2007; Boker, Molenaar, & Nesselroade, 2009; Navarro-Barrientos, Rivera, & Collins, 2011), where they are providing researchers new insight into the dynamics of human behavior and emotion. Dynamical systems modeling enables researchers to examine the complex behavior of a multivariate, time-varying process and the relations between a function and one or more of its derivatives (Ogunnaike & Ray, 1994; Ljung, 1999; Bequette, 2003). The parameters in dynamical systems models include information regarding the shape, magnitude, and speed of the outcome's nonlinear response to change in an independent variable.

Many applications of dynamical systems models to empirical behavioral data have focused on the damped linear oscillator model for self-regulatory processes such as emotional regulation (Bisconti et al., 2004), feelings of intimacy (Boker & Laurenceau, 2006), or even the postural adjustments of infants (Boker & Ghisletta, 2001). Self-regulation occurs when future values of an outcome vary based on the current values of the outcome and its rate of change, with an overall goal of maintaining a balanced state of the outcome variable. For instance, a recently bereaved widow's ability to maintain emotional equilibrium indicates, to some extent, emotional recovery from the loss of a spouse (Bisconti et al., 2004). The ability to model this type of regulatory system is especially relevant to addictive disorders, where core theories hold that drug tolerance and dependence reflect adjustments in homeostatic regulation (Koob & Le Moal, 1997; Solomon, 1977; Stewart, de Wit, & Eikelboom, 1984).

In engineering, dynamical systems models are often used for system identification, a technique to identify the temporal or causal relations between variables of a single system (Ljung, 1999; Bequette, 2003), which in the behavioral sciences would correspond to a single-subject experiment. System identification uses experimental data to identify an appropriate model of how the process behaves naturally over time and how it behaves in response to changes in predictors. Here we use Montgomery's (2005) definition of an experiment: “a test or series of tests in which purposeful changes are made to the input variables of a process or system so that we may observe and identify the reasons for changes that may be observed in the output response” (p. 1). By this definition, the McCarthy et al. (2008) study is an experiment in which the quit attempt is one of the independent variables.

An important reason for conducting system identification is to use the information obtained to develop a controller and optimize the system. Although to date controllers have typically been applied in settings such as automotive, chemical, and industrial engineering, it is possible that behavioral systems can be optimized using the same principles. For example, Rivera et al. (2007) discussed how dynamical systems models and control theory principles can be used to optimize adaptive, time-varying behavioral interventions. They illustrated their proposed methods with a hypothetical example of an intervention using family counseling to prevent the development of conduct disorders in children (Rivera et al., 2007). However, before optimization of behavioral systems can become a reality, a method for conducting system identification based on behavioral ILD is needed.

Objectives of This Article

This article aims to introduce new analytic methods that extend the application of dynamical systems models in the behavioral sciences to include system identification. We demonstrate an alternative method to estimate the derivatives using regression splines, and use mixed effects models to estimate system parameters that address the following research questions in the data collected by McCarthy et al. (2008): Controlling for negative affect, what is the long-term change in nicotine craving related to a quit attempt? How does a quit attempt influence the dynamics of nicotine craving (e.g., Do cravings after a quit attempt fluctuate between many highs and lows, or do they quickly peak and then decline over time)? How long does it take until nicotine cravings following a quit attempt settle? Does the drug bupropion moderate these relations?

Our proposed methods add to the existing literature by addressing the following dynamical systems model complexities: (1) We provide estimation methods for models that have multiple predictor series and are nonlinear in the parameters. (2) Our proposed methods enable researchers to fit these models to multiple subjects to investigate both within-subject and between-subject variability. (3) Our techniques add methods that enable behavioral scientists to use more flexible models to study response processes that show initial change in the opposite direction from the long-term change (called an inverse response). Such methods may be particularly relevant to controlled systems in which output perturbations come under homeostatic control.

The rest of the article is organized as follows. First, we describe the McCarthy et al. (2008) study in greater detail. Next, we define several important terms used in system identification and introduce dynamical systems models. We then give detailed descriptions of standard first-order and second-order, single input-single output, dynamical systems models, as well as direct interpretations of the model parameters and basic model assumptions. Next, we explain how FDA methods can be integrated with dynamical systems models for the purpose of system identification. We demonstrate the proposed procedures by applying them to the data mentioned above. Last, we provide some concluding remarks, review some limitations of the proposed methods, and discuss possibilities for future work.

Methods

Empirical Study

Design

The data we use to demonstrate these methods are from a randomized, placebo-controlled clinical trial of sustained-release bupropion and individual smoking cessation counseling conducted at the University of Wisconsin Center for Tobacco Research and Intervention (McCarthy et al., 2008). Participants were 463 adult daily smokers who were motivated to quit smoking, volunteered, and were eligible for the study. To be included in the study, the participants had to smoke at least ten cigarettes per day, have a baseline expired carbon monoxide level greater than nine parts per million, and provide their informed consent to participate. Participants were excluded based on several physical or mental conditions.

Subjects

A total of 403 participants completed the initial three weeks of assessments prior to the quit day. Prior to the target quit day, participants were randomly assigned to receive either bupropion or placebo, and either eight brief individual cessation counseling sessions or no counseling. Participants completed reports about their smoking behavior, affect, and withdrawal symptoms up to nine times per day for two weeks pre-quit attempt and four weeks post-quit attempt, with assessments as follows: a morning report that assessed current symptoms immediately upon waking up each day; random reports (≤ 7 randomly selected times per day) that assessed real time symptoms throughout the day; and an evening report that assessed the average symptoms since the previous evening report, completed immediately prior to going to bed each night. For a more detailed description of the study, please see McCarthy et al. (2008).

The analyses included in this article used the evening report data, which include one planned observation per day for each participant. Based on previous analyses which indicated no effect of counseling (McCarthy et al., 2008), we limited our analyses to the drug/placebo conditions only, and used a grouping variable, Drug (Drug = 1 if bupropion was given and 0 if a placebo was given). We retained for the analyses only those subjects who began recording their symptoms at least seven days before the quit attempt and continued recording their symptoms for at least fourteen days after the quit attempt (N = 315).

Measures

Craving was measured by averaging each participant's daily scores for four items from the Wisconsin Smoking Withdrawal Scale (WSWS) Craving subscale (Welsch et al., 1999). These four items asked participants to use a 1-11 scale (1 = NO!!! to 11 = YES!!!) to rate their urge to smoke, whether cigarettes were on their mind, whether they were thinking about smoking a lot, and whether they were bothered by the desire to smoke. Negative Affect (NA) was measured by averaging each participant's daily scores for three items from the WSWS. These three items asked participants to use a 1-11 scale (1 = NO!!! to 11 = YES!!!) to rate whether they were bothered by anger/irritability, sad or depressed, and tense or anxious. Quit Attempt (QA) was coded 1 for days that occurred after each participant's target quit day, and 0 for days before the target quit day.

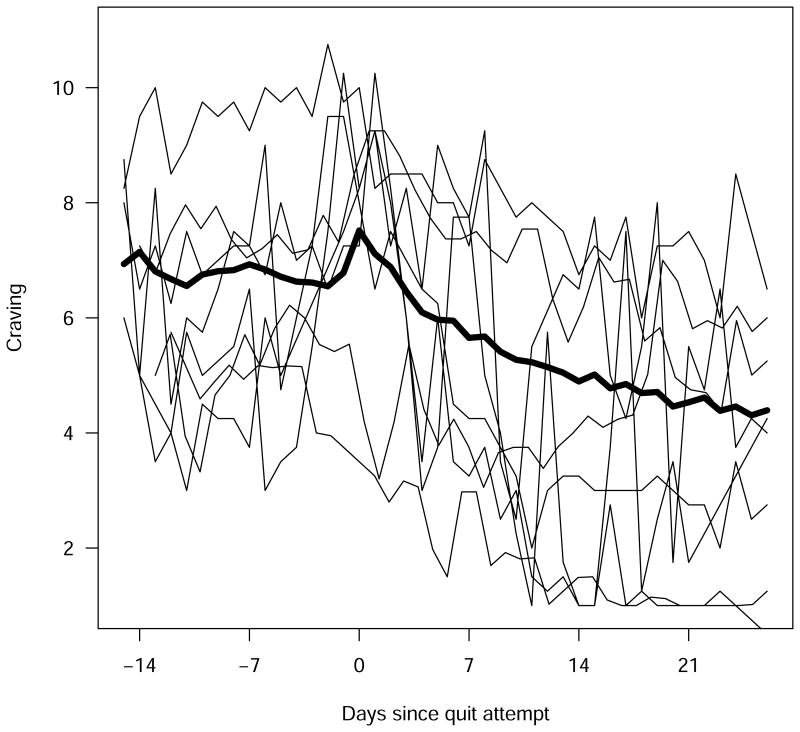
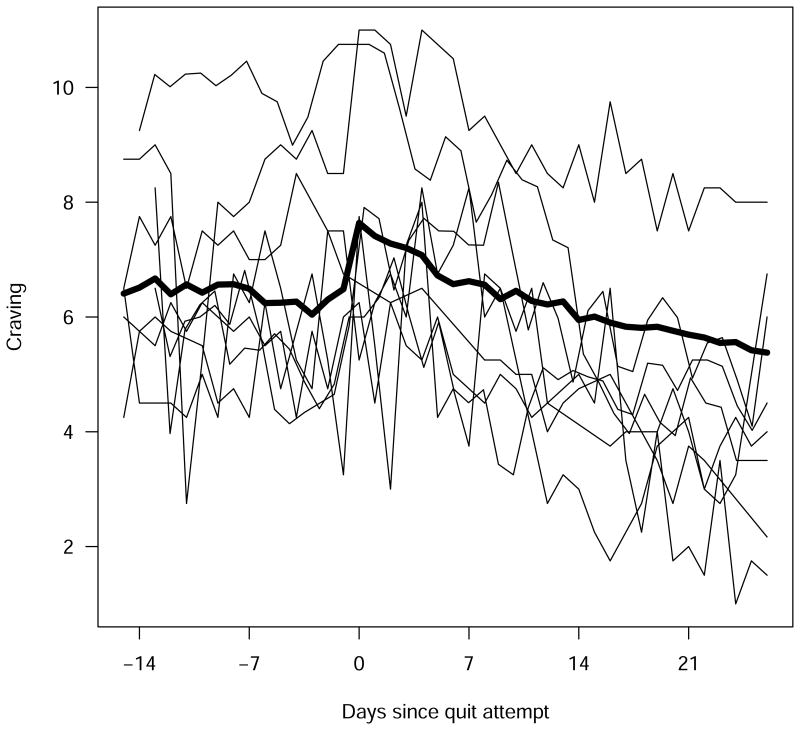
Figures 1 and 2 include plots of observed Craving for a random sample of eight participants from the drug and placebo groups, respectively. Figures 1 and 2 also include the plot of the average observed Craving for each group. We aligned the participants' plots of observed Craving at the assigned quit day, which is represented by Day 0 in Figures 1 and 2. The plots of the data show that, on average, Craving remains fairly steady during the pre-QA period, initially increases near the QA date, and then eventually declines over the four-week post-QA period.

Figure 1.

Plot of observed Craving for a random sample of 8 participants and average of observed Craving from the drug group.

Figure 2.

Plot of observed Craving for a random sample of 8 participants and average of observed Craving from the Placebo group.

Key System Identification Terms

When human behavior dynamics are modeled, an individual represents a single system of a given behavior, that is, an independent unit that produces both measured and (often) unmeasured output variables that vary based on changes to input variables (see Figure 3). Output variables, along with their associated rates of change, correspond to what behavioral scientists call outcome, response, or dependent variables. In the current study, the models fit will include one output, Craving (the individual's average daily level of nicotine craving). Input variables are better known in the behavioral sciences as predictor or independent variables. We will include as inputs two variables: QA (yes or no, depending on whether the day falls before or after the quit attempt) and NA (the individual's average daily level of negative affect).

Figure 3.

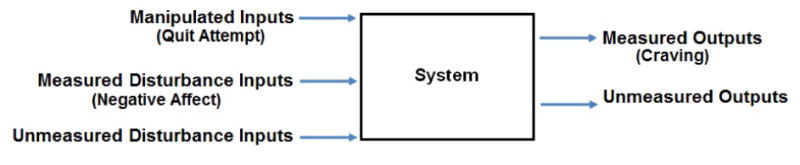
Block diagram of a system with manipulated and disturbance inputs and both measured and unmeasured outputs.

Figure 3 shows that inputs can be classified as either manipulated or disturbance inputs. Manipulated inputs are measured input variables that can be manipulated or controlled. In the current study, QA is a manipulated input because each individual is assigned to quit smoking on a target quit day. By contrast, disturbance inputs cannot be manipulated and may even be unmeasured. Because NA cannot be controlled directly, it is classified as a disturbance input.

Dynamical Systems Models and System Identification

Differential equations

Dynamical systems models are represented by a set of ordinary differential equations (ODEs) fit to ILD, in which one can identify the relations between the derivatives (i.e., rates of change) of the output, the value of the output itself, and any input variables of interest. Even very complex systems typically can be described using relatively simple first- or second-order ODEs. Consider a simple linear growth curve model in which craving is expressed as a function of time:

$${\mathit{\text{Craving}}}_{\mathit{\text{ij}}}=\alpha {\mathit{\text{Time}}}_{\mathit{\text{ij}}}+{\varepsilon }_{\mathit{\text{ij}}},$$ (1)

where j indexes time and i indexes subject. In this simple linear model, α represents the rate of change (i.e., velocity) in Craving as a function of time. Now suppose that the rate of change in Craving is related to the level of Craving. This relation cannot be estimated using standard growth curve models such as (1). Instead, it is necessary to model the rate of change of Craving rather than Craving itself by taking the first derivative of Craving and modeling its relation to Craving:

$$\frac{\mathit{\text{dCraving}}(t_{\mathit{\text{ij}}})}{\mathit{\text{dt}}}=\beta \mathit{\text{Craving}}(t_{\mathit{\text{ij}}})+\varepsilon (t_{\mathit{\text{ij}}})$$ (2)

where j indexes time and i indexes subject. The first derivative of a function with respect to time describes the rate of change in the output, which corresponds to the velocity in the output over time. Equation (2) is called a first-order ODE with constant coefficients. First-order differential equations may be used to model two primary relations between the first derivative of the output and: (1) the level of the output and (2) the level(s) of the input(s) included in the model. For example, a first-order model of Craving and QA uses both the level of Craving and the level of QA to predict the rate of change of Craving. The solution to a differential equation is the function of the output that satisfies the given differential equation. The solution for Equation (2) is Craving(t_ij) = c₀e^(βtij), where c₀ = Craving(0) is the initial condition for the Craving process. Thus, first-order ODEs may be used when the output demonstrates exponential growth (or decay).

To model the acceleration in Craving, the second derivative is used. The second derivative of a function with respect to time describes how the rate of change in the output is itself changing, which corresponds to acceleration in the output. Second-order models may be used to identify four relations between the second derivative of the output and: (1) first derivative of the output, (2) the level of the output, (3) the level(s) of the input(s) included in the model, and (4) the first derivative(s) of the input(s). For example, a second-order model of Craving might model the acceleration of Craving using as predictors the level of Craving, the rate of change of Craving, the level of QA, and the rate of change of QA. Second-order ODEs may be used when the output demonstrates more complex behavior than exponential growth or decay in response to a unit change in input, as when after a QA Craving oscillates between highs and lows. (See Blanchard, Devaney, & Hall, 2002 for more information about differential equation models.)

Interpretation of dynamical system model parameters

Dynamical systems models are quite different from the models behavioral scientists traditionally use (e.g., multiple regression or growth curve models). As discussed above, ODEs include one or more derivatives of the outcome function with respect to time. Also, in contrast to growth curve modeling, time is not explicitly included as a predictor in the model, and the variable on the left-hand side of the equation is a derivative of the output, rather than the level of the output. In addition to having a different model structure from growth curve models, the dynamical systems models have parameters that require different interpretations. We present two standard dynamical systems models fit to the McCarthy et al. (2008) ILD. Because we only use Models I and II to illustrate basic dynamical systems models and describe the parameters, we fit them to the full sample, collapsing over cessation treatment.

Model I: First-order input-output model with one input

One common dynamical systems model for single input-single output systems is the following first-order input-output model:

$${\tau }_1\frac{\mathit{\text{dCraving}}(t_{\mathit{\text{ij}}})}{\mathit{\text{dt}}}=-\mathit{\text{Craving}}(t_{\mathit{\text{ij}}})+K_1\mathit{\text{QA}}(t_{\mathit{\text{ij}}})+e(t_{\mathit{\text{ij}}}),$$ (3)

where t_ij is the jth observed time point for subject i, Craving(t_ij) is the nicotine craving level at time t_ij, dCraving(t_ij)/dt is the first derivative of Craving with respect to time, QA(t_ij) is the QA status at time t_ij and can take values 0 (i.e., before the QA) or 1 (i.e., after the QA), e(t_ij) is a zero mean random error process, and K₁ and τ₁ are system parameters representing the “system gain” and “time constant” (explained below), respectively. The estimated system gains and time constants for the first-order input-output model expressed in Equation (3) can be found in Table 1. Equation (3) is also called a forced ordinary differential equation because of the addition of the input process, QA(t). QA(t) is sometimes referred to as a forcing function, which is a given, known function of time that influences the solution to the ODE. Given the standard assumptions that QA changes from 0 to 1 at t = 0 and that Craving(0) = 0, the solution to Equation (3) is Craving(t_ij) = K₁(1 — e^−tij/τ1) (Bequette, 2003). A graphical representation of this first-order response in Craving to a unit change in QA is shown in Figure 4.

Table 1.

Results of fitting first- and second-order input-output models with single and multiple inputs.

Group	Model	τ̂ (Time Period)	K̂QA (QA Gain)	K̂NA (NA Gain)	ζ̂ (Damping)	τ̂QA (QA Zero)	τ̂NA (NA Zero)	GIC
All	I	1.13	-0.84		-			80574.80
All	II	1.33	-0.89		0.87			80205.21
Drug	III	1.58	-1.50	0.02	-	-	-	80508.41
Placebo		1.11	-0.17	-0.02	-	-	-
Drug	IV	1.57	-1.47	-0.00	0.92	-	-	80298.80
Placebo		1.30	-0.28	-0.01	0.86	-	-
Drug	V	1.57	-1.47	0.02	0.92	-0.97	2.20	79866.56
Placebo		1.30	-0.27	-0.02	0.86	-3.85	1.64
Drug	VI	1.57	-1.47	-0.00	0.92	-0.97	-	80036.92
Placebo		1.30	-0.28	-0.01	0.86	-3.74	-

Figure 4.

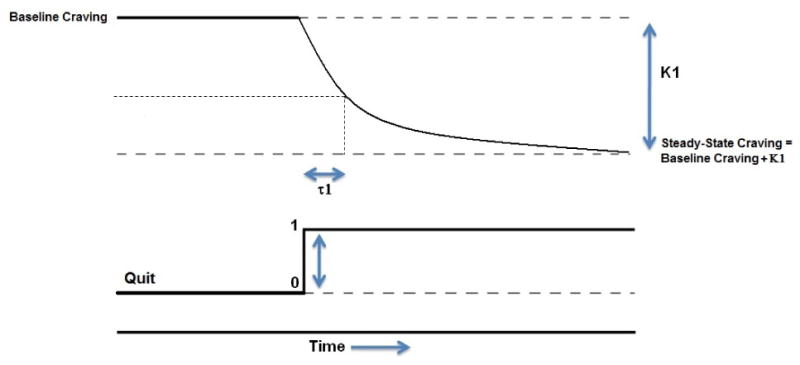
Graphical representation of a first-order system's Craving response to change in Quit Attempt.

The system gain (K₁) is the long-term positive or negative change in Craving in response to a unit change in QA; in other words, it is a measure of the magnitude of response in Craving to a unit change in QA at final time. It is assumed that Craving will eventually settle to a value which is approximately K₁ units different from its baseline value (i.e., the value of Craving prior to the change in QA) within a finite amount of time. This is called the steady-state value of Craving. The estimated gain (i.e., the long-term change) for Equation (3) is -0.84. These results indicate that, on average, a QA is associated with a 0.84 unit decrease in Craving.

The time constant (τ₁) equals the amount of time it takes for post-QA Craving to change in level 63.2%, nearly 2/3, of the system gain; therefore, it represents the speed of response in Craving to a unit change in QA. The dotted vertical line in Figure 4 depicts the point in time at which each Craving function has changed nearly 2/3 K₁ units. Craving attains approximately 95% of its long-term value in three time constants (i.e., 3τ₁). Larger time constants correspond to slower, more gradual change in the output. A time constant equal to zero corresponds to an instantaneous change. The estimated time constant for Equation (3) is 1.13 days. These results indicate that, on average, the length of time for Craving to settle to within 5% of its steady-state response is predicted to be approximately 3.39 (3 × 1.13) days after a QA.

Model II: Second-order input-output model with one input

Now suppose that rather than exhibiting rapid exponential decay to its steady-state value, the response of Craving to a QA changes more like a pendulum, which oscillates before eventually settling to an equilibrium. For oscillatory systems, a second-order input-output model is more appropriate, such as:

$${\tau }_2^2\frac{d^2\mathit{\text{Craving}}(t_{\mathit{\text{ij}}})}{{\mathit{\text{dt}}}^2}+2{\zeta }_2{\tau }_2\frac{\mathit{\text{dCraving}}(t_{\mathit{\text{ij}}})}{\mathit{\text{dt}}}=-\mathit{\text{Craving}}(t_{\mathit{\text{ij}}})+K_2\mathit{\text{QA}}(t_{\mathit{\text{ij}}})+e(t_{\mathit{\text{ij}}}),$$ (4)

where d²Craving(t_ij)/(dt²) is the second derivative, or rate of change of the first derivative, of Craving at time t_ij, and K₂, ζ₂, and τ₂ are system parameters representing the system gain, “damping coefficient”, and “time period”, respectively; these can be found in Table 1. A graphical representation of this second-order response in Craving to a unit change in QA is shown in Figure 5.

Figure 5.

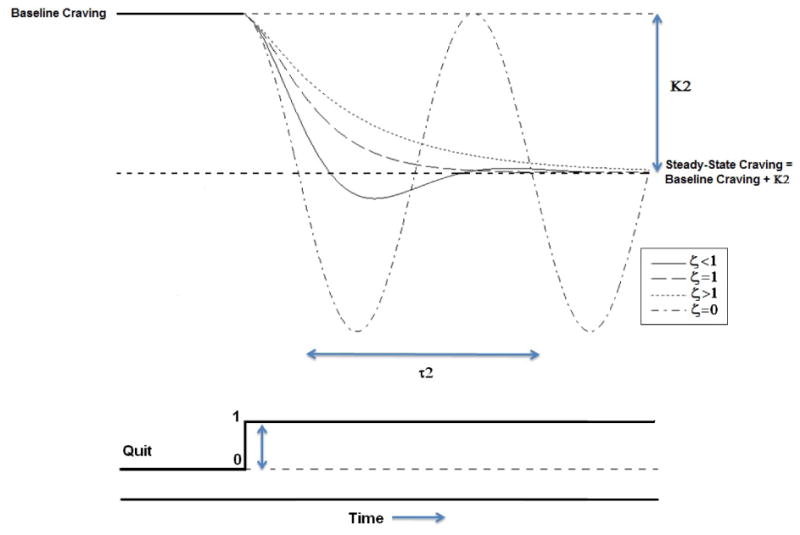
Graphical representation of a second-order system's Craving response to change in Quit Attempt.

The system gain K₂ has the same interpretation as it did in the first-order model. The estimated gain for Equation (4) is -0.89, indicating that on average, a QA is associated with a 0.89 unit decrease in post-QA Craving. The time period τ₂ is the length of time taken by one cycle, or oscillation, of an undamped process. The estimated time period for Equation (4) is 1.33 days. The settling time, or the time it takes for Craving to reach and stay within, say, 2-10% of its steady-state value, is represented in the time period and damping coefficient and can be estimated using a simulation of the predicted trajectory. The estimated settling time for Craving to reach and stay within 5% of its steady-state value is 5.07 days. The damping coefficient ζ₂ primarily describes the shape of the nonlinear response (e.g., oscillation), which factors into the settling time. A damping coefficient between 0 and 1 indicates that the response is oscillatory but eventually settles, depicted by the solid black response line in Figure 5. This is called an underdamped process. The estimated damping coefficient for Equation (4) is 0.87, indicating that the Craving response to a QA is an underdamped process. A damping coefficient equal to 1 indicates that the response is critically damped; that is, Craving displays the fastest possible approach to its steady-state value with no oscillation. The dashed line in Figure 5 is an example of a critically damped process. A damping coefficient greater than 1 indicates that the response does not oscillate, but is slower than the critically damped response. This is called overdamping; the dotted line in Figure 5 is an example of an overdamped process. Zero damping (the dash-dot line in Figure 5) is an undamped process and resembles a sine wave. A negative damping coefficient (not pictured) indicates that the response in Craving to a unit change in QA both oscillates and diverges from equilibrium, suggesting instability in the system. Given the standard assumptions that QA(t) steps from 0 to 1 at t = 0 and that Craving(0) = 0, Equations (5), (6), and (7) are the three possible solutions to Equation (4) (Bequette, 2003). For ζ₂ > 1, the solution is

$$\mathit{\text{Craving}}(t_{\mathit{\text{ij}}})=K_2\left[1+\frac{({\omega }_1{e}^{-t_{\mathit{\text{ij}}}/{\omega }_1}-{\omega }_2{e}^{-t_{\mathit{\text{ij}}}/{\omega }_2})}{({\omega }_1-{\omega }_2)}\right],$$ (5)

where ${\omega }_1={\tau }_2/({\zeta }_2-\sqrt{{\zeta }_2^2-1})$ and ${\omega }_2={\tau }_2/({\zeta }_2+\sqrt{{\zeta }_2^2+1})$. For ζ₂ = 1, the solution is

$$\mathit{\text{Craving}}(t_{\mathit{\text{ij}}})=K_2\left[1-(1+\frac{t_{\mathit{\text{ij}}}}{{\tau }_2})e^{-t_{\mathit{\text{ij}}}/{\tau }_2}\right].$$ (6)

For ζ₂ < 1, the solution is

$$\mathit{\text{Craving}}(t_{\mathit{\text{ij}}})=K_2\left[1-\frac{1}{\sqrt{1-{\zeta }_2^2}}{e}^{-{\zeta }_2{t}_{\mathit{\text{ij}}}/{\tau }_2}\mathit{sin}(\beta t_{\mathit{\text{ij}}}+\varphi )\right],$$ (7)

where $\beta =\sqrt{1-{\zeta }_2^2}/{\tau }_2$ and $\varphi ={tan}^{-1}(\sqrt{1-{\zeta }_2^2}/{\zeta }_2)$.

Dynamical systems models can also be used to examine inverse responses and overshoot. As defined above, an inverse response occurs when Craving exhibits initial change in the opposite direction from its long-term change. An inverse response is evident in the data here; Craving initially increases after a QA but eventually decreases. Overshoot describes a response in which Craving could exhibit early change that exceeded its final steady-state value. Inverse response and overshoot can be modeled in second-order models by including the first derivative(s) of the input(s). We examine these further in models V and VI below.

Model assumptions

Dynamical systems models use deviation variables, which we will denote with superscript (D) (e.g., Craving^(D)(t)). Deviation variables (see Eq. (8)) represent the difference between the values of the system's variables at each time point and the baseline values of the variables, which we will denote with the subscript B. The baseline value is the value of the variable when the system is at its normal, steady-state operating point, that is, the conditions at which the system normally runs.

$$x^{(D)}(t)=x(t)-x_B$$ (8)

The system is assumed to begin in this normal, steady-state operating point so that Craving^(D)(0) = 0 and QA^(D)(0) = 0. In other words, based on these assumptions dynamical systems models are assumed to have zero-valued intercepts.

The deviation scores for Craving were created by taking the difference between Craving at each time point and baseline Craving for each participant: Craving^(D)(t) = Craving(t) − Craving_B. In this study, we calculated the baseline value to be the average Craving value for each participant across the two weeks prior to the QA. This process was repeated for NA.

Model selection

Several methods are available for model selection. First, it is important to plot the data and look for trends. The plots of the observed group means of Craving shown in Figures 1 and 2 indicate that, on average, Craving quickly increases and then decreases in the long run for both the drug and placebo groups. This pattern of change, which as mentioned above is characteristic of an inverse response, suggests that a second-order response model may be necessary. Other observed patterns in Craving over time, such as oscillation, could also be useful in determining the optimal order of the dynamical systems model.

After looking for trends in the plots of the observed data, goodness-of-fit statistics are also useful for determining the best-fitting dynamical systems model. The Akaike information criterion (AIC) or the Bayesian information criterion (BIC) are commonly used fit statistics and are ideal for ILD with an equal number of observations for each subject. The AIC and BIC are calculated using -2 times the log-likelihood of the model, with a penalty added for the increase in model degrees of freedom. For ILD with unequal numbers of measurements for each subject, the participants' covariance matrices have different dimensions. In this case, the AIC and BIC are not appropriate measures of goodness-of-fit. For this reason, we used a Generalized Information Criterion (GIC) instead. GICs use the residual sum of squares of the model in place of -2 times the log-likelihood, thus removing the subjects' covariance matrices from the calculation. We use a GIC with the same penalty used to calculate the AIC: 2 times the model degrees of freedom.

Recall that the dynamical systems models discussed in this article are used to model a complex, nonlinear output response using ODEs. Because ODEs use the derivatives of the output on the left side of the model equations, calculating the residuals based on the derivatives would restrict model comparison capabilities. For example, first-order models could be compared only to other first-order models, and second-order models could be compared only to other second-order models. To enable comparison of GICs between first- and second-order models, we calculated the GIC using the residual sum of squares (RSS) based on the observed and predicted levels of Craving rather than the RSS based on the observed and predicted derivatives of Craving. The predicted Craving function is also called a solution to the ODE. We used a fourth-order Runge Kutta integration procedure to calculate predicted Craving for each of the fitted models.

FDA and System Identification

Derivative Estimation

In intensive longitudinal studies, variables are typically measured at dense, discrete time points. Because the associated derivatives are not directly observed, they must be estimated by first representing the observed data as smooth curves. Ramsay and Dalzell (1991) used generalized smoothing splines, and Ramsay, Hooker, and Graves (2009) provided R and MATLAB code to create smoothed functional data using smoothing splines. Boker and Nesselroade (2002) proposed local linear approximation to estimate first and second derivatives for their damped linear oscillator model. We propose an alternative method using regression splines.

In the present study, 403 participants' nicotine cravings were observed daily for six weeks (two weeks pre-QA and four weeks post-QA). Observed Craving for the i-th participant at time t_ij is denoted y_ij. It is assumed that a smooth function Craving_i(t) underlies participant i's ILD based on the following measurement error model:

$$y_{\mathit{\text{ij}}}={\mathit{\text{Craving}}}_i(t_{\mathit{\text{ij}}})+{\varepsilon }_{\mathit{\text{ij}}}.$$ (9)

We will demonstrate a method that uses a linear combination of basis functions, so that Craving(t) = Σ_kc_kϕ_k(t), where {ϕ_k(t)} is a set of basis functions and {c_k} are constants. One example is the truncated power spline basis, used in the current analysis, where $\{{\varphi }_k(t)\}=\{1,t,\dots ,t^r,{(t-{\xi }_1)}_{+}^r,\dots ,{(t-{\xi }_l)}_{+}^r\}$ for a given degree r and set of knots at ξ₁, …, ξ_l.

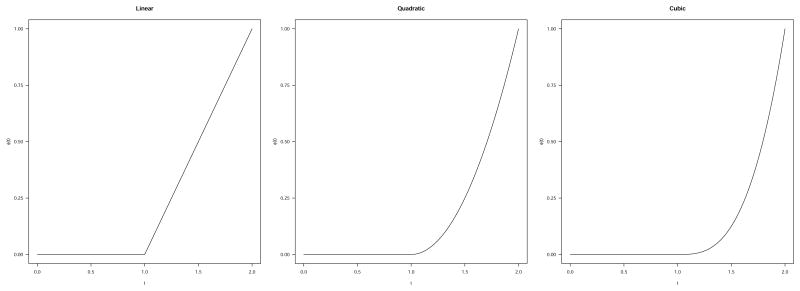
A truncated power function for knot ξ_i is defined by ${(t-{\xi }_i)}_{+}^r$, which is a power function that is truncated to zero to the left of the knot. The truncated power spline basis is then formed by taking the l truncated power functions together with the polynomials 1, t, t², …, t^r. One big advantage of this basis is its simple construction and ease of implementation, resulting in derivatives that are easy to estimate. A disadvantage is that the function can grow to be quite large as t increases. Because of this, we re-scaled the original time scale to [0, 1] for our analyses. Figure 6 shows a simple example of a linear, quadratic, and cubic truncated power function with a knot at t = 1. For more guidance in selecting which basis to use, see chapter 3 in Ramsay, Hooker, and Graves (2009).

Figure 6.

Example linear, quadratic, and cubic truncated power functions with a knot at t = 1.

Using the truncated power spline basis, Craving(t) has the following properties: Craving(t) is a piecewise polynomial of degree r on any subinterval [ξ_j, ξ_j+1) of the interval of observation; has r − 1 continuous derivatives; and has a discontinuous r-th derivative with jumps at the knots (i.e., the points separating the subintervals). Because we planned to use the first and second derivative of Craving and the first derivative of NA in the planned dynamical systems models, we used r = 4 for Craving and r = 3 for NA. As the number of knots decreases, the smoothness of the resulting function increases. We used the AIC to select the optimal number of equally-spaced knots for each participant (ranging from 10 to 30) for both Craving and NA. The optimal number of knots may be different not only between participants, but also for different variables within participant (i.e., Craving and NA). We used relatively high numbers of knots in order to smooth the observed data but still capture the dynamic features of each participant's Craving and NA curves, which is particularly important in the days immediately following the QA. We chose to use equally-spaced knots because the data used in the current analyses were equally spaced as well (e.g., participants reported one time each day, just prior to going to bed each night).

We estimated the measurement error model (9) for each participant and for both Craving and NA using PROC MIXED in SAS/STAT ®software Version 9.2 for Windows.¹ The derivatives of Craving were calculated by using the same linear combination of the derivatives of the basis functions, so that $\frac{\mathit{\text{dCraving}}(t)}{\mathit{\text{dt}}}={\sum }_{k=1}^K{c}_k\frac{d{\varphi }_k(t)}{\mathit{\text{dt}}}$ and $\frac{d^2\mathit{\text{Craving}}(t)}{{\mathit{\text{dt}}}^2}={\sum }_{k=1}^K{c}_k\frac{d^2{\varphi }_k(t)}{{\mathit{\text{dt}}}^2}$. We repeated this process to estimate the first derivative of NA. Example R code to create the basis and SAS code to smooth the data and estimate the derivatives can be found online at http://methodology.psu.edu/people/jtrail.

Estimation Methods

To fit the proposed dynamical systems models to the smoothed data, Ramsay (1996) proposed principal differential analysis, which identifies a linear differential operator that represents the covariation between one or more observed functions and their associated derivatives (Ramsay, 1996; Ramsay, et al., 2009). The dynamical systems model parameters can also be estimated using mixed effects models (Boker & Laurenceau, 2006; Deboeck, Boker, & Bergeman, 2008), which are more familiar in the behavioral sciences. The data analysis for this article was conducted using SAS/STAT mixed effects model software.

Model III: First-order model estimation with multiple inputs

Models I and II are examples of standard dynamical systems models that include only one input, QA. However, dynamical systems models can also be used with multiple inputs. For example, suppose a second input, NA, is introduced into a model in which Craving is the output and QA is a manipulated input. Although NA is a disturbance input and cannot be controlled, changes in NA may still influence post-QA Craving and are important to model. The following first-order model may be used if Craving shows an exponential decay response to change in QA status, controlling for NA:

$${\tau }_1\frac{{\mathit{\text{dCraving}}}^{(D)}(t_{\mathit{\text{ij}}})}{\mathit{\text{dt}}}=-{\mathit{\text{Craving}}}_i^{(D)}(t_{\mathit{\text{ij}}})+K_{\mathit{\text{NA}}}{\mathit{\text{NA}}}_i^{(D)}(t_{\mathit{\text{ij}}})+K_{\mathit{\text{QA}}}{\mathit{\text{QA}}}_i^{(D)}(t_{\mathit{\text{ij}}})+e(t_{\mathit{\text{ij}}}).$$ (10)

Using simple algebra, all of the unknown parameters can be moved to the right side of the equation:

$$\frac{{\mathit{\text{dCraving}}}^{(D)}(t_{\mathit{\text{ij}}})}{\mathit{\text{dt}}}=\frac{-1}{{\tau }_1}{\mathit{\text{Craving}}}_i^{(D)}(t_{\mathit{\text{ij}}})+\frac{K_{\mathit{\text{NA}}}}{{\tau }_1}{\mathit{\text{NA}}}_i^{(D)}(t_{\mathit{\text{ij}}})+\frac{K_{\mathit{\text{QA}}}}{{\tau }_1}{\mathit{\text{QA}}}_i^{(D)}(t_{\mathit{\text{ij}}})+e\ast (t_{\mathit{\text{ij}}}),$$ (11)

where e*(t_ij) = e(t_ij)/τ₁. Note that equation (11) is beginning to resemble a standard repeated measures model without an intercept and with the rate of change of Craving over time as the response variable. However, (11) is a nonlinear model; that is, it is not linear in the parameters. Although there are methods for nonlinear model estimation, a much simpler approach is to parameterize (11) as follows and use linear model methods:

$$\frac{{\mathit{\text{dCraving}}}^{(D)}(t_{\mathit{\text{ij}}})}{\mathit{\text{dt}}}={\beta }_1{\mathit{\text{Craving}}}_i^{(D)}(t_{\mathit{\text{ij}}})+{\beta }_2{\mathit{\text{NA}}}_i^{(D)}(t_{\mathit{\text{ij}}})+{\beta }_3{\mathit{\text{QA}}}_i^{(D)}(t_{\mathit{\text{ij}}})+e\ast (t_{\mathit{\text{ij}}}).$$ (12)

Equation (12) is now a standard, repeated measures, linear model. Estimates of the system parameters may then be calculated using simple, nonlinear functions of the resulting estimates of the βs, which are shown in Equation (13).

$$\begin{array}{lll}{\tau }_1\hfill & =\hfill & -1/{\beta }_1\hfill \\ K_{\mathit{\text{NA}}}\hfill & =\hfill & -{\beta }_2/{\beta }_1\hfill \\ K_{\mathit{\text{QA}}}\hfill & =\hfill & -{\beta }_3/{\beta }_1\hfill \end{array}$$ (13)

Note that because the parameter estimates for the dynamical systems model must be computed nonlinear combinations of the estimated βs, the SAS output does not include standard errors of the estimated gains, time constants, etc. Example SAS code to estimate the βs can be found online at http://methodology.psu.edu/people/jtrail.

To examine the differences in the behavior of Craving between the drug and placebo groups, interactions between Craving, NA, and QA with a grouping variable, Drug, may be added to the model. Including group differences in model (12) gives:

$$\begin{array}{lll}\frac{{\mathit{\text{dCraving}}}^{(D)}(t_{\mathit{\text{ij}}})}{\mathit{\text{dt}}}\hfill & =\hfill & {\beta }_1{\mathit{\text{Craving}}}_i^{(D)}(t_{\mathit{\text{ij}}})+{\beta }_2{\mathit{\text{NA}}}_i^{(D)}(t_{\mathit{\text{ij}}})+{\beta }_3{\mathit{\text{QA}}}_i^{(D)}(t_{\mathit{\text{ij}}})\hfill \\ \hfill & \hfill & +{\beta }_4{\mathit{\text{Craving}}}_i^{(D)}(t_{\mathit{\text{ij}}})\times \mathit{\text{Drug}}+{\beta }_5{\mathit{\text{NA}}}_i^{(D)}(t_{\mathit{\text{ij}}})\times \mathit{\text{Drug}}\hfill \\ \hfill & \hfill & +{\beta }_6{\mathit{\text{QA}}}_i^{(D)}(t_{\mathit{\text{ij}}})\times \mathit{\text{Drug}}+e\ast (t_{\mathit{\text{ij}}}),\hfill \end{array}$$ (14)

where Drug is 1 if the drug is given and 0 if the placebo is given and β₄, β₅, and β₆ will provide opportunities to examine whether there are differences in the system gains and time constants between the bupropion and placebo groups. Note that because there is no intercept in the model, and because the goal of adding the grouping variable is to examine how the system parameters differ between groups, we add Drug only in product terms with Craving, NA, and QA. (14) is a model that is now linear in the parameters and can be estimated using SAS PROC MIXED. Equation (15) contains the nonlinear functions of the βs that are needed to calculate the system gains and time constants for the drug and placebo groups.

$$\begin{array}{lll}{\tau }_1^{(\mathit{\text{Placebo}})}\hfill & =\hfill & -1/{\beta }_1\hfill \\ {\tau }_1^{(\mathit{\text{Drug}})}\hfill & =\hfill & -1/({\beta }_1+{\beta }_4)\hfill \\ K_{\mathit{\text{NA}}}^{(\mathit{\text{Placebo}})}\hfill & =\hfill & -{\beta }_2/{\beta }_1\hfill \\ K_{\mathit{\text{NA}}}^{(\mathit{\text{Drug}})}\hfill & =\hfill & -({\beta }_2+{\beta }_5)/({\beta }_1+{\beta }_4)\hfill \\ K_{\mathit{\text{QA}}}^{(\mathit{\text{Placebo}})}\hfill & =\hfill & {\beta }_3/{\beta }_1\hfill \\ K_{\mathit{\text{QA}}}^{(\mathit{\text{Drug}})}\hfill & =\hfill & -({\beta }_3+{\beta }_6)/({\beta }_1+{\beta }_4)\hfill \end{array}$$ (15)

Table 1 contains the estimated system gains and time constants for the drug and placebo groups for Model III.

Model IV: Second-order model estimation with multiple inputs

To model acceleration in Craving, we increased model complexity to the following standard second-order model:

$${\tau }_2^2\frac{d^2{\mathit{\text{Craving}}}^{(D)}(t_{\mathit{\text{ij}}})}{{\mathit{\text{dt}}}^2}=-{\mathit{\text{Craving}}}_i^{(D)}(t_{\mathit{\text{ij}}})-2{\zeta }_2{\tau }_2\frac{{\mathit{\text{dCraving}}}^{(D)}(t_{\mathit{\text{ij}}})}{\mathit{\text{dt}}}+K_{\mathit{\text{NA}}}{\mathit{\text{NA}}}_i^{(D)}(t_{\mathit{\text{ij}}})+K_{\mathit{\text{QA}}}{\mathit{\text{QA}}}_i^{(D)}(t_{\mathit{\text{ij}}})+e(t_{\mathit{\text{ij}}}).$$ (16)

Using the proposed procedure and adding interactions of Craving, NA, and QA with grouping variable Drug, (16) becomes:

$$\begin{array}{lll}\frac{d^2{\mathit{\text{Craving}}}^{(D)}(t_{\mathit{\text{ij}}})}{{\mathit{\text{dt}}}^2}\hfill & =\hfill & {\beta }_1{\mathit{\text{Craving}}}_i^{(D)}(t_{\mathit{\text{ij}}})+{\beta }_2\frac{{\mathit{\text{dCraving}}}^{(D)}(t_{\mathit{\text{ij}}})}{\mathit{\text{dt}}}+{\beta }_3{\mathit{\text{NA}}}_i^{(D)}(t_{\mathit{\text{ij}}})+{\beta }_4{\mathit{\text{QA}}}_i^{(D)}(t_{\mathit{\text{ij}}})\hfill \\ \hfill & \hfill & +{\beta }_5{\mathit{\text{Craving}}}_i^{(D)}(t_{\mathit{\text{ij}}})\times \mathit{\text{Drug}}+{\beta }_6\frac{{\mathit{\text{dCraving}}}^{(D)}(t_{\mathit{\text{ij}}})}{\mathit{\text{dt}}}\times \mathit{\text{Drug}}\hfill \\ \hfill & \hfill & +{\beta }_7{\mathit{\text{NA}}}_i^{(D)}(t_{\mathit{\text{ij}}})\times \mathit{\text{Drug}}+{\beta }_8{\mathit{\text{QA}}}_i^{(D)}(t_{\mathit{\text{ij}}})\times \mathit{\text{Drug}}+e\ast (t_{\mathit{\text{ij}}}),\hfill \end{array}$$ (17)

where β₅, β₆, β₇, and β₈ provide opportunities to examine differences in the system gains, time periods, and damping coefficients between the bupropion and placebo groups. Equation (18) contains the nonlinear functions of the βs that are needed to calculate the system gains, damping, and time periods for the drug and placebo groups.

$$\begin{array}{lll}{\tau }_2^{(\mathit{\text{Placebo}})}\hfill & =\hfill & \sqrt{-1/{\beta }_1}\hfill \\ {\tau }_2^{(\mathit{\text{Drug}})}\hfill & =\hfill & \sqrt{-1/({\beta }_1+{\beta }_5)}\hfill \\ K_{\mathit{\text{NA}}}^{(\mathit{\text{placebo}})}\hfill & =\hfill & -{\beta }_3/{\beta }_1\hfill \\ K_{\mathit{\text{NA}}}^{(\mathit{\text{Drug}})}\hfill & =\hfill & -({\beta }_3+{\beta }_7)/({\beta }_1+{\beta }_5)\hfill \\ K_{\mathit{\text{QA}}}^{(\mathit{\text{Placebo}})}\hfill & =\hfill & -{\beta }_4/{\beta }_1\hfill \\ K_{\mathit{\text{QA}}}^{(\mathit{\text{Drug}})}\hfill & =\hfill & -({\beta }_4+{\beta }_8)/({\beta }_1+{\beta }_5)\hfill \\ {\zeta }_2^{(\mathit{\text{Placebo}})}\hfill & =\hfill & -0.5{\beta }_2{\tau }_2^{(\mathit{\text{Placebo}})}\hfill \\ {\zeta }_2^{(\mathit{\text{Drug}})}\hfill & =\hfill & -0.5({\beta }_2+{\beta }_6){\tau }_2^{(\mathit{\text{Drug}})}\hfill \end{array}$$ (18)

Table 1 contains the estimated system gains, damping, and time periods for the drug and placebo groups for Model IV.

Model V: Second-order for inverse response model estimation with multiple inputs

The plots of the observed values of Craving in Figures 1 and 2 show that for many subjects, Craving initially increases after the start of the QA even though it decreases in the long run. This suggests that Craving may exhibit an inverse response to change in QA.

This added complexity of Craving's behavior can be modeled in the following way, which adds the first derivative of the inputs to the right side of the equation:

$$\begin{array}{lll}{\tau }_2^2\frac{d^2{\mathit{\text{Craving}}}^{(D)}(t_{\mathit{\text{ij}}})}{{\mathit{\text{dt}}}^2}\hfill & =\hfill & -{\mathit{\text{Craving}}}_i^{(D)}(t_{\mathit{\text{ij}}})-2{\zeta }_2{\tau }_2\frac{{\mathit{\text{dCraving}}}^{(D)}(t_{\mathit{\text{ij}}})}{\mathit{\text{dt}}}\hfill \\ \hfill & \hfill & +K_{\mathit{\text{NA}}}\left[{\mathit{\text{NA}}}_i^{(D)}(t_{\mathit{\text{ij}}})+{\tau }_{\mathit{\text{NA}}}\frac{{\mathit{\text{dNA}}}^{(D)}(t_{\mathit{\text{ij}}})}{\mathit{\text{dt}}}\right]\hfill \\ \hfill & \hfill & +K_{\mathit{\text{QA}}}\left[{\mathit{\text{QA}}}_i^{(D)}(t_{\mathit{\text{ij}}})+{\tau }_{\mathit{\text{QA}}}\frac{{\mathit{\text{dQA}}}^{(D)}(t_{\mathit{\text{ij}}})}{\mathit{\text{dt}}}\right]+e(t_{\mathit{\text{ij}}}).\hfill \end{array}$$ (19)

τ_QA and τ_NA define the “system zeros”, which are important in determining the shape of the response. For example, an inverse response in Craving to a unit change in QA is characterized by τ_QA < 0, with larger negative values corresponding to a larger inverse response.

Using the proposed procedure and adding interactions of the grouping variable Drug with the variables Craving, NA, QA, $\frac{{\mathit{\text{dCraving}}}^{(D)}(t_{\mathit{\text{ij}}})}{\mathit{\text{dt}}}$, $\frac{{\mathit{\text{dNA}}}^{(D)}(t_{\mathit{\text{ij}}})}{\mathit{\text{dt}}}$ and $\frac{{\mathit{\text{dQA}}}^{(D)}(t_{\mathit{\text{ij}}})}{\mathit{\text{dt}}}$, (19) becomes:

$$\begin{array}{lll}\frac{d^2{\mathit{\text{Craving}}}^{(D)}(t_{\mathit{\text{ij}}})}{{\mathit{\text{dt}}}^2}\hfill & =\hfill & {\beta }_1{\mathit{\text{Craving}}}_i^{(D)}(t_{\mathit{\text{ij}}})+{\beta }_2\frac{{\mathit{\text{dCraving}}}^{(D)}(t_{\mathit{\text{ij}}})}{\mathit{\text{dt}}}+{\beta }_3{\mathit{\text{NA}}}_i^{(D)}(t_{\mathit{\text{ij}}})+{\beta }_4\frac{{\mathit{\text{dNA}}}^{(D)}(t_{\mathit{\text{ij}}})}{\mathit{\text{dt}}}\hfill \\ \hfill & \hfill & +{\beta }_5{\mathit{\text{QA}}}_i^{(D)}(t_{\mathit{\text{ij}}})+{\beta }_6\frac{{\mathit{\text{dQA}}}^{(D)}(t_{\mathit{\text{ij}}})}{\mathit{\text{dt}}}+{\beta }_7{\mathit{\text{Craving}}}_i^{(D)}(t_{\mathit{\text{ij}}})\times \mathit{\text{Drug}}\hfill \\ \hfill & \hfill & +{\beta }_8\frac{{\mathit{\text{dCraving}}}^{(D)}(t_{\mathit{\text{ij}}})}{\mathit{\text{dt}}}\times \mathit{\text{Drug}}+{\beta }_9{\mathit{\text{NA}}}_i^{(D)}(t_{\mathit{\text{ij}}})\times \mathit{\text{Drug}}+{\beta }_{10}\frac{{\mathit{\text{dNA}}}^{(D)}(t_{\mathit{\text{ij}}})}{\mathit{\text{dt}}}\times \mathit{\text{Drug}}\hfill \\ \hfill & \hfill & +{\beta }_{11}{\mathit{\text{QA}}}_i^{(D)}(t_{\mathit{\text{ij}}})\times \mathit{\text{Drug}}+{\beta }_{12}\frac{{\mathit{\text{dQA}}}^{(D)}(t_{\mathit{\text{ij}}})}{\mathit{\text{dt}}}\times \mathit{\text{Drug}}+e(t_{\mathit{\text{ij}}}).\hfill \end{array}$$ (20)

Equation (21) contains the nonlinear functions of the βs that are needed to calculate the system gains, damping, time periods, and system zeros for the drug and placebo groups.

$$\begin{array}{lll}\hfill {\tau }_2^{(\mathit{\text{Placebo}})}& =\hfill & \sqrt{-1/{\beta }_1}\hfill \\ \hfill {\tau }_2^{(\mathit{\text{Drug}})}& =\hfill & \sqrt{-1/({\beta }_1+{\beta }_7)}\hfill \\ \hfill K_{\mathit{\text{NA}}}^{(\mathit{\text{Placebo}})}& =\hfill & -{\beta }_3/{\beta }_1\hfill \\ \hfill K_{\mathit{\text{NA}}}^{(\mathit{\text{Drug}})}& =\hfill & -({\beta }_3+{\beta }_9)/({\beta }_1+{\beta }_7)\hfill \\ \hfill K_{\mathit{\text{QA}}}^{(\mathit{\text{Placebo}})}& =\hfill & -{\beta }_5/{\beta }_1\hfill \\ \hfill K_{\mathit{\text{QA}}}^{(\mathit{\text{Drug}})}& =\hfill & -({\beta }_5+{\beta }_{11})/({\beta }_1+{\beta }_7)\hfill \\ \hfill {\zeta }_2^{(\mathit{\text{Placebo}})}& =\hfill & -0.5{\beta }_2{\tau }_2^{(\mathit{\text{Placebo}})}\hfill \\ \hfill {\zeta }_2^{(\mathit{\text{Drug}})}& =\hfill & -0.5({\beta }_2+{\beta }_8){\tau }_2^{(\mathit{\text{Drug}})}\hfill \\ \hfill {\tau }_{\mathit{\text{NA}}}^{(\mathit{\text{Placebo}})}& =\hfill & {\beta }_4/{\beta }_3\hfill \\ \hfill {\tau }_{\mathit{\text{NA}}}^{(\mathit{\text{Drug}})}& =\hfill & ({\beta }_4+{\beta }_{10})/({\beta }_3+{\beta }_9)\hfill \\ \hfill {\tau }_{\mathit{\text{QA}}}^{(\mathit{\text{Placebo}})}& =\hfill & {\beta }_6/{\beta }_5\hfill \\ \hfill {\tau }_{\mathit{\text{QA}}}^{(\mathit{\text{Drug}})}& =\hfill & ({\beta }_6+{\beta }_{12})/({\beta }_5+{\beta }_{11})\hfill \end{array}$$ (21)

Table 1 contains the estimated time period, system gains, damping, and zeros for the drug and placebo groups for Model V. Note that the estimated time periods, system gains, and damping coefficients for model V are similar to those for the standard second-order model results. τ̂_QA is negative for both the drug (τ̂_QA = −0.97) and placebo (τ̂_QA = −3.85) groups, but τ̂_NA is positive for both groups. τ̂_QA for the placebo group is larger in the negative direction than that for the drug group, indicating that on average, Craving in the placebo group has a larger inverse response to change in QA. Because the estimated gains for this model are negative, this has the following implications: (1) controlling for NA, taking bupropion versus a placebo during a QA is associated with a milder initial spike in post-QA Craving. Positive values of τ̂_NA would have indicated that, on average, Craving did not have an inverse response to change in NA but instead may have exhibited overshoot.

Model VI: Second-order for inverse response (to QA only) model estimation with multiple inputs

To determine if the $\frac{\mathit{\text{dNA}}(t)}{\mathit{\text{dt}}}$ term is needed in the model, we fit Model VI, a second-order model for inverse response in Craving to QA; that is, we re-fit model V after removing the $\frac{\mathit{\text{dNA}}(t)}{\mathit{\text{dt}}}$ term. Table 1 contains the estimated time period, system gains, damping, and zeros for the drug and placebo groups for model VI. Note that the estimated time periods, system gains, and damping coefficients for model VI are similar to those for results for models IV and V. The estimated τ̂_QAs for model VI are also similar to those estimated for model V. For model selection, we look to Table 1, which includes the GIC values for the six models presented in this article. Based on the minimum GIC=79866.56, the “best” model is model V, the second-order model for inverse response with multiple inputs. Recall that plots of the mean observed Craving functions (see Figures 1 and 2) indicated that, on average, Craving quickly increases and then decreases in the long run for both the drug and placebo groups. This pattern of change also suggests that the second-order model for inverse response is the appropriate model choice.

Discussion

Empirical Results About Craving Cigarettes After a Quit Attempt

In this article we performed system identification on ILD gathered in the course of a smoking cessation experiment. In part, the appeal of this analytic method is its ability to shed new light on behavioral phenomena. The analysis revealed some interesting aspects of how a QA, NA, and the drug bupropion affect nicotine craving. Craving appears to be a slightly underdamped process, meaning that it may exhibit minor oscillation but levels off fairly quickly, within approximately the first week following a quit attempt. We found that a QA is associated with a pronounced inverse response to Craving; in other words, Craving increases immediately after a quit attempt, and then gradually decreases until it reaches a steady state that is lower than the pre-QA baseline. This inverse response is considerably steeper in the placebo group than in the bupropion group. The bupriopion group took somewhat longer to reach a steady state of Craving, but this steady state of Craving was at a considerably lower level than that reached by the placebo group. Another interesting result is that on average, nicotine cravings leveled off below pre-QA baseline levels for participants who received bupropion, but for those participants who received the placebo, average post-QA Craving leveled off at a level that was only slightly lower than pre-QA baseline Craving. NA was not strongly related to the overall decrease. These results suggest that one effect of bupropion may be to alter the dynamics of Craving; it appears to mitigate the temporary post-QA increase in Craving, and to produce a lower steady state of Craving.

FDA for System Identification of Behavioral Data

The models we have discussed can be applied in situations where there are both controlled and uncontrolled (i.e., disturbance) inputs. In engineering, where these ideas have their roots, most experiments fit in a category that would be labeled “single-subject” by behavioral scientists. The models we have presented here can be applied to single-subject or multiple-subject experiments, and to within-subject and between-subjects experiments. An attractive feature of these models is that any mixed model software may be used for model estimation, such as PROC MIXED in SAS/STAT®software or lme() in R.

Another feature of this approach is that it enables the study of inverse response processes, that is, processes in which there is an initial change or reaction in the opposite direction from the later prevailing trend. This was demonstrated above, when our results indicated that after a quit attempt there is an initial increase in Craving, followed by a downward trend. Models of this type could be useful in many other areas, for example, studies investigating withdrawal from substances other than nicotine, such as alcohol or cocaine; feelings of hunger or craving for particular foods when following a reducing diet; or the side effects of pharmaceuticals.

Notably, FDA is a nonparametric approach, which means that it is not necessary to specify a functional form of change. In fact, the functional form of change per se is typically not a primary focus of investigations that use FDA. Instead, the parameters that are fit provide information about how the rate of change (first-order models) or acceleration (second-order models) of the output reacts to changes in the inputs.

The ILD we analyzed in this study were evenly spaced over time. However, much ILD is not evenly spaced over time. For example, many ILD studies (McCarthy et al., 2008; Shiyko, Lanza, Tan, Li, & Shiffman, 2012) prompt subjects randomly for responses over the course of a day. Others instruct subjects to provide data as events happen, such as when an individual feels a particularly strong craving for a cigarette. Such data collection designs produce complex data structures in which different subjects are observed at different times and contribute different numbers of data points in a given day.

Methods of Smoothing

In this article, we discussed using regression splines to estimate the smooth functions Craving(t) and NA(t), as well as their associated derivatives. There are several methods for nonparametric smoothing; besides regression splines, the most common in statistics literature are local polynomial regression and smoothing splines (Fan & Zhang, 2008). We chose the regression spline method because it is straightforward to implement and provides derivative estimates which are not computationally expensive to produce.

Most smoothing procedures assume that the variable being smoothed is unbounded. This assumption is frequently violated in the behavioral sciences. In the present study, Craving was measured on a scale ranging from 1-11, and then modeled in deviation score form. The smoothing procedure occasionally (in less than one percent of the data points) produced values outside of the valid range. We were unable to find generally accepted guidelines for what to do in this situation. We left the out-of-range values in the analyses, reasoning that a manual truncation would disrupt the estimation. Because bounded data are common in the behavioral sciences, more work is needed in this area.

Process Control

One exciting potential application of FDA in the behavioral sciences is system identification with the ultimate objective of process control (Rivera et al., 2007). Process control is a special topic in control theory: an area in engineering that explores how to influence the behavior of a dynamical system in order to achieve a desired outcome (called the control objective or setpoint), subject to specified constraints (Ljung, 1999; Bequette, 2003). Process control uses feedback or feed-forward controllers in conjunction with the model information obtained through system identification in an attempt to maintain the control objective by varying the manipulated input(s) in response to changes in disturbance variables.

Rivera et al. (2007) discussed the concept of using these control theory principles–particularly feedback control–to develop and improve adaptive, time-varying behavioral interventions. For example, the results of the system identification procedure presented here could form the basis of a controller that would optimize a time-varying adaptive intervention with the objective of efficiently bringing all participants to a goal level of Craving within a defined time frame. Such an approach would add another dimension to development of adaptive interventions. The emphasis would be on building a controller that will produce a system that not only demonstrates statistically significantly better performance than a control group, but, equally importantly, also enables intervention participants to achieve a clearly stated criterion. Examples of such criteria might include the following: for a smoking cessation intervention, a steady state of Craving of no more than a rating of 2; for an intervention to reduce drinking, a steady state of no more than one drinking day per week; for a weight loss intervention, maintenance of a loss of 10 percent of body weight; or for an intervention to combat depression, a steady state of a score below a clinical cutpoint on a depression inventory. By enabling system identification in behavioral ILD, the methodology we propose enables development of such controllers. Once a model of the system has been established, computer algorithms can be used to simulate the dynamical system's behavior based on the estimated model and the application of a controller. These simulations can then used to arrive at the rules that will control the behavioral intervention. This is essentially the same approach to controller development that is used throughout control engineering.

Limitations and Future Directions

In this article, only fixed, time-invariant effects of the inputs were examined. That is, the system gains, time periods, damping, and system zeros were held constant over time and subjects. A valuable tool in FDA is the ability to estimate time-varying effects, in which each effect is allowed to vary as a function of time. Time-varying effects could be used to address such research questions as, Does the effect of NA on post-QA Craving change over time, and is this effect moderated by bupropion? (e.g., Does taking bupropion during a quit attempt break the link between NA and Craving over time?) Additionally, in the behavioral sciences, it is common to include random effects of subject to account for differences between individuals' output responses. For example, subjects who receive bupropion may react differently to the treatment, resulting in different post-QA Craving trajectories. Future work is need to develop methods for including both random effects and time-varying effects.

Another limitation of the current work is that it does not provide methods for testing hypotheses about the system parameters. Important research questions that hypothesis tests could address include whether or not a particular system parameter is statistically significant, as well as whether or not treatment, in the form of bupropion, significantly moderates relations between variables in the system. The parameterization used here to estimate dynamical system parameters includes nonlinear combinations of the estimated βs. Therefore, obtaining the sampling properties of the resulting parameter estimates will require extensive theoretical work.