Cortical Network Modeling for Inverse Kinematic Computation of an Anthropomorphic Finger

Abstract

The performance of reaching movements to visual targets requires complex kinematic mechanisms such as redundant, multijointed, anthropomorphic actuators and thus is a difficult problem since the relationship between sensory and motor coordinates is highly nonlinear. In this article, we present a neural model able to learn the inverse kinematics of a simulated anthropomorphic robot finger (ShadowHand™ finger) having four degrees of freedom while performing 3D reaching movements. The results revealed that this neural model was able to control accurately and robustly the finger when performing single 3D reaching movements as well as more complex patterns of motion while generating kinematics comparable to those observed in human. The long term goal of this research is to design a bio-mimetic controller providing adaptive, robust and flexible control of dexterous robotic/prosthetics hands.

I. Introduction

THE human hand includes multiple joints allowing for an infinite number of different trajectories to move the fingers from one spatial position to another, which is critical in many daily tasks [1]. Such finger flexibility results in a complex neural control scheme that needs to select, plan and execute a particular trajectory in order to take into account task demands (e.g., accuracy) or changing environmental conditions (e.g., external perturbation) [1].

Consequently, when considering the multiple degrees of freedom (DOFs) involved in the control of dexterous robotic hands and fingers, both neuroscientists and roboticists focused on adaptive robot controllers [2],[3].

One fundamental problem for the brain as well as for any robotic controller aiming to command complex kinematic mechanisms, is to learn internal models of forward and inverse sensorimotor transformations (e.g., inverse kinematic) for reaching and grasping. This is a complex problem since the mapping between sensory and motor spaces is generally highly nonlinear and depends on the constraints imposed by the physical features of the human or robotic hand/finger as well as by the environment. In order to solve the inverse kinematic problem, various neural models were proposed; but many of these models did not integrate specific neurophysiological substrate resulting in a very limited biological plausibility (e.g., [4]). Conversely, other computational works proposed biologically plausible neural network models including specific brain structures/functions such as the Cerebellum [5]-[7] or the population vector coding processes found in motor/premotor areas [8]-[11].

Here, in accordance with the latter approach, we present a cortical network model that was able to learn the inverse kinematic. This neural architecture learned the internal inverse kinematic model of a simulated anthropomorphic robot finger (ShadowHand™ finger) having four geometrical DOFs. During an exploration (a motor babbling) phase, random motor commands endogenously generated were used to activate the finger while the corresponding sensorial consequences (e.g., visual) allowed training of the neural model to learn the inverse kinematic of the actuator. The results revealed that, after learning, this neural model was able to control the anthropomorphic finger in order to perform accurate and robust 3D reaching movements (with various levels of complexity) towards spatial targets with kinematics comparable to those previously observed in human. The long term goal of this research is to design a large scale modular cortical neural network model allowing adaptive, robust and flexible control of dexterous robotic/prosthetics hands.

II. Modeling Approach

A. Cortical Modeling and Sensorimotor Information

The proposed neural network model expanded the previous DIRECT (DIrection-to-Rotation Effector Control Transform) model of redundant reaching [8],[9] that functionally reproduces the population vector coding processes evidenced in the motor and premotor cortices [12]. This neural architecture learned neural representations encoding the inverse kinematic to accurately control an anthropomorphic robot finger with four DOFs.

Adaptive performance relied on the integration and processing of five main types of sensorimotor information involved in the control of visually guided movements: i) the neural drive conveying information about motor command for actual performance; ii) the proprioceptive information providing the current state of the finger (e.g., angular position) resulting from the sensory consequences of the motor commands; iii) the visual information related to the finger and the localization of the targets in the 3D space; iv) the task and goal related information involved in motor planning; v) the motor error computed (e.g., by the cerebellum; [5]-[7]). The combination of this sensorimotor information was employed to tune the neural model parameters throughout learning to perform accurate finger movements. Specifically, this architecture learned the internal representations of the inverse kinematic to establish the mapping between spatial displacements of the finger and the motor commands that generate the angular displacements at each joints by integrating visual, proprioceptive and motor command signals of the moving finger. This neural model also included a ‘context field’ (for more details see [13]) which is a set of neurons receiving inputs that determine the context of a motor action. A context field (here, implemented with radial basis functions) changes its activity when a particular joint configuration is recognized as inputs.

B. Cortical Network Architecture

The relationship between spatial and joint velocities of the finger is given by the following (discrete-time) equation:

$$\Delta x=J\left(\theta \right)\Delta \theta$$ (1)

where Δx, Δθ and J are the spatial velocity, the joint velocity of the finger and the finger’s Jacobian matrix, respectively. To obtain a joint rotation vector that moves the finger at a desired spatial velocity, (1) can be rewritten as follow:

$$\Delta \theta =G\left(\theta \right)\Delta x$$ (2)

where G(θ) =J⁻¹(θ) is an inverse of the Jacobian matrix. For a redundant manipulator such as the one used here, a unique inverse does not exist.

The elements of the matrix G(θ) are denoted by g_ij(θ) where index i refers to the actuator space dimension and index j refers to the 3D workspace. The output of the network g_ij(θ) is given by:

$$g_{\mathit{ij}}\left(\theta \right)=\sum _k\left(\frac{A_{\mathit{ijk}}}{\sum _k{A}_{\mathit{ijk}}}\right)\left(w_{\mathit{ijk}}+\sum _m{c}_{\mathit{ijkm}}{z}_{\mathit{ijkm}}\right)$$ (3)

$$c_{\mathit{ijkm}}\left(\theta \right)=\frac{{\theta }_m-{\mu }_{\mathit{ijkm}}}{{\sigma }_{\mathit{ijkm}}}$$ (4)

where g_ij(θ) are the basis functions of the network and k is the index of the basis function, the vector c_ijkm is a measure of the distance between the input value θ and the center of the k^th basis function, and A_ijk is the activation of the basis function (decreases in a Gaussian manner from the center). Here, μ_ijkm and σ_ijkm are the center and the standard deviation along the dimension m of the k^th Gaussian activation function, respectively. Each basis function is associated to a scalar weight w_ijk, related to the magnitude of the data ‘under its receptive field’. The set of weights z_ijkm allow for locally and linearly approximating the slope of the data ‘under its receptive field’.

The learning phase consisted of a babbling process that was performed by successive action-perception cycles during which the motor commands were generated to perform finger movements with various orientations to reach targets located in the 3D workspace (Fig. 1A).

Fig.1.

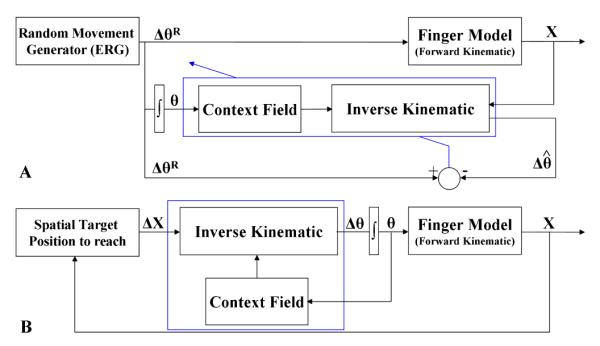
Neural model to learn and perform finger movements. (A) During the learning phase, the Endogenous Random Generator (ERG) generated random angular displacements (Δθ^R) that were transformed into spatial displacements (Δx) of the finger. Such spatial displacements allow the neural model to compute an estimation of angular displacements $\left(\Delta \widehat{\theta }\right)$ and compare them to those randomly generated. (B) After learning, the performance of the neural model was assessed by performing reaching to multiple spatial targets in the 3D workspace. A movement-gating GO signal was employed ([8]) to trigger the generation of the voluntary reaching movement.

Namely, during each action–perception cycle, random finger joint displacements (Δθ^R; R denotes random movements) were generated. These random joint rotations were performed from current joint configurations (denoted by θ) that were provided as inputs to the neural architecture and to the direct kinematics of the finger resulting in spatial displacements (Δx) of the finger. Then, based on these spatial displacements, the neural network computed an estimation $\left(\Delta \widehat{\theta }\right)$ that was compared to the corresponding random joint movement providing thus, an error signal that guided the adaptation of the network parameters (e.g., w_ijk, z_ijkm in equation (3); for further details on the model implementation, see [9],[10],[14]). After learning, a spatial target was provided to the neural model that performed the corresponding movement to reach it (Fig. 1B).

C. Geometrical Modeling of the Actuator

The model of the finger incorporated the geometrical features of the robotic ShadowHand™ finger (Shadow Robot Company Ltd.) which has the properties to mimic the main biomechanical features of an actual human finger including four DOFs (two for the metacarpophaleangeal (MCP; flexion-extension and abduction-adduction), one for the proximal interphalangeal (PIP; flexion-extension) and one for the distal interphalangeal (DIP; flexion-extension)). The direct model of the finger geometry was obtained by employing the Denavit–Hartenberg parameterization (for further details see [14], [15]).

III. Results

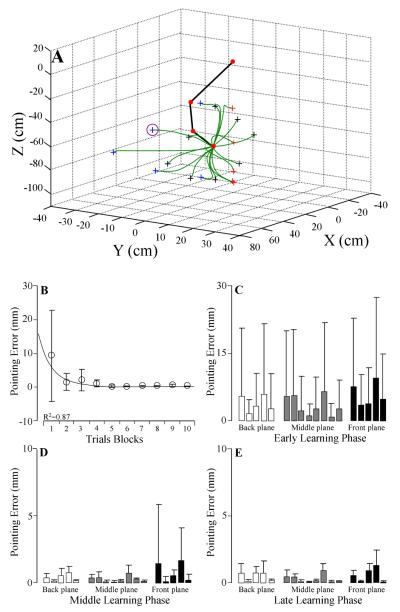
During and after learning of the inverse kinematic of the finger, the performance of the neural model was assessed by performing center-out reaching movements towards multiple targets placed in the 3D Cartesian workspace. These targets were located in three different planes (see Fig. 2A): i) the back plane (n=5) where flexion/extension and adduction movements were combined; ii) in the middle plane (n=8) where only flexion/extension movements were performed and iii) and the front plane (n=5) where flexion/extension and abduction movements were combined.

Fig.2.

Performance of the neural model during three different learning phases. (A) Trajectories during center-out (the stick diagram of the finger represents the initial position) reaching movements performed after learning towards 18 targets placed in the rear (blue color, n=5), middle (black color, n=8) and front (red color, n=5) plane. (B)-(E). Average reaching error and standard deviation during the early, middle and late learning phase for the targets placed in the three planes. For the panel (B), each point represented the average error values for the targets placed in the three planes across a block of 1000 trials. n: number of targets for each plane.

The reaching error and its variability (mean and standard deviation obtained when considering all targets and the three planes) decreased progressively throughout the learning for all the targets (Fig. 2B-E). Namely, when considering all targets, the average pointing errors were equal to 4.17 ± 2.34 mm, 0.40 ± 0.47 mm and 0.40 ± 0.39 mm for the early, middle and late learning periods, respectively. Although the overall error was small, the highest error values were obtained for movement performed in the front plane (Fig. 2C-2E). These results also revealed that, after learning, the angular and linear displacements were sigmoid-shaped and the velocity profiles were generally single-peaked and bell-shaped. The trajectories were slightly curved and the targets were accurately reached. Also, the robustness of the cortical network model was assessed by performing a movement where the finger had to reach a target located in a singular region of the workspace involving a completely outstretched configuration of the effector. This was done by employing both the neural model and a classic Moore-Penrose inverse.

The results revealed that higher velocity variations were found with the classic Moore-Penrose inverse while the neural model appeared to behave correctly around this singular region (Fig. 4A). Finally, to illustrate the potential capabilities of this neural model to generate more complex finger motion, a “triangular loop” was performed by combining successively flexion, abduction-extension and adduction-extension movements bringing the finger in regions where highest reaching errors were found (i.e., front plane, Fig. 2C-D).

Fig.4.

(A) Behavior of the neural model (thick line) and the classic Penrose-Moore inverse (thin line) in a singular region (finger outstretched). (B) Performance of a more complex finger movement (“triangular loop”, from 1 to 3) combining three sub-movements (flexion, abduction/extension, and adduction/extension).

IV. Discussion

We presented a neural architecture functionally similar to the motor and premotor cortices that was able to learn the inverse kinematic computation of an anthropomorphic finger including four DOFs. Specifically, this neural model reproduced the main kinematics features observed in human during finger movements and grip production [1],[16]. Namely, after learning, the angular and linear displacements were sigmoid-shaped and the velocity profiles were generally single-peaked and bell-shaped although for some targets a secondary (small) peak was observed which was also consistent with human data [1]. These specificities need to be further investigated. In addition, in agreement with the experimental results from the literature, this neural model generated slightly curved trajectories and the targets tested were accurately reached [1],[16]. The findings also suggested that this neural model was able to control the finger properly when moving it near singular region. However, when the learned mapping was replaced by the Moore-Penrose pseudoinverse, excessive joint rates were generated as the finger passes near the same singular region (Fig. 4A) resulting in jerky movements not observed in human finger motion [1],[16]. This is due to the fact that this type of neural model learns a mapping that remains zero along singular directions because there is little spatial movement in nearly singular directions [9],[13]. Although the neural model performance was mainly assessed on relatively simple reaching, more complex/ecological motions such as a “triangular loop” could also be correctly executed (Fig. 4B).

Taken together, the present findings suggest that this model can reproduce accurate, flexible and robust ecological human finger reaching movements. This is important since these features contribute to the unique manual ability that is so critical for most of the activity of daily living [1]. This work can be extended to consider several fingers by combining multiple neural models based on the same principles albeit inducing a higher computational cost. However, as previously mentioned, the performance of this neural model was mainly assessed by considering relatively simple center-out reaching movements. Therefore, further assessments need to be performed to extend these results. Namely, additional investigations will further examine the potential of this neural architecture to control this anthropomorphic finger under various conditions (e.g., robustness to multiple types of perturbations) as well as when considering more complex and ecological movements. Also, as a next step, this neural model will be employed to learn the inverse kinematic of an actual anthropomorphic robot finger (ShadowHand™ finger) having the same geometrical features. On the long term, future work will focus on the dynamics of the fingers since this neural model controls a biomechanical system without including any dynamic components (e.g., gravity, inertia). This could be performed by modeling more explicitly structures such as the Cerebellum that has been considered to encode this type of information [5],[6]. In summary, the aim of this research is to design a bio-mimetic controller providing adaptive, robust and flexible control of dexterous robotic/prosthetics hands.

Fig.3.

Typical angular (first row) and linear (second row) kinematics of the fingertip obtained after learning for a reaching movement towards the target in the rear plane (purple circle in Fig.2A). The first, second and third columns represent the position, velocity and acceleration, respectively.