Marker-free dual-axis tilt series alignment

Abstract

Dual-axis tilt series in electron tomography are collected by successively tilting the object about two approximately orthogonal tilt axes. Here we report on the extension of marker-free image registration based on cross-correlation techniques to dual-axis tilt series. A simultaneous geometry refinement yields accurate parameters for the computati on of the final reconstruction. Both, image registration and 3D-reconstruction operate on the combined data from the paired single axis series rather than computing individual single axis tomograms followed by a separate combination step. We show that with simultaneous registration and reconstruction of dual-axis tilt series, tomograms with higher resolution are obtained than by merging separately computed tomograms.

1. Introduction

In recent years electron tomography (ET) has become a routine technique for three-dimensional reconstruction of biological specimens, from whole cells, and cellular organelles to macromolecules or macromolecular assemblies (Baumeister, 2002). In ET, the object is reconstructed from its two-dimensional projections which are recorded with the object positioned in different orientations relative to the electron beam. The most common data collection scheme is a single axis tilt series, where the object is tilted with a goniometer in a typical angular range of ±60° to ±75° using either fixed angular increments or using angular increments that progressively decrease with increasing tilt angle, known as the cosine or Saxton scheme (Saxton et al., 1984). Due to mechanical constraints of the microscope, the goniometer, and the specimen grid, the tilt range is limited. Thus, a considerable part of data required for a faithful reconstruction is unknown. For a single axis tilt series, this is the well-known missing wedge. The effect of the missing wedge on the reconstructed object is an elongation of features in the direction of the optical axis and perpendicular to the tilt axis, and a partial or complete disappearance of features such as filaments and membranes whose Fourier coefficients are located primarily in the missing region.

Combining two tilt series whose tilt axes are approximately perpendicular to each other can reduce these problems. Dual-axis ET results in a better coverage of Fourier space, since only the intersection of the two missing wedges, a smaller pyramidal-shaped region, is unknown. Penczek et al. (Penczek et al., 1995) explored various dual-axis reconstruction schemes with fixed and graduated angular increments. A graduated scheme using larger, constant increments at low tilt angles and smaller increments at higher angles was recommended in cases where radiation damage was of concern. Mastronarde (Mastronarde, 1997) proposed a different approach to increase the resolution of dual-axis tomograms. Two single-axis tomograms were computed separately and subsequently merged after applying a distortion correction to the maps. A study of dual-axis tomography with an iterative algorithm using SIRT, applied to both phantom data and an inorganic specimen showed improved reconstruction quality when compared to weighted back-projection (Tong et al., 2006). An alignment scheme based on determining a set of markers held in common to each part of a dual-axis tilt series has been proposed to overcome problems with separately reconstructing and merging maps (Cantele et al., 2010). For tomography of thick biological specimens in the micrometer range, maps of adequate resolution could be obtained with dual-axis STEM tomography (Sousa et al., 2011).

A critical step in ET is image registration of the collected projection images. The commonly used image registration methods for tilt series, an overview of which can be found in (Amat et al., 2010), are based either on tracking artificially introduced fiducial markers, identifying and tracking intrinsic specimen features, or pattern matching by cross-correlation techniques. In our work, we have exclusively used marker-free alignment, which falls under the category of pattern matching by cross-correlation. The focus of the current study is the extension of the marker-free approach described in previous publications (Winkler and Taylor, 2006; Winkler, 2007) to dual-axis tilt series. The procedure simultaneously aligns both parts of the dual-axis series and refines both the relevant geometric parameters of the individual parts as well as the parameters relating the two parts with each other, i. e. rotation and scale differences.

The reduction of the size of the missing region in dual-axis tomography has also a favorable influence in the further analysis of tomographic data. Subvolumes extracted from single axis tomograms may suffer from the “missing wedge effect” during alignment and classification, i. e. the orientation of the wedge rather than structural features drive the alignment and classification process. Methods have been devised to minimize this effect (Frangakis et al., 2002; Förster et al., 2005, 2008), but obviously the better solution is to reduce the amount of missing data. This is particularly evident for samples where the structural motifs are randomly oriented in the tomograms and therefore the missing wedges have a different orientation relative to the motif. In such a situation, the reduction of a missing wedge to a missing pyramid will increase the data overlap in a cross-correlation calculation and better approximate the ideal situation without missing data. With uniformly oriented motifs such as paracrystalline specimens, the missing wedge effect may not be substantial, but as we show later, dual-axis data will still yield increased resolution compared to single axis data.

2. Theory

2.1. Tilt geometry

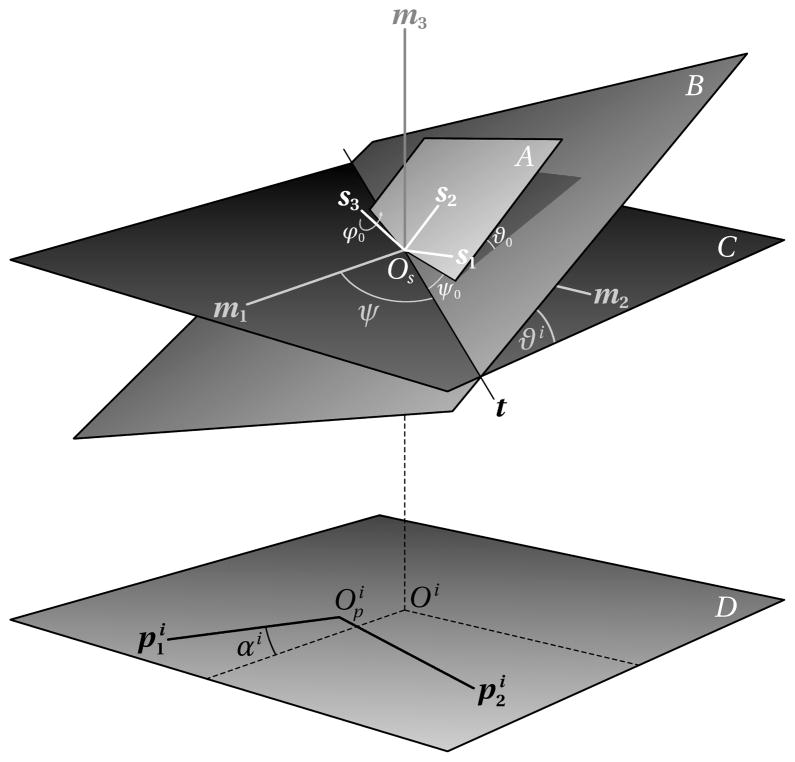
The tilt geometry is defined as shown in Figure 1. Assuming that the tilt series has n images, then for each projection image we define a coordinate system $P^i=\{O_p^i,{\mathbf{p}}_1^i,{\mathbf{p}}_2^i\}$, for i = 1 …n, which is fixed with respect to the pixel raster of the digitized image. The origin $O_p^i$ is usually located at the bottom left corner of the image, but some image file formats can record an arbitrary location. Furthermore, we define a coordinate system M = {O_m, m₁, m₂, m₃ }, fixed with respect to the microscope, and a specimen coordinate system S = {O_s, s₁, s₂, s₃ }, and we assume that the two origins O_m and O_s are identical, and the two planes spanned by the vector pairs m₁, m₂ and ${\mathbf{p}}_1^i,{\mathbf{p}}_2^i$ (the projection plane) are parallel. m₃ is the optical axis and the projection direction. The projection of O_s onto the image plane is denoted as Oⁱ. O_s is implicitly defined by choosing one of the projection images as a reference image, usually the projection of the untilted specimen. The angle ψ measured anti-clockwise from the m₁ axis, indicates the direction of the tilt axis t, and the angles ϑⁱ are the specimen tilts corresponding to the i^th image. To account for in-plane rotations of the images, the angles αⁱ are introduced, which align the image coordinate axes ${\mathbf{p}}_1^i,{\mathbf{p}}_2^i$ with the projected axes m₁, m₂.

Figure 1.

Tilt geometry for single axis tomography

The specimen tilt from the initial, untilted state, in which M and S are identical, is described by the transformation

$$s_j=\sum _{k=1}^3{r}_{jk}^i{\mathbf{m}}_k;j=1\dots 3$$

The coefficients $r_{jk}^i$ can be written as a matrix Rⁱ which is the product of the rotation matrices shown below:

$$R^i=R_0{R}_t^i$$

The rotation about the tilt axis t with the angle ϑⁱ is denoted as $R_t^i$ for the i ^th projection. The rotation R₀ is an additional constant rotation of the specimen itself relative to the supporting specimen grid which can also be expressed by the three Euler angles ψ ₀, ϑ ₀, and ϕ ₀. Besides specimen flatness, this rotation also accounts for unknown or inaccurate tilt angles, for example, when the nominal tilt angles of the goniometer do not correspond to the actual tilt of the specimen and a constant offset might have to be added. The diagram in Figure 1 assumes that the tilt axis is perpendicular to the projection direction. In practice, we specify two angles that define the direction of the tilt axis, which are the tilt azimuth ψ and an elevation angle ϕ. To keep the diagram simple, the elevation angle is not shown in 1. It would be the angle that rotates the tilt axis t out of plane C. The parameter definitions allow the direction of the tilt axis to assume any angle relative to the microscope coordinate system, so that the raw images need not be rotated for processing to fit a particular fixed tilt angle, which would involve an additional interpolation of the images. It is, however, preferable to experimentally orient the tilt axis roughly along one of the coordinate axes of the image raster to maximize the reconstructed area throughout the tilt series.

The tilt geometry definitions above and in Figure 1 are given for a single-axis tilt series. To extend the description to dual-axis tilt series, or even multiple axes, the images need to be grouped by axis, and we simply assign separate parameters ψ (azimuth), ϕ (elevation), and R₀ (specimen orientation) to each group. For some data collection schemes it is also desirable to split images for one particular tilt axis into groups for the processing of the tilt series. An example of such a scheme is a tilt series where the data collection is started at 0° tilt, which requires the stage to be repositioned to 0° after the highest tilt angle has been reached, and the second series be collected with the opposite angular increment. This can lead to slight differences in the common geometric parameters due to hysteresis effects and can be taken into account by grouping the images accordingly for the alignment.

For any single-axis and dual-axis tilt series, an image must be selected arbitrarily to define a reference coordinate system. As already mentioned, this is usually the image at 0° tilt. The second tilt axis for dual-axis tilt series and the orientation angles must be defined in this reference system. For example, in our tilt experiments the specimen was removed from the microscope after the first part of the tilt series had been recorded, and a second tilt series was taken after rotating the grid by approximately 90° and reinserting it into the microscope. In this case, the tilt axis direction remains essentially the same, because it is defined relative to a coordinate system fixed with respect to the microscope. Thus, only the relative orientation of the specimen between the first and second series needed to be determined. It was estimated as the rotation between the two images at 0° tilt. The other parameters, the in-plane rotations and specimen orientation were set to zero initially. Only the tilt angles must be obtained from the tilt experiment. The determination of the tilt axis direction is discussed later, so the remaining parameters to be determined are the locations of the common origin in the raw images. The common origin is assumed to be the center of the region of interest. A useful estimate is the center of the raw images, provided that the tracking during data collection has kept the region of interest well centered.

2.2. Region of interest

For the tilt series alignment to succeed, it is necessary to first identify a region that is held in common among the entire set of images, i. e. a rectangular region of interest should be selected with specimen features, that can be identified in all members of the tilt series, and with areas that are completely contained within the recorded images. With data sets collected on modern computer-controlled microscopes, this task is straightforward as long as the data acquisition software can track the specimen accurately throughout the tilt series. For our tilt series, the size and orientation of the region was determined in such a way as to maximize the common area. For this purpose, a map image was generated that delineates and superimposes the individual coverage of each member of the tilt series (Figure 2). For each series member, a binary representation of the region of interest in the frame of the member images was mapped back to the common frame of reference. The sum of these images forms a map in which higher pixel values (white areas) indicate coverage by a larger number of members. A value equal to the total number of members indicates complete coverage. By applying and varying a threshold when displaying the image, the optimal area can be found by fitting a rectangle into the displayed white area. In the example shown in Figure 2, the staggered appearance is caused by the non-eucentricity of the specimen which moved the region of interest across the field of view during data collection. Since the map is displayed in the specimen frame of reference, in which the tilt axes are oriented approximately vertical and horizontal for the two parts of the dual-axis tilt series, the member contributions appear displaced in approximately orthogonal directions.

Figure 2.

Maximal usable area displayed in the common coordinate frame of the specimen. Contributions from the selected region of interest for each tilt series member are superimposed. The area where all contributions overlap appears white. Various grey levels indicate contributions from fewer members, and black means no contribution. The inscribed dashed rectangle shows the largest area which can be selected relative to the pixel raster and be used for area matching. For display purposes, the total area of the image computed and shown in the figure has been chosen to be about twice the linear dimensions of the usable area.

2.3. Image registration procedure

The raw images of a tilt series cannot be directly used to reconstruct the specimen volume because the projections are usually not in register with the required accuracy. The most probable causes for this are non-eucentricity of the specimen, drift, and errors in specimen tracking during automated data collection. Marker-free image registration is designed to correct these errors. The method has been described previously in detail (Winkler and Taylor, 2006), but a brief summary including the notation introduced in the previous section follows.

Marker-free alignment is carried out in two stages. Initially a coarse alignment is performed: a simple and fast sequential cross-correlation between neighboring images in the tilt series. In order to compare two images at a different tilt angle, the orthogonal projections obtained with the microscope were converted to inclined projections by a stretch perpendicular to the tilt axis (Guckenberger, 1982), the amount of which depends on the tilt angle difference. This compensates the different amounts of foreshortening of the images and ensures that the Fourier transforms cover the same specimen area and have the same array size for numeric computation of the cross-correlation function. Usually, only translational offsets are determined at this stage, but if necessary, there is an option for the correction of the in-plane rotation.

For a refined alignment, equivalent specimen areas were being matched in a second stage with a projection matching approach that we call area matching. Area matching computes a reference projection that is compared to the experimental projection. This is a more time consuming procedure for two reasons: on the one hand the reference is constructed from a preliminary back-projection map, and on the other hand an iterative search algorithms is used to find the optimal alignment parameters which involves the computation of multiple Fourier transforms and cross-correlation functions. The size of the areas was chosen smaller or equal to the maximal usable area determined earlier.

The geometric parameters that need to be determined by the alignment are R₀ (three Euler angles), the angles ψ, ϕ, and αⁱ, as well as Oⁱ, the projections of the common origin O_s. Typically, we keep the tilt angles ϑⁱ fixed in our approach, assuming that the goniometer readings are accurate up to a common offset discussed above. Initial estimates for the parameters are set to zero except for the origins and the tilt azimuth. In many cases, the alignment procedure can tolerate initial values of the azimuth that deviate as much as 10° from the true values. The refinement of an inaccurate value is automatic in the iterative procedure, since it causes a systematic, large variation of the stretch/compression factors which are corrected later by the geometry reevaluation described below.

For both coarse alignment and area matching the raw or preprocessed images are interpolated according to the transformations A_i and a previously chosen region of interest. The resulting interpolated images must have the same size because the cross-correlation function is computed via multiplication of Fourier transforms. The difference between coarse alignment and area matching at this point is the reference construction and the optimization algorithm. Coarse alignment is carried out with a single correlation with the neighboring image in the tilt series; area matching with multiple correlations by varying the geometric parameters and maximizing the correlation coefficient. The reference image in the latter case is a re-projection computed from a previous back-projection map.

The result of the coarse alignment is a new set of Oⁱ, and additionally for area matching, a new set of transformations Aⁱ which are used for the reevaluation of more accurate geometric parameters. The transformations Aⁱ can be written as a product of the (estimated) input transformations Rⁱand a correction C ⁱ. To interpret this correction, we compute the singular value decomposition of the resulting 2×2 matrix:

$$A^i=R^i{C}^i;C^i=US{V}^T$$

The orthogonal matrix U corresponds to an in-plane rotation in the image plane, the diagonal matrix S provides two factors for stretch or compression in two orthogonal directions, the directions being determined by the orthogonal matrix V. It is evident that the alignment process is complete when the correction matrix C ⁱ is the unit matrix and therefore both stretch/compression factors are equal to one. In addition, an isotropic scale factor can be derived from the stretch/compression factors on the basis that no scale change must occur along the tilt axis. This is crucial for dual-axis tilt series, especially when the specimen is removed from the microscope in order to rotate the grid in the specimen holder. Under these circumstances, the magnification can differ measurably between the first and second tilt series.

A new set of geometric parameters $R_f^i$ is evaluated by a least squares fit procedure which attempts to approximate $C_f^i$ with a unit matrix in the equation $A^i=R_f^i{C}_f^i$. In a subsequent alignment cycle, the area matching is then repeated with the new parameters. The stretch/compression factors are monitored during the iterative process of area matching and geometry reevaluation, and can serve as a termination criterion. For more details and illustrations see Winkler and Taylor (Winkler and Taylor, 2006).

2.4. 3D reconstruction

A singular feature of marker-free alignment is the use of re-projections of preliminary maps as references to align the corresponding images. Typically, the alignment process starts with the images at the next higher and lower tilt relative to the image of the untilted specimen, then proceeds towards the more positive or negative tilt angles separately and in parallel. The back-projection reference is computed in a similar way from the already aligned images at each stage of the process. The back-projection calculation follows the procedure outlined by Radermacher (Radermacher, 1992) in section 3.2 and uses weighting functions for an arbitrary tilt geometry (Harauz and van Heel, 1986). This is required since all our tilt series are routinely collected with variable tilt angle increments (Saxton et al., 1984). The weighting functions computed during the alignment process are continuously updated, as images are aligned and merged for the reference computation. Since the geometric parameters of the images do not change any more once they have been aligned, only terms for the newly added images need to be recomputed for the evaluation of the weighting functions, thus speeding up the reference construction.

3. Materials and Methods

3.1. Tilt series acquisition

Dual-axis alignment was applied to sections of actively contracting insect flight muscle (IFM). The raw data of IFM were the same as Wu et al. used for their reconstruction (Wu et al., 2009). The dual-axis tilt series was collected on a FEI CM300-FEG at 300 keV using a Gatan model 670 ultrahigh tilt analytical holder and recorded on a TVIPS Tem-Cam F224 2k× 2k CCD camera. The exact pixel size of 0.69 nm was calculated from the 116 nm axial repeat in IFM. The first part of the series contained 104 images that covered an angular tilt range from −64.4° to 76.8° and was tilted about an axis roughly parallel to the filament axes, the second part had 119 images collected at tilts from −74.8° to 76.8° and the tilt axis was oriented perpendicular to the filament axes. The specimen grid was manually rotated between the collection of the two parts and the rotation angle was calculated by comparing the untilted views. The measured angle between the two untilted images was 98.4°. The initial estimates for the direction of the tilt axes were taken from the prior study cited above. For both parts of the dual axis series the initial azimuth was 88°. The tilt angles were chosen according to the Saxton scheme (Saxton et al., 1984). The increment near the untilted state was 2° and decreased to 0.5° at the highest tilt angles.

3.2. Image preprocessing

Prior to alignment, all raw images were preprocessed in the following way. The preprocessing consisted of two passes. During the first pass density gradients were removed and a median filter applied. In the resulting image, pixels or small areas with density anomalies were identified and recorded as a binary image. These anomalies usually arise during data acquisition in the form of density outliers caused for example by faulty pixels of a CCD camera. Extremely low or high densities due to specimen contamination can be treated in a similar way. In the second pass, local density adjustments based on the binary image were applied to the original image and global corrections such as gradient removal carried out. The resulting images were then used as input to the alignment procedure.

3.3. Tilt series and subvolume processing

The marker-free alignment was carried out with each part of the dual-axis tilt series separately, and also with the two parts combined. For each variant a back-projection map with the dimensions 1800×1372×128 was produced. The three tomograms were translationally and rotationally aligned to the dual-axis tomogram computed by Wu et al. so that their positions for the subvolume extraction could be used without modification. For comparison purposes, additional maps of the two single-axis tilt series were generated by applying the geometric parameters of the combined dual-axis tilt series alignment in the map computation. 515 subvolumes were extracted and processed with previously described methods (Winkler, 2007), and the Fourier shell correlation was computed after three rounds of alignment for a resolution assessment.

3.4. Evaluation of alignment quality and resolution

The monitoring of changes to the geometric parameters as described in an earlier publication (Winkler and Taylor, 2006) is a useful criterion to assess the progress of the iterative alignment. However, it does not reveal much about the quality of the alignment, especially when comparing successive cycles with different processing parameters, for example when the size of the matched area or the sampling interval has changed. In earlier work, we proposed the application of several common resolution criteria to tomographic reconstructions (Taylor et al., 1997). These are useful to estimate the resolution for a final map, but are less suitable to monitor the progress of the alignment for each image individually. Instead of a spatial frequency dependent criterion, the correlation between a computed and a recorded raw image was chosen as a measure to assess the alignment quality. The quality measure uses the cross-correlation coefficient between a selected image and the re-projection of the image from a tomogram that did not include the selected image. The cross-correlation coefficient is computed for each image in the tilt series.

The resolution of the final maps was estimated with Fourier shell correlation of two independently averaged sets of subvolumes. The subvolumes were extracted at the lattice positions of the paracrystalline specimen and aligned with previously described procedures (Winkler, 2007) prior to Fourier shell correlation. For comparison, the calculations were carried out separately with identical positions but with subvolumes from three different maps: the dual-axis map, and the two separately computed single axis maps. A second set of maps computed with identical geometric parameters was used here to separate effects that can be attributed to the tilt series alignment from those attributable to the subvolume alignment. The specimen features in the three maps were in register, so that subvolumes extracted at identical positions contained the same specimen features.

3.5. Software implementation

There are four steps involved in computing a tomogram from a tilt series: (1) parameter setup, (2) initial coarse alignment of the tilt series, (3) refinement of both alignment and geometry, and (4) 3D-reconstruction. Step (2) may not be necessary if the raw data is sufficiently well aligned, otherwise the interactive graphical tool described elsewhere (Winkler, 2007) can be used for coarse alignment. Steps (3) and (4) were implemented as a Python extension module written in C that easily integrates with other software such as SPARX/EMAN2 (Hohn et al., 2007) or Appion (Lander et al., 2009). The basic image processing operations called by the Python extension module are organized in external libraries (Winkler, 2007). The shell scripts and command line programs of the previously described version have been replaced by Python methods. For more technical details see the documentation of the protomo software package (www.electrontomography.org).

4. Results

We have applied the dual-axis method to a data set of a plastic-embedded section of actively contracting IFM. This tilt series has been previously processed (Wu et al., 2009). In the previous study, the two parts of the dual-axis series were individually aligned with our marker-free method and the back-projection maps were subsequently merged in IMOD (Mastronarde, 1997). For the current study these same tilt series were realigned with the new method and the resolution estimated by means of subvolume extraction, alignment, and averaging comparable to the previous work.

4.1. Tilt series processing

Two dual-axis alignment strategies were tested: (A) all images of the first tilt series were aligned, followed by the images of the second tilt series, and (B) all images were aligned strictly in the order of ascending magnitude of the tilt angle, alternating between the first and second series. Thus, with strategy (A) the reference for area matching was first built from images of the entire first tilt series, and images from the second series were merged in later. With strategy (B), the reference contained images from both the first and second tilt series from the beginning of the alignment procedure. In both cases, tilt angles with the same magnitude were processed first before proceeding with the next higher ones. The starting point was the image at 0° tilt of the first series. The 0° tilt image of the second series was removed. In both strategies, the alignment process was started with a small matched area and binned or sampled images of smaller size to speed up the alignment process, since the execution time depends largely on the array size of the Fourier transforms computed from the selected area. In order to cover similar specimen areas with smaller array sizes, the images were sampled by the same factor with which the array size was reduced. If the binning option was selected in the alignment procedure and the sampling factor was not an integer number, the images were first binned with an integer factor less than the specified sampling factor and then interpolated to the desired sampling. Without binning, the interpolation would be carried out directly with the raw images, though this may not be desirable for factors greater than 2 or 3. The matched area was gradually expanded up to the full size of the region of interest, and the sampling factor decreased. For each processing parameter choice, a few cycles of alignment and geometry refinement were carried out. Geometry refinement included the specimen orientation, tilt azimuths, and in-plane rotations. The progress of the alignment in each cycle was monitored by comparing geometry parameter changes numerically and stretch/compression factors graphically with the previous cycles. To automate this process, four cycles were usually executed per alignment stage (Table 1) and the results inspected afterwards. Additionally, before a processing parameter change, a cross-correlation resolution assessment was computed for each stage (Figure 3). In subsequent stages, after more accurate azimuths have been determined, two additional processing parameters were enabled in the geometry refinement: isotropic scale changes and tilt elevation variations. After that, the matched area was increased and unbinned images were used. Table 1 summarizes the parameters of the five alignment stages.

Table 1.

Alignment stages.

Stage	Refined parameters	Sampling factor	Matched area (pixels)
a	azimuth	2	480×480
b	azimuth	2	1000×960
c	azimuth, scale	2	1000×960
d	azimuth, scale, elevation	2	1000×960
e	azimuth, scale, elevation	1	2000×1920

Figure 3.

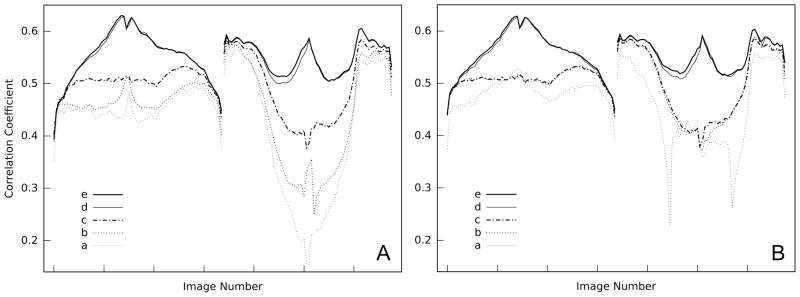
Alignment quality. (A) All images of the first tilt series were aligned first, followed by the images of the second one. (B) All images are aligned strictly in the order of ascending magnitude of the tilt angle, alternating between the first and second series. The left part of each panel represents the first tilt series, the right part the second one. Within each part the tilt angle increases from negative to positive angles with increasing image number. (a) – (e) are the alignment stages listed in Table 1.

Using alignment strategy (A), the improvement in quality progresses slower in the first two stages of alignment compared to strategy (B). Also, the second part of the tilt series starts with much lower cross-correlation coefficients (Figure 3). After inclusion of the isotropic scale factor in the geometry refinement there was no significant difference as measured by the correlation coefficients between the two alignment strategies, and the end result is almost identical. Only the cross-correlation coefficients of the mid-range angles are slightly higher for the second part in strategy (B). A considerable increase in correlation was observed in two instances: the first one when isotropic scale changes were considered (between stages b and c), the second one when the elevation angle was included (between stages c and d), which allows the tilt axis to deviate from a perpendicular orientation relative to the optical axis. Only a marginal improvement was observed in the last stage however, when the original, unsampled images were used that covered the same specimen area as the sampled images of the previous stages.

The comparison of the initial and final tilt azimuths (Table 2) shows only small differences. The initial estimates were chosen based on many tilt series collected previously with the same instrument, so no significant corrections are expected after alignment. It should be noted that the relatively small change in the elevation angle produces an improvement of the alignment for images recorded at lower to mid-range tilt angles as shown in Figure 3.

Table 2.

In-plane rotation between the two images at 0° tilt and tilt axis direction before and after alignment. Note that the two tilt axes are essentially the same, because they are defined in the microscope coordinate system.

	Rotation	First Axis		Second Axis
		ψ	ϕ	ψ	ϕ
Estimated	98.4°	88.1°	0.00°	88.9°	0.00°
Refined	99.0°	88.9°	0.33°	89.7°	0.31°

4.2. Missing data in Fourier space

To illustrate the effect of the missing wedge in single-axis tomograms or the missing pyramid in dual-axis tomograms respectively, three back-projection maps of IFM were computed. The first map (Figure 4A) used those images where the tilt axis was oriented perpendicular to the filament axes, the second map (Figure 4B) the images where the tilt axis was oriented parallel to the filament axes, and finally the third map (Figure 4C) was computed from the complete dual-axis series. All three maps were computed with geometric parameters derived from the alignment of the complete series (C). This eliminates the dependency on alignment quality in the comparison and shows effects that can be attributed to the missing wedge alone. In all three cases, the filaments lie roughly in the specimen plane, so the equatorial and higher layer planes of the filament transform are oriented perpendicular to both the filament axes and the specimen plane. In Figure 4A (tilt axis perpendicular to filaments) the missing wedge orientation removes varying amounts of Fourier coefficients on each layer plane. Most important, the entire equatorial plane except for the single common line is lost, along with varying amounts of the non-equatorial layer planes depending on the distance from the tilt axis. The low-order layer planes of the filament transform are affected more than the higher order layer planes. In IFM, these lower order layer planes have significant amplitude. As a consequence, helically arranged features along the axial direction are not as well rendered as features that extend in lateral directions such as the cross-bridges. In (B), the situation is reversed. The missing wedge cuts across the layer planes and removes a wedge-shaped sector, but that sector is the same for all layer planes and the inner layer planes are not affected any more than the outer layer planes. This wedge orientation is more optimal for imaging the filaments but less so for cross-bridges which appear with less contrast in (B) than in (A) (Taylor et al., 2007). The best definition of both the filaments and cross-bridges is achieved with dual-axis tomography (C) where the volume of missing data in Fourier space is the smallest.

Figure 4.

Central slices through tomograms of insect flight muscle. The thick and thin filaments run vertically. (A) Tomogram computed only from images where the tilt axis is oriented perpendicular to the thin and thick filament axes, and (B) only from images where the tilt axis is parallel to the filament axes. (C) Tomogram computed from the complete dual-axis tilt series. The insets (1), (2), and (3) are global averages of the maps. (1) shows the average in the same orientation as the larger panel with the raw tomogram section; (2) and (3) are sections of the average perpendicular to (1) at the locations indicated by arrows. (2) has the thin filament axis in common with (1) (white arrow), (3) a line midway between thick and thin filaments (black arrow), where the cross-bridges are located. Due to the missing wedge orientation, as explained in the text, helical features of the thin filament are not well rendered and appear with almost no contrast in (A2) whereas crossbridges exhibit high density in (A3). The situation is reversed for (B). For visualization, the contrast was scaled in the same way for all sections.

4.3. Resolution

The Fourier shell correlation was computed from reconstructions of the tilt series with filaments approximately perpendicular to the tilt axis (curve a), filaments approximately parallel to the tilt axis (curve b), and the combined series (curve c) (cf. Figure 5). The observed resolution is lowest when the filament axes are oriented parallel to the tilt axis (curve b). In this orientation, an equal amount of each layer plane is affected by the missing wedge, whereas in the perpendicular orientation (curve a), higher layer planes are less affected as described above, and higher resolution is expected. The combined tilt series yields the best resolution, on one hand because Fourier space is more completely and isotropically sampled, i. e. the volume of the missing pyramid is substantially smaller than that of the missing wedge, and on the other hand because the subvolume alignment prior to the Fourier shell correlation is more robust with double the amount of data that contributed to the reconstruction.

Figure 5.

Fourier shell correlation of IFM subvolumes showing the effect of missing data in Fourier space. Maps were computed from the two separate parts of the dual-axis tilt series and the combined series with identical geometric parameters. In (a) filaments are approximately perpendicular to the tilt axis and in (b) approximately parallel, resulting in missing wedges of different orientation relative to the filaments. (c) represents the combined tilt series with a smaller missing pyramid. The resolution at a correlation coefficient of 0.5 is: (a) 2.79 nm, (b) 2.60 nm, and (c) 2.54 nm.

5. Discussion

5.1. Practical considerations for marker-free alignment

The test specimen that we used in this study was a plastic-embedded, positively stained section with relatively high contrast. With this specimen, we did not encounter some of the problems that frequently occur in the processing of image data from unstained, ice-embedded specimens that exhibit lower contrast. Although we have not processed any dual-axis tilt series from frozen-hydrated specimens, our experience with marker-free alignment of single-axis tilt series can provide some guidelines for dual-axis series in cases where the alignment is less straightforward. First of all, the selection of a region of interest with maximal size may prove to be difficult for tilt series with poor specimen tracking, where considerable shifts would be observed between images. If the shifts occur primarily at the highest tilt angles, unsuitable images are removed from the tilt series altogether when the loss of information is acceptable. If images with out of bound regions are still included, zeros will be back-projected into the reconstructed volume for the missing part of the projection, which will lead to artifacts in the reconstructed volume. In such a situation, we specify a minimum coverage in the alignment procedure in order to detect and ensure that the out of bounds area does not exceed a given percentage of the image area. If the specified criterion is then not met, it is an indication that the size of the region of interest should be decreased.

Generally, for ice-embedded specimens with low contrast it was more critical to select a suitable region of interest than with high-contrast samples. Specimen features that exhibit extreme density differences, for example carbon edges in a cryo-tomogram or large dirt particles, were found to affect the cross-correlation alignment negatively in many instances. Point-like density spikes usually had the same negative effect. While the latter can easily be eliminated during preprocessing, features causing density steps on a larger scale were more difficult to treat. If only peripheral regions were affected, an apodized mask was applied or the region of interest was adjusted to exclude dense features. However, this was only effective if the features of interest were not obstructed by the density anomaly throughout the whole tilt series, especially at high tilts. A special case are tilt series containing high density markers such as gold clusters. Such tilt series could be aligned successfully with the marker-free procedure. It proved to be advantageous to replace the high density markers digitally with a local mean density of the surroundings.

5.2. Improvement of tomogram quality

General experimental and computational improvements specifically relating to the IFM data set have been discussed in detail in Wu et al. (Wu et al., 2009). The main difference between the earlier analysis of this data set and the present work was in the application of our new marker-free dual-axis tomography method and technical improvements of the marker-free alignment and subvolume processing not specifically related to the dual-axis capabilities. The previous subvolume analysis used real space averaging with no missing wedge compensation. Given the paracrystalline nature of the specimen, all subvolumes had nearly identical missing data, so the lack of missing wedge compensation is not expected to have much effect. However, the new approach used simultaneous alignment of the dual-axis tilt series, whereas previously, two separate maps were computed by marker-free alignment that were subsequently merged. Also, the nonperpendicularity of the tilt axis with respect to the electron beam discussed below was not taken into account in the previous study. With the new marker-free dual-axis technique, a resolution of 2.5 nm measured in the global average of extracted cross-bridge repeats (Figure 5) could be obtained, whereas the earlier analysis reported only a maximum of 3.5 nm. In both cases the resolution assessment used the thin filament portion of the cross-bridge repeat, excluding the thick filament, and the 515 subvolumes were extracted at identical positions relative to the specimen structure. The thin filament portion was selected for comparison purposes because it is the only feature held in common in all subvolumes. The cross-bridges themselves are highly variable in structure and placement.

We explored two alignment strategies for dual-axis tilt series which turned out to produce almost identical results as judged by a cross-correlation criterion. Generally, this is the expected outcome provided that the individual alignment steps are carried out correctly. The cross-correlation comparison shows that an alternating, simultaneous merging of the two parts of the dual-axis tilt series yields a more rapid improvement than a consecutive alignment. While the cross-correlation coefficients increased more rapidly between the alignment stages, the same number of alignment cycles was needed to reach the end result. This seems to suggest that both approaches are mostly equivalent, at least for data with a high signal-to-noise ratio. For ice-embedded specimens with a lower signal-to-noise ratio, however, the situation could be different because radiation damage must be considered also, which is cumulative, and affects images that are recorded later in the series more than those recorded earlier. In this case, consecutive alignment might be more robust, because the most degraded images recorded last in the series would be merged into a set of images with the least radiation damage.

The main factor for the observed resolution improvement is attributed to the simultaneous tilt alignment of the marker-free procedure vs. the merging of separately reconstructed maps. This finding is in contrast to other reports (Mastronarde, 1997), where the reconstruction of combined data from the two parts of the dual-axis tilt series was found to produce worse tomograms than separate reconstruction. In the cited report, separate reconstruction was specifically chosen in order to be able to correct the tomograms for distortions. A possible explanation of the different behavior of the two methods is that the tomograms from our test specimens do not suffer much from distortions, so the combination of data in the dual-axis tilt series improves tomogram quality and isotropy of resolution, whereas in the other cases the resolution loss due to distortions outweigh the possible gain in resolution.

5.3. Accuracy and correctness of the tilt geometry

Among factors mentioned above, the quality of the reconstruction also depends on the correct geometric parameters used in the back-projection step. A parameter that might easily be overlooked is the orientation of the tilt axis relative to the electron beam, which is usually assumed to be at a right angle. If not accounted for, a deviation can lead to artifacts and reduced resolution mainly because the actual set of geometric parameters does not accurately reflect the true tilt geometry. In some cases, the beam direction cannot always be corrected by a proper microscope alignment so that a computational solution is required. This has been considered in the context of fiducial-based alignment, where the mathematical marker model was adapted so that it takes into account the non-perpendicularity of the tilt axis with the electron beam (Castaño-Díez et al., 2006). With our marker-free approach we can confirm the quality improvement of 3D-reconstructions when non-perpendicularity of tilt axis and electron beam is taken into account in the geometry refinement. For this purpose, we defined the actual tilt axis direction with two angles: the azimuth measures the direction in a plane perpendicular to the beam, and the elevation angle the out-of-plane direction. Area matching is sensitive enough to detect and correct the discrepancy in foreshortening when the additional elevation is introduced, even if the angle is relatively small. With our test specimens, the small adjustments of the elevation angle of fractions of a degree (Table 2) result in considerable improvement of the alignment quality (Figure 3).

The accuracy of the initial estimate of the tilt axis direction is not so critical in the marker-free alignment if it lies within reasonable limits, because it will be refined during the procedure. It should be noted however, that the tilt azimuth is ambiguous. Adding 180° to the azimuth parameter defines the same tilt axis, but with a reversed sense of rotation. In order for the tilt angles to be correct, the azimuth must also point to the correct quadrant relative to the tilt angles. A possible consequence of an incorrect assignment is a reconstruction with the wrong handedness.