Application of evolutionary algorithm methods to polypeptide folding: Comparison with experimental results for unsolvated Ac-(Ala-Gly-Gly)₅-LysH⁺

Abstract

We present an evolutionary method for finding the low-energy conformations of polypeptides. The application, called foldaway,is based on a generic framework and uses several evolutionary operators as well as local optimization to navigate the complex energy landscape of polypeptides. It maintains two complementary representations of the structures and uses the charmm force field for evaluating the energies. The method is applied to unsolvated Met-enkephalin and Ac-(Ala-Gly-Gly)₅-Lys⁺H⁺. Unsolvated Ac-(Ala-Gly-Gly)₅-Lys⁺H⁺ has been the object of recent experimental studies using ion mobility measurements. It has a flat energy landscape where helical and globular conformations have similar energies. foldaway locates several large groups of structures not found in previous molecular dynamics simulations for this peptide, including compact globular conformations, which are probably present in the experiments. However, the relative energies of the different conformations found by foldaway do not accurately match the relative energies expected from the experimental observations.

The problem of determining the native three-dimensional structure of a polypeptide based only on information about the amino acid sequence is one of the most challenging problems in contemporary computational chemistry. Approaches to this problem are typically divided into three different classes: sequence homology modeling, structural similarity recognition (threading), and nonempirical search techniques. Homology modeling takes advantage of empirical relationships between sequence and three-dimensional structure by using a database of known structural motifs. Threading also employs a database in an effort to find and superimpose structural templates onto the target sequence. In this way, threading measures sequence-structure compatibility rather than mere sequence similarity.

In contrast to these methods, no a priori structural knowledge is required for the nonempirical techniques (1). Instead, the physical relevance of a structure is expressed by means of a potential energy function according to some representation of the polypeptide geometry. According to Anfinsen's thermodynamic hypothesis (2), the native structure of a naturally occurring protein or large polypeptide is simply the conformation for which the free energy attains its global minimum. Therefore, the problem of determining the native structure (ignoring entropic contributions) can be formulated as a global optimization problem, namely, to determine the global minimum of the potential energy function used to model the polypeptide (3, 4).

The two standard approaches for finding minima on large-molecule potential surfaces are molecular dynamics (MD) and Monte Carlo (MC) (5, 6). MD solves Newton's equations, whereas MC randomly samples and selects new geometries based on criteria by using energy. Both MC and MD are used broadly and are very useful, but both can fail to find minima, especially for dense, compact molecular structures.

Because of the complicated nature of polypeptide potential energy functions, finding potential energy minima is a highly nonlinear and quite complex global optimization problem (7). Many different approaches have been developed to address this type of global optimization problem, including deterministic branch-and-bound (8), probabilistic brute-force sampling (9), and pivot algorithms (10). Among the more successful approaches, several are based on the use of genetic algorithms (11-13). Genetic algorithms (14-17) and evolutionary computation (18) are methods that use simulated evolution processes to solve complicated problems. In contrast to most other problem solving techniques, they operate on a pool of individuals, each of which is a solution candidate with an associated fitness that gives a measure of the quality and allows one to rank and compare the solutions to each other. By using different evolutionary operators, the individuals in the parent pool are allowed to breed and mutate, giving a new generation of solution candidates that (in the case of evolutionary progress) will exhibit proportionally better fitness than in the previous generation. This process continues until some stop criterion is reached.

There are many incentives for using this evolutionary framework. First, it is applicable to all optimization problems where representation, modification, and comparison of the quality of solutions are possible. Besides being versatile, this approach is especially efficient for very complex (NP-complete) problems that are difficult to attack with deterministic and conventional methods. Specialized methods may be more efficient computationally, but they are often difficult to implement and have limited applicability.

Methods

Methodology. The application, foldaway, described in this article uses an evolutionary approach to find the low-energy conformations of peptides. foldaway is built by using a generalized framework for evolutionary computation called solution evolution (19), and uses several key evolutionary techniques available in the framework, such as adaptive operator rates and control parameters. We have also made use of an operator in the framework that automatically refines solutions by using local optimization. Thus, new structures generated by the evolutionary operators are subjected to a local optimization procedure. The use of optimization in this way is reminiscent of the MC with optimization approach of Li and Scheraga (20). Our approach also has much in common with the conformational space-annealing (CSA) method of Lee et al. (21, 22). Although CSA is, strictly speaking, a simulated annealing approach, it resembles a genetic algorithm in that it operates on a bank of solutions designed to cover the conformational space. Compared with CSA, our approach is less specialized and no physical intuition is used to generate the starting structures. CSA is also implemented with the ecepp force field, which does not include bond-distance and bond-angle terms in the potential, so these parameters are constrained during optimization (21, 22).

We have tested the methodology described here by using it to determine the low-energy conformations of Met-enkephalin and Ac-(Ala-Gly-Gly)₅-LysH⁺. Met-enkephalin (Tyr-Gly-Gly-Phe-Met) is a small neurotransmitter peptide that has been the object of many computational searches directed at identifying its low-energy conformations (13, 23-25). Thus Met-enkephalin should provide an ideal benchmark to test the ability of foldaway to search the conformational space and locate the global minimum. The conformations adopted by the Ac-(Ala-Gly-Gly)₅-LysH⁺ peptide in the gas phase have recently been studied experimentally by using ion-mobility measurements (26). In these experiments, electrosprayed peptide ions are directed along a drift tube filled with helium buffer gas by a uniform electric field. The time it takes to travel along the drift tube is related directly to the average collision cross section of the ion with the buffer gas. Compact conformations undergo fewer collisions and travel more rapidly through the buffer gas than more open conformations (27-30). Therefore, the cross section can be used as a metric, albeit somewhat limited in its resolution, for determining the structure of an unsolvated peptide ion. The features observed in the experiments are assigned by comparing their collision cross sections with those calculated for trial geometries (which are usually obtained from MD simulations). Studying unsolvated peptides allows one to examine issues like helix propensities in the absence of a solvent (31), so that the intramolecular interactions can be better characterized, and the role of the local environment can be inferred (32-36).

The Ac-(Ala-Gly-Gly)₅-LysH⁺ peptide was designed to have a flat energy landscape with a marginally stable helical state (37). The Ala residues and the C-terminal lysine stabilize the helical conformation (38), whereas the Gly residues destabilize it. Two main conformations were observed for this peptide in the ion-mobility measurements at low temperature (<250 K), which were assigned to an α-helix and a globule (a compact random-looking three-dimensional structure). As the temperature is raised, the α-helix converts into the globular conformation, and at >280 K, only the globule remains.∥ The MD simulations were not able to reproduce the cross section for the globule; even when MD was coupled with simulated annealing, the resulting conformations were not compact enough to match the experimental results. Furthermore, the lowest-energy conformation found in the MD simulations was not the helix or the globule but an unusual, N-terminally untwisted helical conformation with a C-terminal β-turn-type structure (see below), for which the cross section did not match either of main conformations found in the experiment (26). The current studies were motivated by the expectation that a more complete conformational search may yield results in better agreement with the experiment.

The Evolutionary Algorithm (EA) foldaway. foldaway is based on a generalized EA framework, solution evolution (19). solution evolution was first tested on a completely unrelated problem, the optimization of robot welding sequences (39). It has also been tested by searching for the global minima of Lennard-Jones clusters and the energy minimization of spherically distributed charges. As with all EAs, the basic principle behind the method is the development of a population of solutions, which are continually selected and enhanced according to their success in solving the problem at hand. Solutions change, interact, and recombine, exchanging favorable characteristics among themselves. Application-specific control parameters and operator rates can be modified adaptively, enabling a dynamic approximation of the optimal settings throughout and allowing synergistic effects to emerge among the operators.

As a specialization of the generic framework, foldaway is able to take advantage of the well tested generalized methods and also implement operators that are specific to the problem of optimizing the energy of polypeptide structures. The specialization process requires the defining of a “solution” and a fitness function, as well as the defining of various operators to modify solutions.

A solution in foldaway is a set of coordinates defining, unambiguously, a conformation of the polypeptide in space. To allow the various genetic operators to operate on the optimal representation of the peptide, each peptide structure is maintained in two complementary representations, (i) external Cartesian coordinates for all atoms and (ii) and an internal coordinate set consisting of torsion angles, bond angles, and bond lengths. The external coordinates are the preferred basis for the force field implementation (translational and rotational operators) and the geometry optimizers. The internal coordinates are used mainly in the evolutionary operators. Although available to the evolutionary operators, the ω-backbone torsion angles, bond angles, and bond lengths are not actually modified by them. Conformations are converted between the two representations as needed.

The fitness of a conformation is determined by a single objective, the charmm force field (21.3 parameter set) (40) as implemented in the macsimus suite of programs (J. Kolafa; available at www.icpf.cas.cz/jiri/macsimus/default.htm). The CH, CH₂, and CH₃ groups are treated as united atoms.

Before the framework can begin evolving structures, an initial population must be generated. Of the many different ways to accomplish this population generation, the one used here is to take a fully extended conformation and perform a large number of mutations (random changes to the ϕ, ψ, and χ torsion angles), followed by a local minimization. This process is repeated for each initial conformation. A small number of these random conformations are also added into the population at each generation as a way of introducing diversity.

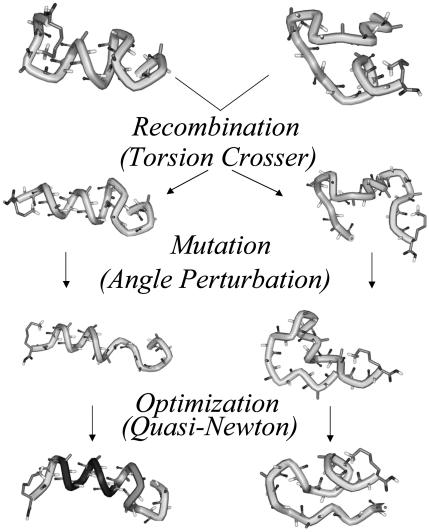
After the initial population has been generated, all subsequent populations are produced by using a combination of the following operations. First, as mentioned above, a small number of random configurations are added to each new population. Second, the most-fit (lowest-energy) conformations from the previous population are retained in the new population. Third, and the largest contributor of new conformations, are structures evolved by recombination and mutation. Two conformations are chosen from the previous generation, and their genetic information (in this case their geometric coordinates) is combined to form two new conformations. These new conformations may then undergo mutations (random changes to ϕ, ψ, and χ torsion angles) and are then optimized by using a local minimization procedure. An example of this process is presented schematically in Fig. 1. The chance of an individual conformation being chosen as a parent is based on its fitness. The more fit (lower in energy) that a conformation is, the more likely it is to be used as a parent. Typically, 10% of the population of each generation results from random conformations, 10% are the most fit (lowest-energy) solutions retained from the previous generation, and 80% result from recombination and mutation.

Fig. 1.

Schematic representation of how the recombination, mutation, and optimization operators work in foldaway by using the Ac-(Ala-Gly-Gly)₅-LysH⁺ polypeptide. Images were produced by using weblab viewer (Molecular Simulations, San Diego). The darker region of the structure on the bottom left is α-helical according to the viewer.

Recombination, or crossover (the process of joining two conformations into one), is the main feature that distinguishes EAs from regular MC techniques and other methods that evolve only a single solution. These operations allow the great leaps through configuration space, and they use information from contemporary and previous conformations to do so. Devising efficient recombination operators for polypeptides requires preserving certain characteristics of the structure. If the crossover is performed in the Cartesian representation, the effect will be too disruptive to be beneficial. Because the internal representation is set up in a residue-by-residue manner, the most efficient recombination can be realized by placing all crossover points along the polypeptide backbone between residues (i.e., at the peptide bond). During the recombination procedure, certain residues or groups of residues are randomly selected and then the internal coordinate information for those residues is swapped between the two conformations.

As mentioned above, when structures have been altered by the evolutionary operators (recombination and/or mutation), they are subjected to local optimization. Thus, the algorithm is not actually wandering around in configuration space but is instead looking at the various wells on the potential energy surface and determining which conformations are lowest in energy. This scheme has been successful in other related applications with the solution evolution framework used here, such as the optimization of homogenous Lennard-Jones clusters and the energy minimization of spherically distributed charges. Several local optimization techniques were tried. The most efficient method found, and the one used for all results presented here, was the limited-memory quasi-Newton (l-bfgs) method of Liu and Nocedal (41). This method uses the gradient of the potential function to build iteratively a better approximation to the inverse Hessian of the function. It is important that the local optimizer used is as efficient as possible because the algorithm spends a large fraction of its time in this optimization step.

A foldaway trial typically consisted of 25 runs each of 300 generations. A population size of 30 proved to be a good compromise between execution time and the ability to explore structures. A run was interrupted, if the best solution (the lowest-energy structure) found in that run was not improved above its fifth significant digit, for 20 consecutive generations.

We are interested not only in finding the lowest-energy conformation but in examining the other low-energy conformations that are adopted by the peptides. Conformations are saved in a solution pool throughout the entire simulation (all 25 runs). The solution pool contains the lowest-energy structure found so far, along with other representative solutions. A solution is added to the pool based on both its fitness (energy) and its dissimilarity to the other solutions in the pool. If a prospective solution is considered unacceptably similar to another solution already in the pool, only the one with the better fitness is kept. The pool has a maximum size (specified at run time), which is maintained by removing the solution with lowest fitness whenever a new solution is added to the pool.

In the present work, we used two metrics of the similarity between the conformations in the solution pool. The first one used was energy. In other words, diversity in the solution pool was enforced by maintaining an energy gap between the solutions. It should be obvious that energy is not a true measure of structural similarity. However, this measure was used only for determining which structures were stored, not which structures were actually produced during the simulation.

The second form of similarity used was a Euclidean distance using the ϕ and ψ angles as coordinates. This dependence can be expressed mathematically as:

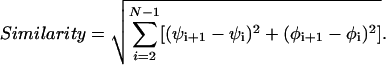1

In this equation, N is the number of residues, and ψ_i and ϕ_i are the ψ and ϕ backbone angles of peptide i. The first and last residues were skipped because the ϕ and ψ angles are not well defined for them. The difference between the angles takes into account that 180° = -180°.

Our choice for the similarity formula was guided by realizing that when we compare two structures in a viewer with a colored ribbon along the backbone, we are actually comparing the backbone torsion angles. The importance of these torsion angles has been recognized in the past (42). This formulation of similarity is more relaxed than the coordinate root mean square deviation (RMSD) method (9, 43, 44), which requires one to determine the optimal rigid-body overlap. Such an inflexible definition is not needed here, and the simple similarity formula seemed to be more appropriate. However, some limitations were seen with the formula when comparing very compact structures, with which it is possible that an RMSD or some other method might work better.

To aid the analysis of the results from foldaway simulations, we implemented a standard data-mining algorithm called k-means (45) to sort the conformations into clusters of similar structures. The k-means algorithm was implemented in a program called motiffinder. The distance criterion for the k-means algorithm is the similarity criterion mentioned above. For the results presented here, the motiffinder program was used only as an initial tool, requiring a human to optimize the parameters and the results.

Results

Met-Enkephalin. The technique, using foldaway, was tested on the penta-peptide Met-enkephalin (Tyr-Gly-Gly-Phe-Met). There have been many studies (13, 21, 23-25) directed at characterizing low-energy conformations of this peptide with computational methods. These studies make Met-enkephalin a suitable subject to test the performance of foldaway in finding the global minimum energy structure as well as its ability to identify other low-energy conformations across the energy landscape. Perez et al. (25) have performed a conformational search for the global energy minimum for the canonical form of Met-enkephalin by using a scheme that used an initial conformational search with the ecepp potential (46), followed by an interactive cycle of minimization and MD simulations with the charmm force field. Calculations were performed with a distance-dependent dielectric constant (ε = r) and separately with ε = 10 and ε = 80. A conformation with a β-II′-type turn around Gly-3 and Phe-4 was found to be the global minimum energy structure for all environments.

We performed 100 foldaway simulations on a Linux-based system with 1.7-GHz processors (Advanced Micro Devices, Sunnyvale, CA). Each simulation (25 runs of 300 generations) took an average of 2.05 h. Preliminary data suggest quadratic scaling of computational effort with peptide size. The calculations were performed by using the charmm force field (21.3 parameter set) with a dielectric constant (ε) of 10. We saved 50 structures from each simulation in the solution pool, and the similarity criterion (see above) was used to determine which structures remained in the pool. After the simulations were finished, the solution pools were combined and motiffinder was used to search for different structural motifs. Five distinct structural motifs were found; all of them are β-turns. In order of increasing energy, starting from the lowest, the motifs are GG β-II, GF β-II′, GF β-V, GF β-II′, and GG β-I′, where the first two letters give the location of the turn (G is Gly, and F is Phe), and the second part of the label gives the type of turn. The dihedral angles and energies for these motifs are summarized in Table 1.

Table 1. Dihedral angles of the lowest-energy conformation of each motif found for Met-enkephalin.

Residue	Angle	1, GG II	2, GF II′	3, GF V	4, GF II′	5, GG I′
Tyr	φ	−157	−156	−98	−154	154
Tyr	ψ	−180	135	−15	122	−67
Tyr	ω	−178	−175	−178	−178	174
Tyr	χ1	61	−158	60	−164	−168
Tyr	χ2	90	83	85	−89	81
Tyr	χ3	1	−174	0	9	−175
Gly	φ	−60	−95	142	−128	56
Gly	ψ	124	59	110	70	44
Gly	ω	−175	179	−171	177	−178
Gly	φ	93	78	81	73	92
Gly	ψ	−93	−88	−90	−99	−60
Gly	ω	175	173	167	174	176
Phe	φ	−90	−108	−83	−73	−76
Phe	ψ	130	−12	144	−24	176
Phe	ω	177	180	−179	170	176
Phe	χ1	−78	65	−176	67	60
Phe	χ2	−75	−81	72	−78	89
Met	φ	−88	−88	−110	−85	−79
Met	ψ	0	0	0	0	0
Met	χ1	−59	−61	−56	−69	−61
Met	χ2	−60	178	−58	178	−61
Met	χ3	171	−65	171	−67	179
Met	χ4	60	60	60	60	60

Motifs are given as motif number and turn type (where G is Gly, and F is Phe). Energy (kJ·mol⁻¹) is 0.0, 4.912, 12.242, 12.623, and 12.853 for motifs 1-5, respectively.

The lowest-energy structure found in the foldaway simulations (which has an energy of -8,418 kJ·mol^-1) has a β-II-type turn around Gly-2 and Gly-3. This motif was found to be the lowest-energy in all 100 foldaway simulations. The global minimum energy conformation found here is not identical to that found by Perez et al. (25). The lowest-energy structure from Perez et al. was a β-II′-type turn around Gly-3 and Phe-4. Perez et al. also found a β-I-type turn around Gly-3 and Phe-4 (only slightly higher than their β-II′-type), which we did not find. These discrepancies probably result from the use of different versions of the charmm force field. After minimizing the lowest-energy Perez structures (β-II′ and β-I) with the version of charmm used in this study, we found their energies to be higher than for the lowest-energy conformations found in the foldaway simulations (by 10.46 kJ·mol^-1 and 3.77 kJ·mol^-1, respectively). We identified fewer distinct conformations (motifs) than Perez et al. (who identified 50 unique minima within 21 kJ·mol^-1 of their global minimum energy conformation) because our automated approach (motiffinder) is set up to identify distinctly different conformations.

Ac-(Ala-Gly-Gly)₅-LysH⁺. The polypeptide chosen as the first test of the ability of foldaway to simulate experimental data was Ac-(Ala-Gly-Gly)₅-LysH⁺. The structures of this peptide have been characterized in the gas phase both experimentally and by using MD simulations (26). Experimental information about the conformations was obtained from ion-mobility measurements, which can separate the different conformations and provide their average collision cross sections. For Ac-(Ala-Gly-Gly)₅-LysH⁺, two conformations were identified in the experiments; these conformations were assigned to a helix and a globule. The helix has a significantly larger cross section than the globule.

foldaway simulations were performed by using the charmm force field (21.3 parameter set) with the dielectric constant ε = 1 (which is appropriate for small peptides in vacuo). The protonation site in the Ac-(Ala-Gly-Gly)₅-Lys peptide is assumed to be the lysine side chain (as indicated by experimental observations) (26). Two sets of foldaway simulations were performed. One simulation used the energy criterion to select solutions retained in the solution pool, whereas the other simulation used the similarity criterion (see above). When the energy criterion was used, the solution pool was limited to 20 structures separated by 5 kJ·mol^-1. When the similarity criterion was used, the solution pool was expanded to contain 50 structures, and at the end of these simulations, the energy spread of the 50 structures was generally <100 kJ·mol^-1 (the energy spread used by using the energy criterion). When the foldaway simulations were completed, each structure in the solution pool was subjected to 55 ps of MD to equilibrate it to 300 K, facilitating comparison with the experimental results. The temperature in the MD was maintained by rescaling the kinetic energies every 0.1 ps. The average potential energy of each structure was determined from the last 35 ps of the MD simulation. The average collision cross section for the final structure from the MD run was then calculated by using an empirical correction to the exact hard-spheres scattering model (47).

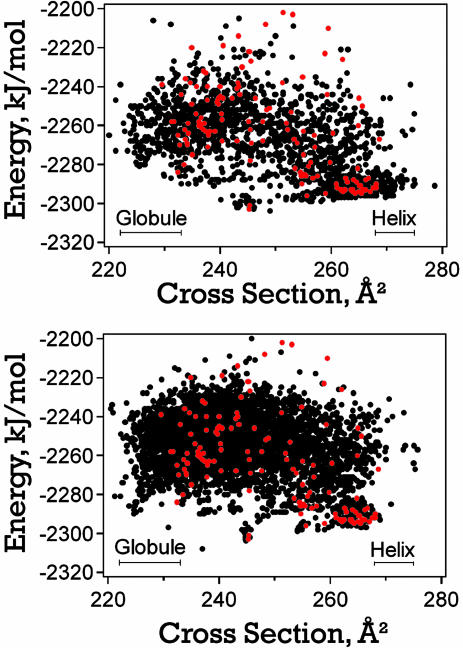
The results are summarized in Fig. 2, which shows plots of the average collision cross section against energy. The black points are local minima from the foldaway simulations, and the red points are local minima from reported MD simulations (26) (which include extended 300-K simulations and simulated annealing runs started from helical and fully extended conformations). Fig. 2 Upper shows results obtained by using the energy criterion to select solutions retained in the solution pool, and Fig. 2 Lower shows results obtained by using the similarity criterion. We performed 100 foldaway simulations (25 runs of 300 generations) by using the energy criterion and 200 simulations by using the similarity criterion. The bars toward the bottom of the plots labeled “Helix” and “Globule” show the expected locations of these conformations from the experimental measurements. Measured and calculated cross sections are expected to agree to within 2% if the conformation used to calculate the cross section is correct. The bars representing the helix and globule incorporate the experimental peak width along with this uncertainty.

Fig. 2.

Plots of the average energy against cross section for the foldaway runs (black points) and previously reported MD simulations (red points) for Ac-(Ala-Gly-Gly)₅-LysH⁺. Upper shows the foldaway results obtained by using the energy criterion to determine which structures are retained in the solution pool. The foldaway results shown in Lower were obtained by using the similarity criterion. Bars show the expected positions of the globular and helical conformations identified in the experiments.

The final structures from the previously reported MD simulations (red points in Fig. 2) were very much dependent on the initial conditions and the temperature schedule that were used during the simulations. This necessity reflects the limited ability of MD to cover the available conformational space. By contrast, all of the foldaway runs were initiated from a fully extended conformation. Runtime parameters were changed only to improve the efficiency of the algorithm in finding low-energy structures and not to affect its ability to move and find new areas of conformational space. In Fig. 2, essentially each MD structure below -2,250 kJ·mol^-1 in energy is surrounded by several foldaway structures, indicating that the EA is capable of finding all low-energy minima found by MD.

Another important aspect of the results shown in Fig. 2 is the presence of compact, low-energy structures. The most compact structure found by the MD simulations has a cross section of 229.5 Ų and a relatively high energy of -2,239 kJ·mol^-1. The lower energy compact conformations found in the MD simulations have cross sections that are on the extreme upper edge of the range expected from the experimental measurements. Conformations with cross sections as small as 220.0 Ų were found in the foldaway simulations (Fig. 2). Furthermore, a plethora of low-energy conformations with cross sections that fall close to the middle of the range expected from the experiments were found.

It is evident from Fig. 2 that the two different methods used to select solutions retained in the solution pool lead to slightly different results. The results obtained with the energy criterion (Fig. 2 Upper) contain more elongated helices (low-energy conformations with cross sections >270 Ų) than were found with the similarity criterion (Fig. 2 Lower). However, the similarity criteria appear to have generated more lower-energy compact globular conformations (structures with cross sections ≈225 Ų) than were found with the energy criterion. The reason that more elongated helices were found by using the energy criterion is not obvious. The similarity criterion is expected to result in a more diverse selection of conformations than the energy criterion. Although the differences between the dihedral angles of different helical conformations can be quite small, it is not clear whether this similarity restriction alone should lead to the absence of the elongated helices from the solution pool.

The enormous number of conformations generated by foldaway precludes the possibility of examining them all individually. Thus, the motiffinder application described above was applied to all of the structures generated in the two sets of trials. The goal of this data-mining approach is to cluster the low-energy conformations into groups or motifs containing similar structures. To simplify the process further, we considered only clusters containing at least one structure with an energy less than -2,280 kJ·mol. For the results obtained by using the similarity criterion, data mining yielded ≈100 clusters containing five or more structures of which ≈30 clusters contained ≥10 structures, and ≈15 clusters contained ≥15 structures. All 100 clusters were analyzed. In some cases, two or more clusters contained similar structures. For example, several clusters contained only helices that tended to differ in the arrangement at the C terminus. Some were slightly unraveled at the C terminus (which enhances hydrogen bonding to the charged lysine side chain), whereas in others, the C terminus remained more helical. These clusters were combined into one helical motif. Ultimately, the number of clusters was reduced to nine main structural motifs. For the data obtained by using the energy criterion, data mining yielded four different structural motifs, all of which were found also in the data set obtained with the similarity criterion.

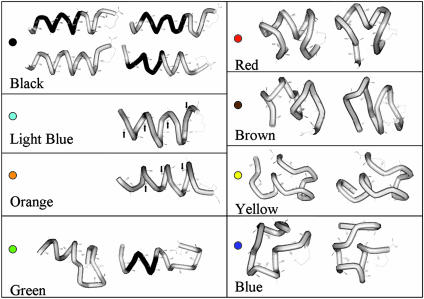
Fig. 3 shows the different structural motifs plotted on the energy-versus-cross section graphs for each foldaway data set. The different colors indicate the different structural motifs. The structural motifs, along with their corresponding colors, are shown in Fig. 4.

Fig. 3.

Structural motifs found by using motiffinder (see text). Different motifs are represented by different colors. Upper shows results obtained by using foldaway with the energy criterion, whereas Lower shows results obtained by using the similarity criterion. The structural motifs are shown in Fig. 4.

Fig. 4.

Structures of each motif shown in Fig. 3 along with their color codes. The images were produced by using weblab viewer (Molecular Simulations). The darker region of the black-motif structure in Left is α-helical according to the viewer.

The motif shown in black is due to helices. It was found in both of the foldaway data sets. The helices are mostly α-helices with a partial <eth>-helix close to the C terminus (see Fig. 4). This arrangement is favored in the simulations because it allows more backbone carbonyl groups to interact with the charged lysine side chain that caps the C terminus. Helices with smaller cross sections tend to have a larger proportion of partial <eth>-helix, whereas helices with larger cross sections tend to have a larger proportion of α-helix and a more unraveled and extended C terminus. It is evident that the helices with the larger cross sections are in better agreement with the measured cross sections (see “Helix” bar in Fig. 4), suggesting a preference for helical conformations with a larger proportion of α-helix. This finding is consistent with previous results for polyalanine-based peptides (38) and recent theoretical studies, which indicate that the charmm force field is too flat along the α-helix-<eth>-helix coordinate (48), and therefore the <eth>-helical regions found in the simulations may be at least partly a force field artifact.

Fig. 4 shows four examples of helices from the motif shown in black. The black-motif helix at the upper left (which has a cross section of 271 Ų and an energy of -2,296 kJ·mol^-1) lies close to the center of the range of cross sections expected from the experimental data. It was found by using the energy criterion. The other black-motif helices are shown to give an idea of the structural diversity in this motif. The black-motif helix at the lower left is a <eth>-helix with a cross section of 260 Ų and an energy of -2,294 kJ·mol^-1. The black-motif helix at the upper right has a cross section of 266 Ų and an energy of -2,297 kJ·mol^-1, whereas the black-motif helix at the lower right has a cross section of 263 Ų and an energy of -2,296 kJ·mol^-1.

The light-blue motif was also found in both foldaway data sets as well as in the previously reported MD simulations. This motif includes the lowest-energy structure found by MD (26) and foldaway by using the energy criterion. As shown in Fig. 4, this structure is a partially unraveled helix with a row of backward-pointing hydrogen bonds. Arrows point to the backward-pointing carbonyl groups. The cross sections of these structures do not match the cross section of the features seen in the experiments.

The orange motif was found in both foldaway data sets, but it was not found in the MD simulations published previously. It is related to the light-blue motif in that it is also a partially unraveled helix with one row of hydrogen bonds facing in the reverse direction. However, in this motif the first backward-pointing carbonyl group is the third residue from the C terminus, whereas in the light-blue motif, the carbonyl group of the C terminus residue was facing backwards. The extra torsional strain at the C terminus and the slight unraveling of the N terminus cause this motif to be slightly higher in energy than the previous motif. The cross sections of these structures also do not match the features observed in the experiments.

There are two varieties of the red motif shown in Fig. 4. This structure is basically a partial helix with both the N- and C-termini unfolded. The red structure Fig. 4 Right has its termini extended in a β-sheet arrangement. This structure was found by foldaway by using both difference criteria, whereas the other variety was only found by using the similarity criteria. The red structure Fig. 4 Left has its termini folded back on top of the helix. This motif makes more compact structures, which have cross sections that lie toward the middle of the range expected for the globule. The less-compact arrangement has cross sections that lie on the upper end of the globule range. No low-energy conformations of either type were found in the MD simulations.

Several other motifs were found from the foldaway data set obtained with the similarity criterion. The green motif includes the lowest-energy conformation found for Ac-(Ala-Gly-Gly)₅-LysH⁺ in these studies (the green motif on the left in Fig. 4). The N-terminal end of this conformation is helical with two hydrogen bonds pointing in the reverse direction. The N terminus, however, is unfolded and consists of a β-sheet like structure. The cross section of this conformation falls outside the range expected for the globule. Note the way that the C-terminal loop is coiled around, maximizing the number of carbonyl groups that interact with the charged amino group of the lysine. Another, higher-energy example of the green motif is shown in Fig. 4 Right. This motif shows the same basic pattern with an α-helical N terminus with a β-sheet arrangement at the C terminus.

The brown motif is similar to the red motif but has a central portion that is more unfolded. Two examples are shown in Fig. 4. Some of the members of this motif have cross sections that fall in the range expected for the globule. The brown motif spans ≈25 Ų. All of the structures have at least one large, centralized, helical turn. The 25-Ų range appears to result from the arrangement of the ends, but the charged lysine side chain is always positioned central to the helical turn.

The yellow motif is partially helical with an unfolded N terminus. This motif also has some members with cross sections that fall within the range expected for the globule, including the lowest-energy conformation found within this range (the orange structure in Fig. 4 Left). The yellow motif has features in common with the green motif. In both motifs the charge is self-solvated by a loop, whereas the N terminus retains a helical character. The yellow motif, however, is obviously more globular than the green motif.

The blue motif is fully unfolded and resembles (slightly) a script “G”. These 20 conformations also have cross sections that lie within the range expected for the globule.

In some cases, the structural motifs have a well defined structure and a well defined structural boundary in Fig. 3. The light-blue motif is an example. In other cases, for example the yellow and brown motifs, the members are interdispersed with other motifs and span relatively large cross sections and energy ranges. It is also evident that some of the motifs share common features. The yellow motif, for example, is similar to the green motif. The red motif has features in common with the brown motif.

Concluding Remarks

We have introduced a generalized EA approach for exploring the energy landscape of unsolvated peptides. The application uses the charmm potential as the objective and uses a dual representation of the conformations. Most of the genetic operators act on the internal (ϕ, ψ) representation, whereas the l-bfgs algorithm and the charmm potential use the external Cartesian coordinates. This dual representation and the use of local minimization differentiate this application from previous attempts at using EAs to fold peptides and proteins (7-9). The EA application foldaway was tested on Met-enkephalin. The lowest-energy conformation found was a β-II-type turn around Gly-2 and Gly-3.

Unlike MD and such approaches as stochastic difference equations (49) or following an assumed progress variable through configuration space (50), EA schemes do not attempt to follow either physical process or causal equations. EA is an optimization technique (not an equation of motion solution), which is both its strength and its weakness. By permitting mutation, recombination, and optimization steps, EA schemes avoid both the local minimum and high barrier problems that can ensnare MD trajectories and the sterically constrained, dense van der Waals repulsion surfaces that can render Metropolis MC ineffective. EA can search in a more global fashion by effectively taking long leaps in configuration space and sampling many structures simultaneously. These attributes account for the much larger set for EA minima than for MD minima shown in Fig. 3; because EA is an ideal optimization scheme, it finds optimal (lowest potential energy) structures very well. But it does not help at all in understanding dynamics; how peptides fold into the motifs in Fig. 4 or the structures in Fig. 3 is beyond EA, just as it is beyond MC.

foldaway found large groups of structures not found in the previously reported MD simulations, and most notable are the compact low-energy structures that fall in the range expected for the globule. Most of the low-energy conformations were found multiple times in the foldaway simulations. However, some conformations (including the one with the lowest energy), were found only once. For the conformations that were found multiple times, the surrounding conformational space is most likely funnel-like, whereas for conformations found only once, the surrounding conformational space is most likely golf course-like (flat with sharp, deep minima that are difficult to find). The fact that the lowest-energy conformation was found only once raises the possibility that there are other even lower-energy conformations that have not been found in these simulations. The lowest-energy conformations that have been found so far still lie outside the range expected for the globule, so the possibility that there are still lower-energy compact structures to be found remains real. However, even if these conformations do exist, they most likely will not be important entropically, so there still appears to be a substantial discrepancy between the experimental results and the theoretical predictions. The most likely cause of this discrepancy now appears to be the force field; in other words, the force field fails to predict the relative energies of the low-energy conformations for the Ac-(Ala-Gly-Gly)₅-LysH⁺ peptide. However, unsolvated Ac-(Ala-Gly-Gly)₅-LysH⁺ has a flat energy landscape, and the energy differences between the low-energy conformations are small, so this peptide provides a severe test of accuracy of the force field.