Membrane potential dynamics of grid cells

Abstract

During navigation, grid cells increase their spike rates in firing fields arranged on a strikingly regular triangular lattice, while their spike timing is often modulated by theta oscillations. Oscillatory interference models of grid cells predict theta amplitude modulations of membrane potential during firing field traversals, while competing attractor network models predict slow depolarizing ramps. Here, using in-vivo whole-cell recordings, we tested these models by directly measuring grid cell intracellular potentials in mice running along linear tracks in virtual reality. Grid cells had large and reproducible ramps of membrane potential depolarization that were the characteristic signature tightly correlated with firing fields. Grid cells also exhibited intracellular theta oscillations that influenced their spike timing. However, the properties of theta amplitude modulations were not consistent with the view that they determine firing field locations. Our results support cellular and network mechanisms in which grid fields are produced by slow ramps, as in attractor models, while theta oscillations control spike timing.

Introduction

Grid cells¹ in the medial entorhinal cortex (MEC) have been hypothesized to form the metric needed for mapping space². A widely held view is that sensory cues specifying location allow error correction and set the grid map's orientation in different environments, while the periodically repeating grid fields are internally generated by path integration of velocity signals^1,3. Extensive modeling efforts have produced two broad conceptual frameworks that explain how grid fields arise by velocity integration^4,5: oscillatory interference models^6-12 and attractor network models^3,13-17.

In oscillatory interference models (Fig. 1a, Supplementary Fig. 1a), grids arise independently in each grid cell. A constant-frequency theta oscillation combines with one or more theta oscillations whose frequency varies with animal velocity to form interference patterns in the membrane voltage^6-12; the amplitude of intracellular theta is largest ‘in field’, with spikes occurring on the peaks of theta cycles. In support, MEC cells exhibit intrinsic oscillations in slices^18,19, grid cells show theta-phase precession²⁰, abolishing theta eliminates grid firing^21,22, and theta and velocity modulated cells have been identified²³. However, grid cells exist in bats without clear theta oscillations²⁴, while theta oscillations may be too noisy for interference-based integration²⁵. The role and importance of theta for grid formation is therefore currently controversial^4,5,26,27 and requires further study.

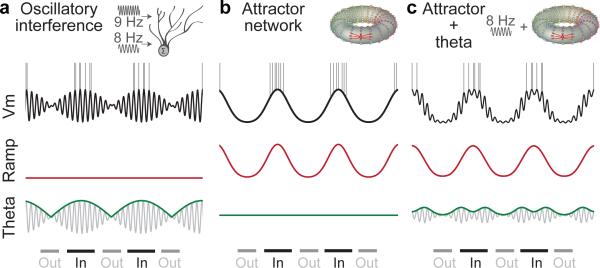
Figure 1. Schematics of membrane potential predicted by different model families, decomposed into low-frequency ‘ramp’ component (red) and a theta frequency component (grey, envelope in green) during in-field (‘In’) and out-of-field periods (‘Out’).

a, Oscillatory interference models. Fields form when theta envelope exceeds threshold; spikes occur on peaks of theta cycles.

b, Attractor network models. Fields form when ramps exceed threshold, without precise spike timing (attractor schematic reproduced from³).

c, Attractor with theta-oscillatory input¹⁷. Fields form when ramps are high and spikes occur on peaks of theta oscillations that also drive the attractor.

Alternatively, in attractor network models (Fig. 1b, Supplementary Fig. 1b), grid fields arise from collective dynamics among cells synaptically connected with a specific topology^3,13-17. Velocity inputs shift the attractor state in the direction of movement. From the perspective of a single grid cell, the moving quasi-stable attractor state of activity generates a slow up and down ramp of synaptically-generated depolarization during field traversal. This ramp defines the cell's firing field as spike threshold is crossed (see simulations in Supplementary Fig. 1b). Despite their theoretical appeal, direct evidence in support of these models has remained scarce.

Interference and network models therefore predict that fundamentally different membrane potential signatures - amplitude modulated theta oscillations and slow up and down ramps - would be the primary drive of firing in grid fields. Here we examine these predictions by direct measurement of the membrane potential of grid cells in mice during navigation in virtual reality (VR)^28-30 (Supplementary Fig. 2).

Grid Cells in Virtual Reality

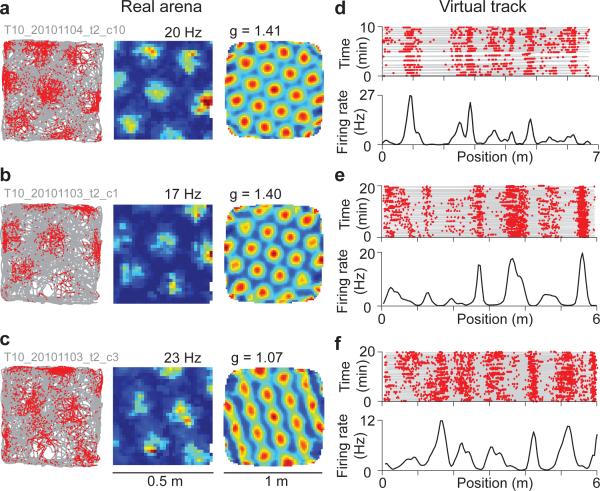
We first used tetrodes (Supplementary Fig. 3) to record MEC neurons in a real two-dimensional (2D) arena (Fig. 2a-c); the same cells were then recorded during navigation along a virtual linear (1D) track (Fig. 2d-f). Units were identified as grid cells from the 2D recordings (Supplementary Fig. 4). Grid cells in VR had increased firing rates at multiple locations along the 1D track (Fig. 2d-f), consistent with grid cell firing on real 1D tracks^20,31. Firing fields and out-of-field periods were defined using a shuffle test (Supplementary Fig. 5). Grid cell peak firing rates, field width, and field spacing were very similar between virtual and real 1D tracks (Supplementary Fig. 6); as in real tracks, grid cell firing rates increased weakly with running speed (Supplementary Fig. 7). These properties suggest that the grid cell circuit operates normally in VR.

Figure 2. Tetrode recordings from grid cells in 2D arenas and virtual linear tracks.

a-c, Grid cells identified in a real arena. Trajectory (grey) and spikes (red dots), firing rate (peak rate above) and autocorrelation function (grid scores above).

d-f, Same cells on a virtual linear track. Top: trajectory (grey) and spikes (red dots). Bottom: firing rate; cells (e) and (f) were recorded simultaneously.

A classifier was implemented that correctly identified the grid cells within the tetrode dataset based on their firing in 1D alone with a high true positive rate (87%) and a low false positive rate (13%, Supplementary Figs. 8-9, Methods). The high success rate allowed us to use this classifier to identify grid cells among our whole-cell recordings from their linear track firing alone.

Whole-cell recordings were performed during navigation as described previously²⁹, but with improved methods for mechanical stability (mean recording duration 10.3 ± 8.9 min; maximum duration 41.3 min, Methods). From 53 recordings, 42 contained enough traversals to measure firing fields. Using our classifier, 27 of these were identified as grid cells (64%, Supplementary Fig. 10). Importantly, the firing field properties of intracellularly recorded grid cells were highly similar to tetrode-recorded grid cells (Fig. 3b,c, Supplementary Fig. 6). A subset of whole-cell recordings had firing fields with highly regular, periodic-like spacing reminiscent of the periodicity of grid cells in 2D environments (Supplementary Fig. 11). The firing rates of highly periodic cells can be viewed as what would be expected if mice ran in a straight line (or ‘slice’) through adjacent firing fields of a grid cell in a 2D environment, along a grid axis. This was also the case for grid cells that were strikingly aperiodic in 1D: their irregular firing fields could also be approximated by slices through 2D grid lattices in a direction not parallel to the grid axes (Supplementary Fig. 12).

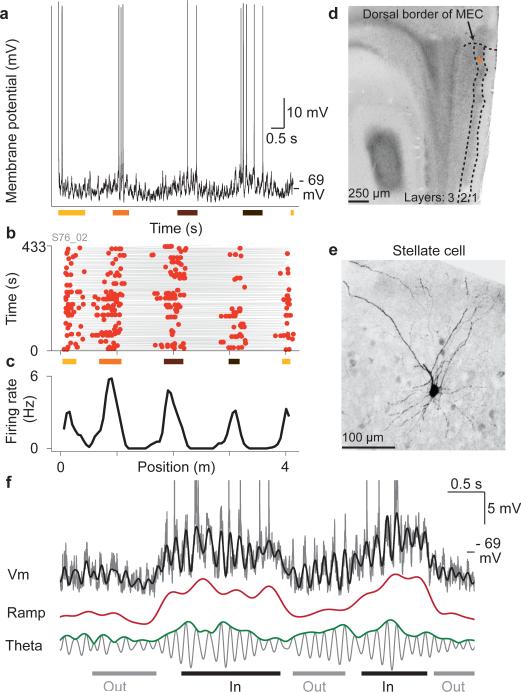
Figure 3. Whole-cell recordings from grid cells.

a, Membrane potential vs. time during a complete run along the virtual track; colored bars indicate grid fields.

b, Trajectory and spikes vs. position; colored bars indicate the same fields as in (a).

c, Firing rate.

d, Soma location (orange dot) in layer 2 of MEC.

e, Stellate morphology.

f, The membrane potential (grey, spikes truncated) could be decomposed into ramp (red) and theta components (grey) and was closely approximated by their sum (black overlay).

Because MEC contains grid cells in two hippocampal-projecting layers (2 and 3) that differ markedly in terms of connectivity and cell type composition³², biocytin fills were used to recover the morphology and layer of 12 grid cells (Fig. 3d,e, Supplementary Figs. 13-14). From the 9 grid cells with identified morphology in layer 2, 6 were stellate and 3 were pyramidal, indicating that both cell types could be grid cells in layer 2, while all 3 grid cells with known morphology in layer 3 were pyramidal (Fig. 4e,f, Supplementary Fig. 14). Using electrode tracts together with electrophysiological properties, 7 additional grid cells with unknown morphology were localized to layer 2 or 3 (Methods).

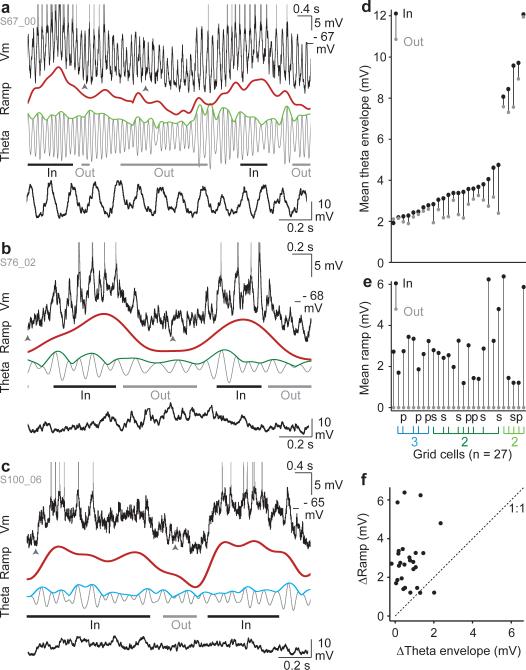
Figure 4. Grid cells exhibit slow intracellular ramps of depolarization and theta oscillations with variable amplitudes.

a, Membrane potential of a large theta grid cell (top, spikes truncated) during two field traversals, and its decomposition into the ramp (red) and theta component (grey). Lower trace: expanded view of Vm (between arrowheads) after spike removal.

b, Same as (a) for a layer 2 small theta cell.

c, Same as (a) for a layer 3 cell.

d, Mean theta envelope during in-field (black dot) and out-of-field (grey dot) periods for all grid cells (n = 27), sorted by out-of-field mean.

e, Same as (d) for the ramp (cells in the same order). Morphology (‘s’, stellate, ‘p’, pyramidal) and layer (3 or 2) indicated underneath; for layer 2, large and small theta cells are light and dark green respectively.

f, ΔRamp vs. ΔTheta envelope for all grid cells (ΔRamp = mean in-field – mean out-of-field ramp; ΔTheta envelope is analogously defined).

Grid cell intracellular recordings displayed two prominent membrane potential signatures: theta oscillations and slower depolarizations that appeared to rise and fall during firing fields (Fig. 3a,f). The slow depolarizations and theta oscillations were extracted from the membrane potential after spike removal using complementary digital filters with nonoverlapping passbands (Supplementary Fig. 15). Because they were the two primary features, the spike-free membrane potential was always well approximated by their sum (Fig. 3f, Supplementary Fig.15). This allowed us to separately study the properties of ramps and theta oscillations with respect to action potential firing in grid cells. The ongoing amplitude of theta oscillations was quantified using an estimate of the peak-to-peak theta envelope (Fig. 3f, Supplementary Fig.15). On the time scale of traversals through sequential firing fields, the slow depolarization component was low between fields, ramping up and down within fields. After subtracting the mean out-of-field value (baseline), we therefore termed the resulting waveform the ‘ramp’ (Supplementary Fig. 15, Methods).

Grid cell intracellular oscillations

Different grid cells displayed a surprisingly wide range of theta oscillation amplitudes (~2-12 mV theta envelope, Fig. 4a-c). A subset of neurons had striking high amplitude oscillations, and were termed ‘large theta cells’ (Fig. 4a,d, Supplementary Figs.16,17,18 part 3). All large theta cells that could be localized were in layer 2 (10 in MEC, 1 in a structure referred to as a 'large dorsal patch'³³). Theta amplitudes were significantly lower in the remainder of layer 2 ‘small theta’ cells (Fig. 4b,d, Supplementary Fig. 18 part 1), and in layer 3 recordings (Fig. 4c,d, Supplementary Fig. 18 part 2; one-way ANOVA F(2,16) = 41.9, p < 10⁻⁶; layer 3 or layer 2 small theta vs. large theta cells, p < 10⁻⁵; layer 3 vs. layer 2 small theta, ns, Tukey HSD test). We note that although these groups differ in mean theta amplitude, they did not differ significantly in terms of their ramp amplitudes (interdecile range mean ± s.e.m, in mV, large theta: 7.3 ± 1.6, layer 2 small theta: 6.4 ± 0.6, layer 3: 8.5 ± 1.3, n.s., one-way ANOVA F(2,16) = 1.0, p > 0.3, Tukey HSD test, all p > 0.3).

Changes in Ramps and Theta Oscillations in Firing Fields

Attractor network models predict that firing fields occur because of a slowly rising and then falling ramp of synaptic input-induced depolarization; the field is located where the depolarization exceeds spike threshold. Conversely, interference models predict that firing fields occur because the theta envelope increases in the field, causing firing on the depolarizing peaks that exceed spike threshold (Fig. 1a, Supplementary Fig. 1a). We found that the mean ramp increased in all grid cells during in-field compared with out-of-field periods (Fig. 4d,e). Theta envelope also increased in all but one cell, but the increases were generally smaller. To quantify their importance to driving in-field firing on a cell-by-cell basis, we first compared the relative amplitude of ΔRamp and ΔTheta envelope in each neuron and found that ΔRamp was larger than ΔTheta envelope in 25/27 grid cells (Fig. 4f). The ratio between the average ΔRamp and ΔTheta envelope was ~4, suggesting that the ramp would be more effective at depolarizing grid cells and driving field formation (mean ± s.e.m, ΔRamp: 2.9 ± 0.3 mV; ΔTheta envelope: 0.72 ± 0.12 mV; ΔRamp > ΔTheta envelope, t(26) = 7.3, p < 10^-7, paired t-test).

The characteristic feature of membrane potential dynamics that forms grid fields should be highly correlated with the firing rate at all times, changing reliably and systematically with position in space. Like the firing rate, this signal should increase as the animal enters a field, reach a peak, then decrease to a minimum between grid fields, and do so consistently on every run through the environment (Fig. 1, Supplementary Fig.1). The ramp was strongly correlated with the firing rate (Fig. 5a, Supplementary Fig. 19), both when averaged across runs through the environment (Pearson's correlation coefficient r = 0.84) and when the ramp on every run was separately correlated with an estimate of the firing rate on that run (r = 0.68, n = 836 runs from 27 grid cells). In contrast, the theta envelope was more weakly correlated with the firing rate, sometimes increasing not only in fields but also between them, sometimes decreasing in the middle of grid fields, and typically varying widely from run to run (Fig. 5a, Supplementary Fig. 19; average, r = 0.46; run-byrun r = 0.22). Moreover, the ramp was less variable than the theta amplitude when pairs of individual runs were compared to each other. The average pairwise correlation between runs for ramp was significantly larger than for theta envelope (r = 0.31 vs. 0.08; t(26) = 7.3, p < 10⁻⁷, one-tailed t-test). Together these results demonstrate that the ramp signal tracks the firing rate much more closely than does the theta amplitude.

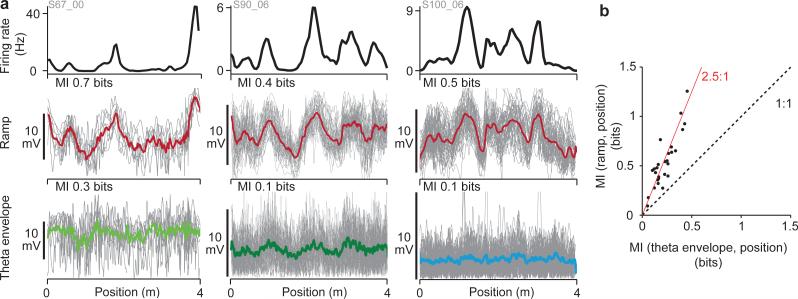
Figure 5. Ramps contain more information about position.

a, Three examples of the firing rate (top), ramp (individual runs, grey; mean, red) and theta envelope (individual runs, grey; mean, green or blue; left: large theta, middle: layer 2 small theta, right: layer 3). Ramps show greater run- to-run reproducibility than theta envelopes.

b, Mutual information (MI) between ramp or theta envelope and position along the track. Information in ramps is always greater than in theta envelope (mean ratio = 2.5).

Because grid cell firing fields occur at specific positions along the track, the characteristic feature of membrane potential that produces firing fields should reliably provide more information about position. Visual inspection of the superimposed runs in Fig. 5a suggests that ramps provide more information, because the theta envelope waveforms are noisier and the averages show less spatial structure. We quantified this by numerically estimating the mutual information between the ramp waveforms and position, and between the theta-envelope waveforms and position (Methods; Supplementary Fig. 20). In essence, these mutual information estimates quantify how much information (in bits) is gained about location along the track from knowing the ramp or theta envelope voltage. All grid cells recorded demonstrated more information about position along the track in ramps than in theta envelope, with a mean ratio of 2.5 between the two quantities (n = 27 grid cells; Fig. 5b).

Because theta was highly variable, we asked whether the increase in theta might be absent in a fraction of individual field traversals, producing counterexamples that would be inconsistent with the basic tenets of the theta interference mechanism. In fact, the theta envelope decreased in nearly a quarter (24%) of field traversals when compared with the out-of-field average, which differs from what interference models predict (examples of in-field firing despite low theta: Fig. 6a, Supplementary Fig. 18). In contrast, the ramp reliably increased in nearly all field traversals (96%). Only field traversals where the cell spiked are included in this analysis. Furthermore, when the theta envelope increased without a simultaneous increase in the ramp, this was insufficient to drive spiking (no firing despite high theta: Fig. 6b, Supplementary Fig. 18). These counterexamples indicated that, even in cells with prominent oscillations, individual field traversals do not necessarily have larger theta envelopes although they nearly always have larger ramps, and that, without the increased ramps, oscillation increases of the magnitudes we observe appear insufficient to drive firing.

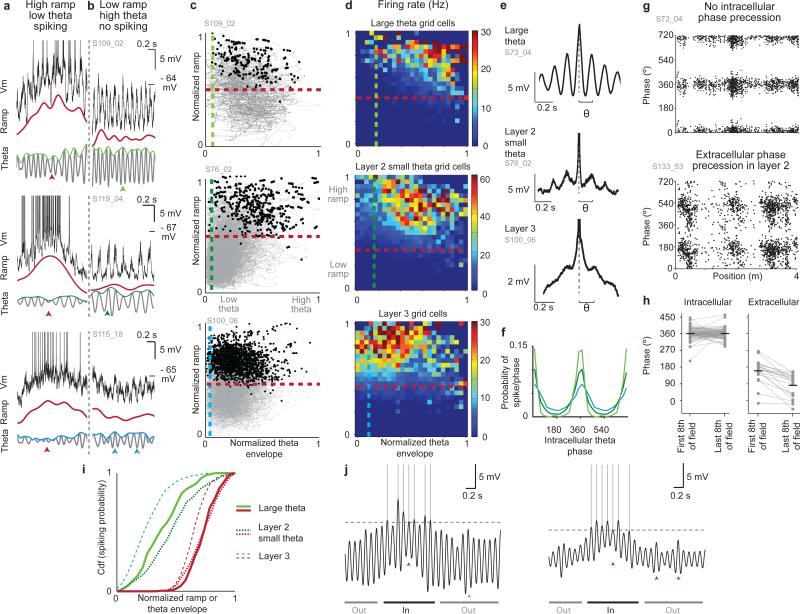
Figure 6. Ramps, not oscillations, are the primary drive of field formation.

a, Example field traversals with spikes fired when the ramp (red) is high although theta envelope (green or blue) is low (red arrowheads; top: large theta, middle: layer 2 small theta, bottom: layer 3).

b, Periods from the same recordings in (a) showing no spiking when theta amplitude is high but the ramp is low (green or blue arrowheads).

c, Normalized ramp and theta envelope for the whole recording (grey) and during spikes (black) for 3 grid cells (top: large theta, middle: layer 2 small theta, bottom: layer 3). 99% of spikes occurred at higher ramps than the dashed red lines and higher theta envelope than the dashed green or blue lines.

d, Average firing rate for the three cell groups in normalized ramp and theta amplitude coordinates. Cells spike for all theta amplitudes, but preferentially above a ramp threshold.

e, Spike-triggered average (aligned to dashed lines) of the Vm from three cells; spikes occur preferentially on intracellular theta peaks.

f, Probability of spiking vs. intracellular theta phase (large theta, light green; layer 2 small theta, dark green; layer 3, blue).

g, Top: intracellular theta phase of spikes in a layer 2 large theta grid cell; Bottom: LFP theta phase of spikes in a different layer 2 grid cell.

h, Mean intracellular (left) and LFP (right) theta phase of spikes fired in the first and last eighth of each field. Horizontal lines are means.

i, Cumulative distribution function of the spiking probability vs. normalized ramp (red) and theta envelope (green or blue) for the cells in (c).

j, Schematics of the membrane potential for large theta (left) and layer 2 small theta cells (right, arrowheads same as (a-b)). Ramps produce firing fields, while spikes are timed by threshold-crossing theta peaks.

Beyond individual counterexamples, we performed a systematic analysis of the value of the ramp and theta envelope amplitudes when grid cells spike. For successive 1 ms time intervals during a recording, we determined the associated normalized ramp and theta envelope amplitude and plotted it as a black dot if the cell spiked or as a small grey dot if the cell did not spike at that time point (Fig. 6c). After binning the data in both dimensions, a firing rate estimate was produced at each location and used to plot the effective firing rate for all normalized ramp and theta envelope pairs averaged across cells in each group (Fig. 6d). The analysis directly demonstrates that cells did not spike when the ramp was low (below red lines in Fig. 6c and d, Supplementary Fig. 21) regardless of the amplitude of theta. Conversely, when the ramp was high, cells spiked even when theta was low (above blue or green lines in Fig. 6c and d). On average, spiking was present for the upper ~53% of the range of the ramp and ~93% of the range of theta values of the respective cells. The contributions of ramp and theta envelope to firing fields can be more directly compared by plotting the cumulative spike probability from these distributions as a function of increasing normalized ramp or theta-envelope (Fig. 6i). When plotted as a function of ramp amplitude (red lines), there is sharp threshold: above this threshold the cumulative probability for spiking rises quickly to 1, while below this value it essentially vanishes. In contrast, the cumulative probability versus theta envelope starts close to 0 and rises immediately, without a threshold, consistent with a cell's ability to spike across the range of available theta envelopes.

Because our recordings were performed in virtual 1D environments where the firing fields of grid cells are less regularly spaced than in 2D environments, we repeated all analyses for the subset of grid cells that had highly regular, periodic-like firing in 1D (7/27 grid cells, Methods, Supplementary Fig. 11 part 1). We found no differences in the relative importance of ramps and theta oscillations to field formation in these highly periodic grid cells (Supplementary Fig. 11 part 2). We also repeated all analyses for large theta and small theta cells separately and obtained the same results (analyses not shown). Finally, we defined highly stable firing fields (Methods, Supplementary Fig. 10) to examine whether small drifts in firing field location could bias any analysis based on field boundaries, and found no qualitative difference in results.

The fact that grid cells fired when the ramp was high regardless of theta envelope but not when the ramp was low suggested that a ramp increase may be necessary to drive firing in grid cells. Consistent with this, when grid cells failed to fire during individual field traversals (‘missed fields’), the ramp was greatly reduced in those field traversals compared to its normal value (mean ± s.e.m ramp in fields with spikes minus mean ramp in missed fields: 2.64 ± 0.47 mV), confirming that the normal in-field increase in ramp was important for driving in-field firing (Supplementary Fig. 22). Although the theta envelope was also reduced, the reduction was much smaller (0.73 ± 0.24 mV; drop in ramp is larger, t(23) = 5.0, p < 10⁻⁴, one-tailed t-test; Supplementary Fig. 22e,f).

Although our data supports the view that ramps are the generator of firing fields, grid cell firing was nevertheless typically theta modulated. Across cell types, spiking occurred preferentially on the peaks of intracellular theta oscillations (Fig. 6e,f; fraction of spikes occurring on the positive half of theta cycles, large theta: 97 ± 2%, layer 2 small theta: 86 ± 3%, layer 3: 74 ± 3%, groups means were statistically different, one-way ANOVA, F(2, 16) = 14.3, p < .001, post-hoc Tukey HSD test, all p <0.05). The fact that the average spiking probability was centered on the peaks of intracellular theta oscillations is consistent with a lack of intracellular phase precession. Consistently, we found that, as in place cells²⁹, grid cells did not exhibit phase precession with respect to intracellular theta oscillations (Fig. 6g,h, Supplementary Fig. 23 part 1). In separate experiments, we performed extracellular recordings from 17 layer 2 cells in MEC where LFP phase precession is expected²⁰, and found phase precession with respect to the LFP in 7/8 grid cells (form 3 mice, Fig. 6g,h, Supplementary Fig. 23 part 2). To quantify the relative importance of theta and ramp amplitude to precise spike timing, a theta-index was calculated for each cell. A regression analysis was performed that estimated this degree of theta modulation as a function of both the amplitude of the cell's ramp and theta envelope. Theta modulation increased with theta envelope amplitude and weakly decreased with ramp amplitude, and the envelope explained a much larger fraction of the variance of theta-index than ramp amplitude (Supplementary Fig. 24). This analysis demonstrates that the amplitude of theta oscillations is the primary determinant of precise, theta-paced spike timing.

Discussion

We demonstrated that the membrane potential dynamics of grid cells includes both ramps and theta oscillations. Compared to changes in theta amplitude, ramps are larger, more reliable, more correlated with firing rate, provide more information about position, and unless they increase sufficiently, spiking does not occur. Ramps were present in grid cells in both hippocampal-projecting MEC layers (2 and 3), and in both stellate and pyramidal cells. The presence and importance of ramps is consistent with the primary membrane potential signature of attractor network models of grid cells. Moreover, on average the ramp peak occurred near the middle of the grid field, as predicted by attractor models (Fig. 1, Supplementary Figs. 1, 25). We also found increases in ramps and theta amplitude in the spatial firing fields of non-grid cells (Supplementary Fig. 26). This has also been observed in place cells²⁹. A suggested explanation for the presence of ramps in place cells in CA1 and non-grid cells in MEC is that they result from summed input from grid cells.

However, in support of interference models, changes of grid scale and theta frequency have been observed dorsoventrally in MEC³¹, in novel environments³⁴, and in HCN1 knockout mice³⁵; these properties can arise naturally in interference models by changing the slope of a proposed linear relationship between velocity and theta frequency⁹. Such velocity-frequency relationships have been observed in rats³⁶. Here, we also found a weak positive correlation between intracellular theta frequency and running speed (Supplementary Fig. 27). However, as shown by the large standard deviations for each speed (Supplementary Fig. 27), intracellular theta oscillations were very noisy. Without frequent error correction, interference models are thought to tolerate only a small degree of variability in the duration of each theta cycle^10,11,25. To be consistent with our data, an interference mechanism would have to produce both ramps and noisy oscillations. For example, this could happen if a biophysical process within grid cells could be shown to transform theta-modulated inputs that arrive and interfere in distal dendrites into ramps and noisy oscillations in the soma.

Although the properties of intracellular theta we measured in grid cells pose challenges to simple forms of interference models, spikes are produced preferentially on the peaks of the theta oscillations (Fig. 6e, Supplementary Fig. 21) and a regression analysis demonstrates that theta index, a measure of how modulated spiking is at that theta frequency, increases with increased amplitude of theta oscillations (Supplementary Fig. 24). Thus intracellular theta oscillations can control the spike timing of grid cells. When this property of theta oscillations is combined with the sharp threshold of ramp amplitude for firing field spiking (Fig. 6i), a conceptual model emerges for how these two signals combine in a grid cell (Fig. 6j). When the ramp amplitude is low, the probability of spiking is low regardless of theta oscillation amplitude because the membrane potential remains hyperpolarized below spike threshold. As ramp amplitude exceeds spike threshold, a firing field is produced. In the field, the cell is transiently more depolarized during the peaks of the theta cycle than during the troughs, increasing the probability of spike generation on the peaks. This applies to both large theta cells (Fig. 6j, left) and small theta cells (Fig. 6j, right), although larger theta oscillations produce more precise spike timing than smaller oscillations (Fig. 6f).

Our data motivates the consideration of a mechanistic conceptual framework that combines theta oscillations and attractor dynamics³⁷. For example, a theta modulated velocity signal could be used to drive an attractor network. In this view, changing the mapping between animal velocity and theta amplitude and frequency would modulate the drive to the attractor and potentially enlarge or shrink the grids. This could provide an explanation for the observed frequency-velocity relationship in rodents³⁶. If velocity inputs are not theta modulated in bats but they are in rodents, this could explain the lack of theta in bat grid cells²⁴ and its importance in rodents^21,22 while maintaining the same integration mechanism across species. A specific model containing some of these features has been recently proposed in which a theta-modulated velocity signal appropriately shifts the attractor state producing path integration and grid cells with both ramps and theta oscillations¹⁷. In general, our data are most consistent with an emerging class of models (Fig. 1c, Supplementary Fig. 1c) where the grids arise from attractor dynamics and theta oscillations control the spike timing of grid cells.

Methods summary

C57BL/6J mice were trained to run for rewards in real and virtual environments²⁹ while recordings were obtained from MEC. Tetrode recordings were performed with a microdrive and headplate assembly that could be used interchangeably for navigation in a real two-dimensional (2D) arena and a virtual 1D track³⁸. Whole-cell recordings were obtained as described previously²⁹, while mice ran along virtual 1D tracks. Biocytin fills were used to recover cell morphology and determine soma location. A complete description of the methods is available as Supplementary Information.