Hydration and mobility of HO^-(aq)

Abstract

The hydroxide anion plays an essential role in many chemical and biochemical reactions. But a molecular-scale description of its hydration state, and hence also its transport, in water is currently controversial. The statistical mechanical quasichemical theory of solutions suggests that 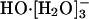is the predominant species in the aqueous phase under standard conditions. This result agrees with recent spectroscopic studies on hydroxide water clusters and with the available thermodynamic hydration free energies. In contrast, a recent ab initio molecular dynamics simulation has suggested that 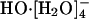is the only dominant aqueous solution species. We apply adiabatic ab initio molecular dynamics simulations and find good agreement with both the quasichemical theoretical predictions and experimental results. The present results suggest a picture that is simpler, more traditional, but with additional subtlety. These coordination structures are labile but the tricoordinate species is the prominent case. This conclusion is unaltered with changes in the electronic density functional. No evidence is found for rate-determining activated interconversion of a 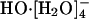trap structure to 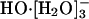mediating hydroxide transport. The view of HO^- diffusion as the hopping of a proton hole has substantial validity, the rate depending largely on the dynamic disorder of the water hydrogen-bond network.

Apreeminent challenge in liquid-state physics is the understanding of aqueous phase chemical transformations on a molecular scale. Water undergoes limited autoprotolysis, which is enhanced in the presence of highly charged metal ions such as Be²⁺ (1, 2). Understanding the hydration and transport of the autoprotolysis products, H⁺ and HO^-, presents unique and interesting challenges for molecular-scale theories of solutions and for simulations. In this paper we focus on HO^-(aq).

Because H⁺ and HO^- constitute the underlying aqueous matrix, it is not unreasonable to expect that their transport in water is different from the transport of other aqueous ions. This anomalous diffusion of the H⁺(aq) and HO^-(aq) has received extensive scrutiny over the years (for example, refs. 3-5), but recently ab initio molecular dynamics (AIMD) capabilities have evolved to provide new information on the solution condition and transport of these species. Over a similar period, the statistical mechanical theory of liquids (especially water) has also become more sophisticated (for example, ref. 6). These two approaches can be complementary, but in typical practice they remain imperfectly connected (but see refs. 2 and 7-11).

In an initial AIMD study (12), HO^-(aq) was observed to be tetrahydrated during the course of the ≈6 ps long simulation. This complex had a lifetime of about 2-3 ps. An approximately square-planar configuration was noted for this 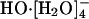complex. That study hinted that transport occurred when converted to a trihydrated () species that has hydrogen-bonding arrangements similar to those in liquid water.

A recent AIMD study (13) reinforced the notion of the 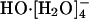species as dominating the equilibrium population distribution at infinite dilution. The proposed mechanism for HO^-(aq) transport was as follows: first the stable (and hence inactive) 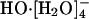converts to the active 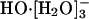species; then the hydrogen bond between the anion and one of the ligating water molecules shortens, thus identifying a transient HO-[H₂O]^- species; a shared proton is transferred along that shortened bond, and a 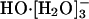species is reconstituted with the hydroxide identity now switched; this active 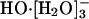species reverts back to an inactive 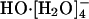species, completing one transport event. Presumably, as in ref. 12, the lifetime of the species was 2-3 ps, but statistical characterization was sketchy.

Discussions of a transport mechanism for HO^-(aq) typically focus on Agmon's (14, 15) extraction of an activation energy for hydroxide transport from the temperature dependence of the experimental mobilities. Near room temperature that empirical parameter is about 3 kcal/mol, but it increases by roughly a factor of 2 for slightly lower temperatures. As a mechanical barrier this value, about 5-6 k_BT, may be low enough to require some subtlety of interpretation (16); the observed temperature sensitivity of the activation energy, and particularly its increase with decreasing temperature, supports that possibility. We note that a standard inclusion of a tunneling correction would be expected to lead to a decrease of activation energy with decreasing temperature.

Ref. 13 framed the consideration of HO^- transport in terms of classical transition state theory and extracted an activation energy from the gas-phase study of Novoa et al. (17). Ref. 13 also considered the importance of tunneling in lowering the barrier for proton transfer by performing path integral calculations. Their combined value of 3.1 kcal/mol was close to Agmon's estimate (14, 15). That experimental number does reflect the influence of the solution medium, and the Arrhenius plots are nonlinear. Additionally, the earlier gas-phase studies (17) had shown that outer shell disposition of the fourth water molecule is lower in energy than 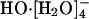, in agreement with subsequent experimental results (18); and, further, with a barrier of 2.5 kcal/mol for conversion of 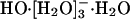to 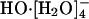, is nearly 1.3 kcal/mol greater than the barrier for the reverse process.

A follow-up classical AIMD study (19), which treated a 1.5 M solution of KOD (1 molecule of DO^- and 1 atom of K⁺ in a 32 water molecule system; D = deuterium, ²H), yielded an estimated diffusion coefficient of DO^- of 1.5 Ų/ps. A tunneling correction for the classical treatment would be expected to increase this rate. The experimental diffusion coefficient for the light water HO^- case is about 0.5 Ų/ps at 298 K (3).

The incongruities in refs. 12 and 13 were noted recently in AIMD simulations of deuterated NaOD and KOD hydroxide solutions with concentrations ranging between 1.5 and 15 M (20). Interestingly, Chen et al. (20) observed that was well represented in the population distribution, and they commented that their results differed somewhat from those obtained in the previous ab initio study (12, 13), which, they noted, suggested 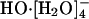to be the “only dominant solvation structure” (20). The distribution of hydration numbers was markedly influenced by the cations there (20). Those results do not permit a consistent extrapolation of HO^-(aq) properties to infinite dilution, but was just a prominent structure, not the only one.

It is clear that earlier simulations have not resolved the most primitive question: What is the coordination state of HO^-(aq) in water without extrinsic complications? Speculations regarding the transport mechanism are somewhat premature in the absence of a clear understanding of this coordination number question. Here we focus on that primitive question first, apply AIMD methods, and find that 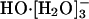is a probable coordination structure. We then discuss the agreement of the present simulation results with inferences based on (i) molecular theory (refs. 21 and 22; ref. 21 is available at http://www.arxiv.org/abs/physics/0211057), (ii) spectroscopic (18) and thermochemical (23) measurements on hydroxide water clusters, (iii) spectroscopic studies (24-27) of aqueous HO^-, and (iv) dielectric dispersion measurements of aqueous HO^- (28). Discussion of the transport can be then framed within the dynamical disorder framework (29-32).

Recent Theoretical and Experimental Background

Recent experimental and theoretical results have addressed the issue of the coordination number of the aquo hydroxide ion. On the theoretical side, the statistical mechanical quasichemical theory of solution has been applied to HO^-(aq) (21, 22). This formally exact approach, with roots in the work of Guggenheim (33, 34), Bethe (35), and Pitzer (36), acquires approximations as applied. But for both hydration of ions in water and standard packing problems, simple approximations have proven effective (2, 6-10, 37-43). In the quasichemical approach, the region around the solute is partitioned into inner and outer shell domains. The inner shell, where chemical effects are important, is treated quantum mechanically. The outer shell contributions can be assessed by using classical force-fields or dielectric continuum models (10). The theory permits a variational check of the partition (8, 44). Quasichemical studies (21, 22) have firmly suggested that 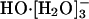is the most prominent solution species. Those results are insensitive to the choice of density functional or ab initio Møller-Plesset second-order perturbation technique.

Recent cluster spectroscopic studies (18) have observed shell closure with formation of 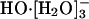in the hydration of HO^-. The fourth water molecule initiates an outer shell around this cluster. This identification of a shell-closure is in agreement with thermochemical measurements that show the same effect (23). Thus theoretical considerations and experiments on hydroxide-water clusters concur on the significance of 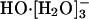as the nominal full inner shell structure.

AIMD Simulations

The AIMD simulations were carried out with the vasp (45, 46) simulation program, wherein the Kohn-Sham equations are solved by usual matrix methods. Thus this corresponds to adiabatic dynamics with tolerance set by the convergence criterion for the electronic structure calculation. The system comprises a hydroxide anion in a periodic cube of 32 water molecules. The box size was 9.8788 Å, consistent with the experimental partial specific volume of the HO^-(aq) (47). This system was initially thermalized by about 10 ps of classical molecular dynamics [using simple point charge/extended (SPC/E, ref. 48) potentials] with a temperature of 300 K and velocity scaling. The dominant HO^- coordination number during this phase was n = 5.

In the first AIMD simulation, RUN1, we used a generalized gradient approximation, PW91 (49, 50), to the electron density functional theory. Ultrasoft pseudopotentials (US-PP) (51, 52) for oxygen were used to describe the core-valence interaction, and an US-PP was used for the hydrogen atoms as well (45, 46). The valence orbitals were expanded in plane waves with a kinetic energy cutoff of 395.76 eV. RUN1 used a 1-fs time step. Self-consistent field (SCF) convergence was accepted when the energy difference between successive iterations fell below 1 × 10^-4 eV. Initially 1.5 ps of AIMD simulations were performed at 300 K, using velocity scaling to maintain the stated temperature. The coordination number at the end of this 1.5-ps simulation was n = 4. The system was then equilibrated for 3.2 ps in the microcanonical ensemble. Then random velocities were reassigned to give a temperature of 300 K, and statistics collected for another 8.2 ps in the microcanonical ensemble. The mean temperature was 332 K. The relative energy fluctuation, 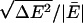, was 8.4 × 10^-5. The drift in the relative energy was about 8 × 10^-6 ps^-1. These values appear quite reasonable (53).

To evaluate the role of chosen density functionals and the time step, we took the terminal configuration from RUN1 and replaced all of the hydrogen atoms by deuterium, thus simulating the classical statistical mechanics of aqueous DO^- in D₂O. The time step was also cut in half to 0.5 ps. After a short microcanonical run with the PW91 density functional and US-PP pseudopotentials, we started RUN2 and RUN3. In both these runs the pseudopotential treatment of atoms was replaced by the projector augmented-wave (PAW; refs. 54 and 55) treatment, which is thought to handle difficult cases involving large electronegativity differences with “exceptional precision” (55). Further, in molecular bonding problems, this method is about as accurate as local basis (such as Gaussian orbital) methods (56). In RUN2 and RUN3, the SCF convergence was accepted when the energy difference between successive iterations fell below 1 × 10^-6 eV. [For comparison, this is an order of magnitude smaller than the “tight” convergence in the gaussian (57) suite of programs.]

RUN2 used the PBE functional (58), which is similar to PW91. RUN2 is not considered further here because it produced a predominant coordination number of n = 3, just as RUN1 did. RUN3 used the revised PBE functional, rPBE (59). The system was equilibrated for 5.9 ps and a further production run of 5.9 ps was conducted. The mean temperature was 313 K. 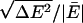was 2.0 × 10^-5. The drift in the relative energy was about 5 × 10^-6 ps^-1.

Fig. 1 introduces the geometric notation used in analyzing the coordination of HO^-(aq). Fig. 2 and Fig. 3 show the coordination number at each time for RUN1 and RUN3, and also the instantaneous temperature observed. Radial distribution functions for those two cases are shown in Fig. 4 and Fig. 5. Table 1 presents the average fractional coordination number populations for RUN1 and RUN3, and Table 2 records averages of hydrogen-bonding angles in the notation of Fig. 1.

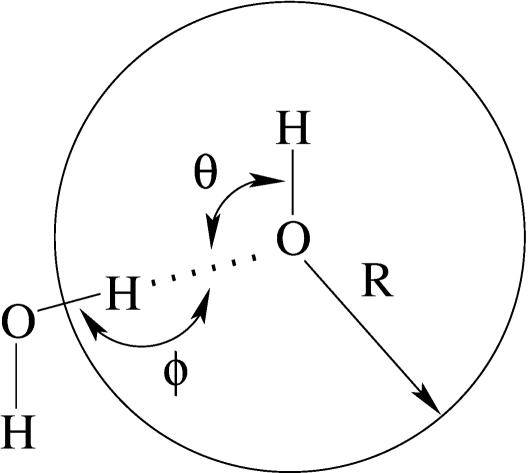
Fig. 1.

R is the radius of the observation volume centered on the hydroxide oxygen. θ and ϕ identify the angles that specify the directionality of the hydrogen bond to water. The hydroxide hydrogen, uppermost here, is not included in the coordination number counts or in the radial distribution functions shown later.

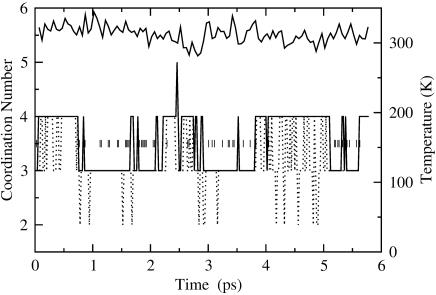
Fig. 2.

RUN1 coordination number and temperature versus time. R = 2.5 Å. The block-averaged temperature is shown with the solid line. The mean temperature is 332 ± 22 K. The short vertical bars at the n = 3.5 level flag hydrogen exchange events, which also change the identity of the hydroxyl. Note that many hydrogen exchange events occur without intercession of the n = 4 configuration.

Fig. 3.

RUN3 coordination number and temperature versus time. The mean temperature is 313 ± 21 K. Other conditions are as in Fig. 2. The dashed line applies to the selection criterion involving R ≤ 2.5, θ ≥ 80°, ϕ ≥ 150°. Note that many hydrogen exchange events occur without intercession of the n = 4 configuration.

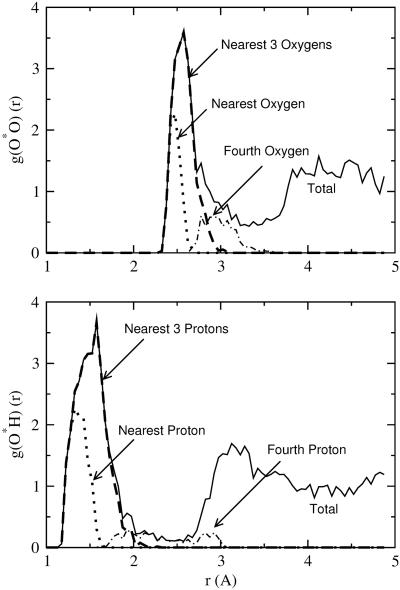
Fig. 4.

Density distribution of water oxygen and proton around the hydroxide oxygen for RUN1, which used PW91. The distributions of the neighboring atoms are also separated into contributions according to distance-order. The hydrogen of the nominal HO chemical bond, otherwise the nearest H, is not included in this distance-ordering.

Fig. 5.

Density distribution of water oxygen and proton around the hydroxide oxygen for RUN3, which used rPBE; otherwise as in Fig. 4.

Table 1.

Relative populations x̂_i = x_i/x₃ for RUN1 and RUN3 and different selection criteria (Fig. 1)

Method	Criteria	x̂1	x̂2	x̂3	x̂4
Quasichemical	—	0.03	0.26	1.0	0.0
PW91/RUN1	R ≤ 2.5	—	—	1.0	0.14
PW91/RUN1	R ≤ 2.5, θ ≥ 80°, φ ≥ 150°	—	0.03	1.0	0.08
rPBE/RUN3	R ≤ 2.5	—	—	1.0	1.02
rPBE/RUN3	R ≤ 2.25	—	0.01	1.0	0.60
rPBE/RUN3	R ≤ 2.5, θ ≥ 80°	—	0.01	1.0	0.43
rPBE/RUN3	R ≤ 2.5, θ ≥ 80°, φ ≥ 150°	—	0.07	1.0	0.36

Table 2.

Mean angles Θ and φ, in degrees, defined in Fig. 1, for RUN1 and RUN3

Method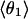
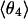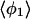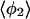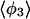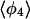PW91/RUN1	107.9 ± 9.2	108.1 ± 10.4	107.0 ± 11.8	97.4 ± 32.8	169.2 ± 9.9	168.1 ± 6.3	166.7 ± 7.1	84.2 ± 38.8
rPBE/RUN3	109.1 ± 9.9	108.0 ± 11.9	103.4 ± 13.1	91.8 ± 24.5	169.8 ± 5.4	168.0 ± 6.0	165.0 ± 7.9	124.9 ± 45.8

The four values for each angle pertain to the four nearest coordinating protons ordered in distance from the anionic oxygen. The values of 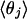j = 1, 2, and 3 are consistent with classic tetrahedral geometry (109.5°). These values are in good agreement with angles (110°) obtained from the optimized 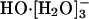cluster. 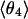is different; θ₄ is typically located closer to the equatorial plane, but with bigger statistical dispersion. 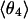is also different from the angle (116°) obtained from the optimized cluster. The angles 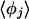indicate that the coordinating OH bond is not collinear with the O^*O vector, and this is consistent with the cluster results. Note specifically that the water oxygen atom determining the angle φ_j does not correspond uniquely to a particular distance order for oxygen atoms; this angle is defined by the distance-ordering of the hydrogen atoms, and the oxygen atoms to which those hydrogens are directly bonded.

Discussion of AIMD Results

For RUN1, it is clear that n = 3 is the predominant state (Figs. 2 and 4 and Table 2). The radial distribution functions shown in Fig. 4 Lower establish that R ≤ 2.5 A is a reasonable, inclusive, even permissive selection criterion; see also ref. 60. Tables 1 and 2 provide guidance on whether many of these n = 4 configurations should be excluded as not hydrogen-bonded. Note that mediating n = 3 to n = 4 interconversions are not required for exchange of the identity of the hydroxide oxygen. RUN3 below provided the same observation.

For RUN3, using the R ≤ 2.5 Å criterion, we find about equal populations of n = 3 and n = 4. Tightening this criteria by 0.25 Å drops n = 4 population by 40% (Table 1) relative to n = 3. It is apparent from Table 2 that many of these n = 4 states are not square-planar. Table 1 shows that even a permissive θ ≥ 80 cutoff excludes many of those n = 4 cases. The configurations thereby excluded are on the “forward” side of the hydroxide-water complex, i.e., θ < π/2 in Fig. 1.

The radial distributions (Figs. 4 and 5) decomposed according to the distance-order of atoms surrounding the hydroxide oxygen, denoted O^*, are similarly interesting. Although the statistical quality is meager, the conventional O atom second shell begins at a distance roughly √2 times the radial location of the first shell. The fourth-nearest oxygen atom, qualitatively described, builds a shoulder on the outside of the principal maximum of the O^*O radial distribution functions. Note that the contributions from the nearest three protons and the nearest three oxygen atoms are concentrated, and that those protons are about 1 Å nearer the hydroxide oxygen. In contrast, the contributions from the fourth-nearest proton and fourth-nearest oxygen are diffuse and overlapping; the contribution from the fourth-nearest proton is not always inside the contribution from the fourth-nearest oxygen. (Of course, those atoms need not be directly bonded.) These observations suggest again that the fourth-nearest water molecule is not always participating in a conventional specific hydrogen bond but is often nonspecifically arranged. This description as a whole is consistent with the hypothesis that the tricoordinated species is a prominent species, although the tetracoordinated species is also present to some extent.

The 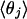results of Table 2 document the interesting point that three nearest coordinating protons are physically equivalent and approximately disposed toward the corners of a tetrahedron. The fourth-nearest proton is distributed broadly about the plane containing the hydroxide oxygen and perpendicular to the OH chemical bond.

These results are only roughly consistent with the inferences formulated upon neutron scattering from 4.6 M NaOD aqueous solutions (61), which report a mean coordination number of 3.7 ± 0.3. This value is not inconsistent with integrals of the results of Figs. 4 and 5, and suggests the natural interpretation of 70% tetracoordinated and 30% tricoordinated species, qualitatively consistent with the view that the tricoordinated species is substantially represented. But the results here suggest the subtlety that the total population obtained by integrating to the first minimum includes a substantial fraction of the fourth-most-distant water molecule that is not involved chemically as the nearer three water molecules are. It should be additionally noted that the interpretation of the neutron scattering data involves empirical potential structure refinement (EPSR) modeling (61) that produces radial distribution functions that have some interesting differences from the recent AIMD results (13, 19, 20), including the present work. For example, with all AIMD results the maximum value of g(O^*O) is less than 6, and the principal peak of g(O^*O) shows perceptible asymmetry on the outer side of the principal maximum, as exemplified by the identification of the contribution of the fourth-most-distant oxygen contribution in Figs. 4 and 5. In contrast, the EPSR model of the neutron scattering data shows maximum values that exceed 6, and that principal peak seems qualitatively less asymmetric. That EPSR-modeled first peak is reported to occur at ≈2.3 Å, which is significantly shorter than the anticipated value 2.45 Å discussed below. It is natural to guess that the higher maximum value (>6) and nearer positioning (≈2.3 Å), relative to AIMD results, are correlated so as to obtain roughly similar net populations. Finally, we note differences in both concentration and temperature, and that close scrutiny of ref. 20 suggests that the hydroxide water coordination number might decrease with decreasing concentration.

Figs. 4 and 5 show the nearest water-oxygen occurring near 2.45 ± 0.1 (2σ) Å of the hydroxide oxygen. This distance is close to the O-O separation in the calculated gas-phase structure of HO·[H₂O]^-, 2.46 Å. We conclude that HO·[H₂O]^- is a prominent subgrouping in the 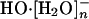(n = 2, 3, or 4) species. The recent theoretical and experimental work noted in the background section above suggests that the structure HO·[H₂O]^- does not provide as natural a description of the thermodynamic hydration free energy as does the species 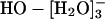that follows from a more conservatively defined inner shell. It seems likely that an inner-shell definition designed (41) to better isolate this HO·[H₂O]^- subgrouping would be excessively complicated. This is one reason why x₁ is not unambiguously separated by the results of Table 1.

The identification of HO·[H₂O]^- as a prominent subgrouping agrees with spectroscopic studies on concentrated hydroxide solutions. The IR and Raman spectra of concentrated hydroxide solutions have been interpreted in terms of HO·[H₂O]^- as a principal structural possibility for those systems (24-27). But the present observations suggest that it is the principal participant in the proton conductivity.

This HO·[H₂O]^- subgrouping also concisely resolves the high effective (not microscopic) hydration numbers extracted from dielectric dispersion measurements (28). A supergrouping of hydrated HO·[H₂O]^-, one involving several more water molecules, could well be relevant to the time scale of the measurement, a possibility also suggested by Agmon (15). Then a dominating species (13, 19, 20) is not a conclusion necessary to the resolution of experimentally obtained effective hydration numbers.

The diffusion coefficient of HO^- is calculated to be 3.1 Ų/ps at 332 K by using PW91 for HO^-, and 1.1 Ų/ps at 313 K by using rPBE for DO^-. For comparison, ref. 19 gives 1.5 Ų/ps for DO^-(aq) presumably at 300 K. The experimental value, calculated from mobility data, is about 0.5 Ų/ps for HO^- (3). Perhaps the agreement of experiment with the lowest of these computed numbers is acceptable, but all these values agree only roughly with experiments. An important background point is that evaluation of diffusion coefficients typically requires longer simulation times, not readily accessible here by AIMD simulation.

Rationalizations why the simulation rates are higher than observed experimental rates would be highly speculative. A quantum mechanical treatment of the water matrix, rather than a classical one, would imply less order, and perhaps that would lead to slower rates. Or it might be that the electron density functionals used here lead to excessive prominence of the HO·[H₂O]^- subgrouping, and that leads to rates that are too high by comparison with experiment. The fact that the empirical activation energies increase with decreasing temperature remains an unexplained point, apparently of qualitative significance.

The transport observed here involved the movement of a proton-hole between two trihydrated species, which is also consistent with the identification of the HO·[H₂O]^- subgrouping and the IR spectra. Second-shell rearrangements do occur, but all-or-nothing breaking and reforming of a hydrogen bond is not necessary (15). There will certainly be rearrangements as the hole settles into its new place. The hole-hopping proposal for HO^- transport, as discussed by Bernal and Fowler (3), and later Stillinger (5), has substantial validity.

We note that AIMD studies on pure liquid water (44) under conventional thermodynamic conditions show that PW91 and PBE predict more strongly structured liquid water compared to experiment, and rPBE softens the structure of liquid water simulated on that basis. The excess chemical potential evaluated in that study (44), on the basis of AIMD results and the quasichemical theory, indicates that PW91 binds liquid water too strongly, whereas rPBE softens the binding. The excess chemical potential of water at 314 K when the rPBE functional was used was -5.1 kcal/mol (compared with -6.1 kcal/mol experimentally), whereas PW91 gives -12 kcal/mol at 330 K. Despite these differences, the hydration structure of HO^-(aq) and the qualitative transport pattern are similar in these two cases. Therefore, the above comparisons can be more optimistic for providing the correct direction to frame discussions on HO^- transport.

Conclusion

Three distinct lines of investigation, theory (22), experiments (18, 23), and the present simulations (and also ref. 21), converge on the common view that 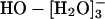is a prominent, likely even dominating, coordination structure for HO^-(aq); this is the most primitive issue underlying current speculations regarding HO^- in aqueous solutions. The present simulation results suggest, in addition, that the coordination number distribution is labile, that less specifically structured n = 4 possibilities are included, and that HO·[H₂O]^- is a prominent subgrouping within larger inner shell structures. This latter point is consistent with interpretations of aqueous phase spectroscopic (24-27) results and also with proposals of high effective solvation numbers on the basis of dielectric dispersion measurements (28).