The unfolding kinetics of ubiquitin captured with single-molecule force-clamp techniques

Abstract

We use single-molecule force spectroscopy to study the kinetics of unfolding of the small protein ubiquitin. Upon a step increase in the stretching force, a ubiquitin polyprotein extends in discrete steps of 20.3 ± 0.9 nm marking each unfolding event. An average of the time course of these unfolding events was well described by a single exponential, which is a necessary condition for a memoryless Markovian process. Similar ensemble averages done at different forces showed that the unfolding rate was exponentially dependent on the stretching force. Stretching a ubiquitin polyprotein with a force that increased at a constant rate (force-ramp) directly measured the distribution of unfolding forces. This distribution was accurately reproduced by the simple kinetics of an all-or-none unfolding process. Our force-clamp experiments directly demonstrate that an ensemble average of ubiquitin unfolding events is well described by a two-state Markovian process that obeys the Arrhenius equation. However, at the single-molecule level, deviant behavior that is not well represented in the ensemble average is readily observed. Our experiments make an important addition to protein spectroscopy by demonstrating an unambiguous method of analysis of the kinetics of protein unfolding by a stretching force.

A mechanical force of a few tens of piconewtons is sufficient to trigger the unfolding and extension of a protein. This process has been studied with the recently developed technique of single-molecule force spectroscopy. In the most typical experiment, a single polyprotein is extended at a constant velocity, while measuring force (1-5). These experiments result in a sawtooth pattern force-extension relationship where each sawtooth peak corresponds to the unfolding of an individual protein module.

Although protein unfolding is known to be dependent on the stretching force (6), this dependency could not be measured directly with constant-velocity experiments where the stretching force is constantly changing in an unpredictable way. Recently, force spectroscopy was refined by the introduction of the force-clamp technique, which, through the use of feedback techniques, could be used to observe the mechanical unfolding of a polyprotein under a relatively constant force. In those early experiments, the thermal-mechanical drift of the cantilevers, as well as the low positioning resolution of the piezoelectric actuators, made it difficult to probe the kinetics of unfolding with sufficient resolution (7). Our improved instrumentation (see Materials and Methods) now makes it possible to examine the force and time dependency of polyprotein unfolding.

Here, we study the mechanical unfolding of the protein ubiquitin, which is a naturally occurring polyprotein of nine identical repeats. Each ubiquitin forms an independently folded protein of 76 amino acids with a characteristic α-β fold, and its folding and unfolding have been studied in detail by using chemical denaturants (8-10) Ubiquitin is involved in protein degradation and other signaling pathways (11, 12). In our experiments an N-C-linked ubiquitin chain (13) was stretched by a mechanical force that was either stepped to a constant value (force-step) or increased at a constant rate (force-ramp). Stretching a polyubiquitin protein under force-clamp conditions produced a staircase-like elongation of the protein where each step increase in length marked the unfolding of a single ubiquitin in the chain. The frequency of occurrence of the step-unfolding events, as well as the force at which they were most likely to be observed, was used as an indication of the kinetic properties of ubiquitin unfolding. The stochastical behavior of protein unfolding under a stretching force is implicitly assumed to lack memory (Markovian; refs. 14 and 15) and to have rates that are exponentially dependent on the pulling force. However, these assumptions remained unproven. The characteristic of Markovian processes is that their probability of occurrence is independent of the previous history. Markovian kinetics has been especially challenging to verify by using constant velocity experiments, which clearly show a memory effect in the data (3, 16). In the constant-velocity experiments, the rate of change of the pulling force and the unfolding probability are history dependent, resulting in an unfolding sequence that cannot be predicted. By contrast, with the force-clamp technique, we can measure the kinetics of unfolding at a well defined force, eliminating many of the ambiguities in the interpretation of the constant-velocity data.

Bond rupture under a stretching force has been modeled as an all-or-none Markovian process showing exponential dwell-time distributions and unbinding rates that were exponentially dependent on the stretching force (17-21). A similar bond-rupture-like process has been used to describe the force-driven unfolding of proteins (1, 2) and RNA hairpins (22). Whereas the forced unfolding of RNA hairpins was shown to be exponentially dependent on the pulling force (22), this assumption remained speculative in the case of proteins. Here, we demonstrate that the force-driven unfolding of a protein can be described as a Markovian process that depends exponentially on the stretching force. These experiments advance force spectroscopy of proteins by providing a direct and well defined approach to studying the kinetics of protein unfolding at the single-molecule level.

Our experiments also demonstrate the advantages of examining unfolding kinetics at the single-molecule level. We show that, although an ensemble average of the single-molecule measurements is well described by a simple two-state model, we observe unfolding events that clearly follow a variant unfolding pathway and that, due to their low frequency of occurrence, are not represented in the ensemble. For example, a protein at room temperature is a very dynamic structure, with a fluctuating bond structure (23). Therefore, their unfolding kinetics might be dependent on their actual conformation when force is applied, leading to either a simple two-state unfolding or to more rare intermediate unfolding states. Similarly, the kinetics of unfolding RNA (24) and the work done on unfolding RNA (25) were shown to vary on each repetition due to thermal fluctuations in the conformation of the RNA structures.

Materials and Methods

Force-Clamp Atomic Force Microscopy. Our custom built atomic force microscope was constructed as described (26). We used a modified Digital Instruments (Veeco Instruments, Santa Barbara, CA) detector head (AFM-689) and a three-dimensional piezoelectric translator “Picocube”; P-363.3CD from Physik Instrumente (Karlsruhe, Germany). The actuator has a displacement range of 6,500 nm in the z axis, with a bandwidth limited by an unloaded resonant frequency of ≈10 kHz, which is somewhat reduced by an aluminum pedestal where the protein sample is placed. Subnanometer resolution results from a fast capacitive sensing of the actuator's position. Our previous force-clamp set-up used a piezoelectric actuator, P841.10, also from Physik Instrumente, equipped with a strain-gage detector of position (7). In those experiments, our positioning accuracy and noise was of several nanometers. By contrast, through the use of a picocube actuator, we have now improved our measurements of protein length to a peak-to-peak noise of ≈0.5 nm, resulting in a significant improvement in our recordings and also in the accuracy of the force-clamp electronics. It is now possible to select “good” low-drift cantilevers that can hold a constant force for many seconds (26). One approach to verify the lack of drift in the system is to test whether the length of a polyprotein remains constant after fully unfolding. We monitored the unfolded length over time to measure the amount of combined drift in the system. It is not rare to find cantilevers where the overall drift in the system (unfolded protein plus cantilever plus piezoelectric actuator) is <2 nm over 10 s or more. Under force-clamp conditions, the force signal had a SD that was bandwidth dependent. A force signal filtered at ≈150 Hz, had a SD = 2.5 pN. For data acquisition and control, we used National Instruments (Austin, TX) boards PCI-6052E and PCI-6703. We wrote all our software in igor pro (WaveMetrics, Lake Oswego, OR), and it is available upon request. The force feedback was built by using analog electronics based around a standard proportional, integral, and differential (PID) amplifier whose output was fed to the piezoelectric positioner. The PID amplifier was driven by an error amplifier that compared a force set-point with the actual force measured. Our analog force-clamp apparatus was typically able to complete a force step in <10 ms and occasionally in <4 ms. The slew-rate of the system depended on the pulling force and varied between ≈5,000 nm/s and up to 100,000 nm/s. The atomic force microscope could be operated in force-step mode, which is used to stretch proteins at a constant force, and force-ramp mode, which is used to stretch proteins at a force that increases linearly with time (F = a·t, where a, the ramp rate, was typically set to 300 pN/s.

Single Protein Recordings. Polyubiquitin chains were cloned and expressed as described (13, 26). Single proteins were picked up by pressing the cantilever onto the sample at 200-800 pN for 2-5 s. The sample was retracted from the cantilever either stepwise to the pulling force (force-step mode) or continuously ramped to the final pulling force (force-ramp mode). The probability of picking up a protein was kept low to reduce the spurious interactions with the cantilever. A single ubiquitin polyprotein was identified as such whenever we observed an uninterrupted staircase composed of several ≈20-nm steps. Such staircases had a variable number of steps ranging from n = 2 to 9.

Results and Discussion

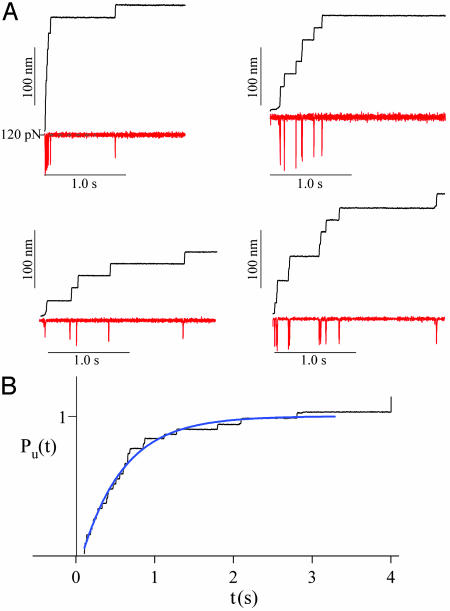
Ubiquitin Unfolds with Markovian Kinetics. Fig. 1A shows four typical recordings of ubiquitin unfolding in response to a step increase in force. The Upper traces show the stepwise increase in the length of the polyprotein as each ubiquitin in the chain unfolds. The Lower traces show the time course of the force, which is punctuated by transient deviations that are due to the finite response time of the feedback in response to each unfolding event. The unfolding of ubiquitin results in a step increase in length of 20.3 ± 0.9 nm (n = 821) measured between 100-200 pN. A single ubiquitin polyprotein was easily identified as a clean staircase of steps of ≈20 nm each. All of the recordings included in this report showed this characteristic fingerprint. Although in all of the examples shown in Fig. 1 A the polyubiquitin chains were subjected to a step-increase in force of similar magnitude, the time evolution of the elongation was different in all cases. This result shows the stochastic nature of the unfolding events triggered by a constant force. The time course of unfolding of an ensemble of ubiquitin chains was obtained by simple summation of several recordings such as those shown in Fig. 1 A. A normalized sum of five stepwise elongation recordings obtained by stepping the force to 120 pN is shown in Fig. 1B. The average time course of these ubiquitin unfolding events can be readily described by a single exponential (Levenberg-Marquardt fit, solid line in Fig. 1B), with a time constant τ = 0.53 s. An exponential time course is consistent with a memory-free Markovian process where the probability of unfolding at any given time is independent of the previous history. However, the exponential behavior of the ensemble average is a necessary but not sufficient condition for Markovian kinetics.

Fig. 1.

Exponential unfolding of ubiquitin at a constant stretching force. (A) Typical length vs. time recordings (black traces) for single ubiquitin chains stretched at a constant force of ≈120 pN (red traces). Under a constant stretching force, the ubiquitin chain elongates in steps of ≈20 nm, marking the unfolding of individual ubiquitins. (B) Average time course of unfolding obtained by summation and normalization of five recordings, including those shown in A. The unfolding time course is well described by a single exponential (blue trace) with a time constant of τ = 0.53 s.

The Unfolding Rates Depend Exponentially on the Pulling Force. Over the past century, a variety of models for the acceleration of mechanical failure by an applied stress have been developed. These models have been variously based on the empirical observations of Arrhenius, the Eyring chemical reaction rate theory, and the Kramers Brownian diffusion rate theory. The basic form of these theories proposes that the time to failure, t_f, is given by t_f ≅ A exp{(ΔE - W)/k_BT} where A is a constant, ΔE is the activation energy of the rupture process, T is the absolute temperature, and W represents any type of additional work done on the system. W can be the result of an electric field, a mechanical force, or a chemical reaction. The principal feature of these models is that the magnitude of an applied stress reduces exponentially the time to failure. George Bell was the first to apply a “time to failure” model to the problem of the rupture of a bond under a mechanical stretching force (17). He predicted that protein-protein bonds, such as those that occur between the cell-adhesion proteins of neighboring cells, would rupture at a rate that would increase exponentially with the stretching force:

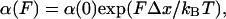1

where F is the stretching force and Δx is the distance to the transition state beyond which the bond will fail (17). Several authors have since examined the consequences of these predictions and confirmed that the rate of bond rupture is indeed exponentially dependent on a stretching force (18, 27). Other consequences of this theory, such as a predicted exponential dependency on the pulling rate (19, 20), also were studied experimentally at the single bond level (18, 21, 27, 28).

The process that leads to the mechanical unfolding of a protein is thought to share many of the same mechanisms as those involved in the mechanical rupture of a protein-protein bond. Indeed, the single-bond rupture model has also been used to describe the all-or-none mechanical unfolding of protein chains (2, 29). However, the principal assumption of this model, that the unfolding rate is exponentially dependent on the stretching force, has never been tested experimentally. Because we can monitor the unfolding time course of a polyubiquitin protein stretched by a constant force, we can examine the way in which the unfolding time constant is affected by the stretching force.

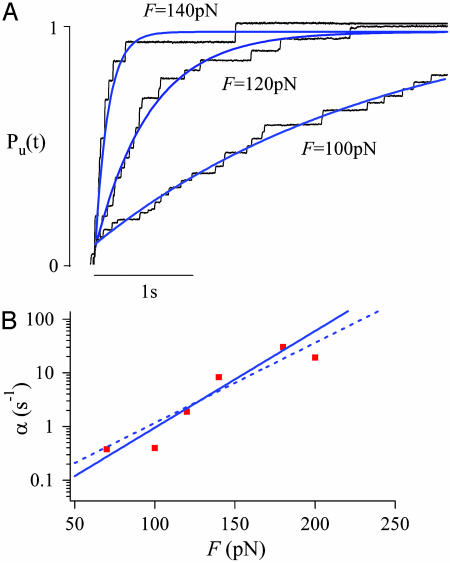
Fig. 2A shows ensemble averages of unfolding time courses obtained at F = 100, 120, and 140 pN. At each stretching force, we added several traces and then normalized the resulting trace as shown before in Fig. 1. The normalized records were fitted [Levenberg-Marquardt (30)] with a single exponential function (continuous line in Fig. 2 A) with time constants τ(100 pN) = 2.77 s; τ(120 pN) = 0.54 s; τ(140 pN) = 0.13 s. It is evident from Fig. 2 A that the rate of polyubiquitin unfolding is strongly dependent on the stretching force. The linear relationship observed in a semilogarithmic plot of the unfolding rate α = 1/τ as a function of the pulling force (red squares; Fig. 2B) directly demonstrates that the unfolding rate of polyubiquitin is exponentially dependent on the pulling force. Our resolution is limited to a range of only ≈130 pN. For forces bigger than 200 pN, the unfolding rate is too fast to be well resolved with the current feedback instrumentation, given that most events will occur within a short time after the force step (<100 ms). For stretching forces below ≈70 pN, the unfolding rate drops significantly and becomes harder to define a baseline. Improvements in the feedback response time as well as decreases in cantilever drift should significantly expand the range of our measurements. A Levenberg-Marquardt (30) fit of Eq. 1 to the data of Fig. 2B (solid line) gives α₀ = 0.015 s^-1 and a distance to transition state of Δx = 0.17 nm.

Fig. 2.

The unfolding rate depends exponentially on the stretching force. (A) Three averaged and normalized ubiquitin unfolding time courses (black traces) obtained at different stretching forces. The blue lines correspond to single exponential fits with time constants of τ = 0.13 s at 140 pN, 0.54 s at 120 pN, and 2.77s at 100 pN, respectively. (B) Logarithmic plot of the unfolding rate, α = 1/τ (red squares), as a function of the stretching force F. A Levenberg—Marquardt fitofEq. 1 to the data (continuous line) gives values of α₀ = 0.015 s^-1, Δx = 0.17 nm. The dashed line corresponds to Eq. 1 evaluated with α₀ = 0.0375 s^-1 and Δx = 0.14 nm.

A Simple Two-State Model for Ubiquitin Unfolding. Given that we have demonstrated that ubiquitin unfolding is consistent with simple Markovian kinetics and that its unfolding rate is exponentially dependent on the pulling force, we are well justified to use a simple two-state kinetic model for ubiquitin unfolding. Given a two-state model with folded (F) and unfolded (U) conformations, we make the simplifying assumption that the refolding rate is negligible over the time of the experiment, and then we calculate the probability of unfolding, P_u, from the following differential equation (19, 20, 31):

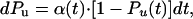2

where α(t) represents the unfolding rate. To change variables from time to force we assume that the stretching force is changing linearly with time as F = a·t, where a is the pulling rate measured in pN/s. By changing variables from time to force in Eq. 2 and then integrating, we obtain the probability of unfolding as a function of a stretching force:

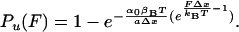3

Hence, this simple model predicts that the unfolding probability is a sigmoidal function of the applied force. We calculate the probability density from Eq. 3:

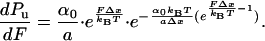4

The probability density predicts the shape of a histogram of the accumulated forces at which ubiquitin is observed to unfold, when pulling the protein with a force that increases at a constant rate (19, 20).

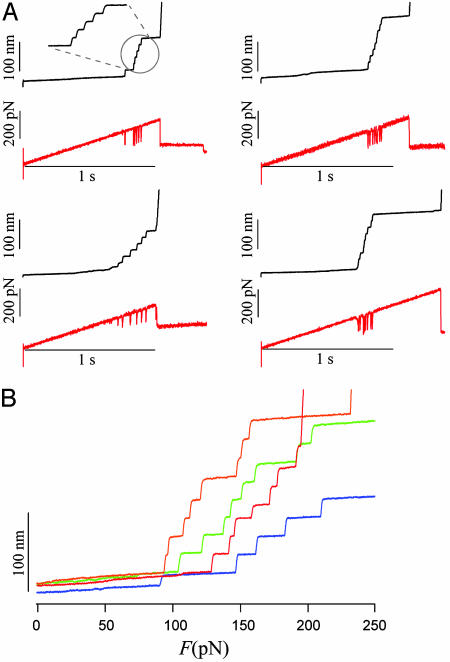
Measurement of Ubiquitin Unfolding Probability and Its Probability Density. Force-clamp measurements of protein unfolding have the very significant advantage that the feedback can be controlled with any type of waveform, which will then be applied as a force to the single protein. To implement the assumptions of our simple two-state model for unfolding, we apply a stretching force that increases linearly with time: the force-ramp method described before by Oberhauser et al. (7). In our experiments, we fixed the pulling rate to a = 300 pN/s. Typical results of these experiment are shown in Fig. 3A. The Upper trace shows the extension vs. time trace whereas the Lower trace shows the force vs. time trace with a ramp rate of a = 300 pN/s. As before, every ubiquitin unfolding event is marked by a step increase in the length of the polyprotein by ≈20 nm and a short imbalance of the feedback that is visible as a brief spike in the force trace (see Fig. 3A). After picking up a single protein, the force increased linearly with time to a maximum typically set to 500 pN. Most proteins break off before reaching this maximum. When the polyprotein breaks off, we lose control of the feedback and the force cannot be increased linearly anymore. Simultaneous with the loss of the feedback, we observe that the piezoelectric positioner will rapidly move several micrometers until it reaches its maximum range. These events are easy to recognize as a discontinuity in both the length and force traces observed toward the end of the recordings. Most ubiquitin unfolding events were observed to occur in a small range of pulling forces between 50 and 200 pN (Fig. 3A).

Fig. 3.

Mechanical unfolding of ubiquitin chains using a force-ramp. (A) Typical length vs. time recordings (black traces) for single ubiquitin chains stretched with a force that increased at a constant rate, a = 300 pN/s (red traces). (B) Length vs. force recordings obtained from data like that shown in (A). Each step increase in length marks the force at which the unfolding event occurred.

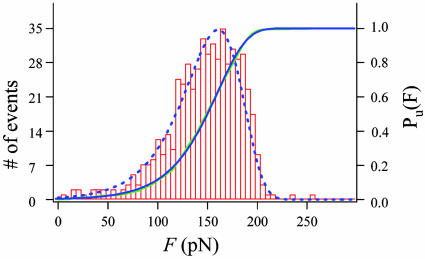
Fig. 3B shows several recordings of ubiquitin unfolding recorded under force-ramp conditions. We plot the polyprotein length vs. the pulling force obtained from traces similar to those shown in Fig. 3A. To reduce noise, we fitted the force trace with a straight line that matched the slope exactly to the set ramp rate. In the plots of Fig. 3B, we used this fit as the ordinate. The plots of Fig. 3B demonstrate a simple method for compiling a large number of unfolding events and the force at which they occurred. Fig. 4 shows a histogram compiling the number of unfolding events observed at a given force. The histogram consists of 538 ubiquitin unfolding events measured with the procedures demonstrated in Fig. 3. This histogram, when normalized, corresponds to the unfolding probability density, dP_u/dF. Integration and normalization of the histogram data yields the unfolding probability P_u (continuous blue line in Fig. 4).

Fig. 4.

The unfolding probability of ubiquitin. Frequency histogram of unfolding forces (n_total = 538) measured from force-ramp experiments like that shown in Fig. 3. We obtained the unfolding probability distribution (P_u^·; green line) by integrating and normalizing the frequency histogram. A fit of the unfolding probability, P_u, with Eq. 3, gave α₀ = 0.0375 s^-1, a = 103 pN/s, and Δx = 0.14 nm. A plot of Eq. 4, evaluated with these parameters, resulted in the dotted line that accurately describes the unfolding force frequency histogram.

We used Eqs. 3 and 4 to explain our data. A least squares fit of the unfolding probability with Eq. 3 produced an excellent fit of the data (green line in Fig. 4) giving α₀ = 0.0375 s^-1, a = 103 pN/s, and Δx = 0.14 nm. The probability density function (Eq. 4) calculated with these values also accurately reproduced our data (blue dotted line, Fig. 4).

The fits of the two state model to the data of Fig. 4 do not recover the correct ramp rate of the experiment (103 pN/s returned by the fit vs. an actual rate of 300 pN/s). One potential source of error is the brief loss of control that occurs during a step-unfolding event (“spikes” in the force traces), which tends to decrease the pulling force (spike amplitude = 87 ± 25 pN and duration = 9.4 ± 5.7 ms; see Fig. 3A). However, these brief spikes occur only during the rapid elongation of the protein that follows unfolding. Hence, the spikes are not likely to affect the unfolding kinetics. It is more likely that the simple two-state kinetic model that we use here does not fully describe the force dependency of ubiquitin unfolding.

Kinetics of Ubiquitin Unfolding Under a Stretching Force. The results of Figs. 2B and 4 demonstrate two types of independent experiments that examine the unfolding of polyubiquitin under a stretching force. When fitted with the two-state model described above, both sets of measurements are consistent. For example, using Eq. 1 together with the values of α₀ and Δx obtained by fitting Eqs. 3 and 4 to the data of Fig. 4 (see above), we can readily explain the force dependency of the rate measured in Fig. 2 (dashed blue line in Fig. 2B). It is interesting to consider that, because the experiments of Fig. 2 were done at constant force, the ramp rate parameter a does not play a role.

That the results of these different types of force-clamp experiments are self-consistent should not be a surprise. However, what is puzzling is that the values obtained for α_0, and Δx are very different from those obtained previously by us by analyzing sawtooth pattern recordings of ubiquitin unfolding under constant velocity conditions. In those experiments, we used Monte Carlo simulations where α₀ was fixed at 0.0004 s^-1 [the value obtained from chemical denaturation data (8)] and where Δx = 0.25 nm was found to describe the data reasonably well (13). These parameters are very different from those that we now obtain from actual fits to the force-clamp data (α₀ = 0.015-0.0375 s^-1 and Δx = 0.14 to 0.17 nm). These discrepancies may result from the very different experimental approaches taken to obtain these data. For example, the sawtooth pattern data obtained by pulling polyproteins at constant velocity is typically analyzed with either Monte Carlo simulations (2, 29) or numerical solutions of the rate equations (32). However, neither technique can actually be used to “fit” data in the sense of exploring the multidimensional space of solutions to minimize the square of the error, as this term usually implies. Typically, a Monte Carlo fit indicates a set of values that can describe the data within a factor of ten or so (2, 13). Furthermore, during a constant velocity experiment (that results in sawtooth patterns of force), the rate of change of the pulling force varies during the experiment in a way that depends on the length of the molecule and on the number of modules that had already unfolded. Given that unfolding is probabilistic, the actual conditions that lead to any given unfolding event are dependent on the previous history and hence cannot be anticipated. Hence, a true analytical model of a sawtooth pattern recording cannot be formulated, much less fitted to the data. By contrast, under force-clamp conditions, the magnitude and the rate of change of the stretching force are established a priori, which we can readily model with simple two-state kinetics (see Eqs. 1-4). This approach represents an important refinement of force spectroscopy, allowing a quantitative measurement of the kinetics of protein unfolding under a stretching force. Although much work is still required to improve this technique, force-clamp data analyzed with analytical representations of kinetic models is likely to represent a far more accurate measure of the unfolding kinetics of a protein under a stretching force.

If these considerations are correct, the force-clamp data measure an unfolding rate at zero force (α₀ = 0.015-0.0375 s^-1) that is 40- to 100-fold faster than that measured by using chemical denaturants (α₀ = 0.0004 s^-1) (8). This large discrepancy may result from the different reaction coordinates in these two different experimental approaches (13, 33, 34).

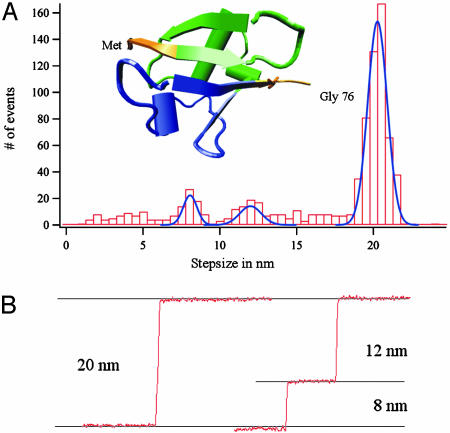
Deviations from Two-State Unfolding. Fig. 5A shows the step-size histogram of 821 single unfolding events. It is clear that the histogram is dominated by the peak centered at 20.3 ± 0.9 nm, which corresponds to the full two-state unfolding of ubiquitin. However, in 5% of these cases, the unfolding events were observed to occur through one or more intermediate states that always added up to the full 20-nm step. These intermediate unfolding steps scattered in size between 2-18 nm and are plotted individually in the histogram. Fig. 5B shows two examples of the most common unfolding events observed. The recording on the Left shows a typical 20-nm step whereas the one on the Right shows an unfolding event broken up into two steps of 8 and 12 nm, respectively. These two smaller steps add up to a full 20-nm step, indicating that the ubiquitin modules unfold in a three-state manner, instead of a two-state manner. Indeed, three-state folding kinetics for ubiquitin had already been observed by using chemical denaturants (9). However, given that the reaction coordinates are very different, it is unlikely that the mechanical unfolding intermediate observed here directly corresponds to that observed in the chemical unfolding studies. For the histogram of Fig. 5A, we have considered only steps that are either 20 nm or that clearly add up to 20 nm. Some of the events showing a 20-nm step broken up into intermediates are likely to correspond to spurious molecules that are picked up in parallel with a ubiquitin chain. When these molecules are stretched, detachment or even unfolding of the second molecule would result in an interruption of the elongation due to an unfolding event. We expect such spurious events to occur at random. Indeed, there is a wide distribution of substeps. However, we can also distinguish two peaks centered at 8.1 ± 0.7 nm and 12.4 ± 1.0 nm. It is unlikely that these well marked peaks result from the random pick-up and rupture of spurious molecules, and therefore they may well be an indication that ubiquitin unfolds by means of an intermediate state. At a stretching force of 100 pN, the 8- and 12-nm steps correspond to the unraveling of 28 aa and 39 aa, respectively. Interestingly, these two step sizes coincide with two well defined structural clusters packing against each other in the ubiquitin fold (Fig. 5A Inset). The first cluster (green) includes β strands I and II, the α helix, and the turn connecting the α helix and β strand III. The second cluster (blue) includes β strands III and IV. Sequential unraveling of these clusters would produce elongations of 11.7 nm and 8.4 nm, respectively, which would explain our data. This sequential unfolding of ubiquitin is similar to the unfolding of BSA (35).

Fig. 5.

Step-size analysis of the mechanical unfolding of ubiquitins. (A) A frequency histogram of the unfolding length step sizes shows one predominant peak at 20.3 ± 0.9 nm and two smaller peaks at 8.1 ± 0.7 nm and 12.4 ± 1.0 nm (n_total = 821). (Inset) Color-coded cartoon representation of the structure of ubiquitin (1UBI). The blue- and green-colored regions match structural features in the ubiquitin fold and would account for an intermediate unfolding step of either 8 or 12 nm (see Deviations from Two-State Unfolding). (B) The most typical examples of length vs. time recordings of ubiquitin unfolding.

It is well known that a protein structure at room temperature is very dynamic, with noncovalent bonds breaking and forming constantly due to the bombardment of the surrounding water molecules (23). Therefore, the exact protein unfolding pathway might depend upon the actual conformation of a protein at the time when a stretching force is applied. This uncertainty will lead to either a simple two-state unfolding or to more rare unfolding trajectories, as observed here. Our experiments again demonstrate the advantages and necessity of examining unfolding kinetics at the single-molecule level, as illustrated for enzymatic reactions by Lu et al. (36) and Zhuang et al. (37), and the mechanical unfolding/folding of RNA hairpins by Liphardt et al. (22).

Although a simple two-state kinetic model is adequate to describe most of our data, it is possible to anticipate a number of ways in which this simple model does not fully describe the unfolding pathway of ubiquitin. The most obvious deficiency is that the folded and unfolded states in reality correspond to a much larger number of conformations. This finding is particularly true of the unfolded state where ubiquitin folding trajectories observed at a low stretching force do not show discrete folding steps but rather a continuous process akin to that of polymer collapse (26). Evidently, a simple two-state kinetic model cannot describe these folding trajectories.

Another likely limitation of a Markovian model is that the lack of memory is likely to be true as long as the times between unfolding events are sufficiently long for having reached thermal equilibrium. At short times, comparable with the relaxation time of the protein, memory effects should appear. Structural memory loss is due to the Brownian motion of the protein. Deformations of the structure triggered by a stretching force, but that fall short of unfolding, will persist for a short time and then will be erased by the Brownian motion of the protein. Recent single-molecule experiments have given increasingly longer estimates of the relaxation times for proteins, up to 25 μs (38). Our own measurements show that unfolding events in a fibronectin module can show a strong correlation within 20 ms (L. Li, H. Huang, C. Badilla-Fernandez, and J.M.F., unpublished work). Hence, a rigorous examination of structural memory in ubiquitin unfolding is likely to show deviations from Markovian behavior when probed in time scales shorter than those reported here. We anticipate that a new class of kinetic models will be necessary to explain the more complex picture that emerges from probing protein unfolding at the single-molecule level.

Conclusion

Using an improved force-clamp technique, we have directly demonstrated at the single-protein level that ubiquitin unfolding is well described by a simple two-state kinetic model and that the unfolding rate closely follows the Arrhenius equation. Our experiments also show the power of single-molecule techniques by capturing lower probability events that deviate from simple two-state kinetics. Although such events are sufficiently rare as not to bias the ensemble averages, they are revealing of the diversity of pathways available to a protein undergoing forced unfolding. We anticipate that the techniques demonstrated in this work will be useful to examine the folding/unfolding kinetics of a wide range of proteins at the single-molecule level.