A Hierarchical Model for Simultaneous Detection and Estimation in Multi-subject fMRI Studies

Abstract

In this paper we introduce a new hierarchical model for the simultaneous detection of brain activation and estimation of the shape of the hemodynamic response in multi-subject fMRI studies. The proposed approach circumvents a major stumbling block in standard multi-subject fMRI data analysis, in that it both allows the shape of the hemodynamic response function to vary across region and subjects, while still providing a straightforward way to estimate population-level activation. An e cient estimation algorithm is presented, as is an inferential framework that not only allows for tests of activation, but also for tests for deviations from some canonical shape. The model is validated through simulations and application to a multi-subject fMRI study of thermal pain.

1 INTRODUCTION

Depending on their scientific goals, researchers in functional magnetic resonance imaging (fMRI) often choose modeling strategies with the intent to either detect the magnitude of activation in a certain brain region, or estimate the shape of the hemodynamic response associated with the task being performed [Poldrack et al., 2011]. While most of the focus in neuroimaging to date has been on detection [Lindquist, 2008], the magnitude of evoked activation cannot be accurately measured without either assuming or measuring timing and shape information as well. In practice, many statistical models of fMRI data attempt to simultaneously incorporate information about the shape, timing, and magnitude of task- evoked hemodynamic responses.

As an example, consider the general linear model (GLM) approach [Worsley and Friston, 1995], which is arguably the dominant approach towards analyzing fMRI data. It models the fMRI time series as a linear combination of several different signal components and tests whether activity in a brain region is related to any of them. Typically the shape of the hemodynamic response is assumed a priori, using a canonical hemodynamic response function (HRF) [Friston et al., 1998, Glover, 1999], and the focus of the analysis is on obtaining the magnitude of the response across the brain. However, it is well-known that the shape of the HRF varies both across space and subjects [Aguirre et al., 1998, Schacter et al., 1997, Handwerker et al., 2004, Badillo et al., 2013a]; thus assuming a constant shape across all voxels and subjects may give rise to significant bias in large parts of the brain [Lindquist and Wager, 2007, Lindquist et al., 2009]. The constant HRF assumption can be relaxed by expressing it as a linear combination of several known basis functions. This can be done within the GLM framework by convolving the same stimulus function with multiple canonical waveforms and including them as multiple columns of the design matrix for each condition. The coe cients for an event type constructed using different basis functions can then be combined to fit the evoked HRF in that particular area of the brain.

The ability to use basis sets to capture variations in hemodynamic responses depends both on the number and shape of the reference waveforms that are used in the model. For example, the finite impulse response (FIR) basis set, consists of one free parameter for every time-point following stimulation in every cognitive event-type that is modeled [Glover, 1999, Goutte et al., 2000]. Therefore, it can be used to estimate HRFs of arbitrary shape for each event type in every voxel of the brain. Another, perhaps more common approach, is to use the canonical HRF together with its temporal and dispersion derivatives to allow for small shifts in both the onset and width of the HRF. Other choices of basis sets include those composed of principal components [Aguirre et al., 1998, Woolrich et al., 2004], cosine functions [Zarahn, 2002], radial basis functions [Riera et al., 2004], spectral basis sets [Liao et al., 2002] and inverse logit functions [Lindquist and Wager, 2007]. For a critical evaluation of a number of commonly used basis sets, see [Lindquist and Wager, 2007] and [Lindquist et al., 2009].

Though basis sets allow the constant HRF assumption to be relaxed in the GLM framework, they are still not without problems, particularly when performing multi-subject analysis. Most analyses of multi-subject fMRI data involve two separate models. A first-level GLM is performed separately on each subject's data, providing subject-specific contrasts of parameter estimates. A second-level model is thereafter used to provide population inference on whether the contrasts are significantly different from zero and assess the e ects of any group-level predictors, such as group status or behavioral performance. However, it is problematic to define appropriate first-level contrasts that truly capture the behavior we are interested in detecting, when multiple basis sets are included in the model. For example, when each condition consists of multiple basis functions it is not self-evident how to properly define a relevant contrast comparing the di erence in activation between the two conditions.

There have been a number of suggestions about how to deal with this issue, most no tably using only the “main” basis set [Kiehl and Liddle, 2001]. In the case of the canonical HRF and its derivatives, this entails only using the coefficient corresponding to the canonical HRF, and treating the coefficients corresponding to the derivatives as nuisance parameters. While this works relatively well for small deviations from the HRFs canonical form, it quickly falls apart as the shape begins to differ. To circumvent this problem [Calhoun et al., 2004] suggested using the norm of the coe cients for the canonical HRF and its derivatives. Another suggestion [Lindquist et al., 2009] is to re-create the HRF after estimation and use the resulting amplitude as the contrast of interest.

In this work we introduce a new approach towards multi-subject analysis of fMRI data that enables us to simultaneously estimate the specific shape of the HRF for a subject in a given voxel, and to obtain a population-level estimate of the magnitude of activation. This approach o ers the flexibility of basis sets while retaining the simplicity of multi-subject inference with a single canonical HRF. We also provide an inferential framework that allows us to test both for activations as well as for any differences in HRF shape from some canonical form.

The idea of performing joint estimation and detection is not new in the neuroimaging literature. For example, Makni and colleagues [Makni et al., 2005, Makni et al., 2008] have suggested a Bayesian approach towards the detection of brain activity that uses a mixture of two Gaussian distributions as a prior on a latent neural response, whereas the hemodynamic impulse response is constrained to be smooth using a Gaussian prior. In this model all parameters of interest are estimated from the posterior distribution using Gibbs sampling. Later work has provided a number of interesting extensions of this model, including to spatial mixture models [Vincent et al., 2010] and reformulating it as a missing data problem that allows for a simplified estimation procedure [Chaari et al., 2013].

Our suggested model takes a different approach. Here the HRF is modeled as a linear combination of B-spline functions (see e.g., [Genovese, 2000] for an early use of spline functions in model fitting). We assume that subject-level HRFs are random draws from a population-level distribution and that for any given voxel the population average response across stimuli will vary only in scale. We provide an efficient algorithm for estimating the model parameters as well as inferential methods. The latter includes both tests of activation and for deviations in the HRF from some canonical form.

This paper is organized as follows. In Section 2 we introduce our hierarchical model. In Sections 3 and 4 we outline an efficient algorithm for estimating the model parameters and performing inference on them. In Sections 5 and 6 we evaluate the performance of the model on a series of simulated data sets and data from an experiment studying the effects of thermal pain. Both the simulated and real data were previously used in a large study of flexible HRF modeling procedures [Lindquist et al., 2009]. The proposed method is shown to outperform each of the previously tested approaches, which include the canonical GLM plus its derivatives, the smooth FIR model, and the inverse logit model. We conclude with a discussion of the suggested approach.

2 METHODS

2.1 The Hierarchical Model

In this section we outline the proposed hierarchical model for simultaneous estimation and detection. For simplicity, we assume only one session per subject and a single experimental group. To study multiple groups, it suffices to apply the model below and the estimation procedure of section 2.2 separately to each group. Similarly, the inference method of section 2.3 easily extends to multiple samples. We assume that all scans have been acquired at the same repetition time Δ and registered to a standard stereotactic space. For the j^th subject (1 ≤ j ≤ n), we model the BOLD response at the v^th voxel (1 ≤ v ≤ V) and t^th scan (1 ≤ t ≤ T_j) as

$$\underset{\mathrm{BOLD}}{\underbrace{y_i(v,t)}}=\sum _{l=1}^L{\int }_0^{t\Delta }\underset{\text{stimulus}}{\underbrace{s_{jl}(t\Delta -\tau )}}\underset{\mathrm{HRF}}{\underbrace{h_{jl}(v,\tau )}}dt+\sum _{\nu =1}^q{d}_{j\nu }\left(v\right)\underset{\text{nuisance}}{\underbrace{{\phi }_{j\nu }\left(t\right)}}+\underset{\text{noise}}{\underbrace{{\epsilon }_j(v,t)}}.$$ (1)

Here the response consists of a linear combination of stimulus-induced signal of interest (represented by the first sum on the right-hand side of the equation), nuisance signal (the second sum) and noise. The stimulus function s_jl is a stick-function that has baseline at zero and takes the value one whenever stimuli of the l^th type are presented. The nuisance signals φ_jν, 1 ≤ ν ≤ q, typically include scanner drift, represented by polynomial and/or cosine basis sets, and physiological noise such as head motion, heart beat, and respiration. The corresponding nuisance parameters d_jν must be estimated from the data. The subject-level HRF h_jl decomposes into

$$h_{jl}(v,\tau )=h_l(v,\tau )+{\eta }_{jl}(v,\tau ),$$ (2a)

where h_l is a population-level HRF (fixed e ect) and η_jl is a subject-specific (random) effect. Hence, each subject-level HRF is assumed to be a random draw from a population with mean h_l. Thus, similar to other recent methods (e.g. [Sanyal and Ferreira, 2012] and [Zhang et al., 2013]) this allows us to borrow strength across subjects to improve subject-specific estimation. The functions h_l(v,·) and η_jl(v,·) are represented using a set of basis functions (B_k)_1≤k≤K:

$$h_l(v,\tau )=\sum _{k=1}^K{\gamma }_{lk}\left(v\right)B_k\left(\tau \right),{\eta }_{il}(v,\tau )=\sum _{k=1}^K{\xi }_{jlk}\left(v\right)B_k\left(\tau \right),$$ (2b)

so estimation reduces to solving for the coefficients γ_lk(v) and ξ_jlk(v). In practice we suggest specifying the B_k as B-splines with regularly spaced knots over a time interval where the HRF is believed to be non-zero, say in the range between 0 and 30 seconds. B-spline basis sets have several desirable features. First, the coefficients of a function in a B-spline basis are very close to the function itself, i.e., the function values at the knots (possibly up to a scaling factor). For this reason, B-spline coe cients are immediately interpretable and inference of local features of the HRF is greatly facilitated. In addition, the compact support of B-splines typically induces sparsity in the design matrices and thus reduces the computational load.

Noting that the shape of the HRF at a given brain location is mostly determined by physiological factors that are independent of the nature of the stimulus, we further assume that the population-level HRFs h_l(v,·), 1 ≤ l ≤ L, have the same shape for all conditions and di er only in scale:

$${\gamma }_{lk}\left(v\right)={\beta }_l\left(v\right){\gamma }_k\left(v\right).$$ (2c)

Here the terms γk(v), 1 ≤ k ≤ K, determine the shape of the HRF, while β_l(v) determines ther amplitude of the response to stimulus of the l^th type. To make these parameters identifiable, we impose the scale constraint Σ_kγk(v)² = 1 and the orientation constraint γ_k0(v) > 0, with k₀ = arg max_k|γ_k(v)|. Assumption (2c) considerably reduces the number of HRF parameters from KL to K + L (the same modeling assumption is used in e.g., [Makni et al., 2005]), which allows one to use a reasonably large number of basis functions while maintaining a good estimation accuracy. On the other hand, the product form of (2c) makes model (1) nonlinear with respect to the parameters β_l(v) and γ_k(v). Note that the shape coe cients γ_k(v) are well defined only if at least one of the HRFs h_l(v,·) is not identically zero, that is, if at least one experimental condition induces an activation at voxel v.

The random effects ξ_jlk(v) in (2b) represent subject-specific deviations from the group-level HRF coefficients γ_lk(v). They are assumed to be independent across subjects and conditions. In addition they are assumed to be Gaussian random vectors with mean zero and correlation structure that is stationary in time and constant in space:

$$\mathrm{Cov}({\xi }_{jlk}\left(v\right),{\xi }_{j^{\prime }{l}^{\prime }{k}^{\prime }}\left(v\right))=\left({\delta }_{j{j}^{\prime }}{\delta }_{l{l}^{\prime }}\right){\sigma }_{\xi l}^2\left(v\right){\rho }_{\xi l}\left(\mid k-k^{\prime }\mid \right).$$ (3)

In the previous equation, ${\sigma }_{\xi l}^2\left(v\right)$ denotes the common variance of the ξ_jlk(v) (1 ≤ j ≤ n, 1 ≤ k ≤ K), ρξl is an autocorrelation function, and δ the Kronecker delta (δ_xy = 1 if x = y, δ_xy = 0 if x ≠ y). Note that ρξl(0) = 1.

To specify the dependence structure of the noise component ε, we consider a partition of the spatial domain $\mathcal{D}$ into neuro-anatomic parcels ${\mathcal{D}}_1,\dots ,{\mathcal{D}}_M$ (e.g., Brodmann areas or any suitable brain atlas). We assume that for each voxel v of a parcel ${\mathcal{D}}_m$, ε_j(v,·) is a stationary Gaussian AR(p) process whose variance ${\sigma }_{\epsilon m}^2$ and structural parameters θ_εm = (θ_ε1m, . . . , θ_εpm) only depend on m. In other words, ${\epsilon }_j(v,t)={\sum }_{k=1}^p{\theta }_{km}{\epsilon }_j(v,t-k)+e_j(v,t)$, where the e_j(v, t), 1 ≤ t ≤ N_j, are i.i.d. normal innovations. The specification of the noise dependence at the parcel level reflects the belief that this noise is spatially smooth. An alternative way to characterize the spatial smoothness of ε would be to model the AR parameters ${\sigma }_{\epsilon }^2$ and θ_ε as smooth functions of v.

Model Summary

For the j^th subject and v^th voxel, the BOLD time course y_j(v) = (y_j(v, 1), . . . , y_j(v, T_j))′ can be expressed in matrix form as

$${\mathbf{y}}_j\left(v\right)={\mathbf{X}}_j(\beta \left(v\right)\otimes \gamma \left(v\right))+{\mathbf{X}}_j{\xi }_j\left(v\right)+{\Phi }_j{\mathbf{d}}_j\left(v\right)+{\epsilon }_j\left(v\right).$$ (4)

As in the standard GLM, the design matrix X_j is the convolution of the stimulus functions s_jl with the basis functions B_k. To be precise, X_j = (X_j1, . . . , X_jL) with X_jl = (x_j1l, . . . , x_jkl) and ${\mathbf{x}}_{jkl}={({\int }_0^{\Delta }{B}_k\left(\tau \right)s_{jl}(\Delta -\tau )d\tau ,\dots ,{\int }_0^{{\tau }_j\Delta }{B}_k\left(\tau \right)s_{jl}(T_j\Delta -\tau )d\tau )}^{\prime }$. We have also written β(v) = (β₁(v), . . . , β_L(v))′ and γ(v) = (γ₁(v), . . . , γ_K(v))′ for the amplitude and scale parameters of the population-level HRF; ε(v) = (ε_j1(v)′)′, . . . , and ε_j1(v))′ for the subject-specific effects; Φ_j = (β_jv (t))1≤v≤q,1≤t≤T_j and d_j(v) = (d_j1(v), . . . , d_jq(v))′ for the nuisance signals; and ε_j(v) = (ε_j(v, 1), . . . , ε_j (v, T_j))′ for the noise. The symbol ⊗ denotes the Kronecker product.

The vector y_j(v) has a multivariate normal distribution with mean and covariance

$$\begin{array}{cc}\hfill {\mu }_j\left(v\right)=& {\mathbf{X}}_j(\beta \left(v\right)\otimes \gamma \left(v\right))+{\Phi }_j{\mathbf{d}}_j\left(v\right),\hfill \\ \hfill {\mathbf{V}}_j\left(v\right)=& {\mathbf{X}}_j({\mathbf{D}}_{\xi }\left(v\right)\otimes {\mathbf{I}}_K){\mathbf{T}}_{\xi }{\mathbf{X}}_j^{\prime }+{\mathbf{V}}_{\epsilon jm},\hfill \end{array}$$ (5)

where ${\mathbf{D}}_{\xi }\left(v\right)=\mathrm{diag}({\sigma }_{\xi 1}^2\left(v\right),\dots ,{\sigma }_{\xi L}^2\left(v\right))$, T_ξ = diag(T_ξ1, . . . , T_ξL) is a block diagonal matrix with T_ξl = (ρξl(|k — k′|)_{1≤k,k′≤K}, I_K is the K × K identity matrix, and V_ξjm is the covariance matrix of ξ_j(v) for $v\in {\mathcal{D}}_m$. Here the first term of V_j(v) corresponds to between-subject variation, while the second term is the within-subject variation.

Table 1 summarizes all model notations.

Table 1.

Notations

j	Subject index
k	Basis function index
l	Condition index
v	Voxel index
n	Sample size
K	Number of basis functions
L	Number of experimental conditions
V	Number of voxels
Bk	Basis function
Tj	Number of brain scans for subject j
yj(v)	fMRI time course for subject j at voxel v
X j	Design matrix for subject j
X jl	Design matrix for subject j, condition l
β(v)	Amplitude parameters for the population HRF at voxel v
γ(v)	Shape parameters for the population HRF at voxel v
ξj(v)	Deviation of subject j from population HRF at voxel v
ξ jl(v)	Deviation of subject j from population HRF for condition l and voxel v
Φ j	Matrix of nuisance signals for subject j
dj (v)	nuisance coefficients for subject j and voxel v
εj(v)	Noise vector for subject j at voxel v
Dξ(v)	Variance coefficients of subject effects at voxel v
T ξ	Correlation matrix for subject effects at voxel v
T ξl	Correlation matrix for subject effects for condition l and voxel v
V εjm	Covariance matrix of the noise for subject j and parcel m
Vj (v)	Covariance matrix of yj (v)

2.2 Estimation

In this section we outline our procedure for estimating the parameters of our model. Our main objective is to estimate the population HRF at each voxel while taking into account the covariance structure of the data. We formulate this objective mathematically as a generalized, penalized, and constrained least squares problem. Since the corresponding objective function is non-convex, our procedure is only guaranteed to yield a local minimum. It is therefore important to select good starting values for the procedure, which we do by constructing a consistent pilot estimator of the HRF. We then provide consistent estimators of the data covariance parameters, after which we optimize the objective function to obtain the final HRF estimates. The entire procedure is performed in the following five steps, each described in detail in a subsequent subsection:

1. For each voxel v, estimate the HRF parameters γ_kl(v) by Penalized Least Squares (PLS). This pilot estimation does not exploit the HRF shape assumption (2c) and does not account for the covariance structure of the data.

2. For each parcel ${\mathcal{D}}_m$, estimate the parameters ${\sigma }_{\epsilon m}^2$ and θ_εm of the AR noise process ε by solving the Yule-Walker equations associated with the predicted errors ${\widehat{\epsilon }}_j\left(v\right)$. The $\widehat{\epsilon }\left(v\right)$ are obtained from a least squares fit on the residuals of step 1.

3. Estimate the temporal correlation parameters ρ_ξl(k) of the subject random effects by Maximum Likelihood (ML). The ML estimates are obtained separately on a small sample of voxels and pooled with a suitable statistic (e.g., trimmed mean or median).

4. For each voxel v, estimate the between-subject variance ${\sigma }_{\xi }^2\left(v\right)$ by Variance Least Squares (VLS).

5. For each voxel v, estimate β(v) and γ(v) again using a generalized, penalized, and constrained least squares approach.

Step 1: Pilot estimation of the HRF

For each voxel v, the HRF scale and shape coe cients β(v) and γ(v) are first estimated by penalized least squares (PLS):

$$\underset{\mathbf{h},\mathbf{d}}{\min }\left\{\sum _{j=1}^n{\Vert {\mathbf{y}}_j\left(v\right)-{\mathbf{X}}_j\mathbf{h}-{\Phi }_j{\mathbf{d}}_j\Vert }^2+n{\lambda }_0{\mathbf{h}}^{\prime }({\mathbf{I}}_L\otimes \mathbf{P})\mathbf{h}\right\},$$ (6)

where h is a vector of length KL that estimates the HRF coefficients γ_lk(v) and d = (d′₁, . . . , d′_n)′ is a vector of length nq that estimates the nuisance signals. The matrix P penalizes departures of h from a linear space of “reasonable” HRFs (e.g., the canonical HRF and its temporal derivative). More precisely, let Ψ be a matrix whose columns contain the coefficients of a few realistic HRFs in the function basis (B_k)_1≤k≤K. Then P = I_K — Ψ(Ψ′Ψ)^–1Ψ′ is the projection on the orthogonal space of Ψ. The smoothing parameter λ₀ > 0 determines the tradeof between fitting the data and closeness to Ψ. It can be selected manually or, for example, by k-fold cross-validation with the subjects randomly partitioned in k subsamples.

Note that the minimization problem (6) is unconstrained and does not rely on (2c). Its solutions are $\widehat{\mathbf{h}}\left(v\right)={({\sum }_{j=1}^n{\mathbf{X}}_j^{\prime }{\mathbf{R}}_j{\mathbf{X}}_j+n{\lambda }_0({\mathbf{I}}_L\otimes \mathbf{P}))}^{-1}{\sum }_{j=1}^n{\mathbf{X}}_j^{\prime }{\mathbf{R}}_j{\mathbf{y}}_j\left(v\right)$ and ${\widehat{\mathbf{d}}}_j\left(v\right)={\left({\Phi }_j^{\prime }{\Phi }_j\right)}^{-1}{\Phi }_j^{\prime }({\mathbf{y}}_j\left(v\right)-{\mathbf{X}}_j\widehat{\mathbf{h}}\left(v\right))$, 1 ≤ j ≤ n, where ${\mathbf{R}}_j={\mathbf{I}}_T-{\Phi }_j{\left({\Phi }_j^{\prime }{\Phi }_j\right)}^{-1}{\Phi }_j^{\prime }$ is the projection matrix on the orthogonal space of Φ_j. The estimator ĥ(v) is consistent and asymptotically unbiased for the γ_lk(v) as the sample size n → ∞ and the smoothing parameter λ₀ → 0. In view of (2c), it follows that ${\widehat{\beta }}_0\left(v\right)={(\Vert {\widehat{\mathbf{h}}}_1\left(v\right)\Vert ,\dots ,\Vert {\widehat{\mathbf{h}}}_L\left(v\right)\Vert )}^{\prime }$ is a consistent estimator of β(v), where ĥ(v) = (ĥ₁(v)′,..., ĥ_L(v)′)′ and the vectors ĥ_l(v), 1 ≤ l ≤ L, have length K. Similarly, the scaled average ${\widehat{\gamma }}_0\left(v\right)={\sum }_{l=1}^L{\widehat{\mathbf{h}}}_l\left(v\right)∕\Vert {\sum }_{l=1}^L{\widehat{\mathbf{h}}}_l\left(v\right)\Vert$ consistently estimates γ(v) when the latter is well-defined, i.e., when the voxel v is activated by at least one experimental condition.

Step 2: Estimation of the noise structure

We turn to the estimation of the noise parameters ${\sigma }_{\epsilon m}^2$ and θ_εm in each parcel ${\mathcal{D}}_m$, 1 ≤ m ≤ M. For each subject 1 ≤ j ≤ n and voxel $v\in {\mathcal{D}}_m$, consider the residual vector ${\mathbf{r}}_j\left(v\right)={\mathbf{y}}_j\left(v\right)-{\mathbf{X}}_j({\widehat{\beta }}_0\left(x\right)\otimes {\widehat{\gamma }}_0\left(v\right))-{\Phi }_j\widehat{\mathbf{d}}\left(v\right)={\mathbf{R}}_j({\mathbf{y}}_j\left(v\right)-{\mathbf{X}}_j({\widehat{\beta }}_0\left(x\right)\otimes {\widehat{\gamma }}_0\left(v\right)))$ resulting from step 1. Given (4) and the consistency of ĥ = ĥ(v) in step 1, it holds that r_j(v) ≈ X_jξ_j + ε_j(v) for n large enough and λ₀ small. The random effects ξ_j(v) and ε_j(v) can thus be predicted by least squares based on r_j(v), yielding

$${\widehat{\xi }}_j\left(v\right)={\left({\mathbf{X}}_j^{\prime }{\mathbf{X}}_j\right)}^{-1}{\mathbf{X}}_j^{\prime }{\mathbf{r}}_j\left(v\right),{\widehat{\epsilon }}_j\left(v\right)={\mathbf{r}}_j\left(v\right)-{\mathbf{X}}_j{\widehat{\xi }}_j\left(v\right).$$

If the design matrix X_j is not full rank, the inverse ${\left({\mathbf{X}}_j^{\prime }{\mathbf{X}}_j\right)}^{-1}$ in the above formula is not defined and can be replaced by its pseudoinverse ${\left({\mathbf{X}}_j^{\prime }{\mathbf{X}}_j\right)}^{+}$. We then solve the Yule-Walker equations (see e.g., [Brockwell and Davis, 2006, p. 239]) associated with ${\widehat{\epsilon }}_j\left(v\right)$, producing consistent estimates of ${\sigma }_{\epsilon m}^2$ and θ_εm for each subject 1 ≤ j ≤ n and voxel $v\in {\mathcal{D}}_m$. By taking the medians of these estimates across subjects and voxels, we obtain robust estimates ${\widehat{\sigma }}_{\epsilon m}^2$ and ${\widehat{\theta }}_{\epsilon m}$.

Step 3: Estimation of the temporal dependence in subject-specific effects

We estimate the temporal correlation parameters ρ_ξl(k), 1 ≤ k ≤ K — 1, 1 ≤ l ≤ L, by Maximum Likelihood (ML). For computational efficiency, ML estimates are separately produced at a small number of voxels and aggregated with a suitable statistic such as the median or trimmed mean. In practice, we propose to select a random sample of about 1000 voxels for the ML estimation. Following a common usage, we first perform a few iterations of the EM algorithm to provide good starting values for the optimization of the likelihood function.

In the rest of this section, we fix a voxel and omit ther index v for conciseness. Writing ${\sigma }_{\xi }^2={({\sigma }_{\xi 1}^2,\dots ,{\sigma }_{\xi L}^2)}^{\prime }$ and ρξ = (ρξ1(1), ρξ1(2), . . . , ρξL(K − 1))′, we optimize the log-likelihood function (multiplied by −2)

$$L(\beta ,\gamma ,\mathbf{d},{\sigma }_{\xi }^2,{\rho }_{\xi },{\sigma }_{\epsilon m}^2,{\theta }_{\epsilon m})=\sum _{j=1}^n\ln \mid {\mathbf{V}}_j\mid +\sum _{j=1}^n{({\mathbf{y}}_j-{\mathbf{X}}_j(\beta \otimes \gamma )-{\Phi }_j{\mathbf{d}}_j)}^{\prime }{\mathbf{V}}_j^{-1}({\mathbf{y}}_j-{\mathbf{X}}_j(\beta \otimes \gamma )-{\Phi }_j{\mathbf{d}}_j)$$ (7)

with respect to ${\sigma }_{\xi }^2$ and ρ_ξ while fixing β, γ, d, ${\sigma }_{\epsilon m}^2$, and θ_εm to their previously estimated values. Note that although we are only concerned here with the estimation of ρ_ξ, the likelihood must also be optimized with respect to ${\sigma }_{\xi }^2$. These variance parameters, which must be estimated at each voxel, will be assessed more e ciently in step 4. The implementation of the EM algorithm and likelihood optimization is described in Appendix A. More details on the EM algorithm for linear mixed models can be found in e.g., ([Pawitan, 2001], chap. 12).

Step 4: Estimation of the between-subjects variance

For each voxel v, we estimate the between-subjects variances ${\sigma }_{\xi }^2\left(v\right)$ by a variance least squares approach (e.g., [Demidenko, 2004], chap. 3) that consists of minimizing the distance between the residual covariance matrix and the theoretical covariance matrix:

$$\underset{{\sigma }_{\xi }^2}{\min }\sum _j{\Vert {\mathbf{r}}_j\left(v\right){\mathbf{r}}_j^{\prime }\left(v\right)-{\mathbf{X}}_j({\mathbf{D}}_{\xi }\left(v\right)\otimes {\mathbf{I}}_K){\widehat{\mathbf{T}}}_{\xi }{\mathbf{X}}_j^{\prime }-{\widehat{\mathbf{V}}}_{\epsilon jm}\Vert }_F^2$$ (8)

subject to the constraint ${\sigma }_{\xi l}^2\ge 0$ for 1 ≤ l ≤ L. Recall that the residuals r_j(v) are defined in step 2 of this section, ${\mathbf{D}}_{\xi }=\mathrm{diag}({\sigma }_{\xi 1}^2,\dots ,{\sigma }_{\xi L}^2)$, and V̂_εjm and T̂_ξ are the estimates of V_ξjm and T_ξ obtained in steps 2-3. The notation ∥A∥_F stands for the Frobenius norm tr(A′ A)^1/2 of a matrix A. Problem (8) is a standard quadratic programming problem that expressed more simply as

$$\underset{{\sigma }_{\xi }^2}{\min }\left\{{\left({\sigma }_{\xi }^2\right)}^{\prime }\mathbf{A}{\sigma }_{\xi }^2-2{\mathbf{b}}^{\prime }{\sigma }_{\xi }^2\right\},$$ (9)

where A is a L × L matrix with (l,l′) entry ${\sum }_{j=1}^n\mathrm{tr}({\mathbf{X}}_{jl}{\widehat{\mathbf{T}}}_{\xi l}{\mathbf{X}}_{jl}^{\prime }{\mathbf{X}}_{j{l}^{\prime }},{\widehat{\mathbf{T}}}_{\xi l^{\prime }}{\mathbf{X}}_{j{l}^{\prime }}^{\prime })$ and b is vector of length L with l^th entry ${\sum }_{j=1}^n\{{\mathbf{r}}_j^{\prime }\left(v\right){\mathbf{X}}_{jl}{\widehat{\mathbf{T}}}_{\xi l}{\mathbf{X}}_{jl}^{\prime }{\mathbf{r}}_j\left(v\right)-\mathrm{tr}\left({\widehat{\mathbf{T}}}_{\xi l}{\mathbf{X}}_{jl}^{\prime }{\widehat{\mathbf{V}}}_{\epsilon jm}{\mathbf{X}}_{jl}\right)\}$. The solutions to (8)-(9) can be computed by various methods (e.g., [Nocedal and Wright, 2006], p. 449) that are widely available in software packages.

Step 5: Generalized least squares estimation of the HRF

The pilot estimation of the HRF can be improved upon in two ways: (i) by accounting for the dependence structure of the BOLD signal, and (ii) by imposing the form (2c) to the HRF estimates. To integrate these features in the estimation, we use a penalized, constrained, generalized least squares approach. For a given voxel v, let ${\widehat{\mathbf{V}}}_j\left(v\right)={\mathbf{X}}_j({\widehat{\mathbf{D}}}_{\xi }\left(v\right)\otimes {\mathbf{I}}_K){\widehat{\mathbf{T}}}_{\xi }{\mathbf{X}}_j^{\prime }+{\widehat{\mathbf{V}}}_{\epsilon jm}$ be the estimate of V_j(v) resulting from steps 1-4. We seek to solve

$$\underset{\beta ,\gamma ,\mathbf{d}}{\min }\left\{\sum _{j=1}^n{\Vert {\mathbf{y}}_j\left(v\right)-{\mathbf{X}}_j(\beta \otimes \gamma )-{\Phi }_j{\mathbf{d}}_j\Vert }_{{\widehat{\mathbf{v}}}_j^{-1}\left(v\right)}^2+n\lambda {\gamma }^{\prime }\mathbf{P}\gamma \right\}$$ (10)

under the constraint ∥k∥² = 1. Like in the pilot estimation, the nuisance parameter d can be eliminated from (10). To that intent, let ${\tilde{\mathbf{R}}}_j\left(v\right)={\mathbf{I}}_T-{\Phi }_j{\left({\Phi }_j^{\prime }{\widehat{\mathbf{V}}}_j^{-1}\left(v\right){\Phi }_j\right)}^{-1}{\Phi }_j^{\prime }{\widehat{\mathbf{V}}}_j^{-1}\left(v\right)$ be the projection matrix on the orthogonal space of Φ_j in the metric ${\widehat{\mathbf{V}}}_j^{-1}\left(v\right)$. Then (10) is equivalent to ${\min }_{\beta ,\gamma }\{{\sum }_{j=1}^n{\Vert {\tilde{\mathbf{R}}}_j\left(v\right){\mathbf{y}}_j\left(v\right)-{\tilde{\mathbf{R}}}_j\left(v\right){\mathbf{X}}_j(\beta \otimes \gamma )\Vert }_{{\widehat{\mathbf{V}}}_j^{-1}\left(v\right)}^2+n\lambda {\gamma }^{\prime }\mathbf{P}\gamma \}$.

Because of the tensor product $\beta \otimes \gamma$ and the quadratic constraint ∥γ∥² = 1, problem (10) is nonlinear and has no closed-form solutions. However, (10) is a separable least squares problem: for a fixed γ, solving (10) with respect to βreduces to a generalized least squares problem that admits a closed-form solution. For a fixed β, solving (10) with respect to γ is a quadratically constrained quadratic program that requires little more than a singular value decomposition. As a result, (10) can be e ciently solved in an iterative way.

For conciseness, we omit the index v from notations in the remainder of the section. Let $\mathrm{M}={\sum }_{j=1}^n{\mathbf{X}}_j^{\prime }{\tilde{\mathbf{R}}}_j^{\prime }{\widehat{\mathbf{V}}}_j^{-1}{\tilde{\mathbf{R}}}_j{\mathbf{X}}_j$ and $\eta ={\sum }_{j=1}^n{\mathbf{X}}_j^{\prime }{\widehat{\mathbf{V}}}_j^{-1}{\tilde{\mathbf{R}}}_j{\mathbf{y}}_j$. The solutions $\widehat{\beta }$ and $\widehat{\gamma }$ of (10) are obtained by cycling through the following equations until convergence:

$$\widehat{\beta }={\left[{({\mathbf{I}}_L\otimes \widehat{\gamma })}^{\prime }\mathrm{M}({\mathbf{I}}_L\otimes \widehat{\gamma })\right]}^{-1}{({\mathbf{I}}_L\otimes \widehat{\gamma })}^{\prime }\eta ,$$ (11)

$$\widehat{C}=\underset{C}{\arg \min }\left\{{\eta }^{\prime }(\widehat{\beta }\otimes {\mathbf{I}}_K){\left[{(\widehat{\beta }\otimes {\mathbf{I}}_K)}^{\prime }\mathrm{M}(\widehat{\beta }\otimes {\mathbf{I}}_K)+n\lambda \mathbf{P}+{C_I}_K\right]}^{-1}{(\widehat{\beta }\otimes {\mathbf{I}}_K)}^{\prime }\eta +C\right\},$$ (12)

$$\widehat{\gamma }={[{(\widehat{\beta }\otimes {\mathbf{I}}_K)}^{\prime }\mathbf{M}(\widehat{\beta }\otimes {\mathbf{I}}_K)+n\lambda \mathbf{P}+\widehat{C}{\mathbf{I}}_K]}^{-1}{(\widehat{\beta }\otimes {\mathbf{I}}_K)}^{\prime }\eta ,$$ (13)

with $\widehat{\gamma }$ initially set to the pilot estimator ${\widehat{\gamma }}_0$. Equation (11) corresponds to the generalized least squares problem that updates $\widehat{\beta }$ for a given $\widehat{\gamma }$. Equations (12)-(13) correspond to the quadratically constrained quadratic program that updates $\widehat{\gamma }$ for a given $\widehat{\beta }$ using the method of Lagrange multipliers. The Lagrange multiplier Ĉ is computed by performing the singular value decomposition of ${(\widehat{\beta }\otimes {\mathbf{I}}_K)}^{\prime }\mathrm{M}(\widehat{\beta }\otimes {\mathbf{I}}_K)+n\lambda \mathbf{P}$ and numerically finding the root of a monotone function (see e.g., [Golub and Van Loan, 2013, chap. 6] for details).

2.3 Inference

In this section we discuss the sampling distribution of the HRF estimates and illustrate how to perform inference on model parameters. As before, we omit the voxel index v from notations for conciseness. Recall that for a given voxel, the HRF shape parameter γ is well defined only if at least one condition induces an activation in the voxel. Under this assumption, for a sufficiently large sample size n and sufficiently small smoothing parameter γ, the sampling distributions of $\widehat{\beta }$ and $\widehat{\gamma }$ can be respectively approximated by $N(\beta ,{\left[{({\mathbf{I}}_L\otimes \gamma )}^{\prime }\mathrm{M}({\mathbf{I}}_L\otimes \gamma )\right]}^{-1})$ and $N(\gamma ,{\left[{(\beta \otimes {\mathbf{I}}_K)}^{\prime }\mathrm{M}(\beta \otimes {\mathbf{I}}_K)\right]}^{-1})$, where the matrices V̂_j are replaced by the true covariances V_j in M and where N(μ,Σ) denotes the multivariate normal distribution with mean μ and covariance matrix Σ. Further, neglecting the uncertainty about γ (and about the covariance matrices V_j) in the estimation of β and vice-versa, we obtain

$$\begin{array}{cc}\hfill \widehat{\beta }\approx & N\left(\beta ,{\left[{({\mathbf{I}}_L\otimes \widehat{\gamma })}^{\prime }\mathrm{M}({\mathbf{I}}_L\otimes \widehat{\gamma })\right]}^{-1}\right),\hfill \\ \hfill \widehat{\gamma }\approx & N\left(\gamma ,{[{(\widehat{\beta }\otimes {\mathbf{I}}_K)}^{\prime }\mathrm{M}(\widehat{\beta }\otimes {\mathbf{I}}_K)}^{-1}\right).\hfill \end{array}$$ (14)

The first result allows us to perform inference to detect activation, as is commonly performed in the GLM setting. The second results allows us to test hypotheses regarding the shape of the HRF. For example, after computing the values of γ that correspond to the canonical the HRF,we could test for deviations in the shape across brain based on the fact that ${(\widehat{\gamma }-\gamma )}^{\prime }{\left[{(\beta \otimes {\mathbf{I}}_K)}^{\prime }\mathrm{M}(\widehat{\beta }\otimes {\mathbf{I}}_K)\right]}^{-1}(\widehat{\gamma }-\gamma )$ follows a χ² distribution with K degrees of freedom. A theoretical justification of (14) is provided in Appendix B.

Recall that the above inference procedures rely on the assumption that the voxel under study is activated in at least one condition (otherwise γ is not well defined). This assumption amounts to the fact that at least one of the unconstrained HRF coefficients γ_lk is not zero. It can easily be tested using the pilot estimator ĥ of the γ_lk defined in (6). More precisely, ĥ has a normal distribution with asymptotic bias zero and asymptotic variance ${\left({\sum }_{j=1}^n{\mathbf{X}}_j^{\prime }{\mathbf{R}}_j{\mathbf{X}}_j\right)}^{-1}\left({\sum }_{j=1}^n{\mathbf{X}}_j^{\prime }{\mathbf{R}}_j{\mathbf{V}}_j{\mathbf{R}}_j{\mathbf{X}}_j\right){\left({\sum }_{j=1}^n{\mathbf{X}}_j^{\prime }{\mathbf{R}}_j{\mathbf{X}}_j\right)}^{-1}$ for large n and small λ₀. If the null hypothesis γ_lk = 0 for all k, l fails to be rejected, then no further inference should be performed for this voxel. Another sensible approach is to use (14) first to test for activations in all voxels and then to infer the HRF shape in activated voxels.

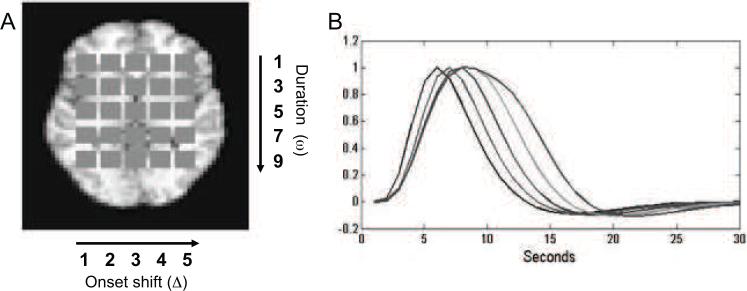
2.4 Simulations

The basic framework for this simulation study is similar to the one found in Lindquist et al. (2008), where a number of different HRF modeling approaches were evaluated. Inside a static brain slice, with dimensions 51 × 40, a set of 25 identically sized squares, with dimensions 4 × 4, were placed to represent active regions (see Fig. 1A). Within each square, we simulated BOLD fMRI signal based on different stimulus functions, which varied systematically across the squares in terms of onset and duration. From left to right the onset of activation varied from the first to the fifth TR. From top to bottom, the duration of activation varied from one to nine TRs in steps of two. To create the response, we convolved the stimulus function in each square with SPMs canonical HRF, using a modified nonlinear convolution that includes an exponential decay to account for refractory effects with stimulation across time, with the net result that the BOLD response saturates with sustained activity in a manner consistent with observed BOLD responses (Wager et al., 2005). This procedure gave rise to a set of 25 distinct HRF shapes. Fig. 1B shows examples of the 5 HRFs with no onset shift, which are representative of the remaining HRFs.

Figure 1.

Overview of simulation set-up (A) A set of 25 equally sized squares were placed within a static brain image to represent regions of interest. BOLD signals were simulated based on different stimulus functions, which varied systematically across the squares in their onset and duration of neuronal activation. From left to right the onset of activation varied between the squares from the first to the fifth TR. From top to bottom, the duration of activation varied from one to nine TR in steps of two. (B) The five HRFs with varying duration. The plot illustrates di erences in time-to-peak and width attributable to changes in duration.

In total we performed five simulation studies in order to evaluate the properties of the proposed model. Below follows a description of each.

Simulation 1

In this simulation the TR was assumed to be 1s long and the inter-stimulus interval was set to 30s. This activation pattern was repeated to simulate a total of 10 epochs. To simulate a sample of subjects and group random-effects, we generated 15 subject datasets, which consisted of the BOLD time series at each voxel plus white noise, creating a plausible e ect size (Cohen's d= 0.5) based on observed e ect sizes in the visual and motor cortex (Wager et al., 2005). The value of ${\sigma }_{\epsilon }^2$ was set to 3. In addition, a random between-subject variation with a standard deviation of size one third of the within-subject variation was added to each subject's time course.

Simulation 2

The second simulated data set was constructed in precisely the same manner as outlined in Simulation 1, except here instead of using white noise to simulate within-subject variation we used an AR(1) noise process with θ_ε = 0.3.

Simulation 3

The third simulated data set was constructed, using the exact same process with AR(1) noise described in Simulation 2, expect here instead of using SPMs canonical HRF we used a subject-specific HRF. These were randomly generated using 20 B-spline basis sets with weights drawn from a normal distribution with mean equal to the weights corresponding to the canonical HRF and standard deviation 0.1.

Simulation 4

The fourth simulated data set was constructed in precisely the same manner as outlined in Simulation 1, except here we allowed for two separate conditions. For both conditions the inter-stimulus interval was set to 30s and the activation pattern was repeated to simulate a total of 10 epochs. However, the two conditions were interleaved to begin 15s apart from one another. The β value for the two conditions were set to 0.5 and 1, respectively. All other parameters were set according to the description of Simulation 1.

Simulation 5

The fifth simulated data set was constructed in precisely the same manner as outlined in Simulation 1, except here we used a fast event-related design. The inter-stimulus interval was randomized across each trial using a uniform distribution between 10 and 20s. All other parameters were set according to the description of Simulation 1.

For each of the five simulations, the basic data sets of dimensions 51 × 40 × 300 were fit voxel-wise using both using the standard GLM/OLS approach and our proposed hierarchical approach. For Simulations 1-3 an event-related stimulus function with a single spike repeated every 30s was used for fitting the models to the data set described above. For Simulation 4 this was supplemented by a second stimulus function with a single spike repeated every 30s corresponding to the timing of the second condition. Finally, in Simulation 5 we used a stimulus function with a single spike repeated according to the outcomes of the randomization scheme outlined above.

This implies that for each simulation the square in the upper left-hand corner of Fig. 1A is correctly specified for the standard GLM while the remaining squares have activation profiles that are mis-specified to various degrees. When fitting our method we used 20 B-spline basis functions of order 6. While our proposed method provides multi-subject estimates and a framework for direct inference on these parameters, the standard OLS (ordinary least squares) approach to multi-subject analysis in fMRI involves using a two-stage model. It begins by fitting individual regression coefficients for each subject using a standard GLM. Thereafter group estimates of the parameters are obtained by averaging across subjects and variance components are obtained by computing the variance of the estimates across subjects. Since this analysis is performed on the estimated regression coefficients, the variance will contain contributions from both the standard error of the estimates and the between-subject variance components. This method is the most popular method in the neuroimaging community for estimating the parameters of a mixed-e ects model [Mumford and Nichols, 2009].

After estimation we performed population level inference to determine whether β was significantly different from 0. In each case we performed a one-sided test. In order to control for multiple comparisons we used an FDR-controlling procedure with q = 0.05 [Genovese et al., 2002].

2.5 Experimental Data

All subjects (n = 20) provided informed consent in accord with the Declaration of Helsinki, and the Columbia University Institutional Review Board approved all procedures. Subjects were all right-handed, as assessed by the Edinburgh Handedness Inventory, and free of self-reported history of psychiatric and neurological disorders, excessive ca eine or nicotine use, and illicit drug use. They were pre-screened during an initial calibration session to ensure that stimuli were painful and that they could rate pain reliably (r ≥ .65) between applied temperature and pain rating). During fMRI scanning, 48 thermal stimuli, 12 at each of 4 temperatures, were delivered to the left forearm using a Peltier device (TSA-II, Medoc, Inc.) with an fMRI-compatible 1.5 mm-diameter thermode. Temperatures were calibrated individually for each participant before scanning to be warm, mildly painful, moderately painful, and near tolerance. Heat stimuli were preceded by a 2s warning cue and 6s anticipation period, lasted 10s in duration (1.5s ramp up/down, 7s at peak), and were followed by a 30s inter-trial interval (ITI). At a time 14s into the ITI, participants were asked to rate the painfulness of the stimulus on an 8-point visual analogue scale using an fMRI-compatible trackball (Resonance Technologies, Inc.). Functional T2*-weighted EPI-BOLD images (TR = 2s, 3.5 × 3.5 × 4mm voxels, ascending interleaved acquisition) were collected during 6 functional runs each consisting of 6 minutes 8s. Images were corrected for slice-timing acquisition delay and realigned to adjust for head motion using SPM5 software (http://www.fil.ion.ucl.ac.uk/spm/). A high-resolution anatomical image (T1-weighted spoiled-GRASS [SPGR] sequence, 1 × 1 × 1mm voxels, TR = 19ms) was collected after the functional runs and coregistered to the mean functional image using a mutual information cost function (SPM5, with manual checking and adjustment of starting values to ensure satisfactory alignment for each participant), and was then segmented and warped to the Montreal Neurologic Institute template (avg152T1.nii) using SPM5's “generative” segmentation [Ashburner and Friston, 2005]. Warps were applied to functional images. Functional images were smoothed with a 6 mm-FWHM Gaussian kernel, high-pass filtered with a 120s (.0083 Hz) discrete cosine basis set (SPM5), and windsorized at 2 standard deviations prior to analysis. Each of the models described above was fit to data from each voxel in a single axial slice (z = −22mm) that covered several pain-related regions of interest, including the anterior cingulate cortex. Separate HRFs were estimated for stimuli of each temperature, though we focus on the responses to the highest heat level in the results.

We fit the data using our proposed hierarchical approach with 12 B-spline basis functions of order 6. As the fMRI data consisted of 6 functional runs for each subject, we combined the results across runs in a manner corresponding to a fixed-effects model, assuming the same HRF for all runs for a given subject and voxel. As an alternative it would be possible to extend our model to allow β to be a random effect across runs in a manner analogous to that outlined in [Badillo et al., 2013b]. After estimation we performed population level inference to determine whether β was significantly different from 0. In each case we performed a one-sided test. In order to control for multiple comparisons we used an FDR-controlling procedure with q = 0.05 [Genovese et al., 2002].

3 RESULTS

3.1 Simulations

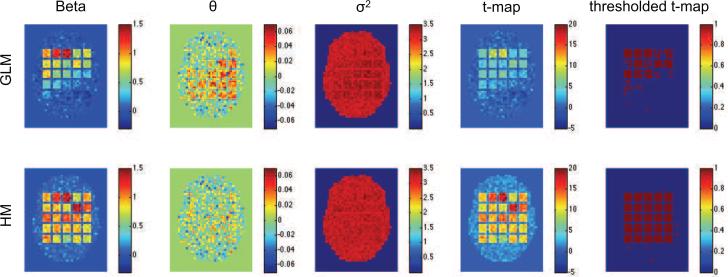
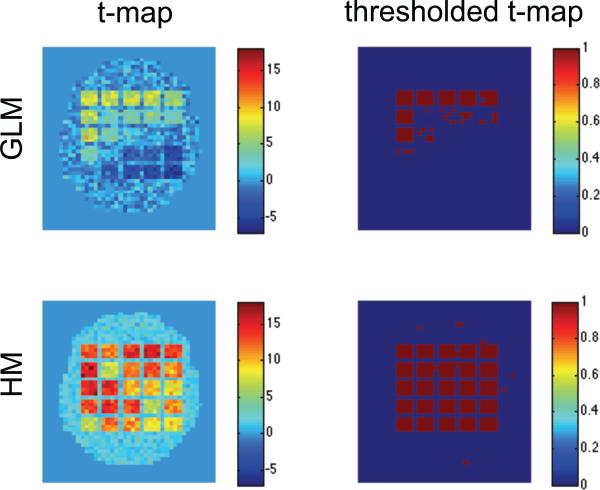
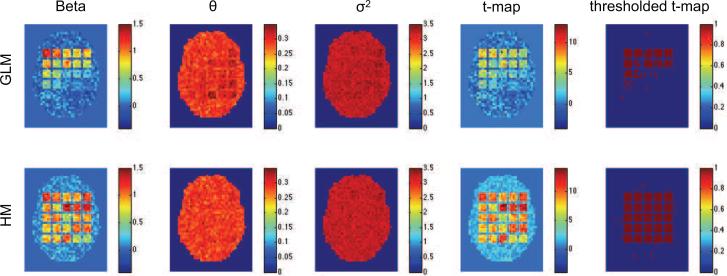
Figs. 2-4 show results of the first three simulation studies. Each contains estimates of β, θ_ε, ${\sigma }_{\epsilon }^2$, the t-map, and the thresholded t-map, obtained using both the standard GLM/OLS approach and our hierarchical model. In each case, GLM/OLS (first row) gives reasonable results for delayed onsets within 3s and widths up to 3s, corresponding to squares in the upper left-hand corner. However, its performance worsens dramatically as onset and duration increase. As pointed out in Lindquist et al. (2008) this is natural as the GLM is correctly specified for the square in the upper left-hand corner, but not well equipped to handle large deviations from this model. Interestingly, in Fig. 2 we see that this model misspecification gives rise to a positive autocorrelation in several of the most severely effected squares, even though we used white noise in that particular simulation.

Figure 2.

Results of the first simulation shown for the standard GLM/OLS approach (top row), and our hierarchical model (bottom row). From left-to-right the columns represent the estimated values of β, θ_ε, ${\sigma }_{\epsilon }^2$, t-map and thresholded t-map.

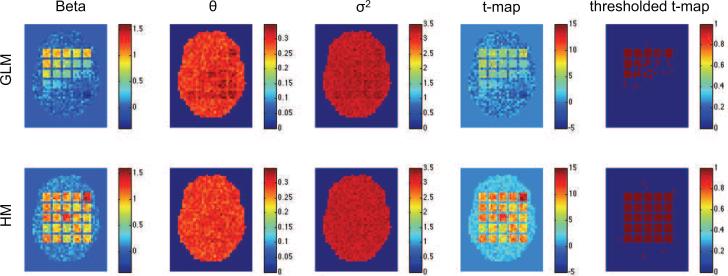
Figure 4.

Results of the third simulation shown for the standard GLM/OLS approach (top row), and our hierarchical model (bottom row). From left-to-right the columns represent the estimated values of β, θ_ε, ${\sigma }_{\epsilon }^2$, t-map and thresholded t-map.

Almost all of these problems are solved using our hierarchical model. Clearly, irrespective of the shape of the underlying HRF we were able to efficiently recover both β and the variance component in each square. Clearly, these improved estimations lead to significantly improved sensitivity and specificity in the population-level hypothesis tests.

The results of Simulation 4 are shown in Fig. 5. Here the first column contains the t-map corresponding to the test of whether the contrast, β₁ − β₂, between the parameters of the two conditions was significantly different from zero, while the second column shows the analogous thresholded t-maps. Again, our hierarchical model is able to detect significant regions with both high sensitivity and specificity. In contrast, the GLM/OLS approach performs poorly, even in the upper-left hand corner where it is expected to be optimal.

Figure 5.

Results of the fourth simulation shown for the standard GLM/OLS approach (top row), and our hierarchical model (bottom row). From left-to-right the columns represent the estimated and thresholded t-map for testing whether the contrast between the two conditions was significantly different from 0.

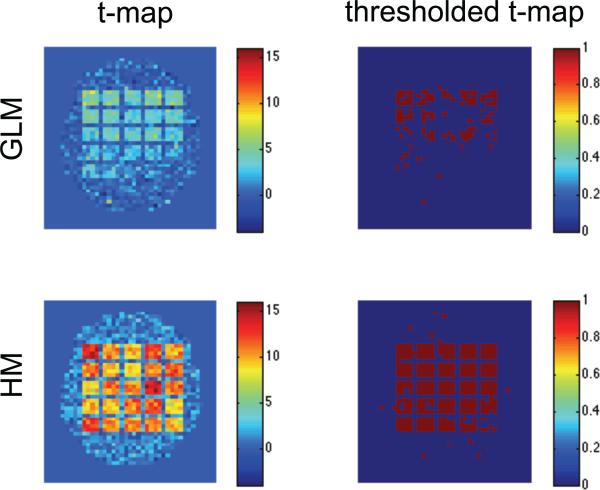
Fig. 6 shows results for Simulation 5 where we used a rapid event-related task. The first column contains the t-map corresponding to testing whether the parameter β was significantly different from zero, and the second column corresponds to the thresholded t-maps. The GLM/OLS approach performs somewhat better than in the other simulations, perhaps due to the increased number of trials. However, our hierarchical model is again able to detect significant regions with both a high degree of sensitivity and specificity.

Figure 6.

Results of the fifth simulation shown for the standard GLM/OLS approach (top row), and our hierarchical model (bottom row). From left-to-right the columns represent the estimated and thresholded t-map.

To illustrate further, we see in Fig. 7 the results of 100 replications of the first simulation. Fig. 7A shows the portion of times the standard GLM/OLS approach gave significant results in each voxel across the simulated brain. Fig. 7B shows the same results for our hierarchical model. Clearly, our hierarchical model is able to consistently detect truly activated regions, while avoiding spurious findings. Not surprisingly, the GLM/OLS approach only performs well in squares where it is correctly defined. Fig 7C shows the portion of times the estimated HRF significantly deviated from SPMs canonical form (α < 0.05). This test was performed by first computing values of γ corresponding to the canonical HRF and thereafter using the χ² test described in Section 2.3. The results show, again not surprisingly, that the HRF in voxels in the lower right-hand corner of the brain deviate significantly from the canonical form. Interestingly, these voxels corresponds closely to voxels that were erroneously deemed non-active in Fig. 7A. This leads us to believe that our approach could have an alternative use as a diagnostic tool for assessing the performance of standard GLM analyses.

Figure 7.

The results of 100 replications of the first simulation. (A) The portion of times the standard GLM/OLS approach gave significant results in each voxel. (B) The same results for our hierarchical model. Clearly the hierarchical model is able to effectively separate signal from noise in a more consistent manner than the GLM/OLS. (C) The portion of times the estimated HRF deviated from the canonical form using our model.

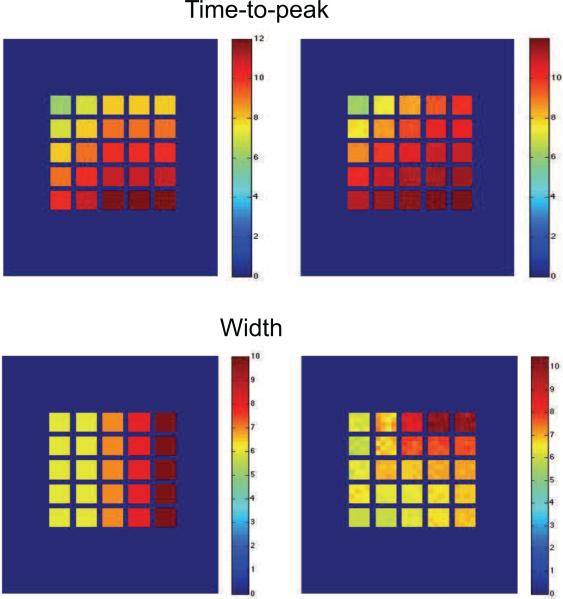
Fig 8 shows the methods ability to recover the time-to-peak and width of the underlying HRF used to generate the data. The left hand column shows the true values and the right hand columns the mean estimated values across the 100 replications. Clearly we are able to extremely accurately capture the true value of the time-to-peak. However, it appears that the estimates of the width, while close are somewhat confounded by the changes in onset, with the best results occurring when there are no onset shifts present.

Figure 8.

The results of 100 replications of the first simulation. (Top row) The true and estimated values of the time-to-peak for the group-level HRF. (Bottom row) Same results for the width.

3.2 Experimental Data

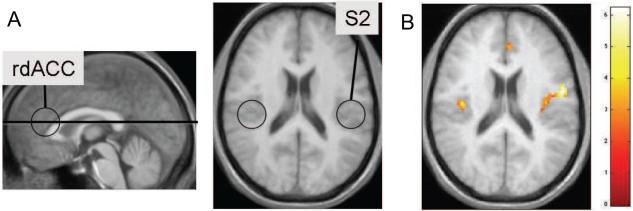
The results of the pain experiment are shown in Fig. 9 for a single axial slice (z = −22mm). The location of the slice used and an illustration of key areas of interest are shown in Fig. 9A. The highlighted areas are the rostral dorsal anterior cingulate cortex (rdACC) and the secondary somatosensory cortex (S2); two brain regions known from previous work to be involved in the processing of pain intensity [Ferretti et al., 2003, Peyron et al., 2000]. Activation in S2 is thought to be related to sensory-discriminant aspects of pain-processing, while rdACC has been shown to be related to expectancy [Atlas et al., 2012].

Figure 9.

(A) The location of the slice and an illustration of areas of interest. Both rdACC and S2 are regions known to process pain intensity. (B) A statistical map obtained using the proposed herarchical model.

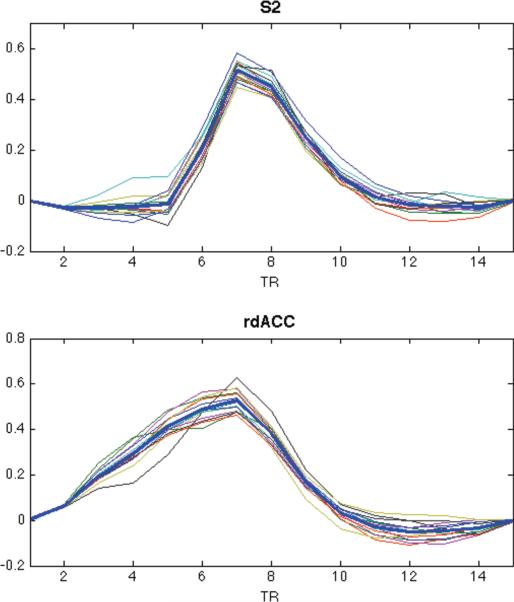
In Fig. 10 we see examples of the estimated HRFs, obtained using our approach, from voxels chosen because they lay in the center of the rdACC and S2, respectively. These results include both the subject-specific and group-level estimates. The shapes of both group-level HRFs are significantly different from the canonical HRF (p < 0.01) using the g=x² test. Note that the shapes of the HRFs are also quite different from one another. For rdACCC, the width of the response is significantly wider from what we would expect from the canonical HRF. While for S2, the onset is significantly delayed. However, interestingly both HRFs appear to reach their peak at roughly the same time point following activation.

Figure 10.

Estimates of the subject-specific HRF computed using voxels from the rdACC and S2. The group-level estimates are shown in bold.

Due to the apparent variability in the HRF across the slice, it would be problematic to analyze this data set using a canonical HRF or one that uses a constrained basis set. In fact, the GLM showed no activation in either rdACC or S2. However, the flexibility of our approach allows for large deviations in the shape of the HRF across voxels. In Fig. 9B we see an activation map obtained using our method. In particular, note that there is significant activation in S2 in response to the noxious stimulation. In previous analysis of this data set [Lindquist et al., 2009], activations in this region were particularly difficult to detect using standard GLM methods (e.g., the canonical HRF plus its temporal and dispersion derivatives, or the finite impulse response (FIR) basis set). The inverse-logit (IL) model was the only approach that showed activation in S2 contralateral to noxious stimulation. The activation shown here is extremely robust in comparison.

4 DISCUSSION

In this paper we introduce a new approach towards the simultaneous detection of activation and the estimation of the HRF for multi-subject fMRI. The suggested approach circumvents a number of shortcomings in the standard approach for performing group analysis. In these approaches there is often a tension between flexible modeling of the HRF at the first level and straightforward inference in the second level. For example, if multiple basis sets are used in the first-level GLM, then it is difficult to determine an approriate contrast to bring forward to the second-level. Often, researchers use only a subset of the basis functions and therefore potentially ignore important information contained in those left behind. The proposed approach allows the shape of the hemodynamic response function to vary across regions and subjects, as when using basis sets, while still providing a straightforward way to estimate population-level activation using all the information from the first level analysis.

An additional benefit of our model is that the suggested inferential framework not only provides a means for performing the standard tests for determining whether a voxel is significantly active, but also allows one to test whether the estimated HRF deviates from some canonical shape (e.g., SPMs canonical HRF). This type of inference has been under-utilized in the field, but we feel it can be extremely useful for diagnostic purposes, as it can help identify regions that would normally not be deemed active when using a canonical HRF.

In addition, our method could prove useful in situations when the standard HRF is either ill-fitting, such as in studies of young or elderly populations, or when the exact onset time or width of activation is unknown and added flexibility is needed to properly fit the data. An example of the latter is the thermal pain data presented in this paper. In previous studies [Lindquist et al., 2009], activations in S2 were particularly difficult to detect using either the canonical HRF plus its temporal and dispersion derivatives, or the finite impulse response (FIR) basis set. However, using our approach, the activation was extremely robust in comparison.

To date the method has only been implemented in a voxel-wise manner. Hence, we make the common, but rather implausible, assumption of independence between voxels with regards to both the HRF shape and amplitude. However, we do allow for the possibility of a parcel-specific noise structure. We are currently in the process of extending the method to also estimate spatial dependences in the data. For that purpose two types of approaches can be considered: one consists in spatially regularizing the estimation in local neighborhoods; the other is to integrate a functional parcellation of the brain. In the latter case, one can either resort to an existing atlas (see e.g. [Karahanoğlu et al., 2013]) or define a data-driven parcellation (see e.g., [Chaari et al., 2012] for such a parcellation at the subject level). To make the manuscript more manageable we decided to limit our discussion of this issue until a later time.

The presented simulations and data set are identical to those used in a previous study [Lindquist et al., 2009], where we evaluated the performance of seven different HRF models. These included: SPMs canonical HRF; the canonical HRF plus its temporal derivative; the canonical HRF plus its temporal and dispersion derivatives; the finite impulse response (FIR) basis set; a regularized version of the FIR model (denoted the smooth FIR); a nonlinear model with the same functional form as the canonical HRF but with 6 variable parameters; and the inverse logit (IL) model. The results of that work showed that it was surprisingly di cult to accurately recover true task-evoked changes in BOLD signal and that there were substantial differences among models in terms of power, bias and parameter confusability. While the derivative models were accurate for very short shifts in latency they became progressively less accurate as the shift increased. The IL model and the smooth FIR model showed the least amount of biases, and the IL model showed by far the least amount of confusability of all the models that were examined. Both these methods were clearly able to handle even large amounts of model misspecification and uncertainty about the exact timing of the onset and duration of activation.

The suggested model clearly outperformed each of the 7 other models in the same battery of tests. For space purposes we only present the canonical HRF for comparison purposes, and we encourage interested readers to look back at [Lindquist et al., 2009], for more results. The hierarchical model was found to have a superb balance of sensitivity and specificity that none of the other models was able to obtain. In addition, in the previous work the IL model was the only model that showed significant activation in S2 contralateral to noxious stimulation. Here the proposed model shows extremely robust signal in this region. For these reasons we believe the proposed model is a useful approach towards e ectively modeling multi-subject fMRI data.

A Matlab implementation of the proposed methodology is available upon request. The code runs in a reasonable time for fMRI data sets of moderate size. By optimizing the code and running it in parallel on voxels and/or on subjects, our methodology can scale up to large fMRI data. Specifically, step 1 of the estimation algorithm can be solved in closed form and requires few matrix multiplications. Step 2 is also very fast due to the definition of the noise parameters at the parcel level and to the computational efficiency of the Yule-Walker equations. Step 3 (maximum likelihood/EM algorithm) would be very slow if it was run for each voxel but is in reality only carried for a small number of voxels. Step 4 consists in a large number of standard quadratic programming problems that can be solved quickly and in parallel. Step 5 is arguably the slowest part of the estimation procedure because of the necessity to compute inverse data covariance matrices. However, linear algebra tricks can reduce the dimension of the matrices to be inverted from the number of scans (T_j) to the number of regressors (KL).

Highlights.

• Model for joint detection of activation and estimation of the HRF in multi-subject fMRI studies.

• Allows the HRF to vary across regions and subjects, while allowing for group-level inference.

• Inferential framework allows for tests of activation and deviations from canonical HRF shape.

• Validated through simulations and application to a multi-subject fMRI study of thermal pain.

Figure 3.

Results of the second simulation shown for the standard GLM/OLS approach (top row), and our hierarchical model (bottom row). From left-to-right the columns represent the estimated values of β, θ_ε, ${\sigma }_{\epsilon }^2$, the t-map and the thresholded t-map.

Appendix

A Estimation of the dependence in subject effects

A.1 EM algorithm

We fix a voxel and omit the index v from notations. Since the random effects ξ_j are independent, identically distributed, and stationary, it holds that ${\sigma }_{\xi l}^2=\mathbb{E}\left({\Vert {\xi }_{jl}\Vert }^2\right)∕K$ for each subject (1 ≤ j ≤ n) and condition (1 ≤ l ≤ L). Hence, we first estimate ${\sigma }_{\xi l}^2$ by the empirical average ${\sigma }_{\xi l}^{2\left(0\right)}=(1∕n){\sum }_{j=1}^n{\Vert {\widehat{\xi }}_{jl}\Vert }^2∕K$. We initially assume working independence for the ξ_jl so that ${\rho }_{\xi l}^{\left(0\right)}\left(k\right)={\delta }_{0k}$ for each lag (1 ≤ k ≤ K − 1) and condition. At the (r + 1)^th iteration (r ≥ 0) of the EM algorithm, the E-step computes the conditional expectation of (minus twice the logarithm of) the complete likelihood, i.e., the likelihood of the augmented data (y₁, . . . , y_n, ξ₁, . . . , ξ_n). The conditioning variables are y₁, . . . , y_n, the current estimators ${\sigma }_{\xi }^{2\left(r\right)}$, ${\rho }_{\xi }^{\left(r\right)}$, and ${\widehat{\beta }}_0$, ${\widehat{\gamma }}_0$, ${\widehat{\sigma }}_{\epsilon m}^2$, ${\widehat{\theta }}_{\epsilon m}$. Up to constant terms, the conditional expectation is

$$Q({\sigma }_{\xi }^2,{\rho }_{\xi }\mid {\rho }_{\xi }^{2\left(r\right)},{\rho }_{\xi }^{\left(r\right)})=nK\ln \mid {\mathbf{D}}_{\xi }\mid +n\ln \mid {\mathbf{T}}_{\xi }\mid +\sum _{j=1}^n{\xi }_j^{{\left(r\right)}^{\prime }}{\mathbf{T}}_{\xi }^{-1}({\mathbf{D}}_{\xi }^{-1}\otimes {\mathbf{I}}_K){\xi }_j^{\left(r\right)}+\sum _{j=1}^n\mathrm{tr}\left\{{\mathbf{T}}_{\xi }^{-1}({\mathbf{D}}_{\xi }^{-1}\otimes {\mathbf{I}}_K){\mathbf{B}}_j^{\left(r\right)}\right\},$$ (15)

where ${\mathbf{B}}_j^{\left(r\right)}={[{\mathbf{X}}_j^{\prime }{\widehat{\mathbf{V}}}_{\epsilon jm}^{-1}{\mathbf{X}}_j+{\left({\mathbf{T}}_{\xi }^{\left(r\right)}\right)}^{-1}({\left({\mathbf{D}}_{\xi }^{\left(r\right)}\right)}^{-1}\otimes {\mathbf{I}}_K)]}^{-1}$, ${\xi }_j^{\left(r\right)}={\mathbf{B}}_j^{\left(r\right)}{\mathbf{X}}_j^{\prime }{\widehat{\mathbf{V}}}_{\epsilon jm}^{-1}{\mathbf{r}}_j$ is the predicted random effect for the j^th subject, and r_j is the residual vector defined in step 2 of section 2.2.

For 1 ≤ l ≤ L, the derivative of Q with respect to ${\sigma }_{\xi l}^2$ is

$$\frac{\partial Q}{\partial {\sigma }_{\xi l}^2}=\frac{nK}{{\sigma }_{\xi l}^2}-\frac{1}{{\sigma }_{\xi l}^4}\sum _{j=1}^n{\xi }_{jl}^{{\left(r\right)}^{\prime }}{\mathbf{T}}_{\xi l}^{\left(r\right)}-\frac{1}{{\sigma }_{\xi l}^4}\sum _{j=1}^n\mathrm{tr}\left\{{\mathbf{T}}_{\xi l}^{-1}{\mathbf{B}}_{jll}^{\left(r\right)}\right\},$$ (16)

where the matrix ${\mathbf{B}}_j^{\left(r\right)}$ has been partitioned in blocks ${\mathbf{B}}_{jl{l}^{\prime }}^{\left(r\right)}$, 1 ≤ l, l′ ≤ L, of size K × K. Writing ${\mathbf{C}}_j^{\left(r\right)}={\sum }_{j=1}^n({\xi }_{jl}^{\left(r\right)}{\xi }_{jl}^{{\left(r\right)}^{\prime }}+{\mathbf{B}}_{jll}^{\left(r\right)})$ and equating (16) with zero, we get

$$\begin{array}{cc}\hfill {\sigma }_{\xi l}^2=& \frac{1}{nK}\left(\sum _{j=1}^n{\xi }_{jl}^{{\left(r\right)}^{\prime }}{\mathbf{T}}_{\xi l}^{\left(r\right)}+\sum _{j=1}^n\mathrm{tr}\left\{{\mathbf{T}}_{\xi }^{-1}{\mathbf{B}}_{jll}^{\left(r\right)}\right\}\right)\hfill \\ \hfill =& \frac{1}{nK}\mathrm{tr}\left({\mathbf{T}}_{\xi l}^{-1}{\mathbf{C}}_l^{\left(r\right)}\right).\hfill \end{array}$$ (17)

After plugging (17) in (15), the variance-profile function Q_p to be optimized in the M step of the algorithm is

$$\begin{array}{cc}\hfill Q_p({\rho }_{\xi }\mid {\sigma }_{\xi }^{2\left(r\right)},{\rho }_{\xi }^{\left(r\right)})=& nK\ln \mid {\mathbf{D}}_{\xi }\mid +n\ln \mid {\mathbf{T}}_{\xi }\mid +n\hfill \\ \hfill =& nK\sum _{l=1}^L\ln \left(\mathrm{tr}\left({\mathbf{T}}_{\xi l}^{-1}{\mathbf{C}}_l^{\left(r\right)}\right)\right)-nK\ln \left(nK\right)+n\sum _{l=1}^L\ln \mid {\mathbf{T}}_{\xi l}\mid +n.\hfill \end{array}$$ (18)

For computational speed, we may use any suitable gradient-based optimazation method. Let D_k be the K × K whose (i,j) entry 1 if |i — j| and 0 otherwise. then ${\mathbf{T}}_{\xi l}={\sum }_{k=0}^{K-1}{\rho }_{\xi l}\left(k\right){\mathbf{D}}_k$ and the gradient of Q_p is

$$\frac{\partial Q_p}{\partial {\rho }_{\xi l}\left(k\right)}=-nK\frac{\mathrm{tr}({\mathbf{T}}_{\xi l}^{-1}{\mathbf{D}}_k{\mathbf{T}}_{\xi l}^{-1}{\mathbf{C}}_l^{\left(r\right)}}{\mathrm{tr}({\mathbf{T}}_{\xi l}^{-1}{\mathbf{C}}_l^{\left(r\right)}}+n\mathrm{tr}\left({\mathbf{T}}_{\xi l}^{-1}{\mathbf{D}}_k\right)$$ (19)

for 1 ≤ k ≤ K−1 and 1 ≤ l ≤ L. The box constraints −1 ≤ ρξl(k) ≤ 1 and positive definiteness of T_ξl are enforced during the optimization. The updated variance estimator ${\sigma }_{\xi l}^{2(r+1)}$ is obtained by plugging ${\rho }_{\xi }^{(r+1)}$ in (17). Writing ${\Gamma }^{\left(r\right)}=(\mathrm{vec}\left({\mathbf{T}}_{\xi 1}^{-1}{\mathbf{C}}_1^{\left(r\right)}{\mathbf{T}}_{\xi 1}^{-1}\right),\dots ,\mathrm{vec}\left({\mathbf{T}}_{\xi L}^{-1}{\mathbf{C}}_L^{\left(r\right)}{\mathbf{T}}_{\xi L}^{-1}\right))$, D = (vecD₁),...., vec(D_K−)), ${\mathbf{t}}^{\left(r\right)}={(\mathrm{tr}\left({\mathbf{T}}_{\xi 1}^{-1}{\mathbf{C}}_1^{\left(r\right)}\right),\dots ,\mathrm{tr}\left({\mathbf{T}}_{\xi L}^{-1}{\mathbf{C}}_L^{\left(r\right)}\right))}^{\prime }$, and $\mathbf{S}=(\mathrm{vec}\left({\mathbf{T}}_{\xi 1}^{-1}\right),\dots ,\mathrm{vec}\left({\mathbf{T}}_{\xi L}^{-1}\right))$, the gradient (19) can be compactly written as

$$\frac{\partial Q_p}{\partial {\rho }_{\xi }}=-nK\frac{\mathrm{vec}\left({\mathbf{D}}^{\prime }{\Gamma }^{\left(r\right)}\right)}{{\mathbf{t}}^{\left(r\right)}\otimes 1_{K-1}}+n\mathrm{vec}\left({\mathbf{D}}^{\prime }\mathbf{S}\right),$$

where the division is taken element-wise and 1_K−1 is a vector containing (K−1) ones.

A.2 Maximum Likelihood Estimation

For a given voxel v, the partial derivatives of the likelihood function (7) are

$$\frac{\partial L}{\partial {\sigma }_{\xi l}^2}=\sum _{j=1}^n\mathrm{tr}\left({\mathbf{X}}_{jl}^{\prime }{\mathbf{V}}_j^{-1}\left(v\right){\mathbf{X}}_{jl}{\mathbf{T}}_{\xi l}\right)-\sum _{j=1}^n{\mathbf{r}}_j^{\prime }{\mathbf{V}}_j^{-1}\left(v\right){\mathbf{X}}_{jl}{\mathbf{T}}_{\xi l}{\mathbf{X}}_{jl}^{\prime }{\mathbf{V}}_j^{-1}\left(v\right){\mathbf{r}}_j\left(v\right)$$ (20)

and

$$\frac{\partial L}{\partial {\rho }_{\xi l}\left(k\right)}={\sigma }_{\xi l}^2\sum _{j=1}^n\mathrm{tr}\left({\mathbf{X}}_{jl}^{\prime }{\mathbf{V}}_j^{-1}\left(v\right){\mathbf{X}}_{jl}{\mathbf{D}}_k\right)-{\sigma }_{\xi l}^2\sum _{j=1}^n{\mathbf{r}}_j^{\prime }{\mathbf{V}}_{j-1}^{}\left(v\right){\mathbf{X}}_{jl}{\mathbf{D}}_k{\mathbf{X}}_{jl}^{\prime }{\mathbf{V}}_j^{-1}\left(v\right){\mathbf{r}}_j\left(v\right)$$ (21)

for 1 ≤ k ≤ K − 1 and 1 ≤ l ≤ L. Based on (20)-(21) and a suitable gradient-based optimization procedure, we obtained the ML estimators ${\widehat{\sigma }}_{\xi l}^2\left(v\right)$ and ${\widehat{\rho }}_{\xi l}(k,v)$. We then define the aggregated correlation estimate ${\widehat{\rho }}_{\xi l}\left(k\right)$ as the median of the ${\widehat{\rho }}_{\xi l}(k,v)$ across voxels where the estimation was carried.

B Sampling distribution of the HRF estimators

Here we provide the theoretical justification of the large-sample approximation (14) to the sampling distribution of the estimators $\widehat{\beta }\left(v\right)$ and $\gamma \left(v\right)$.

First, the estimators used in this paper rely on standard statistical procedures whose consistency properties are well documented in the literature. In step 1, the penalized least squares estimator ĥ(v) of the HRF coefficients γ_lk(v) is consistent as n → ∞ and λ₀ → 0. Note that increasing the number of scans T_j reduces the influence of the noise ε on the estimation but not the sampling variability (subject effects ξ). In fact, the variance of the pilot estimator ĥ(v) is dominated by the sampling variability: it is of order $\mathcal{O}({\sum }_j{T}_j^2∕{\left({\sum }_j{T}_j\right)}^2)$, i.e. $\mathcal{O}(1∕n)$ if the T_j are of comparable size. Also, the parameter λ₀ governing the penalty on HRF shapes lying outside the null space Ψ must go to zero to render the pilot estimator asymptotically unbiased. In step 2, the Yule-Walker estimators of the noise parameters ${\sigma }_{\epsilon m}^2$ and θ_εm are consistent as max_j T_j → ∞. The consistency of steps 3-5 derives from the large-sample properties of least squares- and maximum likeklihood estimators and from the consistency of the previous estimation steps. Note that the estimators of the noise and random effects parameters are averaged across subjects and space (except for the variance estimators ${\widehat{\sigma }}_{\xi l}^2\left(v\right)$). As a consequence, their variance is generally small in comparison to the variance of the HRF estimators.

We now turn to the large-sample distribution of $\widehat{\beta }\left(v\right)$ and $\gamma \left(v\right)$. Assuming that for each subject, stimuli of each type are presented sufficiently often, the design matrices X_j are of order $\mathcal{O}\left(\sqrt{T_j}\right)$ in norm and the matrix M = M(v) is of order $\mathcal{O}\left({\sum }_j{T}_j\right)$ in probability. Given the consistency of $\widehat{\gamma }\left(v\right)$, V̂ _j(v)the normality of the data, and the fact that Var(η) ≈ M, one can apply Slutsky's theorem and the Law of Large Numbers in (11) to obtain the large-sample approximation $\widehat{\beta }\left(v\right)\to N(\beta \left(v\right),{\left[{({\mathbf{I}}_L\otimes \beta \left(v\right))}^{\prime }\mathrm{M}({\mathbf{I}}_L\otimes \gamma \left(v\right))\right]}^1)$ (with ${\widehat{\mathbf{V}}}_j^{-1}\left(v\right)$ in M replaced by ${\widehat{\mathbf{V}}}_j^{-1}\left(v\right)$) as n, Σ_j T_j → ∞ and λ → 0. Turning to the estimator $\widehat{\gamma }\left(v\right)$, simple algebraic manipulations in (11) and (13) show that $\widehat{C}=-n\lambda \widehat{\gamma }{\left(v\right)}^{\prime }\mathbf{P}\widehat{\gamma }\left(v\right)$. In other words, the terms ĈI_K and nλP in (13) are of order $\mathcal{O}\left(n\lambda \right)$ in probability and thus negligible in comparison to M. Applying the same arguments as with $\widehat{\beta }\left(v\right)$ in (11), we obtain the limit distribution $\widehat{\gamma }\left(v\right)\to N(\gamma \left(v\right),{\left[{(\beta \left(v\right)\otimes {\mathbf{I}}_K)}^{\prime }\mathrm{M}(\beta \left(v\right)\otimes {\mathbf{I}}_K)\right]}^{-1})$.