Abstract
This paper extends earlier work on spatial modeling of fMRI data to the temporal domain, providing a framework for analyzing high temporal resolution brain imaging modalities such as electroencapholography (EEG). The central idea is to decompose brain imaging data into a covariate-dependent superposition of functions defined over continuous time and space (what we refer to as topographic latent sources). The continuous formulation allows us to parametrically model spatiotemporally localized activations. To make group-level inferences, we elaborate the model hierarchically by sharing sources across subjects. We describe a variational algorithm for parameter estimation that scales efficiently to large data sets. Applied to three EEG data sets, we find that the model produces good predictive performance and reproduces a number of classic findings. Our results suggest that topographic latent sources serve as an effective hypothesis space for interpreting spatiotemporal brain imaging data.
Keywords: fMRI, Bayesian, decoding, variational, multivariate
1. Introduction
Brain imaging techniques like electroencephalography (EEG) and magnetoencephalography (MEG) offer a time-resolved window onto the neural correlates of cognitive processing. In this paper, we propose a new statistical model that characterizes the spatiotemporal distribution of neural signals and their relationship to experimental covariates. The essential innovation of this model is the decomposition of the data into parameterized functions defined over continuous space and time—what we term topographic latent sources.1 These functions provide a parsimonious and interpretable characterization of the data. As we demonstrate below, they can also be used to decode mental states from brain activity with higher accuracy than many currently used methods. We refer to our model as topographic latent source analysis (TLSA).
Our work builds on a previous version of TLSA for functional magnetic resonance imaging (fMRI) data developed in Gershman et al. (2011). TLSA decomposes fMRI data into latent sources defined over 3D image volumes, but does not model the timecourse of event-related brain activity (but see Manning et al., 2014). In light of the poor temporal resolution of fMRI data, this is of little consequence for many experiments. However, for MEG and EEG the timecourse is of fundamental interest, necessitating the spatiotemporal model developed in this paper. The basic design principle underlying TLSA is the same for fMRI and MEG/EEG: the brain pattern is decomposed into a covariate-dependent superposition of topographic latent sources. In the case of spatiotemporal data, the latent sources are defined over both space and time.
In addition to extending TLSA to the spatiotemporal domain, this paper presents a new algorithm for Bayesian parameter estimation. In our previous paper (Gershman et al., 2011), we used Markov chain Monte Carlo methods (Robert and Casella, 2004) to approximate the posterior over parameters with a set of samples. However, these methods scale poorly with data set size, sometimes requiring days to run. Here, we develop an efficient variational inference algorithm (Jordan et al., 1999; Attias, 2000) that can analyze large data sets in minutes. We have made Matlab (Mathworks Inc., Natick, MA) software implementing this algorithm available online.2
In the remainder of this paper, we describe spatiotemporal TLSA and our inference algorithm. We also describe how mental state decoding, neural reconstruction, and classical hypothesis testing can be carried out in this framework. We then apply TLSA to three EEG data sets and compare it to several alternative models. Our empirical results suggest that for this data set, TLSA provides superior predictive power compared to these alternatives, demonstrating its usefulness as a tool for analyzing spatiotemporal brain patterns.
2. Materials and Methods
In this section, we describe the generative model underlying TLSA and present an approximate inference algorithm for inverting the generative model given data. We then explain how classical hypothesis testing can be applied to the parameter estimates, as well as how the model can be used to decode experimental covariates (e.g., mental states) from brain activity. Finally, we describe the three data sets analyzed which we analyzed, and the alternative algorithms to which we compared TLSA.
2.1. Terminology
We first introduce some basic terminology and notation. In order to preserve flexibility in how the data are represented, we assume that brain patterns can be described by a set of neural “features.” For example, the voxel is a standard feature for fMRI data. We represent EEG data in terms of features that are conjunctions of electrodes and time points within a trial. Thus, an EEG feature might correspond to an electrode's signal measured at a particular time point. Alternatively, one could use spectral features, such as the power in a frequency band at a particular electrode and time point.
Let C be the number of covariates (experimental parameters, stimuli, or tasks), N be the number of observations (e.g., trials), K be the number of latent sources, S be the number of participants, and V be the number of neural features (e.g., electrodes and time points within a trial epoch). The model consists of the following variables:
, the design matrix containing each covariate's time series for subject s.
, the weight matrix encoding how each covariate loads on each source. Weights are analogous to coefficients in a regression analysis.
, the matrix of basis pattern for each latent source. Each basis pattern represents the latent source function evaluated at all the feature locations (see below for more details).
, the pattern of neural activity at each observation.
, the location matrix, specifying, in D-dimensional coordinates, the location of each neural feature. For EEG data, the location corresponds to the Cartesian 3D coordinates of the electrode and a particular time point within the trial (thus, D = 4). In practice, we also normalize the coordinates to [0, 1].
We will use lowercase letters to denote scalar elements of a matrix (e.g., xsnc denotes the element in row n and column c of matrix Xs). Bold lowercase letters denote vectors (rows or columns of a matrix).
2.2. Generative model
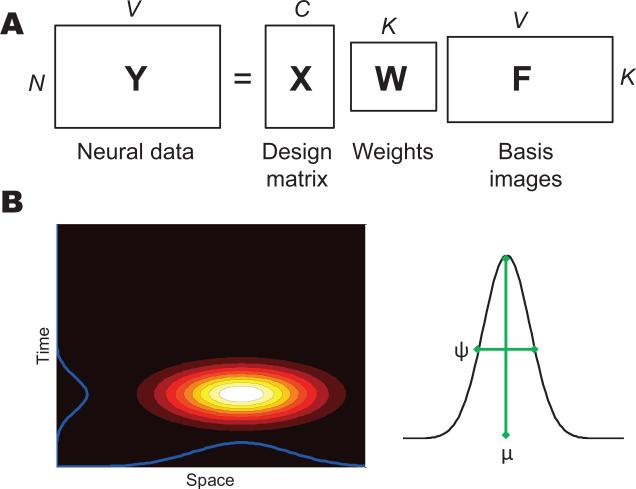
The observed neural data is assumed to arise from a covariate-dependent superposition of K latent latent sources (Figure 1A):
| (1) |
where is a Gaussian noise term and τs ~ Gamma(ν, ρ) is the noise precision.3 The basis pattern matrix is constructed by evaluating a parameterized spatial basis function φ(·; ω) at the measured feature locations Rs = {rsv}:
| (2) |
where is a vector of parameters for source k.
Figure 1. Model schematic.
(A) Matrix factorization representation of the generative process. (B) Construction of a spatiotemporal latent source.
Of particular interest are basis functions that are spatially and temporally localized. In our earlier work on fMRI (Gershman et al., 2011), we used a radial basis function, parameterized by ω = {μ , ψ}:
| (3) |
where μ ∈ [0, 1]D is the source center and ψ > 0 is a width parameter. We can extend this basis function to the spatiotemporal domain by distinguishing spatial (μa, ψa) and temporal (μt, ψt) parameters:
| (4) |
where ra is the spatial component of the neural feature location, and rt is the temporal component (note that μt and rt are scalars, since time is one-dimensional). The spatiotemporal basis function can be understood as the product of spatial and temporal “receptive fields.” This construction is illustrated in Figure 1B.
We extend this generative model hierarchically to model sharing of latent sources across subjects, while still allowing within-subject variation. To do this, we we specify a group-level “template,” . This template captures the spatiotemporal structure of the latent source that is conserved across subjects. The corresponding subject-level parameters for each individual subject are then assumed to arise from a stochastic deformation of the group-level parameters: . Thus, a given source is identifiable in all subjects, but the precise shape of this source is allowed to vary between subjects. The amount of variation is controlled by the precision matrix Λ.
Because the covariance structure of the subject-level parameters is generally unknown, we introduce a prior on Λ. For simplicity, we assume that Λ is diagonal: Λ = diag(λ1, . . . , λM), with λm ~ Gamma(β, β). When β → 0, the coupling between subjects disappears, and each subject is modeled independently (i.e., non-hierarchically). In the analyses reported below, we compare the hierarchical (β > 0) and non-hierarchical (β = 0) models. In the non-hierarchical setting, the group-level parameters have no meaning, and therefore we treat this as a special case by placing the group-level prior directly over the subject-level parameters: .
2.3. Inference
The goal of inference is to compute the posterior over the latent variables θ = {τ, ω, W} given data {X, Y}:
| (5) |
where the normalizing constant is also known as the marginal likelihood (or model evidence). For brevity, we leave the dependence on hyperparameters {β, ν, ν0, , ν, ρ} implicit.
Since the normalizing constant of the posterior is intractable, we must resort to approximations. In previous work (Gershman et al., 2011), we described a Monte Carlo algorithm for approximating Eq. 5 with a set of samples. However, this algorithm was prohibitively slow for large data sets, and introduced additional variability into the parameter estimates (due to the inherently stochastic nature of the algorithm). In this section, we describe a variational inference algorithm (Jordan et al., 1999) for deterministically approximating the posterior.
The basic idea of variational inference is to approximate the posterior p(θ|X, Y) with another distribution q(θ) whose parameters we optimize to minimize a divergence measure between the two distributions. The standard divergence measure used for this purpose is the Kullback-Leibler (KL) divergence:
| (6) |
The KL divergence is equal to 0 when the two distributions are the same. However, we cannot directly minimize KL[q(θ)∥p(θ|X, Y)] with respect to q(θ), because it requires computing the intractable posterior. Instead, we can equivalently maximize a lower bound on the log marginal likelihood, ln :
| (7) |
where is the expectation with respect to q and is the entropy of q. is related to the KL divergence by the equality
| (8) |
Thus, maximizing is equivalent to minimizing KL[q(θ)||p(θ|X, Y)]. Importantly, does not require computing the intractable posterior.
We assume a “mean-field” approximation in which q factorizes into a set of component distributions:
| (9) |
where i indexes a subset of the parameters. In this paper, we consider the following factorization:
| (10) |
To keep the notation simple, we have omitted the subscript indexing each q-distribution, allowing it to be specified by context.
Maximization of proceeds by coordinate ascent, iteratively updating each q−distribution while holding the others fixed. If each q-distribution is in the conjugate-exponential family, the updates take the following form:
| (11) |
In other words, the updates proceed by iteratively taking the expectation of the complete data log probability under the factorized posterior while holding all q-distributions except qi fixed. The complete set of update equations are described in Appendix A.
One impediment to applying the coordinate ascent updates is that the q-distributions for the source parameters ω are not generally in the conjugate-exponential family, due to the non-linearity induced by ϕ. Following the work of Chappell et al. (2009), we use a linearization of the likelihood that allows us to obtain closed-form updates (see Appendix B). The cost of this approximation is that is no longer a strict lower bound on ln . However, linearization often works quite well in practice (Friston et al., 2007; Chappell et al., 2009; Braun and McAuliffe, 2010; Gershman et al., 2012), and we confirm this empirically below.
2.4. Hypothesis testing
After fitting the model to data, we are often interested in testing null hypothesis of the form , where [η1, . . . , ηC] is a contrast vector. We adopt a standard mixed-effects approach to this problem by first calculating the contrast for each subject and source (where ŵ denotes the posterior mean estimator of ω), and then performing a t-test across subjects for each source separately. The resulting p-values can be corrected for multiple comparisons (e.g., using false discovery rate or Bonferroni correction). Compared to conventional mass-univariate analysis, the number of comparisons is dramatically smaller for TLSA, since in general K < < V . Thus, hypothesis testing on latent sources can potentially improve sensitivity.
Note that in order for this analysis to give sensible results, the sources must be aligned across subjects. This will happen naturally when we employ the hierarchical model (i.e., when β > 0). However, for the non-hierarchical model (β = 0) there is no constraint on the source parameters to be similar across subjects, and hence comparing the weight matrices across subjects is meaningless.
2.5. Decoding and reconstructing brain patterns
Given new neural data y, we are often interested in the conditional distribution over the covariates x that gave rise to it (Friston et al., 2008). This decoding problem arises, for example, in experiments where the model has been trained on trials for which the covariates are known, and then used to infer the unknown covariates on the remaining trials. Bayes’ rule specifies how the desired conditional distribution should be computed:
| (12) |
Here we have implicitly conditioned on the training data. As can be seen from this equation, Bayesian decoding requires a prior on covariates, p(x). However, TLSA, in its basic form described above, does not specify a distribution over covariates. This distribution is likely to vary substantially from experiment to experiment, and therefore we will not attempt a general specification. Instead, we choose computationally expedient priors that allows us to perform Bayesian decoding analytically. To keep things simple, we define the likelihood term p(y|x) using the expected values of the latent variables under the variational posterior, .
In the case of real-valued covariates, we choose p(x) to be multivariate Gaussian, with parameters equal to the sample mean x0 and covariance matrix Σ0 of the training data, collapsing across subjects. Given this prior, the posterior over covariates is also Gaussian:
| (13) |
| (14) |
| (15) |
where A = ŴF̂ and is the estimated precision (see Appendix A). We have suppressed the subject index here for notational convenience.
For discrete covariates, these will typically belong to a finite set, small enough that we can exhaustively enumerate all possible values of x. Analogous to the strategy for the continuous case, we can use the sample proportions of each covariate from the training data to construct a prior p(x). Bayesian decoding is then straightforward to implement, since the normalization constant in Bayes’ rule is (typically) a tractable summation.
We can also ask the converse question (the reconstruction problem): Given covariates x, what is the conditional distribution over neural data y? This distribution is multivariate Gaussian with mean ŷ = xŴF̂ and covariance . In other words, we simply run TLSA in “forward mode” with the estimated parameters to predict what the neural data should look like on a particular trial.
2.6. Implementation details
For all our analyses with TLSA, we use the following hyperparameter settings (unless specified otherwise): β = 0.01, ν = 1, ρ = 1. Because we normalize the feature coordinates to [0, 1], the parameters of the radial basis function only take meaningful values in [0, 1]. In order to reconcile this with the Gaussian prior on ω, we use a logit transformation to map ω to real values. We set for the source centers (corresponding to the center of the space-time volume) and for the source widths. For the prior precision matrix, we set . Unless otherwise indicated, we ran the variational inference algorithm for 200 iterations. We have found that the results of TLSA are remarkably robust to variations in these parameters, and we give some examples of this robustness in the Results section.
The variational inference algorithm will typically converge to a local optimum. It is therefore sensitive to the initial values of the parameters. We use a simple initialization procedure that consists of the following steps:
A grand average pattern (averaging over subjects and trials) is constructed, normalized to have a maximum value of 1. Although covariate-specific information is lost in this average, it will still capture gross patterns of regional activity.
A single source is centered at the maximum of the average pattern, with its width initialized to the prior mean.
The basis pattern for the newly created source is subtracted from the average pattern, and the average pattern is then renormalized.
Steps 2 and 3 are repeated until the parameters of all K sources are selected.
This procedure is designed to place sources in regions of the pattern that are not yet accounted for by existing sources. Note that the only parameters being initialized here are the source parameters (ω); the other parameters are automatically set by the updates described in Appendix A.
2.7. EEG data sets
In this paper, we analyze two previously unpublished EEG data sets (a standard visual oddball experiment and an item recognition data set) as well as a data set from the 3rd Brain-Computer Interface (BCI) competition (del Millán, 2004).
2.7.1. Oddball data
Ten participants between 18 and 41 years of age were recruited from the university community at The Ohio State University. All participants were right-handed and spoke and read English fluently. Participants provided written consent in accordance with requirements of the local IRB and were paid $10/hour for their time. Data from participants for whom there were excessive motion artifacts, recording noise, or experimenter error (n = 4) were not included in the analyses, leaving data from 6 participants for the analyses reported below.
Stimuli consisted of X's or O's presented in a large font at the center of the screen. The task was simply to specify if the stimulus was an X or O by pressing J or K on the keyboard with the right hand as quickly and accurately as possible following each stimulus onset. Which key corresponded to an X or O response was counterbalanced across blocks in order to eliminate any keyboard response artifacts. The experiment consisted of 1 practice and 8 experimental blocks with 40 stimuli each (32 common and 8 rare). A custom program written using the Python experiment programming library (PyEPL; Geller et al., 2007) and running on a desktop computer with a 24in LCD display was used to generate the study lists for each participant, control the timing of the tasks, present the stimuli, and record participant responses.
2.7.2. Item recognition data
Twenty-three participants between 18 and 30 years of age were recruited from the university community at The Ohio State University. All participants were right-handed and spoke and read English fluently. Participants provided written consent in accordance with requirements of the local IRB and were paid $10/hour for their time. Of the participants, 12 were selected for the present analysis because they exhibited good behavioral performance and did not have excessive motion artifacts, recording noise, or experimenter error.
Stimuli consisted of lists of words presented one at a time in a large font at the center of the screen. Each word presentation lasted 1.6 s with a 0.3 to 0.7 s jittered interstimulus interval. Participants were told to remember the words for a subsequent recognition memory task that occurred after each of the study-lists. Each study list comprised 36 unique items, split evenly into weak and strong conditions. Weak items were presented once on the study list, whereas strong items were presented three times, once in each third of the list. The recognition task that followed each list tested memory for each studied word along with the same number of matching lures, giving rise to 72 total test items per list, in random order. Participants indicated whether the test word was old or new by pressing the J or K key on the keyboard with their right hand as quickly and accurately as possible following each stimulus onset. Participants had 1.8 s to make their response, followed by a 0.4 to 0.8 s jittered interstimulus interval. The experiment consisted of 13 study/test blocks. For the analyses presented here we compared correctly recognized strong items, which were presented three times during the study list, and correctly rejected lures, which were not previously presented, to illustrate the canonical parietal old/new effect (Rugg and Curran, 2007).
2.7.3. Mental imagery data from the BCI competition
This data set was taken from the publicly available data sets collected as part of the 3rd Brain-Computer Interface (BCI) competition.4 A complete description of the data set can be found in del Millán (2004). Three participants performed three different tasks over the course of 4 sessions: (1) Imagination of repetitive self-paced left-hand movements, (2) Imagination of repetitive self-paced right-hand movements, and (3) Generation of words beginning with the same random letter. Participants were not provided with feedback. EEG signals were recorded with Biosemi system using a 32-channel cap (sampling rate: 512 Hz).
2.7.4. Preprocessing
EEG data from 96 (oddball data) or 64 (item recognition data) channels were recorded on a Brain Products, Inc., ActiCHamp system with active electrodes, digitized at 1000 Hz, rereferenced to linked mastoids, and then high-pass filtered 0.25 Hz with a zero-phase distortion Butterworth filter. Eye-movement artifacts were corrected using a wavelet independent components analysis method (WICA) that has proven to be quite robust at removing eye artifacts without introducing spurious correlations between the electrodes (Castellanos and Makarov, 2006). After these preprocessing steps, the item presentation events were separated into distinct non-overlapping epochs and baseline corrected to the average of the 250 ms prior to visual stimulus onset. Finally, the data were z-scored within each subject and feature separately. Data from 0 to 900 ms post-stimulus were used in the analyses reported below.
For the spatial component of the neural feature location (ra), we used the 3D Cartesian coordinate of each electrode. For the temporal component (rt), we used the time (in milliseconds) of each measurement. All features were separately normalized to the [0, 1] range.
For the mental imagery data, we used the precomputed power spectral density (PSD) features provided by the BCI competition. The raw EEG potentials were first spatially filtered by means of a surface Laplacian. Then, the PSD in the 8-30 Hz band was estimated every 62.5 seconds (i.e., at a sampling rate of 16 Hz) over the previous second of data with a frequency resolution of 2 Hz. The PSD features were provided for the 8 centro-parietal channels C3, Cz, C4, CP1, CP2, P3, Pz, and P4. The resulting EEG data is a 96-dimensional vector (8 channels × 12 frequency components).
2.8. Alternative models
The alternative models we consider in this paper are summarized as follows:
Gaussian naive Bayes (GNB): each class-conditional distribution over neural features is modeled as a multivariate Gaussian.
- Shrinkage linear discriminant analysis (SLDA): similar to GNB, each class-conditional distribution is modeled as a multivariate Gaussian, using optimal shrinkage of the covariance matrix as suggested by Schäfer et al. (2005). Classification is performed by projecting the neural input onto a separating hyperplane:
where w is a V × 1 weight vector and ∈ is a threshold parameter. Observation n is assigned to one class if t(yn) > 0, and to the other class if t(yn) < 0. This algorithm has been shown to achieve state-of-the-art performance in brain-computer interface applications (Blankertz et al., 2011).(16) L2-regularized logistic regression: logistic regression with a weighted penalty on the L2 norm of the regression coefficients. We set the regularization parameter to 0.01, but the results were not sensitive to this choice.
Bilinear discriminant component analysis (BDCA; Dyrholm et al., 2007): discriminant analysis that finds a separating hyperplane in a subspace projection of the neural data. The discriminant function is bilinear in the spatial and temporal components of the data, with Gaussian process priors enforcing smoothness (over space and time) of the parameter estimates. BDCA uses the same discriminant function as SLDA, but regularizes it differently. Let W denote the reorganization of w into a matrix where rows index electrodes and columns index time points. BDCA assumes that W is the product of two low rank matrices, W = UVΤ, where (following Dyrholm et al.) we set the rank to be 1. Thus U and V are row vectors, with each component of U corresponding to an electrode, and each component of V corresponding to a time point. By placing Gaussian process priors on these vectors, the estimate of w is regularized in a spatiotemporally local fashion. We optimize the hyperparameters of the Gaussian processes (which control the spatial and temporal smoothness of W) using nested cross-validation.
Of these models, only GNB models the conditional distribution p(Y|X). Logistic regression and BDCA model the conditional p(X|Y). This means that logistic regression and BDCA cannot be used for tasks involving the distribution of neural data, such as the reconstruction task.
For all the models above, the set of features was the concatenation of neural activity across all time points and electrodes. The sampling rate was the same as used by TLSA (see previous section for details).
3. Results
In this section, we evaluate the predictive accuracy of TLSA on the oddball, item recognition and mental imagery EEG data sets and compare it to several alternative models. We then illustrate how TLSA can be used for classical hypothesis testing.
3.1. Prediction performance
In the prediction task for the oddball data set, our goal is to decode whether a trial was rare or common; for the item recognition data set, our goal is to decode whether a trial was old or new. To evaluate predictive performance on held-out data, we used a cross-validation procedure in which we broke each subject's data into 6 sets of trials, fitting the models to 5 of the sets and testing on the 6th. For the oddball data, each training set contained 40 trials from each condition, and each test set contained 200 common trials and 40 rare trials. For the item recognition data, the training and test sets contained an irregular number of old and new items (on average, there were slightly over twice as many new items as old items). We repeated this procedure so that each set appeared once as the test set. We found that we could improve the performance of TLSA by averaging all the training trials within each condition, reducing X to two rows. Averaging in this way, a common technique in multivariate decoding analyses of event-related fMRI (Yang et al., 2012), is helpful in reducing noise.
Decoding performance was quantified using the area under the receiver operating curve (AUC), which quantifies the degree to which a classifier is able to distinguish between two classes. Higher values of AUC indicate better performance; an AUC of 0.5 indicates chance performance. Reconstruction performance was quantified using the mean squared error (MSE)
| (17) |
where ŷsnv denotes the model prediction. Lower values of MSE indicate better performance.
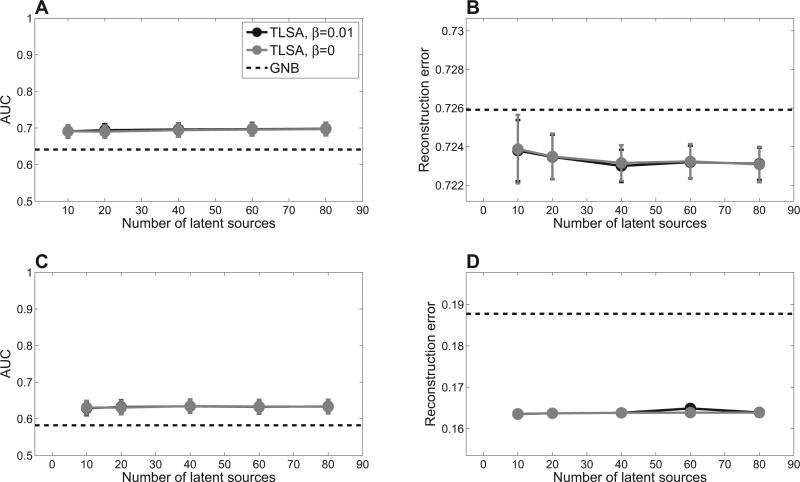
We initially restricted our comparison to TLSA and GNB, since the latter is the only generative model among the alternatives and hence can be compared on both prediction and reconstruction. Our prediction results (Figure 2) indicate the superior performance of TLSA compared to GNB. Consistent with our earlier work on fMRI data (Gershman et al., 2011), the hierarchical model (β = 0.01) does not seem to perform better than the non-hierarchical model (β = 0) in which each subject is analyzed separately. However, as we mentioned above, the hierarchical model is essential for drawing group-level inferences, since it ensures identifiability of sources across subjects.
Figure 2. Prediction results.
Top row shows results for the oddball data set; bottom row shows results for the item recognition data set. (A,C ) Mental state decoding accuracy quantified by the area under the receiver operating curve (AUC). Higher values indicate better performance. (B,D) Brain pattern reconstruction performance quantified by mean squared error. Error-bars represent standard error of the difference between TLSA and GNB across subjects.
Another pattern evident in Figure 2 is that the results are relatively insensitive to the number of sources, as long as this number is greater than 10. This is reassuring, because it means that one need not fit many models with different numbers of sources in order to find the optimal model. The caveat, of course, is that this conclusion is data-dependent; other, more complex data sets may require a larger number of sources. In the remainder of this article, we restrict our attention to the hierarchical model (β = 0.01) with K = 40.
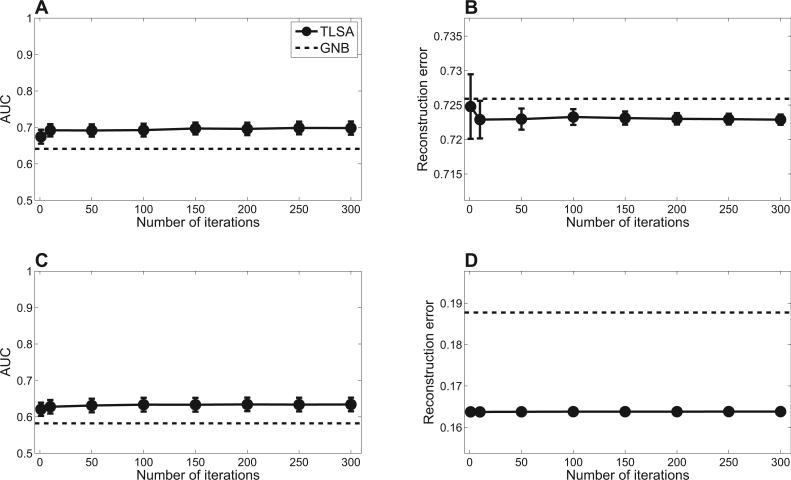
We next evaluated the sensitivity of our results to changes in the number of iterations of the variational inference algorithm. As shown in Figure 3, prediction performance is essentially the same with as few as 50 iterations, but falls o with fewer. This indicates that TLSA can produce a reasonable approximation of the posterior in roughly the same amount of time that it takes to fit a mass-univariate generalized linear model, the standard workhorse of brain imaging analysis.
Figure 3. Prediction performance is insensitive to the number of iterations of the variational inference algorithm.
Top row shows results for the oddball data set; bottom row shows results for the item recognition data set. (A,C ) Mental state decoding accuracy quantified by the area under the receiver operating curve (AUC). (B,D) Brain pattern reconstruction error. Error-bars represent standard error of the difference between TLSA and GNB across subjects.
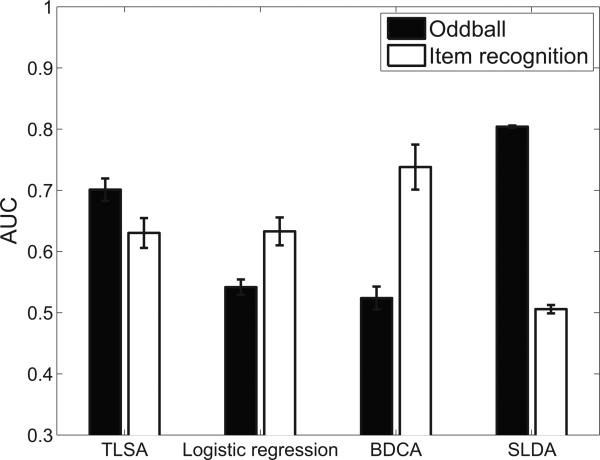
Figure 4 shows a comparison of TLSA with the three discriminative models described in the Materials and Methods: L2-regularized logistic regression, SLDA, and BDCA. Note that we do not compare reconstruction performance, which is outside the scope of the discriminative models (they do not model the distribution of neural data). Our results demonstrate that for the oddball data set, the mental state decoding accuracy of TLSA is second only to SLDA, whereas for the item recognition data set, TLSA is second only to BDCA. TLSA is the only model that performs consistently well across the two data sets.5 This is noteworthy given that these models are designed to directly model the conditional distribution over covariates given neural data, and hence are ideally suited to mental state decoding.
Figure 4. Comparison against discriminative models.
Error-bars represent standard error of the mean.
3.2. How well does TLSA capture the spatiotemporal statistics of neural data?
In contrast to conventional mass-univariate analyses, TLSA builds a spatiotemporal model of neural data from a set of basis functions. We chose these, for simplicity, to be radial basis functions. How well do superpositions of these functions capture the spatiotemporal statistics of the EEG data?
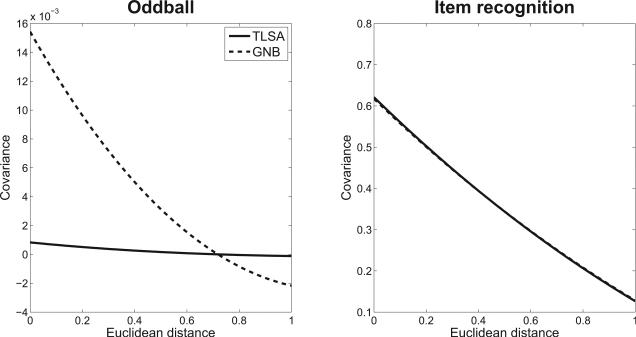
One way to investigate this question is to analyze the spatiotemporal correlation structure of the residuals (i.e., the neural activity after subtracting the model predictions). Both TLSA and GNB predict that these residuals should be uncorrelated (white) Gaussian noise. We can test this prediction by looking at the covariance of the residuals between two neural features as a function of their spatiotemporal distance. If the residuals are independent, this function will be a straight line (i.e., the correlation will be insensitive to distance). Alternatively, if there exists unmodeled spatiotemporal structure, the covariance function will (typically) be a monotonically decreasing function of distance.
We analyzed the residuals for TLSA and GNB fit to the oddball and item recognition data, using the same cross-validation procedure described above: The trials were divided into 6 subsets, the models were fit to 5 of the subsets, and then the residuals of the 5th subset were analyzed by fitting a third-order polynomial to the residuals as a function of squared distance in the coordinate system defined by R. Figure 5 shows the results of the residual analysis. The covariance function for TLSA in the oddball data is nearly straight, indicating that the model is capturing most of the spatiotemporal structure of the data that isn't just noise. In contrast, the covariance function for GNB is monotonically decreasing, indicating that it is failing to model some of the spatiotemporal structure. The story is different for the item recognition data set, where the covariance was generally stronger compared to the oddball data, declining at about the same rate for both TLSA and GNB. Thus, our analyses provide mixed evidence for the claim that TLSA is able to capture the spatiotemporal structure of EEG data better than GNB. One explanation for this discrepancy is that when covariance is stronger overall (as in the item recognition data set), it is harder to attain a flat covariance function with either model.
Figure 5. Covariance function of residuals.
The x-axis represents Euclidean distance between features, and the y-axis represents average covariance between pairs of features separated by a particular distance. (Left) Oddball data set. (Right) Item recognition data set.
3.3. Hypothesis testing illustrations
In this section, we illustrate how TLSA can be used to do hypothesis testing by replicating the analysis of two widely replicated event-related potentials: the P300 in the oddball paradigm, and the parietal old/new effect in the item recognition paradigm.
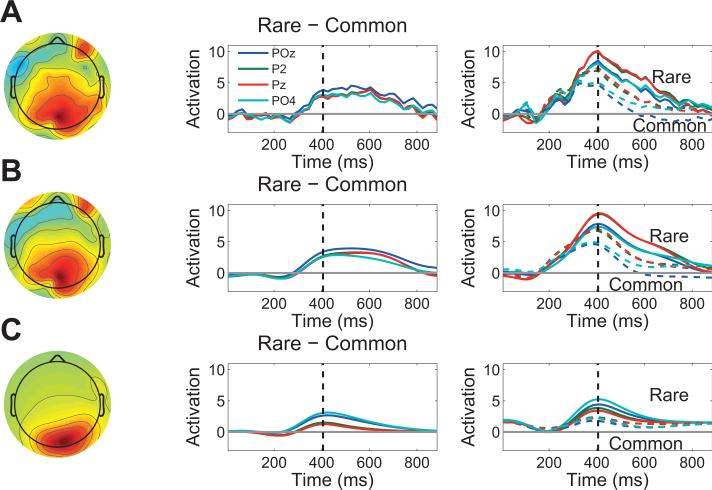
The P300 event-related potential, a positive-going deflection over parietal cortex with a typical latency of 300-500 ms post-stimulus (Squires et al., 1975), is revealed by the contrast rare − common; we replicated this effect in our oddball data (Figure 6A). For TLSA, we constructed the rare − common contrast for each source (with K = 40) and computed a p-value based on a paired-sample t-test across subjects. Figure 6B shows the unthresholded contrast pattern, and Figure 6C shows the thresholded contrast pattern (i.e., the contrast based on the 3 sources that passed the significance threshold of p < 0.05, uncorrected). The thresholded contrast pattern shows fewer loci of activation compared to the mean contrast in Figure 6A, because these other loci did not survive thresholding. These TLSA contrast analyses show a cleaner extraction of the parietal old/new effect compared to the conventional ERP.
Figure 6. Analysis of the P300 in the oddball data set.
(A) Event-related potential: grand average topography at 400 ms post-stimulus (left) and time course (middle) of the rare − common contrast. Electrodes are indicated in the legend. The right panel shows the grand average time course for each condition separately; dashed lines represent the common condition, solid lines represent the rare condition. (B) Topography and time course of the rare − common contrast using latent sources without thresholding. The topography and time courses are obtained by using the latent sources to predict the data at each electrode and time point. (C ) Same as in (B), but using only sources that passed a significance threshold of p < 0.05.
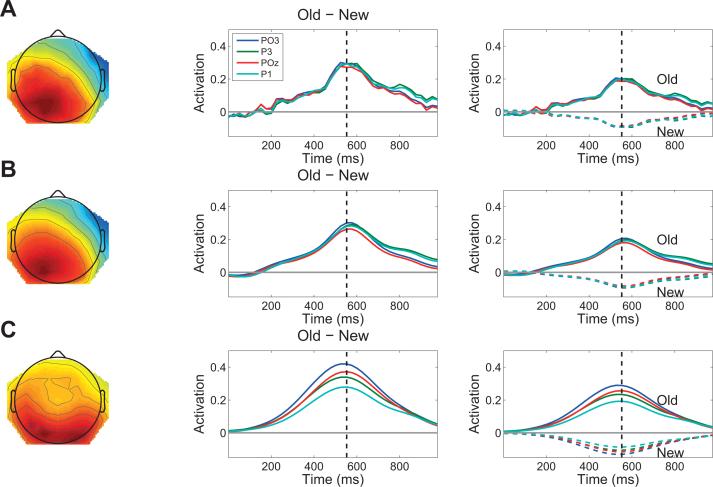
We next examined the parietal old/new effect, a positive-going deflection over parietal cortex with a typical latency of 400-500 ms post-stimulus (Rugg and Curran, 2007). This waveform is revealed by the old − new contrast, an effect we replicated in our item recognition data (Figure 7A). Figure 7B shows the unthresholded contrast pattern, and Figure 7C shows the thresholded contrast pattern (i.e., the contrast based on the 7 sources that passed the significance threshold of p < 0.05, uncorrected). As with the P300, the TLSA contrast shows a cleaner extraction of the parietal old/new effect compared to the conventional ERP.
Figure 7. Analysis of the parietal old/new effect in the item recognition data set.
(A) Event-related potential: grand average topography at 550 ms post-stimulus (left) and time course (middle) of the old − new contrast. Electrodes are indicated in the legend. The right panel shows the grand average time course for each condition separately; dashed lines represent the common condition, solid lines represent the rare condition. (B) Topography and time course of the old − new contrast using latent sources without thresholding. The topography and time courses are obtained by using the latent sources to predict the data at each electrode and time point. (C ) Same as in (B), but using only sources that passed a significance threshold of p < 0.05.
These results demonstrate that TLSA is able to effectively recover standard event-related potential findings; the difference from conventional analyses is that we are applying hypothesis tests to the latent sources rather than to individual electrodes and time windows, dramatically reducing the number of hypothesis tests.
3.4. Performance on BCI competition data with spectral features
Our final analysis applies TLSA to a publicly available dataset from the 3rd BCI competition (del Millán, 2004). As described in the Materials and Methods section, the experiment involved 3 different mental imagery tasks, and the challenge was to decode which of these 3 tasks a participant was engaging in. Our goal in analyzing this data set is to demonstrate that TLSA can yield classification results that are competitive with state-of-the-art algorithms.
In addition, we show that TLSA can be applied to spectral features, simply by replacing spatiotemporal basis functions with spatiospectral basis functions; no modification of the underlying generative model or algorithm is required. In this setting, rt represents one of 12 frequency bands in the 8-30 range, and (μt, ψt) are parameters of a spectral source in frequency space. Note that we are not computing the PSD of the latent sources, but rather modeling the PSD of the data as a linear superposition of latent sources defined in a spatiospectral feature space.
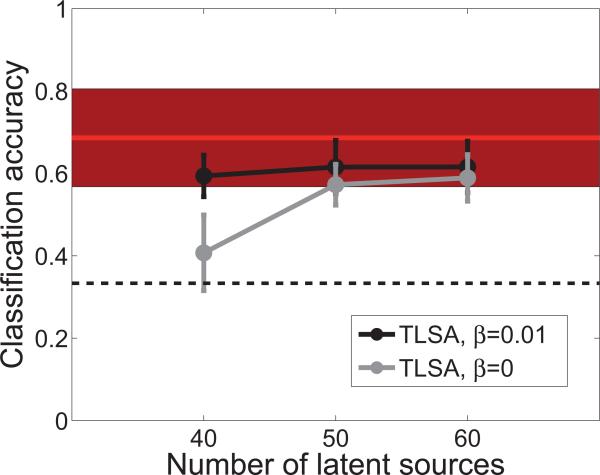
The data set consists of PSD features for 8 central electrodes, computed every 62.5 seconds. Following the BCI competition guidelines, we trained the model on the first 3 sessions and evaluated it on the 4th session (3488 time points per participant, on average). The classification results are shown in Figure 8. In general, both hierarchical and non-hierarchical versions of TLSA perform better than chance, although the hierarchical version appears to do better with 40 latent sources. As a comparison, we show the performance of the algorithm that won the BCI competition, which uses a distance-based discriminant analysis (Galán, Oliva, & Guárdia6). This comparison shows that the classification accuracy of TLSA is comparable to the state-of-the-art.
Figure 8. Performance on the mental imagery data set from the BCI competition.
The x-axis shows the number of latent sources used by TLSA. Results are shown separately for the hierarchical model (β = 0.01) and the non-hierarchical model (β = 0). The dashed line shows chance performance on the 3-way classification, and the red line shows performance of the winning algorithm (filled region shows the standard error across participants).
4. Discussion
We have developed a statistical model for MEG and EEG that decomposes spatiotemporal brain patterns into topographic latent sources. These sources naturally capture the statistical structure of activation patterns that are smooth and localized in space and time (or frequency, in the case of spectral data). Our application of TLSA to three EEG data sets demonstrated the predictive power of our approach: TLSA was able to consistently decode mental states and reconstruct brain patterns with high accuracy. We also illustrated how TLSA can be used for classical hypothesis testing, while avoiding the explosion of multiple comparisons that attend standard mass-univariate analyses (this is true as long as the number of sources is less than the number of neural features, which is almost always the case).
An important contribution of this paper is the development of an efficient variational inference algorithm. For multi-subject data sets with tens of thousands of features and hundreds of covariates, this algorithm typically takes less than 15 minutes to run on a laptop computer. The algorithm can be applied generically to MEG/EEG and fMRI data (simply by modifying the basis function), and permits the use of any differentiable basis function.7 We are thus in a position to begin applying TLSA to larger and more complex data sets.
4.1. Related work
Dimensionality reduction methods have a long history in EEG analysis (Makeig et al., 2004; Lotte et al., 2007). Unsupervised methods, such as independent component analysis (Makeig et al., 1997; Vigário et al., 2000), find projections of the neural data onto a low-dimensional subspace, but ignore covariate information. This runs the risk of finding projections that are not useful for decoding mental states. An alternative approach is to search for discriminative projections of the data (e.g., Müller-Gerking et al., 1999; Lobaugh et al., 2003). The discriminative dimensionality reduction method most related to TLSA is BDCA (Dyrholm et al., 2007), which we described earlier. This method finds a discriminating hyperplane that is the product of two low-rank matrices, corresponding to spatial and temporal dimensions of the neural data. BDCA imposes smoothness on these matrices using Gaussian process priors, analogous to how TLSA imposes smoothness on the basis pattern matrix using topographic latent sources.
TLSA can be viewed as a method for supervised dimensionality reduction based on a generative model of the neural data. In contrast, discriminative models are limited by the fact that they do not model the distribution of the neural data; consequently, they cannot be used for tasks such as reconstructing neural data from covariates. More generally, modeling the distribution of the neural data is useful for exploratory data analysis, where researchers might want to investigate questions about the spatiotemporal statistics of neural signals, rather than conditioning on them for the purposes of mental state decoding.
Another distinguishing characteristic of TLSA is its unit of analysis, namely topographic latent sources. None of its parameters are directly connected to the neural features, which means that features can be removed or modified (e.g., the time series can be down-sampled) without changing the underlying model. Most models of MEG and EEG data take as their unit of analysis to be the neural features themselves, typically by fitting parameters (e.g., regression weights) to these features. Thus, the neural features cannot be changed without constituting a new model. Furthermore, any inferences about spatially or temporally extended regions of activation require post hoc analysis of the feature-specific parameters. In contrast, TLSA models these regions of activation directly.
4.2. Limitations and future directions
It is important to keep in mind that while TLSA is a generative model, it does not express the true physical process giving rise to EEG signals. In particular, scalp topography arises from intracranial current sources, produced by the superposition of post-synaptic potentials. The mapping from dipoles to EEG signals can be captured by a lead field, which models passive conduction of the electric field. Instead of modeling the spatiotemporal statistics of the EEG activity directly (as in TLSA), an alternative approach would be to model the underlying current sources, using the lead field as part of the likelihood function. Haufe et al. (2011) have pursued this approach, using radial basis functions to describe the current sources. We could potentially extend this approach to modeling spatiotemporal current sources.
A similar idea can be applied to modeling spectral features of EEG data. One approach, developed by Dähne et al. (2014), is to first decompose the raw EEG data into its electrical sources, and then compute spectral features of these sources (rather than of the raw data). They show that this approach is able to recover the underlying brain activity with a high signal-to-noise ratio. In principle one could define a version of TLSA that modeled the spectral features extracted by the approach of Däahne et al. (2014).
As we have developed it, TLSA is modular in the sense that any differentiable basis function can be used in combination with our inference algorithm. This means that it is possible to explore more complex families of latent sources, such as deformable volumetric primitives (e.g., Terzopoulos et al., 1988) or splines (Wahba, 1990). It is an interesting empirical question whether these more complex families will outperform the simpler radial basis functions used in this paper. We conjecture that by using more complex sources, the neural data can be well-modeled with a smaller number of sources.
Another potentially useful extension of TLSA is to place a Bayesian nonparametric prior over the source weights. This would allow us to model uncertainty in the number of sources (K), and thereby automatically infer K from the data. For example, we have explored using the beta process (Thibaux and Jordan, 2007; Paisley and Carin, 2009) as a prior on Ws. However, posterior inference with this model is substantially more expensive compared to TLSA with a fixed number of sources. It remains an open question whether the use of nonparametric priors is of sufficient practical value to merit the computational costs. Our results suggest that, at least for the EEG data sets analyzed in this paper, the predictive performance of TLSA is largely insensitive to K.
4.3. Conclusion
Capturing the intricate spatiotemporal statistics of neural signals continues to be a challenging problem. TLSA departs from most models by fitting parameterized continuous functions to the data. These functions provide a low-dimensional and interpretable description of the data. The effectiveness of this approach, both for prediction and hypothesis testing, suggests that TLSA is a promising addition to the neuroimaging tool kit.
Highlights.
A model is presented for decomposing brain imaging data into topographically organized regions.
We describe a fast variational algorithm for fitting the model to data.
The model achieves high predictive accuracy on three EEG data sets.
Acknowledgments
We thank Minqi Jiang and Jeremy Manning for helpful discussions. This research was supported by the NSF/NIH Collaborative Research in Computational Neuroscience Program, grant number NSF IIS-1009542. Samuel J. Gershman was supported by a National Science Foundation Graduate Research Fellowship.
Appendix A: variational inference algorithm
In this section, we derive the complete variational updates. We use “hat” notation (e.g., ) to denote variational parameters, but in some cases we will also use this notation to denote the expected value of a parameter under the variational posterior, .
Update for λm
For this update we need to calculate:
| (18) |
It can be shown that q′(λm) is a Gamma distribution:
| (19) |
where
| (20) |
Update for ω0k
For this update we need to calculate:
| (21) |
It can be shown that the updated q-distribution for ω0k is a Gaussian:
| (22) |
where
| (23) |
| (24) |
and is derived below.
Update for ωsk
For this update we need to calculate:
| (25) |
Using the linearization of the likelihood (Eq. 35), it can be shown that q′(ωsk) is multivariate Gaussian (Chappell et al., 2009):
| (26) |
where
| (27) |
| (28) |
and represents the value of from the previous iteration. is defined below.
Update for τs
For this update we need to calculate:
| (29) |
Using the linearization of the likelihood (Eq. 35), it can be shown that q′(τs) is a Gamma distribution (Chappell et al., 2009):
| (30) |
where
| (31) |
| (32) |
where is the summed squared error and ŷns = xnsŴsF̂s is the predicted brain pattern. Under the approximate posterior, the expectation of τs is .
Update for Ws
We choose q(Ws) = δ[Ws, Ŵs, where δ[·, ·] is the delta function whose value is 1 if its arguments are equal, and 0 otherwise. By placing an infinitely broad prior on Ws, such as , the optimal setting of Ŵs is the maximum likelihood estimate. This is equivalent to solving the following linear system:
| (33) |
where ⊗ denotes the Kronecker product and vec(·) denotes the operation that reshapes a matrix into a column vector. This linear system can be solved efficiently with matrix factorization methods (e.g., the LU decomposition), without explicitly constructing the Kronecker product.
Appendix B: linearized likelihood
Conditional on , the log-likelihood is given by:
| (34) |
Note that Es is implicitly a function of .
Due to the fact that φ(·; ω) is generally a non-linear function of ω, the Gaussian prior we placed on ω will not be conjugate to the likelihood, and hence all expectations involving ω will be analytically intractable at the subject-level. We can obtain a linearized approximation by using a first-order Taylor series expansion around the posterior mode (which for a Gaussian is also the mean). Expressing the predicted brain patterns Ŷ s as a function of ωsk, the linearized approximation is:
| (35) |
where Jsk is the NV × M Jacobian matrix of partial derivatives with respect to ωsk:
| (36) |
Under this linearization, the likelihood is a linear-Gaussian function of ω, and thus we obtain a closed-form variational update (see Appendix A). Using this linearization means that the variational lower bound on the log marginal likelihood (Eq. 7) no longer strictly holds. In practice we find that the algorithm converges reliably to good solutions (in the sense of visual inspection and predictive performance), though we cannot guarantee that such solutions represent local optima of the lower bound.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Our use of the word “source” is different from its use in source reconstruction for MEG and EEG (Grech et al., 2008). The source reconstruction problem is to find the current source generating signals measured on the scalp. In this paper, we are focused on modeling the spatiotemporal distributions of signals, rather than their precise anatomical localization (which is known to be an ill-posed problem).
We use the gamma distribution parameterized in terms of shape and scale ν and scale ρ.
We found that SLDA produced dramatically different performance depending on the shrinkage method, but no method performed consistently well across both data sets.
First-order differentiability is required in order to implement the linearized likelihood described in Appendix B.
Contributor Information
Samuel J. Gershman, Department of Brain and Cognitive Sciences, Massachusetts Institute of Technology, Cambridge, MA 02139, USA.
David M. Blei, Department of Computer Science, Princeton University, 35 Olden Street, Princeton, NJ 08540, USA
Kenneth A. Norman, Department of Psychology and Princeton Neuroscience Institute, Princeton University, Princeton, NJ 08540, USA
Per B. Sederberg, Department of Psychology, The Ohio State University, Columbus OH 43210, U.S.A
References
- Attias H. A variational bayesian framework for graphical models. Advances in Neural Information Processing Systems. 2000;12:209–215. [Google Scholar]
- Blankertz B, Lemm S, Treder M, Haufe S, Müller K-R. Single-trial analysis and classification of erp componentsa tutorial. NeuroImage. 2011;56:814–825. doi: 10.1016/j.neuroimage.2010.06.048. [DOI] [PubMed] [Google Scholar]
- Braun M, McAuli e J. Variational inference for large-scale models of discrete choice. Journal of the American Statistical Association. 2010;105:324–335. [Google Scholar]
- Castellanos N, Makarov V. Recovering eeg brain signals: artifact suppression with wavelet enhanced independent component analysis. Journal of Neuroscience Methods. 2006;158:300–312. doi: 10.1016/j.jneumeth.2006.05.033. [DOI] [PubMed] [Google Scholar]
- Chappell M, Groves A, Whitcher B, Woolrich M. Variational bayesian inference for a nonlinear forward model. IEEE Transactions on Signal Processing. 2009;57:223–236. [Google Scholar]
- Dähne S, Meinecke FC, Haufe S, Höhne J, Tangermann M, Müller K-R, Nikulin VV. Spoc: A novel framework for relating the amplitude of neuronal oscillations to behaviorally relevant parameters. NeuroImage. 2014;86:111–122. doi: 10.1016/j.neuroimage.2013.07.079. [DOI] [PubMed] [Google Scholar]
- del Millán J. Proceedings. 2004 IEEE International Joint Conference on. Vol. 4. IEEE; 2004. On the need for on-line learning in brain-computer interfaces. In Neural Networks, 2004. pp. 2877–2882. [Google Scholar]
- Dyrholm M, Christoforou C, Parra L. Bilinear discriminant component analysis. The Journal of Machine Learning Research. 2007;8:1097–1111. [Google Scholar]
- Friston K, Chu C, Mourão-Miranda J, Hulme O, Rees G, Penny W, Ashburner J, et al. Bayesian decoding of brain images. NeuroImage. 2008;39:181–205. doi: 10.1016/j.neuroimage.2007.08.013. [DOI] [PubMed] [Google Scholar]
- Friston K, Mattout J, Trujillo-Barreto N, Ashburner J, Penny W, et al. Variational free energy and the laplace approximation. NeuroImage. 2007;34:220–234. doi: 10.1016/j.neuroimage.2006.08.035. [DOI] [PubMed] [Google Scholar]
- Geller A, Schleifer I, Sederberg P, Jacobs J, Kahana M. Pyepl: A cross-platform experiment-programming library. Behavior Research Methods. 2007;39:950–958. doi: 10.3758/bf03192990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gershman S, Blei D, Pereira F, Norman K. A topographic latent source model for fMRI data. NeuroImage. 2011;57:89–100. doi: 10.1016/j.neuroimage.2011.04.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gershman S, Ho man M, Blei D. Langford J, Pineau J, editors. Nonparametric variational inference. Proceedings of the 29th International Conference on Machine Learning. 2012:767–774. [Google Scholar]
- Grech R, Cassar T, Muscat J, Camilleri K, Fabri S, Zervakis M, Xanthopoulos P, Sakkalis V, Vanrumste B. Review on solving the inverse problem in eeg source analysis. Journal of Neuroengineering and Rehabilitation. 2008;5:25. doi: 10.1186/1743-0003-5-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haufe S, Tomioka R, Dickhaus T, Sannelli C, Blankertz B, Nolte G, Müller K-R. Large-scale eeg/meg source localization with spatial flexibility. NeuroImage. 2011;54:851–859. doi: 10.1016/j.neuroimage.2010.09.003. [DOI] [PubMed] [Google Scholar]
- Jordan M, Ghahramani Z, Jaakkola T, Saul L. An introduction to variational methods for graphical models. Machine Learning. 1999;37:183–233. [Google Scholar]
- Lobaugh N, West R, McIntosh A. Spatiotemporal analysis of experimental di erences in event-related potential data with partial least squares. Psychophysiology. 2003;38:517–530. doi: 10.1017/s0048577201991681. [DOI] [PubMed] [Google Scholar]
- Lotte F, Congedo M, Lécuyer A, Lamarche F, Arnaldi B. A review of classification algorithms for eeg-based brain–computer interfaces. Journal of Neural Engineering. 2007;4:1–13. doi: 10.1088/1741-2560/4/2/R01. [DOI] [PubMed] [Google Scholar]
- Makeig S, Debener S, Onton J, Delorme A, et al. Mining event-related brain dynamics. Trends in Cognitive Sciences. 2004;8:204–210. doi: 10.1016/j.tics.2004.03.008. [DOI] [PubMed] [Google Scholar]
- Makeig S, Jung T, Bell A, Ghahremani D, Sejnowski T. Blind separation of auditory event-related brain responses into independent components. Proceedings of the National Academy of Sciences. 1997;94:10979–10984. doi: 10.1073/pnas.94.20.10979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manning JR, Ranganath R, Norman KA, Blei DM. Topographic factor analysis: a bayesian model for inferring brain networks from neural data. PLoS One. 2014 doi: 10.1371/journal.pone.0094914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller-Gerking J, Pfurtscheller G, Flyvbjerg H. Designing optimal spatial filters for single-trial eeg classification in a movement task. Clinical Neurophysiology. 1999;110:787–798. doi: 10.1016/s1388-2457(98)00038-8. [DOI] [PubMed] [Google Scholar]
- Paisley J, Carin L. Proceedings of the 26th Annual International Conference on Machine Learning. ACM; 2009. Nonparametric factor analysis with beta process priors. pp. 777–784. [Google Scholar]
- Robert C, Casella G. Monte Carlo Statistical Methods. Springer; New York: 2004. [Google Scholar]
- Rugg MD, Curran T. Event-related potentials and recognition memory. Trends in Cognitive Sciences. 2007;11:251–257. doi: 10.1016/j.tics.2007.04.004. [DOI] [PubMed] [Google Scholar]
- Schäfer J, Strimmer K, et al. A shrinkage approach to large-scale covariance matrix estimation and implications for functional genomics. Statistical applications in genetics and molecular biology. 2005;4:32. doi: 10.2202/1544-6115.1175. [DOI] [PubMed] [Google Scholar]
- Squires N, Squires K, Hillyard S. Two varieties of long-latency positive waves evoked by unpredictable auditory stimuli in man. Electroencephalography and Clinical Neurophysiology. 1975;38:387–401. doi: 10.1016/0013-4694(75)90263-1. [DOI] [PubMed] [Google Scholar]
- Terzopoulos D, Witkin A, Kass M. Constraints on deformable models: Recovering 3d shape and nonrigid motion. Artificial Intelligence. 1988;36:91–123. [Google Scholar]
- Thibaux R, Jordan M. Hierarchical beta processes and the indian bu et process. International Conference on Artificial Intelligence and Statistics. 2007;11:564–571. [Google Scholar]
- Vigário R, Sarela J, Jousmiki V, Hamalainen M, Oja E. Independent component approach to the analysis of eeg and meg recordings. Biomedical Engineering, IEEE Transactions on. 2000;47:589–593. doi: 10.1109/10.841330. [DOI] [PubMed] [Google Scholar]
- Wahba G. Spline Models for Observational Data. Society for Industrial Mathematics. 1990 [Google Scholar]
- Yang Z, Fang F, Weng X. Recent developments in multivariate pattern analysis for functional mri. Neuroscience Bulletin. 2012;28:399–408. doi: 10.1007/s12264-012-1253-3. [DOI] [PMC free article] [PubMed] [Google Scholar]