Semi-Adiabatic Shinnar Le-Roux Pulses and their Application to Diffusion Tensor Imaging of Humans at 7T

Abstract

The adiabatic Shinnar Le-Roux (SLR) algorithm for radiofrequency (RF) pulse design enables systematic control of pulse parameters such as bandwidth, RF energy distribution and duration. Some applications, such as diffusion weighted imaging (DWI) at high magnetic fields, would benefit from RF pulses that can provide greater B₁-insensitivity while adhering to echo time and specific absorption rate (SAR) limits. In this study, the adiabatic SLR algorithm was employed to generate 6-ms and 4-ms 180° semi-adiabatic RF pulses which were used to replace the refocusing pulses in a twice refocused spin echo (TRSE) diffusion weighted echo planar imaging (DW-EPI) sequence to create two versions of a twice refocused adiabatic spin echo (TRASE) sequence. The two versions were designed for different trade offs between adiabaticity and echo time. Since a pair of identical refocusing pulses are applied, the quadratic phase imposed by the first is unwound by the second, preserving the linear phase created by the excitation pulse. In vivo images of the human brain obtained at 7T demonstrate that both versions of the TRASE sequence developed in this study achieve more homogeneous signal in the diffusion weighted images than the conventional TRSE sequence. Semi-adiabatic SLR pulses offer a more B₁-insensitive solution for diffusion preparation at 7T, while operating within SAR constraints. This method may be coupled with any EPI readout trajectory and parallel imaging scheme to provide more uniform coverage for DTI at 7T as well as 3T.

Introduction

Adiabatic radiofrequency (RF) pulses can be powerful replacements for conventional windowed sinc or Shinnar Le-Roux (SLR) pulses in MR pulse sequences to provide greater immunity to B₁-inhomogeneity when operating at high magnetic fields or when using surface coils with non-uniform B₁ profiles. One of the advantages of the adiabatic SLR algorithm described in 2010 [1], is that the designer has greater control over pulse and spectral profile characteristics. Therefore trade offs can more easily be made between aspects of pulse performance such as spatial selectivity, bandwidth, duration, maximum amplitude and adiabaticity. Adiabatic pulses often have high time-bandwidth (TBW) products resulting in good selectivity, but also high RF power deposition as measured by the specific absorption rate (SAR). Sometimes, a certain amount of B₁-insensitivity is desired but bandwidth (BW) and duration of the RF pulse need to be lower in order to adhere to echo time (TE) and SAR limits. Using the adiabatic SLR algorithm, these parameters can be traded off for degree of adiabaticity. Furthermore, the adiabatic SLR method allows the pulse designer to apply additional quadratic phase across the pulse profile in order to achieve a more uniform distribution of RF energy. One application in which a short, low-BW, B₁-insensitive pulse would be useful is diffusion tensor imaging (DTI) in the presence of the non-uniform B₁ field that is observed at 7 Tesla (7T).

The higher signal-to-noise ratio (SNR) offered at 7T has been shown to increase the SNR and directional certainty of DTI-based parameters such as fractional anisotropy (FA) [2,3]. However, DTI at 7T faces major challenges including B₀ and B₁-inhomogeneity and shortening of white matter T₂ values, from 71 ms at 3T to 47 ms at 7T [4], offsetting the SNR benefits offered by the higher magnetic field. Nonetheless, development of an optimized DTI sequence is essential for developing a complete neuroimaging protocol at 7T. Although some techniques have been proposed that provide solutions for better excitation or readout of magnetization at 7T [5–9], the optimal sequence structure for 7T DTI has yet to be established.

Readout-segmented echo planar imaging (EPI) combined with parallel imaging may be used to contend with the severe B₀ artifact [5]. Fast Spin Echo (FSE or TSE) sequences have also been used at 7T instead of EPI to reduce susceptibility artifacts [6]. However, in order to reduce signal loss due to B₁-inhomogeneity, alternative approaches for excitation of the magnetization must be explored. A simple Stejskal-Tanner pulse sequence utilizes a single refocusing pulse and allows for shorter TEs but is not easily translated to an adiabatic sequence and must be coupled with post-processing eddy current compensation methods that result in some data blurring. Looking forward, as stronger gradient sets are used to shorten echo times and achieve higher b values, diffusion gradients will be driven to a higher maximum value, increasing the severity of eddy current distortions which scale with maximum gradient amplitude.

A twice-refocused spin echo (TRSE) diffusion preparation which utilizes two 180° RF pulses, is regulary used in clinical scans and has shown value in substantially reducing eddy current distortions [10, 11]. A TRSE approach cancels eddy current effects through the use of appropriately chosen bipolar diffusion gradients [10, 12]. It is particularly well suited to the use of adiabatic refocusing pulses because the second identical adiabatic 180° pulse perfectly refocuses quadratic phase induced by the first one, leaving no net phase in the final echo. This is important because quadratic phase across the final slice would result in signal loss. Echo time for TRSE sequences may be shortened by the use of stronger diffusion gradients, while inherently compensating for the resultant increase in eddy current effects. Furthermore, the twice refocused approach may be used to perform reduced field of view imaging at high resolutions [13]. In this case a second 180° pulse is necessary to reset inverted spins outside the desired slice or to provide a third dimension of selectivity. Therefore it is of value to investigate twice refocused approaches to diffusion weighted imaging at 7T, in addition to single refocused approaches.

Our objective was to increase the B₁-insensitivity of the TRSE sequence while not significantly increasing the effective TE and operating within SAR limits for similar acquisition times. This was achieved by replacing the 180° RF pulses in the TRSE sequence with semi-adiabatic SLR pulses which were specifically designed to minimize pulse duration and peak B₁ at adiabatic threshold, while maintaining a high degree of adiabaticity. The semi-adiabatic SLR pulses achieve higher quality slice profiles with lower SAR and peak amplitude than conventional hyperbolic secant (HS) [14–16] pulses designed to have similar BW and pulse duration. Using a twice-refocused adiabatic spin echo (TRASE) sequence has been previously proposed and shown to improve image homogeneity in phantoms at 3T and 7T and DWI of animals at 14.1T [7,8,17].

This work shows that semi-adiabatic SLR pulses can substantially improve the performance of the standard TRSE sequence at 7T and provide more uniform SNR in the presence of B₁-inhomogeneity. Two different variants of the semi-adiabatic SLR pulses with different pulse durations, BW, and B₁-insensitivity were tested. Although this method could be applicable at both 3T and 7T, results are obtained in the human brain at 7T in order to demonstrate improved performance in the presence of severe B₁-inhomogeneity.

Methods

RF Pulse and Pulse sequence Design

Our first step was to design an adiabatic SLR 180° pulse to replace the 180° pulses in the TRASE DWI sequence. The adiabatic SLR algorithm [1] was used to generate an adiabatic full passage 180° pulse.

The pulse was designed to have physical spectral bandwidth of 2.32 kHz, pulse duration of 6 ms and fractional transition width (FTW) of 0.5. The sampling rate, f_s, in Hz for the filter was set to 119 kHz. Values used as inputs for the finite impulse response filter design function “firls” in MATLAB (The Mathworks, Natick, MA, USA) were

$$\begin{array}{cc}\hfill f_{\mathit{\text{FIR}}}& =\text{firls}(N,F,A,W)\hfill \\ \hfill N& =355\hfill \\ \hfill F& =\frac{1}{\pi }[00.01\pi 0.03\pi \pi ]\hfill \\ \hfill A& =[1100]\hfill \\ \hfill W& =[0.1/8\text{sqrt}(0.01/2)]\hfill \end{array}$$ (1)

As described in [1], N is the number of samples. F is a vector of frequency band edges given in the range [0, π] but normalized to [0,1]. The vector A specifies the desired amplitude of the frequency response of the resultant filter and, in this case, is set for a lowpass filter. W contains the relative ripple amplitudes in the pass- and stopbands.

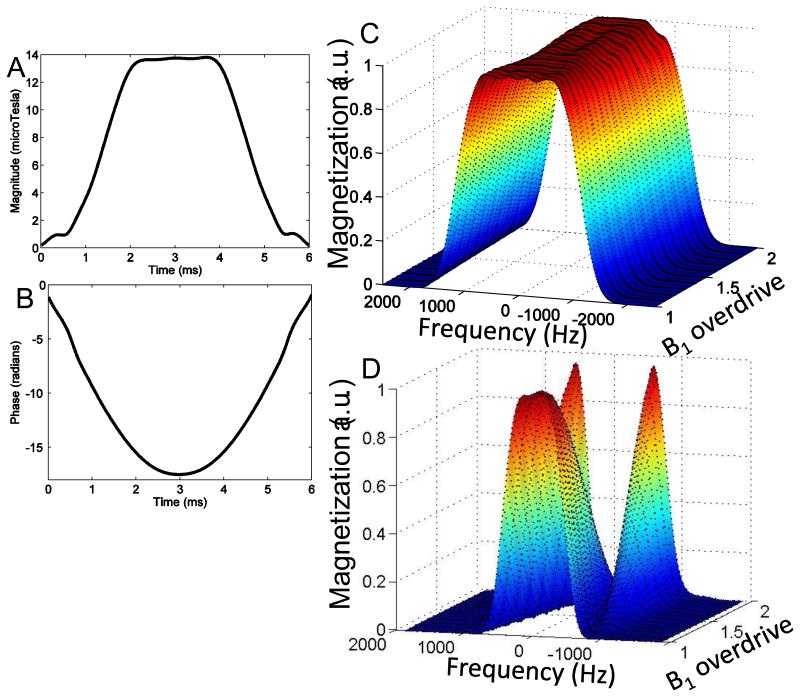
Quadratic phase was applied to spread RF energy as uniformly as possible over the pulse duration and reduce peak B₁. Lower peak RF amplitude allows for a greater range of B₁ immunity before the hardware limit for the RF coil/amplifier combination is reached. The constant, k, determines the number of cycles of quadratic phase that are applied across the spectral profile. A k value of 2000 was used. This resulted in a maximum pulse amplitude of 13.8 µT at adiabatic threshold. The amplitude and phase waveforms for the 6 ms adiabatic SLR 180° pulse are shown in Figs. 1 A and B.

Figure 1.

RF (A) amplitude and (B) phase waveforms for 6 ms semi-adiabatic SLR 180° RF pulse designed for version 1 of the twice-refocused adiabatic DWI sequence. Simulated slice profile for (C) the semi-adiabatic pulse used in the TRASE sequence and (D) a conventional 180° used in a TRSE sequence for a range of B₁ overdrive factors. The B₁ overdrive factor is equal to the amplitude at which the pulse is operated divided by the amplitude of the pulse at adiabatic threshold. The semi-adiabatic pulse profile remains fairly invariant as B1 is overdriven, while a conventional 180° varies significantly. However the 6 ms semi-adiabatic pulse duration results in a longer minimum TE than the conventional twice refocused DWI sequence.

Simulations were performed in MATLAB by calculating the Cayley-Klein parameters, α and β, for the piecewise-constant RF pulse as described in [18]. The expressions for the Cayley-Klein parameters represent a series of rotations and may be used to generate the spectral profile for the pulse. Note that this is equivalent to the calculations performed by a discrete-time Bloch simulator [18]. To isolate the effect of the 180° pulse, a refocusing slice profile given by β² is calculated, where the initial transverse magnetization is assumed to be 1.

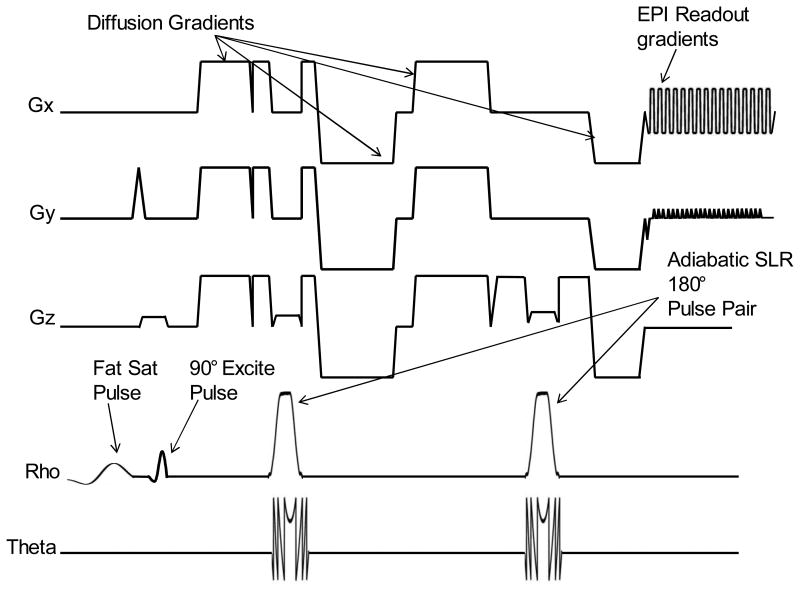
The simulated slice profile behavior plotted for RF overdrive factors ranging from 1 to 2 is shown in Fig. 1 C. The RF overdrive factor is equal to the amplitude at which the pulse is operated divided by the amplitude of the pulse at adiabatic threshold. Therefore, a RF overdrive factor of 1.2 would mean a 20% increase of pulse amplitude above the adiabatic threshold. There is slight variation in profile shape as the pulse is overdriven, but when compared to the drastically varying slice profile for a conventional 180° pulse shown in Fig. 1 D, the fidelity of the profile is largely maintained, demonstrating near-adiabatic behavior. The TRASE DW-EPI sequence utilizing a pair of identical semi-adiabatic SLR pulses for refocusing and bipolar diffusion gradients is shown in Fig. 2. The crusher area is larger for the second 180° pulse in order to prevent the formation of a coherence pathway. An imperfect 180° will have 90° component resulting in a stimulated echo if the crusher area is the same. Thus, unequal crusher areas are utilized.

Figure 2.

RF amplitude, phase and gradient waveforms for TRASE DWI sequence with semi-adiabatic SLR pulses.

Although the 6-ms pulse achieves good adiabatic behavior, the increased pulse duration and BW, when compared to the conventional 180° pulses results in a 10 ms increase in echo time. Additionally, SAR is proportional to the TBW product of pulses, so it is prudent to minimize TBW to that required for a certain application. Longer TEs are disadvantageous given the shortening T₂s at 7T, however, the effective TE for a TRASE sequence is different than that for a TRSE sequence, as magnetization is spin-locked during a adiabatic pulse and experiences slower decay.

In order to achieve more comparable TEs and lower SAR, a second version of the pulse was developed with lower BW and shorter duration. This was achieved by redesigning the spectral profile and truncating the waveforms further, which resulted in some variation of profile shape and approximately 5% signal loss as B₁ was varied, or equivalently less robust adiabatic behavior. The second version of the semi-adiabatic SLR 180° pulse, for which RF waveforms and simulated slice profile for a range of B₁ are shown in Figs. 3 A–C, was designed to have a 1.65kHz bandwidth and was highly truncated to a 4 ms duration with a peak RF amplitude of 11.7 µT. A k value of 3000 was used when setting the quadratic phase. The inputs into the firls function in MATLAB were

Figure 3.

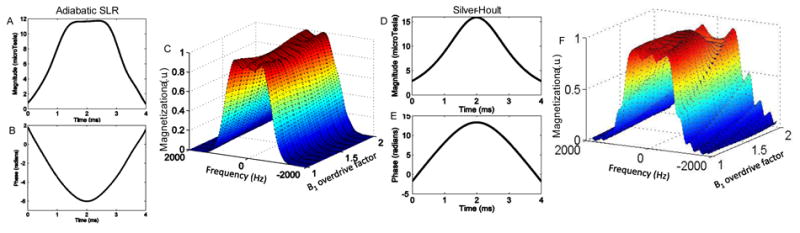
RF (A) amplitude and (B) phase waveforms for 4-ms semi-adiabatic SLR 180° RF pulse designed for shorter TE twice-refocused DWI sequence. (C) Simulated slice profile for the pulse for a range of B₁ amplitudes. Because the pulse is highly truncated, there is some variation in the slice profile amplitude and shape as B¹ is overdriven. A trade off exists between adiabaticity and pulse duration. Amplitude and phase waveforms for a comparative HS pulse are shown in (D) and (E). Deterioration of slice profile and loss of adiabatic behavior result from severe truncation as shown in the simulated profile in (F)

$$\begin{array}{cc}\hfill f_{\mathit{\text{FIR}}}& =\text{firls}(N,F,A,W)\hfill \\ \hfill N& =355\hfill \\ \hfill F& =\frac{1}{\pi }[00.007\pi 0.017\pi \pi ]\hfill \\ \hfill A& =[1100]\hfill \\ \hfill W& =[0.1/8\mathit{\text{sqrt}}(0.01/2)]\hfill \end{array}$$ (2)

A conventional HS adiabatic pulse designed to have 4-ms duration and similar BW suffers from severe deterioration of the spatial profile as the B₁ amplitude is increased. Pulse waveforms and simulated profiles for a comparative HS pulse are shown in Figs 3 D–F. Variation in the slice profile shown in F occurs because manipulation of the hyperbolic secant modulation function to yield a 1.6 kHz pulse with 4-ms duration results in severe truncation of the pulse waveform and loss of adiabaticity. In this case, conflicting pulse design requirements for BW, pulse duration, adiabaticity and profile shape cannot be simultaneously satisfied for the conventional HS pulse. Additionally, the RF energy distribution of the HS pulse is not as uniform as the adiabatic SLR pulse, resulting in higher peak amplitude and more limited range of adiabatic operation for the same hardware limits. SAR for the HS pulse is also 38% greater than the SLR pulse at adiabatic threshold. In order to produce similar slice profile behavior with a 4-ms HS pulse, the BW would have to be increased by 70%, resulting a more than doubling of the SAR when compared to the 4-ms adiabatic SLR pulse.

The 6-ms and 4-ms adiabatic SLR pulses resulted in two versions of the sequence in Fig. 2. Version 1, utilizing 6 ms refocusing pulses with 94.8 ms TE and Version 2 utilizing 4 ms refocusing pulses with 88.8 ms TE. The minimum TE of the TRSE sequence was 83.8 ms.

The RF energy deposition as defined by the SAR value for the 6 ms semi-adiabatic SLR pulse was calculated and compared to the 4 ms semi-adiabatic SLR pulse. At adiabatic threshold, the SAR for the 4 ms pulse was 54% of the SAR of the 6 ms pulse. When compared to a windowed sinc 180° RF pulse with a TBW product of 3 (similar to that used in the conventional TRSE sequence), the 4 ms semi-adiabatic SLR pulse deposits 2.8 times the RF energy of the windowed sinc pulse. Both pulses operate within conservative SAR limits with a marginal increase in total acquisition time. Pulse bandwidth, profile shape and maximum pulse amplitude at adiabatic threshold are factors determining the calculated SAR value.

In Vivo Experiments

Three healthy volunteers were scanned with a product TRSE sequence and Version 1 of our TRASE sequence. Scans were performed at 7T (Echospeed whole-body magnet; GE Healthcare, Waukesha, WI, USA) using a Nova Medical (Wilmington, MA) 2 channel quadrature transmit and 32-channel parallel-receive head coil. Sequence parameters were: 45 slices, 3 mm slice thickness, 128×128 grid, 24 cm FOV, TE/TR=83.8ms/5.5s and scan time=2:56 s for the product TRSE and TE/TR=94.8/6.5s and scan time=3:28 s for TRASE. The same b value of 1000 s/mm² was used for both sequences. A slightly longer TR was used for the TRASE sequence to ensure operation within SAR limits for all scans. Chemical saturation was used for fat suppression. Full DTI data sets were acquired with 32 diffusion encoded directions. B₁ maps were also obtained using adiabatic Bloch Siegert B₁⁺ mapping [19]. The experiment was repeated using Version 2 of the sequence on 6 healthy volunteers. All scan parameters remained the same except the TE for the TRASE sequence shortened to 88.8 ms.

Diffusion weighted images were acquired in 32 directions. Effects on diffusion weighted images due to residual eddy currents and subject motions were corrected by performing image registration using tools available in FSL. The resulting images were applied to a linear least square fitting algorithm, followed by tensor decomposition to create mean diffusivity (MD), fractional anisotropy (FA) and color-coded FA maps. The latter steps were implemented as a plugin DTIMap of a DICOM viewer platform OsiriX (free and open-source software

SNR measurement in parallel imaging accelerated images is not trivial due to spatial variation of g-factor. Since the same FOV and acceleration factor were used in both the standard and TRASE acquisitions, the g-factor distribution is the same in both methods. Therefore the signal cross-sections were compared in selected regions to reflect the SNR improvement of the TRASE method. To further explore the measurement accuracy of processed images, e.g. FA map, a relatively homogeneous ROI was chosen in a region of peak B₁ and the standard deviation of FA values was calculated. The standard deviation consists of two components: (1) intrinsic spatial variation of FA values (2) noise/inaccuracy in the FA measurement. Since the intrinsic spatial variation of the FA values is the same in the two methods, the standard deviation reflects the inaccuracy in the measurement of FA values

Results

Figure 4 shows diffusion weighted images in one direction for a slice of the brain of a representative volunteer obtained using (A) product TRSE and (B) Version 1 of our TRASE sequence for DWI. The B₁ profile of the slice is shown in Fig. 4 D . The main area of signal loss due to a peak in the B₁ profile at the center of the brain is indicated by the white arrow in Fig. 4 A. This signal is largely recovered by the TRASE sequence as shown by Fig. 4 B. Central cross sections through these two images are shown in Fig. 4 C, demonstrating appreciable signal increase afforded by the TRASE sequence at the center of the brain.

Figure 4.

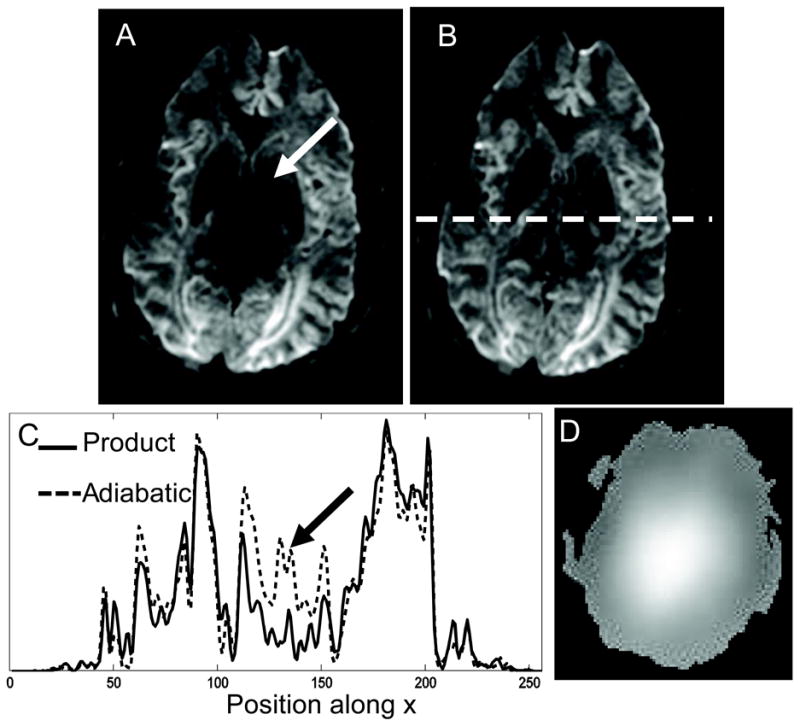
Diffusion weighted image along one direction for a chosen slice of the brain obtained using (A) the product TRSE sequence and (B) version 1 of the proposed TRASE sequence using 6 ms semi-adiabatic SLR pulses. The white arrow in (A) indicates area of signal loss due to overdriven 180° pulses caused by B1 inhomogeneity. (C) Cross section as indicated by the white dotted line in (B) across both images. Black arrow indicates signal difference at center. (D) B₁ map of the slice.

FA maps for the same slice of the brain in Fig. 4 are shown in Figs. 5 A and B for the product TRSE and TRASE sequences, respectively. Zoomed regions of the color-coded and grayscale FA maps of the chosen slice, containing structures such as the thalamus and corticospinal tracts, are shown in Figs. 5 (C,D) and (E,F), respectively. An elliptical ROI indicated with the yellow outline on Figs. 5 E and F shows a region over which the standard deviation (STD) of FA values was calculated. The STD measured in an ROI will include contributions from true tissue contrast and noise. Since the true tissue contrast should be the same between the two methods, the STD measured will reflect imaging noise. Still, a region was outlined only on one side of the brain to minimize the contribution from tissue contrast. For this data set, the STD over the ROI was 0.33 for the conventional TRSE sequence and 0.17 for the TRASE FA maps. Therefore, in the thalamic region, where there is a peak in the B₁ field, FA map obtained by the semi-adiabatic SLR TRASE sequence benefits from less noise when compared to the product TRSE sequence.

Figure 5.

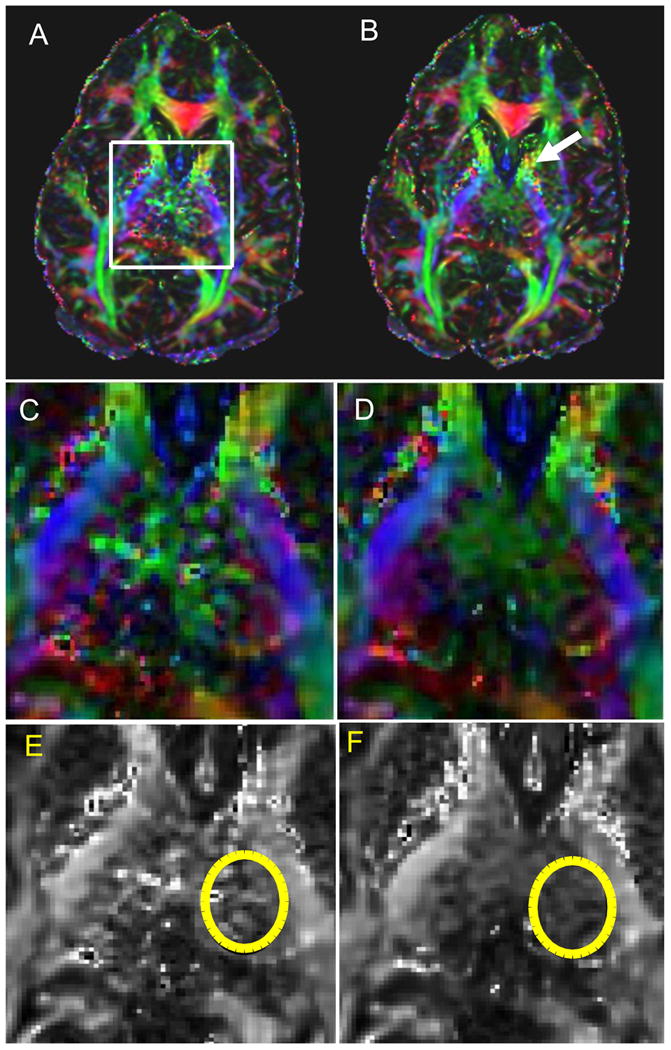
Fractional anisotropy maps of the slice of the brain shown in Fig. 4 generated from the DTI dataset obtained using (A) TRSE and (B) TRASE sequence. White box indicates area of increased noise in the FA map due to B₁-induced signal loss in the diffusion weighted images. Color FA maps zoomed into the region indicated by the white box in (A) are shown in C and D for the TRSE and TRASE sequences, respectively. E and F show the grayscale versions of the zoomed FA maps in C and D. Yellow ellipses on E and F indicate areas for which noise in the FA measurement was calculated and compared for the two sequences. STD of the FA measurement was 0.17 for the TRASE sequence, while it was 0.33 for the conventional TRSE sequence. The white arrow in B indicates a region where the TRASE sequence exhibits noisier FA values than the TRSE sequence. This may be due to the longer pulse duration for the adiabatic refocusing pulses.

The white arrow in Fig. 5 B indicates a region where the TRASE sequence exhibits noisier FA values than the TRSE sequence. This region is approximately in the anterior limb of the internal capsule, which should have comparable T₂ values to other white matter regions. However, the region is proximate to regions with lower T₂ values, such as the putamen. Therefore, signal loss in this region may be due to T₂-decay occurring over longer TE required to accomodate longer pulses and crusher durations in the TRASE sequence. Another possibility is that the TRASE sequence, which utilizes long quadratic phase pulses, may have greater sensitivity to pulsatile motion due to imperfect refocusing of the phase of moving spins. For these reasons, it was necessary to explore Version 2 of the sequence that utilizes shorter adiabatic RF pulses with lower bandwidth and achieves a shorter minimum TE.

Figures 6 and 7 show in vivo results from two representative volunteers using Version 2 of the TRASE sequence. For both Figs. 6 and 7, A and B show raw diffusion weighted images for one diffusion direction obtained using the conventional TRSE sequence and Version 2 of the TRASE sequence, respectively. Comparative cross sections along the central area of the raw DWI images indicated by the white dotted line on B are shown in E. Signal intensity at the center of the brain is approximately doubled when using the TRASE sequence instead of TRSE. The B₁-map for the chosen slice is provided in F. Color-coded FA maps can be seen in C and D. Zoomed in color-coded and grayscale FA maps are shown in (G,H) and (I,J), respectively. The area over which the STD was calculated for the FA maps is indicated by the yellow ellipse on I and J. For the dataset in Fig. 6, the STD value was 0.37 for the TRSE sequence compared with 0.11 for the TRASE sequence. The white arrows in Fig. 6 D indicate white matter tracts in which greater SNR and directional certainty is achieved by the TRASE sequence when compared to TRSE. For the dataset in Fig. 7, STD value was 0.36 for the TRSE sequence compared with 0.27 for the TRASE sequence. The two volunteer datasets shown in Figs. 6 and 7 demonstrate that the improvement offered by the TRASE sequence when compared to the conventional sequence can vary. This is because the degree of B₁-inhomogeneity is subject-specific and will depend on the shape and size of the head. TRASE achieves better immunity to the B₁-variations that do exist, providing consistently improved performance at high fields, as was observed in all our volunteer scans. In the regions of the brain where there is relatively slowly varying B₁, Version 2 of the sequence generally outperforms Version 1, likely due to shorter pulse durations and TE. Signal intensity in the raw images and noise in the FA maps are similar or better than those achieved by TRSE.

Figure 6.

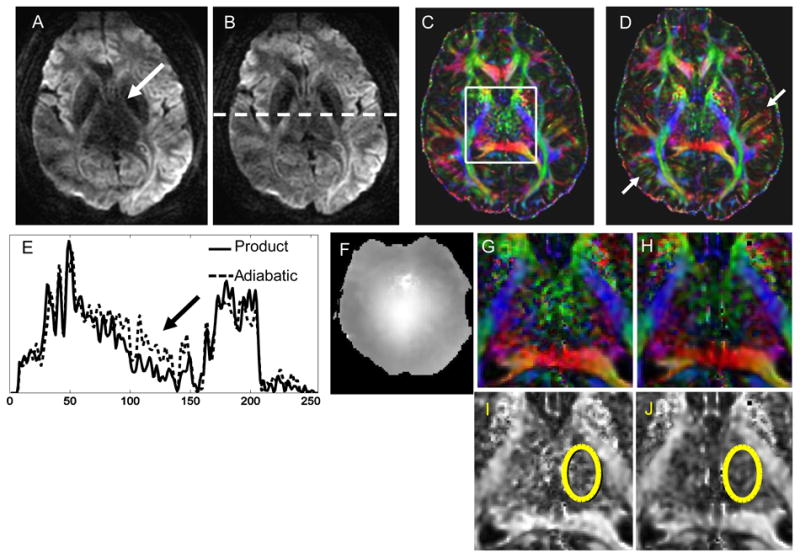
Diffusion weighted image along one direction for a chosen slice of the brain of volunteer 1 obtained using (A) the product TRSE sequence and (B) version 2 of the proposed TRASE sequence using 4 ms semi-adiabatic SLR pulses. Color FA maps were calculated and are shown in (C) and (D). Cross sections of the raw images are provided in (E) and a B₁ map of the slice is shown in (F). (G) and (H) show a zoomed central region of the FA maps and (I) and (J) are the grayscale FA maps of this region. Yellow ellipses show a region from which the STD was calculated for both sequences. The STD for the region indicated by the ellipse was 0.37 for the TRSE sequence and 0.11 for version 2 of TRASE, indicating appreciable reduction in noise of the FA measurement achieved by TRASE. Other regions that demonstrate improved SNR and accuracy of directional encoding by the TRASE sequence are indicated by the white arrows in (D)

Figure 7.

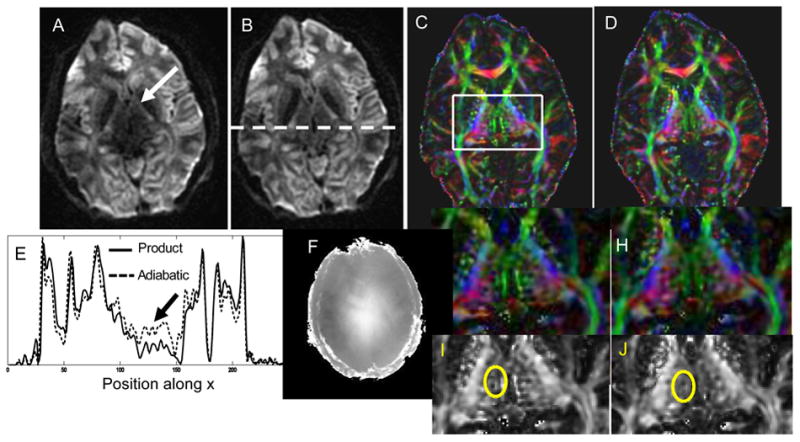
Data obtained using Version 2 of the TRASE sequence on a second volunteer and compared the TRSE sequence. (A,B) show raw images from TRSE and TRASE, respectively. (C,D) are the corresponding FA maps. Zoomed versions of the FA maps in color and grayscale are shown in (G,H) and (I,J), respectively. Cross sections of the raw images (E) and the B₁-map of that slice (F) are also provided. STD values in the illustrated region on grayscale map are 0.36 and 0.27 for TRSE and TRASE, respectively.

Discussion

In vivo data obtained at 7T demonstrate that semi-adiabatic SLR pulses provide significant improvement in the SNR and uniformity of diffusion weighted images acquired using a twice-refocused sequence while maintaining similar TEs and aquisition times. This method for diffusion preparation may be coupled with improved readout trajectories that compensate for B₀-inhomogeneity, resulting in robust DTI sequences for use at 7T. Using the adiabatic SLR method, it was possible to systematically trade off adiabaticity for pulse duration and bandwidth, resulting in shorter, lower SAR pulses that provided improved slice profiles in the presence of severe B₁-inhomogeneity, when compared to conventional HS pulses. Several techniques exist to design adiabatic pulses with more uniformly distributed RF power [15,20–26], however the adiabatic SLR algorithm was chosen for pulse design because it allowed for easier manipulation of pulse parameters.

Another advantage of using the adiabatic SLR method to generate an adiabatic 180° pulse is that a matched-phase 90° pulse can also be created using the method described in [27,28]. This pulse pair could be used in a single-refocused Stejskal-Tanner diffusion preparation. The advantages of this matched-phase adiabatic single-refocused approach are that lower SAR values and shorter echo times can be achieved. This approach would also have utility at very high diffusion b values with powerful gradients such as the 300 mT/m gradients used for the Human Connectome Project, where concomitant Maxwell field terms make it necessary to use a single refocused approach [29,30]. However, the B₁-insensitivity would never be as robust as the adiabatic twice-refocused approach, as the efficacy of phase-matching would deteriorate as the B₁ value deviates from the adiabatic threshold. Additionally, eddy-current effects would no longer be inherently compensated. Nevertheless, it would be valuable to compare the two approaches, which is a target for future work.

This study was focused on improving the B₁-insensitivity of the DTI sequence at 7T. It is noteworthy that other areas also need improvement and the image quality of the FA maps shown are not representative of current state-of-the-art 7T systems. The gradient set used in this study, with a maximum amplitude of 50 mT/m and slew rate of 200 mT/m/s, was not optimal for diffusion imaging and although parallel imaging was used, readout-segmented EPI [5] and reduced field of view imaging were not employed. Stronger gradients and optimized readout techniques would enable echo times shorter than 80 ms, at which the advantages of operation at 7T would become apparent. Since the gradient Maxwell terms mentioned above grow as the square of the ratio between the gradient strength and B₀, there is still a large range of gradient strengths between 50 mT/m and 300 mT/m for which a TRASE approach would be usable. SNR could have also been increased by doubling the number of averages or diffusion directions that were collected, increasing overall scan time to 7 mins, which remains a reasonable acquisition time at 7T, considering subject motion. Our objective was to show that artifacts due to B₁-inhomogeneity may be mitigated by the use of carefully designed adiabatic SLR pulses, while not requiring a significant increase in echo time and while remaining within SAR limits. This was successfully demonstrated in vivo.

New installations of 7T scanners already have stronger gradient sets with a 70 mT/m maximum gradient amplitude, which would enable 10-15 ms reductions in echo time. These experiments were performed at 7T to show improved performance of the semi-adiabatic SLR pulses for DTI in the presence of severe B₁-inhomogeneity. However, this technique is directly translatable to 3T, at which tissue T₂ values are longer, relaxing the requirement for short echo times. Both body and brain diffusion applications could benefit from additional B₁-insensitivity at 3T. Adiabatic approaches to excitation may be be combined with any EPI readout scheme, including the readout-segmented EPI sequence with GRAPPA presented in [5]. This way, both B₁ and B₀ field inhomogeneities may be compensated, enabling uniform whole brain coverage for DTI and allowing us to truly capitalize on the SNR advantage offered at high fields.

Abbreviations

RF

radiofrequency

SLR

Shinnar Le-Roux

TBW

time-bandwidth

SAR

Specific absorption rate

BW

bandwidth

TE

echo time

DTI

diffusion tensor imaging

7T

7 Tesla

SNR

signal-to-noise ratio

FA

fractional anisotropy

EPI

echo planar imaging

FSE

Fast Spin Echo

TSE

Turbo Spin Echo

TRSE

twice-refocused spin echo

TRASE

twice-refocused adiabatic spin echo

FTW

fractional transition width

MD

mean diffusivity