A Novel Spatiotemporal Analysis of Peri-Ictal Spiking to Probe the Relation of Spikes and Seizures in Epilepsy

Abstract

The relation between epileptic spikes and seizures is an important but still unresolved question in epilepsy research. Preclinical and clinical studies have produced inconclusive results on the causality or even on the existence of such a relation. We set to investigate this relation taking in consideration seizure severity and spatial extent of spike rate. We developed a novel automated spike detection algorithm based on morphological filtering techniques and then tested the hypothesis that there is a pre-ictal increase and post-ictal decrease of the spatial extent of spike rate. Peri-ictal (around seizures) spikes were detected from intracranial EEG recordings in 5 patients with temporal lobe epilepsy. The 94 recorded seizures were classified into two classes, based on the percentage of brain sites having higher or lower rate of spikes in the pre-ictal compared to post-ictal periods, with a classification accuracy of 87.4%. This seizure classification showed that seizures with increased pre-ictal spike rate and spatial extent compared to the post-ictal period weremostly (83%) clinical seizures, whereas no such statistically significant (α = 0.05) increase was observed peri-ictally in 93% of sub-clinical seizures. These consistent across patients results show the existence of a causal relation between spikes and clinical seizures, and imply resetting of the preceding spiking process by clinical seizures.

INTRODUCTION

Epilepsy affects 1% of the world's population and is currently the most common neurological disorder after stroke and Alzheimer's disease. It is characterized by two hallmarks: seizures and spikes.⁸ While the nature and role of seizures (ictal states) have been widely investigated, the role of interictal (between seizures) spikes in epilepsy, and importantly in ictogenesis (seizure generation), is still elusive. Interictal spikes (IS) are abnormally synchronized discharges of thousands of neurons, manifested in the electroencephalogram (EEG) as localized in space and time, a couple of hundreds of milliseconds in duration and of high amplitude (>50 μV), electrographic activity frequently followed by slow waves.⁷ Elucidation of the cause and effect of spikes may provide additional clues to the process of epileptogenesis^10,16 and new treatment paradigms for epilepsy. For example, after validation of the relation of spikes to upcoming seizures, significant changes in interictal or pre-ictal (before seizures) spiking could be used to detect seizure susceptibility or predict impending seizures respectively, and intervene in time to avert seizures’ occurrence.

Investigation of the spiking process and its relation to seizures has been a topic of intense debate in the epilepsy community.⁴⁰ Increased rate of epileptic spikes has been observed in the pre-ictal as well as the post-ictal (after seizures) periods, thus raising doubts whether epileptic spikes are actually precursors or aftershocks to seizures.^{4,11,13,14,25,26,32,38} Lange et al.,²⁵ in their studies of the spatiotemporal evolution of preictal spike activity in human temporal lobe epilepsy, found that the degree of bilateral dependence in medial temporal lobe spiking increased prior to onset of temporal lobe seizures, thus indicating that spikes may herald the interictal to ictal transition. In a more recent publication, White et al. came to the same conclusion using a status epilepticus animal model of epilepsy.⁴¹ On the other hand, Engel et al. reported that a high interictal spike rate was associated with a low probability of occurrence of seizures.¹¹ Along similar lines, Avoli et al.,^1,2 treated combined slices of mouse hippocampus and entorhinal cortex in vitro with chemical convulsants and concluded that “interictal activity controls rather than promotes ictal events.” These findings appear to be in agreement with studies reporting that interictal spikes are followed by periods of prolonged inhibition (increase of the threshold for generation of epileptic discharges).^5,6 Also, Gotman¹³ reported that, in amygdala kindled cats, spiking appears as a result of seizures. Post-ictal increase in spike rate in human focal epilepsy was also observed.^12,15,22,23 However, it was also noted¹⁵ that seizures occurred irrespectively of interictal spike rate being high or low, thus weakening the hypothesis that spikes beget seizures and the existence of a causal relationship between spikes and seizures. Finally, studies on the effect of anti-epileptic drugs (AEDs) on spike rate suggested that spike rate is not affected much by AEDs^9,15 while seizure rate and seizure severity are. This was interpreted as possible evidence that mechanisms of spike generation may be different from those of seizure generation.

To address these conflicting reports in the literature, we applied a novel peri-ictal spatiotemporal analysis of the EEG per seizure to all 94 seizures recorded at the epilepsy monitoring unit (EMU) from a cohort of 5 patients with temporal lobe epilepsy. Consistency of findings across patients was an implicit goal we set. Our analytical scheme included: a) the development and validation of a novel tool (data-adaptive morphological filter) for automated and reliable detection of epileptic spikes from the EEG, b) measurement of spatiotemporal pre-ictal vs. post-ictal changes in spike rate per seizure, and c) seizure severity as a confounding factor of the relation between spikes and seizures. We tested the hypothesis that seizures are preceded by increased spike rate in a large number of brain sites and are followed by spike rate suppression in the immediate post-ictal period.

MATERIALS AND METHODS

Data-Adaptive Morphological Filtering (DAMF)

Morphological filters (MF) are a class of nonlinear filters used to identify and extract characteristic morphologies from multi-dimensional signals. The theory behind mathematical morphology was developed by Matheron and Serra in 1964 and has been widely applied to detect edges and perform pattern recognition in images.^{28,30,31,36,37,39,44} MF typically rely on structure elements of predefined shape depending on the shape of the patterns to be detected and extracted from signals. There is no general theory for selection of an appropriate structure element. Commonly used structure elements include squares, disks, parabolas etc.

Application of morphological filtering to spike detection has been performed in the past using various structure elements.^30,31,44 However, the characteristics of EEG change over time (EEG is a non-stationary signal), so the design of a structure element should take this into account, that is, the structure element should ideally be adaptive to such changes. Along these lines, we developed a new MF with data-adaptive structure elements. We have called this modified morphological filter “DAMF.”

Morphological Filter Operators

Morphological filtering includes four operations formulated on the basis of Minkowski's addition and subtraction. Assuming two sets X and Y in Euclidian space, their Minskowski sum is defined as²⁹

$$X\oplus Y=\{x+y\mid x\in X,y\in Y\}$$ (1)

that is, every element in X is added to every element in Y to produce the Minkowski sum. Minkowski subtraction is defined similarly as:

$$X\ominus Y=\{x-y\mid x\in X,y\in Y\}$$ (2)

Then, the four basic morphological operators are

$$\begin{array}{cc}\hfill & \text{Erosion}:(X\ominus Y^S)\left(t\right)=\underset{\tau }{\min }\{x\left(t\right)-y(-(t-t))\},\tau \in \mathbb{R}\hfill \\ \hfill & \text{Dilation}:(X\oplus Y^S)\left(t\right)=\underset{\tau }{\max }\{x\left(t\right)+y(-(t-t))\},\tau \in \mathbb{R}\hfill \\ \hfill & \text{Opening}:\left(X^S\right)\left(t\right)=[(x\ominus y^s)\oplus y]\left(t\right)\hfill \\ \hfill & \text{Closing}:(X\cdot Y^S)\left(t\right)=[\left(x^S\right)\ominus y]\left(t\right)\hfill \end{array}$$ (3)

where x(t) is the raw data series, y(t) is the structure element, y^S(t) = y(–t), and $\mathbb{R}$ is the set of real numbers. The symbols $\oplus ,\ominus ,\circ$,. indicate Minkowski addition, Minkowski subtraction, and Opening and Closing respectively. Erosion of x(t) typically attenuates the peaks, whereas dilation of x(t) enlarges its valleys. The Opening (O) operation is erosion followed by dilation, thus smoothing the signal from below. The Closing (C) operation is dilation followed by erosion and has the effect of smoothing the signal from above by filling up its valleys. Combination of Opening and Closing operations (OC or CO) can be used to eliminate spikes in x(t). To eliminate spikes in the positive as well as negative directions, we followed the approach in Wilcoxon.⁴² Then, OC(t) = x(t) o y₁(t). y₂(t) and CO(t) = x(t). y₁(t) o y₂(t), where y₁(t), y₂(t) are two different y(t) structure elements that can separate the background EEG from upward and downward spikes in x(t) respectively. Thus, if we define x̂(t) as

$$\widehat{x}\left(t\right)=x\left(t\right)-\frac{OC\left(t\right)+CO\left(t\right)}{2}$$ (4)

x̂(t) contains just the spikes in x(t) and is devoid of any background EEG activity (see Fig. 1a). Then, a hard threshold T_th, e.g., equal to a multiple of standard deviations (σ) from the mean of x̂(t), can be used to detect and extract the spikes from x̂(t). The threshold T_th is the only pre-determined parameter (but still adaptive since σ is a function of x̂(t))) in such a spike detection algorithm; all other involved parameters are data-adaptive and do not need to be pre-determined. The effect of T_th on spike detection is shown in the Results section, together with the evaluation of the algorithm via a Receiver Operating Characteristics (ROC) analysis.

FIGURE 1.

Epileptic spike detection via DAMF. (a) EEG raw signal (x(t)) recorded from a single channel, intermediate (OC(t) and CO(t) signals) and output (x̂(t)) signal. (b) Data adaptive structure elements for DAMF from EEG data; EEG epochs in (a) and (c), and the derived structure elements from them in (b) and (d) respectively.

Data-Adaptive Structure Element

Selection of an appropriate structure element improves the efficiency and accuracy of a spike detector. Xu et al.⁴⁴ proposed parabolic structure elements y(t), whose width and height are optimized to extract peaks in a signal while at the same time suppress the background activity. We herein propose a modified version of Xu's algorithm for the design of the optimal structure elements without a pre-determined shape as follows.

We first define the nth order difference of x(t) as:

$$d^n\left(t\right)=\mid x(t+n)-x\left(t\right)\mid$$ (5)

Subsequently, if D(n) is the 75% quintile of these dⁿ(t) values, D(n) approximates the significant values of dⁿ(t), we define the structure element y(t) as:

$$y(M-n)=y(M+n)=-{\alpha }_{\mathrm{opt}}D\left(n\right)$$ (6)

where n ∈ [1, M – 1], $M=\frac{n_{\mathrm{opt}}+1}{2}$, n_nopt abd α_opt are the optimal length and amplitude of the structure element respectively, and are estimated from the data according to the iterative process delineated in the next section (also note that for n = 0, y(M) = 0). Thus, the structure element y(t) carries information about the average local variation of the signal under consideration.

Optimization of Structure Element

The length and amplitude of the structure element are critical in optimal detection of epileptic spikes. We used the K-criterion detailed in Xu et al.⁴⁴ for selection of the optimal amplitude α_opt and length n_opt of the structure element. First, an available EEG record was divided in 10.24 s epochs. We have found in the past that such an EEG epoch's duration is short enough to compensate for the effect of the nonstationarity of the EEG on the estimation (and convergence) of measures of EEG dynamics in patients with focal epilepsy.^18,20 For each 10.24 s EEG epoch x(t), we estimate two structure elements y₁(t) and y₂(t) (see Fig. 1b). The shape of the structure elements is estimated from Eq. 6. To reduce the effect of noise and EEG scaling on the detector performance, we normalized (subtracting the mean value and dividing by the standard deviation) and filtered the raw EEG data between 0.1 and 30 Hz by a fourth order Butterworth filter. The optimal length n_opt and amplitude α_opt of each structure element y(t) are selected by the following iterative procedure:

1. Initialize amplitude α₁ and length n₁ of y₁(t). Initialize amplitude α₂ and length n₂ of y₂(t)

2. Estimate x̂(t) using Eq. 4

3. Estimate the number of zero crossings, N_pz of x̂(t) as

   $$N_{\mathrm{pz}}=\sum _{t=1}^{N-1}ϴ(\widehat{x}\left(t\right)\cdot \widehat{x}(t+1)),$$ (7)

   where $ϴ\left(x\right)=\{\begin{array}{c}1,x\le 0\hfill \\ 0,x>0\hfill \end{array}\phantom{\}}$ is the Heaviside function and N is the length of the signal x̂(t)

4. Estimate R_pz = N_pz/N. The quantity R_pz is the zero-crossing rate of x̂ and reflects the degree at which the background activity in x(t) is attenuated.

5. Estimate I_f = x̃/x̄ where $\stackrel{‒}{x}=\frac{1}{N}{\sum }_{t=1}^N\mid \widehat{x}\left(t\right)\mid$ and x̃ = max(|x̂(t)|). The quantity I_f is the pulse index of x̂ and is sensitive to the transient component of x̂(t).

6. Estimate K = I_f/R_pz. A larger value of K means that spike components are better extracted from the background.

7. Repeat steps 1–6 for different values of α₁, α₂, n₁, n₂. In the search for optimal parameters per EEG epoch of 10.24 s, we tried values of α₁ and α₂ from 0.1 to 2 with a step size of 0.1 and for n₁ and n₂ from 5 to 21 sample points with step size of 2 (i.e., from 25 to 100 ms since the EEG was sampled at 200 Hz).

8. Select the values of n₁, n₂, α₁, α₂ for which K attains its maximum value as the optimal set of parameter values for spike detection in the 10.24 s EEG epoch per channel under consideration.

9. Finally, from the x̂(t) that is generated with the above optimal set of parameters for DAMF, extract the spikes as the outliers in x̂(t) using a “hard” (pre-determined) statistical threshold T_th = [multiple of standard deviation σ of x̂(t)] per EEG epoch. Then, “Spike at t = t* if |x̂(t*)| > T_th”.

10. Store the occurrence times t* of the detected spikes per epoch and recorded channel for subsequent spatiotemporal analysis of spike rates.

EEG Data

Long-term EEG recordings from five patients with temporal lobe epilepsy, who underwent phase II (with intracranial electrodes) pre-surgical evaluation at the EMU of Shands Hospital at the University of Florida for possible resection of their epileptogenic focus, were included in this study. The existence of relatively frequent interictal spiking in the EEG data was the only additional criterion for inclusion in this study from a database of a total of 10 patients. Informed consent for analysis of their EEG data had been obtained from all patients. The EEGs were recorded using an average common reference with band pass filter settings of 0.1–70 Hz. Depth electrodes were placed in the right and left hippocampi (RTD and LTD respectively), two subdural strips were placed on the right and left orbitofrontal lobes (ROF and LOF respectively), and two subdural strips were placed on the right and left subtemporal lobes (RST and LST respectively). The EEGs were sampled at 200 Hz and transferred to computer media for further analysis. The recordings included 7–30 clinical seizures (seizures with clinical manifestations) and subclinical seizures (seizures without clinical manifestations) over a period of 5–13 days per patient (see Table 1). The seizures were marked by visual analysis of EEG by two EEG certified neurologists.

TABLE 1.

Clinical information from five patients with temporal lobe epilepsy.

			# Recorded seizures (94)
Patient	# Electrodes	Available EEG recording (h)	Clinical (53)	Subclinical (41)	Epileptogenic focus (temporal lobe)
P1	28	200.2	23	7	Right Hippocampus
P2	28	143.4	8	10	Right Hippocampus
P3	28	149.6	6	16	Left Hippocampus
P4	28	322.8	10	7	Right Hippocampus
P5	28	268.6	6	1	Right Hippocampus

RESULTS

Evaluation of DAMF's Performance for Spike Detection

To evaluate the performance of the DAMF spike detection algorithm, epileptic spikes were visually marked by an EEG certified neurologist (WK) in a 2-h continuous interictal EEG recording from one of our patients (P1). A total of 144 spikes were identified in one of the channels of this EEG record. We ran DAMF on sequential non-overlapping 10.24 s EEG epochs from that channel to evaluate DAMF's sensitivity and specificity based on the expert physician's assessment. In Fig. 2 we show the results of DAMF from a 3 min segment of this EEG record using a T_th = 2σ and optimal values for α₁, α₂, n₁, n₂ per 10.24 s epoch. Over the whole 2-h record, the means of the optimal values of α₁, α₂, n₁, n₂ for the structure elements y₁(t) and y₂(t) were found to be 1.3, 1.7, 11 and 15 respectively. The algorithm's sensitivity was estimated as the percentage of the spikes marked by the physician and detected by DAMF. The false detection rate (FDR) was estimated as the ratio of the total number of false spike detections by the algorithm to the duration of record. Sensitivity and FDR values from this 2-h EEG record were estimated at different spike detection thresholds T_th, from 1.5σ to 4σ in steps of 0.001σ, and are plotted as a ROC curve in Fig. 3. The performance of DAMF was also compared with the one by a commercially available and widely used in clinical practice spike detection software (Persyst⁴³). Persyst's spike detection is achieved by pattern recognition and the use of the company's own database of possible spike morphologies (patterns). The spikes identified and given as output by the algorithm depend upon a user's provided perception-based threshold from 0.5 to 1. Based on spike morphologies and corresponding evaluation by experts, both stored in Persyst's database, a perception value of 0.75 indicates that 75 out of 100 EEG reviewers would have agreed that the detected event was a spike. The perception values are automatically assigned by the algorithm to each detected spike. Control on Persyst software was limited to the selection of the perception threshold by the user. Therefore, we used the perception threshold as a parameter in the construction of the ROC curve for Persyst's algorithm with a range of 0.5–1 in steps of 0.01. The ROC curve for Persyst's algorithm is also shown in Fig. 3. We observe that the spike detector based on DAMF consistently outperformed the one by Persyst sensitivity and specificity-wise. A possible reason is that Persyst's algorithm was presumably optimized from a standard database of spikes from scalp instead of intracranial EEG recordings. Another reason may be that DAMF's parameters are neither predetermined nor selected from a pre-existing database but estimated continuously over time, optimized per each EEG epoch.

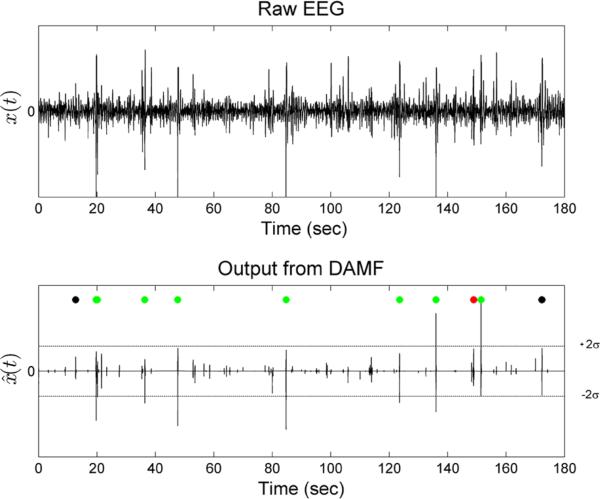
FIGURE 2.

Performance over time of the epileptic spike detection by DAMF. Top panel: A 3 min segment from a 2 h interictal, single channel, EEG data x(t) from patient 1. Bottom panel: The output signal x̂(t) from DAMF. DAMF was applied to 10.24 s non-overlapping EEG epochs from x(t) for structure element selection and optimization and with a final threshold T_th = 2σ (dotted horizontal lines) for spike extraction from each epoch. Green dots (7 of them) are placed over detected spikes that also qualified as epileptic spikes by our expert physician (true positives). Black dots (2 of them) are placed where the algorithm failed to detect spikes that were however recognized by the physician. Red dots (1 of them) are placed where the algorithm detected spikes that were not recognized as spikes by the physician (false positives). The performance of DAMF in terms of sensitivity and specificity in this EEG segment was: sensitivity = 7/9 = 0.78 and specificity = 1 false positive every 3 min = 0.33 false positives per minute.

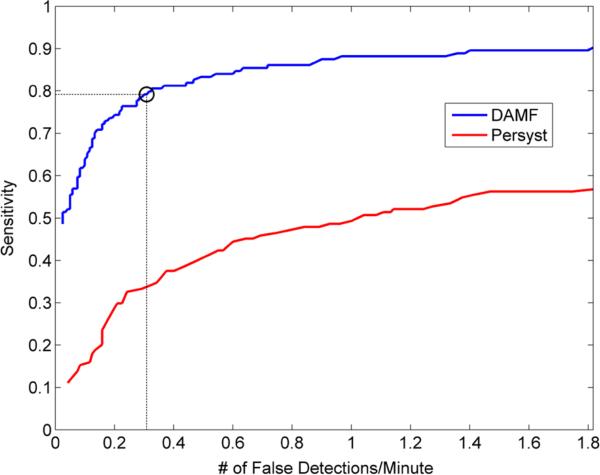
FIGURE 3.

ROC curves for evaluation of the performance of DAMF and Persyst-based spike detection. The algorithms were run on a 2-h single channel EEG recorded interictally from patient 1. The sensitivity and specificity values for the DAMF ROC curve were estimated with threshold T_th values from 1.5σ to 4σ in steps of 0.001σ. The sensitivity and specificity values for the Persyst ROC curve were estimated with their perception threshold T_th values from 0.5 to 1 in steps of 0.01. It is observed that DAMF presents a superior performance over Persyst spike detection algorithm for any specified pair of sensitivity and specificity values. Based on these results, we decided to run DAMF for spike detection in the peri-ictal periods of all recorded seizures with T_th = 2σ, thus expecting a sensitivity of 0.79 and corresponding specificity of 0.30 false spike detections per minute (dotted lines in the figure).

Single Channel Analysis of Peri-Ictal Spike Rate Across Seizures

Following validation of DAMF, a single channel analysis of spike rates was performed peri-ictally per seizure and patient as follows. At every seizure onset (t_SZ), we defined a 20 min pre-ictal window w₁(t) =[t_SZ – 20min, t_SZ] and a 20 min post-ictal window w₂ = [t_SZ + D_SZ, t_SZ + D_SZ + 20min], with D_SZ = 5 min selected to be larger than the observed duration of any of the seizures in our datasets. Epileptic spikes were detected by running DAMF with T_th = 2σ. For this threshold, the expected sensitivity is 0.79 and specificity is 0.30 false detections per minute (see dotted lines in ROC curve in Fig. 3). Per 10.24 s non-overlapping EEG epoch and electrode, the times of spike occurrences were then recorded. The spike rate (number of spikes/10.24 s) at each recording electrode was then calculated. Thus, spike rates $S_{\mathrm{PRE}}^{i,k}$ and $S_{\mathrm{POST}}^{i,k}$ were estimated every 10.24 s for every brain site i and seizure k in the 20-min pre-ictal and post-ictal windows respectively (see Fig. 4).

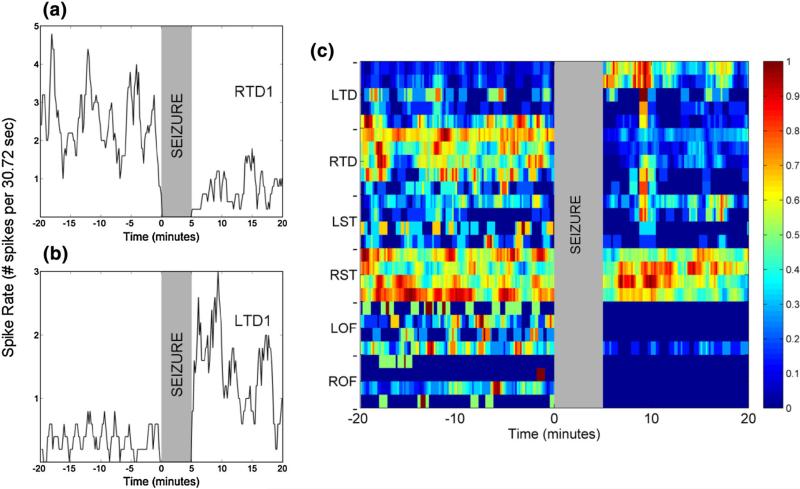
FIGURE 4.

Peri-ictal spike rate 20 min before $\left(S_{\mathrm{PRE}}^{i,k}\right)$ and 20 min after $\left(S_{\mathrm{POST}}^{i,k}\right)$ seizure k = 1 from patient 1 with an epileptogenic focus in right hippocampus (RTD1, 2 and 3). Spike rates inside the 5 min gray shaded vertical zone in the graphs (ictal period) are not shown. Panel a: At electrode RTD1 [most anterior right hippocampus—focal electrode (i = 7)]. Panel b: At electrode LTD1 [most anterior left hippocampus—non-focal electrode (i = 1)]. Panel c: At all electrodes (i = 1–28) and color-coded (maximum value of spike rate corresponds to red color and minimum value to blue color). We observe that pre-ictal spike rates per electrode may be higher (panel a) or lower (panel b) than the corresponding post-ictal rates. They may also stay unchanged [e.g., right subtemporal area (RST) in panel c].

We then estimated the mean pre-ictal $\left({\widehat{S}}_{\mathrm{PRE}}^{i,k}\right)$ and mean post-ictal $\left({\widehat{S}}_{\mathrm{POST}}^{i,k}\right)$ spike rate within the windows w₁(t) and w₂(t) respectively, thus creating a distribution of ${\widehat{S}}_{\mathrm{PRE}}^{i,k}$ and ${\widehat{S}}_{\mathrm{POST}}^{i,k}$ values per seizure k, brain site i and patient. For every brain site i and patient, paired Wilcoxon signed-rank test³⁹ were performed on the distribution of ${\widehat{S}}_{\mathrm{PRE}}^{i,k}$ and ${\widehat{S}}_{\mathrm{POST}}^{i,k}$ with k = 1,..., N_SZ,, where N_SZ = number of seizures per patient. The null hypothesis (H0) that the median value $\left({\stackrel{‒}{S}}_{\mathrm{PRE}}^i\right)$ of ${\widehat{S}}_{\mathrm{PRE}}^{i,k}$ is equal to the median value $\left({\stackrel{‒}{S}}_{\mathrm{POST}}^i\right)$ of ${\widehat{S}}_{\mathrm{POST}}^{i,k}$ across seizures per brain site i and patient $({\stackrel{‒}{S}}_{\mathrm{PRE}}^i={\stackrel{‒}{S}}_{\mathrm{POST}}^i)$ was tested at significance level α = 0.05. If the null hypothesis was rejected, we checked whether the alternate hypothesis (H1: ${\stackrel{‒}{S}}_{\mathrm{PRE}}^i={\stackrel{‒}{S}}_{\mathrm{POST}}^i$ or ${\stackrel{‒}{S}}_{\mathrm{PRE}}^i<{\stackrel{‒}{S}}_{\mathrm{POST}}^i$) was true using the Z-test.¼Thus, for every brain site i and patient, we obtained a p value indicating whether the pre-ictal spike rate is higher, lower or equal to the post-ictal spike rate across a patient's seizures. The results of this analysis are presented in Fig. 5 and the number of brain sites per patient showing pre-ictal spike rates equal to, larger than, or less than the post-ictal spike rates across seizures is presented in Table 2.

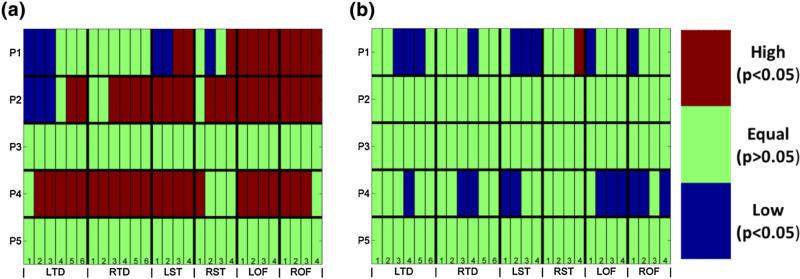
FIGURE 5.

Single channel analysis of peri-ictal spiking ${\stackrel{‒}{S}}_{\mathrm{PRE}}^i$ vs. ${\stackrel{‒}{S}}_{\mathrm{POST}}^i$ in the EEG from five patients (P1–P5). Channel nomenclature is on the horizontal axis (28 channels: from LTD1 through ROF4) and patient number on the vertical axis. The results of analysis are presented in (a) for clinical seizures and (b) for subclinical seizures. The results are color-coded for visualization purposes. Red denotes significantly higher pre-ictal spike rate than average post-ictal spike rate at a particular brain site averaged over the seizures in the same patient $({\stackrel{‒}{S}}_{\mathrm{PRE}}^i>{\stackrel{‒}{S}}_{\mathrm{POST}}^i)$. Blue color denotes significantly lower average pre-ictal spike rate than average post-ictal spike rate at a particular brain site over the seizures in the same patient $({\stackrel{‒}{S}}_{\mathrm{PRE}}^i>{\stackrel{‒}{S}}_{\mathrm{POST}}^i)$. Green color denotes no significant change in spike rate between pre-ictal and post-ictal periods for brain site i over all seizures in the same patient $({\stackrel{‒}{S}}_{\mathrm{PRE}}^i>{\stackrel{‒}{S}}_{\mathrm{POST}}^i)$. Wilcoxon signed-rank test was performed on the peri-ictal spike rates with statistical significance level of α = 0.05.

TABLE 2.

Single channel analysis of peri-ictal spike rate.

	Clinical			Subclinical
	Fraction of brain sites across seizures with			Fraction of brain sites across seizures with
Patient	${\stackrel{‒}{S}}_{\mathrm{PRE}}^i={\stackrel{‒}{S}}_{\mathrm{POST}}^i$	${\stackrel{‒}{S}}_{\mathrm{PRE}}^i>{\stackrel{‒}{S}}_{\mathrm{POST}}^i$	${\stackrel{‒}{S}}_{\mathrm{PRE}}^i<{\stackrel{‒}{S}}_{\mathrm{POST}}^i$	${\stackrel{‒}{S}}_{\mathrm{PRE}}^i={\stackrel{‒}{S}}_{\mathrm{POST}}^i$	${\stackrel{‒}{S}}_{\mathrm{PRE}}^i>{\stackrel{‒}{S}}_{\mathrm{POST}}^i$	${\stackrel{‒}{S}}_{\mathrm{PRE}}^i<{\stackrel{‒}{S}}_{\mathrm{POST}}^i$
P1	0.39	0.39	0.21	0.64	0.04	0.32
P2	0.14	0.75	0.11	1.00	0	0
P3	1.00	0	0	1.00	0	0
P4	0.18	0.82	0	0.61	0	0.39
P5	1.00	0	0	1.00	0	0
Avg	0.54	0.39	0.06	0.85	0.01	0.14

From Fig. 5 and Table 2, we observe that single channel analysis of changes of peri-ictal spike rates across seizures per patient produces inconsistent results across patients. For two patients (P2 and P4) we observe that a large number of electrodes exhibit statistically significant (α = 0.05) increase in spike rate in the preictal period of clinical seizures when compared to post-ictal period, whereas in two other patients (P3 and P5) no significant change in peri-ictal spike rate was observed. For one patient (P1) the results were inconsistent across sites, with some electrode sites showing increased spike rate pre-ictally and some sites increased spike rate post-ictally. It is noteworthy that inconsistency in these results is in agreement with ones in the literature.^{9,12,13,15,22} We also observe that patients P3 and P5 had on average equal pre-ictal and post-ictal spike rates across their clinical and subclinical seizures. Patients P1, P2 and P4 exhibited mixed results with tendency for higher spike rate pre-ictally at more sites than post-ictally. In essence, to some degree, these results justify the conflicting results in the literature as, depending on the electrode site analyzed, the average pre-ictal spike rate across seizures was found to be larger, equal or lower than the post-ictal spike rate.

Analysis of Peri-Ictal Spike Rate Across Sites Per Seizure: A Spatiotemporal Approach

Although seizures of a patient may visually look similar, we have shown in the past that the spatio-temporal dynamics of the transition to seizures can be quite different from one seizure to another, even in the same patient.^17–20,35 Therefore, in an attempt to further elucidate the changes in peri-ictal spiking, we set out to repeat the analysis of the previous section per seizure and patient. Mann–Whitney U Test was performed to compare the distributions of $S_{\mathrm{PRE}}^{i,k}$ and $S_{\mathrm{POST}}^{i,k}$, and test the null hypothesis (H0) that $S_{\mathrm{PRE}}^{i,k}=S_{\mathrm{POST}}^{i,k}$ against the alternate hypothesis (H1) that $S_{\mathrm{PRE}}^{i,k}\ne S_{\mathrm{POST}}^{i,k}$ at significance level α = 0.05. In case the null hypothesis was rejected, we checked whether $S_{\mathrm{PRE}}^{i,k}>S_{\mathrm{POST}}^{i,k}$ or $S_{\mathrm{PRE}}^{i,k}>S_{\mathrm{POST}}^{i,k}$ using the Z-test. We define F₊(k) as the fraction of brain sites at seizure k for which higher spike rate is observed in the pre-ictal than the post-ictal period

$$F_{+}\left(k\right)=\frac{1}{N_{\mathrm{e}}}\sum _{i=1}^{N_{\mathrm{e}}}ϴ\left(S_{\mathrm{PRE}}^{i,k}>S_{\mathrm{POST}}^{i,k}\right),$$ (8)

where N_e is the number of brain sites we record from, and Θ(n) = 1 if n is true, and Θ(n) = 0 if n is false. Similarly, F–(k) is defined as the fraction of brain sites at seizure k for which lower spike rate is observed in the pre-ictal than the post-ictal period

$$F_{\_}\left(k\right)=\frac{1}{N_e}\sum _{i=1}^{N_e}ϴ\left(S_{PRE}^{i,k}<S_{POST}^{i,k}\right)$$ (9)

(Obviously, if we denote by F₀(k) the fraction of sites for which $S_{\mathrm{PRE}}^k=S_{\mathrm{POST}}^k$, it is: F₊(k) F₋(k)+F₀(k) = 1.)

Using F₊(k) and F₋(k) as the two features in a 2-D feature space, the seizures of each patient were classified using a K-means classifier.²⁷ Figure 6 illustrates the results of such a seizure classification per patient. Two well-separated clusters were formed for all seizures per patient. The red cluster represents the class of seizures where median spike rate across brain sites is larger in the pre-ictal compared to post-ictal periods (large F₊, small F₋), which we denoted as Class 1 seizures. The blue cloud with smaller F₊ than F₋ values (located mostly in the lower left corner) we denoted as Class 2 seizures. Interestingly 83% of Class 1 seizures were complex partial seizures or seizures with secondary generalization (in general clinical seizures) and 93% of Class 2 seizures were subclinical seizures. It is remarkable that these results were so consistent across patients. The results of the classification per patient are tabulated in Table 3. Of note is that, across all patients, the center of Class 1 cluster had F₊ > F₋, whereas the center of Class 2 cluster had F₊ < F₋. Performance of the classifier was quantified by estimating its Rand index and classification accuracy.³³ Rand index ranges from 0 to 1, with 1 in our case denoting that every seizure in each class derived by the K-means classifier (Class 1 or Class 2) is correctly classified as clinical or subclinical (with Class 1 denoting clinical seizures and Class 2 subclinical seizures). Classification accuracy is a more global (overall) index of classification than Rand index. For example, a classification value of 90% denotes that 90 out of 100 seizures were correctly classified by K-means, and the misclassified 10 of them might be either all subclinical or all clinical, etc. In our classification scheme, the Rand index ranged between 0.71 and 0.86, and seizure classification accuracy was between 83 and 91% across patients (see Table 3).

FIGURE 6.

Classification of seizures per patient using the fraction of brain sites that have higher pre-ictal than post-ictal spike rate (F₊) and the fraction of brain sites that have lower pre-ictal than post-ictal spike rate (F₋). Each seizure in the feature space is denoted by a star, where the coordinates of its position are its F₊ and F₋ values, and its color is red if it is a clinical seizure and blue if it is a subclinical seizure. Classification into two classes was performed using a K-means clustering algorithm for all seizures per patient. The red cloud includes seizures classified as Class 1 (mostly clinical seizures) and the blue cloud seizures classified as Class 2 (mostly sub-clinical seizures).

TABLE 3.

Classification of seizures into two classes based on F₊ and F_–.

	Class 1 ($F_{+}^{\mathrm{c}}>F_{-}^{\mathrm{c}}$)				Class 2 ($F_{+}^{\mathrm{c}}<F_{-}^{\mathrm{c}}$)
Patient	Cluster center ($F_{+}^{\mathrm{c}},F_{-}^{\mathrm{c}}$)	Resetting power $F_{+}^{\mathrm{c}}-F_{-}^{\mathrm{c}}$	Seizure type		Cluster center ($F_{+}^{\mathrm{c}},F_{-}^{\mathrm{c}}$)	Resetting power $F_{+}^{\mathrm{c}}-F_{-}^{\mathrm{c}}$	Seizure type		Rand Index	Accuracy (%)
			Clinical	Sub-clinical			Clinical	Sub-clinical
P1	0.45, 0.28	0.17	18/23 (78%)	0/7	0.13, 0.27	–0.14	5/23	7/7 (100%)	0.71	83
P2	0.69, 0.13	0.56	8/8 (100%)	2/10	0.18, 0.19	–0.01	0/8	8/10 (80%)	0.79	89
P3	0.65, 0.10	0.55	4/6 (67%)	0/16	0.10, 0.15	–0.05	2/8	16/16 (100%)	0.83	91
P4	0.85, 0.06	0.79	9/10 (90%)	1/7	0.06, 0.40	–0.34	1/10	6/7 (86%)	0.78	88
P5	0.5, 0.09	0.41	5/6 (83%)	0/1	0.05, 0.29	–0.24	1/6	1/1 (100%)	0.71	86
Total avg.	0.62, 0.13	0.50	44/53 (83%)	3/41	0.10, 0.26	–0.16	9/53	38/41 (93%)	0.76	87.4

These classification results suggest that a clinical seizure is preceded by more brain sites with “higher pre-ictal than post-ictal spike rate” than ones with “lower pre-ictal than post-ictal spike rate.” This implies that occurrence of clinical seizures tends to reduce spike activity across brain sites and may be related to the homeostatic role of epileptic seizures (resetting of pathological brain dynamics) as postulated previously by Iasemidis et al.^3,21,34 For example, if we define the resetting power of a seizure as:

$$\mathrm{RP}=F_{+}^{\left(\mathrm{c}\right)}-F_{-}^{\left(\mathrm{c}\right)},$$ (10)

where F^(c)₊, F^(c)₋ are the center of each cluster, we see from Table 3 that, across all patients, Class 1 seizures (mostly clinical; 44 clinical and 3 subclinical seizures) have higher resetting power RP per patient compared to Class 2 seizures (mostly subclinical; 38 subclinical and 9 clinical seizures). It is also noteworthy that the sign of RP is reversed in the two classes: it is positive for the clinical seizures and negative for the subclinical seizures. This means that resetting of dynamics may work in the opposite direction in the two classes of seizures, since in the overwhelming majority of clinical seizures in our patients spike rate is post-ictally reduced across sites, while in the majority of subclinical seizures is increased. A possible explanation for this finding is that subclinical seizures may not be as effective in resetting the brain as clinical seizures are. An alternative, more dynamic, explanation is that the brain is en route towards a higher instability state, with higher spike rate and subclinical seizures occurrence, until clinical seizures occur to temporarily reset this pathology.

DISCUSSION

In this study, we focused on seizures and spikes, the current neurophysiological hallmarks of epilepsy. The motivation for this study was a persistent debate in the literature about the dynamics of epileptic spikes and their relation to seizures.^12,14,15 Proof of a causal relation between spikes and seizures could contribute to further elucidation of the mechanisms of ictogenesis and the development of new treatment modalities for epilepsy.

Towards this goal, we first developed a novel data-adaptive algorithm for automated spike detection from the EEG based on the concept of morphological filters (DAMF), and compared its performance to an expert physician's judgment and the performance of a commercially available algorithm for spike detection. The favorable evaluation of our spike detection algorithm encouraged us to then proceed with an automated spatiotemporal analysis of spike rates in long-term intracranial EEG data recorded from five temporal lobe epilepsy patients. In particular, we analyzed 10.24 s successive epochs from 40 min of peri-ictal EEG (20 min before and 20 min after a seizure) for each of 94 recorded seizures. Analysis of spike rates, averaged over seizures for each recording site in the same patient, produced mixed results across patients, similar to the inconclusive ones in the literature: different brain sites showed either increase, decrease or no change in pre-ictal vs. post-ictal spike rates.

Assuming that seizures are different from each other even in the same patient and switching into averaging of preictal and postictal spike rates across sites per seizure and patient, we achieved consistency across patients but still not statistically significant results (p < 0.01) in most of the patients (see Table 4). Finally, motivated by our past results on brain dynamics in epilepsy and resetting of abnormal pre-ictal dynamics by seizures,^21,24,34 we attempted a spatio-temporal analysis relating the spike rates in the preictal and post-ictal periods per site and seizure. In particular, instead of spatial averaging the spike rates over all sites separately in the pre-ictal and post-ictal periods, we estimated the fraction of sites that exhibited a positive (F₊) or negative (F₋) change in spike rate peri-ictally per seizure (Eqs. 8–10). This approach led to consistent results in all patients.

TABLE 4.

Mean and standard deviation of spatially averaged pre-ictal and post-ictal spike rates across Class 1, Class 2 and all seizures per patient; P_v (p value from non-parametric Wilcoxon test) of the difference between the spatially averaged pre-ictal and post-ictal spike rates across Class 1, Class 2 and all seizures per patient.

	Class 1 seizures			Class 2 seizures			All seizures (Class 1 + Class 2)
Patient	$\mu \left({\tilde{S}}_{\mathrm{PRE}}\right)\pm \sigma \left({\tilde{S}}_{\mathrm{PRE}}\right)$	$\mu \left({\tilde{S}}_{\mathrm{POST}}\right)\pm \sigma \left({\tilde{S}}_{\mathrm{POST}}\right)$	P v	$\mu \left({\tilde{S}}_{\mathrm{PRE}}\right)\pm \sigma \left({\tilde{S}}_{\mathrm{PRE}}\right)$	$\mu \left({\tilde{S}}_{\mathrm{POST}}\right)\pm \sigma \left({\tilde{S}}_{\mathrm{POST}}\right)$	P v	$\mu \left({\tilde{S}}_{\mathrm{PRE}}\right)\pm \sigma \left({\tilde{S}}_{\mathrm{PRE}}\right)$	$\mu \left({\tilde{S}}_{\mathrm{POST}}\right)\pm \sigma \left({\tilde{S}}_{\mathrm{POST}}\right)$	P v
P1	1.75 ± 0.63	1.66 ± 0.54	0.71	1.45 ± 0.73	1.44 ± 0.63	0.79	1.62 ± 0.68	1.57 ± 0.58	0.86
P2	0.90 ± 0.34	0.51 ± 0.22	0.017	0.47 ± 0.33	0.48 ± 0.30	0.96	0.71 ± 0.39	0.50 ± 0.25	0.097
P3	0.82 ± 0.23	0.21 ± 0.15	0.028	0.70 ± 0.27	0.71 ± 0.31	0.94	0.72 ± 0.26	0.63 ± 0.33	0.18
P4	1.02 ± 0.38	0.25 ± 0.12	0.004	0.59 ± 0.40	0.76 ± 0.33	0.32	0.84 ± 0.43	0.46 ± 0.34	0.008
P5	0.28 ± 0.13	0.11 ± 0.06	0.016	0.25 ± 0.12	0.31 ± 0.01	1.0	0.27 ± 0.12	0.16 ± 0.11	0.13

A significant by-product of this analysis was the finding that peri-ictal spike rates differ in subclinical and clinical seizures (seizure classification accuracy of 87.4%). In particular, (a) statistically significant higher spike activity occurs before than after clinical seizures with the possibility of seizures themselves resetting it to lower values, and (b) no statistically significant changes in spike activity occur around subclinical seizures, however with a tendency to higher spike rates post-ictally. These findings support the view that increased pre-ictal spike activity and subclinical seizures may be manifestations of the brain moving to more unstable dynamical states, and that clinical seizures may result to resetting of this route, thus contributing to more stable brain dynamical states. It is noteworthy that the mean duration of subclinical seizures was significantly (p < 0.05) shorter than the one of clinical seizures across all patients with the exception of P3 for whom it was still shorter but with p > 0.05 (see Fig. 7). This observation suggests that duration of epileptic seizures might have an antagonist effect on post-ictal spiking, reflecting a passive physiological mechanism for resetting by seizures (e.g., prolonged ictal activity in clinical seizures may more severely deplete critical neurotransmitters and deactivate critical neuroreceptors for generation and propagation of spike activity). However, there is always the possibility that subclinical seizures reset only a very small portion of the brain that we either did not have recording access to (limitation of recording) or that its dynamical behavior is masked by a much bigger portion of the brain we record from (limitation of the algorithm's normalization). The latter points out to a possible future improvement of our approach by giving a special consideration to the peri-ictal behavior of the epileptogenic focus vs. the rest of the sites we record from. (In this study we refrained from giving a special consideration to particular brain sites in order to avoid introducing a potential bias to our results from patient to patient and seizure to seizure.)

FIGURE 7.

Distribution of duration of subclinical and clinical seizures for the five patients. Clinical seizures tend to have significantly (p < 0.05) longer duration compared to clinical seizure for all patients except P3.

In conclusion, our results from the small cohort of patients with epilepsy we analyzed point out to a consistent across patients causal relationship between clinical seizures and spikes, as well as to a resetting power of clinical seizures upon pre-ictal spike activity. This behavior was not evident in peri-ictal periods of sub-clinical seizures. The possibility that the relationship between spikes and seizures may depend on the type of seizures and the applied spatiotemporal meta-analysis could partially explain the inconclusive and at times conflicting results in the literature about epileptic seizures and spikes, and potentially lead to further elucidation of the mechanisms of ictogenesis and epileptogenesis.