Self-assembled tunable photonic hyper-crystals

Abstract

We demonstrate a novel artificial optical material, the “photonic hyper-crystal”, which combines the most interesting features of hyperbolic metamaterials and photonic crystals. Similar to hyperbolic metamaterials, photonic hyper-crystals exhibit broadband divergence in their photonic density of states due to the lack of usual diffraction limit on the photon wave vector. On the other hand, similar to photonic crystals, hyperbolic dispersion law of extraordinary photons is modulated by forbidden gaps near the boundaries of photonic Brillouin zones. Three dimensional self-assembly of photonic hyper-crystals has been achieved by application of external magnetic field to a cobalt nanoparticle-based ferrofluid. Unique spectral properties of photonic hyper-crystals lead to extreme sensitivity of the material to monolayer coatings of cobalt nanoparticles, which should find numerous applications in biological and chemical sensing.

Over the last few decades a considerable progress has been made in developing artificial optical materials with novel and often counterintuitive properties. Revolutionary research by Yablonovitch and John on photonic crystals¹,² was followed by the development of electromagnetic metamaterial paradigm by Pendry³. Even though considerable difficulties still exist in fabrication of three-dimensional (3D) photonic crystals and metamaterials, both fields exhibit considerable experimental progress⁴,⁵. On the other hand, on the theoretical side these fields are believed to be complementary but mutually exclusive. Photonic crystal effects typically occur in artificial optical media which are periodically structured on the scale of free space light wavelength λ, while electromagnetic metamaterials are required to be structured (not necessarily in a periodic fashion) on the scale, which is much smaller than the free space wavelength of light. For example, in metal nanowire-based hyperbolic metamaterials⁶ schematically shown in Fig. 1A the inter-wire distance must be much smaller than λ. Here we report experimental realization of 3D “photonic hyper-crystals” which bridge this divide by combining the most interesting properties of hyperbolic metamaterials and photonic crystals.

Figure 1.

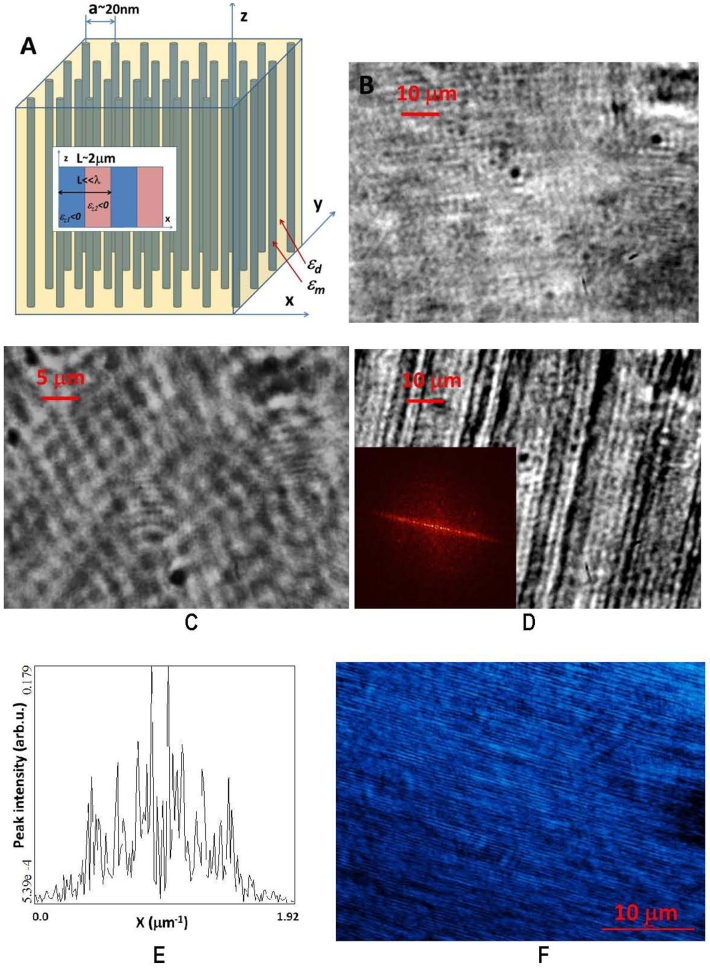
(A) Experimental geometry of the ferrofluid-based hyperbolic metamaterial. The array of self-assembled cobalt nanocolumns has typical separation a ~ 20 nm between the nanocolumns. The inset shows a photonic hyper-crystal structure formed by periodic arrangement of cobalt rich and cobalt sparse regions with typical periodicity L ~ 2 μm, so that periodic modulation of hyperbolic metamaterial properties on a scale L ≪ λ is achieved in the LWIR spectral range where λ ~ 10 μm. Since photon wave vector in hyperbolic metamaterials is not diffraction-limited, periodic modulation of hyperbolic metamaterial properties on a scale L ≪ λ would lead to Bragg scattering and formation of band structure. (B–F) Microscopic images of cobalt nanoparticle-based ferrofluid reveal subwavelength modulation of its spatial properties: frames (B) and (D) show microscopic images of the diluted cobalt nanoparticle-based ferrofluid before and after application of external magnetic field. The pattern of self-assembled stripes visible in image D is due to phase separation of the ferrofluid into cobalt reach and cobalt poor phases. The stripes are oriented along the direction of magnetic field. The inset shows Fourier transform image of frame D. Its cross section presented in panel E shows a histogram of different periods present in the image. A movie taken during this experiment when the external magnetic field was turned on and off is available in the supporting on-line material. A microscopic image of the sample taken along the axes of the nanowires is shown in frame C. Panel F demonstrates that the original undiluted ferrofluid exhibits similar phase separation in external magnetic field, even though on much smaller scale.

Our concept of the photonic hyper-crystal⁷ is based on the fact that dispersion law of extraordinary photons in hyperbolic metamaterials⁸

does not exhibit the usual diffraction limit. In such uniaxial metamaterials the in-plane ε_xy and out-of-plane ε_z components of the dielectric permittivity tensor have opposite signs (e.g. the metal wire array hyperbolic metamaterial shown in Fig. 1A may have ε_z < 0 and ε_xy > 0 ⁸), so that the photon wave vector components k_i are not bounded at a given frequency of light ω. Existence of large k-vector modes in a broad range of frequencies is responsible for such unusual effects as hyperlens-based super-resolution imaging⁸,⁹,¹⁰,¹¹ and broadband divergence of photonic density of states in hyperbolic metamaterials¹². On the other hand, this also means that periodic modulation of hyperbolic metamaterial properties on a scale L ≪ λ (see inset in Fig. 1A) would lead to Bragg scattering of extraordinary photons and formation of photonic band structure no matter how small L is⁸. Thus, so formed “photonic hyper-crystals” would combine the most interesting properties of hyperbolic metamaterials and photonic crystals. For example, similar to classic photonic crystal effect predicted by John², strong localization of photons may occur in photonic hyper-crystals. However, unlike usual photonic crystals where light localization occurs on a scale ~ λ, photonic hyper-crystals may exhibit light localization on deep subwavelength scale. Similar to surface plasmon resonance (SPR)¹³ and surface enhanced Raman (SERS)¹⁴ - based sensing, engineered localization of light on deep subwavelength scale in photonic hyper-crystals should find numerous applications in biological and chemical sensing.

Band structure and field distribution inside a photonic hyper-crystal may be obtained in a straightforward manner. While both ε_xy and ε_z may exhibit periodic spatial dependencies, let us consider the relatively simple case of coordinate-independent ε_xy > 0 and periodic ε_z(z) < 0 with a period L ≪ λ. Aside from the relative mathematical simplicity of this model, it also corresponds to the most readily available low-loss realizations of a hyperbolic metamaterials such as the composites formed by metallic nanowires in a dielectric membrane¹⁵ (where ε_xy > 0 and ε_z(z) < 0), and planar layered metal-dielectric¹⁶,¹⁷ and doped semiconductor metamaterials¹⁸. Taking into account the translational symmetry of the system in x and y directions, we can introduce the in-plane wave vector (k_x, k_y) so that the propagating waves can be expressed as

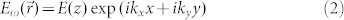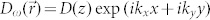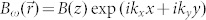The uniaxial symmetry of this medium reduces the ordinary and extraordinary waves to respectively the TE (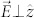) and TM (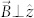) - polarized modes. Introducing the wavefunction 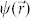as the z-component of the electric displacement field of the TM wave

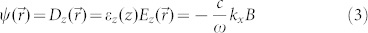for the wave equation we obtain

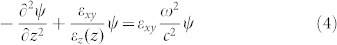In this wave equation the periodic ε_xy/ε_z ratio acts as a periodic effective potential. As usual, solutions of eq.(4) may be found as Bloch waves

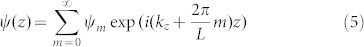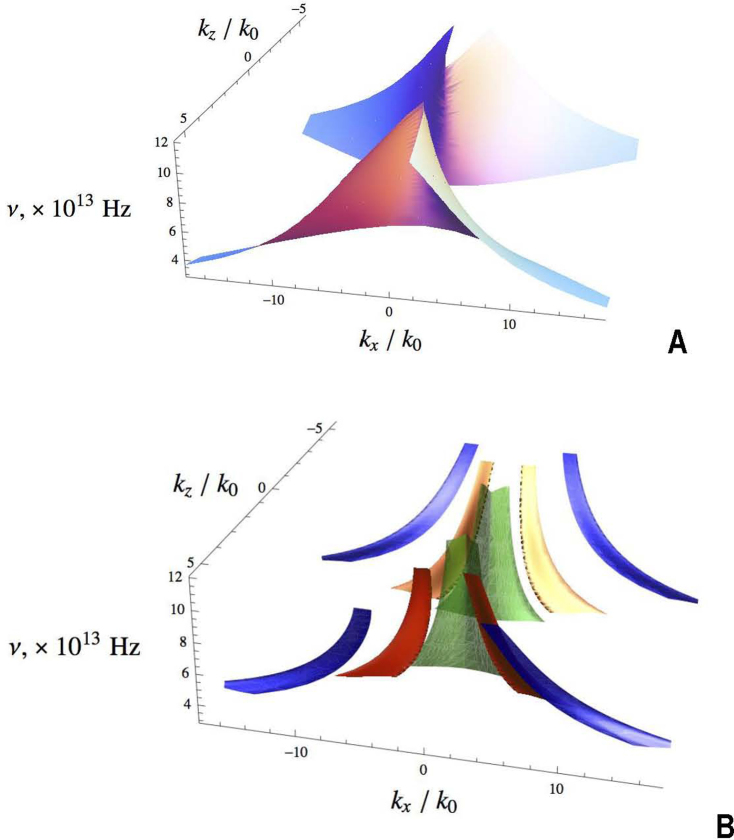
where k_z is defined within the first Brillouin zone 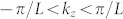. Strong Bragg scattering is observed near the Brillouin zone boundaries at k_z ~ π/L ≫ π/λ, leading to the formation of photonic bandgaps in both the wavenumber and the frequency domains. This behavior is illustrated in Fig. 2, where we compare the dispersion diagram for an example of such nanowire-based photonic hyper-crystal to its effective medium counterpart. The material parameters of photonic hyper-crystal are based on the parameters of stratified ferrofluid described below. However, we should emphasize that Fig. 2A is presented as an illustration only, since in real experiment we cannot separate magnetic field-induced hyperbolic properties of the ferrofluid from its photonic hyper-crystal properties (or vice versa), at the actual wavelengths where both properties coexist.

Figure 2.

Comparison of the effective medium dispersion of a nanowire-based hyperbolic metamaterial (A) to the exact solution for photonic crystal (B). The hyper-crystal unit cell in (B) is assumed to be 1000 nm, with one half of the cell is filled with the same ferrofluid while another half is pure kerosene. The ferrofluid aligned by external magnetic field applied in the z-direction, is characterized by the material parameters described in Fig. 3. The stratified ferrofluid is assumed to form layers with the normal along the x-direction. The effective medium dispersion in panel (A) uses the dielectric permittivity tensor obtained by the homegenization of the electromagnetic response of the hyper-crystal unit cell. This is an artificial result that would be expected if we could experimentally isolate magnetic field induced hyperbolic behaviour of the ferrofluid from its photonic hyper-crystal behaviour. In both panels, the wavevector components are given in units of the free-space wavenumber k₀.

Similar to the usual photonic crystals², adiabatic chirping of L leads to strong field enhancement which, unlike that in the conventional photonic crystals, occurs on a deep subwavelength scale. We should also mention that the most interesting case appears to be the epsilon-near-zero (ENZ) situation where ε_z approaches zero near a periodic set of planes. As has been demonstrated in Ref. 19, electric field of the extraordinary wave diverges in these regions. These periodic field divergences appear to be most beneficial for sensing applications.

In order to validate the photonic hyper-crystal concept we have developed an experimental technique which uses three-dimensional self-assembly of cobalt nanoparticles in the presence of external magnetic field. Magnetic nanoparticles in a ferrofluid are known to form nanocolumns aligned along the magnetic field²⁰. Moreover, depending on the magnitude of magnetic field, nanoparticle concentration and solvent used, phase separation into nanoparticle rich and nanoparticle poor phases may occur in many ferrofluids²¹. This phase separation occurs on a 0.1–1 micrometer scale. Therefore, it can be used to fabricate a self-assembled photonic hypercrystal.

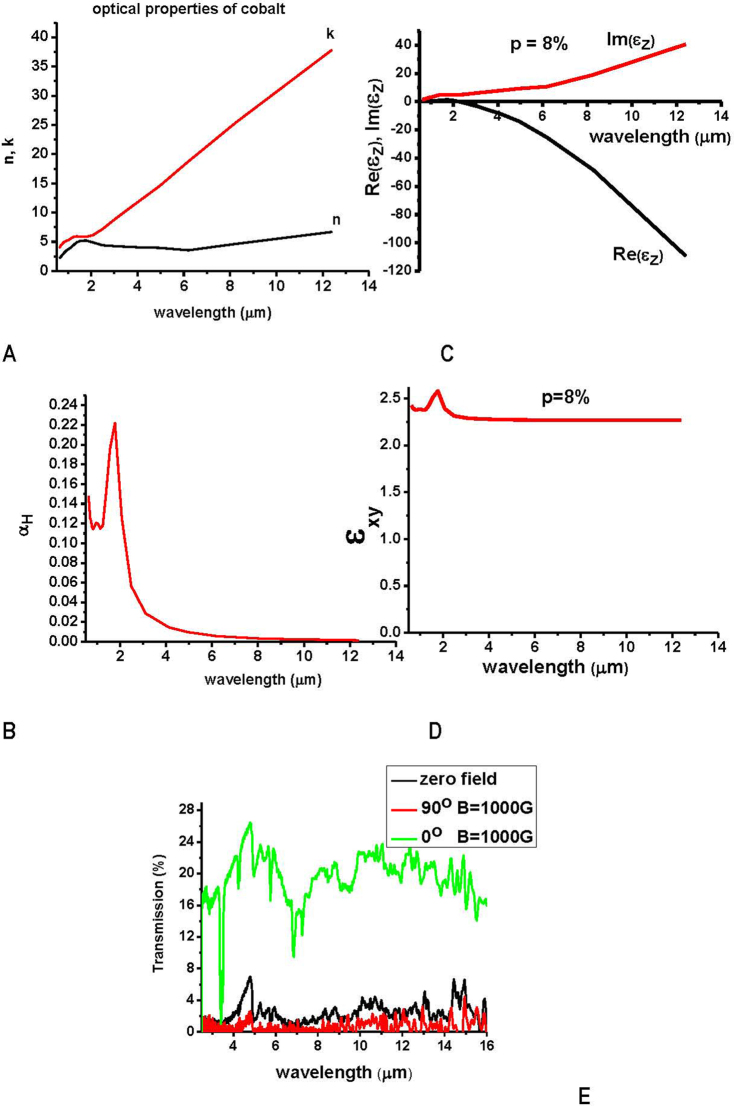
For our experiments we have chosen cobalt magnetic fluid 27-0001 from Strem Chemicals composed of 10 nm cobalt nanoparticles in kerosene coated with sodium dioctylsulfosuccinate and a monolayer of LP4 fatty acid condensation polymer. The average volume fraction of cobalt nanoparticles in this ferrofluid is p = 8.2%. Cobalt behaves as an excellent metal in the long wavelength infrared range (LWIR), as evident by Fig. 3A: the real part of its refractive index, n, is much smaller than its imaginary part, k²². Thus, real part of ε, Reε = n²- k², is negative, and its absolute value is much larger than its imaginary part, Imε = 2nk. Therefore, it is highly suitable for fabrication of hyperbolic metamaterials. The structural parameter of such a metamaterial falls into a few nanometers range: the cobalt nanoparticle size is 10 nm, while average inter-particle distance at 8.2% volume fraction is about 19 nm. Therefore, the metamaterial properties may be described by effective medium parameters on spatial scales ~100 nm. On the other hand as demonstrated below, ferrofluid begins to exhibit hyperbolic behavior in the range of free space wavelengths ~10000 nm and above - in the so called long wavelength infrared (LWIR) frequency range. Thus, in between 100 nm and 10000 nm there exists an ample range of spatial scales which enable photonic hyper-crystal behavior described above. For example, if the effective medium parameters of ferrofluid are modulated on the scale of ~2000 nm (as evident from Fig. 1D) the large k-vector modes which exist in the metamaterial in the LWIR range will experience Bragg scattering due to this modulation.

Figure 3.

(A) Optical properties of cobalt as tabulated in Ref. 22: real (n) and imaginary (k) parts of the cobalt refractive index are plotted in the long wavelength IR range. (B) Critical volume fraction of cobalt nanoparticles corresponding to ferrofluid transition to hyperbolic metamaterial phase shown as a function of free space light wavelength. (C,D) Wavelength dependencies of ε_z and ε_xy at α(∞) = 8.2%. While ε_xy stays positive and almost constant, ε_z changes sign around λ = 3 μm. (E) Polarization-dependent transmission spectra of 200 μm - thick ferrofluid sample measured using FTIR spectrometer are consistent with hyperbolic character of ε tensor.

Electromagnetic properties of these metamaterials may be understood based on the Maxwell-Garnett approximation via the dielectric permittivities ε_m and ε_d of cobalt and kerosene, respectively. Volume fraction of cobalt nanoparticles aligned into nanocolumns by external magnetic field, α(B), depends on the field magnitude. At very large magnetic fields all nanoparticles are aligned into nanocolumns, so that α(∞) = p = 8.2%. We will assume that at smaller fields the difference α(∞)-α(B) describes cobalt nanoparticles, which are not aligned and distributed homogeneously inside the ferrofluid. Dielectric polarizability of these nanoparticles may be included into ε_d leading to slight increase in its value. Using this model, the diagonal components of the ferrofluid permittivity may be calculated using Maxwell-Garnett approximation as follows²³:

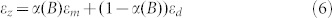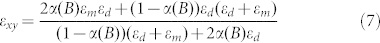Calculated wavelength dependences of ε_z and ε_xy at α(∞) = p = 8.2% are plotted in Figs. 3CD. While ε_xy stays positive and almost constant, ε_z changes sign to negative around λ = 3 μm. If the volume fraction of cobalt nanoparticles varies, this change of sign occurs at some critical value α_H:

The value of α_H as a function of wavelength is plotted in Fig. 3B. This plot indicates that the original ferrofluid diluted with kerosene at a 1:10 ratio remains a hyperbolic medium above λ = 5 μm. More interestingly, such a diluted ferrofluid develops very pronounced phase separation into periodically aligned cobalt rich and cobalt poor phases (with periodicity L ~ 2 μm) if subjected to external magnetic field. Optical microscope images of the diluted ferrofluid before and after application of external magnetic field are shown in Figs. 1B and 1D. The periodic pattern of self-assembled stripes visible in image D appears due to phase separation. The stripes are oriented along the direction of magnetic field. A movie taken during this experiment when magnetic field was turned on and off is available in the supporting on-line material. It clearly demonstrates the tunability of the medium by external magnetic field. The stripe periodicity L ~ 2 μm appears to be much smaller than the free space wavelength in the hyperbolic frequency range. Therefore, created self-assembled optical medium appears to be a photonic hyper-crystal. We should also note that the original undiluted ferrofluid exhibits similar phase separation in external magnetic field, even though on much smaller ~0.3 μm spatial scale (see Fig. 1F).

Polarization dependencies of ferrofluid transmission as a function of magnetic field and nanoparticle concentration measured in a broad 0.5 μm–16 μm wavelength range conclusively prove hyperbolic crystal character of ferrofluid anisotropy in the long wavelength IR range at large enough magnetic field. Fig. 3E shows polarization-dependent transmission spectra of 200 μm thick undiluted ferrofluid sample obtained using FTIR spectrometer. These data are consistent with hyperbolic character of ε tensor of the ferrofluid in B = 1000 G. Ferrofluid transmission is large for polarization direction perpendicular to magnetic field (perpendicular to cobalt nanoparticle chains) suggesting dielectric character of ε in this direction. On the other hand, ferrofluid transmission falls to near zero for polarization direction along the chains, suggesting metallic character of ε in this direction. However, these measurements are clearly affected by numerous ferrofluid absorption lines, whose behaviour will be addressed later. In order to be conclusive, LWIR data must be supported by polarization measurements in the visible range presented in Fig. 4. Main features of these dependencies may indeed be understood based on the Maxwell-Garnett approximation (eqs.(6,7)). At small magnetic fields α(B) ≪ p and we obtain

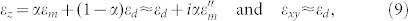where ε″_m is the imaginary part of ε_m. This absorption-related anisotropy is primarily responsible for the polarization dependence of ferrofluid transmission. Results presented in Figs. 4AB were obtained at λ = 1.55 μm by measuring transmission of ferrofluid placed inside a d = 10 μm wide quartz cuvette (note that ε_quartz ~ ε_d in the visible and near IR ranges). If ferrofluid inside the cuvette may be considered as a homogeneous medium, its transmission as a function of light polarization ϕ should behave as

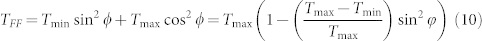where T_min is transmission for polarization direction parallel to magnetic field and T_max is transmission for polarization direction perpendicular to magnetic field. Since electric field equals 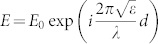after passing through a ferrofluid layer of thickness d, the contrast between transmissions can be estimated using expressions for ε_z and ε_xy from eq.(9):

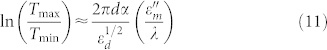Equation (11) may be used to verify Maxwell-Garnett approximation and measure α(B).

Figure 4.

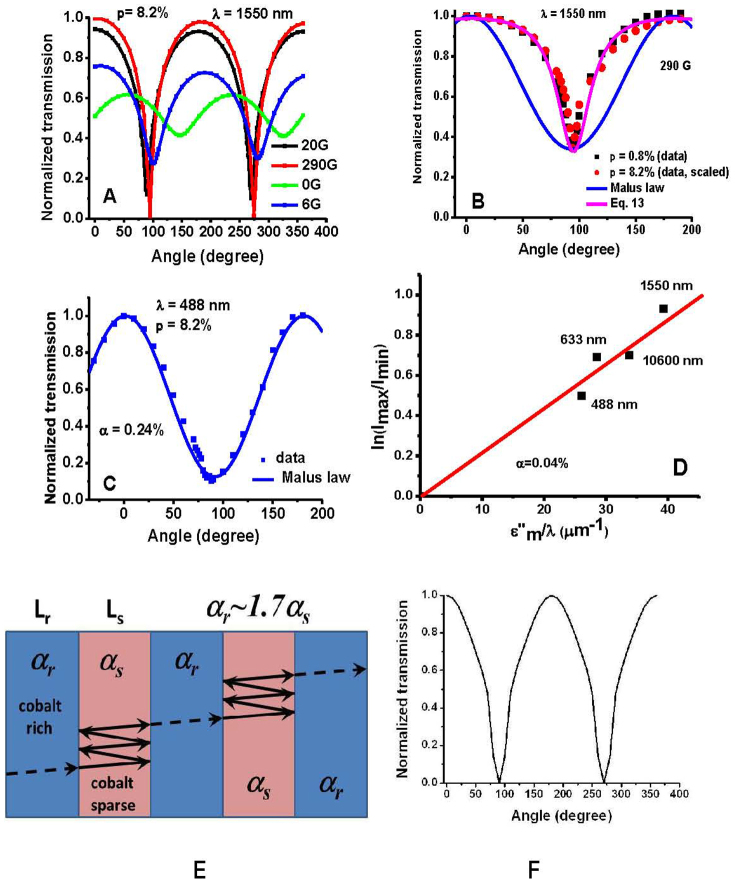
(A,B) Experimentally measured transmission of the cobalt based ferrofluid at λ = 1.55 μm as a function of cobalt concentration, external magnetic field and polarization angle. As shown in panel (B), in the absence of phase separation polarization curves exhibit the Malus law sin²ϕ dependencies. On the other hand, in the phase separated state polarization curves exhibit universal “polarization notch” behaviour indicating long range order of periodically aligned cobalt nanocolumns. (C) Experimentally measured transmission of the ferrofluid at α(∞) = 8.2%, λ = 488 nm and B = 1630 G. (D) Polarization contrast measurements (data points) in the 0.5–10.6 μm range provide experimental validation of Maxwell-Garnett approximation (red line) at low nanoparticle concentrations. (E) Visible and near IR light propagation through a stratified ferrofluid. Due to much higher absorption in the cobalt rich phase, ferrofluid may be represented as multiple Fabry-Perot - like resonators separated by strongly absorptive regions of cobalt rich phase. (F) Calculated transmission of such a model stratified ferrofluid at λ = 1.55 μm.

At λ = 1.5 μm and large fields, polarization curves depart from the Malus law, showing much sharper minima (Fig. 4A), which will be discussed later. However, in the visible range, or in smaller fields, polarization curves indeed obey the Malus law exhibiting sin²ϕ dependence (see Fig. 4C). Moreover, low field measurements in Fig. 4D performed on the same sample at four different wavelengths across a very broad 0.5–10.6 μm wavelength range follow the Maxwell-Garnett result given by Eq. 11 (note that α = 0.0004 ≪ p in this case, since only a small fraction of particles are aligned into nanocolumns in a week magnetic field). These measurements give substantial support to our model.

Let us demonstrate that these measurements conclusively point towards hyperbolic character of ferrofluid anisotropy in the long wavelength IR range. As an example, let us calculate α(B)) for the polarization curve in Fig. 4C measured at B = 1630 G. While polarization contrast is quite large for this curve: T_max/T_min ~ 10, it fits Malus law sin²ϕ dependence rather well. Based on Eq. 11, calculated α(B)) equals 0.002 in this experiment performed at λ = 488 nm. Therefore, at λ = 14 μm where Re(ε_m) = −2100 the real parts of the dielectric permittivity tensor components are

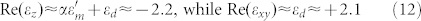meaning that the magnetized ferrofluid does indeed exhibit hyperbolic metamaterial behaviour on spatial scales above ~100 nm.

On the other hand, polarization dependent transmission of phase separated ferrofluid samples shown in Fig. 1D supports long range order of periodically aligned (with periodicity L ~ 2 μm) cobalt rich and cobalt sparse regions in a magnetized ferrofluid. Using Eqn. (11), experimentally observed contrast between transmission of the cobalt rich and cobalt sparse regions in Figs. 1D and 1F may be used to evaluate volume fractions of cobalt nanoparticles α_r and α_s in these phases. In both cases the ratio α_r/α_s falls into the 1.6–1.8 range. Moreover, it is clear from Fig. 4A that polarization curves measured at large magnetic fields deviate strongly from the Malus law sin²ϕ dependence. As shown in Fig. 4B, polarization dependencies of the phase separated ferrofluid measured at different nanoparticle concentrations may be scaled to a universal “polarization notch” curve described by two parameters:

As illustrated in Fig. 4E, such a “polarization notch” dependence arise naturally due to multiple scattering of light by periodically spaced nanoparticle rich and nanoparticle poor phases seen in Fig. 1D. Due to much higher absorption in the cobalt rich phase (α_r ~ 1.7α_s), ferrofluid may be represented as multiple Fabry-Perot like resonators separated by strongly absorptive regions of cobalt rich phase. Let us consider light propagation through one of such Fabry-Perot resonators formed by a single cobalt sparse region. Transmission amplitude t through such an elementary resonator is given by a coherent sum of all the multiple scattering events in which the wave experiences multiple polarization-dependent reflections from the phase boundaries:

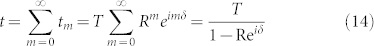where δ is the phase accumulated by the wave upon double pass between the phase boundaries, and T and R are the transmission and reflection coefficients for a single inter-phase boundary (note that T + R = 1 when losses at boundaries are neglected). Resulting transmission through a single resonator formed by the nanoparticle rich and nanoparticle poor phases is thus

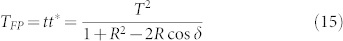Since R exhibits strong polarization dependence due to alignment of cobalt nanoparticles by external magnetic field, the universal “polarization notch” curve given by eq.(13) finds natural explanation. Within the scope of model presented in Fig. 4E the overall transmission of ferrofluid is

where T_FF is given by eq.(10) and N is the number of effective Fabry-Perot resonators from Fig. 4E. Since the cuvette size in experiments presented in Fig. 4 is d = 10 μm, the number of resonators N is small. Calculated transmission of such a model stratified ferrofluid is presented in Fig. 4F. For simplicity we have assumed that interfaces between cobalt rich and cobalt sparse regions behave as ideal polarizers, so that R ≈ sin²ϕ. However, even such an oversimplified model reproduces polarization notch behavior of stratified ferrofluid. Note that in order for this model to be valid, polarization state of light must be conserved during propagation, indicating a well-ordered ferrofluid state. In principle, such mechanism as Anderson localization may also lead to polarization-dependent changes in transmission (see for example24) which study effects of polarization on Anderson localization in one-dimensional random stacks. However, the described effect consists in strong polarization dependencies near the Brewster angle (see for example Fig. 11 from²⁴). Therefore, they are not applicable to our experiments, which have been conducted at normal incidence. Moreover, long range ordering of our samples is clearly demonstrated by Fig. 1. Relatively small amount of disorder visible in these images does not justify application of Anderson localization theory. Thus, our microscopy results in Fig. 1C–E, and detailed examination of polarization-dependent transmission of the ferrofluid presented in Fig. 4 strongly indicate both hyperbolic character of the medium in the long wavelength IR range, and its well-ordered periodicity. These data conclusively prove that the magnetized ferrofluid may indeed be considered as a self-assembled photonic hyper-crystal.

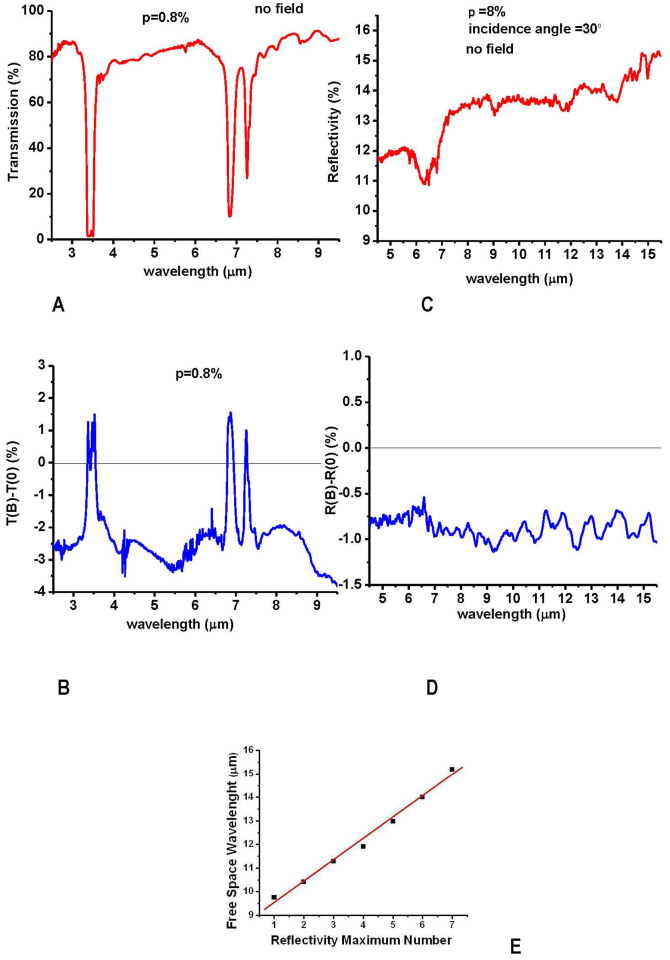
As summarized in Fig. 5, fabricated photonic hyper-crystals exhibit all the typical features associated with the hyperbolic metamaterials. For example, Figs. 5A and 5B demonstrate modulation of the metamaterial absorption lines due to hyperbolic order induced by the external magnetic field. Radiation lifetime engineering due to broadband divergence of the photonic density of states in hyperbolic metamaterials¹² has been predicted in²⁵ and experimentally confirmed in¹⁶,¹⁷,²⁶. Absorption lines of kerosene offer natural target for testing this effect in fabricated photonic hyper-crystals. Absorption spectra measured using FTIR spectrometer with and without external magnetic field are consistent with the decrease of the radiation lifetime of kerosene molecules in the hyperbolic state. Shorter lifetime leads to decrease in absorption line amplitude, which is detected in Fig. 5B. Reduced reflection has been reported recently as another experimental signature of hyperbolic metamaterials²⁷. Due to broadband divergence of photonic density of states, roughened surface of a hyperbolic metamaterial scatters light preferentially inside the medium, resulting in reduced reflectance. In case of photonic hyper-crystals, periodic modulation of the hyper-crystal surface plays the same role, facilitating coupling of external light into the large k vector modes of photonic hyper-crystal. Figs. 5C and 5D demonstrate such magnetic field induced reduced reflectivity of the ferrofluid. Moreover, Fig. 5D shows evidence of weak periodic modulation of reflectivity at λ > 9 μm with period close to 1 micrometer: reflectivity maxima in Fig. 5D are plotted as a function of free space light wavelength in Fig. 5E. These reflectivity maxima are consistent with Bragg scattering of incoming LWIR light due to periodic modulation of ferrofluid concentration observed in Fig. 1. Such a Bragg-like scattering is difficult to explain without considering large k-vector modes in hyperbolic metamaterials. Coincidentally, our numerical calculations (see eq.(12)) indeed indicate hyperbolic behavior of ferrofluid in the LWIR range.

Figure 5.

(A) FTIR transmission spectrum of the diluted (α(∞) = 0.8%) ferrofluid in zero magnetic field reveals strong kerosene absorption lines. (B) Measured differential FTIR transmission spectrum T(H)-T(0) indicate a decrease in absorption line amplitude, which is consistent with the decrease of the kerosene radiation lifetime in the hyperbolic metamaterial state. (C) FTIR reflection spectrum of the ferrofluid in zero magnetic field. (D) Measured differential FTIR reflection spectrum R(H)-R(0) indicates reduced reflectivity in the hyperbolic state. (E) Reflectivity maxima in Fig. 5D plotted as a function of free space light wavelength show evidence of Bragg-like scattering of large k-vector hyperbolic metamaterial modes.

Finally, we would like to illustrate photonic hyper-crystal potential in chemical and biological sensing, which is made possible by spatially selective field enhancement effects described above. This potential is revealed by detailed measurements of magnetic field induced transmission of photonic hyper-crystals in the broad IR spectral range presented in Figs. 6A and 6B. FTIR spectral measurements are broadly accepted as a powerful “chemical fingerprinting” tool in chemical and biosensing. Therefore, broadly available magnetic field-tunable photonic hyper-crystals operating in the IR range open up new valuable opportunities in chemical analysis. Our experimental data presented in Fig. 6 clearly illustrate this point. The FTIR transmission spectrum of the diluted (p = 0.8%) ferrofluid in Fig. 6A exhibits clear set of kerosene absorption lines, which is consistent with other published data (see for example ref. 28). On the other hand, magnetic field induced transmission spectrum of the p = 8.2% ferrofluid shown in Fig. 6B contains a very pronounced absorption line at λ ~ 12 μm (~840 cm⁻¹), which cannot be attributed to kerosene. Quite naturally this absorption line may be attributed to fatty acids, since cobalt nanoparticles are coated with a monolayer of surfactant composed of various fatty acids, such as lactic, oleic etc. acids as shown in Fig. 6D. Detailed comparison of Fig. 6B with the 10–14 μm portion of lactic acid FTIR absorption spectrum shown in Fig. 6C indeed indicates a close match. The fatty acid line appears to be about as strong as λ ~ 14 μm (~695 cm⁻¹) line of kerosene, even though the oscillator strength of these molecular lines is about the same, while the amount of kerosene in the sample is ~ two orders of magnitude larger (a monolayer coating of fatty acids on a 10 nm cobalt nanoparticle occupies no more than 1% of ferrofluid volume). This paradoxical situation clearly indicates local field enhancement effects. Another strong evidence of field enhancement is provided by measurements of extinction coefficient of the ferrofluid presented in Fig. 6E. Ferrofluid subjected to magnetic field exhibits pronounced resonances around the fatty acid absorption line at λ ~ 12 μm and the kerosene absorption line at λ ~ 14 μm. These resonances provide clear evidence of field enhancement by cobalt nanoparticle chains. We expect that further optimization of photonic hyper-crystals geometry will lead to much stronger sensitivity of their optical properties to chemical and biological inclusions, indicating a very strong potential of photonic hyper-crystals in biological and chemical sensing.

Figure 6.

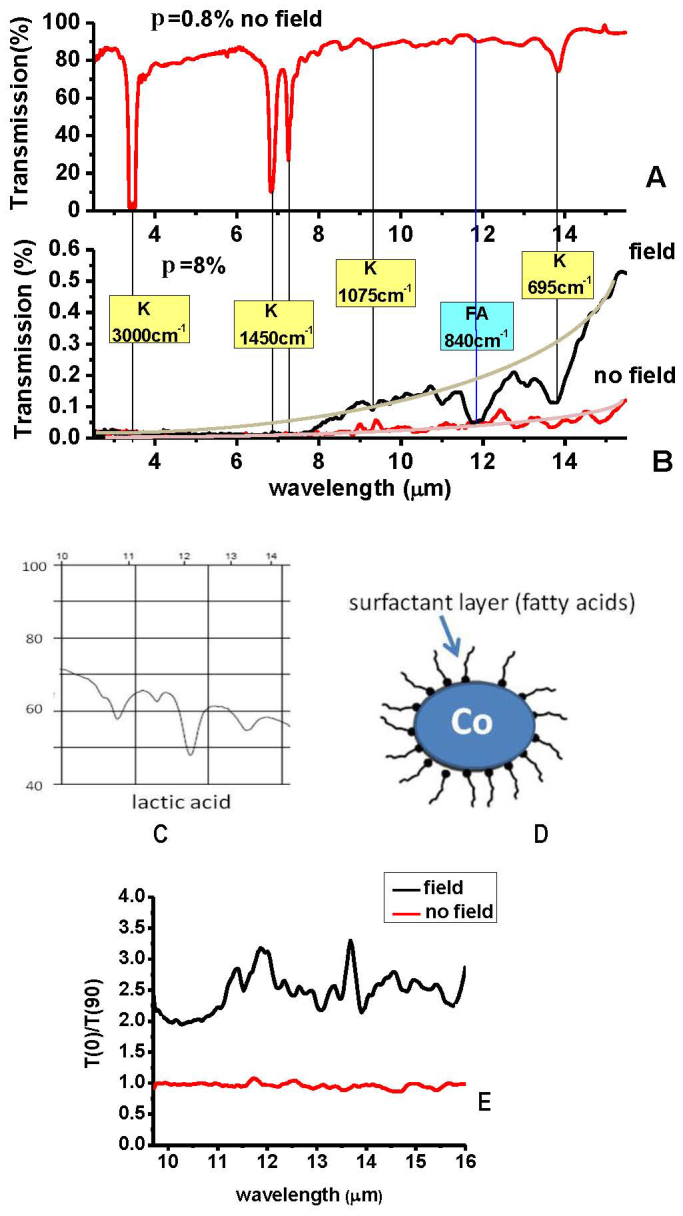
(A) FTIR transmission spectrum of diluted (α(∞) = 0.8%) ferrofluid exhibits clear set of kerosene absorption lines. (B) Transmission spectra of the α(∞) = 8.2% ferrofluid measured with and without application of external magnetic field. Magnetic field induced transmission spectrum contains a very pronounced absorption line at λ ~ 12 μm (~840 cm⁻¹), which can be attributed to lactic acid. Kerosene absorption lines are marked with yellow boxes, while the fatty acid line at 840 cm⁻¹ is marked with a green box. (C) The 10–14 μm portion of lactic acid FTIR absorption spectrum. (D) Schematic view of cobalt nanoparticle coated with a monolayer of fatty acids, such as lactic and oleic acid. (E) Extinction coefficient (the ratio T(0)/T(90) of ferrofluid transmissions at 0 and 90 degrees) of ferrofluid subjected to external magnetic field exhibits pronounced resonances around the fatty acid absorption line at λ ~ 12 μm and the kerosene absorption line at λ ~ 14 μm. These resonances provide clear evidence of field enhancement by cobalt nanoparticle chains.

Author Contributions

I.S., V.S. and E.N. wrote the main manuscript text, V.S., B.Y., D.L. and I.S. collected experimental data. E.N. developed the theory of photonic hyper-crystals. All authors reviewed the manuscript.