Abstract
Fluorescence fluctuation imaging is a powerful means to investigate dynamics, interactions, and stoichiometry of proteins inside living cells. Pulsed interleaved excitation (PIE) is the method of nanosecond alternating excitation with time-resolved detection and allows accurate, independent, and quasi-simultaneous determination of fluorescence intensities and lifetimes of different fluorophores. In this work, we combine pulsed interleaved excitation with fluctuation imaging methods (PIE-FI) such as raster image correlation spectroscopy (RICS) or number and brightness analysis (N&B). More specifically, we show that quantitative measurements of diffusion and molecular brightness of Venus fluorescent protein (FP) can be performed in solution with PIE-RICS and compare PIE-RICS with single-point PIE-FCS measurements. We discuss the advantages of cross-talk free dual-color PIE-RICS and illustrate its proficiency by quantitatively comparing two commonly used FP pairs for dual-color microscopy, eGFP/mCherry and mVenus/mCherry. For N&B analysis, we implement dead-time correction to the PIE-FI data analysis to allow accurate molecular brightness determination with PIE-NB. We then use PIE-NB to investigate the effect of eGFP tandem oligomerization on the intracellular maturation efficiency of the fluorophore. Finally, we explore the possibilities of using the available fluorescence lifetime information in PIE-FI experiments. We perform lifetime-based weighting of confocal images, allowing us to quantitatively determine molecular concentrations from 100 nM down to <30 pM with PIE-raster lifetime image correlation spectroscopy (RLICS). We use the fluorescence lifetime information to perform a robust dual-color lifetime-based FRET analysis of tandem fluorescent protein dimers. Lastly, we investigate the use of dual-color RLICS to resolve codiffusing FRET species from non-FRET species in cells. The enhanced capabilities and quantitative results provided by PIE-FI make it a powerful method that is broadly applicable to a large number of interesting biophysical studies.
Introduction
As of this writing, there is a large push in the biophysical sciences to extract more information from individual experiments and perform more-quantitative analyses. One of the tools that is routinely used to investigate biomolecular mobility, concentration, and interactions in vitro and in live cells is fluorescence fluctuation spectroscopy (FFS). FFS started with fluorescence correlation spectroscopy (FCS) in the early 1970s, which quantifies fluctuations in fluorescence intensity with time (1–3). The introduction of fast confocal laser scanning microscopy (CLSM) in the second half of the 1980s (4) made it possible to determine molecular properties in a spatio-temporally resolved manner, but it took several years before the FFS methodology was combined with CLSM to perform fluorescence fluctuation imaging (FFI). The earliest report of FFI was image correlation spectroscopy (ICS) in which the size and concentration of immobile molecular aggregates were determined by spatial correlation analysis (5). Many developments of the ICS method have appeared in literature, including, quantitative analysis of temporal and spatio-temporal fluorescence intensity variations in CLSM images and/or image series (6,7).
Dual-color FFI techniques allow detailed investigations of the interactions of differentially labeled molecules from images at the ensemble (7–10) and single-molecule level (11). However, multicolor imaging systems typically suffer from crosstalk (or spectral bleed-through) of photons from the more blue-shifted fluorophore into the detection channel of the red-shifted fluorophore. Crosstalk reduces the sensitivity and dynamic range of multicolor FFI and complicates data analysis. In the mid-2000s, methodologies in which excitation lasers were alternated on the microsecond (alternating laser excitation, ALEX) and nanosecond timescales (pulsed interleaved excitation, PIE) were introduced to allow quasi-simultaneous and independent multicolor imaging (12,13). Combining ALEX or PIE with established fluorescence techniques has been proven to increase their sensitivity and robustness considerably. For example, with PIE it is possible to perform quantitative point fluorescence cross-correlation spectroscopy measurements, even when the sample undergoes Förster resonance energy transfer (FRET) (13). PIE also allows us to perform highly accurate single-pair FRET experiments when combined with multiparameter fluorescence detection (14).
In this work, we describe the advantages and challenges of combining PIE with fluctuation imaging (PIE-FI). In particular, we combined PIE with raster ICS (RICS) and the number and brightness (N&B) analysis method (15,16). RICS exploits the spatio-temporal information encoded in a single CLSM image to extract the diffusion coefficient and concentration of fast diffusing molecules (15). N&B makes it possible to determine the concentration and stoichiometry of fast diffusing molecular complexes (16). We use PIE-RICS to investigate diffusion of the Venus fluorescent protein (FP) (17) under different conditions and compare the performance of two interesting FP pairs with dual-color PIE-FI on tandem heterodimers of eGFP-mCherry and mVenus-mCherry in cells. We also combine PIE with N&B to measure a fluorophore-specific absolute brightness and apply PIE-NB to studying eGFP oligomer maturation inside cells. Finally, we exploit the available fluorescence lifetime information for dual-color fluorophore-specific lifetime imaging and for a lifetime-weighted RICS analysis. We apply the latter approach to 1), measure concentrations accurately in vitro in the pM range with single-color PIE-RICS; and 2), to resolve dual-color codiffusing FRET species from non-FRET species based on their fluorescence lifetime with dual-color PIE-RICS in cells.
Materials and Methods
Details of the reagents used, sample preparation, and cell culture can be found in the Supporting Material.
Microscopy
All experiments were performed on a home-built, dual-color PIE dual-color detection microscope (see Fig. S1 in the Supporting Material). Laser powers in this work were measured in the excitation path; the total laser power at the sample was ∼40% of this value. The point-spread function (PSF) was always positioned close to the coverslip (<10 μm), to limit refractive-index related problems (18). Unless stated otherwise, the (12.5-μm)2-sized images were recorded at (300-pixel)2 resolution and 1-s time frame (pixel size δr = 41.7 nm, pixel dwell time τp = 11.11 μs, line time τl = 3.333 ms). Per experiment, 5–400 frames were recorded depending on the concentration and brightness of the molecules under investigation. Data analysis was performed with software written in the software MATLAB (The MathWorks, Ismaning, Germany), which is available upon request and can be used to analyze fluctuation images obtained with most (also non-PIE) CLSMs. More details of the setup are given in the Supporting Material.
Results and Discussion
Robust measurement of fluorescent protein diffusion with PIE-RICS
RICS with PIE-FI
To test for potential effects of pulsed excitation on RICS data, we performed PIE-FI experiments on Venus fluorescent protein (FP) diluted in aqueous buffer. We recorded photons with 475-nm pulsed excitation and dual-color detection, while performing rapid laser scanning of 100 image frames (see Materials and Methods for imaging settings). Because the arrival time of all photons with respect to the exciting laser pulse is available with PIE, the data can be represented directly in a microscopic arrival time histogram per detector, which we will refer to as a microtime histogram (Fig. 1 A). The majority of photons were detected in the green detection channel (Fig. 1 A, top panel) and ∼13% of the total emission of Venus FP was detected as crosstalk in the red detection channel (Fig. 1 A, lower panel). This value is close to what is expected based on the known absorption coefficients and quantum yield of Venus FP and filters and transmission coefficients of the setup (see Table S1 and Fig. S2 in the Supporting Material). Next, we used time gating (19) to perform further analysis only with photons detected in a specific PIE channel (Fig. 1 A, gray hatched areas). Photons in the FGG(t) PIE channel include green emission photons after 475-nm excitation of the green fluorophore and photons in the FGR(t) PIE channel include red emission photons after 475-nm excitation. With the scan-timing information available as well as the arrival times of all recorded photons with respect to the start of the experiment (i.e., macrotimes), we constructed a macrotime image series, IGG(x,y,f), where GG denotes the FGG(t) PIE channel; x- and y- are the fast and slow scanning axis of the laser, respectively; and f is the number of the image frame. The average macrotime image is displayed in Fig. 1 B. The homogeneous intensity over the field of view suggests that the PSF is uniform throughout the image. We verified this uniformity quantitatively with point FCS measurements (see Fig. S3). We subsequently used IGG(x,y,f) to calculate a series of spatial autocorrelation functions (ACFs),
| (1) |
where ξ and ψ are the spatial lag (in pixels), and
is the spatial average intensity with X and Y being the respective dimensions of the image; I1 = I2 for an autocorrelation analysis; and I1 ≠ I2 when two different images are used for a cross-correlation analysis. A fast Fourier transform algorithm (5) was used for calculating G(ξ,ψ,f) and the resulting two-dimensional ACF series was averaged over all image frames F. A typical average two-dimensional ACF, 〈G(ξ,ψ)〉F, of Venus FP in solution is shown in Fig. 1 C (top view) and in Fig. 1 D (side view). The central region (30 × 30 to 50 × 50 pixels) in 〈G(ξ,ψ)〉F was fitted with a RICS model for free diffusion in a three-dimensional Gaussian point-spread function (PSF) (8),
| (2) |
where γ = 2−3/2 is the geometrical factor for a three-dimensional Gaussian PSF (20,21); N is the average number of molecules in the PSF; D is the diffusion coefficient; τp is the pixel dwell time; τl is the line time; ωr ≈ 0.2 μm and ωz ≈ 1 μm are the radial and axial dimensions of the PSF, respectively; and δr is the pixel size. The size of the PSF was determined by point FCS measurements on reference dyes. Because fast scanning increases the effective lateral PSF size, where possible, ωr was used as a fitting parameter in addition to N and D. To show both the data as well as the fit in the same graph, it is useful to show only the G(ξ,0) or G(0,ψ) correlation curves (Fig. 1 F). Because photon counting detectors do not exhibit afterglowing (in contrast to analog photomultiplier tubes) (22), only G(0,0) has to be omitted from the fitting for ACFs calculated from a single APD.
Figure 1.
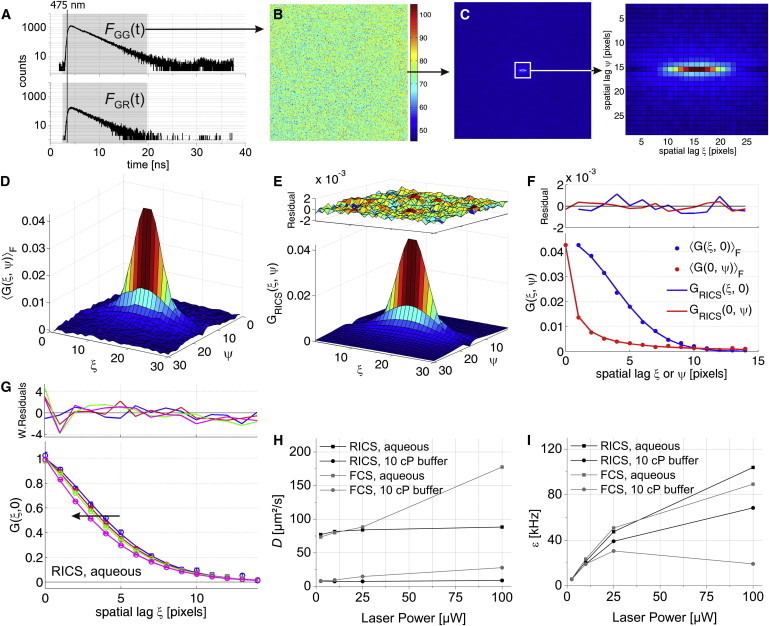
PIE-RICS experiments on Venus FP. (A) Logarithmic microtime histograms of all photons detected in the green (top) and red (bottom) detection channel during five images. (Gray hatching) The different PIE channels. (B) The average macrotime image (F = 100) with photons detected in the FGG(t) PIE channel from 100-nM Venus FP freely diffusing in buffer and measured at 5 μW excitation power. (C) Typical average spatial ACF of the data in panel B. (D) Three-dimensional representation of the data plotted in panel C. (E) Three-dimensional fit and residual plot for the 100-nM Venus ACF plotted in panels C and D. (F) The x- and y-cross sections of the RICS correlation function, fit, and residuals for the data plotted in panels C and D. (G) Experimental G(ξ,0) from RICS (symbols) at 2.5 (blue), 10 (red), 25 (green), and 100 μW (pink) excitation power in an aqueous buffer. (Solid line) Fit to Eq. 3. (Plot on the upper panel) Weighted residuals. (Black arrow) Trend with increasing laser power. To allow a direct comparison of their shape, the correlation functions were normalized to the amplitude of the fit function by multiplying the data and fit with N(1-Fb)γ-1. (H and I) The apparent diffusion coefficient (H) and brightness (I) of Venus FP are plotted as a function of laser power. The results from single-point FCS experiments are shown for comparison.
Diffusion coefficient measurements
Because fast photophysics (blinking, photobleaching) of yellow FPs is known to render quantitative estimations of D difficult when measured with FCS (23), we verified the performance of PIE-RICS for measuring D of Venus FP by measuring the laser power dependence of 〈G(ξ,ψ)〉F in an aqueous buffer. A shift of the spatial ACF to a faster timescale was observed when increasing the laser power (Fig. 1 G). We fitted the resulting data with a RICS model including a blinking term,
| (3) |
where Fb and τb are the fractional amplitude and relaxation time of the fast process, respectively, and GRICS(ξ,ψ) is the normal RICS model from Eq. 2. Furthermore, we performed complementary (PIE-)FCS and PIE-RICS experiments both in an aqueous buffer and in a more viscous sucrose/buffer mixture (10-cP buffer) that mimics free cellular diffusion of Venus FP and determined the apparent D (Fig. 1 H and see Fig. S4). Clearly, D depended much less on the laser power when measured with PIE-RICS. The average D in aqueous buffer was determined to be 82.8 ± 4.6 μm2/s and in the 10-cP buffer 7.8 ± 0.7 μm2/s.
Brightness determination
For the same experiments on Venus FP, we determined the apparent peak molecular brightness ε at the center of the PSF (20,21,24) by dividing the average count rate by N:
| (4) |
The maximum apparent molecular brightness that could be achieved with PIE-RICS as a function of laser power was much higher for PIE-RICS than with FCS (Fig. 1 I and see Fig. S4). When PIE-RICS was performed with all photons detected after blue excitation by using the summed FGG+GR(t) = FGG(t) +FGR(t) time gate, the obtained D and N stayed the same (data not shown) but the brightness was larger by ∼10% (10.3 kHz/mol at 5 μW excitation power) as compared to the complementary RICS analysis with photons from the FGG(t) time gate (9.2 kHz/mol).
Hence, it is possible to perform quantitative RICS measurements with PIE. Interestingly, PIE-RICS measurements on Venus FP were more robust than point PIE-FCS experiments. The fast laser scanning used with PIE-RICS limits the total illumination time per FP, allowing it to cope better with blinking and/or bleaching and, as a result, yields a higher maximal apparent brightness and correct D at higher laser intensities (Fig. 1, H and I). Therefore, it would be the method of choice for accurately measuring FPs with considerable dark state formation, such as mRFP1 or mCherry (25). Additionally, when measuring in cells, RICS provides the advantage of acquiring a spatially averaged D. Conversely, point FCS would provide a much more precise choice of the measurement location and would be preferable when the sample exhibits localized fluctuating image heterogeneities that cannot be removed from the image series by preprocessing the data before the RICS analysis. Other scanning-based techniques such as line- or circle-FCS could also be used to circumvent blinking or bleaching problems (26,27). Finally, because ωr is an independent fitting parameter in RICS, it allows an accurate quantification of D, as has been shown before for dual-foci scanning FCS (27). Alternatively, two-focus FCS also provides accurate measurements of D with high spatial resolution and benefits from the full time resolution of FCS (28). However, two-focus FCS is still sensitive to artifacts due to fast fluorophore photophysics and care should be taken when performing any fluorescence fluctuation method with fluorescent proteins.
Imaging protein-protein interactions in living cells with dual-color PIE-RICS
Dual-color RICS with PIE-FI
The real advantage of PIE-FI comes when multicolor and/or lifetime imaging experiments are performed. To demonstrate the possibilities of PIE when multiple excitation wavelengths are used, we performed PIE-FI on HeLa cells expressing eGFP and mCherry FP and analyzed the data with the cross-correlation RICS method (ccRICS) (8). The emission of eGFP after 475-nm excitation is detected in the FGG(t) and FGR(t) PIE channels, while the red emission photons of mCherry excited with interleaved 561-nm excitation are detected in the FRR(t) PIE channel (Fig. 2 A). Put simply, direct mCherry emission and crosstalk of the eGFP are temporally separated in the red detection channel. Next, we determined the eGFP and mCherry-specific macrotime images from the FGG(t) and FRR(t) PIE channels, respectively, to show the specific cellular distribution of both fluorophores in the absence of crosstalk (Fig. 2 B). Then, a portion of the cell was selected for the RICS analysis (Fig. 2 B, white squares). Before image correlation with Eq. 1, macrotime images were spatially homogenized with a 10-frame moving average correction (Eq. S3 in the Supporting Material) (29). This homogenization is necessary to ensure that spatial correlations within images are only caused by fast diffusing molecules. The result of spatial correlation analysis with macrotime images calculated from different PIE channels is displayed in Fig. 2 C.
Figure 2.
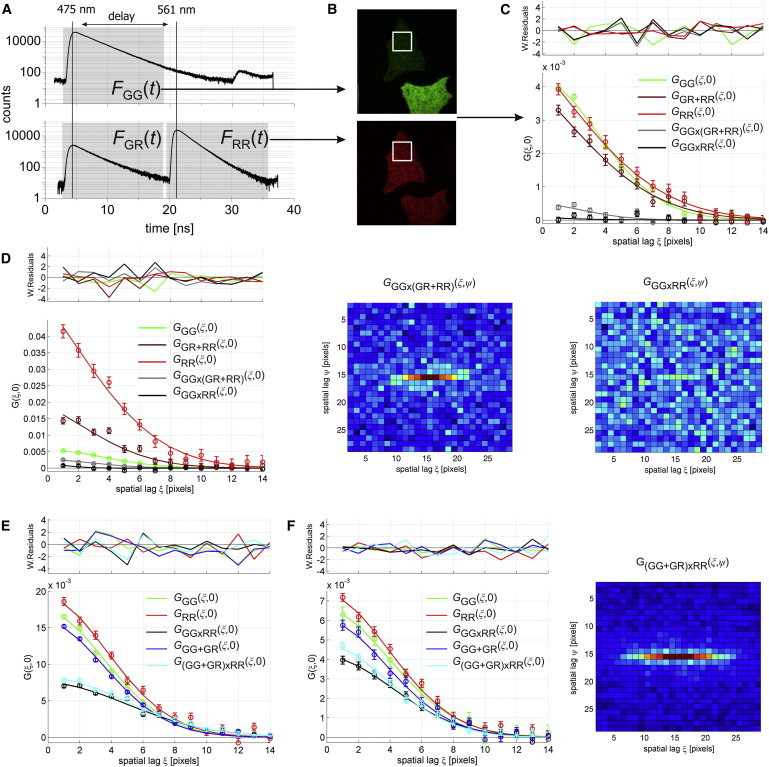
Dual-color PIE-RICS in the cytosol of living HeLa cells. (A) Logarithmic microtime histograms recorded in cells expressing eGFP and mCherry FP at similar concentrations. (Gray hatching) The different PIE channels. (B) Confocal macrotime images of HeLa cells expressing eGFP and mCherry with photons from the FGG(t) (eGFP) and FRR(t) (mCherry) PIE channels. (Open box) Subcellular region where PIE-FI was performed. Various correlation functions are shown for PIE-RICS experiments performed in live cells expressing (C) eGFP and mCherry at similar concentrations, (D) with an excess of eGFP, (E) eGFP-mCherry tandem construct, and (F) mVenus-mCherry tandem construct. Error bars represent the standard deviation and were used for weighted fitting to Eq. 2. In panels D and F, top views of selected CCFs are shown. The plus-sign in the figure legend indicates the combination of PIE channels into a single macrotime image, while the multiplier sign indicates the cross-correlation calculation of two macrotime images.
The spatial ACF of the red fluorophore in the presence of crosstalk
The amplitude of the red non-PIE spatial ACF GGR+RR calculated from images containing all red detected photons (Fig. 2 C, dark red curve) is given by
| (5) |
where is the ratio of total green versus total red molecules in the PSF; is the ratio of double-labeled versus total red molecules; β is the crosstalk parameter describing the relative brightness of the green versus red fluorophore in macrotime images calculated with photons from the combined FGR+RR(t) PIE channel (see Table S1 for the expected β); and is the total number of molecules carrying a red fluorophore. The higher the or β, the more the red spatial ACF amplitude will deviate from the normal curve where the amplitude is inversely proportional to . The amplitude of GRR in the absence of crosstalk (Fig. 2 C, red curve) is simply defined as
| (6) |
The GRR(ξ,ψ) ACF scales inversely, and only with , making it straightforward to calculate the absolute concentration when PIE-RICS is used. We performed a similar experiment in cells expressing eGFP in considerable excess with respect to mCherry (Fig. 2 D). In this case, a concentration calculated from the amplitude of GGR+RR would be far from the absolute value without correcting for crosstalk. A concentration calculated from the amplitude of GRR, however, is still independent of crosstalk.
The spatial cross-correlation function
When PIE is not used for the cross-correlation analysis, a false-positive cross-correlation amplitude is clearly observed as shown in Fig. 2, C and D (gray curves) when the FGG(t) and FGR+RR(t) PIE channels were used for determining the images. When the crosstalk-free FGG(t) and FRR(t) PIE channels are used instead, this amplitude drops below the background level (Fig. 2, C and D, black curves and Fig. 2 D, top views). Thus, even in cells with a large overexpression of eGFP, no false-positive cross-correlation is observed when PIE was used.
As a positive control, we analyzed the eGFP-mCherry fusion protein, which is known to constitute a good model FP pair for both dual-color fluorescence cross-correlation spectroscopy (30) and FRET (31) (Fig. 2 E). The high amplitude of the GGG×RR(ξ,ψ) crosstalk-free spatial CCF confirms the linked diffusion of the two fluorescent proteins. This amplitude is given by (13)
| (7) |
where fE is the FRET efficiency; is the total number of molecules carrying a green fluorophore; and is the fraction of double-labeled molecules NGR versus . FRET and/or incomplete double-labeling thus influence the observed cross-correlation amplitude. Assuming the FRET-lowered brightness of the eGFP in the FGG(t) PIE channel is compensated by the FRET-increased brightness of mCherry FP in the FGR(t) PIE channel, G(GG+GR)×RR(0,0) can be defined as
| (8) |
Hence, the absolute concentration of double-labeled species can be calculated from Eq. 8, even if fE and are not known. It can be seen in Fig. 2 E that the amplitude G(GG+GR)×RR (cyan curve) is indeed slightly higher than that of GGG×RR (black curve). Thus, under the right conditions, Eq. 8 represents the CCF amplitude as if no FRET or cross-talk were occurring, and can be used for straightforward quantification of interactions.
The spatial ACF of the green fluorophore in the presence of FRET
The amplitude of the spatial ACF from the macrotime image with FGG(t) photons when the system undergoes FRET is given by
| (9) |
Again, assuming the FRET-lowered brightness of eGFP in the FGG(t) PIE channel is compensated by the FRET-increased brightness of mCherry FP in the FGR(t) channel, GGG+GR(0,0) is given by
| (10) |
Under conditions of incomplete double-labeling and in the presence of FRET, concentrations calculated from GGG(0,0) will be too low whereas the correct and absolute concentrations can be calculated with GGG+GR(0,0), even if fE and/or are not known. The effect of FRET on the green ACF can be seen in Fig. 2 E where the amplitudes of GGG (green curve) and GGG+GR (blue curve) are slightly offset.
eGFP-mCherry versus mVenus-mCherry
PIE-FI is not limited to dual-color imaging of fluorophores with significantly separated emission spectra such as eGFP and mCherry, but can also be performed on constructs with significantly more crosstalk provided the green emission filter still blocks all photons coming from the red fluorophore. To demonstrate this, we measured the cross-correlation PIE-RICS of a mVenus/mCherry tandem. The crosstalk of mVenus into the red detection channel is significantly higher than that of eGFP because its emission spectrum is more red-shifted (see Table S1). In cells expressing an mVenus-mCherry tandem, a high CCF amplitude was observed, even higher than for eGFP-mCherry (Fig. 2 F). This suggests a higher fraction of double-labeled species exist. Additionally, the difference when correcting the green ACF and CCF for FRET was bigger than for eGFP-mCherry, suggesting a higher fE. We analyzed the ACFs and CCF quantitatively with Eqs. 6, 8, and 10 to assess the percentage of species having a fluorescent green and red fluorophore (Table 1). We calculated , the percentage of fluorescent eGFP molecules that are attached to a fluorescent mCherry, and , the percentage of fluorescent mCherry molecules that are attached to a fluorescent eGFP. For mVenus-mCherry, both and were higher than for eGFP-mCherry. It is known that mVenus folds and maturates more efficiently than eGFP, which would explain the larger fraction of fluorescent mVenus in the tandem constructs (17). The reason for the larger fraction of fluorescent mCherry in the mVenus-mCherry construct might be due to a more efficient folding of mCherry when attached to mVenus.
Table 1.
Dual-color PIE-RICS analysis
| Protein | fGR,GT [%] | fGR,RT [%] |
|---|---|---|
| eGFP-mCherry | 37 ± 4 | 73 ± 8 |
| mVenus-mCherry | 48 ± 7 | 85 ± 11 |
Dual-color PIE-RICS is definitely the more robust approach for quantifying such protein-protein interactions inside cells, because there can be a significant crosstalk if different fluorescent proteins are used as labels and because any effect of FRET can be removed from the experimental data. Also, because PIE-FI allows a straightforward, quantitative analysis of fluorophores, even with limited spectral separation, it holds great promise for multicolor imaging. Fluorescence cross-correlation analysis methods, when performed properly, allow the determination of binding affinities, even in live cells (30,32,33). In the past, quantification of intracellular binding affinities has proven difficult because of the presence of crosstalk and/or FRET (32,33), which can be simplified with PIE-FI. Fluctuation measurements on ternary complexes have mostly been limited to the theory and proof-of-principle experiments (34,35). The application of PIE-FI has the potential for imaging multiple fluorophores simultaneously and quantitatively in cells for the study of, for example, ternary and perhaps even quaternary complexes.
Absolute brightness and stoichiometry measurements with PIE-NB
N&B analysis with PIE-FI
The same data that is used for RICS analysis can, in principle, be further analyzed with the number and brightness analysis (N&B) to extract the concentration and absolute brightness, and thus stoichiometry, of molecules and complexes (16). In general, the average molecular number image n(x,y) and absolute brightness image ε(x,y) can be calculated from the first and second moments of the pixel intensities,
| (11) |
| (12) |
where
is the mean fluorescence intensity image and
is the temporal variance image of pixel (x,y) over all frames F in the image series. The temporal variance of the signal from a pixel is very sensitive to the statistics of photon emission, and photon counting detectors such as APDs have a nonnegligible dead time (36), which is even worse for time-correlated single-photon counting (TCSPC) electronics. Detection dead time reduces the number of detected photons and hence the measured variance at high count rates. Therefore, we investigated whether it is possible to perform a quantitative N&B analysis with PIE-FI.
We measured an aqueous solution of ATTO488 for 100 frames and calculated the histogram of the mean pixel intensity 〈I(x,y)〉F (Fig. 3 A) and a photon counting histogram (11.11 μs bin time) of the individual pixels (Fig. 3 B). Even at the relatively low average count rate of ∼75 kHz, there is a significant probability that individual pixels have a high (approximately MHz) count rate. After calculating the images from the raw photon files and preceding PIE-NB brightness analysis, we calculated the dead-time-corrected pixel intensity IC(x,y,f) using (37),
| (13) |
where IM(x,y,f) is the measured photon count in pixel (x,y,f); τp is the pixel dwell time; and τdead is the dead time. The relation between the registered and corrected count rate per pixel as a function of dead time is illustrated in Fig. 3 C for a pixel dwell time of 11.11 μs. The effect of a 100-ns dead time correction on the experimental histograms is depicted in black in Fig. 3, A and B. To calibrate the dead-time characteristics of our hardware, we measured the whole-image average brightness for a broad dilution series of ATTO488 with Eq. 12 after correcting the image series with Eq. 13 using different values for τdead (Fig. 3 D). Two nonlinear regimes can be distinguished, at very low count rates (<10 kHz) and at very high count rates. Whereas the low signal nonlinearity has different origins (see Accurate Measurements at Picomolar Concentrations), a dead-time correction should correct the high count rate nonlinearity as seen for τdead ∼100 ns (Fig. 3 D). This dead time corresponds well with the reported value for the TCSPC card that was used for the experiments (SPC-140, 100 ns; Becker & Hickl, Berlin, Germany).
Figure 3.
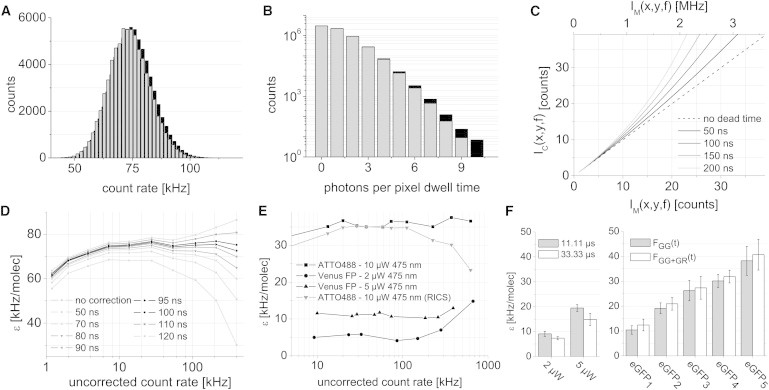
Determining the absolute molecular brightness with PIE-FI microscopy. (A) Histogram of the mean intensity per pixel from a series of 100 images of a 20-nM aqueous solution of ATTO488 at 20 μW excitation power and 11.11 μs pixel dwell time. (B) The photon counting histogram of absolute pixel counts for the same image series analyzed in panel A. (Gray histograms) Raw (not dead-time-corrected) data. (Black histograms) Same data corrected for a 100-ns detection dead time as given by Eq. 13. (C) The relationship between the measured (IM) and corrected (IC) photon counts is plotted assuming a pixel dwell time of 11.11 μs for different detection dead times. The x axis is displayed in counts per pixel dwell time (lower axis) and in megacounts per second (upper axis). (D) The experimental dependence of the measured brightness of ATTO488 determined from samples of various concentration (and hence count rate) assuming different detection dead-time corrections. (E) Dead-time-corrected brightness analysis of ATTO488 and Venus FP in a 10-cP buffer. (F) Molecular brightness measurements of eGFP and eGFP oligomers in live cells. (Left bar chart) Dependence of the apparent monomeric eGFP brightness on laser power and pixel dwell time. (Right bar chart) Molecular brightness for different eGFP tandem constructs ranging from monomers to pentamers.
The average PIE-NB brightness of the dye in the linear range of the concentration range was 75 ± 2 kHz/mol, when the dye was excited at 20 μW of 475-nm light. The average brightness calculated from a PIE-RICS analysis on the same data with Eq. 4 was slightly higher (82 ± 2 kHz/mol), suggesting that a pixel dwell time of 11.11 μs is still too long to accurately sample the temporal pixel variance needed for proper PIE-NB brightness for a freely diffusing fluorophore in solution. When analyzing the same dye in 10-cP buffer, the PIE-NB brightness (36 ± 1 kHz/mol) and PIE-RICS brightness (35 ± 1 kHz/mol) at 10 μW excitation power were in the linear range and indeed very similar, demonstrating that it is possible to measure the brightness accurately with PIE-FI, either from the spatial (PIE-RICS) or the temporal (PIE-NB) pixel variance (Fig. 3 E). In the 10-cP buffer, we studied the brightness of Venus FP at two laser powers. The average brightness was 5.1 ± 0.8 kHz/mol at 2 μW and 11.0 ± 0.5 kHz/mol at 5 μW, agreeing well with what was obtained from the PIE-RICS experiments (Fig. 1 F).
PIE-NB in cells
Using proper correction for the large dead time of the TCSPC detection system used for PIE, we tested the performance of PIE-NB in living cells expressing eGFP. For the N&B analysis, images need not be spatially homogeneous as for RICS analysis, but it is still necessary to remove variance due to drift of the cell and the slow motion of large cellular structures (16). As very few photons are typically detected per pixel with PIE-FI, it is helpful to use spatial averaging as well as temporal averaging to remove slow fluctuations (see Eq. S6 in the Supporting Material). Spatial averaging can be done as the pixel size is generally fivefold less than the radial waist of the PSF.
First, we measured the effect of laser power and pixel dwell time on the obtained apparent eGFP brightness. The measured brightness at a 11.11-μs pixel dwell time and 2 μW or 5 μW excitation power (Fig. 3 F, left panel) were similar to what was expected considering the performance of the microscope (see Table S1). A longer pixel dwell time reduced the apparent PIE-NB brightness due to motion of the eGFP in the PSF while measuring at the pixel.
Brightness analysis of eGFP oligomers in cells
We used PIE-NB to investigate the molecular brightness of different homo-oligomers of eGFP, which have been previously used for characterizing the cytosolic dynamics of large rod-like molecules (38) (Fig. 3 F, right panel). The PIE-NB brightness of the oligomers increased with size, although their brightness was not an integer multiple of the monomer brightness. It is known that not all fluorescent proteins mature and fluoresce. We used the measured brightness to estimate the average maturation efficiency of eGFP using
| (14) |
where ε(n) is the observed brightness of the n-mer; ε (1) is the brightness of a monomer; and p is the maturation probability. The maturation probabilities estimated from measurements on the dimer were ∼91%, for the trimer 84%, and for the tetramer and pentamer ∼73%. Interestingly, the brightness does not continue linearly with oligomer size. This suggests that higher-order oligomer constructs have a more difficult time maturating than monomers or dimers. Alternatively, it is also possible that the decrease in the molecular brightness for the higher order oligomers is due to an increasingly higher probability for singlet-singlet or singlet-triplet annihilation, as has been proven before for dendrimers (39) and DsRed tetramers (40). Taken together, these experiments demonstrate that quantitative N&B analysis can be performed with PIE-FI, when the appropriate dead-time correction is applied.
Using the fluorescence lifetime information from PIE-FI
Accurate measurements at picomolar concentrations
The fluorescence lifetime information available from PIE with TCSPC detection brings additional benefits when performing PIE-FI experiments. One example is measurements at picomolar concentrations. At low signal, uncorrelated noise (Raman scattering, laser reflections, detector dark counts, background light) or correlated noise (detector afterpulsing) contaminates the fluorescence signal, as can be seen in a microtime histogram of a PIE-FI series of an aqueous solution of ATTO488 for concentrations varying from 100 nM to 6.1 pM (Fig. 4 A). Whereas at high concentration (100 nM) most detected photons are coming from fluorescence, at low (195-pM, 100-nM diluted 29-fold) and very low (6.1-pM, 100-nM diluted 214-fold) concentrations, the scattering signal makes up a larger fraction of the detected photons. Correcting for scattering is difficult due to the nonlinear weighting of the different species in a correlation analysis. The amplitude of the PIE-RICS ACF determined over four orders of magnitude in concentration is shown in Fig. 4 B. Due to scattering, the amplitude does not vary linearly with concentration below ∼1 nM. One way to reduce the effect of noise is to use time gating. The scattering photons come immediately with the excitation pulse, whereas the majority of fluorescence photons are delayed. By selecting photons that arrive after the instrument response function (IRF) has decayed, as illustrated with the FGG,gated(t) channel in Fig. 4 A, it is possible to suppress the detection of scattered photons and perform quantitative measurements at subnanomolar concentrations (Fig. 4 B).
Figure 4.
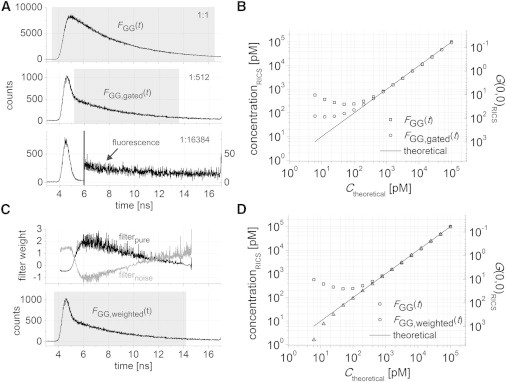
Measuring picomolar concentrations with RLICS. (A) Experimental microtime histograms of a 100-nM (top), 195-pM (middle), and 6-pM (bottom) ATTO488 solution. (Shaded hatching) Nongated and gated FGG(t) PIE channels. At 6 pM, the y scale was expanded 10 times from 6 ns onward to show the fluorescence. (B) Theoretical versus RICS-measured concentration of a dilution series of ATTO488 from 100 nM to 6 pM in twofold dilution steps with photons from the respective hatched PIE channels in panel A. For reference, the experimental GGG(0,0) value from the RICS experiment determined by fitting the ACF to Eq. 2 is given on the right y axis. (C) (top) Experimental lifetime weighting filters calculated from the data in the FGG(t) PIE channel (bottom). (D) Theoretical versus measured concentration for the same dilution series as in panel B, when lifetime weighting is used. The nonweighted data and experimental GGG(0,0) from the RICS experiment are given for comparison.
A very elegant approach to avoid problems with scattering during the correlation analysis is to use a lifetime weighting approach as was done previously in fluorescence lifetime correlation spectroscopy (FLCS) (41). This is possible, as long as a filter pattern can be designed that differs substantially between the different species (42,43). In raster lifetime image correlation spectroscopy (RLICS), each photon in the macrotime image is weighted by the species filter (Fig. 4 C and see Eq. S8 in the Supporting Material), dependent on the microtime of the detected photon. As the filters can have negative values, it is possible that the total pixel intensity after filtering is very close to zero, or even zero, which would adversely affect the amplitude of the ACF. Therefore, we first apply a precorrelation image rescaling
| (15) |
where min(I) is the absolute value of the lowest pixel intensity in the image series. Spatial ACFs were then calculated per frame with Eq. 1 and the average spatial ACF over all frames was rescaled to its original amplitude (44),
| (16) |
where
is the spatially averaged pixel intensity over all frames F. The PIE-channel selected for the analysis and the RLICS amplitude as a function of concentration are shown in Fig. 4, C and D. Clearly, the range at which the concentration could be accurately determined was significantly improved to <∼30 pM. Considering an image size of 156.25 μm2, this corresponds to an average of N < 10 molecules in the whole image. Below ∼30 pM concentration, the measured concentrations were lower than expected, most likely due to dilution artifacts at low concentration.
Resolving FRET species with lifetime-weighted PIE-FI
The fluorescence lifetime information available with PIE makes it possible to quantify FRET in PIE-FI experiments. We demonstrate this by further analyzing the eGFP/mCherry and mVenus/mCherry data presented in Fig. 2. First, from cells coexpressing mCherry and either eGFP or mVenus, we extracted the fluorescence lifetime of the respective protein in the absence of FRET by performing a convolution fitting (i.e., Eq. 17 with n = 1) of the microtime histogram constructed with all photons from the FGG(t) PIE channel (for eGFP or mVenus) or the FRR(t) PIE channel (for mCherry),
| (17) |
where Np is the total number of photons in the decay; fs is the fraction of scattering in the decay; tshift is the temporal shift of the IRF; the asterisk is the convolution function; c is the contribution of uncorrelated background; fx and τx are the fractional contribution and excited state fluorescence lifetime of component i; n is the number of lifetime components; and T is the number of time channels included in the fitting (45). The values fs, fx, τx, and c were allowed to vary during fitting. The fluorescence decay of eGFP and mVenus could be approximated well with a single exponential (Fig. 5, A and B, and Table 2) and the resulting lifetimes agreed well with reported values (46,47). The fluorescence decay of mCherry in the FRR(t) PIE channel could be fitted reasonably well with a single exponential model and the recovered lifetime was 1.50 ± 0.06 ns, close to what has been reported as the major component governing the fluorescence decay of mCherry (25).
Figure 5.
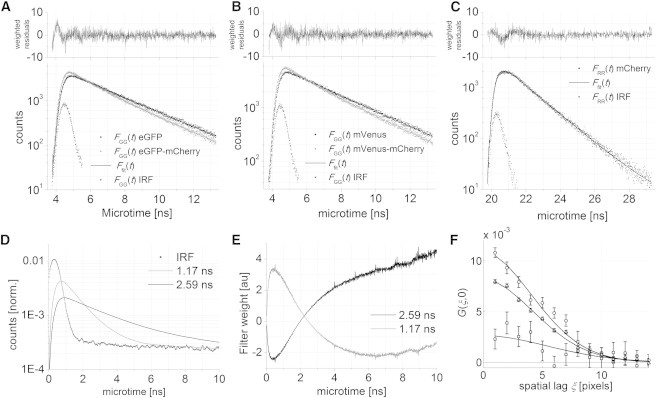
Dual-fluorophore pseudo-FLIM and dual-color RLICS analysis. Fluorescence lifetime analysis of image data for (A) eGFP and eGFP-mCherry, (B) mVenus and mVenus-mCherry, and (C) mCherry. (D) Calculated idealized fluorescence decay of FRET-quenched (1.17 ns) and unquenched (2.59 ns) eGFP in an eGFP-mCherry tandem convoluted with the experimental IRF. (E) Lifetime weighting filters calculated from the data in panel D. (F) Unfiltered (triangles), FRET-species filtered (circles), and non-FRET species filtered (squares) GGG×RR(ξ,0) of the eGFP-mCherry tandem measured in live cells.
Table 2.
Dual-color lifetime analysis
| Protein | PIE channel | τ1 [ns] | f1 [%] | τ2 [ns] | fE | χ2r |
|---|---|---|---|---|---|---|
| eGFP | FGG(t) | 2.60 ± 0.04 | — | — | — | 2.01 |
| eGFP-mCherry | FGG(t) | 2.59 ± 0.04 | 64 ± 4 | 1.17 ± 0.11 | 0.55 ± 0.04 | 1.54 |
| eGFP-mCherry | FRR(t) | 1.46 ± 0.04 | — | — | — | 2.56 |
| mVenus | FGG(t) | 2.99 ± 0.02 | — | — | — | 2.18 |
| mVenus-mCherry | FGG(t) | 2.88 ± 0.03 | 64 ± 1 | 1.05 ± 0.11 | 0.63 ± 0.04 | 1.76 |
| mVenus-mCherry | FRR(t) | 1.50 ± 0.02 | — | — | — | 1.97 |
| mCherry | FRR(t) | 1.50 ± 0.06 | — | — | — | 2.73 |
Reconvolution fitting with Eq. 17 was performed on datasets with ∼1E6 photons. The value τ1,2 is the fluorescence lifetime; f1 is the fraction of the first lifetime component; fE is the FRET efficiency, calculated with Eq. 18; and χ2r is the reduced fit quality parameter calculated from the anisotropy-free part of the fluorescence decay (45).
In cells expressing the heterodimer tandems, the fluorescence of the green fluorophore was quenched by the close proximity of the mCherry FRET acceptor (Fig. 5, A and B). A biexponential model was necessary to fit the fluorescence decay (Eq. 17 with n = 2), yielding one fluorescence lifetime close to that of the donor-only species and one strongly quenched fluorescence lifetime (Table 2). From the lifetimes values, the FRET efficiency was determined:
| (18) |
For eGFP-mCherry, fE = 0.55 was close to the previously reported value of a similar construct (Table 2) (46). The mVenus/mCherry pair clearly exhibited a higher fE of 0.63, consistent with the higher calculated R0 for the mVenus/mCherry pair (see Table S1). The fraction of the donor fluorophore population exhibiting a fast lifetime component was similar for both samples, suggesting that mCherry acts equally well as a FRET acceptor in both constructs. To verify whether the photophysical properties of mCherry are independent of the presence of the proximal FRET donor, we also analyzed its fluorescence lifetime directly in the tandem constructs. For all constructs, the directly excited fluorescence lifetime of mCherry stayed constant (Table 2).
Species-RICS in cells
It is possible to separate different species with the same color during FCS experiments based on their fluorescence lifetime with FLCS (41) or based on other parameters, such as their anisotrophy, with filtered FCS (48). With the lifetime information available in PIE-FI, we tested whether we can separate species based on their fluorescence lifetime inside living cells using a species-RICS approach. To do this, we analyzed a dual-color PIE-RICS dataset of cells expressing the eGFP-mCherry tandem dimer. Cross-correlation of mCherry with only those eGFP species having a quenched fluorescence lifetime should result in a higher CCF amplitude than the non-species-specific CCF. Likewise, cross-correlation with those eGFP species having a donor-only lifetime should result in a zero CCF amplitude.
Using the ideal fluorescence decay of eGFP and FRET-quenched eGFP convoluted with the IRF (see Eq. S7 in the Supporting Material) as input (Fig. 5 D), we created the two lifetime filters for the RLICS analysis (Fig. 5 E). Using the microtime histograms and weighting filters, we calculated two weighted macrotime image series of the donor, IGG,D(x,y,f), weighted for the non-FRET species and IGG,DA(x,y,f), weighted for the FRET species. The RLICS CCF with the (nonweighted) macrotime image series of mCherry, IRR(x,y,f) is shown in Fig. 5 F. The CCF amplitude indeed increased when weighting the data with the filter for the FRETing donor. Similarly when weighting the data with the filter for the nonFRETing donor, the CCF amplitude decreased. As the cross-correlation amplitude did not decrease to zero, this suggests that the factor 2 difference in the fluorescence lifetime is not ideal for lifetime-weighted fitting. This proof-of-principle experiment shows that the fluorescence lifetime information encoded in a species-RICS experiment can be used to specifically study subspecies with the same color, yet different lifetimes.
Conclusion
In this work, we introduced pulsed interleaved excitation fluctuation imaging (PIE-FI), to our knowledge a novel microscopy modality in which we have combined PIE with existing techniques for fluctuation analysis such as RICS, ccRICS, N&B, and FLCS. We showed that RICS can be well performed using pulsed lasers. For fluorophores that are sensitive to photo-induced blinking and -bleaching, RICS shows definite advantages over single-point FCS measurements and the determined diffusion coefficient and brightness was more robust as a function of laser power. Crosstalk-free ccRICS could be performed with PIE, making it possible to directly obtain quantitative results from the amplitude of the ACFs and CCF. If direct excitation of the red fluorophore with green excitation is negligible, one can also correct for FRET when performing PIE-FI. The one disadvantage of using PIE-FI when performing an N&B analysis is the significant dead time of the TCSPC detection cards. However, by correcting for the effects of the dead-time, quantitative N&B analysis can be performed. From the quantitative results obtained from PIE-FI measurements, interactions and the stoichiometry of complexes can be determined. From the N&B measurement on different GFP oligomers, we could show that the folding efficiency of GFP decreases with the size of these oligomers.
In addition to the advantages of removing crosstalk for cross-correlation measurements, the TCSPC information available from the PIE-FI data can be used to enhance the functionality of fluctuation imaging experiments. Raster lifetime ICS (RLICS) has a dual advantage: the amount of uncorrelated noise does not need to be known a priori, and even correlated noise such as detector afterpulsing can be removed from the correlation function because, on the microtime level, it is detected as a constant offset in each time-to-amplitude converter channel. With RLICS we were able to perform quantitative concentration measurements down to <30 pM. In measurements of FP tandems in live cells, we used the lifetime information available in the PIE-RICS experiment to quantify the FRET efficiency. It was even possible to use lifetime filtering to discriminate between FRETing and non-FRETing complexes and analyze the species separately.
Of course, there are more imaging applications that can be enhanced using PIE than we have presented here. Recently, a new superresolution method based on fluctuation imaging has been introduced, stochastical optical fluctuation imaging (SOFI) (49,50). SOFI increases the resolution of an image series obtained using wide field microscopy when the fluorophores are stochastically blinking by analyzing the temporal correlation functions generated from pixels in the image. By combining SOFI with PIE, it would be possible to perform crosstalk-free multicolor SOFI. However, due to the slow imaging rates obtainable with the raster scanning implementation of PIE, SOFI-PIE may not be of practical use in this form. To overcome this difficulty, groups are working on the development of area detectors with lifetime resolution such as the one described by Michalet et al. (51) that would make PIE-SOFI possible. With the availability of the fluorescence lifetime information in PIE-SOFI, a multispecies SOFI analysis based on different labels distinguished based on their lifetime as in FLCS would be possible.
Altogether, PIE-FI provides new functionalities and enhances the analysis capabilities of different fluctuation imaging techniques. It is also straightforward to implement and can, in principle, be incorporated into any raster-scanning microscope (even commercial systems) as long as the scanning and detection modules can be synchronized (29,52,53). Therefore, we expect PIE-FI to become the new standard in advanced fluorescence microscopy.
Acknowledgments
We thank Prof. Masataka Kinjo and Prof. Shintaro Mikuni (Laboratory of Molecular Cell Dynamics, Faculty of Advanced Life Science, Hokkaido University, Sapporo, Japan), Prof. Atsushi Miyawaki (Laboratory for Cell Function Dynamics, RIKEN Brain Science Institute, Japan), and Prof. Roger Y. Tsien (Howard Hughes Medical Institute, University of California at San Diego, La Jolla, CA) for providing plasmids encoding fluorescent proteins. We thank Prof. Enrico Gratton (Laboratory for Fluorescence Dynamics, University of California, Irvine, CA) for fruitful discussions regarding the implementation of the dead-time correction for the PIE-NB analysis. We are indebted to Dr. Volodymyr Kudryavtsev and Dr. Martin Sikor for helping in the development of data acquisitioning and analysis software and for fruitful discussions. MSc. Doortje Borrenberghs (Laboratory for Photochemistry and Spectroscopy, KU Leuven, Belgium) is thanked for cloning pmVenus-mCherry and pmVenus-C1 plasmids and for purifying Venus FP.
J.H. is grateful for a postdoctoral fellowship and travel grant from the Research Foundation Flanders. D.C.L. acknowledges financial support of the Deutsche Forschungsgemeinschaft through the Excellence Initiative Nanosystems Initiative Munich, Sonderforschungbereich grant No. 1032, and the Ludwig-Maximilians-Universität through the Center for Nano Science and the Ludwig-Maximilians-Universität Innovative BioImaging Network.
Contributor Information
Jelle Hendrix, Email: jelle_hendrix@hotmail.com.
Don C. Lamb, Email: d.lamb@lmu.de.
Supporting Material
References
- 1.Elson E.L., Magde D. Fluorescence correlation spectroscopy. I. Conceptual basis and theory. Biopolymers. 1974;13:1–27. doi: 10.1002/bip.1974.360130103. [DOI] [PubMed] [Google Scholar]
- 2.Magde D., Elson E.L., Webb W.W. Fluorescence correlation spectroscopy. II. An experimental realization. Biopolymers. 1974;13:29–61. doi: 10.1002/bip.1974.360130103. [DOI] [PubMed] [Google Scholar]
- 3.Magde D., Webb W.W., Elson E. Thermodynamics Fluctuations in a Reacting System-Measurement by Fluorescence Correlation Spectroscopy. Phys. Rev. Lett. 1972;29:705–708. [Google Scholar]
- 4.White J.G., Amos W.B., Fordham M. An evaluation of confocal versus conventional imaging of biological structures by fluorescence light microscopy. J. Cell Biol. 1987;105:41–48. doi: 10.1083/jcb.105.1.41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Petersen N.O., Höddelius P.L., Magnusson K.E. Quantitation of membrane receptor distributions by image correlation spectroscopy: concept and application. Biophys. J. 1993;65:1135–1146. doi: 10.1016/S0006-3495(93)81173-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wiseman P.W., Brown C.M., Horwitz A.F. Spatial mapping of integrin interactions and dynamics during cell migration by image correlation microscopy. J. Cell Sci. 2004;117:5521–5534. doi: 10.1242/jcs.01416. [DOI] [PubMed] [Google Scholar]
- 7.Wiseman P.W., Squier J.A., Wilson K.R. Two-photon image correlation spectroscopy and image cross-correlation spectroscopy. J. Microsc. 2000;200:14–25. doi: 10.1046/j.1365-2818.2000.00736.x. [DOI] [PubMed] [Google Scholar]
- 8.Digman M.A., Wiseman P.W., Gratton E. Detecting protein complexes in living cells from laser scanning confocal image sequences by the cross correlation raster image spectroscopy method. Biophys. J. 2009;96:707–716. doi: 10.1016/j.bpj.2008.09.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Digman M.A., Wiseman P.W., Gratton E. Stoichiometry of molecular complexes at adhesions in living cells. Proc. Natl. Acad. Sci. USA. 2009;106:2170–2175. doi: 10.1073/pnas.0806036106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Toplak T., Pandzic E., Wiseman P.W. STICCS reveals matrix-dependent adhesion slipping and gripping in migrating cells. Biophys. J. 2012;103:1672–1682. doi: 10.1016/j.bpj.2012.08.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Semrau S., Holtzer L., Schmidt T. Quantification of biological interactions with particle image cross-correlation spectroscopy (PICCS) Biophys. J. 2011;100:1810–1818. doi: 10.1016/j.bpj.2010.12.3746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kapanidis A.N., Lee N.K., Weiss S. Fluorescence-aided molecule sorting: analysis of structure and interactions by alternating-laser excitation of single molecules. Proc. Natl. Acad. Sci. USA. 2004;101:8936–8941. doi: 10.1073/pnas.0401690101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Müller B.K., Zaychikov E., Lamb D.C. Pulsed interleaved excitation. Biophys. J. 2005;89:3508–3522. doi: 10.1529/biophysj.105.064766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kudryavtsev V., Sikor M., Lamb D.C. Combining MFD and PIE for accurate single-pair Förster resonance energy transfer measurements. ChemPhysChem. 2012;13:1060–1078. doi: 10.1002/cphc.201100822. [DOI] [PubMed] [Google Scholar]
- 15.Digman M.A., Brown C.M., Gratton E. Measuring fast dynamics in solutions and cells with a laser scanning microscope. Biophys. J. 2005;89:1317–1327. doi: 10.1529/biophysj.105.062836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Digman M.A., Dalal R., Gratton E. Mapping the number of molecules and brightness in the laser scanning microscope. Biophys. J. 2008;94:2320–2332. doi: 10.1529/biophysj.107.114645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Nagai T., Ibata K., Miyawaki A. A variant of yellow fluorescent protein with fast and efficient maturation for cell-biological applications. Nat. Biotechnol. 2002;20:87–90. doi: 10.1038/nbt0102-87. [DOI] [PubMed] [Google Scholar]
- 18.Enderlein J., Gregor I., Fitter J. Art and artifacts of fluorescence correlation spectroscopy. Curr. Pharm. Biotechnol. 2004;5:155–161. doi: 10.2174/1389201043377020. [DOI] [PubMed] [Google Scholar]
- 19.Lamb D.C., Schenk A., Nienhaus G.U. Sensitivity enhancement in fluorescence correlation spectroscopy of multiple species using time-gated detection. Biophys. J. 2000;79:1129–1138. doi: 10.1016/S0006-3495(00)76366-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ivanchenko S., Lamb D.C. Fluorescence correlation spectroscopy: principles and developments. In: Brnjas-Kraljevic J., Pifat-Mrzljak G., editors. Supramolecular Structure and Function. Springer-Verlag, Berlin; Germany: 2011. pp. 1–30. [Google Scholar]
- 21.Thompson N.L. Fluorescence correlation spectroscopy. In: Lakowicz J.R., editor. Topics in Fluorescence Spectroscopy. Plenum Press; New York: 1991. [Google Scholar]
- 22.Gielen E., Smisdom N., Ameloot M. Measuring diffusion of lipid-like probes in artificial and natural membranes by raster image correlation spectroscopy (RICS): use of a commercial laser-scanning microscope with analog detection. Langmuir. 2009;25:5209–5218. doi: 10.1021/la8040538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Schwille P., Kummer S., Webb W.W. Fluorescence correlation spectroscopy reveals fast optical excitation-driven intramolecular dynamics of yellow fluorescent proteins. Proc. Natl. Acad. Sci. USA. 2000;97:151–156. doi: 10.1073/pnas.97.1.151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hendrix J., Lamb D.C. Pulsed interleaved excitation: principles and applications. Methods Enzymol. 2013;518:205–243. doi: 10.1016/B978-0-12-388422-0.00009-1. [DOI] [PubMed] [Google Scholar]
- 25.Hendrix J., Flors C., Engelborghs Y. Dark states in monomeric red fluorescent proteins studied by fluorescence correlation and single molecule spectroscopy. Biophys. J. 2008;94:4103–4113. doi: 10.1529/biophysj.107.123596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Petrásek Z., Schwille P. Precise measurement of diffusion coefficients using scanning fluorescence correlation spectroscopy. Biophys. J. 2008;94:1437–1448. doi: 10.1529/biophysj.107.108811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ries J., Schwille P. Studying slow membrane dynamics with continuous wave scanning fluorescence correlation spectroscopy. Biophys. J. 2006;91:1915–1924. doi: 10.1529/biophysj.106.082297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Dertinger T., Pacheco V., Enderlein J. Two-focus fluorescence correlation spectroscopy: a new tool for accurate and absolute diffusion measurements. ChemPhysChem. 2007;8:433–443. doi: 10.1002/cphc.200600638. [DOI] [PubMed] [Google Scholar]
- 29.Brown C.M., Dalal R.B., Gratton E. Raster image correlation spectroscopy (RICS) for measuring fast protein dynamics and concentrations with a commercial laser scanning confocal microscope. J. Microsc. 2008;229:78–91. doi: 10.1111/j.1365-2818.2007.01871.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Foo Y.H., Naredi-Rainer N., Wohland T. Factors affecting the quantification of biomolecular interactions by fluorescence cross-correlation spectroscopy. Biophys. J. 2012;102:1174–1183. doi: 10.1016/j.bpj.2012.01.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tramier M., Zahid M., Coppey-Moisan M. Sensitivity of CFP/YFP and GFP/mCherry pairs to donor photobleaching on FRET determination by fluorescence lifetime imaging microscopy in living cells. Microsc. Res. Tech. 2006;69:933–939. doi: 10.1002/jemt.20370. [DOI] [PubMed] [Google Scholar]
- 32.Oyama R., Takashima H., Yanagawa H. Protein-protein interaction analysis by C-terminally specific fluorescence labeling and fluorescence cross-correlation spectroscopy. Nucleic Acids Res. 2006;34:e102. doi: 10.1093/nar/gkl477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Shi X., Foo Y.H., Wohland T. Determination of dissociation constants in living zebrafish embryos with single wavelength fluorescence cross-correlation spectroscopy. Biophys. J. 2009;97:678–686. doi: 10.1016/j.bpj.2009.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Heinze K.G., Jahnz M., Schwille P. Triple-color coincidence analysis: one step further in following higher order molecular complex formation. Biophys. J. 2004;86:506–516. doi: 10.1016/S0006-3495(04)74129-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hwang L.C., Gösch M., Wohland T. Simultaneous multicolor fluorescence cross-correlation spectroscopy to detect higher order molecular interactions using single wavelength laser excitation. Biophys. J. 2006;91:715–727. doi: 10.1529/biophysj.105.074120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hillesheim L.N., Müller J.D. The photon counting histogram in fluorescence fluctuation spectroscopy with non-ideal photodetectors. Biophys. J. 2003;85:1948–1958. doi: 10.1016/S0006-3495(03)74622-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Becker W. Springer, Heidelberg; Germany: 2005. Advanced Time-Correlated Single Photon Counting Techniques. Springer Series in Chemical Physics, Vol. 81. [Google Scholar]
- 38.Pack C., Saito K., Kinjo M. Microenvironment and effect of energy depletion in the nucleus analyzed by mobility of multiple oligomeric EGFPs. Biophys. J. 2006;91:3921–3936. doi: 10.1529/biophysj.105.079467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hofkens J., Maus M., De Schryver F. Probing photophysical processes in individual multichromophoric dendrimers by single-molecule spectroscopy. J. Am. Chem. Soc. 2000;122:9278–9288. [Google Scholar]
- 40.Cotlet M., Hofkens J., De Schryver F.C. Identification of different emitting species in the red fluorescent protein DsRed by means of ensemble and single-molecule spectroscopy. Proc. Natl. Acad. Sci. USA. 2001;98:14398–14403. doi: 10.1073/pnas.251532698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Böhmer M., Wahl M., Enderlein J. Time-resolved fluorescence correlation spectroscopy. Chem. Phys. Lett. 2002;353:439–445. [Google Scholar]
- 42.Kapusta P., Wahl M., Enderlein J. Fluorescence lifetime correlation spectroscopy. J. Fluoresc. 2007;17:43–48. doi: 10.1007/s10895-006-0145-1. [DOI] [PubMed] [Google Scholar]
- 43.Rüttinger S., Kapusta P., MacDonald R. On the resolution capabilities and limits of fluorescence lifetime correlation spectroscopy (FLCS) measurements. J. Fluoresc. 2010;20:105–114. doi: 10.1007/s10895-009-0528-1. [DOI] [PubMed] [Google Scholar]
- 44.Schwille P., Korlach J., Webb W.W. Fluorescence correlation spectroscopy with single-molecule sensitivity on cell and model membranes. Cytometry. 1999;36:176–182. doi: 10.1002/(sici)1097-0320(19990701)36:3<176::aid-cyto5>3.0.co;2-f. [DOI] [PubMed] [Google Scholar]
- 45.Maus M., Cotlet M., Seidel C.A. An experimental comparison of the maximum likelihood estimation and nonlinear least-squares fluorescence lifetime analysis of single molecules. Anal. Chem. 2001;73:2078–2086. doi: 10.1021/ac000877g. [DOI] [PubMed] [Google Scholar]
- 46.Padilla-Parra S., Audugé N., Tramier M. Quantitative comparison of different fluorescent protein couples for fast FRET-FLIM acquisition. Biophys. J. 2009;97:2368–2376. doi: 10.1016/j.bpj.2009.07.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Sarkar P., Koushik S.V., Gryczynski Z. Photophysical properties of Cerulean and Venus fluorescent proteins. J. Biomed. Opt. 2009;14:034047. doi: 10.1117/1.3156842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Felekyan S., Kalinin S., Seidel C.A. Filtered FCS: species auto- and cross-correlation functions highlight binding and dynamics in biomolecules. ChemPhysChem. 2012;13:1036–1053. doi: 10.1002/cphc.201100897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Dedecker P., Mo G.C., Zhang J. Widely accessible method for superresolution fluorescence imaging of living systems. Proc. Natl. Acad. Sci. USA. 2012;109:10909–10914. doi: 10.1073/pnas.1204917109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Dertinger T., Colyer R., Enderlein J. Fast, background-free, 3D super-resolution optical fluctuation imaging (SOFI) Proc. Natl. Acad. Sci. USA. 2009;106:22287–22292. doi: 10.1073/pnas.0907866106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Michalet X., Colyer R.A., Weiss S. Single-quantum dot imaging with a photon counting camera. Curr. Pharm. Biotechnol. 2009;10:543–558. doi: 10.2174/138920109788922100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Hendrix, J., and D. C. Lamb. Implementation and application of pulsed interleaved excitation for dual-color FCS and RICS. In Fluorescence Spectroscopy and Microscopy: Methods and Protocols. Y. Engleboroghs and A.J.W.G. Visser, editors. Springer-Humana Press, Heidelberg, Germany. In press. [DOI] [PubMed]
- 53.Gielen E., Smisdom N., Ameloot M. Diffusion of myelin oligodendrocyte glycoprotein in living OLN-93 cells investigated by raster-scanning image correlation spectroscopy (RICS) J. Fluoresc. 2008;18:813–819. doi: 10.1007/s10895-007-0308-8. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


