Using phylogenetic information and chemical properties to predict species tolerances to pesticides

Abstract

Direct estimation of species' tolerance to pesticides and other toxic organic substances is a combinatorial problem, because of the large number of species–substance pairs. We propose a statistical modelling approach to predict tolerances associated with untested species–substance pairs, by using models fitted to tested pairs. This approach is based on the phylogeny of species and physico-chemical descriptors of pesticides, with both kinds of information combined in a bilinear model. This bilinear modelling approach predicts tolerance in untested species–compound pairs based on the facts that closely related species often respond similarly to toxic compounds and that chemically similar compounds often have similar toxic effects. The three tolerance models (median lethal concentration after 96 h) used up to 25 aquatic animal species and up to nine pesticides (organochlorines, organophosphates and carbamates). Phylogeny was estimated using DNA sequences, while the pesticides were described by their mode of toxic action and their octanol–water partition coefficients. The models explained 77–84% of the among-species variation in tolerance (log₁₀ LC₅₀). In cross-validation, 84–87% of the predicted tolerances for individual species were within a factor of 10 of the observed values. The approach can also be used to model other species response to multivariate stress factors.

1. Introduction

Organisms are adapted to exploit the resources of their habitats and withstand a range of environmental conditions found therein. Stress or disturbance occurs when conditions depart from that range [1]. Toxic stress occurs when exposure to chemical substances is sufficient to disrupt important physiological processes, leading to depression or complete failure of functions that are necessary for growth, reproduction or survival. Such disruption depends on a broad array of interactions, at the molecular level, between physico-chemical properties of the compound and biochemical traits (e.g. receptors and enzymes) of the organism. Hence, tolerance to toxic stress can be regarded as a complex species trait integrating an array of subordinate biochemical and physiological features. On the other hand, chemical compound toxicity results from the physico-chemical properties of the compounds; these properties can be regarded as features of the compounds. Toxic stress therefore arises from complex interactions between the characteristics of the organisms and those of the chemical compounds.

Understanding the effects of toxicity on living organisms is mandatory to assess the impact of chemical pollution on the environment [2]. An appreciable proportion of the numerous chemical compounds that are developed, produced and used by humans eventually reach ecosystems. These ecosystems are themselves populated by many different species, each of them having its particular susceptibilities towards each of those compounds. The exhaustive testing of every possible species-substance combination is impossible in practice because ecosystems are generally inhabited by hundreds to thousands of species and affected by environmental mixtures containing hundreds, sometimes thousands, of different compounds [3].

To our knowledge, most approaches proposed so far have addressed this problem as two separate issues: compound multiplicity and species diversity. Quantitative structure–activity relationships (QSAR) [4–10] seek to address compound multiplicity by predicting physiological effects of chemical compounds on single biological endpoints from their molecular structure. QSAR parameters are estimated using observed effects of compounds (e.g. their level of toxicity from a given mode of action) on target organisms and descriptors of its chemical structure and properties. Phylogenetic modelling [3], on the other hand, seeks to address species diversity by estimating species' unknown tolerances to toxic compounds or other stressors from that of other related species with known values. This approach relies on the fact that traits which influence tolerance are subject to evolutionary change, and therefore that the effects of these traits can be modelled as phylogenetic signals. These signals can be regarded as a combination of large-scale phylogenetic structures and small-scale structures. A large-scale structure arises from an evolutionary change that occurred early in the phylogeny, with observable effects on lineages shared by a large number of species. A small-scale structure, on the other hand, arises from changes that occurred recently in the phylogeny, thereby only affecting a few, closely related, species. Here, we demonstrate that chemical compound multiplicity and species diversity can be addressed as a single problem.

Bilinear modelling is an extension of multivariate linear regression where a table of response variables is fitted using two different tables of descriptors [11]. The first table contains descriptors of the variation among the rows of the multivariate response data (i.e. as in multiple regression), whereas the second table contains descriptors of the variation among the columns of the multivariate response. A bilinear model can therefore be used to relate a multivariate response, such as the tolerance of many species to multiple compounds, to descriptors of the species' phylogenetic signal component [3,12] and descriptors of the molecular structure and/or physico-chemical properties [10], as those used for QSAR.

The objective of this study is to demonstrate how bilinear modelling can be used to develop models addressing the issue of predicting the tolerance of multiple species to multiple compounds. To exemplify the modelling approach, we applied it to the modelling of multiple species tolerances to acute toxicity by multiple pesticides, using phylogenetic eigenvectors and physico-chemical properties as predictors. The ability of the models to make external predictions of tolerance to pesticides was also assessed.

2. Material and methods

(a). Data sources

We obtained tolerance data from the US Environmental Protection Agency ECOTOX database [13]. We selected data of median lethal concentrations (LC₅₀) after 96 h of exposure excluding entries with inequality indications (i.e. greater than or smaller than). The mortality was selected as the endpoint because it is the one for which data are the most abundant. We performed a quality check when multiple LC₅₀ values were found for one substance-species combination (see section ‘Data quality check’ in the electronic supplementary material for details). From the resulting dataset, we selected the species and pesticides that allowed us to build the species-by-pesticides table having the largest number of elements, without missing information. The data for any given model were assembled in a multivariate response matrix LC₅₀ = [LC_50i,j] whose rows i represent individual species and whose columns j represent a set of pesticides, and LC_50i,j is the log₁₀ of the concentration of pesticide j causing 50% death for species i after 96 h. We obtained the octanol–water partition coefficients (k_ow) for each pesticide from the KOWWIN software [14].

(b). Phylogenetic analysis

We estimated the phylogenies using DNA sequences obtained online from the US National Center for Biotechnology Information's GenBank website (http://www.ncbi.nlm.nih.gov/genbank/; database: Nucleotide). We collected the available DNA sequences for the whole mitochondrial genomes as well as for the nuclear 28S, 18S and 5.8S rRNA transcripts and their internal transcribed spacers (ITS 1 and ITS 2). We used sequences for the complete genes, whenever possible, and took the longest sequences available when only partial sequences could be found. When a sequence for a widespread gene was not available for a given species and no other species in the same genus or family was in the dataset, we used that of a related species instead. Then, we performed multiple DNA sequences alignment separately for each individual gene using the program Muscle v. 3.8.31 ([15]; http://www.drive5.com/muscle). After alignment, we concatenated the sequences for all genes into a single super-alignment and estimated the phylogeny using the maximum-likelihood method [16,17], which was computed by program fdnaml within software EMBOSS v. 6.3.1 [18].

(c). Modelling approach

Phylogenetic eigenvector regression [19,20] is an approach whereby eigenvectors are used as descriptors in a regression model. For this study, we used a particular type of such eigenvectors called phylogenetic eigenvector maps (PEM) [12]. PEM allows one to calculate phylogenetic eigenvectors that are fine-tuned to the processes through which traits have evolved (neutral evolution or natural selection). In its simplest form, PEM calculation involves the estimation of a selection strength parameter a that take values between 0 (purely neutral evolution) and 1 (strong natural selection).

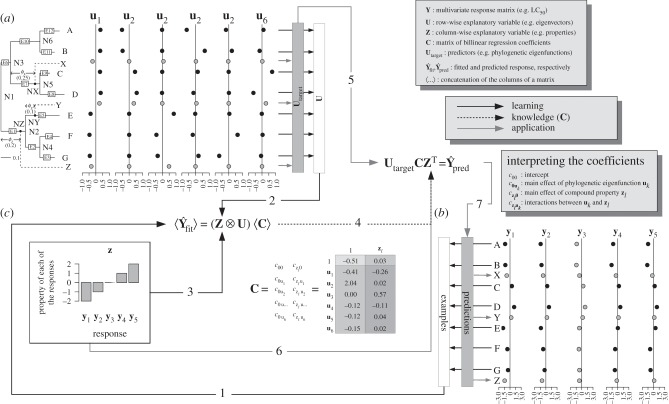
Calculation of PEMs and of the species scores used to make predictions is described in [12]; here, we will only summarize the method. These calculations involve the singular value decomposition of a weighted influence matrix (i.e. a mathematical representation of the edges linking the nodes and leaves of the tree) whose columns are centred on 0. These eigenvectors allow one to decompose species trait variation into components associated with different phylogenetic resolution levels; they are used as descriptors in the bilinear models for predicting tolerance to toxic substances. One can then obtain scores for new species for which predictions are to be made (we will hereafter refer to them as the ‘target’ species) using calculations similar to those that are made when a new point is added to an ordination diagram [21,22]. These scores can be used in models to predict tolerance (figure 1). Note that these are true out-of-sample predictions because the target species are not used to estimate the parameters of the bilinear model.

Figure 1.

Example flowchart of bilinear model calculation. (a) Y is a multivariate response matrix whose values for y₁, y₂, y₄, and y₅ are known for seven model species A − G (black markers), whereas the values that are being predicted (grey markers) are those of three target species X, Y and Z for all the responses (y_X,…, y_Y,… and y_Z,…, respectively) as well as those of all species for response y₃. Two kinds of information are available in the form of row-wise and column-wise descriptors and predictors. (b) The row-wise design matrix U contains the species loadings of the model species on the phylogenetic eigenvectors u_k (black markers), whereas the matrix of row-wise predictors U_target contains the target species scores on the phylogenetic eigenfunctions (grey markers). (c) The column-wise design matrix Z contains a descriptor z_l (e.g. a chemical property; there could have been many column-wise descriptors); here, it is also used as a predictor as it is known for all response variables. Model building proceeds as follows: using the observed response variables (1) together with the species loadings (2) and the column-wise descriptor(s) (3), we calculate C, the matrix of bilinear regression coefficients. This matrix contains the intercept, the main effects of the individual phylogenetic eigenvectors u_k, the main effects of the individual properties z_l and the interactions among the row-wise and column-wise descriptors. The model interrogation proceeds as follows: we pre-multiply C, which was estimated from data (4), with the design matrix containing U_target (5) and post-multiply it with the transpose of Z (6), yielding predicted values (7).

In this study, we used phylogenetic eigenvectors to explain the among-species variation in LC₅₀; let U = [u_i,k] be a design matrix of phylogenetic eigenvectors whose elements u_i,k are the loadings of species i (rows) on eigenvectors k (columns). As mentioned in the Introduction, a bilinear model requires a second set of descriptors. In our study, these descriptors are properties of the pesticides that we used to explain variation in the columns of matrix LC₅₀. Let Z = [z_j,l] be a design matrix of descriptors of the chemical properties l of pesticides j. LC₅₀ can be represented as the matrix product

2.1

where C = [c_j,l] is a matrix of bilinear regression coefficients, and E = [ɛ_i,j] is a matrix of error terms (see section ‘Estimating the matrix of bilinear regression coefficients’ in the electronic supplementary material for details).

The design matrix describing the among-row variation (U) had a centring variable (i.e. a column of ones to estimate the intercept) in addition to the phylogenetic eigenvectors. The design matrix describing the among-column variation (Z) included a centring variable, contrasts variables depicting the different modes of action of the pesticides and the log₁₀ of the octanol–water partition coefficient (i.e. the proportion of the compound dissolving in octanol solvent compared with that dissolving in water solvent) as a descriptor of pesticides in LC₅₀, and p × q columns, where p and q are the numbers of columns in U and Z, respectively. We regularized the bilinear models in order to maximize the ability of the models to predict LC₅₀. Regularization was performed by the forward selection of a subset of the modelling terms (elements c_j,l) on the basis of the Akaike information criterion with correction for small sample sizes (AIC_c [23]). We chose the subset that minimized AIC_c, thereby obtaining models minimizing information loss. Elements of C that were found to be irrelevant for prediction were given a value of 0, resulting in a sparse bilinear model.

We used cross-validation to evaluate the ability of models to make dependable and accurate predictions. For each model, cross-validation was performed by first selecting a given species i, then performing the aforementioned model construction procedure using the n − 1 remaining species, predicting the LC₅₀ for species i, and finally repeating the procedure for each and every species in the dataset. In addition to cross-validation of the species, we obtained predictions for tolerance to other pesticides not used in model estimation and compared them to their observed values. Following these predictive validations, we assessed models performance at the global and observation scales using the prediction coefficient P² and the deviation factor d_i,j, respectively (see section ‘Metrics of model performance’ in the electronic supplementary material for calculation details).

Model calculation and cross-validation were performed using the R language and environment v. 3.0.1 [24] and R package ape v. 3.0–8 [25].

(d). Candidate models

To explore the performance of our modelling approach under different circumstances of data availability, we defined three bilinear LC₅₀ models from the data described in table 1. All models span three modes of action: acetylcholinesterase inhibition (AChE), γ-amino butyric acid-triggered chloride channel antagonism (GABA) and sodium channel modulation (NaM).

Table 1.

The pesticides, their properties used for phylogenetic bilinear modelling (mode of action, NaM: Na⁺ channel modulator, AChE: Acetylcholinesterase inhibitor and GABA: GABA-gated Cl⁻ channel antagonist; and log₁₀ octanol–water partition coefficient), the models in which they are used and the model(s) for which predictions were calculated.

CAS no.	name	log10 kow	mode of action	used	predictions
50293	DDT	6.91	NaM	1−3
55389	fenthion	4.09	AChE	2, 3	1
56382	parathion	3.83	AChE	1−3
58899	lindane	3.72	GABA	1−3
60571	dieldrin	5.40	GABA	1−3
63252	carbaryl	2.36	AChE	2, 3	1
115297	endosulfan	3.83	GABA		1−3
121755	malathion	2.75	AChE	1−3
122145	fenitrothion	3.30	AChE		1−3
333415	diazinon	3.81	AChE		1−3
2921882	chlorpyrifos	4.96	AChE	2, 3	1, 2
8001352	toxaphene	3.30	GABA	3	1, 2

The first model (M1) incorporates five pesticides: malathion and parathion (AChE), lindane and dieldrin (GABA) and DDT (NaM), as well as 25 species. The 25 species included two amphibians, 13 fish species, six crustaceans and four insects; total number of observations: 125. The two other models included more pesticides; the cost was that they had smaller numbers of species, given the available data. We obtained a second model (M2) by adding the pesticides carbaryl and fenthion (AChE) and dropping six species, which left 19 species for modelling (13 fish species, five crustaceans and one insect, total number of observations: 126). In a third model (M3), we added chlorpyrifos (AChE) and toxaphene (GABA), which required dropping four more species, leaving 15 species for modelling (10 fish species, four crustaceans and one insect, total number of observations: 117).

We obtained predictions for each of these three models by using data for the pesticides that were not used to estimate model parameters. These other pesticides span three additional compounds: endosulfan (GABA), fenitrothion and diazinon (both AChE).

To represent the difference in the effects of the three modes of actions in the column-wise descriptor matrices (Z), we defined two orthogonal contrast variables called MOA₁ and MOA₂ (see section ‘Orthogonal contrast variables’ in the electronic supplementary material for more details).

We found DNA sequences for most species, with the exception of the Isopode (Crustacea) Asellus brevicaudus and the Hemiptera (Insecta) Notonecta undulata, for which we substituted the congeneric species Asellus aquaticus in the first case, and for which information was only available at the genus level in the second case. The most widespread DNA sequences were the mitochondrial large ribosomal subunit (16S; 25 species, of which 12 were complete and 13 were partial), the cytochrome oxidase subunit 1 (COX1; 24 species: 13 complete, 11 partial), the mitochondrial small ribosomal subunit (12S; 23 species: 13 complete, 10 partial), the nuclear small ribosomal subunit (18S; 21 species: height complete, 13 partial) and cytochrome b (CYTB; 21 species: 13 complete, height partial). Most of the remaining 39 sequences that were available for fewer than 19 species were complete mitochondrial DNA sequences for species whose entire mitochondria can be found on GenBank.

3. Results

With a few exceptions, the phylogeny we estimated from DNA data placed most species within their recognized taxonomic group (see section ‘Estimated phylogeny’ in the electronic supplementary material for more details on the phylogeny and common species names). The PEM used to calculate models M1 and M2 had small selection strength parameters (a, table 2) indicating nearly neutral and neutral trait evolution, respectively, whereas M3 had much higher value of a, indicating a stronger intervention of natural selection, on average, when pesticides chlorpyrifos and toxaphene are used in the model. The number of bilinear regression terms involved in the models ranged from 24 (M1, five main effect and 19 interaction terms; table 2; see ‘tables of bilinear model coefficients’ in the electronic supplementary material for more details on bilinear model parameters) to 11 (M3, five main effect and six interaction terms; M2 had 19 terms, with nine main effect and 10 interaction terms). The models had adjusted R² 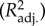ranging from 0.77 to 0.84 (from 0.16 to 0.30 when using only chemical descriptors). The prediction coefficients (P²) obtained by comparing observed LC₅₀ values with those predicted following leave-one-out jack-knives ranged from 0.49 to 0.73 (table 2 and figure 2). The percentages of these individual jack-knifed predictions having an absolute deviation factor (|d|) lower than 10 (i.e. a variation often observed between studies for the same species–compound combination) ranged from 84 to 87%, whereas from 0 to 2.3% of the predictions deviated from observations by a factor of 100 or more. The most extreme deviations by model were observed for species A. brevicaudus and pesticide malathion in models M1 (d = −246) and M2 (d = −313), as well as for Cyprinus carpio and dieldrin in model M3 (d = −97).

Table 2.

Comparison of three phylogenetic bilinear model: sample size, selection strength (a), number of bilinear regression terms, adjusted coefficient of determination 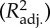, prediction coefficient (P²) and the percentages of deviation factor values (d) that are below given values for jack-knife (performed for one species at a time using a model developed using the remaining species) and external (using all the species of a given model and predicting for pesticides that were not in the models) predictions.

parameter			M1	M2	M3
sample size	species		25	18	13
	compounds		5	7	9
	total		125	126	117
selection strength (a)			0.06	0.00	0.57
number of terms	chemistry		1	3	2
	phylogeny		4	6	3
	interaction		19	10	6
adjusted R2	chemistry alone		0.16	0.30	0.19
	all terms		0.80	0.84	0.77
P2	jack-knife		0.49	0.64	0.73
	external		0.54	0.48	0.74
deviation factor	jack-knife	|d| < 10	84%	87%	86%
		|d| < 100	98%	98%	100%
	external	|d| < 10	61%	65%	87%
		|d| < 100	97%	97%	100%

Figure 2.

The observed LC₅₀ (filled squares) and values predicted using phylogeny (unfilled circles) following leave-one-out jack-knife runs on the datasets used to build model M1 (a; 25 species and five pesticides), M2 (b; 19 species and seven pesticides) and M3 (c; 15 species and nine pesticides).

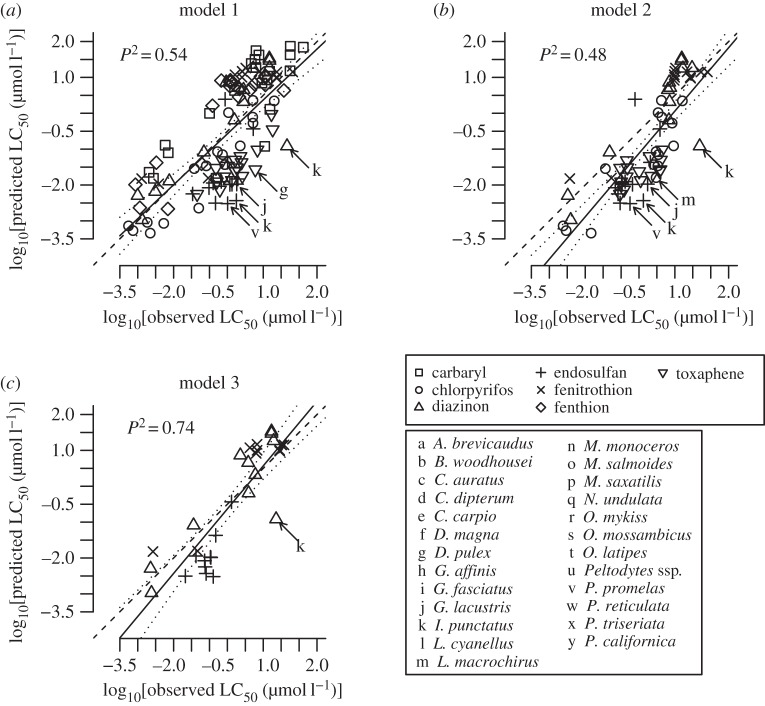
The numbers of predictions made for pesticides not used in the models were 118 for M1, 68 for M2 and 31 for M3. They had P²s ranging from 0.48 to 0.74 (table 2 and figure 3). From 61 to 87% of the predictions were within an absolute deviation factor of 10 of the observed LC₅₀ values, whereas from 0 to 3% of the predictions deviated by a factor 100 or greater. Most of the extreme predictions by model were overestimates of Ictalurus punctatus tolerance to endosulfan (M1: d = 152) and diazinon (M2: d = 127, M3: d = 58). A small prediction bias was evidenced for model M2 (the 95% confidence limits of the regression line did not include the 1 : 1 line in the whole range of observed values), the latter having a tendency to predict LC₅₀s were smaller than the observed values. For models M1 and M3, the 1 : 1 line fit within the 95% confidence limits of the regression line and no prediction bias was evident.

Figure 3.

(a–c) Observed LC₅₀ values as a function of those predicted using three phylogenetic bilinear models, for pesticides other than that used to build the models, with regression lines (solid; dotted: 95% confidence limits; dashed: 1 : 1 relationship), and coefficients of prediction (the letters used as markers represent the different pesticides). Species labels are only shown when predictions deviated from observations by a factor of more than 50.

4. Discussion

In this paper, we developed an approach to predict tolerance using species phylogenetic patterns of pesticide tolerance coupled with properties used as proxies of the activity of the compounds. The models presented here as examples used relatively simple column-wise descriptor matrices encompassing only the mode of toxic action (in the form of orthogonal contrast variables) and log₁₀ k_ow. This modelling approach (i.e. using phylogenetic eigenvectors within a bilinear model) has, however, a much wider application scope; it can be applied whenever one wants to model multiple species attributes towards sets of environmental conditions that species are exposed to. For example, one may want to predict multiple species reactions (e.g. physiological, behavioural and immunological endpoints) to a mixture of toxic stresses observed in situ using descriptors for this mixture in addition to phylogenetic eigenvectors. Still, despite the fact that we used relatively simple bilinear models for expository purposes, we were able to predict from half to two-thirds of the out-of-sample variation in LC₅₀ values (0.50–0.66) for jack-knifes and from half to three-quarters (0.48–0.74) for a set of external compounds. We stress that these were true out-of-sample predictions, and therefore are honest assessments of the information content in phylogenetic trees about the relationships between pesticide properties and species tolerances.

(a). Candidate models

The challenge in selecting tolerance data was to obtain a broad phylogeny that encompassed species from as many higher taxonomic groups as possible with, ideally, several representative species for each of these groups, while having complete sets of values for as many pesticides as possible. The three models covered the following cases: (M1) many species, but few substances, (M3) many substances, but few species, and (M2) an intermediate model between these two extremes. As a consequence of data availability and the requirement that the response matrix (Y) be complete (no missing value for any element y_i,j), all three models were implemented using modest numbers of species, compared with those typically inhabiting ecosystems, and very few compounds, compared with the many chemicals that are found in ecosystems.

Although these models may be useful for several applications, we hope that enhanced models, with many more species and compounds, will be developed. We propose the following four steps to maximize the development of phylogenetic bilinear models in the near future. First, it is necessary to pinpoint, within the pool of currently unavailable data, those data whose estimation using bioassays would maximize the size of the response matrix Y in the training data. To do so, an online database can be queried to highlight unavailable species–pesticide pairs associated with either many species or many pesticides. For example, if a particular species is lacking tolerance data about only one pesticide, then a bioassay on that species–pesticide pair will permit the addition of all measured tolerances for that particular species to the response matrix. Second, the suites of bioassays to estimate LC₅₀ should be performed for the still missing species–pesticide combinations with the most useful predictive information. Third, the quality of the explanatory variables could be improved. For example, the phylogeny could be re-estimated using DNA sequence for the poorly resolved species. Furthermore, more descriptors of chemical activity (e.g. new metrics of molecular structure, enzymatic assays) should also be considered in order to improve models. It is noteworthy that using the toxic mode of action limits the scope of application of models to compounds with modes of action that are known and represented in the models. Future efforts to seek better descriptors of chemical activity for use in phylogenetic bilinear tolerance models should therefore focus on those that are easy to estimate (e.g. using descriptors of molecular structure and activity, in vitro tests) and applicable to many (ideally all) compounds. Fourth, the phylogenetic bilinear model should be re-estimated to account for any new information provided by the previous three steps. We view these four steps as an iterative procedure of model building. The tools for such a procedure could conceivably be implemented within a web-based interface, with data provided from collaborators worldwide.

Another relevant matter to increase the scope of phylogenetic bilinear LC₅₀ models beyond pesticides is to focus the efforts on a standard set of species and compounds. Standard species could be chosen, for instance, on the basis of their representativeness of the taxonomic group to which they belong and to maximize the number of high-order taxonomic groups that the models represent. Similarly, standard chemical compounds can be chosen on the basis of their representativeness of the chemical group they belong to (e.g. alkanes, ketones, alcohols, etc.). By increasing sample size, orienting sampling effort to add more representative species and compounds, and developing better descriptors of chemical activity, it would be possible to extend the scope of applications of phylogenetic bilinear tolerance models. A potential future application could be to accurately estimate the toxicity of compounds that have not yet been synthesized, including designer drugs. We anticipate that such models would be very useful to the chemical industry and government regulation authorities by giving scientists an early warning to avoid or ban harmful compounds and make the industry focus on more benign alternatives.

(b). Model performance

The developed models explained between 77 and 84% of the variability in the acute compound toxicity (table 2) and were therefore in the range of previous models (61–85%) that used existing empirical data to make predictions [3]. Regarding the ability of the three models to make predictions, it became apparent that the local representation of phylogeny was very important for the final performance. Most outliers in M1 were related to single branches in the phylogenetic tree, e.g. Morone saxatilis (DDT), A. brevicaudus and Metapenaeus monoceros (for both malathion and parathion). In M2, the latter species was removed, while for A. brevicaudus, another outlier for fenthion was included. For M3 finally, both M. saxatilis and A. brevicaudus were removed, with the best prediction results, respectively. Hence, to increase the prediction power for species not included in the model, it is suggested to have at least one related species in the phylogenetic tree.

Generally, a number of other ecotoxicological models for single biological endpoints (e.g. acute toxicity for Daphnia magna or Pimephales promelas) are available, applying physico-chemical properties or read-across methodologies to make quantitative predictions [6,9,10]. Thereby, models predicting baseline toxicity from k_ow usually explain more variability than those for diverse chemical classes using read-across. However, these models are restricted to single species, while the proportions of variability they explain (e.g. 73–87% for fishes and 85% for Daphnids) are in the same range as that of the models presented here (table 2). Hence, owing to the wide taxonomic range of species covered, the models developed in this paper are particularly useful to identify the taxonomic groups at highest risk for a certain compound. Given the widespread distribution of pollution [26], these models might also help explain why certain species have been lost from certain areas while others remain [27]. Moreover, the predictions might support mixture toxicity models that usually suffer from a low number of test data for each compound [28].

(c). Assumptions

Bilinear modelling is an adaptation of multivariate regression analysis with the addition of a second table of descriptors. Therefore, it has the same assumptions as multivariate regression. An assumption that is of concern in this study is that the response variable should have independent and identically distributed residuals. Hence, as LC₅₀ are taken from multiple species having different degrees of common ancestry, their values are indeed expected to lack statistical independence, because of phylogenetic autocorrelation, which is induced by phylogenetic processes. The latter processes, however, are themselves described by the phylogenetic eigenvectors acting as a fixed effect in the bilinear models, thereby directly controlling for the lack of independence originating from phylogenetic correlation. When one uses ordinary least squares to fit models—as we did in this study—residuals must be normally distributed for parametric tests of significance to be correct. Linear models with distribution other than normal may also be used; it is straightforward to fit generalized linear models [11].

Perhaps the most relevant assumption of any modelling method, including bilinear regression, is the adequacy of descriptors. In this study, row-wise descriptors were phylogenetic eigenvectors, whereas column-wise descriptors were more standard variables (i.e. orthogonal contrasts and log₁₀ k_ow, a quantitative variable). We can enumerate three main assumptions underlying the adequacy of phylogenetic eigenvectors as descriptors.

The first assumption is that the phylogenetic tree is estimated without systematic and significant error. This assumption is similar for any model whose descriptors need to be estimated by some other method prior to modelling. In cases where the reliability of phylogeny is questionable, Monte Carlo simulations can be used to assess the impact of phylogenetic estimation errors on the correctness and accuracy of tolerance estimates. It is also noteworthy that while this study did no DNA sequencing, future modelling efforts would ideally be granted with that possibility. Nowadays, DNA sequencing is cheaper than performing a suite of bioassays. We therefore regard the bioassays as the most demanding constraint to model development.

The second assumption is that traits evolve in a steady fashion along the branches of the phylogenetic tree. In this paper, we used PEM, a method enabling one to fine-tune eigenvectors to represent the evolutionary dynamics of traits (i.e. neutral evolution versus evolution by stabilizing or directional selection) and specify different evolutionary rates adapted to particular parts of a tree. However, in this expository treatment we did not use that latter functionality.

The third assumption is that the test species are sufficient and adequate to dependably represent the patterns of trait variation. Hence, when a group shows extreme trait variability, many representative species are necessary to correctly describe the patterns of trait variation within it. As a word of caution, it is noteworthy that, in practice, the possibility of large trait variation over small phylogenetic distances can never be entirely overruled. In this study, for instance, species A. aquaticus was substantially more tolerant to malathion and parathion than the other Malacostraca species present in the data. When the latter species was withdrawn during cross-validation, the resulting phylogenetic model naively inferred relative sensitivity of that group to these pesticides leading to the highest deviation values we observed. In general, a species showing small inter-population variability in tolerance may include outlying populations that are highly tolerant (or sensitive; [29,30]). In such a situation, it may not be practical to estimate tolerance from a phylogeny as one would need intra-specific phylogeny and tolerance data focused on the evolutionary event that led to the emergence of these outstandingly tolerant populations [3]. Although not explored in this paper, trait data may be used either in place of or in combination with phylogenetic data, in order to directly measure the species characteristics that lead to variation in tolerance [12].

(d). Directions

We hope that this study will inspire scientists to pursue the implementation of phylogenetic models in various fields, such as ecotoxicology, environmental sciences, pharmacology and beyond, to other disciplines where it is relevant. We also hope that it will inspire ecotoxicologists to develop more powerful tolerance models and make them available to the people who need them [31].

Funding statement

G.G. was funded by NSERC grant no. 7738–07 to P.L., and S.C.W. was funded by an NSERC PDF and NSERC grant no. 7738–07 to P.L. The work of P.v.d.O. was supported by the European Commission through the Project HEROIC (FP7–282896; Coordination Action funded under the 7th Framework Program).