Sources of Individual Differences in Children’s Understanding of Fractions

Abstract

Longitudinal associations of domain-general and numerical competencies with individual differences in children’s understanding of fractions were investigated. Children (n = 163) were assessed at 6 years of age on domain-general (nonverbal reasoning, language, attentive behavior, executive control, visual-spatial memory) and numerical (number knowledge) competencies; at 7 years on whole-number arithmetic computations and number line estimation; and at 10 years on fraction concepts. Mediation analyses controlling for general mathematics ability and general academic ability revealed that numerical and mathematical competencies were direct predictors of fraction concepts whereas domain-general competencies supported the acquisition of fraction concepts via whole-number arithmetic computations or number line estimation. Results indicate multiple pathways to fraction competence.

Competence with fractions is an integral part of overall mathematical proficiency, laying the foundation for learning the advanced mathematics that is critical for obtaining full economic opportunity and meaningful participation in society (e.g., Moses & Cobb, 2001; National Mathematics Advisory Panel [NMAP], 2008). Yet fractions represent a primary source of difficulty for many students (Hecht, Close, & Santisi, 2003; NMAP, 2008; Siegler et al., 2012; Tatsuoka, Corter, Tatsuoka, 2004). For example, only 40% of fourth graders in the U.S. can compare unit fractions—such as explaining whether ¼ is smaller or larger than 1/5 (National Center for Education Statistics [NCES], 2007), and only half can identify pictorial representations of equivalent fractions (NCES, 2009). These difficulties remain well into high school (e.g., Calhoon, Emerson, Flores, & Houchins, 2007). Further, difficulty with fractions is not only a U.S. phenomenon; several countries around the world report fractions as challenging for students to master (e.g., Chan, Leu, & Chen, 2007; Tatsuoka et al., 2004). Thus, a pressing need exists to improve understanding of the developmental precursors of fraction knowledge, with the goal of providing theoretical insight into and practical guidance about the identification and treatment of fraction difficulties.

This longitudinal study focused on identifying early predictors of fourth-grade children’s understanding of core fraction concepts (e.g., fractions represent the division of whole units into parts; fractions can be used to describe proportions and magnitudes; an infinite number of fractions exist between any two values; Siegler & Pyke, 2013). We focused specifically on fraction concepts because conceptual understanding tends to have larger effects on the development of procedural proficiency and has more generalized effects on new learning than does procedural knowledge (e.g., Hecht et al., 2003; Rittle-Johnson, Siegler, & Alibali, 2001).

Development of Fraction Competence

Children begin schooling with an informal understanding of fraction concepts that does not depend on knowledge of formal mathematical symbols. For instance, Mix, Levine, and Huttenlocher (1999) found that 4-year-olds can reason with informal fraction problems involving solutions less than or equal to one whole, whereas the ability to reason with mixed-number fractions (i.e., greater than one) emerges around 6-years-old. Mix et al. demonstrated that children have at least an implicit understanding of some fraction-related concepts long before fractions are formally introduced in school. This intuitive knowledge, however, does not easily translate into symbolic knowledge of fractions. For example, whereas young children have an informal understanding of the part-whole notion of fractions, not until seventh grade do they consistently demonstrate an understanding of part-whole relations with symbolic fraction notation (Stafylidou & Vosniadou, 2004).

It has been suggested that learning formal fractions suffers in part because of what Ni and Zhou (2005) call the whole-number bias. Many children apply their understanding of whole number properties when solving fraction problems (Stafylidou & Vosniadou, 2004). This is problematic because, for example, whole numbers follow a stable order sequence (e.g., 5 always follows 4 in the counting sequence), and each number in the sequence has a greater magnitude than the previous number (e.g., 5 is always larger than 4). Over-generalization of such properties contributes to difficulty in understanding, for example, that ¼ is larger than 1/5.

At this time, the cognitive competencies that support the conceptual leap from whole numbers to fractions are not well understood. Such understanding is critical not only given the importance of fraction competence for more advanced mathematics and for competing in the U.S. workforce (NMAP, 2008; Siegler et al., 2012), but also for generating hypotheses about the processes by which such a conceptual leap is achieved in fractions as well as other domains of learning. This includes, for example, moving from comprehension of stories to informational text—another stumbling block for learners that occurs around the same time that fractions become salient in the school curriculum—or at other developmental stages, such as the transition to algebra, which involves operating on functions rather than numbers, whole or rational.

Theoretical Accounts of Fraction Learning

Previous studies have shown that mathematical skills are predicted by a combination of (a) domain-general competencies—the global processes that contribute to cognitive development and learning across several domains (e.g., attentive behavior, executive control)—and (b) specific numerical competencies, such as the ability to represent and manipulate small exact quantities (Fuchs et al., 2010b; Geary, 2011; LeFevre et al., 2010). Few studies, however, have assessed the early competencies that support the later development of fraction concepts, even though this knowledge may have implications for preventative work with young students to avoid subsequent difficulty.

Two previous studies are particularly relevant in specifying a theoretical model of fraction development. Hecht et al. (2003) proposed that domain-general competencies predict fraction knowledge directly and indirectly through intervening mathematical skills hypothesized as necessary to become proficient with fractions, such as fraction concepts and whole-number computations. According to this model, domain-general competencies influence learning across all academic domains and thus support the acquisition of both fraction skill and intervening mathematical competencies. In a test of their model with fifth graders, Hecht et al. found that domain-general competencies were better predictors of the intervening mathematical skills than of fraction skills. Specifically, attentive behavior (children’s ability to pay attention during instruction) and executive control (the general purpose control mechanism that regulates the maintenance and processing of cognitive subprocesses involved in immediate awareness; Miyake, Friedman, Emerson, Witzki, & Howerter, 2000) were related to fraction skills primarily through their association with the intervening mathematical precursor skills. Further, there was a differential relation between fraction skills and the intervening mathematical competencies: Whereas fraction concepts was related to all fraction skills (estimation, computations, and word problems), fluency with whole-number combinations was related only to fraction computations.

These findings indicate that domain-general and mathematical competencies do not share uniform relations with fraction learning. Moreover, Hecht et al. (2003) tested the effects of only attentive behavior and executive control, even though other domain-general competencies, such as language and nonverbal reasoning, have been implicated in more recent research (e.g., Seethaler, Fuchs, Star, & Bryant., 2011; Jordan et al., 2013). Further, Hecht et al. considered mathematical competencies only as intervening variables in the developmental sequence of fraction learning. More recent studies have shown that early numerical competencies, including the ability to fluently process, represent, and manipulate small exact quantities, are also foundational for later mathematical development independent of domain-general competencies (e.g., Fuchs et al., 2010b; Geary, 2011; Geary, Bailey, & Hoard, 2009).

More recently, LeFevre et al. (2010) proposed an alternative model of general mathematical development. The model proposes that three “pathways” are involved in processing numerical information and that these pathways play distinct roles in mathematical development. The linguistic pathway is a domain-general system hypothesized to support the development of symbolic representational systems, including the symbolic number system. Thus, the linguistic pathway should predict performance on measures that require knowledge of the formal number system, such as whole-number computations and fraction concepts. The quantitative pathway is a cognitive system involved in processing numerosity independent of the symbolic number system, such as through subitizing, or apprehending small collections of objects without counting. The quantitative pathway is thought to support the development of mathematical skills that require children to represent and manipulate quantities, including estimating quantities and understanding proportional magnitudes. Finally, the spatial attention pathway represents a complex set of domain-general cognitive competencies—attentional capacity, executive control, nonverbal reasoning, visual-spatial memory—that are involved in processing numerical information separate from linguistic and quantitative skills. As such, the spatial attention pathway is hypothesized to influence mathematical outcomes generally versus having a distinct association with specific tasks.

In a longitudinal study with children from 4.5 to 7.5 years of age, LeFevre et al. (2010) found that the three pathways differentially predicted various mathematical outcomes (i.e., whole-number computations, numeration, geometry, measurement, and number line estimation). The linguistic pathway—a composite including vocabulary, phonological skills, and number identification—was uniquely related to all mathematical outcomes, presumably because these outcomes required knowledge of the symbolic number system. The quantitative pathway—a composite including subitizing and a nonverbal calculation task—was uniquely related to numeration, whole-number computations, and number line estimation, ostensibly because these tasks require numerical magnitude processing specifically. Finally, the spatial attention pathway, representing several domain-general competencies, explained unique variance across tasks tapping both the symbolic number system and those tapping magnitude processing.

In thinking about the cognitive competencies that may support the conceptual leap from whole-number to fraction understanding and how to design interventions to support such a leap, the LeFevre et al. (2010) model requires further specification for two reasons. First, the composites used to operationalize the pathways do not permit a sufficiently fine-grained analysis of specific processes. For instance, a relation between the linguistic composite and mathematical outcomes could reflect the influence of language skills or number identification, thus obscuring the potential of these findings to provide insight on early indicators of later difficulty or directions for early intervention. Similarly, the spatial attention pathway represented several domain-general competencies, even though previous research suggests that domain-general competencies contribute differentially to various outcomes (Hecht et al., 2003; Jordan et al., 2013; Seethaler et al., 2011). For example, Jordan et al. (2013) found that executive control shared a unique association with fraction procedures but not fraction concepts, whereas language and attentive behavior shared unique associations with fraction concepts but not fraction procedures. Second, Hecht et al. (2003) found that domain-general competencies may not be robust predictors of fraction knowledge. This suggests the need to consider intervening specific numerical precursor skills in the developmental sequence of fraction learning.

Study Purpose and Overview

This longitudinal study examined a model of fraction development that considered how first- and second-grade domain-general and numerical competencies predict individual differences in fraction concepts at the end of fourth grade. We targeted fourth grade because wide individual differences in fraction knowledge exist at that time, even though formal fraction instruction only begins in fourth grade. This signals the need to identify early precursors of later difficulty so schools can identify children at risk of poor fraction development and provide targeted intervention using strategies that align with the competencies involved in the conceptual leap from whole number to fractions.

We initiated the study at the start of first grade, when the range of individual differences on early domain-general and numerical competencies is already wide, based on informal learning experiences, and because the role of first-grade competencies has been established for the whole-number mathematics learning that occurs in the primary grades, prior to the introduction of fractions (e.g., Fuchs et al., 2010a,b; Geary, 2011; Geary et al., 2009). It is worth noting that we do not intend to imply that domain-general competencies and their relation with achievement— mathematics or otherwise—are fixed at first grade. Instead, we intended to examine the potential of domain-general competencies to serve as risk indicators of later fraction difficulty. Domain-general competencies tend to become stable around first grade, and changes in individual differences in these competencies after first grade do not tend to alter the nature of their association with mathematical development (e.g., Li & Geary, 2013; Sameroff, Seifer, Baldwin, & Baldwin, 1993).

Building on prior research, we studied five domain-general competencies. First, nonverbal reasoning is hypothesized to play a role in the conceptual leap from whole-number to fractions because fraction knowledge is not intuitive and, compared to whole numbers, involves greater symbolic complexity (Seethaler et al., 2011), which invokes the type of mental flexibility, manipulation of symbolic associations, and maintenance of multiple representations reflected in measures of nonverbal reasoning. In a similar way, language skills are needed to operate in symbolically complex domains, and linguistic skills play a vital role in the way children understand and represent mathematical concepts (e.g., LeFevre et al, 2010; Vukovic & Lesaux, 2013), including fraction concepts (Miura, Okamoto, Vlahovic-Stetic, Kim, & Han, 1999; Jordan et al., 2013). Third, attentive behavior is required to profit from classroom instruction and to complete fraction tasks that involve a complex sequence of steps (e.g., comparing fractions with different numerators and denominators; Hecht et al., 2003). In such tasks, executive control is also thought to play a supporting role by helping students hold the sequential set of decisions in mind while completing subsequent steps of the problem-solving process (Siegler & Pyke, 2013). Finally, visual-spatial memory, which is specialized for the maintenance of visual-spatial information in immediate awareness, may play a role in the conceptual leap because successful completion of fraction problems demands that children store visual-spatial representations in mind while manipulating these representations to solve fraction problems (LeFevre et al., 2010). Note that whereas the spatial attention pathway in LeFevre et al. represented several domain-general competencies, this study considered the independent effects of nonverbal reasoning, attentive classroom behavior, executive control, and visual-spatial memory, consistent with other researchers (Hecht et al., 2003; Seethaler et al., 2011).

We also considered specific numerical competencies in our model. In line with previous researchers (e.g., Geary, 2011; LeFevre et al., 2010), we hypothesized that number knowledge (e.g., representing and manipulating exact quantities less than 10) represents a unique pathway to later fraction learning, separate from domain-general competencies. Number knowledge is thought to be foundational to fraction learning by providing the building blocks for understanding abstract concepts relating to number, magnitude, and proportional reasoning.

We proposed two types of intervening mathematical skills—in this case whole-number computations and number line estimation—in the developmental progression from the basic first-grade competencies to relatively sophisticated fourth-grade fraction concepts. The first, competence with whole-number arithmetic, may interfere with fraction development due to whole-number bias (e.g., Ni & Zhou, 2005; Siegler & Pyke, 2013; Stafylidou & Vosniadou, 2004). Indeed, Hecht et al. (2003) found that fluency with whole-number combinations was not especially predictive of fraction skill. Yet, Siegler and Pyke (2013) demonstrated that unlike low-achieving students, high achievers were less susceptible to whole-number bias, suggesting that mastery of whole-number computations is foundational for fractions learning. Given that instruction in the early school tends to favor whole-number development, it is critical to examine whether whole-number computations is a precursor of fraction knowledge.

Second, we examined children’s rudimentary proportional reasoning ability via a number-line estimation task. The ability to accurately place Arabic numerals on a number line with two endpoints (e.g., 0 and 100) requires estimating a specific magnitude relative to the whole (Barth & Paladino, 2011; Slusser, Santiago, & Barth, 2013). Such proportion judgments—even with whole numbers—may be foundational for later fraction knowledge, given that both tasks require an understanding of proportional magnitudes.

We measured whole-number computations and number line estimation in second grade because wide individual differences exist in both skills by this time (e.g., Geary et al., 2009; Siegler & Booth, 2004). Further, measuring these skills at a separate time point than the first-grade competencies allowed for an examination of a fundamental developmental question surrounding the relative contribution of whole-number and proportional reasoning to fraction learning and the interplay between these skills and early competencies.

Specifically, the literature provides surprisingly little insight into: (a) whether fraction acquisition is an extension of the same learning pathway stemming from early cognitive competencies and whole-number skills; (b) whether fraction learning follows a learning trajectory from early cognitive competencies and proportional reasoning; (c) whether fraction learning develops independent of both whole-number computations and proportional reasoning; or (d) some combination thereof. Thus, this study sought to assess the extent to which fraction concepts was an extension of earlier forms of mathematical learning or if the conceptual leap required in fraction learning relies predominantly on early domain-general or numerical competencies. Beginning to unravel the developmental course of fraction learning is critical for informing instruction while generating hypotheses for parallel conceptual leaps that occur in the intermediate grades and for other forms of learning at other developmental stages.

Method

Participants

The data were collected with a sample of children in a Southeastern metropolitan school district who participated in a larger research project designed to examine the first-grade predictors of emerging competence with whole-number arithmetic (Fuchs et al., 2010b). We expanded the scope of the original project to fraction outcomes at end of fourth grade. The analytic sample was restricted to the 163 children with complete data in first, second, and fourth grade who also did not receive any special intervention as part of the larger project (because intervention was designed to disrupt the predictive value of important variables). In the larger project, an additional 80 students (~16 children/year; 6.6% annual attrition) would have qualified for participation, but they had moved and thus could not be assessed in fourth grade. Students in the present sample were not significantly different from the 80 children who exited the study on any of the first-grade predictor variables.

The sample’s mean age in first grade was 6 years 6 months (SD = 4 months); in second grade, 7 years 11 months (SD = 4 months); and in fourth grade, 10 years 0 months (SD = 4 months). About half of the children were female (n =76 girls, 46.6%). According to school records, 76.7% of the sample received subsidized lunch; 55.2% were Black, 21.5% White non-Hispanic origin, 13.5% White Hispanic origin, and 9.8% fell into other categories or information was not provided. There were no sex differences on any of study measures but the White non-Hispanic group outperformed the other groups on all study measures, as did the students who did not receive subsidized lunch. Given these differences, racial/ethnic identity and lunch status were controlled in all analyses. Note that all children received the same curriculum.

Measures of First-Grade Predictors

Nonverbal reasoning

The Matrix Reasoning subtest of the Wechsler Abbreviated Scale of Intelligence (WASI; Wechsler, 1999) measures nonverbal reasoning with pattern completion, classification, analogy, and serial reasoning tasks. Children complete an incomplete gridded pattern by pointing to or stating the number of the correct response from five possible choices. As reported in the test manual, reliability is between .89 and .94 for first grade.

Language

We considered two indicators of language ability: vocabulary and listening comprehension. With the Vocabulary subtest from the WASI (Wecshler, 1999), children orally define a series of words. Responses are awarded a score of 0, 1, or 2 depending on conceptual quality. As reported by the test developer, split-half reliability is between .86 and .92. With the Listening Comprehension test of the Woodcock Diagnostic Reading Battery (WDRB; Woodcock, 1997), children listen to a short passage and supply the single word missing at the end of the passage. Reliability, as reported by the test developer, is .80. We created a single language ability latent composite for use in subsequent analyses (see preliminary analyses below).

Attentive behavior

We used the Strengths and Weaknesses of ADHD Symptoms and Normal Behavior scale (SWAN; Swanson et al., 2004) to index attentive behavior. The SWAN is an 18-item teacher rating scale that measures children’s attentive behavior and activity levels. It samples items from the Diagnostic and Statistical Manual of Mental Disorders-IV (APA, l994) criteria for Attention-Deficit/Hyperactivity Disorder for inattention (9 items) and hyperactivity/impulsivity (9 items). Teachers rate each item on a seven-point scale ranging from 1 (far below average) to 7 (far above average). The reported score represents the average rating across the nine attentive behavior items. SWAN correlates well with other dimensional assessments of behavior related to attention (www.adhd.net). Alpha in this study was .98.

Executive control

We measured executive control with a task that did not involve numbers to avoid artificially inflating the relation between executive control and mathematical outcomes based on superficial task features (see Raghubar, Barnes, & Hecht, 2010). With the Listening Recall subtest from the Working Memory Test Battery for Children (WMTB-C; Pickering & Gathercole, 2001), children hear a series of sentences and first determine if each sentence is true (storage demand); they then recall the last word in each sentence (processing demand). There are six items at span levels from 1–6. Passing four items at a span level moves the child to the next span level. At each span level, the number of items to be remembered increases by one. Failing three items terminates the subtest. We report the trials correct score. As per the test developer, test-retest reliability is .83.

Visual-spatial memory

We assessed visual-spatial memory with two tasks from the WMTB-C (Pickering & Gathercole, 2001). With Mazes Memory, the tester presents a maze with more than one solution and a picture of an identical maze with a path showing one solution. The picture is removed after 3 sec; then the child duplicates the path. Note that the time constraint distinguishes this task from a spatial reasoning task (McGrew, 2005). Block Recall uses a board with nine raised blocks, each with a number on one side, which only the tester sees. The tester taps a block (or series of blocks); the child duplicates the tapping. Passing four items at a level moves the child to the next level. At each span level, the number of items to be remembered increases by one. Failing three items terminates the subtest. As per the test developer, test-retest reliability is .63 – .68. Given the correlation between subtests (r = .41, p <.001), we report the mean score across both subtests.

Number knowledge

The Number Sets Test (Geary et al., 2009) indexes the speed and accuracy with which children understand and operate with whole numbers less than 10, while partitioning sets and transcoding between quantities (sets of objects, such as circles and stars) and symbols (Arabic numerals). Children are presented with two pages of domino-like stimuli in which the squares of the domino are either objects (e.g., circles, stars), Arabic numerals, or blank. At the top of the page, the target sum (5 or 9) is shown. The child is instructed to “circle any groups that can be put together to make the top number”; and “work as fast as you can without making many mistakes.” For example, on the first page, the child circles any domino in which all squares (mostly 2-square dominos but also some 3-square dominos), when added, result in 5 (e.g., domino with two circles and three stars). The student has 60 s for the target sum 5; 90 s for the target sum 9. Signal detection methods are applied to the number of hits and false alarms to generate a d' variable representing sensitivity to quantities (Geary et al., 2009). Children who correctly identify many target quantities and commit few false alarms have high scores. Individual differences in d' are likely related to (a) acuity of the cognitive systems for representing exact small quantities or approximate larger ones (Koontz & Berch, 1996); (b) implicit or explicit understanding of addition (Levine, Jordan, & Huttenlocher, 1992); and (c) understanding of cardinal value and that numbers are composed of sets of smaller-magnitude numbers (Butterworth, 2010).

Measures of Second-Grade Intermediate Numeracy Skills

Number line estimation

With the Number Line Estimation task (Siegler & Booth, 2004), children estimate where whole numbers fall on a number line. Stimuli are 24 number lines displayed across the center of a standard computer screen. Each number line is 25 cm and has a start point of 0 and an endpoint of 100 with a target number printed approximately 5 cm above it in a large font (72 pt). Target numbers are 3, 4, 6, 8, 12, 17, 21, 23, 25, 29, 33, 39, 43, 48, 52, 57, 61, 64, 72, 79, 81, 84, 90, and 96. Stimuli are presented in random order for each child. The tester first explains a number line that includes the 0 and 100 endpoints and is marked in increments of 10. After the tester judges that the child recognizes the concept, a number line containing only the endpoints 0 and 100 is presented, and the child points to where 50 should go. A model number line with the endpoints and the location of 50 marked is then presented, and the child compares his or her response to the model. The tester explains how “the number 50 is half of 100, so we put it halfway in between 0 and 100 on the number line.” Next, the tester teaches the child to use the arrow keys to place a red pointer on the line where 50 should fall on the computer screen. Then, the measure is administered. For each item, the tester says, “If this is zero (pointing) and this is 100 (pointing), where would you put N?” There is no time constraint. We used the absolute value of the difference between the correct placement and the child’s placement (i.e., estimation of accuracy), averaged across trials; smaller values indicate greater accuracy. This accuracy score correlates with mathematics achievement (Siegler & Booth, 2004). Cronbach’s alpha on the sample was .93.

Arithmetic computation

With the Arithmetic subset of the Wide Range Achievement Test-3 (WRAT-3; Wilkinson, 1993), children complete written calculation problems of increasing difficulty that are presented in horizontal or vertical format. Items are not read to the children. Most of this second-grade sample completed whole number addition and subtraction problems with single- and double-digits, with and without regrouping; some children also completed simple multiplication problems. In the present sample, alpha was .87.

Fourth-Grade Conceptual Understanding of Fractions

Understanding of fraction concepts was assessed using 17 released fraction items from recent National Assessments of Educational Progress (NCES 2007, 2009). With the NAEP items, testers read each problem aloud (with up to one rereading upon student request). Eight items assess the part-whole interpretation of fractions (e.g., Shade 3/8 of the rectangle above.); eight assess the measurement interpretation of fractions (e.g., Which picture shows that 2/3 is the same as 6/9?); and one asks how many fourths make a whole. Students select an answer from four choices (10 problems); write an answer (3 problems); shade a portion of a fraction (1 problem); mark a number line (1 problem); write a short explanation (1 problem); or write numbers, shade fractions, and explain the answer (1 problem with multiple parts). Alpha was .73.

Control Variables

All analyses included controls for the demographic characteristics noted and general achievement levels in first grade. To index general academic ability, we used the Reading subtest of the WRAT-3 (Wilkinson, 1993) consistent with previous research (Siegler & Pyke, 2013). Children read words of increasing difficulty. Alpha is .94 at age 6. To index general mathematics ability, we used the Concepts & Applications test (Fuchs, Hamlett, & Fuchs, 1990), consistent with previous research (Fuchs et al., 2010a,b). With 25 items, this test samples numeration, concepts, geometry, measurement, applied computation, money, charts, and word problems. For example, items require counting arrays of items, writing the number after, identifying smaller/larger quantities, and identifying operators within number sentences. Alpha was .93.

Procedure

At the beginning of first grade, children were assessed on nonverbal reasoning, language, attentive behavior, executive control, visual-spatial memory, and number knowledge. In spring of second grade, children were assessed on number line estimation and whole-number computations. In spring of fourth grade, children were assessed on the NAEP fraction items. Testing occurred individually in a quiet room for all tasks except for number knowledge in first grade and NAEP items in fourth grade, which were group administered. Graduate student testers were trained to criterion at each testing occasion and used standard directions for administration. Reliability across testers was assessed on percentage of agreement in scoring, based on audiotapes of children’s responses; agreement exceeded 99%.

Data Analytic Plan

Mediation analysis following Baron and Kenny (1986) and using the Preacher and Hayes (2008) SPSS macro was used to examine the extent to which fraction concepts were an extension of earlier forms of mathematical learning or if the conceptual leap required in fraction learning relied predominantly on early domain-general or numerical competencies. Mediation analysis has the advantage of allowing researchers to investigate direct associations, which in this study was used to examine the relation between first-grade competencies and fourth-grade fraction concepts, while holding constant the intermediate mathematical skills (and control variables). Importantly, mediation analysis also provides estimations of the statistical significance of indirect associations, which was used in the current study to evaluate whether whole-number computations and proportional reasoning interrupted the association between first-grade competencies and fourth grade fraction concepts. Bootstrapping (5000 draws to estimate standard errors) was used to construct 95% confidence intervals for the indirect associations. Bootstrapping is particularly valuable for estimating indirect associations because it makes fewer assumptions than other tests of indirect effects (e.g., shape of sampling distribution and standard error of indirect effect), for which traditional z-statistics are known to be biased (Fiedler, Schott, & Meiser, 2011; Gelfand, Mensinger, & Tenhave, 2009; Hayes, 2009; MacKinnon, Fairchild, & Fritz, 2007). We remind readers that because mediation analyses are correlational, causation should not be inferred.

Results

Preliminary Analyses

See Table 1 for sample means in standard scores (as available) as well as raw scores, which were used in subsequent analyses. As the standard scores indicate, the sample performed in the average range on all standardized measures. Table 1 also shows correlations among all first-grade competencies, second-grade mathematical skills, and fourth grade fraction concepts. The first-grade competencies were moderately to strongly correlated with the second-grade mathematics skills and fourth-grade fraction concepts. The second-grade mathematics skills were also moderately to strongly correlated with fourth-grade fraction concepts.

Table 1.

Means Raw Scores, Mean Standard Scores, and Correlations Among First-, Second- and Fourth-Grade Variables

		Raw Score	Standard Score	Correlations
		M (SD)	M (SD)	1.	2.	3.	4.	5.	6.	7.	8.	9.	10.	11.	12.
1.	G1 Reading	20.61 (4.94)	105.12 (15.32)	--
2.	G1 Concepts & Applications	11.22 (5.16)		.69	--
3.	G1 Nonverbal Reasoning	8.71 (5.23)	48.94 (9.26)	.43	.52	--
4.	G1 Language Composite	0.00 (1.00)		.58	.60	.39	--
5.	G1 Vocabulary	17.28 (6.76)	41.24 (10.68)	.53	.49	.39	.90	--
6.	G1Listening Comprehension	14.08 (5.18)	87.39 (16.55)	.52	.60	.31	.90	.63	--
7.	G1 Attentive Behavior	39.06 (12.60)		.55	.66	.42	.50	.44	.45	--
8.	G1 Listening Recall	5.40 (4.11)		.58	.64	.45	.65	.59	.58	.54	--
9.	G1 Visual-spatial memory	11.26 (3.34)		.40	.45	.46	.35	.32	.31	.39	.47	--
10.	G1 Number Knowledge	0.21 (1.04)		.49	.66	.48	.50	.46	.44	.58	.53	.43	--
11.	G2 Number Line Estimation	12.93 (6.59)		−.43	−.53	−.33	−.47	−.43	−.41	−.34	−.36	−.38	−.43	--
12.	G2 Arithmetic Computations	21.47 (3.31)	94.95 (13.50)	.50	.53	.38	.50	.51	.39	.52	.48	.40	−.50	−.46	--
13.	G4 NAEP Fractions	11.79 (4.24)		.56	.68	.49	.53	.48	.48	.57	.50	.41	.67	−.52	.58

Note. G1 = grade 1; G2 = grade 2; G4 = grade 4; NAEP = National Assessments of Educational Progress. Standardized scores for nonverbal reasoning and vocabulary represent T-score values (mean = 50, SD = 10); standardized scores for listening comprehension represent standard scores (mean = 100; SD = 15). All correlations had p values <.001.

Exploratory analyses were conducted to investigate the appropriateness of forming a latent language composite based on the vocabulary and listening comprehension variables. One factor was extracted, which accounted for 81.23% of the variance and was well defined by both variables (standardized loadings = .90). We used this latent composite in subsequent analyses.

Mediation Analyses: Unraveling the Developmental Course of Fraction Learning

The primary analyses focused on examining the direct and indirect associations between the first- and second-grade variables and fourth-grade fraction concepts. All analyses included controls for beginning of first-grade general mathematics achievement and reading achievement, demographic variables (i.e., racial/ethnic identity and subsidized lunch status), and all first-grade competencies. For instance, when testing the specific association of nonverbal reasoning, we controlled for language, attentive behavior, executive control, visual-spatial memory, number knowledge, concepts and applications, reading, racial/ethnic identity, and subsidized lunch status. Results are summarized in Figure 1.

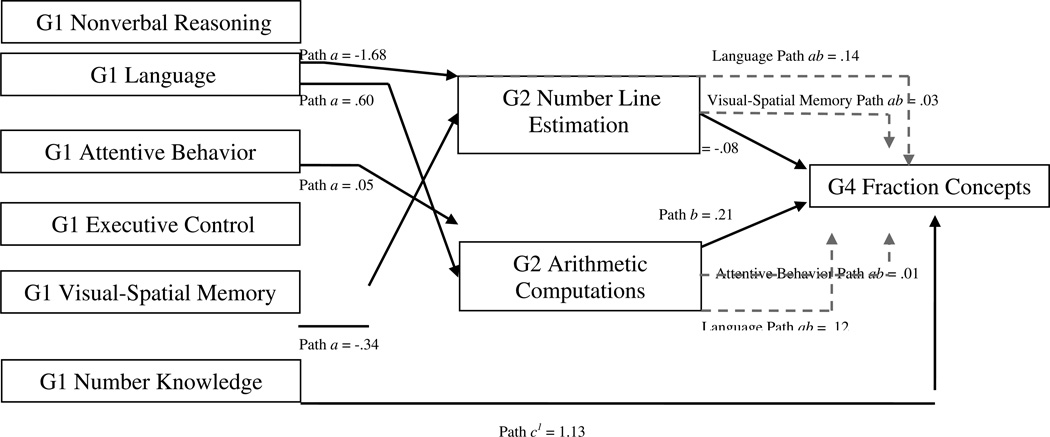
Figure 1.

Direct and indirect associations between first-grade competencies (left), second-grade intervening mathematical skills (middle), and fourth-grade fraction concepts (right). Analyses controlled for demographic characteristics, general mathematics ability, and general academic ability. Solid black lines indicate significant direct associations. Broken gray lines indicate significant indirect associations. Nonsignificant paths are not displayed. Note that paths are negative for number line estimates because lower scores indicate greater accuracy.

As shown at the top of Table 2, the association of both second-grade mathematics skills with fourth-grade fraction concepts—b paths—was statistically significant, holding constant first-grade competencies and controls. Thus second-grade mathematical skills met criteria for potential mediation between first-grade competencies and fourth-grade fraction concepts. The middle panel of Table 2—a paths—shows that first-grade language was the only variable that was significantly associated with both second-grade number line estimation and second-grade whole-number computations, after controlling for all control variables. First-grade visual-spatial memory had a significant association with second-grade number line estimation, whereas first-grade attentive behavior had a significant association with second-grade whole-number computations. First-grade nonverbal reasoning, executive control, and number knowledge did not have significant associations with second-grade number line estimation or second-grade whole-number computations, after accounting for control variables. First grade number knowledge had a direct association with fourth-grade fraction concepts.

Table 2.

Coefficients for Paths a, Paths b, and Paths c¹ in Mediation Models

Path	Coefficient (SE)	t-Value	p-Value
Path b: Effect of Grade 2 Skills on Grade 4 Fractions Concepts
Number line estimation → Fraction concepts	−083 (.04)	−1.98	.050
Arithmetic computations → Fraction concepts	.206 (.09)	2.35	.020
Path a: Effect of Grade 1 Predictor on Grade 2 Skill
Nonverbal reasoning → Number line estimation	.061 (.11)	0.56	.578
Nonverbal reasoning → Arithmetic computations	.008 (.05)	0.15	.884
Language ability → Number line estimation	−1.675 (.62)	−2.69	.008
Language ability → Arithmetic computations	.600 (.30)	2.00	.047
Attentive behavior → Number line estimation	.047 (.05)	0.97	.336
Attentive behavior → Arithmetic computations	.054 (.02)	2.33	.021
Executive control → Number line estimation	.207 (.16)	1.31	.193
Executive control → Arithmetic computations	.021 (.08)	0.27	.787
Visual-spatial memory → Number line estimation.	− 340 (.16)	−2.17	.032
Visual-spatial memory → Arithmetic computations	.019 (.08)	1.44	.153
Number knowledge → Number line estimation	− 581 (.61)	−0.95	.344
Number knowledge → Arithmetic computations	.313 (.29)	1.06	.290
Path c1: Direct Effect of Grade 1 Predictor on Grade 4 Fraction Concepts
Nonverbal reasoning → Fractions Concepts	.071 (.06)	1.29	.200
Language ability → Fractions Concepts	.218 (.32)	0.67	.503
Attentive behavior → Fractions Concepts	.025 (.02)	1.01	.315
Executive control → Fractions Concepts	− 052 (.08)	−0.64	.521
Visual-spatial memory → Fractions Concepts	−006 (.08)	−0.07	.943
Number knowledge → Fractions Concepts	1.128 (.31)	3.63	.000

Note. In all models, the effects of the other first grade predictor variables were controlled, as were the effects of grade 1 reading and math ability, racial/ethnic and subsidized lunch status.

Table 3 displays the total and indirect associations of the first-grade competencies on fourth-grade fraction concepts; 95% confidence intervals that do not cover 0 are statistically significant. First-grade language had a significant indirect association with fourth-grade fraction concepts via both second-grade number line estimation and whole-number computations. First-grade attentive behavior had a statistically significant indirect association via second-grade whole-number computations. First-grade visual-spatial memory had a statistically significant indirect association via second-grade number line estimation; the indirect association via second-grade whole-number computation appeared significant but could not be considered as a mediator given the nonsignificant a path from visual-spatial memory to whole-number computation.

Table 3.

Indirect Effects of First Grade Predictors on Fourth Grade Fraction Concepts

Path	Indirect Effect (path ab)	Bootstrapped 95% CI
Total Effect of Nonverbal Reasoning	.067 (.06)	−.0088 to .0125
Via Grade 2 number line estimation	.0004 (.00)	−.0061 to .0076
Via Grade 2 arithmetic computations	.0010 (.00)	−.0046 to .0086
Total Effect of Language Ability	.2592 (.11)	.0846 to .5335
Via Grade 2 number line estimation	.1399 (.08)	.0218 to .3598
Via Grade 2 arithmetic computations	.1193 (.08)	.0106 to .3306
Total Effect of Attentive Behavior	.0069 (.01)	−.0076 to .0279
Via Grade 2 number line estimation	−.0037 (.00)	−.0162 to .0028
Via Grade 2 arithmetic computations	.0106 (.01)	.0011 to .0304
Total Effect of Executive control	−.0147 (.02)	−.0626 to .0367
Via Grade 2 number line estimation	−.0180 (.02)	−.0633 to .0056
Via Grade 2 arithmetic computations	.0033 (.02)	−.0235 to .0429
Total Effect of Visual-spatial memory	.0498 (.03)	.0124 to .1226
Via Grade 2 number line estimation	.0280 (.02)	.0034 to .0779
Via Grade 2 arithmetic computations	.0218 (.02)	.0007 to .0788
Total Effect of Number Knowledge	.1166 (.11)	−.0558 to .3829
Via Grade 2 number line estimation	.0522 (.06)	−.0383 to .2234
Via Grade 2 arithmetic computations	.0644 (.07)	−.0268 to .2821

Note. In all models, the effects of the other first grade predictor variables were controlled, as were the effects of grade 1 reading ability, grade 1 general math ability, racial/ethnic and subsidized lunch status. Confidence intervals that do not cover 0 are statistically significant.

Discussion

The goal of this study was to begin to unravel the developmental course of fraction learning, especially whether conceptual understanding of fractions is an extension of earlier forms of mathematical learning or if the conceptual leap from whole-number understanding to fraction knowledge is predicated on other forms of learning. At this time, the developmental precursors of fraction knowledge are poorly understood, which is especially problematic considering the central role fractions play in economic and social opportunities in adulthood (NMAP, 2008; Siegler et al., 2012). We tested the relative contributions of domain-general and numerical competencies to the prediction of fraction concepts. Overall, results suggest that domain-general and numerical competencies play different roles in the conceptual leap from whole numbers to fractions, findings which may also be relevant for understanding conceptual leaps occurring in other academic domains or at other developmental stages.

Domain-General Competencies Support Building Blocks for Later Learning

The associations between domain-general competencies and children’s later understanding of fraction concepts were all mediated by second-grade mathematical skills. Indeed, the findings suggest that domain-general competencies—language, visual-spatial memory, and attentive behavior in particular—at school entry facilitate the learning of mathematical skills that provide the building blocks for later fractions learning, but are not direct antecedents of fraction learning. These findings lend strength to the idea that learning fraction concepts is an extension of earlier forms of mathematical learning, and that domain-general competencies play a secondary role to mathematical skills. This does not mean that domain-general competencies assessed simultaneously with fractions concepts would not be important but does indicate that early competencies operate through intermediate mathematical skills.

That language was associated with intervening mathematical skills but was not a direct antecedent of fraction concepts contrasts with the hypothesis that linguistic skills influence the kinds of mathematical learning that depend on the symbolic number system, including fractions (LeFevre et al., 2010). Whereas LeFevre et al. (2010) found that their linguistic composite measured at 4.5 years of age predicted all mathematical outcomes (i.e., whole-number computations, numeration, geometry, measurement, and number line estimation) three years later, a more complex association emerged in this study, with language skills predicting subsequent whole-number computations and number line estimation which in turn predicted later fraction concepts. These findings thus suggest that early language competencies play a more nuanced role in fraction development than proposed by LeFevre et al. It is possible that early language competencies promote the development of intervening mathematical skills rather than directly support how children understand fraction concepts. For example, language capability helps children cognitively represent large numbers (i.e., ≥ 5) with precision, which is needed to manipulate exact quantities, as with whole-number computations (e.g., 5 + 9), and to estimate exact magnitudes relative to each other, as in making number line estimations (e.g., accurately placing 5 on a number line). Early language competency may therefore be needed to master second-grade mathematical skills, which in turn impart an advantage in learning more nuanced features of number necessary for fourth-grade fraction knowledge, such as understanding the difference between 5 and 1/5. Thus, poor early language competency may forecast children’s difficulty making the conceptual leap from whole number to fractions, signaling the need to ensure mastery of mathematical language in the early years to provide a solid foundation for learning both whole numbers and fractions.

In this study, visual-spatial memory and attentive behavior were associated with fraction concepts whereas executive control and nonverbal reasoning were not. This finding thus suggests that not all domain-general competencies associated with the spatial-attention pathway proposed by LeFevre et al. (2010) are associated with mathematical learning—fractions in this case—a finding that would have been obscured had we considered a composite spatial-attention variable. Early visual-spatial competencies may reflect the ease with which children learn to (a) map spatial representations of magnitude onto precise symbolic representations (by second grade, children have developed mappings between nonverbal magnitude representations and Arabic numerals up to around 100), and (b) hold in memory spatial and symbolic representations of magnitude in order to make proportion judgments (e.g., accurately placing 5 on a 0–100 number line). Early visual-spatial memory may thus be needed to integrate the visual-spatial and symbolic representations necessary to make accurate number line estimations, which may in turn assist children in interpreting visual-spatial and symbolic connections related to fourth-grade fractions, such as producing a visual representation of 1/5. If so, the present findings would suggest that children with weak visual-spatial memory may have difficulty making the transition to fractions unless they receive early support in learning to integrate visual-spatial and symbolic representations of magnitude, as in making number line estimations.

Attentive behavior in this study was associated with whole-number computations, consistent with a substantial body of research (e.g., Fuchs et al., 2006, 2010a,b), but not with number line estimation or fraction concepts, in contrast to previous findings (Hecht et al., 2003; Jordan et al., 2013). Whereas Hecht et al. (2003) and Jordan et al. (2013) investigated this association in third through fifth graders, this study focused on younger children. This may mean that in the early school years, attentive behavior matters specifically for the acquisition of procedural skills whereas conceptual development depends less on attentive behavior. Attentive behavior may help children master the sequenced procedures needed to solve arithmetic problems, which becomes especially important when children learn regrouping in second grade. This early attentive ability needed to master second-grade mathematical rules and procedures may in turn support the conceptual leap to fractions in fourth grade, when children must distinguish between the rules and procedures related to whole numbers versus fractions (e.g., multiplying whole numbers always results in a larger number, whereas multiplying fractions does not). These findings suggest that poor attentional capacity is a risk factor for later fraction learning. Teachers may need to be intentional in directing and ensuring children’s attention during mathematical instruction in ways that focus on rules and procedures, especially for students who exhibit poor attentive behavior.

It must be noted that the findings as they relate to teasing apart the roles of executive control and visual-spatial memory are exploratory and our interpretations thus speculative. Researchers have noted the problem of task impurity with measures of executive processes, whereby tasks designed to measure specific executive functions often place demands on several executive processes and/or non-executive processes (e.g., Best, Miller, & Jones, 2009; Miyake et al., 2000), making it difficult to interpret findings pertaining to any one measure. One solution has been to use a latent variable approach to capitalize on the underlying competencies rather than surface features of the task, an approach not possible in this study. Although our results are consistent with the finding that visual-spatial memory has broader effects on mathematical learning than does executive control (Bull, Espy, & Wiebe, 2008; St Clair-Thompson & Gathercole, 2006), and that attentive behavior is important for learning whole-number procedures (e.g., Fuchs et al., 2006, 2010a,b), this study should be replicated using multiple measures of executive processes.

Multiple Pathways to Fraction Competence

The second main finding was that fraction concepts had roots in earlier forms of mathematical learning and in early numerical competencies. This lends support to the idea that not only is learning fractions an extension of earlier forms of mathematical learning, but also that there may be multiple pathways to fraction competence. Specifically, the findings suggest that children may learn fractions through (a) the same learning pathway as whole-number development; (b) a proportional reasoning learning trajectory; or (c) a yet unspecified developmental course stemming from early numerical competencies.

In this study, number knowledge was the only first-grade competency that directly predicted fourth-grade fraction concepts. This corroborates LeFevre et al. (2010) and Butterworth (2010) who proposed a quantitative pathway as a unique source of individual differences in mathematical skill independent of domain-general competencies. Interestingly, first-grade number knowledge was not associated with second-grade arithmetic computations or number line estimation, a somewhat surprising finding given that both second-grade tasks required numerical processing. Thus, the findings suggest a unique pathway to fraction learning that is independent from whole-number computations and proportional reasoning. Butterworth and colleagues posit that the ability to recognize, represent, and manipulate small numerosities provides the building blocks for learning arithmetic in particular (e.g., Butterworth, 2010; Gelman & Butterworth, 2005). By contrast, our results suggest that the fluency with which children can identify, process, and manipulate small quantities, as assessed with the Number Sets Test (Geary et al., 2009), matters specifically for fraction learning. This fluency may serve as a proxy for children’s later ability to make the conceptual leap from whole-number understanding to fraction understanding, although the underlying mechanism remains to be identified. In any case, results suggest that the Number Sets Test, a highly efficient measure, may be diagnostically useful in forecasting children’s difficulty with fraction concepts, thereby providing a means of identifying students for early intervention. It also suggests that an emphasis on number knowledge and fluency in recognizing and manipulating small quantities may be a target for early intervention to prevent fraction difficulty.

That second-grade number line estimation was uniquely associated with fraction concepts two years later suggests that children’s rudimentary proportional reasoning ability also provides a foundation for learning fractions. This finding corroborates Jordan et al. (2013) with a different sample spanning a longer developmental period and while considering mediating effects. In Jordan et al., third-grade number line estimation made the largest unique contribution to fourth-grade fraction concepts above the effects of third-grade whole-number skills, language, and attentive behavior. Together, results indicate that children—even those as young as second grade—who make accurate number line estimations seem also to have an advantage in learning fraction concepts. Given the increased emphasis on the number line in the Common Core State Standards, this finding is likely relevant to practitioners. Results also suggest that proportional reasoning might have a different learning trajectory separate from whole-number concepts and procedures. This corroborates Mix et al.’s (1999) finding that children have an informal understanding of fractions before formal fraction instruction occurs. This study identified two developmental precursors of number line estimation, namely, language and visual-spatial memory. Future research is needed to further specify this learning trajectory, especially the extent to which non-symbolic proportional reasoning (e.g., Spence & Krizel, 1994) and the approximate number system (ANS; Halberda, Mazzocco, & Feigenson, 2008; Libertus, Feigenson, & Halberda, 2011) are involved. Although Jordan et al. (2013) found that the ANS in third grade did not uniquely predict fourth-grade fraction outcomes, few studies have considered how non-symbolic proportional reasoning contributes to the development of fraction knowledge independent of whole-number competencies or how the ANS contributes to number line development in the early school years.

Finally, results suggest that whole-number skills are developmental precursors of fraction learning. Hecht et al. (2003) found that whole-number arithmetic computations were predictive of procedural fraction skill. This study extends these findings to indicate that whole-number computations are also predictive of children’s understanding of fraction concepts. Although the iterative relation between conceptual and procedural knowledge has been well documented (e.g., Rittle-Johnson & Alibali, 1999; Rittle-Johnson et al., 2001), a unique contribution of this study is the finding that whole-number procedural skill predicted conceptual understanding of fractions two years later. This finding is especially striking given that general mathematics ability, general academic ability, and proportional reasoning were controlled. This finding provides strong support for the hypothesis that the conceptual leap from whole number to fractions depends in part on mastery of whole-number concepts and procedures (NMAP, 2008; Siegler & Pyke, 2013). Thus, findings suggest that the whole-number bias may be alleviated in part by addressing gaps in children’s understanding of whole-number procedures and principles.

Limitations and Conclusions

Readers should note that, as with all studies, specific measures were selected to operationalize constructs, and varying the methods for indexing key abilities or expanding the models to incorporate additional competing predictors could alter findings. Also, this study did not examine all potential competencies that might have an influence on children’s fraction development, most notably the ANS (e.g., Halberda et al., 2008) and non-symbolic proportional reasoning (e.g., Spence & Krizel, 1994). Future research is needed to determine which domain-general and numerical competencies are involved in later fractions learning, including specifying the independent pathways identified in this study. We further note that like other correlational analyses, evidence of significant associations in our model cannot be interpreted as causal nor can it be assumed that the proposed model represents the only or best solution. For instance, a significant mediated association could reflect that the intermediate mathematical skill is a correlate of either the true (untested) mediator or of fraction concepts and not necessarily a causal mechanism. It is thus important to replicate the present findings.

Finally, although difficulty with fractions is not just a U.S. phenomenon (e.g., Chan et al., 2007; Tatsuoka et al., 2004), it is interesting to consider the role of school context in explaining the development of fraction knowledge. Specifically, the observed findings may depend on the type of instruction provided at that time in American schools, where the dominant focus is part-whole understanding. A second type of understanding, the measurement interpretation of fractions, reflects cardinal size. This type of interpretation, often represented with number lines, has until recently been assigned a subordinate role, addressed later and with less emphasis. Yet, an instructional focus on the measurement interpretation is in keeping with the Common Core State Standards’ explicit emphasis on understanding of fraction equivalence and ordering. A schooling context that emphasizes the measurement interpretation may result in different findings. Future research is needed to tease apart how differences in instruction, for example part-whole vs. measurement interpretation, facilitate or hinder fraction learning.

With these caveats in mind, we offer two conclusions. First, domain-general competencies may be foundational for fraction concepts only insofar as they promote the development of intermediate mathematical skills. Not all domain-general competencies, however, are necessarily implicated. Language ability appears to matter generally for mathematical development, whereas visual-spatial memory matters for number line estimation, and attentive behavior matters for arithmetic computations. Nonverbal reasoning and executive control did not emerge as salient predictors of children’s understanding of fraction concepts. Second, early numerical and mathematical competencies may be direct antecedents and powerful longitudinal predictors of children’s understanding of fraction concepts.

Competence with fractions plays a pivotal role in determining success in and out of school. Our findings suggest that children develop fraction competence through multiple pathways, indicating that a breakdown in learning fractions may occur at any point along any particular pathway, beginning with early domain-general and numerical competencies. Just as reading comprehension difficulties may result from decoding or language comprehension deficits (among other sources), fraction difficulties may stem from multiple origins that require different instructional interventions. For example, children with adequate whole-number knowledge may nonetheless experience difficulty learning fractions because of weaknesses in understanding number generally or in understanding proportional reasoning. Such weaknesses might further reflect underlying difficulties in domain-general functioning, such as language or visual-spatial memory, or gaps in mathematical content related to number and proportional reasoning. Each, in turn, would have different instructional implications. Future research is needed to specify the precise sequence of learning that occurs along different trajectories in order to inform diagnostic assessments and corresponding instructional interventions.