Primordial chemistry and enzyme evolution in a hot environment

Abstract

Ever since the publication of Darwin’s Origin of Species, questions have been raised about whether enough time has elapsed for living organisms to have reached their present level of complexity by mutation and natural selection. More recently, it has become apparent that life originated very early in Earth’s history, and there has been controversy as to whether life originated in a hot or cold environment. This review describes evidence that rising temperature accelerates slow reactions disproportionately, and to a much greater extent than has been generally recognized. Thus, the time that would have been required for primordial chemistry to become established would have been abbreviated profoundly at high temperatures. Moreover, if the catalytic effect of a primitive enzyme (like that of modern enzymes) were to reduce a reaction’s heat of activation, then the rate enhancement that it produced would have increased as the surroundings cooled, quite aside from changes arising from mutation (which is itself highly sensitive to temperature). Some nonenzymatic catalysts of slow reactions, including PLP as a catalyst of amino acid decarboxylation, and the Ce^IV ion as a catalyst of phosphate ester hydrolysis, have been shown to meet that criterion. The work reviewed here suggests that elevated temperatures collapsed the time required for early evolution on Earth, furnishing an appropriate setting for exploring the vast range of chemical possibilities and for the rapid evolution of enzymes from primitive catalysts.

Catalysis and transition state binding by enzymes

Since the time of Pasteur, biologists and chemists have marveled at the power of enzymes to enhance the rates of reactions. Individual enzyme molecules are present at such low concentrations in cells that biological reactions must proceed very rapidly at their active sites—often in a matter of milliseconds—if these reactions are to be of any use to a cell with a division time measured in hours. On the other hand, if biological reactions were not very slow in the absence of enzymes, then biologically important molecules would disintegrate too rapidly to be of any use to living organisms. So the very existence of life can be said to depend on the difference in rate between uncatalyzed reactions and enzyme-catalyzed reactions.

What is responsible for this difference in rate? Transition state theory (also known as the theory of absolute reaction rates) provides a useful way of describing the action of a catalyst (Fig. 1).

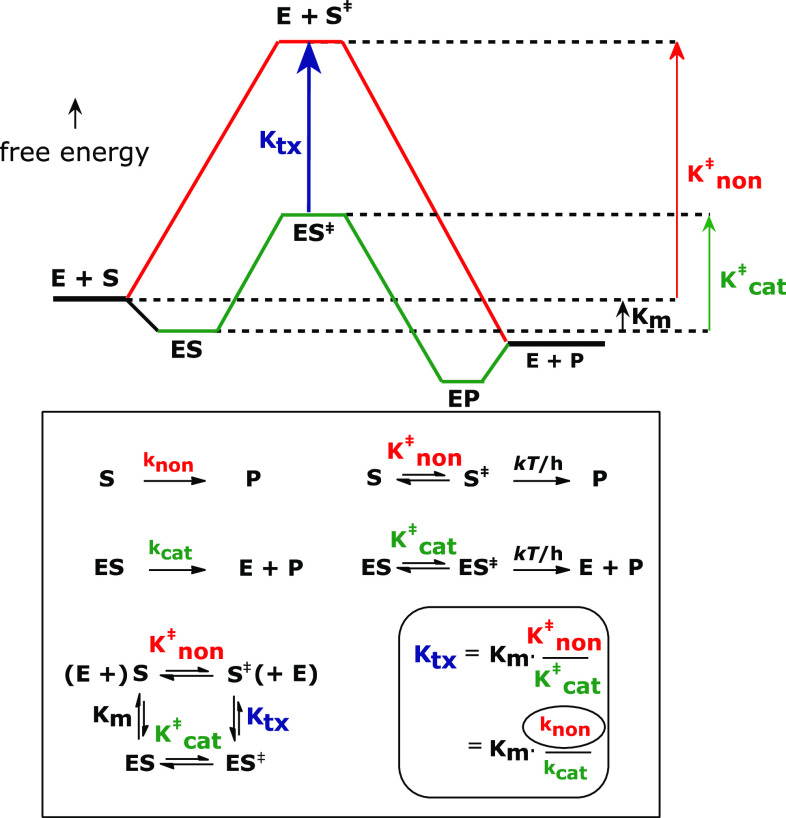
Fig. 1.

Free energy diagram for enzyme catalysis, showing the path of the nonenzymatic reaction (red) and the enzyme reaction (green). Estimation of the dissociation constant of the enzyme from the altered substrate in the transition state requires knowledge of the rate constant of the uncatalyzed reaction

In the absence of a catalyst (red line), every reaction passes from the ground state S to the transition state S^‡, in a process with a nominal equilibrium constant ($K_{\text{non}}^{‡}$) that is highly unfavorable. The transition states of all reactions are understood to decompose to products with the same absolute rate constant kT/h (where k = Boltzmann’s constant, T = absolute temperature, and h = Planck’s constant), so that one reaction is faster than another to the extent—and only to the extent—that the equilibrium constant of activation (K ^‡) is larger for the first reaction than for the second.

The rate constant (k _cat) of an enzyme reaction, which describes the rate of product formation from the enzyme-substrate complex ES (green line), can be treated in the same way. If k _cat exceeds k _non by a known factor (the rate enhancement), then $K_{\text{cat}}^{‡}$ exceeds $K_{\text{non}}^{‡}$ by the same factor. It follows algebraically that the enzyme’s binding affinity for the substrate (roughly the reciprocal of K _m) increases by that same factor as the complex proceeds from the ground state (ES) to the transition state (ES^‡), where binding becomes exceedingly strong (the reciprocal of K _tx). A stable analogue of S^‡ should therefore be a powerful reversible inhibitor. That inference remains valid even if—as is sometimes the case—the enzymatic and nonenzymatic reactions proceed by mechanisms that differ, or if the rate of the enzyme reaction is limited by the physical release of the reaction product [1].

Measuring benchmark rates of uncatalyzed reactions

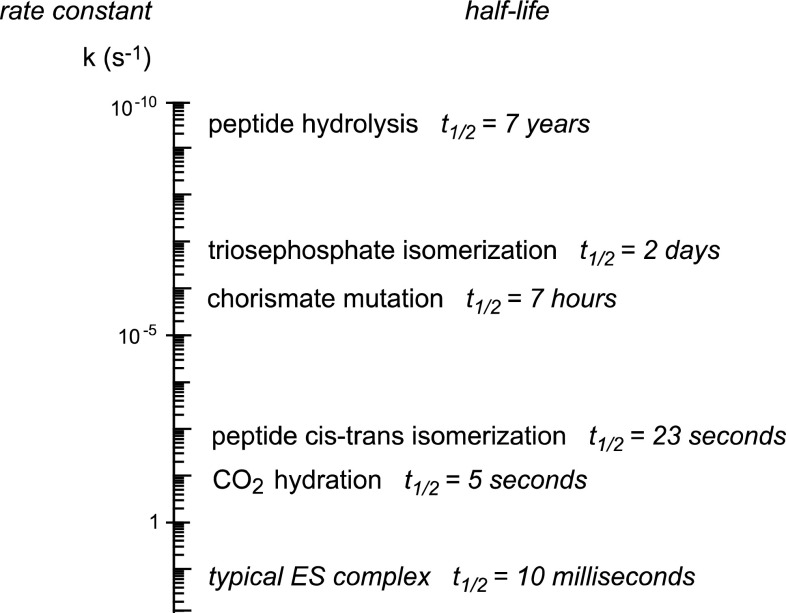
That principle led to the discovery of powerful enzyme inhibitors. In addition to more practical applications, these molecules, usually termed transition state analogues, have proven useful in distinguishing between alternative mechanisms by which an enzyme might act, and (in conjunction with exact structural methods) in revealing enzyme-substrate interactions that are important for catalysis. However, when attempts were made to compare the binding affinities of real analogues with the transition state affinities that would be expected in theory, it became apparent that a significant piece of information was missing. The rate constants of most biological reactions in the absence of a catalyst were simply unknown. Experiments involving extremely sensitive methods for product formation such as the release of a radioactive product from a matrix-bound substrate [2], had shown that half-lives could be as long as several years (Fig. 2). However, it was clear that a different approach would be needed to measure the rates of any processes much slower than that at ordinary temperatures, with half-lives that might extend to centuries or even longer.

Fig. 2.

Rate constants and half-lives of nonenzymatic reaction at 25 °C known in 1994

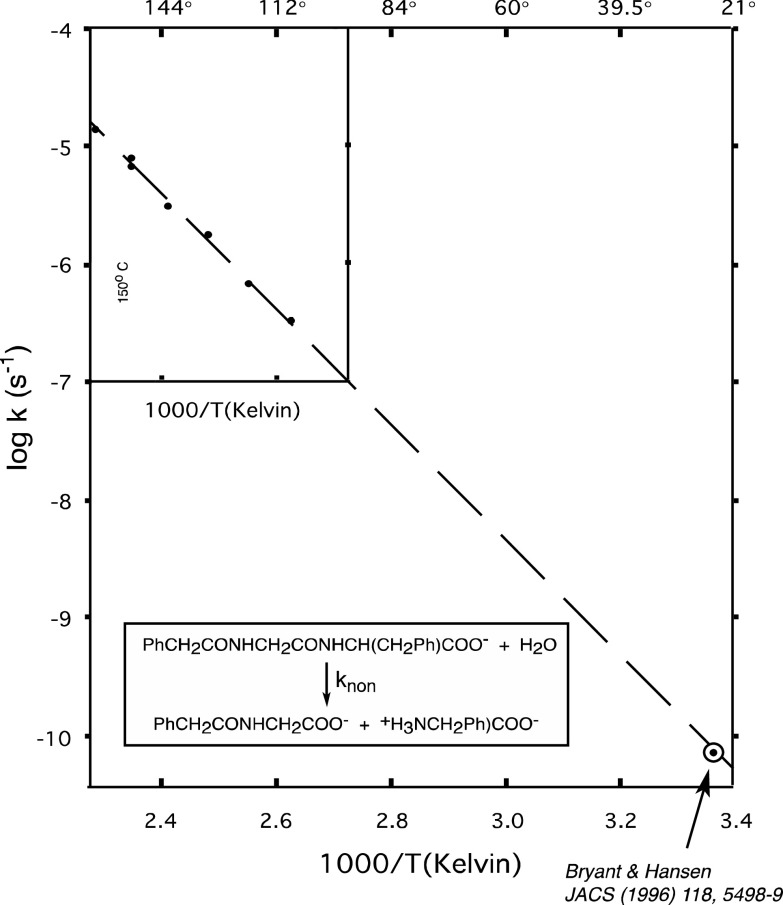
Virtually all chemical processes are accelerated by heat. One of the most general ways to monitor the rates of very slow reactions is to determine reaction rates at elevated temperatures and extrapolate the results to ordinary temperatures using the Arrhenius equation, according to which the logarithm of the rate constant varies with the reciprocal of the absolute temperature. For most simple reactions, that relationship turns out to be remarkably linear, as exemplified by the results for peptide hydrolysis in Fig. 3. A regression line through the values between 95 and 170 °C intersects a value determined at 25 °C based on a hypersensitive fluorescence assay [3, 4], showing that this Arrhenius plot is linear over a range of >10⁵-fold in rate constants. Although curvature would be expected in those cases where heat capacities of activation are significant, curvature is very seldom observed except in those processes in which the rate-limiting step changes with temperature.

Fig. 3.

Arrhenius plot for peptide hydrolysis at pH 7, showing points gathered at elevated temperatures (inset) and a single point measured at 25 °C (bullseye)

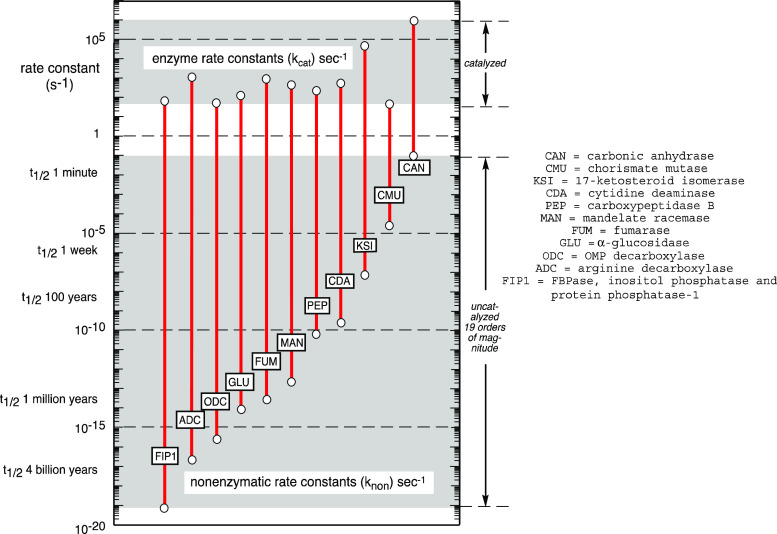
For peptide hydrolysis, the extrapolated half-life for the uncatalyzed reaction is ~500 years at 25 °C, but some reactions have been found to be much slower, with half-lives of 130,000 years for phosphodiester hydrolysis [5], 10⁸ years for the decarboxylation of orotidine 5′-phosphate⁵, and 10¹² years for the reaction of water with phosphomonoester dianions [6]. Shown on a logarithmic vertical scale, Fig. 4 compares the rate constants of some enzyme reactions (across the top) with the rate constants of the corresponding uncatalyzed reactions (across the bottom). Each of these comparisons is for reactions whose mechanisms are similar in the presence and absence of the enzyme, not for reactions in which the enzymatic and nonenzymatic reactions involve different sites or mechanisms of bond breaking. The rate enhancement (k _cat/k _non) produced by each of these enzymes is indicated by the length of the vertical line (note that this is a logarithmic scale), and range from 10⁷-fold for carbonic anhydrase to 10²¹-fold for phosphate monoesterases that catalyze direct water attack on the substrate.

Fig. 4.

Rate constants for reactions in the presence and absence of enzymes, plotted on a logarithmic scale. The length of each red line represents the rate enhancement produced by each enzyme, identified by abbreviations shown on the right

Evolutionary questions

In the course of gathering information about enzyme rate enhancements for the purpose of estimating the affinities expected of ideal transition state analogue inhibitors, we stumbled unexpectedly on information that might be relevant to two vexing evolutionary questions. Ever since the time of Kelvin [7], critics of Darwinian evolution have argued that not enough time had passed for these and other biological processes to evolve to their present level of complexity. Moreover, although the age of the earth is now understood to be ~4.6 billion years, cyanobacteria appear to have been flourishing within the first ~1 billion years after its birth [8]. Figure 4 shows that in the absence of an enzyme, some biological reactions are slow on a geological—or even a cosmological—time-scale. How did these reactions get started before enzymes were available to catalyze them? And how might enzyme evolution itself have gotten started?

How did biological reactions get started before enzymes were available?

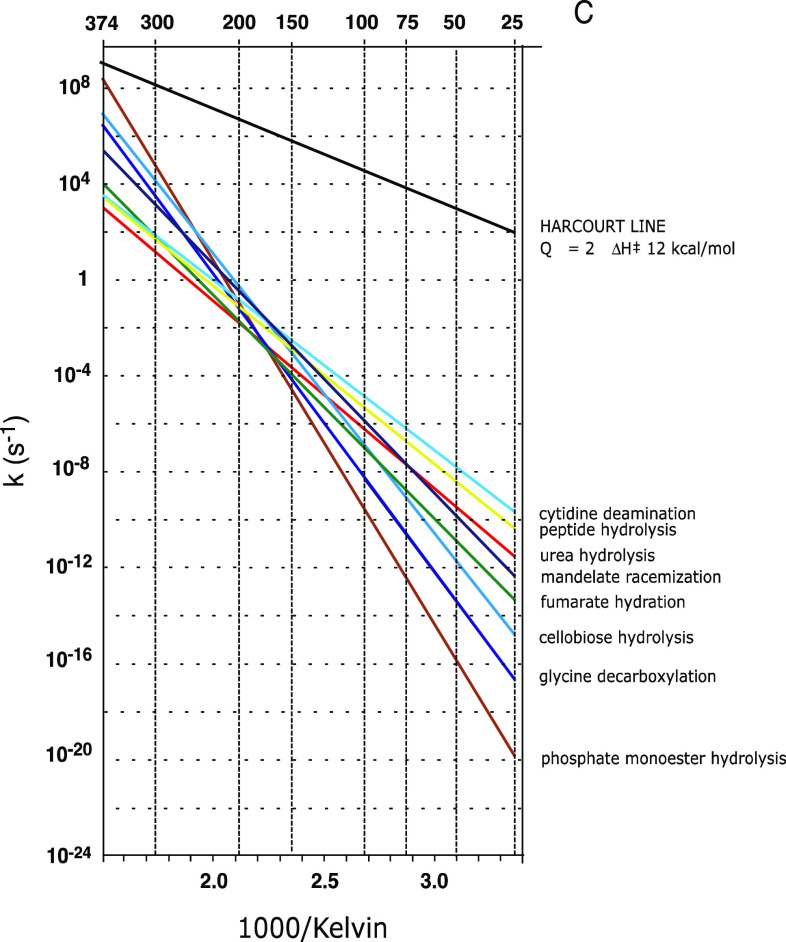
Consider the temperature dependence of chemical reactions in the absence of a catalyst. Vernon Harcourt, the first chemist to examine the effects of temperature systematically, noticed in 1862 that the rate of the iodine clock reaction roughly doubled with a 10 °C increase in temperature (sometimes paraphrased: “Q ₁₀ = 2”) [9]. For reasons that appear in retrospect to have been related to the limited range of reaction rates that are convenient to follow at ordinary temperatures, Harcourt’s observation emerged as a generalization applicable to all reactions in the minds of many chemists, and continues to appear in many prominent textbooks, and in fact, it is true that Q ₁₀ does equal 2 for a few biologically important reactions such as the dehydration of carbonic aid, which proceeds spontaneously, in the absence of an enzyme, with t _1/2 ~30 s [10].

However, that statement is not true as a generalization. Compare the slope of the black “Harcourt line” (for which Q ₁₀ = 2) in Fig. 5 with the slopes of the colored lines representing various reactions that have been examined recently. The slopes of these Arrhenius plots are seen to be much greater than that of the Harcourt line, and to vary greatly among themselves. The slower a reaction is at low temperature (toward the right side of Fig. 2), the more sensitive to temperature it tends to be.

Fig. 5.

Arrhenius plots for some biological reactions in the absence of enzymes

Now consider the result of compounding these effects over a substantial temperature range for reactions with different ΔH^‡ values. Some modern thermophilic organisms grow at temperatures as high as 122 °C, while some psychrophiles grow at temperatures well below 0 °C. Without going to these extremes, let us consider the effect of raising the temperature from 25° to 100 °C. The rate of peptide and urea hydrolysis (t _1/2 = 600 years at 25 °C), a reaction with a Q ₁₀ of 4 (ΔH^‡ = 24 kcal/mol), increases 4,000-fold when the temperature is raised from 25 to 100 °C. The rate of sucrose hydrolysis (t _1/2 = 10¹² years at 25 °C) with a Q ₁₀ of 8 (H^‡ = 36 kcal/mol) increases 200,000-fold in going from 25 to 100 °C. The rate of hydrolysis of phosphate monoester dianions, one of the slowest reactions known (t _1/2 = 10¹² years at 25 °C), with Q ₁₀ = 16 (H* = 48 kcal/mol) increases 10,000,000-fold in going from 25 to 100 °C.

The startling magnitude of these temperature effects on slow reactions suggests a provisional answer to the question of how very slow biological reactions got started on a primitive earth. If early biomimetic chemistry began while Earth was still warm, then the elevated temperature of the surroundings would have collapsed the time required for their occurrence, especially for the slowest reactions [11].

However, did life arise while the earth was still warm? The discovery of ancient cyanobacteria suggests that the first organisms originated within the first of the 4.6 billion years of Earth’s history, not long after the end of the Late Heavy Bombardment [8]. The most primitive branches of the tree of life appear to have been largely populated by thermophilic organisms [12], and the genetic code appears to have been established while the earth was still warm [13]. Moreover, recent reconstructions of the probable amino acid sequences of ancestral enzymes yield proteins with much higher temperatures of denaturation than their modern counterparts [14]. If life did indeed arise while the earth was still warm, then the kinetic burden imposed on early chemical evolution by the sluggishness of most biological reactions at ordinary temperatures would have been alleviated.

How did enzyme evolution get started? A hypothesis

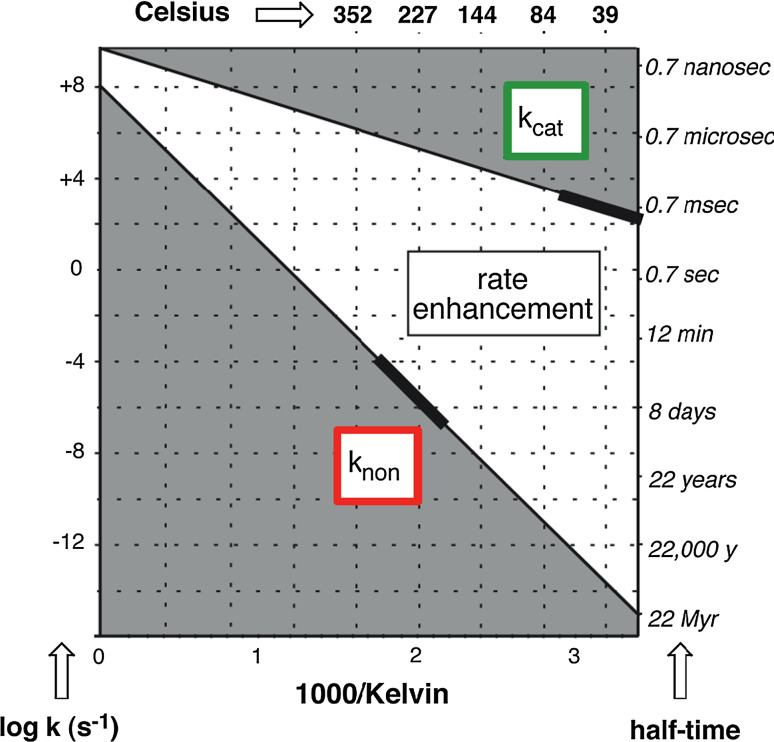
Modern enzymes exhibit rate enhancements as large as 10²¹-fold [6]. Moreover, numerous enzymes have been found to act on their substrates with second order rate constants that approach the physical limits imposed by enzyme-substrate encounter in solution, with values of k _cat/K _m that approach 10⁹ M⁻¹ s⁻¹. [15] What circumstances would have permitted enzymes to evolve to their present state of near-perfection within the limited time available? The magnitude of this problem becomes apparent if one considers the decarboxylation of orotidine 5′-phosphate, an essential step in the biosynthesis of pyrimidine nucleotides, and thus of DNA. In the absence of the decarboxylase, the half-life of this reaction is ~78 million years at 25 °C in neutral solution [5]. If a “primitive” enzyme enhanced the rate of this reaction by a factor of 10³, 10⁶, or even 10⁹, for example, that enzyme would have been of little use in a primitive organism’s struggle for existence. How did the earliest enzyme reactions get a toehold, so that natural selection could begin to do its work?

Efforts to address that question have tended to be constrained by the conditions of life as we know it, and at 25 °C, the barriers to reaction are formidable indeed. However, as we have seen for simple reactions, the picture changes markedly if we consider a much warmer environment in which spontaneous reactions occur much more rapidly. Figure 6 shows the temperature dependence rate of glycoside hydrolysis in the presence and absence of a bacterial α-glycosidase [16]. The enzyme reaction is far more rapid at ordinary temperatures, but because it is much less sensitive to temperature than the spontaneous reaction, the rate enhancement (k _cat/k _non) produced by the enzyme (the white area between the lines in Fig. 6) becomes less and less impressive with increasing temperature.

Fig. 6.

Arrhenius plots for the enzymatic and nonenzymatic reactions catalyzed by a α-glucosidase. The bold segments of the lines show the range of temperatures over which rate measurements were conducted. Reprinted with permission from Wolfenden et al. (1999) J. Amer. Chem. Soc. 121, 7419–7420. Copyright 1999 American Chemical Society

Now reverse this process and consider a potential scenario on the early earth, in which a primitive enzyme, perhaps a metal ion or a simple organic acid or base, might have produced a small enhancement in the rate of a reaction at elevated temperatures. As the surroundings cooled, the rate enhancement produced by that proto-enzyme would have increased automatically, quite apart from any improvements that might have resulted from the effects of selective pressure over time.

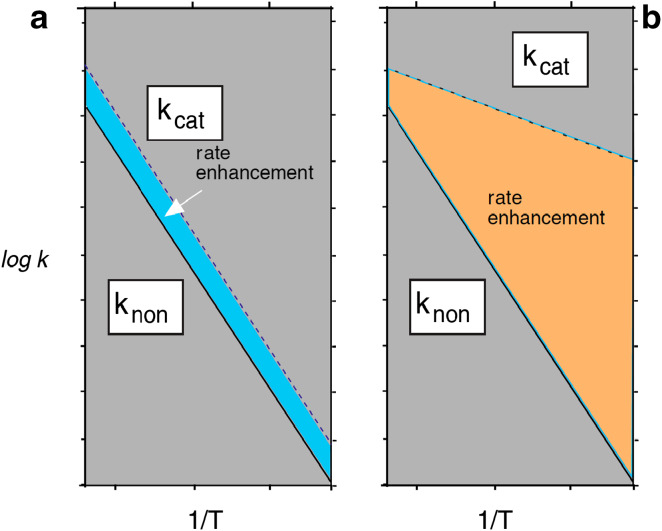
The plausibility of that scenario depends on whether, and to what extent, a primitive catalyst might have achieved its effect by lowering the enthalpy of activation (orange wedge, Fig. 7), as opposed to achieving its effect by enhancing the entropy of activation (blue wedge, Fig. 7). It would therefore be of interest to know whether nonenzymatic catalysts, such as might have been present on the hot surface of a primitive earth, follow either of those extreme scenarios. Figure 8 shows some nonenzymatic catalysts or other environments for which rate enhancements have been reported. These include five proteins (including a catalytic antibody, two designed enzyme mimics and a designed interface between two protein subunits), three metal ions and several nonaqueous environments (cyclohexane, hexamethylphosphoramide and the vapor phase).

Fig. 7.

Variation with temperature of two catalysts, one of which (a) enhances a reaction’s entropy of activation (blue) without affecting the enthalpy of activation, while the other (b) lowers the enthalpy of activation (orange) without affecting the entropy of activation

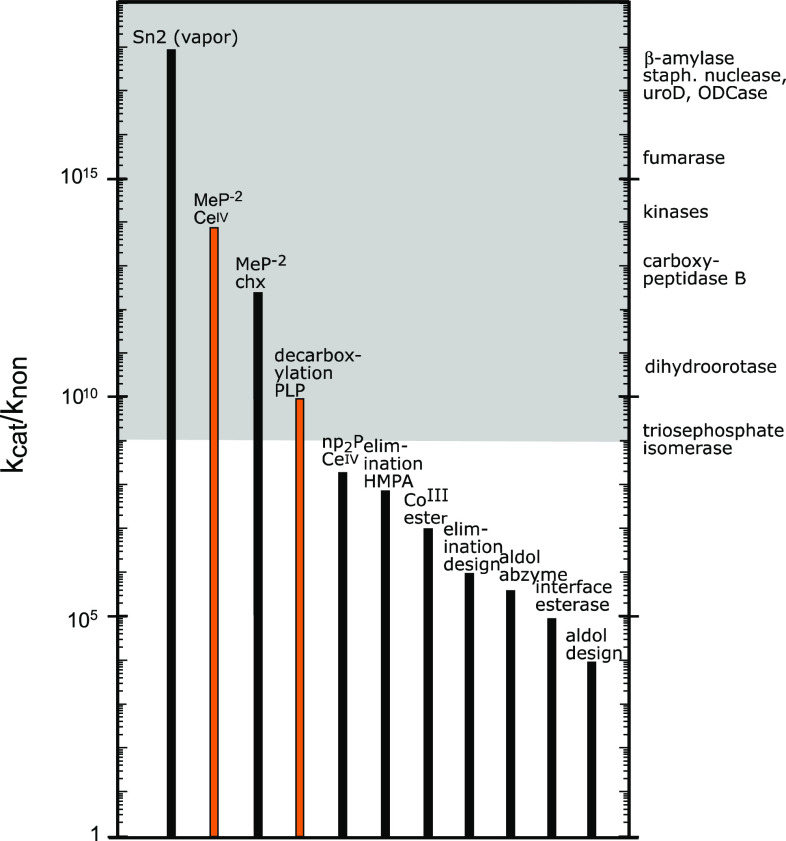
Fig. 8.

Rate enhancements produced by some nonenzymatic catalysts, compared with some enzymes (right margin)

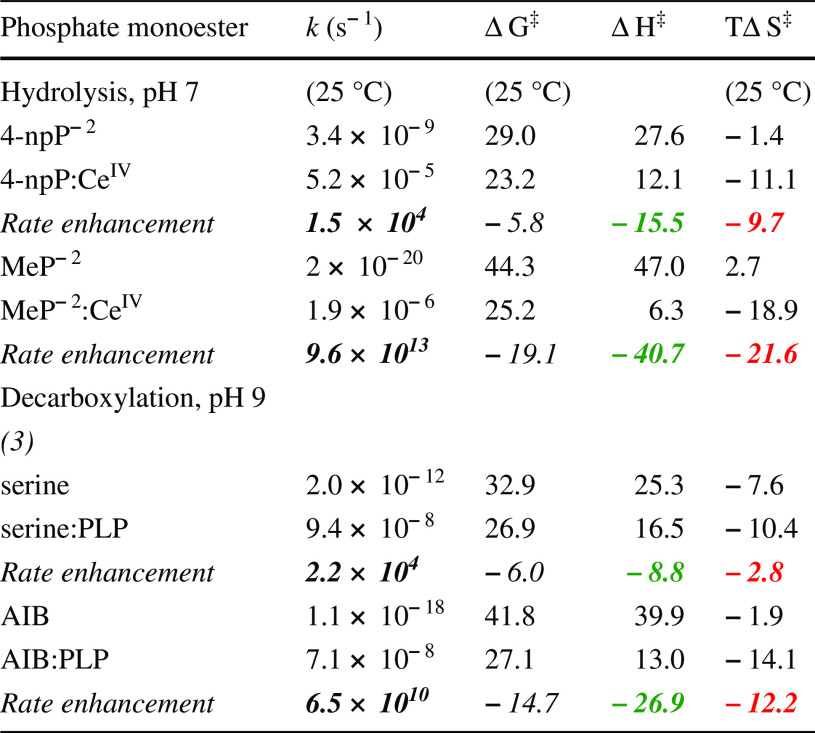
Highlighted in orange are pyridoxal phosphate (PLP) and Ce^IV, which generate rate enhancements approaching those produced by some enzymes (k _cat/k _non values for some enzyme reactions are shown along the right vertical axis of Fig. 8). PLP is a thermostable coenzyme that survives lengthy exposure to a warm environment, is required in a variety of biological reactions, and has been shown to catalyze amino acid decarboxylation in the absence of an enzyme [17]. Cerium, which is the most abundant of the rare earth elements and composes 0.05 % by weight of the earth’s crust, is also the only lanthanide that is stable in the +4 state. Soluble complexes of Ce^IV have been shown to catalyze the hydrolysis of phosphoric acid esters. [18, 19] When the rate enhancements produced by PLP and Ce^IV were examined as a function of temperature, the effects of these powerful catalysis were found to be based entirely on a reduction of ΔH^‡. Instead of being favorable, their effects on TΔS^‡ were actually found to be unfavorable (Table 1) [11].

Table 1.

Effects of nonenzymatic catalysts on thermodynamics of activation (kcal/mol, where ΔG^‡ = ΔH^‡ − TΔS^‡) [11]

In each case, the effect of the catalyst on ΔH^‡ is favorable (green), but its effect on TΔS^‡ is unfavorable (red)

Footnotes to Table 1

(1) 4-npP⁻² = 4-nitrophenyl phosphate dianion, (2) MeP⁻² = methyl phosphate dianion, (3) PLP = pyridoxal phosphate, (4) AIB = 2-aminoisobutyric acid

If the catalytic effect of a primordial enzyme were enthalpic, then the rate enhancement that it produced would have increased as the environment cooled (Fig. 7b), quite apart from any benefits conferred by mutation and natural selection. It may therefore be of historical interest that, with the notable exception of the peptidyl transferase site of the ribosome (see below), most modern enzymes resemble α-glycosidase (Fig. 6) in that the enthalpy of activation (ΔH^‡) is much less positive for the enzyme reaction than for the uncatalyzed reaction. For a randomly chosen set of enzymes catalyzing the cleavage of bonds of seven different types, the value of ΔH^‡ associated with k _cat is reduced by ~16 kcal/mol [11]. Such a catalyst produces a 300-fold larger rate enhancement at 25° than at 100 °C. If k _cat/K _m (or transition state affinity) is considered, that effect becomes even more pronounced because K _m values tend to increase with increasing temperature.

In the exceptional case of the peptidyl transferase center of the ribosome, which produces only a modest rate enhancement (10⁷-fold), catalysis is achieved entirely by rendering the entropy of activation more favorable. Indeed, the ribosome actually renders the enthalpy of activation less favorable [20, 21]. The dominance of entropy in this case appears to be in keeping with the relative importance of substrate specificity, rather than rate enhancement, in the function of the ribosome.

It seems reasonable to infer that the enthalpic basis of catalysis by most modern enzymes may reflect their origin in more primitive catalysts for which a reduction of ΔH^‡ (rather than an increase in TΔS^‡) offered a selective advantage in a gradually cooling environment. The means by which that was accomplished would have varied from case to case, but typically involves the formation of new electrostatic and hydrogen bonds in the transition state [16].