Joint Modeling Approach for Semicompeting Risks Data with Missing Nonterminal Event Status

Abstract

Semicompeting risks data, where a subject may experience sequential non-terminal and terminal events, and the terminal event may censor the non-terminal event but not vice versa, are widely available in many biomedical studies. We consider the situation when a proportion of subjects’ non-terminal events is missing, such that the observed data become a mixture of “true” semicompeting risks data and partially observed terminal event only data. An illness-death multistate model with proportional hazards assumptions is proposed to study the relationship between non-terminal and terminal events, and provide covariate-specific global and local association measures. Maximum likelihood estimation based on semiparametric regression analysis is used for statistical inference, and asymptotic properties of proposed estimators are studied using empirical process and martingale arguments. We illustrate the proposed method with simulation studies and data analysis of a follicular cell lymphoma study.

1 Introduction

In many biomedical studies, patients may experience multiple distinct causes of failures. With competing risks data, the first occurrence of any cause censors the occurrences of all other causes. When only one of the two failure causes (terminal) can censor the other but not vice versa, the risks are called semicompeting (Fine et al, 2001). Semicompeting risks data is more informative than competing risks data. An example of semicompeting risks data involves time to disease progression (non-terminal event) and mortality (terminal event).

When non-terminal event can be missing, different underlying models may lead to seemingly identical competing risks observations. The observation of terminal event such as death is usually well defined and objective. However, absence of non-terminal event may be interpreted as right censoring when the event has not occurred yet, or left censoring when the non-terminal event occurred but was not registered. Further, upon absence of the non-terminal event it may be unknown which of the two possibilities takes place. In cancer, recurrence or progression and death often represent semicompeting risks data. Here disease progression may be established through a series of clinical and/or radiologic measurements. Observation of such non-terminal events may be missing (unobserved) dependent on what procedures are performed and how they are registered in the database. As a result, an unknown proportion of subjects may have their non-terminal events occurred but unobserved, such that the observed semicompeting risks data become a mixture of “true” semicompeting risks data and terminal event only data with unknown non-terminal event status. This situation may occur by design when a mortality database that does not have recurrence information is combined with a clinical dataset where such information is partially or fully available.

Because non-terminal and terminal events are usually driven by the same disease and thus correlated, censoring of the non-terminal event by the terminal event is informative. Ignoring the dependent censoring structure or the association may lead to biased estimation or efficiency loss (Zheng and Klein, 1995; Huang and Zhang, 2008).

Understanding the association between the events is interesting in itself as an important component of the disease natural history useful in prognostic and therapeutic studies. Learning about the disease natural history through an observation of a non-terminal event and adapting treatment to this knowledge is an interesting problem.

In statistical literature, semicompeting risks have been addressed in a semiparametric instead of a fully nonparametric framework due to the non-identifiability issue (Peng and Fine, 2007). A copula model for the two event times has been repeatedly considered under a restriction on the upper wedge $T_1^{\ast }\le T_2^{\ast }$ of the positive quadrant, where $T_1^{\ast },T_2^{\ast }$ are potential times to non-terminal and terminal events, respectively. In the one-sample setting, Fine et al (2001) proposed a semiparametric estimation approach based on Clayton copula (Clayton, 1978), and Wang (2003) extended this framework to more general copula models. This approach has also been extended to the regression setting by postulating separate marginal regression models for non-terminal and terminal events (Peng and Fine, 2007; Hsieh et al, 2008; Chen, 2012). It is noted that all of these models proceed from latent failure times and are similar in spirit to the competing risks models in the same class, e.g., Fine and Gray (1999). Therefore, the interpretation of the marginal distribution of the non-terminal event in this framework is hypothetical.

Alternatively, multistate illness-death models (Kalbfleisch and Prentice, 2002; Hougaard, 2000), Figure 1, can be adopted. Associations can be incorporated through effects on transition intensity functions. Let λ_ij(t|t_i) be the intensity of transition from state i to state j, where t_i is the time spent in state i. Markov or semi-Markov illness-death models represent specific assumption on the form of λ_ij. A variety of proportional hazards (PH) models have been considered by Andersen et al (1991) and Kalbfleisch and Prentice (2002)(p.270) (Markov models); Andersen et al (2000) and Shu et al (2007) (semi-Markov models).

Fig. 1.

The three-state illness-death model

In this paper we extend the PH framework to incorporate a possibility that non-terminal event is unobserved either because it is censored or because the observation is missing, and it is generally unknown which of the two possibilities takes place.

A shared-frailty effect (Nielsen et al, 1992; Govindarajulu et al, 2011) has been a popular tool to induce positive dependence. Xu et al (2010) incorporates gamma frailty into the illness-death model to model semicompeting risks data. However, conditional specification of the model where non-terminal event affects the risk for the terminal event may be more attractive when the dependence cannot be assumed positive. Specifically we use an idea similar to so-called Markov modulated models based on intensity processes (e.g., (Kalbfleisch and Prentice, 2002) Section 9.2, (Cook and Lawless, 2007) Section 5.3) used with recurrent data analysis. This leads us to an approach similar to transformation models in survival analysis (Chen et al, 2002; Tsodikov, 2003; Chen, 2009).

Partial-likelihood-based approaches conditioning on the past history become inappropriate when the past history is not fully observable (Andersen and Keiding, 2002). Therefore our paper is based on a full likelihood approach.

The paper is organized as follows. In Section 2, we describe the illness-death model and its properties in terms of bivariate survival distributions, the data structure to be used throughout the paper, as well as the likelihood construction when missing non-terminal event is possible. The maximum likelihood estimation procedure and asymptotic properties of the estimators for regression coefficients are discussed in Section 3 and 4. We present Monte Carlo simulation studies and a data analysis of follicular cell lymphoma patients in Section 5, and conclude the article with a discussion in Section 6.

2 Model and Data Structure

2.1 Notation and Model

Let $T_1^{\ast }$ and $T_2^{\ast }$ be the potential times to non-terminal and terminal events, respectively; Z(t) be the covariate vector of dimension d; $N_1^{\ast }(t)=I(T_1^{\ast }<t)$ be the counting processes for non-terminal event. Throughout the paper, suppressing subscripts, we denote S,f and λ as survival, density and hazard functions, respectively. We define the joint distribution of $T_1^{\ast }$ and $T_2^{\ast }$ through the marginal and conditional hazard functions, respectively:

$$\begin{array}{l}{\lambda }_1(t\mid Z(t))=\underset{\mathit{\Delta }\to 0}{lim}P(T_1^{\ast }\in [t,t+\mathit{\Delta })\mid T_1^{\ast }\ge t,T_2^{\ast }\ge t,Z(t))/\mathit{\Delta }\\ =h_0(t)\eta (Z(t)),\end{array}$$ (1)

$$\begin{array}{l}{\lambda }_2(t\mid Z(t),N_1^{\ast }(t))=\underset{\mathit{\Delta }\to 0}{lim}P(T_2^{\ast }\in [t,t+\mathit{\Delta })\mid T_2^{\ast }\ge t,Z(t),N_1^{\ast }(t))/\mathit{\Delta }\\ =h_0^{\ast }(t)\theta (Z(t))\mu {(Z(t))}^{N_1^{\ast }(t)},\end{array}$$ (2)

where η(Z(t)) = e^β_ηZ(t), θ(Z(t)) = e^β_θZ(t), μ(Z(t)) = e^{β_μ0+β_μZ(t)}, and h₀, $h_0^{\ast }$ are the baseline hazard functions. For brevity, we consider time-independent covariate Z from now on, and keep in mind that the proposed model may accommodate external time-dependent Z(t) as well.

The proposed specification can be viewed as a combination of two commonly used models: 1) a Cox proportional hazard (PH) model for $T_1^{\ast }$; and 2) a Cox PH model for $T_2^{\ast }$ with the counting process for $T_1^{\ast }$ as a time-dependent covariate. Alternatively, one may view the proposed model in terms of an illness-death process (Figure 1), where λ₁ is the transition hazard between state 0 and 1 (λ₀₁), λ₂ is the path transition hazard between state 0 and 2 which may depend on whether state 1 occurs (λ₁₂) or not (λ₀₂). Furthermore, μ(Z) may be interpreted as the hazard ratio between λ₀₂ and λ₁₂, which defines the dependence between non-terminal and terminal events, as discussed in Section 1. μ(Z) = 1 corresponds to no dependence between $T_1^{\ast }$ and $T_2^{\ast }$; μ(Z) > 1 or μ (Z) < 1 represent positive or negative dependence between $T_1^{\ast }$ and $T_2^{\ast }$ the occurrence of $T_1^{\ast }$ accelerating or decelerating the occurrence of $T_2^{\ast }$.

The model (1) and (2) defines a bivariate distribution for ( $T_1^{\ast },T_2^{\ast }$) on the positive quadrant of (t₁ ≥ 0, t₂ ≥ 0). For semicompeting risks (observed) data, observations are restricted to the upper wedge 0 ≤ t₁ ≤ t₂ and are positively correlated even if the potential times are not. Following Xu et al (2010), define $T_1^{\ast }=\infty$ if terminal event occurs before non-terminal event, such that there is no probability mass in the lower wedge t₂ < t₁ < ∞. The probability model for ( $T_1^{\ast },T_2^{\ast }$) is taken to be absolutely continuous with joint density f₁(t₁, t₂) defined in the upper wedge 0 < t₁ ≤ t₂, and continuous along the line at t₁ = ∞ with density f_∞(t₂), t₂ > 0, such that ${\int }_0^{\infty }{\int }_{t_1}^{\infty }{f}_1(t_1,t_2){dt}_2{dt}_1+{\int }_0^{\infty }{f}_{\infty }(t_2){dt}_2=1$. This definition provides validity for the marginal distribution of $T_1^{\ast }$, which is not well defined in semicompeting risks data. We further denote S₁ and S_∞ as the survival functions correspond to f₁ and f_∞, respectively.

In the following we assume proportionality relationship between $T_1^{\ast }$ and $T_2^{\ast }$, i.e., $h_0=h_0^{\ast }=h$. In cancer studies this assumption can be justified through a common tumor growth process driving the risks of observed events proportional to a common baseline hazard serving as a surrogate of the growth pattern. We will discuss approaches to relax this assumption in Section 6. By denoting η = η(Z), θ = θ(Z), μ = μ(Z), μ̄ = 1 − μ, $H(t)={\int }_0^{t}h(x)dx$, and $D_k=-\frac{\partial }{\partial t_k}$ for k = 1, 2, we can subsequently derive the joint probability density functions (f) and survival functions (S) of $T_1^{\ast }$ and $T_2^{\ast }$ on the upper wedge 0 ≤ t₁ ≤ t₂ as

$$\begin{array}{l}{S}_1(t_1,t_2)=S(t_1,t_2,t_1\le t_2)=\frac{\eta \theta \mu }{\eta +\theta \overline{\mu }}\left\{\frac{e^{-H(t_1)(\eta +\theta \overline{\mu })-H(t_2)\theta \mu }}{\theta \mu }-\frac{e^{-H(t_2)(\eta +\theta )}}{\eta +\theta }\right\},\\ f_1(t_1,t_2)=D_1{D}_2{S}_1(t_1,t_2)=h(t_1)h(t_2)\eta \theta \mu e^{-H(t_1)(\eta +\theta \overline{\mu })-H(t_2)\theta \mu },\\ D_1{S}_1(t_1,t_2)=h(t_1)\eta e^{-H(t_1)(\eta +\theta \overline{\mu })-H(t_2)\theta \mu },\\ D_2{S}_1(t_1,t_2)=\frac{h(t_2)\eta \theta \mu }{\eta +\theta \overline{\mu }}\left\{e^{-H(t_1)(\eta +\theta \overline{\mu })-H(t_2)\theta \mu )}-e^{-H(t_2)(\theta +\eta )}\right\}.\end{array}$$

These model quantities are derived by integrating the densities presented in Supplemental Materials Section A. We note that the integration goes over H as an argument due to the proportionality assumption. When the subject fails before the non-terminal event occurs, i.e., t₂ < t₁ (t₁ redefined as = ∞ in this case) the probability density and survival functions are

$$f_{\infty }(t_2)=h(t_2)\theta e^{-H(t_2)(\theta +\eta )},S_{\infty }(t_2)=\frac{\theta }{\theta +\eta }{e}^{-H(t_2)(\theta +\eta )}.$$

Kendall’s τ is a popular global measure of dependence between bivariate survival times. One can show that the Kendall’s τ on the upper wedge 0 ≤ t₁ ≤ t₂ is given by:

$$\tau =4\times {\int }_0^{\infty }{\int }_0^y{S}_1(x,y)f_1(x,y)\mathit{dxdy}-1=\frac{\theta \mu }{\eta +\theta +\theta \mu }.$$

Remarkably, this measure does not depend on the baseline hazard function, a consequence of the proportionality assumption.

The crossratio function (Clayton, 1978; Oakes, 1989) is commonly used to measure the local dependence between bivariate survival times. For the upper wedge of 0 ≤ t₁ ≤ t₂, the crossratio function γ(t₁, t₂) is as follows:

$$\begin{array}{l}\gamma (t_1,t_2)=\frac{S_1(t_1,t_2)f_1(t_1,t_2)}{\{D_1{S}_1(t_1,t_2)\}\{D_2{S}_1(t_1,t_2)\}}=\frac{{\lambda }_2(t_2\mid T_1=t_1)}{{\lambda }_2(t_2\mid T_1>t_1)}=\frac{{\lambda }_1(t_1\mid T_2=t_2)}{{\lambda }_1(t_1\mid T_2>t_2)}\\ =1+\frac{\eta +\theta \overline{\mu }}{\eta +\theta }\frac{1}{e^{(H(t_2)-H(t_1))(\eta +\theta \overline{\mu })}-1}.\end{array}$$

We notice that γ(t₁, t₂) cannot be written in terms of S(t₁, t₂) alone, and thus the corresponding copula does not belong to the Archimedean class (Oakes, 1989).

2.2 Observed Data Structure and Counting Process Notation

2.2.1 Conventional Semicompeting Risks Data

Let V* be the censoring time independent of ( $T_1^{\ast },T_2^{\ast }$), given Z; ξ be the maximum follow-up time in the study. Suppose ( $T_{1i}^{\ast },T_{2i}^{\ast },V_i^{\ast }$, Z_i), i = 1, …, n are n independent and identically distributed replicates of ( $T_1^{\ast },T_2^{\ast }$, V*, Z), such that the observed semicompeting risks data for subject i, i = 1, ···, n, consists of { $T_{1i}^{\ast }$, T̃_i, ${\delta }_{ki}^{\ast },{\stackrel{\sim }{\delta }}_{2i}^{\ast }$, Z_i; k = 1, 2, 0 ≤ t ≤ ξ}, where $T_i^{\ast }=min(T_{1i}^{\ast },T_{2i}^{\ast },V_i),{\stackrel{\sim }{T}}_i=min(T_{2i}^{\ast },V_i)$ with $V_i=min(V_i^{\ast },\xi ),{\delta }_{ki}^{\ast }=I(T_i=T_{ki}^{\ast })$, k = 1, 2 are competing risks cause of failure indicators, ${\stackrel{\sim }{\delta }}_{2i}^{\ast }={\delta }_{1i}^{\ast }I({\stackrel{\sim }{T}}_i=T_{2i}^{\ast })$ is an indicator of terminal event observed after the non-terminal one, and where I(·) is the indicator function. Because 0 ≤ T_i ≤ T̃_i, the observations are restricted to the upper wedge. Furthermore, if ${\delta }_{1i}^{\ast }=0,{\delta }_{2i}^{\ast }=1,{\stackrel{\sim }{\delta }}_{2i}^{\ast }=0$, then $T_i={\stackrel{\sim }{T}}_i=T_{2i}^{\ast }$ and $T_{1i}^{\ast }=\infty$ by definition.

2.2.2 Semicompeting Risks with Missing Non-terminal Events

When non-terminal event can be unobservable (missing), the observed semi-competing risks data become a mixture of subjects whose disease history is completely or partially observed. Throughout the paper, we distinguish the observed status of one’s non-terminal event from the missing status indicator showing whether one’s non-terminal event status can be observed. The former is an observed event status (i.e., ${\delta }_1^{\ast }$); the latter is assumed to be a binary unobserved missing data indicator variable following a missing at random (MAR) mechanism (Little and Rubin, 2002). Let M_i = 1 if the non-terminal event is unobservable, and M_i = 0 if it is observable. It is natural to assume $Pr(M_i=1)=p=\frac{exp({\beta }_p)}{1+exp({\beta }_p)}$, where p is following a logistic model (or other link functions as applicable). Covariates can be easily added to this formulation. The complete data is given by ( $T_{1i}^{\ast },T_{2i}^{\ast },V_i^{\ast }$, M_i, Z_i), i = 1, …, n, n independent and identically distributed replicates of ( $T_1^{\ast },T_2^{\ast }$, V*, M, Z). The observed semicompeting risks data in presence of missing non-terminal event are similar {T_i, T̃_i, δ_ki, δ̃_2i, Z_i; k = 1, 2, 0 ≤ t ≤ ξ}, where ${\stackrel{\sim }{T}}_i=min(T_{2i}^{\ast },V_i),{\delta }_{2i}=I(T_i=T_{2i}^{\ast })$, but $T_i^{\ast },{\stackrel{\sim }{\delta }}_{1i}^{\ast },{\delta }_{2i}^{\ast }$ are modified into $T_i=min(T_{1i}^{\ast },T_{2i}^{\ast },V_i)I(M_i=0)+min(T_{2i}^{\ast },V_i)I(M_i=1),{\delta }_{1i}=I(T_i=T_{1i}^{\ast })I(M_i=0)$, and ${\delta }_{2i}={\delta }_{1i}I({\stackrel{\sim }{T}}_i=T_{2i}^{\ast })$. In other words, observing non-terminal event (δ_1i = 1) implies M_i = 0; not observing non-terminal event (δ_1i = 0) indicates either (i) non-terminal event has occurred but is unobservable (M_i = 1), or (ii) non-terminal event has not occurred yet.

In counting process notation, for subject i, let $N_{ki}^{\ast }=I(T_{ki}^{\ast }\le t)$, k = 1, 2, be the underlying counting processes for non-terminal (k = 1) and terminal (k = 2) events, Y_i(t) = I(T_i ≥ t) be the at-risk process for the first-occurring event regardless of event type, Ỹ_i(t) = I(T̃_i ≥ t > T_i) be the at-risk process for the terminal event occurring after the observed non-terminal one, and let $N_{1i}(t)={\delta }_{1i}{N}_1^{\ast }(t)$ and $N_{2i}(t)={\delta }_{2i}{N}_2^{\ast }(t)$ be the observed counting processes of the first-occurring non-terminal and terminal events, respectively, and ${\stackrel{\sim }{N}}_{2i}(t)={\int }_0^t{\stackrel{\sim }{Y}}_i(x){dN}_2^{\ast }(x)={\stackrel{\sim }{\delta }}_{2i}{N}_2^{\ast }(t)$ be the observed counting process of terminal event occurring after non-terminal event. In addition, we assume $Pr(T_1^{\ast }=T_2^{\ast })=0$.

The observed semicompeting risks data are thus expressed through the three counting processes N_1i(·),N_2i(·), Ñ_2i(·), and two corresponding at-risk processes Y_i(·), Ỹ_i(·) for subject i. By definition, N_1i(·) + N_2i(·) ≤ 1, and Ñ_2i(·) = 0 if δ_2i = 1 or M_i = 1.

2.3 Likelihood with Missing non-terminal Event Status

Following Section 2, the likelihood contribution of subject i will take one of the following four forms (where the Pr notation is informal and context dependent, and is understood as a density where appropriate):

• If both non-terminal and terminal events are observed sequentially, i.e., (T_i < T̃_i, δ_1i = 1, δ_2i = 0, δ̃_2i = 1):

  $$\begin{array}{l}{\mathcal{L}}_{1i}^{\ast }=Pr(T_{1i}^{\ast }=T_i,T_{2i}^{\ast }={\stackrel{\sim }{T}}_i,M_i=0)\\ =Pr(M_i=0)Pr(T_{1i}^{\ast }=T_i,T_{2i}^{\ast }={\stackrel{\sim }{T}}_i\mid M_i=0)\\ =(1-p)\times f_1(T_i,{\stackrel{\sim }{T}}_i)=(1-p)\times h(T_i)h({\stackrel{\sim }{T}}_i){\eta }_i{\theta }_i{\mu }_i{e}^{-H(T_i)({\eta }_i+{\theta }_i{\overline{\mu }}_i)-H({\stackrel{\sim }{T}}_i){\theta }_i{\mu }_i}.\end{array}$$
• If non-terminal event is observed, but terminal event is censored, i.e., (T_i < T̃_i, δ_1i = 1, δ_2i = 0, δ̃_2i = 0):

  $$\begin{array}{l}{\mathcal{L}}_{2i}^{\ast }=Pr(T_{1i}^{\ast }=T_i,T_{2i}^{\ast }\ge {\stackrel{\sim }{T}}_i,M_i=0)\\ =Pr(M_i=0)Pr(T_{1i}^{\ast }=T_i,T_{2i}^{\ast }\ge {\stackrel{\sim }{T}}_i,\mid M_i=0)\\ =(1-p)\times D_1{S}_1(t_1,t_2){\mid }_{(T_i,{\stackrel{\sim }{T}}_i)}=(1-p)\times h(T_i){\eta }_i{e}^{-H(T_i)({\eta }_i+{\theta }_i{\overline{\mu }}_i)-H({\stackrel{\sim }{T}}_i){\theta }_i{\mu }_i}.\end{array}$$
• If non-terminal event is not observed, and terminal event is observed, i.e., (T_i = T̃_i, δ_1i = 0, δ_2i = 1, δ̃_2i = 0):

  $$\begin{array}{l}{\mathcal{L}}_{3i}=Pr(T_{1i}^{\ast }<T_i,T_{2i}^{\ast }=T_i,M_i=1)+Pr(T_1^{\ast }>T_i,T_2^{\ast }=T_i)\\ =p\times D_2{S}_1(t_1,t_2){\mid }_{(0,T_i)}+f_{\infty }(T_i)\\ =p\times h(T_i)\frac{{\eta }_i{\theta }_i{\mu }_i}{{\eta }_i+{\theta }_i{\overline{\mu }}_i}\{e^{-H(T_i){\theta }_i{\mu }_i}-e^{-H(T_i)({\eta }_i+{\theta }_i)}\}+h(T_i){\theta }_i{e}^{-H(T_i)({\eta }_i+{\theta }_i)}\end{array}$$
• If neither event is observed, i.e., (T_i = T̃_i, δ_1i = 0, δ_2i = 0, δ̃_2i = 0):

  $$\begin{array}{l}{\mathcal{L}}_{4i}=Pr(T_{1i}^{\ast }\le T_i,T_{2i}^{\ast }\ge T_i,M_i=1)+Pr(T_{1i}^{\ast }\ge T_i,T_{2i}^{\ast }\ge T_i)\\ =p\times \frac{{\eta }_i}{{\eta }_i+{\theta }_i{\overline{\mu }}_i}\{e^{-H(T_i){\theta }_i{\mu }_i}-e^{-H(T_i)({\eta }_i+{\theta }_i)}\}+e^{-H(T_i)({\eta }_i+{\theta }_i)}.\end{array}$$
  Note that we can alternatively express ${\mathcal{L}}_{1i}^{\ast }$ and ${\mathcal{L}}_{2i}^{\ast }$ as

  $$\begin{array}{l}{\mathcal{L}}_{1i}^{\ast }=Pr(T_{1i}^{\ast }=T_i,T_{2i}^{\ast }={\stackrel{\sim }{T}}_i,M_i=0)={\mathcal{L}}_{1i}\times {\stackrel{\sim }{\mathcal{L}}}_{1i},\\ {\mathcal{L}}_{2i}^{\ast }=Pr(T_{1i}^{\ast }=T_i,T_{2i}^{\ast }\ge {\stackrel{\sim }{T}}_i,M_i=0)={\mathcal{L}}_{1i}\times {\stackrel{\sim }{\mathcal{L}}}_{2i},\end{array}$$

  where

  • ${\mathcal{L}}_{1i}=Pr(M_i=0)Pr(T_{1i}^{\ast }=T_i\mid M_i=0)=(1-p)\times h(T_i){\eta }_i{e}^{-H(T_i)({\eta }_i+{\theta }_i)}$,

  • ${\stackrel{\sim }{\mathcal{L}}}_{1i}=Pr(T_{2i}^{\ast }={\stackrel{\sim }{T}}_i\mid T_{1i}^{\ast }=T_i,M_i=0)=h({\stackrel{\sim }{T}}_i){\theta }_i{\mu }_i{e}^{-[H({\stackrel{\sim }{T}}_i)-H(T_i)]{\theta }_i{\mu }_i}$,

  • ${\stackrel{\sim }{\mathcal{L}}}_{2i}=Pr(T_{2i}^{\ast }={\stackrel{\sim }{T}}_i\mid T_{1i}^{\ast }=T_i,M_i=0)=e^{-[H({\stackrel{\sim }{T}}_i)-H(T_i)]{\theta }_i{\mu }_i}$,

  such that the contribution from non-terminal event is separated from the terminal event. Therefore, the contribution of subject i in the log-likelihood is

  $$\begin{array}{l}{\ell }_i={\delta }_{1i}{\stackrel{\sim }{\delta }}_{2i}log({\mathcal{L}}_{1i}^{\ast })+{\delta }_{1i}(1-{\stackrel{\sim }{\delta }}_{2i})log({\mathcal{L}}_{2i}^{\ast })+{\delta }_{2i}log({\mathcal{L}}_{3i})+(1-{\delta }_{i1}-{\delta }_{2i})log({\mathcal{L}}_{4i})\\ =\{{\delta }_{1i}log({\mathcal{L}}_{1i})+{\delta }_{2i}log({\mathcal{L}}_{3i})+(1-{\delta }_{i1}-{\delta }_{2i})log({\mathcal{L}}_{4i})\}+{\delta }_{1i}\{{\stackrel{\sim }{\delta }}_{2i}log({\stackrel{\sim }{\mathcal{L}}}_{1i})+(1-{\stackrel{\sim }{\delta }}_{2i})log({\stackrel{\sim }{\mathcal{L}}}_{2i})\}.\end{array}$$ (3)

Using notation ℓ_1i = δ_1i log( ) + δ_2i log( ) + (1 − δ_i1 − δ_2i) log( ), ℓ_2i = δ_1i{δ̃_2i log( 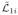) + (1 − δ̃_2i) log( )}, and ${\ell }_1={\sum }_{i=1}^n{\ell }_{1i},{\ell }_2={\sum }_{i=1}^n{\ell }_{2i}$, we can write the full log-likelihood as

$$\ell =\sum _{i=1}^n{\ell }_i=\sum _{i=1}^n\{{\ell }_{1i}+{\ell }_{2i}\}={\ell }_1+{\ell }_2.$$

Such likelihood partition can be easily recognized from the illness-death model formulation, where ℓ₁ corresponds to the contributions from first-occurring events (a competing risks type likelihood), and ℓ₂ corresponds to the additional likelihood contributions from the terminal events if the preceding non-terminal events are observed.

3 Nonparametric Maximum Likelihood Estimation

3.1 Martingale Theory

Let us denote β = (β_η, β_θ, β_μ0, β_μ, β_p) and the full parameter set Ω = (β, H(·)), where β is finite-dimensional and H(·) is the infinite-dimensional parameter. Using the NPMLE approach, we treat H(·) as a nondecreasing step function with jumps dH only at the time points where events are observed (Tsodikov, 2003; Zeng and Lin, 2006; Chen, 2009). Therefore {dH} is viewed as the collection of the jump sizes of H at the observed event times.

The following martingales (at the true model) can be constructed based on observed counting processes with respect to filtration

$$\mathcal{F}(t-)=\sigma \{N_{1i}(x),N_{2i}(x),{\stackrel{\sim }{N}}_{2i}(x),Y_i(x),{\stackrel{\sim }{Y}}_i(x),Z_i:x\in [0,t),i=1,\cdots ,n\},$$

$$\begin{array}{l}{dM}_{ki}(t)={dN}_{ki}(t)-Y_i(t){\mathit{\Theta }}_{ki}(H(t),\beta )dH(t),k=1,2,\\ d{\stackrel{\sim }{M}}_{2i}(t)=d{\stackrel{\sim }{N}}_{2i}(t)-{\stackrel{\sim }{Y}}_i(t){\stackrel{\sim }{\mathit{\Theta }}}_{2i}(\beta )dH(t),\end{array}$$

where

• ${\mathit{\Theta }}_{1i}(H(t);\beta )=\frac{(1-p)\times {\eta }_i{e}^{-H(t)({\eta }_i+{\theta }_i)}}{p\times \frac{{\eta }_i}{{\eta }_i+{\theta }_i{\overline{\mu }}_i}\{e^{-H(t){\theta }_i{\mu }_i}-e^{-H(t)({\eta }_i+{\theta }_i)}\}+e^{-H(t)({\eta }_i+{\theta }_i)}}$,

• ${\mathit{\Theta }}_{2i}(H(t);\beta )=\frac{p\times \frac{{\eta }_i{\theta }_i{\mu }_i}{{\eta }_i+{\theta }_i{\overline{\mu }}_i}\{e^{-H(t){\theta }_i{\mu }_i}-e^{-H(t)({\eta }_i+{\theta }_i)}\}+e^{-H(t)({\eta }_i+{\theta }_i)}}{p\times \frac{{\eta }_i}{{\eta }_i+{\theta }_i{\overline{\mu }}_i}\{e^{-H(t){\theta }_i{\mu }_i}-e^{-H(t)({\eta }_i+{\theta }_i)}\}+e^{-H(t)({\eta }_i+{\theta }_i)}}$,

• Θ̃_2i(β) = θ_iμ_i.

Θ_ki(H(t); β), k = 1,2 and Θ̃_2i(β) can be derived through the following probabilistic argument,

$$\begin{array}{l}E\{{dN}_{ki}(t)\mid {\mathcal{F}}_i(t-)\}=Y_i(t)Pr({dN}_{ki}(t)=1\mid Y_i(t)=1)=Y_i(t){\mathit{\Theta }}_{ki}(H(t);\beta )dH(t),\\ E\{d{\stackrel{\sim }{N}}_{2i}(t)\mid {\mathcal{F}}_i(t-)\}={\stackrel{\sim }{Y}}_i(t)Pr(d{\stackrel{\sim }{N}}_{2i}(t)=1\mid {\stackrel{\sim }{Y}}_i(t)=1)={\stackrel{\sim }{Y}}_i(t){\stackrel{\sim }{\mathit{\Theta }}}_{2i}(\beta )dH(t),\end{array}$$

where k = 1,2, and

$$\begin{array}{l}Pr({dN}_{1i}(t)=1\mid Y_i(t)=1)=\frac{Pr(T_{1i}^{\ast }=t,T_{2i}^{\ast }\ge t,M_i=0)}{Pr(T_1^{\ast }\le t,T_2^{\ast }\ge t,M_i=1)+Pr(T_1^{\ast }\ge t,T_2^{\ast }\ge t)},\\ Pr({dN}_{2i}(t)=1\mid Y_i(t)=1)=\frac{Pr(T_1^{\ast }<t,T_2^{\ast }=t,M_i=1)+Pr(T_1^{\ast }>t,T_2^{\ast }=t)}{Pr(T_1^{\ast }\le t,T_2^{\ast }\ge t,M_i=1)+Pr(T_1^{\ast }\ge t,T_2^{\ast }\ge t)},\\ Pr(d{\stackrel{\sim }{N}}_{2i}(t)=1\mid {\stackrel{\sim }{Y}}_i(t)=1)=\frac{Pr(T_{1i}^{\ast }=t^{\ast },T_{2i}^{\ast }=t,M_i=0)}{Pr(T_{1i}^{\ast }=t^{\ast },T_{2i}^{\ast }\ge t,M_i=0)}.\end{array}$$

3.2 Score Function and Estimating Equation

For any functional J that depends on the path H̄ (x) of the function H(y), y ∈ [0, x], define a derivative as

$$\frac{\partial J(\overline{H}(x))}{\partial dH(t)}={\frac{dJ(\overline{H}(x)+a\times f)}{da}|}_{a=0,f=1(y-t)},$$

where 1(x) = 1 when x ≥ 0 and 0 otherwise, and the function f(y) = 1(y − t) serves as a direction of perturbation of the argument of J. For example, using this definition $\frac{\partial H(x)}{\partial dH(t)}=1(x-t),\frac{\partial dH(x)}{\partial dH(t)}=d1(x-t)={\delta }_D(x-t)dx$, where δ_D is a Dirac’s delta function representing a limit of normal density when variance approaches zero. Suppose now that $J(\overline{H}(\tau ))={\int }_0^{\tau }\phi (H(x))dH(x)$, where φ(y) is a differentiable function of its argument. Differentiating J as a composite functional gives

$$\frac{\partial J(\overline{H}(\tau ))}{\partial dH(t)}=I(t<\tau ){\int }_t^{\tau }{\phi }^{\prime }(H(x))dH(x)+\phi (H(t)).$$

Also this definition of the functional derivative corresponds to taking a derivative with respect to a jump of H at time t if H is a step-function.

Denote the functional derivative with respect to {dH(t)} and β of Θ_ki(H(t); β) and Θ̃_2i(β) as:

$$\begin{array}{l}{\mathit{\Theta }}_{ki,H}(H(t);\beta )=\partial {\mathit{\Theta }}_{ki}(H(t);\beta )/\partial dH(t),\\ {\mathit{\Theta }}_{ki,\beta }(H(t);\beta )=\partial {\mathit{\Theta }}_{ki}(H(t);\beta )/\partial \beta ,{\stackrel{\sim }{\mathit{\Theta }}}_{2,i\beta }(\beta )=d{\stackrel{\sim }{\mathit{\Theta }}}_{2i}(\beta )/d\beta \end{array}$$

In order to link the martingales M_ki(t) and M̃_2i(t) with the likelihood, we note that the denominator of Θ_ki(H(t); β), k = 1,2 represents the probability of neither of the events occurring by the time t in the presence of the missing data mechanism (compare to the contribution ). As this is a survival function, we can express it through the respective cumulative hazard as

$$p\times \frac{{\eta }_i}{{\eta }_i+{\theta }_i{\overline{\mu }}_i}\{e^{-H(t){\theta }_i{\mu }_i}-e^{-H(t)({\eta }_i+{\theta }_i)}\}+e^{-H(t)({\eta }_i+{\theta }_i)}=exp\left\{-{\int }_0^t\sum _{k=1}^2{\mathit{\Theta }}_{ki}(H(x);\beta )dH(x)\right\}.$$

Applying this expression to the terms of the log-likelihood ℓ = ℓ₁ + ℓ₂ in Section 2.3, and moving to the counting process notation, we get the compact counting process forms

$${\ell }_1=\sum _{i=1}^n\sum _{k=1}^2\left\{{\int }_0^{\xi }[log\mathit{dH}(x)+log{\mathit{\Theta }}_{ki}(H(x);\beta )]{dN}_{ki}(x)-Y_i(x){\mathit{\Theta }}_{ki}(H(x);\beta )dH(x)\right\}$$ (4)

$${\ell }_2=\sum _{i=1}^n\left\{{\int }_0^{\xi }[log\mathit{dH}(x)+log{\stackrel{\sim }{\mathit{\Theta }}}_{2i}(\beta )]d{\stackrel{\sim }{N}}_{2i}(x)-{\stackrel{\sim }{Y}}_i(x){\stackrel{\sim }{\mathit{\Theta }}}_{2i}(\beta )dH(x)\right\},$$ (5)

By taking derivative of the re-expressed log-likelihood with respect to {dH} using the differentiation rules defined above, we obtain the following score function for H(t):

$$U_{H(t)}=\sum _{i=1}^n{\int }_0^t\{\sum _{k=1}^2[{dN}_{ki}(x)-Y_i(x){\omega }_{ki}(\overline{H}(\xi ),x;\beta ){\mathit{\Theta }}_{ki}(H(x);\beta )dH(x)]+d{\stackrel{\sim }{N}}_{2i}(x)-{\stackrel{\sim }{Y}}_i(x){\stackrel{\sim }{\mathit{\Theta }}}_{2i}(\beta )dH(x)\},$$ (6)

where

$${\omega }_{ki}(\overline{H}(\xi ),t;\beta )=1-\frac{{\int }_{t+}^{\xi }{\psi }_{ki}(H(x);\beta ){dM}_{ki}(x)}{{\mathit{\Theta }}_{ki}(H(t);\beta )};{\psi }_{ki}(H(t);\beta )=\frac{\partial log{\mathit{\Theta }}_{ki}(H(t);\beta )}{\partial dH(y)}=\frac{{\mathit{\Theta }}_{ki,H}(H(t);\beta )}{{\mathit{\Theta }}_{ki}(H(t);\beta )},y<t.$$

We note that ω is a functional of H that invokes its full path H̄(ξ). The score function for β is

$$U_{\beta }=\sum _{i=1}^n{\int }_0^{\xi }\{\sum _{k=1}^2\left[\frac{{\mathit{\Theta }}_{ki,\beta }(H(x);\beta )}{{\mathit{\Theta }}_{ki}(H(x);\beta )}{dN}_{ki}(x)-Y_i(x){\mathit{\Theta }}_{ki,\beta }(H(x);\beta )dH(x)\right]\frac{{\stackrel{\sim }{\mathit{\Theta }}}_{2i,\beta }(\beta )}{{\stackrel{\sim }{\mathit{\Theta }}}_{i2}(\beta )}d{\stackrel{\sim }{N}}_{2i}(x)-{\stackrel{\sim }{Y}}_i(x){\stackrel{\sim }{\mathit{\Theta }}}_{2i,\beta }(\beta )dH(x)\}.$$ (7)

Solutions to the above estimating equations (6) and (7) set to zero, gives an NPMLE of {dĤ} and β̂.

The NPMLE is obtained by maximizing the log-likelihood ℓ, or equivalently, solving the system of score functions (6) and (7). Note that the pro- posed method is semiparametric and thus the dimension of the parameter Ω = (β, {dH}) is of the same order as the sample size. We can write the NPMLE of H based on U_H(t) as

$$\begin{array}{c}\widehat{H}(t)=\sum _{i=1}^n{\int }_0^t\frac{{\sum }_{k=1}^2{dN}_{ki}(x)+d{\stackrel{\sim }{N}}_{2i}(x)}{S_0(\overline{H}(\xi ),x;\beta )},\text{where}\\ S_0(\overline{H}(\xi ),x;\beta )={\sum }_{i=1}^n\left[{\sum }_{k=1}^2{Y}_i(t){\omega }_{ki}(\overline{H}(\xi ),t;\beta ){\mathit{\Theta }}_{ki}(H(t);\beta )+{\stackrel{\sim }{Y}}_i(t){\stackrel{\sim }{\mathit{\Theta }}}_{2i}(\beta )\right].\end{array}$$ (8)

Note that Ĥ can viewed as a weighted Breslow-type estimator (Breslow, 1975), and has a close connection to the estimator proposed by Chen (2009) for semiparametric transformation models. The weights ω_ki have unit expectation at the true model parameters by martingale properties of score function. Therefore, maximization of the likelihood with respect to H can be done by an iterative reweighting algorithm (Chen, 2009). Given β, starting with initial weights ω⁽⁰⁾ = 1 and initial values dH⁽⁰⁾(t) (for example based on the Nelson-Aalen estimator), we repeat the following steps until convergence:

1. Fix weights ω^(k) and solve the estimating equation (8) and obtain the solution H^(k+1). The weights being fixed, $S_0^{\omega }$ in (8) only depends on the current value H(t) rather than its full path, and the problem of solving for H is recurrent where a value of H for the next point of jump is found by solving a univariate algebraic equation, the solutions for all previous jumps available from the previous steps.

2. Update weights ω^(k+1) using H^(k+1).

By replacing dH(t) and H(t) in the loglikelihood by the point of convergence dĤ (t) and Ĥ(t) of the above procedure, we obtain the profile likelihood ℓ_pr(β) that can be maximized by conventional finite-dimensional methods.

4 Asymptotic Properties

We use a combination of empirical process and martingale theory following a general line of (Zeng and Lin, 2007, 2010; Chen, 2009, 2010).

Regularity conditions are listed in the Supplemental Materials Section C. Based on the score functions (6) and (7), we can write the score equations for Ω = (β, {dH}) in martingale form

$$U_{\beta }=\sum _{i=1}^n{\int }_0^{\xi }\left\{\sum _{k=1}^2\frac{{\mathit{\Theta }}_{ki,\beta }(H(x);\beta )}{{\mathit{\Theta }}_{ki}(H(x);\beta )}{dM}_{ki}(x)+\frac{{\stackrel{\sim }{\mathit{\Theta }}}_{2i,\beta }(\beta )}{{\stackrel{\sim }{\mathit{\Theta }}}_{2i}(\beta )}d{\stackrel{\sim }{M}}_{2i}(x)\right\},$$ (9)

and

$$U_{H(t)}=\sum _{i=1}^n{\int }_0^t\left\{\sum _{k=1}^2\left[{dM}_{ki}(x)+{\int }_{x^{+}}^{\xi }[{\psi }_{ki}(H(u);\beta ){dM}_{ki}(u)]dH(x)\right]+d{\stackrel{\sim }{M}}_{2i}(x)\right\}.$$

After exchanging the integration over u and x, it is not difficult to show:

$$U_{H(t)}=\sum _{i=1}^n{\int }_0^{\xi }\left\{\sum _{k=1}^2{\epsilon }_{ki}(u,t;\beta ,H){dM}_{ki}(u)+I(u\le t)d{\stackrel{\sim }{M}}_{2i}(u)\right\},$$ (10)

where ε_ki(u, t; β,H) = I(u ≤ t)+ ϕ_ki(H(u); β)H(u ∧ t). As we show in the Supplementary Materials Section B, the linear transform ${\int }_0^{\xi }{\epsilon }_{ki}(u,t;\beta ,H){dM}_{ki}(u)$ and ${\int }_0^{\xi }I(u\le t)d{\stackrel{\sim }{M}}_{2i}(x)$ is a martingale when ε_ki(u, t; β,H) does not depend on t for u ≤ t as is the case here. Therefore, the score functions U_β and U_H(t) are both martingales under the true model.

In the following we present the consistency and weak convergence results for the proposed NPMLE Ω̂ = (β̂, Ĥ (t)) with details given in the Supplementary Materials Section C.

Theorem 1 Assuming regularity conditions hold, with probability one, β̂ converges to β⁰, Ĥ(t) converges to H⁰(t) uniformly in the interval [0, ξ], where H⁰(t), β⁰ are the true values of H(t), β.

Consider a linear functional

$$n^{1/2}\left\{a^T(\widehat{\beta }-{\beta }^0)+{\int }_0^{\xi }b{(t)}^{T}d(\widehat{H}(t)-H^0(t))\right\},$$ (11)

where a is real vector, b(t) is a function with bounded total variation in [0, ξ], and let B be the vector consisting of the values of b(t) evaluated at the observed failure times corresponding to the set {dH}, and ε^T = (a^T ,B^T ). We have

Theorem 2 Assuming regularity conditions hold, n^1/2{β̂ − β⁰, Ĥ (t) − H⁰(t)} converges weakly to a zero-mean Gaussian process. In addition, nε^T ( )⁻¹ε converges in probability to the asymptotic variance-covariance function of the linear functional (11), where is the negative Hessian matrix of the observed log-likelihood function with respect to Ω̂.

For a differentiable functional F(Ω) of Ω, based on the functional delta method (Andersen et al, 1993) Section II.8), n^1/2{F(Ω̂) − F(Ω)} converges weakly to a zero-mean Gaussian process with variance-covariance function Ḟ(Ω)^T ( )⁻¹ Ḟ (Ω), where Ḟ (Ω) is the gradient of F(Ω) with respect to Ω, can be consistently estimated by n⁻¹ , with the explicit expression of is derived in the Supplementary Materials Section C.3.

5 Numerical Examples

5.1 Simulation Studies

Data on two event times $T_1^{\ast }$ and $T_2^{\ast }$ are simulated based on the marginal and conditional specifications. We consider the following true models: (i) all non-terminal events are observable (scenario I, p = 0); or (ii) 30% subjects’ non-terminal events are unobservable due to the MAR missingness mechanism (scenario II, p = 0.3). For scenario II, it is important to distinguish that while 30% subjects’ non-terminal events are unobservable, the actual observed non-terminal event proportion may vary depending on the censoring distribution. Both scenarios assume a common baseline hazard h(t) = 0.1, with two covariates Z₁ and Z₂ included in regression models of $T_1^{\ast }$ and $T_2^{\ast }$, where Z₁ is generated from a uniform distribution U(0, 1), and Z₂ is generated from a binomial distribution with a success probability of 0.5. The true logarithmic hazard ratios for $T_1^{\ast }$ and $T_2^{\ast }$ are β_η1 = 0.5, β_η2 = 1, β_θ1 = −0.5, β_θ2 = 0.5, and β_μ0 = 1, β_μ1 = 0.5, β_μ2 = 0. Under independent right censoring time from a uniform distribution U(0, 10), in scenario I, 31.1% of subjects have both non-terminal and terminal events, 14.9% only have a non-terminal event and censored terminal event, 22.6% have only a terminal event, and 31.5% have neither non-terminal nor terminal events; in scenario II, on average 30% of subjects’ non-terminal events are missing, the proportions with different types of events being 22.1%, 10.9%, 31.2%, and 35.8%, respectively. For each simulation scenario, 1,000 datasets are generated.

Under both scenarios, the simulated datasets were analyzed by the proposed method with and without accounting for missing non-terminal events (Model I and II, respectively), as well as by the Markov illness-death model based on partial likelihood (Kalbfleisch and Prentice, 2002),p.270). The performance of all these methods was assessed under sample sizes of n = 250 and n = 400. The Markov model assumes a set of baseline hazards, one for each transition intensity, λ_jk(t) = λ_jk0(t) exp(β_jkZ_j), for j < k, j = 0, 1, k = 1, 2. Compared with the Markov model, Model II is more parsimonious since it assumes proportional baseline hazards, such that (i) β_η and β_θ have same interpretations as β₀₁ and β₀₂; (ii) β_μ0 in our proposed model can be viewed as the log hazard ratio between λ₁₂₀ and λ₀₂₀; (iii) β_μ can be viewed as the interaction between Z and the occurrence of $T_1^{\ast }$, and β_μ = β₁₂ − β₀₂. For comparison purpose, β₁₂ in the Markov model is expressed in terms of β_μ based on the above relationship. In addition, β_p = logit(p) is expressed in p and the corresponding asymptotic standard deviation is obtained through Delta method.

In the computation of hazard estimators, initial values for the algorithm are taken from a Nelson-Aalen estimator. Convergence criterion was specified as the magnitude of relative improvement in the full likelihood falling below tolerance of 10⁻⁶. Tolerance for the solution of the hazard equation was taken one order of magnitude smaller (10⁻⁷) compared to the likelihood maximization over the finite-dimensional parameter vector. The computation aspects of the iterative reweighting algorithm are discussed and compared with the direct maximization approach (Zeng and Lin, 2007) in Supplementary Materials Section D.

The simulation results are summarized in Tables 1 and 2, respectively.

Table 1.

Simulation results for a model with two covariates; no missing non-terminal events except by right censoring

	Parameter
	βη1 = 0.5	βη2 = 1	βθ1 = −0.5	βθ2 = 0.5	βμ0 = 1	βμ1 = 0.5	βμ2 = 0	p = 0
	n = 250, Model I
Bias	0.052	0.039	−0.102	−0.072	−0.028	0.096	0.092	0.047
SE	0.301	0.194	0.446	0.314	0.375	0.625	0.412	0.044
ASD	0.300	0.192	0.463	0.301	0.366	0.627	0.399	0.048
CP	94.5%	94.2%	95.2%	93.7%	95.1%	94.2%	95.2%	96.2%
	n = 250, Model II
Bias	−0.011	0.005	−0.019	−0.010	−0.009	0.003	0.021	-
SE	0.307	0.192	0.406	0.273	0.376	0.606	0.373	-
ASD	0.288	0.184	0.391	0.257	0.354	0.565	0.358	-
CP	93.7%	93.4%	93.7%	93.3%	94.0%	93.5%	93.7%	-
	n = 250, Markov Model
Bias	0.017	0.013	−0.006	0.000	-	−0.006	0.009	-
SE	0.341	0.204	0.489	0.298	-	0.653	0.397	-
ASD	0.329	0.199	0.487	0.285	-	0.638	0.384	-
CP	94.8%	94.8%	94.6%	94.7%	-	94.6%	94.1%	-
	n = 400, Model I
Bias	0.050	0.029	−0.086	−0.061	−0.017	0.087	0.069	0.043
SE	0.227	0.153	0.357	0.236	0.282	0.481	0.304	0.037
ASD	0.236	0.151	0.364	0.233	0.285	0.491	0.309	0.036
CP	94.8%	94.4%	96.0%	94.6%	95.4%	95.0%	95.2%	95.3%
	n = 400, Model II
Bias	−0.014	−0.003	−0.024	−0.008	−0.006	0.009	0.013	-
SE	0.245	0.152	0.339	0.211	0.289	0.477	0.285	-
ASD	0.226	0.145	0.307	0.202	0.276	0.441	0.280	-
CP	93.6%	93.4%	93.2%	93.6%	93.5%	92.8%	93.8%	-
	n = 400, Markov Model
Bias	0.005	0.003	0.000	0.007	-	−0.003	−0.006	-
SE	0.263	0.161	0.373	0.229	-	0.484	0.291	-
ASD	0.257	0.156	0.381	0.223	-	0.497	0.300	-
CP	94.8%	94.2%	96.0%	94.2%	-	96.2%	95.9%	-

Model I: Proposed model with missingness

Model II: Proposed model without missingness

SE: Empirical Standard Errors

ASD: Asymptotic Standard Deviations

CP: 95% Coverage Probability

Table 2.

Simulation results a model with two covariates, missing non-terminal events present

	Parameter
	βη1 = 0.5	βη2 = 1	βθ1 = −0.5	βθ2 = 0.5	βμ0 = 1	βμ1 = 0.5	βμ2 = 0	p = 0.3
	n = 250, Model I
Bias	−0.098	−0.017	0.015	−0.004	0.014	−0.044	0.022	−0.025
SE	0.382	0.249	0.632	0.383	0.497	0.862	0.525	0.127
ASD	0.394	0.254	0.605	0.367	0.475	0.835	0.509	0.131
CP	93.7%	94.8%	93.2%	94.6%	94.1%	93.8%	94.9%	93.1%
	n = 250, Model II
Bias	−0.335	−0.162	0.489	0.248	0.130	−0.462	−0.214	-
SE	0.356	0.217	0.335	0.221	0.449	0.622	0.383	-
ASD	0.325	0.210	0.343	0.222	0.411	0.597	0.373	-
CP	81.3%	87.0%	70.0%	80.4%	91.9%	87.5%	89.8%	-
	n = 250, Markov Model
Bias	−0.069	−0.100	0.250	0.199	-	−0.232	−0.174	-
SE	0.406	0.237	0.401	0.244	-	0.658	0.398	-
ASD	0.391	0.235	0.403	0.237	-	0.640	0.392	-
CP	94.8%	93.3%	91.0%	87.4%	-	92.6%	92.4%	-
	n = 400, Model I
Bias	−0.041	−0.025	0.029	0.000	0.029	−0.040	0.007	−0.016
SE	0.302	0.212	0.488	0.332	0.372	0.678	0.424	0.113
ASD	0.305	0.206	0.473	0.327	0.362	0.659	0.419	0.110
CP	94.5%	94.3%	93.7%	94.9%	94.3%	93.8%	94.8%	94.0%
	n = 400, Model II
Bias	−0.325	−0.177	0.493	0.249	0.148	−0.507	−0.224	-
SE	0.278	0.177	0.273	0.177	0.328	0.482	0.285	-
ASD	0.256	0.165	0.269	0.175	0.321	0.468	0.292	-
CP	74.5%	78.8%	54.3%	69.6%	92.1%	80.2%	88.7%	-
	n = 400, Markov Model
Bias	−0.062	−0.116	0.252	0.200	-	−0.270	−0.186	-
SE	0.314	0.194	0.301	0.194	-	0.485	0.295	-
ASD	0.308	0.185	0.316	0.186	-	0.499	0.305	-
CP	93.1%	88.4%	87.3%	80.1%	-	92.7%	91.0%	-

Model I: Proposed model with missingness

Model II: Proposed model without missingness

SE: Empirical Standard Errors

ASD: Asymptotic Standard Deviations

CP: 95% Coverage Probability

When the observed data do not contain missing non-terminal events (scenario I, Table 1), as expected, we find Model II performs best. Slight small-sample bias of the NPMLE for regression coefficients β reduces as sample size increases. The estimated mean asymptotic standard errors obtained from the observed information matrix are quite close to the empirical standard errors, and the resultant 95% confidence intervals attain appropriate coverage probabilities. We also find that the method allowing for missing non-terminal events (Model I) also achieves almost unbiased estimates, and maintains the 95% coverage probability at nominal levels, especially with large sample size of n = 400. The model with no missing non-terminal events, p = 0, in Model I gives a reasonably small bias of 0.04–0.05, considering the fact that p = 0 (logit(p) = −∞) is on the boundary of parameter space for this model. The estimates from the Markov model, while unbiased, are less efficient than results from Model II, since the more parsimonious model is correctly specified.

When missing non-terminal events (30%) are present (scenario II), our proposed method incorporating the missing mechanism (Model I) is superior. As sample size increases, we find diminishing bias of the proposed estimators, good correspondence between asymptotic standard errors and empirical standard errors, and correct 95% coverage probability at nominal levels. Neither method assuming complete data can match its performance, as expected. The Markov model allowing different baseline hazards for different transition intensities has slightly smaller bias than Model II due to its higher flexibility. Both methods ignoring missing data provide biased estimates and unreliable statistical inference.

5.2 Data Analysis

We apply the proposed method to a follicular cell lymphoma dataset collected at the Princess Margaret Hospital, Toronto, between 1967 and 1996 (Pintilie, 2006). Follicular cell lymphoma is a common type of non-Hodgkin lymphoma (NHL), a slow-growing lymphoma arising from B-cells. It mainly affects older adults with few early warning signs, and is usually difficult to cure (unlike the Hodgkin’s lymphoma). It is characterized by a relatively high cancer relapse rate even with very good response to treatment.

In this observational study cohort, 517 patients with early stage disease (I or II) were treated with either radiation alone (RT, 80.0%) or with radiation and chemotherapy (RT+CMT, 20.0%). Patients who had complete treatment response are included in the analysis. The times to cancer relapse and death are available as outcome variables, and are measured in years from the date of cancer diagnosis. Other variables assessed at the time of diagnosis include patients’ age (mean 56.6 years, sd 14.0 years) and haemoglobin level (mean 139.1 g/l, sd 15.3 g/l). The median follow-up time is 8.9 years. Among the 354 (68.5%) and 163 (31.5%) patients with stage I and II cancers, respectively, 301 (85.0%) and 113 (69.3%) were treated by RT alone (p<.0001). Two-sample t-tests find the distributions of patients’ age are significantly different between treatment groups (p=0.032) and clinical stages (p=0.0002), while the distributions of hemoglobin level are similar between treatment groups (p=0.469) and clinical stages (p=0.202).

Among the 517 patients, 162 (31.3%) had prior relapse before death, 74 (14.3%) died without a prior recorded relapse, 88 (17.0%) had relapse and were censored afterwards, and 193 (37.3%) were censored for both events. Like in many other cancer studies, it is plausible to expect that patients who died without recorded relapse or were censored for both events may have experienced a relapse that went missing.

We first fit a model for time to relapse and time to death separately: (i) a Cox PH model for time to relapse under independent censoring assumption for death; and (ii) a Cox PH model on time to death with relapse as a time-dependent covariate. The results are summarized in Table 3. The baseline covariates included for regression analysis are treatment group, clinical stage, and patients’ age (centered at its sample mean 56.6 years and standardized by its sample standard deviation 14.0 years). We find the effect of patients’ hemoglobin level at baseline is always insignificant for all methods, and there-fore it is not included in the final model. After adjusting for other covariates, separate analysis finds that stage II, older age patients treated by RT had shorter time to relapse, and those diagnosed at older age also had shorter time to death without relapse. In addition, patients with relapse prior to time t are expected to have about 10 times (HR=exp(2.33),p<.0001) the risk of dying at subsequent times as compared with a patient who has not experienced a relapse, and older patients may live longer than younger patients if both had relapse before (p=0.085). This finding suggests a strong positive association between relapse and death, as expected.

Table 3.

Results of separate Cox PH analyses, and the proposed model accounting for possibly missing relapse

Coefficients	Separate Analysis			Proposed Model
	Estimate	SE	P-value	Estimate	SE	P-value
	Time to relapse
RT vs RT+CMT	0.641	0.196	0.001	1.554	0.227	<.0001
Stage I vs II	−0.463	0.139	.0009	−0.451	0.166	0.007
Age	0.269	0.068	<.0001	0.329	0.087	<.0001
	Time to death without relapse
RT vs RT+CMT	0.219	0.351	0.533	−1.868	0.695	0.007
Stage I vs II	−0.440	0.277	0.112	−1.400	0.522	0.007
Age	1.098	0.147	<.0001	1.097	0.289	<.0001
	Time to death with relapse
Relapse	2.332	0.413	<.0001	1.634	0.315	<.0001
RT vs RT+CMT	−0.630	0.431	0.144	1.304	0.745	0.080
Stage I vs II	0.235	0.325	0.470	1.296	0.554	0.019
Age	−0.299	0.173	0.085	−0.373	0.310	0.229
Prob. of missing relapse	-	-	-	0.295	0.036	<.0001

Our proposed illness-death models taking account of missing relapse was applied to the follicular cell lymphoma dataset (Table 3). We estimated that, among all patients who had experienced cancer relapse, 29.5% (se=3.6%,p<.0001) were not recorded as relapsed. With this important correction to the observed semicompeting risks data, we find that cancer relapse is positively associated with death, as the risk of death for a patients with prior relapse is about 5 times that of a patient without relapse (HR=exp(1.634),p<.0001). Compared with the other models, not only our model finds similar effects of clinical stage, patient’s age, a stronger effect of treatment on time to relapse, but also concludes that stage I, younger patients receiving RT lived longer if they did not have relapse. Furthermore, a patient with stage I cancer and prior relapse is expected to die sooner (p=0.019). This result is not surprising, as many early-stage cancers become more aggressive and lethal once they relapse. In fact, our alternative analysis of time to death using a Cox PH model with relapse as a time-dependent covariate also suggests a similar but insignificant finding (p=0.470).

One important feature of our proposed joint model for semicompeting risks data is a measure of dependence between times to relapse and death based on covariate-specific Kendall’s τ (Figure 2). The estimated Kendall’s τ from Model I and Model II show similar trends but are otherwise slightly different. Older patients, except for those stage II patients who received RT+CMT, tend to have stronger dependence between relapse and death; stage II patients who received RT+CMT seem to have the strongest dependence among all patients.

Fig. 2.

Estimated Kendall’s τ. Model I: accounting for possibly missing relapse; Model II: assuming no missing relapse except due to censoring

In summary, our proposed method is in general agreement with separate analyses identified additional significant covariate effects. In particular, our proposed model supports a positive correlation between relapse and death, especially for stage I patients. Based on our simulation results in Section 5.1, the nontrivial proportion of unobserved patients’ relapse status (29.5%) was estimated. Failing to recognize missing relapses may lead to diluted covariate effects and misleading biased estimates.

6 Discussion

We have developed an illness-death model for semicompeting risks that recognizes that an unknown proportion of non-terminal events may be missing at random (left censored) rather than right censored, if not observed prior to death or a censoring event. The inherent difficulty on top of the semicompeting risks problem is that, both the time to non-terminal event and its status may be unobserved in this situation. In addition to offering a general treatment for the missingness of non-terminal event, the proposed illness-death model incorporates positive and negative dependence between non-terminal and terminal events. Dependent censoring issues were taken into account by the proposed joint model in a natural way.

Time to non-terminal event may be viewed as a mixture of exact, left and right censored data with partially missing status and dependent censoring. The PH assumption of common baseline hazard allowed a methodology similar to the one used with transformation models avoiding irregular convergence rates of current status data. The same assumption of proportionality between hazards for non-terminal and terminal events yielded close-form expressions for the model and likelihood contributions facilitating an explicit evaluation of the properties of the model such as measures of local and global dependence.

The conventional methodology for Markov multistate models, including illness-death models and progressive multistate models, are mainly based on partial likelihood. While these methods are flexible in analyzing multiple outcome data like semicompeting risks and recurrent event data, limited research has been conducted to address the situations when states are not always observable.

One advantage of our proposal is that the score functions retain a martingale structure, such that the martingale central limit theorems can be used to establish weak convergence. Empirical processes (a Glivenko-Cantelli argument) and functional differentiation are used to establish uniform law of large numbers implying consistency.

Relaxing the missing at random assumption does not appear to be difficult if an alternative model for the missing data mechanism is identified.

Under the proportional hazards assumption between the non-terminal and terminal risks, even if the non-terminal event is never observed (p=1), the model remains identifiable. Identifiability conditions can be expressed as an intergo-differential equation with the cumulative incidence of terminal event on the one side and its model-based counterpart on the other side. Uniqueness of solution can be guaranteed by regularity conditions for such equations. With non-terminal event unobservable, it represents a frailty variable whose distribution is parameterized by the same hazard H. Formal identifiability result can then be established similar to how this is done with univariate frailty models. By implication, a more informative partially observable non-terminal event setting will keep the model identifiable.

The PH assumption can be relaxed without altering the basic framework of this paper by linking the baseline hazards for the terminal and non-terminal events using a parametric transformation. While we can justify the PH assumption using mechanistic models of cancer, for other diseases models parameterized by two infinite dimensional parameters represent an interesting issue for future research.

Fig. 3.

Precision of likelihood maximization by the computation time (precision is measured as the L2 norm of the difference between the limiting value of the likelihood as the tolerances tend to −∞ and the maximal likelihood value achieved under a stopping rule): Iterative Reweighting (IW), Direct Maximization (DM)

Fig. 4.

Numerical efficiency by different sample sizes at tolerance level 1e-6: Iterative Reweighting (IW), Direct Maximization (DM) 28 Chen Hu, Alex Tsodikov