An Elegant Algorithm for the Construction of Suffix Arrays

Abstract

The suffix array is a data structure that finds numerous applications in string processing problems for both linguistic texts and biological data. It has been introduced as a memory efficient alternative for suffix trees. The suffix array consists of the sorted suffixes of a string. There are several linear time suffix array construction algorithms (SACAs) known in the literature. However, one of the fastest algorithms in practice has a worst case run time of O(n²). The problem of designing practically and theoretically efficient techniques remains open.

In this paper we present an elegant algorithm for suffix array construction which takes linear time with high probability; the probability is on the space of all possible inputs. Our algorithm is one of the simplest of the known SACAs and it opens up a new dimension of suffix array construction that has not been explored until now. Our algorithm is easily parallelizable. We offer parallel implementations on various parallel models of computing. We prove a lemma on the ℓ-mers of a random string which might find independent applications. We also present another algorithm that utilizes the above algorithm. This algorithm is called RadixSA and has a worst case run time of O(n log n). RadixSA introduces an idea that may find independent applications as a speedup technique for other SACAs. An empirical comparison of RadixSA with other algorithms on various datasets reveals that our algorithm is one of the fastest algorithms to date. The C++ source code is freely available at http://www.engr.uconn.edu/~man09004/radixSA.zip.

1. Introduction

The suffix array is a data structure that finds numerous applications in string processing problems for both linguistic texts and biological data. It has been introduced in [1] as a memory efficient alternative to suffix trees. The suffix array of a string T is an array A, (|T | = |A| = n) which gives the lexicographic order of all the suffixes of T. Thus, A[i] is the starting position of the lexicographically i-th smallest suffix of T.

The original suffix array construction algorithm [1] runs in O(n log n) time. It is based on a technique called prefix doubling: assume that the suffixes are grouped into buckets such that suffixes in the same bucket share the same prefix of length k. Let b_i be the bucket number for suffix i. Let q_i = (b_i, b_i+k). Sort the suffixes with respect to q_i using radix sort. As a result, the suffixes become sorted by their first 2k characters. Update the bucket numbers and repeat the process until all the suffixes are in buckets of size 1. This process takes no more than log n rounds. The idea of sorting suffixes in one bucket based on the bucket information of nearby suffixes is called induced copying. It appears in some form or another in many of the algorithms for suffix array construction.

Numerous papers have been written on suffix arrays. A survey on some of these algorithms can be found in [2]. The authors of [2] categorize suffix array construction algorithms (SACA) into five based on the main techniques employed: 1) Prefix Doubling (examples include [1] - run time = O(n log n); [3] - run time = O(n log n)); 2) Recursive (examples include [4] - run time = O(n log log n)); 3) Induced Copying (examples include [5] - $\text{run}\text{time}=O(n\sqrt{logn})$); 4) Hybrid (examples include [6] and [7] - run time = O(n² log n)); and 5) Suffix Tree (examples include [8] - run time = O(n log σ) where σ is the size of the alphabet).

In 2003, three independent groups [7, 9, 10] found the first linear time suffix array construction algorithms which do not require building a suffix tree beforehand. For example, in [7] the suffixes are classified as either L or S. Suffix i is an L suffix if it is lexicographically larger than suffix i + 1, otherwise it is an S suffix. Assume that the number of L suffixes is less than n/2, if not, do this for S suffixes. Create a new string where the segments of text in between L suffixes are renamed to single characters. The new text has length no more than n/2 and we recursively find its suffix array. This suffix array gives the order of the L suffixes in the original string. This order is used to induce the order of the remaining suffixes.

Another linear time algorithm, called skew, is given in [9]. It first sorts those suffixes i with i mod 3 ≠ 0 using a recursive procedure. The order of these suffixes is then used to infer the order of the suffixes with i mod 3 = 0. Once these two groups are determined we can compare one suffix from the first group with one from the second group in constant time. The last step is to merge the two sorted groups, in linear time.

Several other SACAs have been proposed in the literature in recent years (e.g., [11, 12]). Some of the algorithms with superlinear worst case run times perform better in practice than the linear ones. One of the currently best performing algorithms in practice is the BP R algorithm of [12] which has an asymptotic worst-case run time of O(n²). BP R first sorts all the suffixes up to a certain depth, then focuses on one bucket at a time and repeatedly refines it into sub-buckets.

In this paper we present an elegant algorithm for suffix array construction. This algorithm takes linear time with high probability. Here the probability is on the space of all possible inputs. Our algorithm is one of the simplest algorithms known for constructing suffix arrays. It opens up a new dimension in suffix array construction, i.e., the development of algorithms with provable expected run times. This dimension has not been explored before. We prove a lemma on the ℓ-mers of a random string which might find independent applications. Our algorithm is also nicely parallelizable. We offer parallel implementations of our algorithm on various parallel models of computing.

We also present another algorithm for suffix array construction that utilizes the above algorithm. This algorithm, called RadixSA, is based on bucket sorting and has a worst case run time of O(n log n). It employs an idea which, to the best of our knowledge, has not been directly exploited until now. RadixSA selects the order in which buckets are processed based on a heuristic such that, downstream, they impact as many other buckets as possible. This idea may find independent application as a standalone speedup technique for other SACAs based on bucket sorting. RadixSA also employs a generalization of Seward’s copy method [13] (initially described in [14]) to detect and handle repeats of any length. We compare RadixSA with other algorithms on various datasets.

2. A Useful Lemma

Let Σ be an alphabet of interest and let S = s₁s₂ … s_n ∈ Σ^*. Consider the case when S is generated randomly, i.e., each s_i is picked uniformly randomly from Σ (1 ≤ i ≤ n). Let L be the set of all ℓ-mers of S. Note that |L| = n − ℓ + 1. What can we say about the independence of these ℓ-mers? In several papers analyses have been done assuming that these ℓ-mers are independent (see e.g., [15]). These authors point out that this assumption may not be true but these analyses have proven to be useful in practice. In this Section we prove the following Lemma on these ℓ-mers.

Lemma 1

Let L be the set of all ℓ-mers of a random string generated from an alphabet Σ. Then, the ℓ-mers in L are pairwise independent. These ℓ-mers need not be k-way independent for k ≥ 3.

Proof

Let A and B be any two ℓ-mers in L. If x and y are non-overlapping, clearly, Prob[A = B] = (1/σ)^ℓ, where σ = |Σ|. Thus, consider the case when x and y are overlapping.

Let P_i = s_is_i+1 … s_i+ℓ−1, for 1 ≤ i ≤ (n − ℓ + 1). Let A = P_i and B = P_j with i < j and j ≤ (i + ℓ − 1). Also let j = i + k where 1 ≤ k ≤ (ℓ − 1).

Consider the special case when k divides ℓ. If A = B, then it should be the case that s_i = s_i+k = s_i+2k = ···= s_i+ℓ; s_i+1 = s_i+k+1 = s_i+2k+1 = ···= s_i+ℓ+1; ···; and s_i+k−1 = s_i+2k−1 = s_i+3k−1 = ···= s_i+ℓ+k−1. In other words, we have k series of equalities. Each series is of length (ℓ/k) + 1. The probability of all of these equalities is ${\left(\frac{1}{\sigma }\right)}^{\ell /k}{\left(\frac{1}{\sigma }\right)}^{\ell /k}\cdots {\left(\frac{1}{\sigma }\right)}^{\ell /k}={\left(\frac{1}{\sigma }\right)}^{\ell }$.

As an example, let S = abcdefghi, ℓ = 4, k = 2, A = P₁, and B = P₃. In this case, the following equalities should hold: a = c = e and b = d = f. The probability of all of these equalities is (1/σ)²(1/σ)² = (1/σ)⁴ = (1/σ)^ℓ.

Now consider the general case (where k may not divide ℓ). Let ℓ = qk + r for some integers q and r where r < k. If A = B, the following equalities will hold: s_i = s_i+k = s_i+2k = ···= s_{i+⌊(ℓ+k−1)/k⌋k}; s_i+1 = s_i+1+k = s_i+1+2k = ···= s_{i+1+⌊(ℓ+k−2)/k⌋k}; ···; and s_i+k−1 = s_i+k−1+k = s_i+k−1+2k = ···= s_{i+k−1+⌊(ℓ/k)⌋k}.

Here again we have k series of equalities. The number of elements in the qth series is $1+\lfloor \frac{\ell +k-q}{k}\rfloor$, for 1 ≤ q ≤ k. The probability of all of these equalities is (1/σ)^x where $x={\sum }_{q=1}^k\lfloor \frac{\ell +k-q}{k}\rfloor$.

$$\begin{array}{c}x=\lfloor \frac{(q+1)k+r-1}{k}\rfloor +\lfloor \frac{(q+1)k+r-2}{k}\rfloor +\cdots +\lfloor \frac{(q+1)k}{k}\rfloor \\ +\lfloor \frac{(q+1)k-1}{k}\rfloor +\lfloor \frac{(q+1)k-2}{2}\rfloor +\cdots +\lfloor \frac{(q+1)k-(k-r)}{k}\rfloor \\ =(q+1)r+(k-r)q=kq+r=\ell .\end{array}$$

The fact that the ℓ-mers of L may not be k-way independent for k ≥ 3 is easy to see. For example, let S = abcdefgh, ℓ = 3, A = P₁, B = P₃, and C = P₄. What is Prob.[A = B = C]? If A = B = C, then it should be the case that a = c, b = d = a, b = c = e, and c = f. In other words, a = b = c = d = e = f. The probability of this happening is (1/σ)⁵ ≠ (1/σ)⁶.

Note: To the best of our knowledge, the above lemma cannot be found in the existing literature. In [16] a lemma is proven on the expected depth of insertion of a suffix tree. If anything, this only very remotely resembles our lemma but is not directly related. In addition the lemma in [16] is proven only in the limit (when n tends to ∞).

Our Basic Algorithm

Let S = s₁s₂ ···s_n be the given input string. Assume that S is a string randomly generated from an alphabet Σ. In particular, each s_i is assumed to have been picked uniformly randomly from Σ (for 1 ≤ i ≤ n). For all the algorithms presented in this paper, no assumption is made on the size of Σ. In particular, it could be anything. For example, it could be O(1), O(n^c) (for any constant c), or larger.

The problem is to produce an array A[1 : n] where A[i] is the starting position of the ith smallest suffix of S, for 1 ≤ i ≤ n. The basic idea behind our algorithm is to sort the suffixes only with respect to their prefixes of length O(log n) (bits). The claim is that this amount of sorting is enough to order the suffixes with high probability. By high probability we mean a probability of ≥ (1 − n^−α) where α is the probability parameter (typically assumed to be a constant ≥1). The probability space under concern is the space of all possible inputs.

Let S_i stand for the suffix that starts at position i, for 1 ≤ i ≤ n. In other words, S_i = s_is_i+1 ···s_n. Let P_i = s_is_i+1 ···s_i+ℓ−1, for i ≤ (n − ℓ). When i > (n − ℓ), let P_i = S_i. The value of ℓ will be decided in the analysis. A pseudocode of our basic algorithm follows.

Algorithm SA1.

Sort P1, P2, …, Pn using radix sort;

The above sorting partitions the Pi’s into buckets where equal ℓ-mers are in the same bucket;

Let these buckets be B1, B2, …, Bm where m ≤ n;

for i := 1 to m do

if |Bi| > 1 then sort the suffixes corresponding to the ℓ-mers in Bi using any relevant algorithm;

Lemma 2

Algorithm SA1 has a run time of O(n) with high probability.

Proof

Consider a specific P_i and let B be the bucket that P_i belongs to after the radix sorting step in Algorithm SA1. How many other P_j’s will there be in B? Using Lemma 1, Prob.[P_i = P_j] = (1/σ)^ℓ. This means that Prob.[∃j : i ≠ j&P_i = P_j] ≤ n(1/σ)^ℓ. As a result, Prob.[∃j : |B_j| > 1] ≤ n²(1/σ)^ℓ. If ℓ ≥ ((α + 2) log_σ n), then, n²(1/σ)^ℓ ≤ n^−α.

In other words, if ℓ ≥ ((α + 2) log_σ n), then each bucket will be of size 1 with high probability. Also, the radix sort will take O(n) time. Note that we only need to sort O(log n) bits of each P_i (1 ≤ i ≤ n) and this sorting can be done in O(n) time (see e.g., [17]).

Observation 1

We could have a variant of the algorithm where if any of the buckets is of size greater than 1, we abort this algorithm and use another algorithm. A pseudocode follows.

Algorithm SA2.

1	Sort P1, P2, …, Pn using radix sort;
	The above sorting partitions the Pi’s into buckets where equal ℓ-mers are in the same bucket;
	Let these buckets be B1, B2, …, Bm where m ≤ n;
2	if |Bi| = 1 for each i, 1 ≤ i ≤ m
3	then output the suffix array and quit;
4	else use another algorithm (let it be Algorithm SA) to find and output the suffix array;

Observation 2

Algorithm SA1 as well as Algorithm SA2 run in O(n) time on at least (1 − n^−α) fraction of all possible inputs. Also, if the run time of Algorithm SA is t(n), then the expected run time of Algorithm SA2 is (1 − n^−α)O(n) + n^−α(O(n) + t(n)). For example, if Algorithm SA is the skew algorithm [9], then the expected run time of Algorithm SA2 is O(n) (the underlying constant will be smaller than the constant in the run time of skew).

Observation 3

In general, if T (n) is the run time of Algorithm SA2 lines 1 through 3 and if t(n) is the run time of Algorithm SA, then the expected run time of Algorithm SA2 is (1 − n^−α)T (n) + n^−α(T (n) + t(n)).

The case of non-uniform probabilities

In the above algorithm and analysis we have assumed that each character in S is picked uniformly randomly from Σ. Let Σ = {a₁, a₂, …, a_σ}. Now we consider the possibility that for any s_i ∈ S, Prob.[s_i = a_j] = p_j, 1 ≤ i ≤ n; 1 ≤ j ≤ σ. For any two ℓ-mers A and B of S we can show that $\mathit{Prob}.[A=B]={\left({\sum }_{j=1}^{\sigma }{p}_j^2\right)}^{\ell }$. In this case, we can employ Algorithms SA1 and SA2 with ℓ ≥ (α + 2) log_1/P n, where $P={\sum }_{j=1}^{\sigma }{p}_j^2$.

Observation 4

Both SA1 and SA2 can work with any alphabet size. If the size of the alphabet is O(1), then each P_i will consist of O(log n) characters from Σ. If |Σ| = Θ(n^c) for some constant c, then P_i will consist of O(1) characters from Σ. If |Σ| = ω(n^c) for any constant c, then each P_i will consist of a prefix (of length O(log n) bits) of a character in Σ.

3. Parallel Versions

In this Section we explore the possibility of implementing SA1 and SA2 on various models of parallel computing.

3.1. Parallel Disks Model

In a Parallel Disks Model (PDM), there is a (sequential or parallel) computer whose core memory is of size M. The computer has D parallel disks. In one parallel I/O, a block of size B from each of the D disks can be fetched into the core memory. The challenge is to devise algorithms for this model that perform the least number of I/O operations. This model has been proposed to alleviate the I/O bottleneck that is common for single disk machines especially when the dataset is large. In the analysis of PDM algorithms the focus is on the number of parallel I/Os and typically the local computation times are not considered. A lower bound on the number of parallel I/Os needed to sort N elements on a PDM is $\frac{N}{DB}\frac{log(N/B)}{log(M/B)}$. Numerous asymptotically optimal parallel algorithms have been devised for sorting on the PDM. For practical values of N, M, D, and B, the lower bound basically means a constant number of passes through the data. Therefore, it is imperative to design algorithms wherein the underlying constants in the number of I/Os is small. A number of algorithms for different values of N, M, D, and B that take a small number of passes have been proposed in [18].

One of the algorithms given in [18] is for sorting integers. In particular it is shown that we can sort N random integers in the range [1, R] (for any R) in $(1+\nu )\frac{log(N/M)}{log(M/B)}+1$ passes through the data, where ν is a constant < 1. This bound holds with probability ≥ (1 − N^−α), this probability being computed in the space of all possible inputs.

We can adapt the algorithm of [18] for constructing suffix arrays as follows. We assume that the word length of the machine is O(log n). This is a standard assumption made in the algorithms literature. Note that if the length of the input string is n, then we need a word length of at least log n to address the suffixes. To begin with, the input is stored in the D disks striped uniformly. We generate all the ℓ-mers of S in one pass through the input. Note that each ℓ-mer occupies one word of the machine. The generated ℓ-mers are stored back into the disks. Followed by this, these ℓ-mers are sorted using the algorithm of [18]. At the end of this sorting, we have m buckets where each bucket has equal ℓ-mers. As was shown before, each bucket is of size 1 with high probability.

We get the following:

Theorem 1

We can construct the suffix array for a random string of length n in $(1+\nu )\frac{log(n/M)}{log(M/B)}+2$ passes through the data, where ν is a constant < 1. This bound holds for ≥ (1 − n^−α) fraction of all possible inputs.

3.2. The Mesh and the Hypercube

Optimal algorithms exist for sorting on interconnection networks such as the mesh (see e.g., [19] and [20]), the hypercube (see e.g., [21]), etc. We can use these in conjunction with Algorithms SA1 and SA2 to develop suffix array construction algorithms for these models. Here again we can construct all the ℓ-mers of the input string. Assume that we have an interconnection network with n nodes and each node stores one of the characters in the input string. In particular node i stores s_i, for 1 ≤ i ≤ n. Depending on the network, a relevant indexing scheme has to be used. For instance, on the mesh we can use a snake-like row-major indexing. Node i communicates with nodes i + 1, i + 2, …, i + ℓ − 1 to get s_i+1, s_i+2, …, s_i+ℓ−1. The communication time needed is O(log n). Once the node i has these characters it forms P_i. Once the nodes have generated the ℓ-mers, the rest of the algorithm is similar to the Algorithm SA1 or SA2. As a result, we get the following:

Theorem 2

There exists a randomized algorithm for constructing the suffix array for a random string of length n in O(log n) time on a n-node hypercube with high probability. The run time of [21]’s algorithm is O(log n) with high probability, the probability being computed in the space of all possible outcomes for the coin flips made. Also, the same can be done in $O(\sqrt{n})$ time on a $\sqrt{n}\times \sqrt{n}$ mesh with high probability.

Observation

Please note that on a n-node hypercube, sorting n elements will need Ω(log n) time even if these elements are bits, since the diameter of the hypercube is Ω(log n). For the same reason, sorting n elements on a $\sqrt{n}\times \sqrt{n}$ mesh will need $\mathrm{\Omega }(\sqrt{n})$ time since $2(\sqrt{n}-1)$ is the diameter.

3.3. PRAM Algorithms

In [9] several PRAM algorithms are given. One such algorithm is for the EREW PRAM that has a run time of O(log² n), the work done being O(n log n). We can implement Algorithm SA2 on the EREW PRAM so that it has an expected run time of O(log n), the expected work done being O(n log n). Details follow. Assume that we have n processors. 1) Form all possible ℓ-mers. Each ℓ-mer occupies one word; 2) Sort these ℓ-mers using the parallel merge sort algorithm of [22]; 3) Using a prefix computation check if there is at least one bucket of size > 1; 4) Broadcast the result to all the processors using a prefix computation; 5) If there is at least one bucket of size more than one, use the parallel algorithm of [9].

Steps 1 through 4 of the above algorithm take O(log n) time each. Step 5 takes O(log² n) time. From Observation 3, the expected run time of this algorithm is (1 − n^−α)O(log n) + n^−α(O(log n) + O(log² n)) = O(log n). Also, the expected work done by the algorithm is (1−n^−α)O(n log n)+n^−α(O(n log n)+ O(n log² n)) = O(n log n).

4. Practical Implementation

In this section we discuss the design and implementation of the RadixSA algorithm. The following is the pseudocode of the RadixSA algorithm:

Algorithm RadixSA.

1.	radixSort all suffixes by d characters
2.	let b[i] = bucket of suffix i
3.	for i := n down to 1 do
4.	if (b[i].size > 1) then
5.	if detectPeriods(b[i])then
6.	handlePeriods(b[i]);
7.	else radixSort all suffixes j ∈ b[i] with respect to b[j + d]

A bucket is called singleton if it contains only one suffix, otherwise it is called non-singleton. A singleton suffix is the only suffix in a singleton bucket. A singleton suffix has its final position in the suffix array already determined.

We number the buckets such that two suffixes in different buckets can be compared by comparing their bucket numbers. The for loop traverses the suffixes from the last to the first position in the text and sorts the bucket in which the current suffix resides. This order ensures that after each step, suffix i will be found in a singleton bucket. This is easy to prove by induction. Thus, at the end of the loop, all the buckets will be singletons. If each bucket is of size O(1) before the for loop is entered, then it is easy to see that the algorithm runs in O(n) time. In lines 5 and 6 we detect periodic regions of the input. This is discussed in the next section.

Even if the buckets are not of constant size (before the for loop is entered) the algorithm is still linear if every suffix takes part in no more than a constant number of radix sort operations. The order in the for loop is deceptively simple but it sorts the buckets in an order which favors quick breakdown of non-singleton buckets. Intuitively, say a pattern P = a₁a₂a₃ … a_k appears multiple times in the input. After the initial radix sort, we will have the suffixes which start with a₁ in a bucket b₁, the suffixes which start with a₂ in a bucket b₂ and so on. Assume that the initial sorting depth D is much smaller than k. If we sort these buckets in the order b₁, b₂, …, b_k most of them remain the same, except that now we know we have them sorted by at least 2D characters. On the other hand, our algorithm will sort these buckets in the order b_k, b_k−1, …, b₁. If bucket b_k separates into singleton buckets after sorting, then all the other buckets will subsequently separate into singletons. This way, every suffix in these buckets is placed in a singleton bucket at a constant cost per suffix. Due to this traversal order, in practice, our algorithm performs a small number of accesses to each suffix, as we show in the results section.

Table 4 shows an example of how the algorithm works. Each column illustrates the state of the suffix array after sorting one of the buckets. The order in which buckets are chosen to be sorted follows the pseudocode of RadixSA. The initial radix sort has depth 1 for illustration purpose. The last column contains the fully sorted suffix array.

However, the algorithm as is described above has a worst case runtime of $O(n\sqrt{n})$ (proof omitted). We can improve the runtime to O(n log n) as follows. If, during the for loop, a bucket contains suffixes which have been accessed more than a constant C number of times, we skip that bucket. This ensures that the for loop takes linear time. If at the end of the loop there have been any buckets skipped, we do another pass of the for loop. After each pass, every remaining non-singleton bucket has a sorting depth at least C + 1 times greater than in the previous round (easy to prove by induction). Thus, no more than a logarithmic number of passes will be needed and so the algorithm has worst case runtime O(n log n).

4.1. Periods

In lines 5 and 6 of the RadixSA pseudocode we detect periodic regions of the input as follows: if the suffixes starting at positions i, i − p, i − 2p, … appear in the same bucket b, and bucket b is currently sorted by d ≥ p characters, it is easy to see that we have found a periodic region of the input, where the period P is of length p. In other words, suffix i is of the form P S_i+p+1…n, suffix i − p is of the form P P S_i+p+1…n, suffix i − 2p is of the form P P P S_i+p+1…n and so on. We can easily see that these suffixes can be placed in separate buckets based on the relationship between suffixes i and i + p by the following rule. If suffix i is less than suffix i + p, then suffix i − p is less than suffix i, suffix i − 2p is less than i − p, and so on. The case where i is greater than i + p is analogous.

The depth of each bucket increases after each sorting, therefore periods of any length are eventually detected. This method can be viewed as a generalization of Seward’s copy method [13] where a portion of text of size p is treated as a single character.

4.2. Implementation Details

Radix sorting is a central operation in RadixSA. We tried several implementations, both with Least Significant Digit (LSD) and Most Significant Digit (MSD) first order. The best of our implementations was a cache-optimized LSD radix sort. The cache optimization is the following. In a regular LSD radix sort, for every digit we do two passes through the data: one to compute bucket sizes, one to assign items to buckets. We can save one pass through the data per digit if in the bucket assignment pass we also compute bucket sizes for the next round [23]. We took this idea one step forward and we computed bucket counts for all rounds before doing any assignment. Since in our program we only sort numbers of at most 64 bits, we have a constant number of bucket size arrays to store in memory. To sort small buckets we employ an iterative merge sort.

To further improve cache performance, in the bucket array we store not only the bucket start position but also a few bits indicating the length of the bucket. Since the bucket start requires ⌈log n⌉ bits, we use the remaining bits, up to the machine word size, to store the bucket length. This prevents a lot of cache misses when small buckets are the majority. For longer buckets, we store the lengths in a separate array which also stores bucket depths.

The total additional memory used by the algorithm, besides input and output, is 5n + o(n) bytes: 4n for the bucket array, n bytes for bucket depths and lengths, and a temporary buffer for radix sort.

5. Experimental Results

One of the fastest SACAs, in practice, is the Bucket Pointer Refinement (BPR) algorithm [12]. Version 0.9 of BPR has been compared [12] with several other algorithms: deep shallow [24], cache and copy by Seward [13], qsufsort [25], difference-cover [26], divide and conquer by Kim et al. [4], and skew [9]. BPR 0.9 has been shown to outperform these algorithms on most inputs [12]. Version 2.0 of BPR further improves over version 0.9. We compare RadixSA with both versions of BPR.

Furthermore, a large set of SACAs are collected in the jSuffixArrays library [27] under a unified interface. This library contains Java implementations of: DivSufSort [28], QsufSort [25], SAIS [11], skew [9] and DeepShallow [24]. We include them in the comparison with the note that these Java algorithms may incur a performance penalty compared to their C counterparts.

We tested all algorithms on an Intel core i3 machine with 4GB of RAM, Ubuntu 11.10 Operating System, Sun Java 1.6.0 26 virtual machine and gcc 4.6.1. The Java Virtual Machine was allowed to use up to 3.5 GB of memory. As inputs, we used the datasets of [12] which include DNA data, protein data, English alphabet data, general ASCII alphabet data and artificially created strings such as periodic and Fibonacci strings¹.

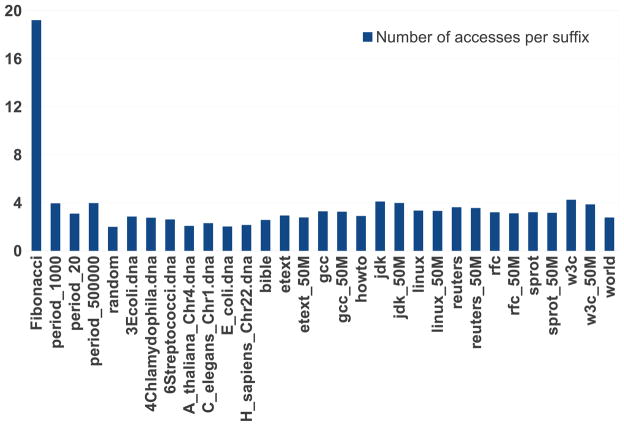
For every dataset, we executed each algorithm 10 times. The average run times are reported in table 2 where the best run times are shown in bold. Furthermore, we counted the number of times RadixSA accesses each suffix. The access counts are shown in figure 1. For almost all datasets, the number of times each suffix is accessed is a small constant. For the Fibonacci string the number of accesses is roughly logarithmic in the length of the input.

Table 2.

Comparison of run times on datasets from [12] on a 64-bit Intel CORE i3 machine with 4GB of RAM, Ubuntu 11.10 Operating System, Sun Java 1.6.0 26 and gcc 4.6.1. Run times are in seconds, averaged over 10 runs. Bold font indicates the best time. ML means out of memory, TL means more than 1 hour.

Dataset			Run time
Name	Length	|Σ|	RadixSA	BPR2	BPR.9	DivSuf Sort	QSuf Sort	SAIS	skew	Deep Shallow
Fibonacci	20000000	2	7.88	12.48	14.05	6.81	26.44	5.50	14.53	369.48
period 1000	20000000	26	2.12	3.52	5.71	3.15	20.42	6.59	23.27	TL
period 20	20000000	17	1.44	1.95	43.39	1.83	11.05	2.83	7.15	TL
period 500000	20000000	26	2.78	4.60	6.31	4.74	23.32	8.56	25.68	2844.37
random	20000000	26	2.25	3.34	4.87	6.35	5.02	11.75	22.05	5.69
3Ecoli.dna	14776363	5	2.23	2.67	3.43	4.00	13.85	6.14	19.62	433.54
4Chlamydophila.dna	4856123	6	0.61	0.67	0.90	1.71	3.24	1.93	5.24	4.80
6Streptococci.dna	11635882	5	1.63	1.79	2.38	2.88	7.08	4.98	14.88	4.26
A thaliana Chr4.dna	12061490	7	1.27	1.74	2.40	3.02	5.13	5.37	15.71	3.52
C elegans Chr1.dna	14188020	5	1.61	1.95	2.65	3.21	6.91	5.69	17.18	6.92
E coli.dna	4638690	4	0.41	0.51	0.58	1.36	1.72	1.96	5.04	1.37
H sapiens Chr22.dna	34553758	5	4.40	5.66	8.21	7.76	15.31	15.59	49.70	10.98
bible	4047391	63	0.51	0.48	0.80	1.24	1.38	1.56	4.64	1.08
etext	105277339	146	19.40	23.09	43.46	26.56	62.63	54.70	ML	119.96
etext 50M	50000000	120	8.13	9.74	17.26	11.94	26.40	24.46	88.57	79.07
gcc	86630400	150	13.84	15.58	24.50	15.84	46.20	33.62	135.12	80.78
gcc 50M	50000000	121	7.21	9.56	13.26	8.31	28.43	17.73	68.65	264.90
howto	39422104	197	5.96	6.35	10.26	8.41	17.64	16.67	64.73	16.33
jdk	69728898	113	12.07	12.54	26.86	12.74	39.92	24.66	102.76	58.22
jdk 50M	50000000	110	8.32	8.30	17.05	8.91	26.30	17.58	71.31	36.98
linux	116254720	256	19.27	19.34	29.67	21.17	61.99	44.47	ML	58.71
linux 50M	50000000	256	7.62	7.60	10.50	8.84	27.54	18.18	76.10	31.92
reuters	114711150	93	19.76	25.08	60.72	25.07	74.78	49.17	ML	87.57
reuters 50M	50000000	91	7.84	9.53	20.41	10.24	26.94	20.29	77.25	33.68
rfc	116421900	120	21.18	22.08	42.75	22.55	66.28	47.99	ML	42.14
rfc 50M	50000000	110	8.23	8.39	14.85	9.24	24.80	19.61	76.64	16.63
sprot	109617186	66	18.48	22.79	47.07	25.52	69.58	50.40	ML	48.69
sprot 50M	50000000	66	7.57	9.10	16.81	10.88	28.07	21.69	78.47	20.03
w3c	104201578	256	18.82	18.78	35.94	20.01	74.09	38.29	ML	1964.80
w3c 50M	50000000	255	7.93	8.33	17.67	8.73	25.95	17.26	71.42	36.59
world	2473399	94	0.30	0.27	0.42	0.91	0.86	0.91	2.35	0.78

Figure 1.

Average number of times RadixSA accesses each suffix, for datasets from [12].

6. Discussion and Conclusions

In this paper we have presented an elegant algorithm for the construction of suffix arrays. This algorithm is one of the simplest algorithms known for suffix arrays construction and runs in O(n) time on a large fraction of all possible inputs. It is also nicely parallelizable. We have shown how our algorithm can be implemented on various parallel models of computing.

We have also given an extension of this algorithm, called RadixSA, which has a worst case runtime of O(n log n). RadixSA uses a deceptively simple heuristic to select the order in which buckets are processed so as to reduce the number of operations performed. As a result, RadixSA performed a small number of accesses per suffix on all but one of the inputs tested (the Fibonacci string). This heuristic, together with a careful implementation designed to increase cache performance, makes RadixSA very efficient in practice.

The RadixSA heuristic could find application as an independent speedup technique for other algorithms which use bucket sorting and induced copying. For example, BPR could use it to determine the order in which it chooses buckets to be refined. A possible research direction is to improve RadixSA’s heuristic. Buckets can be processed based on a topological sorting of their dependency graph. Such a graph has at most n/2 nodes, one for each non singleton bucket, and at most n/2 edges. Thus, it has the potential for a lightweight implementation.

An interesting open problem is to devise a randomized algorithm that has a similar performance.

Table 1.

Example of suffix array construction steps for string ‘cdaxcdayca‘. b[suffix] stands for the bucket of suffix. Underlines show the depth of sorting in a bucket at a given time. The initial radix sort has depth 1 for illustration purpose.

Initial buckets	Sort b[a]	Sort b[ca]	Sort b[dayca]	Sort b[cdayca]
a	a	a	a	a
ayca	axcdayca	axcdayca	axcdayca	axcdayca
axcdayca	ayca	ayca	ayca	ayca
ca	ca	ca	ca	ca
cdayca	cdayca	cdayca	cdayca	cdaxcdayca
cdaxcdayca	cdaxcdayca	cdaxcdayca	cdaxcdayca	cdayca
dayca	dayca	dayca	daxcdayca	daxcdayca
daxcdayca	daxcdayca	daxcdayca	dayca	dayca
xcdayca	xcdayca	xcdayca	xcdayca	xcdayca
yca	yca	yca	yca	yca