Distribution of normal human left ventricular myofiber stress at end diastole and end systole: a target for in silico design of heart failure treatments

Abstract

Ventricular wall stress is believed to be responsible for many physical mechanisms taking place in the human heart, including ventricular remodeling, which is frequently associated with heart failure. Therefore, normalization of ventricular wall stress is the cornerstone of many existing and new treatments for heart failure. In this paper, we sought to construct reference maps of normal ventricular wall stress in humans that could be used as a target for in silico optimization studies of existing and potential new treatments for heart failure. To do so, we constructed personalized computational models of the left ventricles of five normal human subjects using magnetic resonance images and the finite-element method. These models were calibrated using left ventricular volume data extracted from magnetic resonance imaging (MRI) and validated through comparison with strain measurements from tagged MRI (950 ± 170 strain comparisons/subject). The calibrated passive material parameter values were C₀ = 0.115 ± 0.008 kPa and B₀ = 14.4 ± 3.18; the active material parameter value was T_max = 143 ± 11.1 kPa. These values could serve as a reference for future construction of normal human left ventricular computational models. The differences between the predicted and the measured circumferential and longitudinal strains in each subject were 3.4 ± 6.3 and 0.5 ± 5.9%, respectively. The predicted end-diastolic and end-systolic myofiber stress fields for the five subjects were 2.21 ± 0.58 and 16.54 ± 4.73 kPa, respectively. Thus these stresses could serve as targets for in silico design of heart failure treatments.

heart failure is a worldwide epidemic that contributes considerably to the overall cost of health care in developed nations. The number of people afflicted with this complex disease is increasing at an alarming pace, a trend likely to continue as the population ages and life span expands. Ventricular wall stress is an important quantity that is related to several physical processes of the heart (66), including ventricular remodeling (15). During ventricular concentric remodeling, an increase in ventricular wall stress during pressure overload is hypothesized to lead to compensatory hypertrophy, whereby an increase in systolic ventricular wall stress leads to the overall thickening of ventricular wall as myocyte width increases (16). This process translates into eventual heart failure in the case of pathological cardiac hypertrophy (32).

Since ventricular wall stress affects ventricular remodeling, which, in turn, determines the clinical course of heart failure (6), normalization of ventricular wall stress is the cornerstone of many existing and new treatments or devices for heart diseases and heart failure. These treatments include surgical ventricular restoration (SVR), which seeks to normalize left ventricular (LV) geometry (10, 40), injection of polymer-based material into ventricular wall, which seeks to augment ventricular wall thickness (38, 50), and a ventricular partitioning device, which can reduce end-diastolic (ED) ventricular myofiber stress (36, 42).

However, information is lacking about regional ventricular wall stress in normal humans that can be easily used as a target for computational studies of ventricular stress normalization. Such information can, in principle, be used to optimize the injection pattern in polymer injection-based therapies, as our laboratory described previously (64). Although the Young-Laplace law can be used to estimate the average ventricular wall stress in normal humans, it is still a largely simplified law, and its prediction differs from that of a detailed computational ventricular model that used the finite-element (FE) method (70). Moreover, it is impossible to use the Young-Laplace law to determine regional ventricular wall stress.

To bridge the gap in our knowledge of ventricular wall stress in normal humans, we used the FE method to construct computational models of the LV of five normal subjects and validated these models individually through comparison with myocardial strain measurements from tagged magnetic resonance imaging (MRI) in each subject. The primary goals of this work were to take the first step toward determining 1) a reference ED and end-systolic (ES) LV myofiber stress field that can be used as a target for ventricular wall stress normalization; and 2) a reference set of diastolic and systolic material parameters for normal humans that can be used in other computational models of the normal human LV.

MATERIALS AND METHODS

Subject-specific geometries, volumes, and strains.

Five normal human volunteers (three men and two women; age 36 ± 11 yr) were used for the study and underwent MRI with Spatial Modulation of Magnetization (SPAMM) (1, 68). This study was reviewed and approved by the University of California San Francisco review board, and subjects provided written, informed consent. Series of orthogonal short-axis and long-axis images were acquired for each subject. The short-axis images were 1.1-mm pixel size, and each short-axis slice was separated by 5 mm. The short-axis slices contained two orthogonal series of tags forming a grid. The radial long-axis slices were oriented circumferentially at an interval of 30° around the LV and contained one series of tags that was orthogonal to the ventricular long axis. The tag spacing was 6 mm in both short-axis and long-axis images.

In each subject, we used the medical images analysis software MeVisLab (http://www.mevislab.de) to extract the relaxed LV geometries in the magnetic resonance (MR) images by manually segmenting the LV endocardium and epicardium in the images that correspond to the beginning of diastole. To avoid errors in measuring volume due to ventricular motion, segmentation was performed in both short-axis and long-axis slices, starting from just below the valves to the LV apex. The segmented contours were used to reconstruct the LV endocardial and epicardial surfaces. Then a fully hexahedral FE mesh of the LV wall was constructed using the meshing software TrueGrid (http://truegrid.com). The FE mesh in each of the five LV models consisted of ∼5,000 nodes and 3,500 elements (Fig. 1). We verified that this mesh density was sufficient to achieve numerical convergence and extracted the LV endocardial surfaces from the MR images corresponding to end systole (ES) and end diastole (ED) in each subject. The ES and ED volumes (ESV and EDV, respectively) of each subject were computed from these surfaces, and these volumes were used to personalize the LV computational models, as described in the section Model personalization.

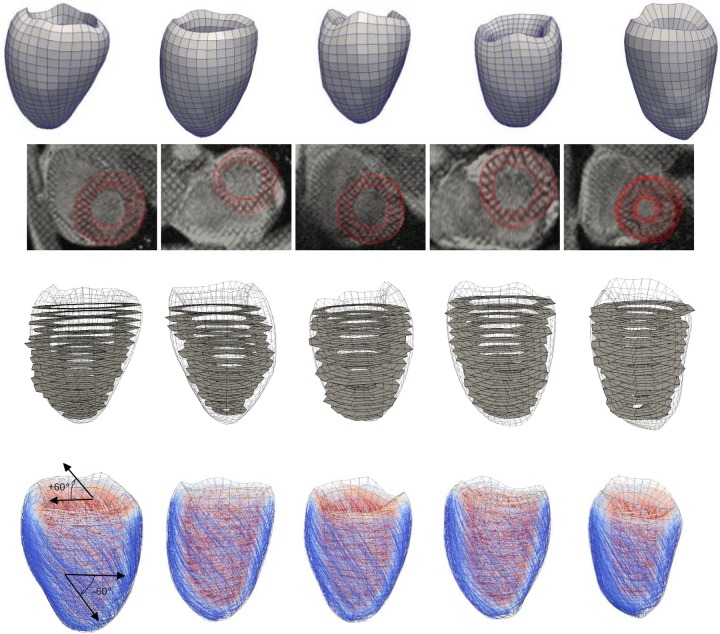
Fig. 1.

First row: subject-specific left ventricular geometries at beginning of diastole, extracted from magnetic resonance images. Second row: match between the finite-element (FE) meshes and the magnetic resonance images. Third row: two-dimensional sectors used to compute strain from the tagged magnetic resonance images, superimposed onto the three-dimensional FE meshes shown as wire frames. Fourth row: rule-based fiber orientation map (color denotes helix angle with respect to the circumferential direction when viewed from the epicardium, from −60°, blue, to +60°, red), superimposed onto the FE meshes shown as wire frames.

Last, the systolic regional strains in the LV wall of each subject were computed from the tagged MR images by semi-automatically segmenting the tag lines in the tagged MR images using the tag segmentation software FindTags (24) and then computing the deformation gradient associated with the segmented tag lines using accompanying B-spline-based motion tracking technique software (TTT; Laboratory of Cardiac Energetics, Bethesda, MD) (44, 45). Through-plane motion was accounted for by including both the short-axis and long-axis tag lines in the analysis.

FE modeling.

We used the FE method to calculate the mechanical response of the LV of each subject due to volume and pressure changes during diastole and systole. To use the FE method, one must prescribe a material law describing the myocardial stress-strain relationship and the appropriate boundary conditions.

Myofiber aggregate structure of the myocardial tissue was described using a rule-based approach (41). Based on previous histological studies (52), we assumed that the myofiber orientation can be defined by a linear variation of the fiber helix angle from +60° at epicardium to −60° at endocardium throughout the LV wall. In practice, we used the Visualization ToolKit (VTK) library (http://www.vtk.org) to assign a local myofiber orientation to each element of the FE LV models.

The material law used here has been described extensively (39, 53, 63). The key points are summarized here, and the details are given in appendix a. Briefly, two different material laws were used to account for the passive material behavior that persists in the entire cardiac cycle and the active material behavior that only occurs during systole. The passive material behavior was described using a quasi-incompressible transversely isotropic Fung law that was tailored to the myocardium by Guccione et al. (18). This law is parameterized by four parameters (C₀, b_f, b_t, b_fs) that describe the nonlinearity and the degree of anisotropy of the tissue diastolic mechanical properties. Specifically, C₀ is a scaling factor, b_f controls stiffness in the local muscle fiber direction, b_t controls stiffness in the plane perpendicular to the local myofiber direction, and b_fs controls rigidity under shearing deformation. By fixing the ratios b_f to b_t and b_fs, to values in Ref. 62, the law can be reparameterized by two independent parameters: C₀, and a factor B₀ that determines the level of nonlinearity of the stress-strain relationship (appendix a). These parameters were identified for each subject, as described in the next section. To account for the incompressibility of the myocardial tissues (due its large water content), the deformation is decomposed into its volumetric and deviatoric components. The volumetric deformation (i.e., deformation that leads to a change in volume) is constrained by imposing a high bulk-to-shear modulus ratio (26).

The active material behavior was described by a stretch-dependent active force law (19, 23). In this law, the active force is a function of the current sarcomere length, peak intracellular calcium concentration, and the time from activation. Following Ref. 57, the generated active force is orthotropic, with maximal contractile force developing in the local myofiber direction and a contractile force 40% of the maximum developing in the local sheet direction. The active force law has a single parameter T_max, which reflects the overall contractility of the myocardial tissue, and was identified for each subject as described in Model personalization, below.

In terms of model boundary conditions, the basal line was fixed to account for the rather large stiffness of the annulus compared with the myocardium itself. Mechanical loading of the LV was imposed by prescribing a change in the LV chamber volume based on the volume data acquired from MR images, as described in the previous section. Specifically, the ED and ES phases were calculated by prescribing an LV chamber volume equal to the measured EDV and ESV in each subject, respectively.

The inertial and body forces were neglected in the computation, as they can be shown (using basic dimensional analysis) to be small compared with the elastic forces internal to the LV. The FE LV models were implemented using the FE software Abaqus/Standard (http://www.3ds.com/products-services/simulia/portfolio/abaqus) with user-defined material subroutines written using the LMT++ library (13, 35). Unlike previous studies, which used explicit FE methods (39, 53, 63), we used a fully implicit solver in Abaqus/Standard. Details of the implementation and its numerical validation can be found in Ref. 12.

Model personalization.

Unlike previous studies where only a single scaling parameter C₀ was calibrated using EDV and ED pressures, and the exponential terms describing the nonlinearity of the stress-strain relationship were fixed (39, 53, 62), here we calibrated two parameters, namely, the scaling parameter C₀ and the parameter (reparameterized from the exponential terms) that defines the nonlinearity of the stress-strain relationship B₀. However, there is an infinite combination of these two parameters for each given set of EDV and ED pressure. To find a unique and subject-specific value for these two parameters, we also minimized the distance of the calculated passive pressure-volume response to that found experimentally (34), in addition to matching the measured EDV and ED pressure. Klotz et al. (34) showed that, when scaled appropriately, the LV ED pressure-volume relationship can be defined by a single curve that is independent of species and etiology.

The parameters C₀ and B₀ were determined by an optimization process that contains two intertwined loops. The first loop was used to optimize B₀ so that the distance to the “Klotz” curve was minimized, whereas the second loop (which was run at every iteration of the previous loop) was used to optimize C₀ for a given B₀, so that the calculated ED pressure matches the prescribed ED pressure at the ED phase of the computation. A normal ED pressure of 9 mmHg was used.

The single parameter T_max that defines the tissue contractility was determined sequentially for each subject once the passive material parameters C₀ and B₀ were found. In each subject, T_max was scaled accordingly, so that the calculated ES pressure matches the prescribed ES pressure at the ES phase of the computation. A normal ES pressure of 120 mmHg was used. In a recent study, our laboratory carried out a sensitivity analysis and showed that a pressure change within the normal range did not modify the study's conclusions (40).

These optimization problems were solved with Abaqus/Standard as the forward solver, and the python optimization library NL-Opt (http://ab-initio.mit.edu/wiki/index.php/NLopt) as the inverse solver. Typically, fewer than 20 iterations of the derivative-free bound optimization by quadratic approximation algorithm (47) were required to reach convergence. More details on the implementation can be found in Ref. 12.

Model validation.

To validate our modeling approach, we compared the regional strains computed from our FE model to those measured from tagged MRI. Only the core of the ventricles were considered, and not the most apical and basal regions. Since the measured MRI strains are systolic strains that were referenced to the ED configuration, whereas the FE-computed strains were referenced to the beginning of diastole configuration, we converted the computed strains into systolic strains by using the basic transformation composition principles (53).

RESULTS

Subject-specific data and models.

All results are presented here as means ± SD.

In general, the LV geometries from the reconstructed LV models at the beginning of diastole were ellipsoidal with a sphericity (defined by the short-to-long axis dimension ratio) of 74 ± 3.7% (Fig. 1). The LVs had ESV = 52 ± 12.0 ml and EDV = 117 ± 23.7 ml, and the average ejection fraction of the five LVs was 56 ± 3.95% (Fig. 2). Stroke volumes and ejection fractions were in the normal range for healthy humans (46).

Fig. 2.

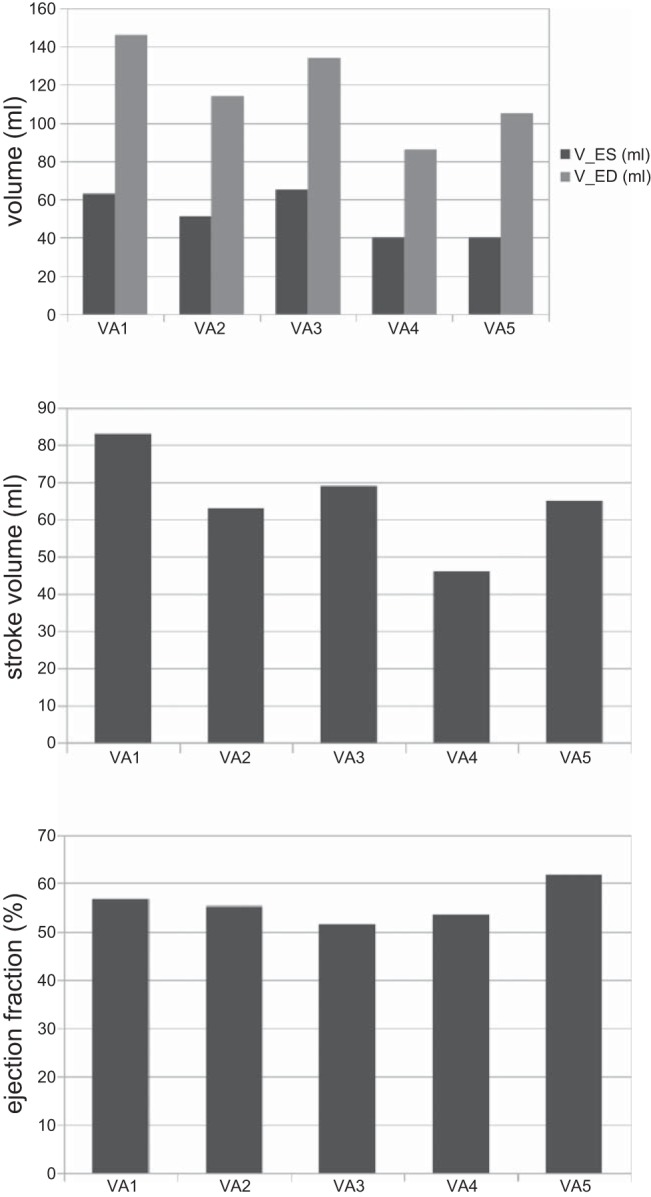
Top: end-systole (V-ES) and end-diastole volumes (V-ED) for all subjects (VA1–VA5), extracted from magnetic resonance imaging (MRI). V-ES = 52 ± 12.0 ml. V-ED = 117 ± 23.7 ml. Middle: corresponding stroke volumes. Stroke volume = 65 ± 13 ml. Bottom: corresponding ejection fractions. Ejection fraction = 56 ± 3.95%.

Strain data (see Table 2) correlated well with published data. Specifically, in Ref. 43, a study on 31 healthy volunteers, circumferential strain values were −23 ± 4, −22 ± 3, −16 ± 5, and −16 ± 4% in the anterior, lateral, inferior, and septal sectors of an equatorial slice, respectively, which correlates well with the overall average of −17.6 ± 5.8% we report here. Similarly, in Ref. 43, the longitudinal strain values were −15 ± 3, −14 ± 4, −15 ± 3, and −15 ± 3% in the anterior, lateral, inferior, and septal sectors of an equatorial slice, which correlates well with the overall average of −13.9 ± 2.9% found in the present study.

Table 2.

Mean and SD of the circumferential and longitudinal strain differences between magnetic resonance imaging-measured and finite-element-computed strains, for each subject, as well as averaged across all five subjects

	VA1	VA2	VA3	VA4	VA5	Average
ECCFE, %	−13.0 ± 4.1	−16.6 ± 4.1	−13.3 ± 4.3	−14.2 ± 3.5	−14.1 ± 6.2	−14.2 ± 4.4
ECCMRI, %	−17.9 ± 4.1	−21.5 ± 3.8	−16.6 ± 5.6	−15.5 ± 7.3	−16.5 ± 7.9	−17.6 ± 5.8
ECCFE − ECCMRI, %	4.9 ± 4.4	5.0 ± 4.8	3.3 ± 5.7	1.3 ± 6.6	2.4 ± 9.8	3.4 ± 6.3
EllFE, %	−16.0 ± 5.3	−10.6 ± 8.9	−12.1 ± 4.8	−15.0 ± 3.8	−12.9 ± 4.4	−13.3 ± 5.5
EllMRI, %	−13.5 ± 2.6	−12.5 ± 4.0	−14.4 ± 2.1	−15.0 ± 3.1	−14.0 ± 2.6	−13.9 ± 2.9
EllFE − EllMRI, %	−2.5 ± 7.3	1.9 ± 10.2	2.3 ± 4.4	0.0 ± 3.4	1.1 ± 4.4	0.5 ± 5.9

E, strain; CC, circumferential; FE, finite element; MRI, magnetic resonance imaging; ll, longitudinal.

The diastolic parameters that can reproduce 1) the measured EDV at a normal ED pressure; and 2) an ED pressure-EDV relationship that best matches the experimental results of Ref. 34 in each individual LV model were, on average, C₀ = 0.115 ± 0.008 kPa and B₀ = 14.4 ± 3.18 (Table 1). The resultant normalized ED pressure-EDV curves from each of the five LV models were best fit (in a least squares sense) to the “Klotz” curve (34) that defines the pressure-volume relationship of multiple species and etiologies (Fig. 3). Additionally, the systolic parameter that could reproduce the measured ESV at a prescribed ES pressure of 120 mmHg in each individual LV model was, on average, T_max = 143 ± 11.1 kPa (Table 1).

Table 1.

Subject-specific values of the passive and active material parameters

	VA1	VA2	VA3	VA4	VA5	Average	SD
C0, kPa	0.117	0.121	0.105	0.107	0.123	0.115	0.00817
B0	12.4	15.0	18.3	16.0	10.1	14.4	3.18
Tmax, kPa	130	149	148	132	155	143	11.1

Parameters were calibrated so as to match end-diastole volumes and pressures and to minimize the distance of the pressure-volume relationship to the Klotz curve (for passive parameters), and so as to match end-systole volumes and pressures (for active parameters). VA1–VA5, subjects 1–5; C₀, scaling factor; B₀, factor that determines the level of nonlinearity of the stress-strain relationship; T_max, factor that reflects the overall contractility of the myocardial tissue.

Fig. 3.

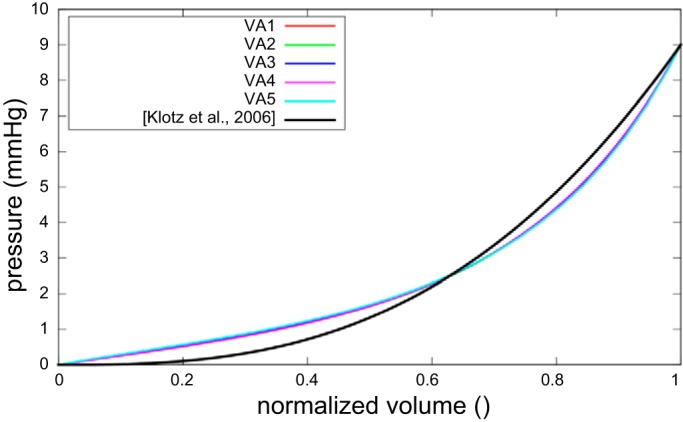
Normalized end-diastole pressure-volume relationships of the five subjects after optimization of the passive material parameters, compared with the Klotz curve (34).

Model validation.

The average circumferential strain difference between MR imaging and FE modeling was 3.4 ± 6.3% and agrees with previous studies (63) (Table 2). The average longitudinal strain difference was 0.5 ± 5.9% (Table 2). As an illustration, Figure 4 compares, for a midventricle slice of the third subject, MRI and FE circumferential and longitudinal strains as a function of the circumferential position.

Fig. 4.

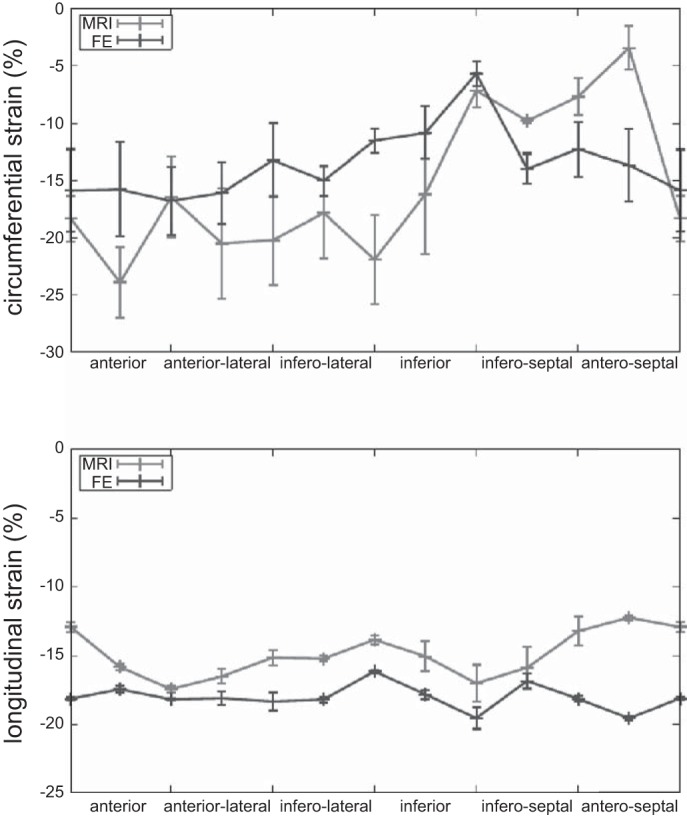
Systolic circumferential and longitudinal strains predicted by the FE model after calibration of the passive and active material parameters, compared with the MRI strains. This plot corresponds to one midventricle slice of the third subject. Values are means ± SD.

Myofiber stress distribution.

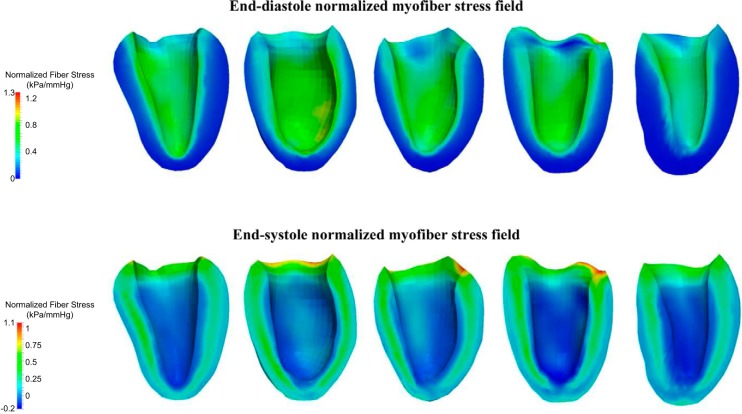
The ED and ES myofiber stress patterns across the five subjects are shown in Fig. 5. The ED myofiber stress was larger near the subendocardial wall than in the subepicardial wall. Also, the transmural variation of the ES myofiber was nonmonotonic and was maximal at the LV midwall.

Fig. 5.

Top: end-diastole normalized myofiber stress field for each subject. Bottom: end-systole normalized myofiber stress field for each subject. Stress is normalized with respect to the ventricular pressure, in mmHg.

The volumetric-averaged ED and ES myofiber stress distributions across the five subjects are shown in Fig. 6. The mean volumetric-averaged myofiber stress was 2.21 ± 0.58 kPa at ED, and 16.54 ± 4.73 kPa at ES.

Fig. 6.

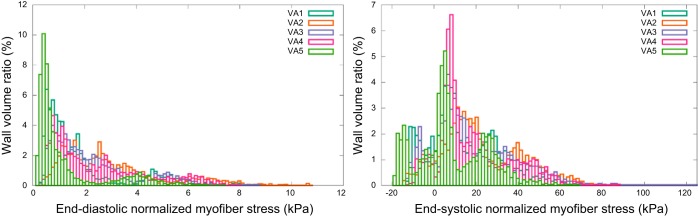
End-diastolic and end-systolic myofiber stress distribution, normalized with respect to the ventricular pressure, in mmHg. Wall volume ratio is the ratio of wall volume subject to a given fiber stress, divided by the total wall volume.

DISCUSSION

Our study details significant advancements in FE models of human global and regional LV mechanics, especially in terms of comparing these models to in vivo strain measurements. We included five unique FE models customized with 1) in vivo geometry measured with MRI; 2) diastolic material parameter values formally optimized to best fit (in a least squares sense) subject-specific ED pressures and EDV, as well as the ED pressure-EDV relationship measured previously by Klotz et al. (34); 3) myocardial contractility parameter values best fit to subject-specific ES pressures and ESV; and 4) agreement to in vivo strains measured with tagged MRI throughout the LV. No previous biomechanical models of the LV have been so rigorously validated: 950 ± 170 strain comparisons were made per subject. These five FE models have allowed us to take the first step in establishing a normal range of myofiber stress and its distribution at ED and ES in humans. This data could serve as a reference target for in silico optimization studies of cardiac procedures and devices aimed at treating heart failure by normalizing ventricular wall stress.

Comparison with modeling studies of heart failure treatments.

Recently, we performed two patient-specific FE modeling studies of such heart failure treatments. The first was of SVR, a procedure designed to treat heart failure by surgically excluding infarcted tissues from the dilated failing LV. To elucidate and predict the effects of geometrical changes from SVR in combination with coronary artery bypass grafting (SVR + CABG) on LV function and wall stress, our laboratory (40) created patient-specific FE LV models before and after surgery using untagged MRI. Our results predicted that decreased diastolic distensibility in patients compromised the postsurgical improvement in systolic function. By simulating restoration of the LV back to its measured baseline sphericity, we showed that diastolic and systolic function improved, whereas peak myofiber stress was reduced substantially (by 50%: from 141.2 ± 45.1 to 70.3 ± 15.0 kPa) after SVR, and the resultant LV myofiber stress distribution became more uniform. This reduction in myofiber stress after SVR may help reduce adverse remodeling of the LV. Overall, our patient-specific FE model results were consistent with what the Surgical Treatment for Ischemic Heart Failure trial speculated would be the neutral outcome, that “the lack of benefit seen with SVR is that benefits anticipated from surgical reduction of LV volume (reduced wall stress and improvement in systolic function) are counter-balanced by a reduction in diastolic distensibility.” Thus, using our normal human myofiber stress results to optimize the design of SVR for treating heart failure may not be worthwhile.

Our second patient-specific FE modeling study of heart failure treatment was of a polymer gel injected into the LV. Data obtained from clinically relevant large-animal preparations and FE LV modeling indicate that adding noncontractile material to a damaged LV wall can potentially reduce elevated myofiber stress (59). Algisyl-LVR is a proprietary biopolymer gel under clinical development that is injected into strategic areas of the heart muscle, where it remains as a permanent implant to prevent or reverse the progression of heart failure in patients who have a dilated LV. To quantify the effects of Algisyl-LVR + CABG, we (38) created patient-specific FE LV models using untagged MRI before and after treatment. The LV become more ellipsoidal after Algisyl-LVR + CABG than after SVR + CABG, and both EDV and ESV decreased substantially 3 mo after Algisyl-LVR + CABG in all patients (EDV: from 264 ± 91 to 146 ± 86 ml; ESV: from 184 ± 85 to 86 ± 76 ml), whereas ejection fraction increased from 32 ± 8 to 47 ± 18%. These rather remarkable changes were accompanied by an ∼35% decrease in ED and ES myofiber stress. Specifically, volumetric-averaged ED myofiber stress decreased from 6.6 ± 1.9 to 4.4 ± 1.8 kPa, and volumetric-averaged ES myofiber stress decreased from 37.1 ± 13.2 to 23.1 ± 12.8 kPa. Posttreatment myofiber stress became more uniform in the LV. Overall, our patient-specific FE model results support the novel concept that Algisyl-LVR + CABG treatment leads to decreased myofiber stress, restored LV geometry, and improved function. Thus, using the normal human myofiber stress results from the present study to optimize the design of Algisyl-LVR for treating heart failure probably would be worthwhile.

Implications for designing treatments for heart failure.

To develop a method for automatically optimizing medical devices for treating heart failure, our laboratory previously used experimentally measured ED and ES LV pressures and EDV and ESV in dogs with coronary microembolization-induced heart failure (64). Specifically, the FE simulation-based method we developed automatically optimizes the injection pattern of polymeric “inclusions” according to a specific objection function using commercially available software tools. The optimization resulted in an intuitive optimal injection pattern (i.e., the one with the greatest number of inclusions) when the objective function was weighted to minimize mean ED and ES myofiber stress and ignore LV stroke volume. In contrast, the optimization resulted in a nonintuitive optimal pattern (i.e., 3 inclusions longitudinally × 6 inclusions circumferentially) when both myofiber stress and stroke volume were incorporated into the objective function with different weights.

Now, we are in a position to design optimal Algisyl-LVR injection patterns to treat individual heart failure patients. Patient-specific FE LV models before treatment can be created using untagged MRI, as described in Refs. 38 or 40. Patient-specific ED and ES LV myofiber stress distributions can be automatically computed for all possible Algisyl-LVR injection patterns, as described in Ref. 64. Rather than simply minimizing myofiber stress and/or maximizing stroke volume, the normal human LV myofiber stress results from the present study can be used in the objective function. For example, “Patient 1” in Ref. 38 had a baseline ejection fraction of 40%, a 3-mo posttreatment ejection fraction of 65.4%, and a 6-mo posttreatment ejection fraction of 75.9%, which is greater than the normal range at rest (62.3 ± 6.1%) assessed using radionuclide angiocardiography (46). Apparently then, a less aggressive treatment (e.g., fewer injections) may have been more appropriate. Perhaps an FE simulation-based design of an optimal Algisyl-LVR injection pattern for that patient (aimed at posttreatment ED and ES LV myofiber stress distributions best fitting those obtained in the present study for normal human subjects) would have arrived at an injection pattern that resulted in a 6-mo posttreatment ejection fraction closer to 62.3%. Because at least 6 mo are apparently required after this heart failure treatment to reach a steady state as far as reverse LV remodeling is concerned, chronic patient-specific FE LV modeling, as described in Ref. 33, may also be required in the optimal treatment design.

It is especially interesting how the average ED and ES myofiber stresses in the present study (2.21 ± 0.58 and 16.54 ± 4.73 kPa, respectively) appear to represent critical thresholds near which post-Algisyl-LVR + CABG treatment ejection fractions become normal (see Table 1 of Ref. 38). In Patient 1 in Ref. 38, ejection fraction increased from 40 to 65.4% when average ED and ES stresses decreased from 5.6 to 3.1 kPa and from 29.6 to 12.7 kPa, respectively. In Patient 2, however, ejection fraction increased from 23.7% to only 29.2% when average ED and ES stresses decreased from 8.7 to 6.4 kPa and from 52.4 to 37.4 kPa, respectively. Similarly, in Patient 3 (3 mo after treatment), ejection fraction increased from 35.1% to only 47.0% when average ED and ES stresses decreased from 5.4 to 3.6 kPa and from 29.4 to 19.3 kPa, respectively. Six months after treatment, however, ejection fraction in Patient 3 became 61.9% when average ED and ES stresses became 2.8 and 12.8 kPa, respectively.

A noninvasive method for estimating regional myocardial contractility would be valuable for designing and evaluating new surgical and medical strategies to treat and/or prevent infarction-induced heart failure. Adverse LV remodeling after myocardial infarction (MI) is responsible for nearly 70% of heart failure cases. Previous studies in clinically relevant large-animal preparations using state-of-the-art MRI tissue tagging and FE modeling algorithms have demonstrated that a spatially progressive loss of contractile function in perfused myocardium outside the infarct zone is central to the mechanism by which an initially well-tolerated acute myocardial loss progressively leads to chronic symptomatic heart failure (14, 20, 28, 49). These animal studies have established that loss of contractile function occurs initially and is most severe in the perfused border zone adjacent to the infarct. Recently, our laboratory (62) published the first use of a fully validated tissue tagging and analytic modeling technique to assess regional contractile function in the remodeled human heart of a 62-yr-old man who suffered a MI in 1985 and had recently had complete revascularization. Myofiber systolic contractile stress that developed in the border zone (T_{max B}) and in regions remote from the MI (T_{max R}) were quantified using cardiac catheterization, MRI, and the FE method. The resulting FE model of the patient's beating LV could simulate the reduced systolic strains measured using tagged MRI at matching LV pressures and volumes. T_{max B} (73.1 kPa) was greatly reduced relative to T_{max R} (109.5 kPa). These results were independent of assumptions relating to border zone myofiber orientation. These findings from our laboratory's earlier study are consistent with those of the present study. For example, our average calibrated value of T_max = 143 ± 11.1 kPa is comparable to the value T_{max R} = 109.5 kPa and well above the value T_{max B} = 73.1 kPa.

Historical context.

The models developed in this study are solved fully implicitly. This might seem a detail to noncomputational scientists, but it is the only way to fully trust the obtained numerical results. Indeed, explicit methods will always return a result, but there is no guarantee that the numerical result obtained using an explicit method is close to the exact solution of the equations of the model (which is analytically intractable, see Ref. 37 for a more detailed discussion on computational cardiac mechanics). In contrast, implicit methods, which involve a rather complex iterative process, will only “converge” if the numerical result is close to the exact solution. Commercial FE software can simulate “contact” problems associated with medical devices for treating cardiac disease (see, for example, Refs. 5, 36, 61, 65). The commercial implicit FE software that we used (Abaqus/Standard) also can simulate such contact problems, but has only very recently been used to realistically simulate regional diastolic cardiac mechanics (60).

Despite intense interest by clinicians, engineers, and physiologists in quantifying ventricular wall stress, no FE ventricular model published before 1981 compared predictions of myocardial deformation or strain against experimental measurements under physiological conditions. The reasons for this are twofold: 1) no FE software available before 1970 could simulate finite or large deformation comparable to that which occurs in the beating LV (e.g., 20% midwall myofiber strain between ES and ED); and 2) such experimental deformation measurements were not made until the mid-1980s. In 1974, Janz et al. (29, 30) first showed the importance of using finite deformation theory rather than classical or infinitesimal deformation theory, at least for FE simulation of diastolic LV filling. It then took until 1985 for a cardiologist and two bioengineers to accurately quantify transmural distributions of three-dimensional (3D) finite myocardial strain in the normal beating canine LV using high-speed biplane cineradiography of closely spaced columns of lead beads (56).

Two major advances in FE ventricular modeling and validation in the late 1980s and 1990s were the development of 1) FE software that could simulate finite deformation of an anisotropic material (e.g., Refs. 3, 4, 7, 8, 17), and 2) MRI methods for noninvasively measuring regional 3D strain throughout the LV myocardium of beating hearts (e.g., Refs. 1, 11, 69). Remarkably, the SPAMM method developed by Axel and Dougherty (1) in 1989 is still the most widely used MRI method for measuring regional LV 3D myocardial strain. One explanation for its longevity and popularity is it has been validated using a deformable phantom (67).

To the best of our knowledge, our laboratory was the first to use FE LV modeling and systolic myocardial 3D strain measurements to estimate regional myocardial contractility in vivo. Specifically, we used cardiac catheterization, biplanar SPAMM, and the implicit FE method of Costa et al. (7, 8) to measure regional systolic myocardial material properties in the beating hearts of four sheep with LV aneurysm (57) and six sheep with LV aneurysm repaired surgically (58). With knowledge of these myocardial material properties, we could quantify the effect of aneurysm plication on regional myocardial stress distributions. Although those two previous studies were significant advances in FE modeling of hearts with MI, because of long computation times, they both used a manually directed pseudo-optimization. In other words, a formal nonlinear optimization of material constants was not feasible. Therefore, we began using commercial explicit FE software (LS-DYNA) and optimization software (LS-OPT) to develop and validate a computationally efficient formal optimization of regional myocardial contractility (39, 51, 53, 54, 62, 63).

A recent study (2) that presented a proof-of-concept simulator for a four-chamber human heart model created from computer topography and MR images illustrated the governing equations of excitation-contraction coupling and discretized them using an explicit FE environment (Abaqus/explicit). To illustrate the basic features of their model, the authors visualized the electrical potential and mechanical deformation across the human heart throughout its cardiac cycle. Thus their single subject-specific model is better than our five subject-specific models in terms of the number of heart chambers simulated and the ability to predict regional cardiac electrical potential and mechanical deformation throughout the cardiac cycle. To compare their simulation against common metrics of cardiac function, however, they extracted only the pressure-volume relationship and showed that it agreed well with clinical observations. As our laboratory (53) and others (see, for example, Ref. 27) have pointed out, it is impossible to determine myocardial material properties (in the form of 3D constitutive equations) from ventricular pressure-volume relations alone.

Study limitations.

From the perspectives of chamber blood-flow and myocardial physiology, the normal human heart is an amazing and incredibly complex organ or pump. We make no claims about our subject-specific LV FE models being able to realistically simulate all of those coupled phenomena. Moreover, our models can realistically simulate only a limited scope of regional LV mechanics. Nevertheless, within that scope, our models are state-of-the-art in their realism and the rigor with which they have been validated.

The realism and validity of our subject-specific models is limited to only one heart chamber, the LV, and two time points in the cardiac cycle: the end of LV filling and the end of LV ejection. Nevertheless, our laboratory has found ED and ES LV pressure-volume relationships and mean myofiber stresses to be extremely valuable in evaluating the efficacy of novel medical and/or surgical procedures and devices for treating ischemic cardiomyopathies (5, 9, 21, 22, 31, 33, 36, 38, 40, 48, 54, 58, 59, 61, 64, 65, 70).

Another limitation is that we used generic fiber orientation maps, and not subject-specific ones. However, precise myofiber orientation measurements are usually only possible ex vivo, which is the main reason why very few normal human datasets exist. Although recent studies have proven the feasibility of in vivo diffusion tensor imaging (25, 55), the densification of such sparse data is still an open question, and modified scanners with specific scanning sequences are required.

In terms of the mechanical model itself, one limitation is the anisotropy, which is considered fixed at 40% cross-fiber stiffness and active force. However, it is not possible to uniquely identify an anisotropic constitutive material law solely based on a pressure-volume relationship. Moreover, it was shown that 40% cross-fiber stiffness and active force gave the best agreement with ex vivo biaxial tissue stretching (57).

Another limitation is that we studied only three men and two women. Although to facilitate the use of our work by the community, we made the data freely available at https://simtk.org/home/normalhumanlvs. We plan to study more normal human subjects and make the new data freely available there as well.

Conclusion.

In conclusion, in this paper, we derived LV myofiber stress distributions at ED and ES for five normal human subjects, based on MRI and personalized computational cardiac mechanics modeling. Model personalization involved deriving the range of normal passive and active myocardial mechanical properties. The models were validated by comparing the systolic strains predicted by the model to the ones measured in vivo by MRI. The validated myofiber stress fields presented here can be used as a target for future in silico studies of cardiac procedures. To do so, the stress fields could be mapped onto a specific geometry corresponding to a diseased heart and then used in the optimization procedure.

GRANTS

This work was supported by National Institutes of Health Grants R01-HL-077921 and R01-HL-118627 (J. M. Guccione) and K25-NS058573–05 (G. Acevedo-Bolton); and Marie-Curie International Outgoing Fellowship within the 7th European Community Framework Program (M. Genet).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: M.G., L.C.L., R.N., Z.Z., and L.G. analyzed data; M.G. and L.C.L. interpreted results of experiments; M.G. prepared figures; M.G. and L.C.L. drafted manuscript; M.G., L.C.L., K.O., S.K., and J.M.G. edited and revised manuscript; M.G., L.C.L., R.N., H.H., G.A.-B., Z.Z., L.G., K.O., S.K., and J.M.G. approved final version of manuscript; H.H. and G.A.-B. performed experiments; K.O., S.K., and J.M.G. conception and design of research.

Appendix A: Constitutive Model for the Normal Myocardium

The material law used for the myocardium has already been described extensively, for instance in Refs. 39, 53, 63. It is only briefly recalled here. Basically, it is divided into passive and active parts.

The passive part consists in a quasi-incompressible transversely isotropic Fung law, originally proposed for the myocardium in Ref. 18. Transverse (i.e., sheet and sheet normal) stiffness is 40% of myofiber stiffness. Quasi-incompressibility is imposed by decomposing the transformation gradient into volumetric and isovolumic parts and using a high bulk modulus (compared to the shear modulus) for the volumetric deformation (26), such that the total free energy potential is written as:

$$\psi (\underset{¯}{\underset{¯}{E}})=\frac{1}{K}\left[\frac{J^2-1}{2}-\ln (J)\right]+\overline{\psi }(\underset{¯}{\underset{¯}{\overline{E}}})$$

where K is the bulk modulus, J is the Jacobian of the deformation gradient [i.e., $J=\det (\underset{¯}{\underset{¯}{F}})$], and $\underset{¯}{\underset{¯}{\overline{E}}}$ is the isochoric Green-Lagrange strain tensor that is defined as $\underset{¯}{\underset{¯}{\overline{E}}}=({\underset{¯}{\underset{¯}{\overline{F}}}}^T\underset{¯}{\underset{¯}{\overline{F}}}-\underset{¯}{\underset{¯}{1}})/2$ with $\underset{¯}{\underset{¯}{\overline{F}}}$ the isochoric part of the deformation gradient [i.e., $\underset{¯}{\underset{¯}{\overline{F}}}=J^{-1/3}\underset{¯}{\underset{¯}{F}}$, such that $\det (\underset{¯}{\underset{¯}{\overline{F}}})=1$]. The isochoric part of the free energy potential is written as:

$$\overline{\psi }(\underset{¯}{\underset{¯}{\overline{E}}})=\frac{c_0}{2}\left[e^{Q(\underset{¯}{\underset{¯}{\overline{E}}})}-1\right]$$

with:

$$Q(\underset{¯}{\underset{¯}{\overline{E}}})=b_f{\overline{E}}_{ff}^2+b_t\left({\overline{E}}_{ss}^2+{\overline{E}}_{nn}^2+\frac{{\overline{E}}_{sn}^2+{\overline{E}}_{ns}^2+{\overline{E}}_{sn}{\overline{E}}_{ns}+{\overline{E}}_{ns}{\overline{E}}_{sn}}{2}\right)+b_{ft}\left(\frac{{\overline{E}}_{fs}^2+{\overline{E}}_{sf}^2+{\overline{E}}_{fs}{\overline{E}}_{sf}+{\overline{E}}_{sf}{\overline{E}}_{fs}}{2}+\frac{{\overline{E}}_{fn}^2+{\overline{E}}_{nf}^2+{\overline{E}}_{fn}{\overline{E}}_{nf}+{\overline{E}}_{nf}{\overline{E}}_{fn}}{2}\right)$$

where C₀ is a first scaling factor, which must be identified for each subject, and b_f, b_t, and b_ft are three parameters that, considering that transverse stiffness is 40% of fiber stiffness and that shear stiffness is average between normal and transverse stiffness, are defined by:

$$\{\begin{array}{c}{b}_f=B_0\\ b_t=0.40B_0\\ b_{ft}=\frac{b_f+b_t}{2}=0.70B_0\end{array}$$

where B₀ is a second scaling factor, determining the level of nonlinearity of the stress-strain relationship, which must be identified for each subject.

The active part consists in stretch-dependent active force law, originally proposed for the myocardium in Refs. 19 and 23. Active contraction is orthotropic, with full contractile force in the local myofiber direction, 40% contractile force in the local sheet direction, and no contraction in the local sheet normal direction. The contractile force is written as:

$$T(t,E_{ff})=\frac{T_{\max }}{2}\frac{{\text{Ca}}_0^2}{{\text{Ca}}_0^2+{\text{ECa}}_{50}^2(E_{ff})}\left\{1-\cos \left[\omega (t,E_{ff})\right]\right\}$$

with:

$${\text{ECa}}_{50}(E_{ff})=\frac{{\text{Ca}}_{0_{\max }}}{\sqrt{e^{B[l(E_{ff})-t_0]}-1}}$$

$$\omega (t,E_{ff})=\{\begin{array}{c}\pi \frac{t}{t_0}\text{when}0\le t\le t_0\\ \pi \frac{t-t_0+t_r[l(E_{ff})]}{t_r}\text{when}{t}_0\le t\le t_0+t_r[l(E_{ff})]\\ 0\hspace{0.17em}\text{when}\hspace{0.17em}t\ge t_0+t_r[l(E_{ff})]\end{array}$$

$$t_r(l)=ml+b$$

and

$$l(E_{ff})=l_r\sqrt{2E_{ff}+1}$$

where E_ff is the Lagrangian strain tensor component aligned with the local muscle fiber direction in the unloaded reference configuration; T_max is the law's scaling factor, which must be identified for each subject; Ca₀ = 4.35 μM is the peak intracellular calcium concentration; Ca_0max = 4.35 μM is the maximum peak intracellular calcium concentration; B = 4.75 μm⁻¹ governs the shape of peak isometric tension-sarcomere length relation; l₀ = 1.58 μm is the sarcomere length at which no active tension develops; t₀ = 100 ms is the time to peak tension; m = 1.0489 s/μm and b = −1.429 s govern the shape of linear relaxation duration-sarcomere length relaxation; and ECa₅₀ is the length-dependent calcium sensitivity.