Comparison of monovalent and divalent ion distributions around a DNA duplex with molecular dynamics simulation and a Poisson-Boltzmann approach

Abstract

The ion atmosphere created by monovalent (Na⁺) or divalent (Mg²⁺) cations surrounding a B-form DNA duplex were examined using atomistic molecular dynamics (MD) simulations and the nonlinear Poisson-Boltzmann (PB) equation. The ion distributions predicted by the two methods were compared using plots of radial and two-dimensional cation concentrations and by calculating the total number of cations and net solution charge surrounding the DNA. Na⁺ ion distributions near the DNA were more diffuse in PB calculations than in corresponding MD simulations, with PB calculations predicting lower concentrations near DNA groove sites and phosphate groups and a higher concentration in the region between these locations. Other than this difference, the Na⁺ distributions generated by the two methods largely agreed, as both predicted similar locations of high Na⁺ concentration and nearly identical values of the number of cations and the net solution charge at all distances from the DNA. In contrast, there was greater disagreement between the two methods for Mg²⁺ cation concentration profiles, as both the locations and magnitudes of peaks in Mg²⁺ concentration were different. Despite experimental and simulation observations that Mg²⁺ typically maintains its first solvation shell when interacting with nucleic acids, modeling Mg²⁺ as an unsolvated ion during PB calculations improved the agreement of the Mg²⁺ ion atmosphere predicted by the two methods and allowed for values of the number of bound ions and net solution charge surrounding the DNA from PB calculations that approached the values observed in MD simulations.

Introduction

Interactions between nucleic acids, such as DNA and RNA, and counterions are key to many nucleic acid functions including genome packaging, DNAzyme and RNAzyme activity, and protein binding.^1–8 Counterions enable proper folding and function of nucleic acids by partially neutralizing the negatively charged phosphate groups that are located along the nucleic acid backbone. The counterions not only bind at specific sites, forming long-lasting interactions that can be observed in crystal structures of functional RNAs and ribosomal subunits, but they also interact diffusely and create an “ion atmosphere” surrounding the nucleic acids.^4,9–11 The ion atmosphere is constantly in flux, with binding events lasting 100s or 1000s of picoseconds for monovalent and divalent cations, respectively, making explicit structural determination using traditional methods ineffective. Therefore, while its existence is accepted, a detailed understanding of the ion atmosphere, including its spatial distribution, its composition, and how it differs from bulk solution, has remained elusive.^12–15

Because of the inability to determine its structure using traditional experimental methods, understanding of the ion atmosphere surrounding nucleic acids has been, until recently, mostly based on computational techniques such as solving the Poisson-Boltzmann (PB) equation or atomistic molecular dynamics (MD) simulations. The PB equation, which uses a mean-field approximation to describe electrolytes within a continuum based solvent model, has become the standard by which macromolecular electrostatic interactions are described. PB theory has been used to study the electrostatic potentials that surround DNA and RNA, salt effects on ligand and protein binding to DNA,^7,16,17 nucleic acid pK_a shifts,¹⁸ and ion distributions around nucleic acids.^12,19–22 Despite its widespread use, the PB equation models ions as an ideal gas within a constant dielectric medium, preventing it from including ion-ion correlations and limiting its use in observing specific microscopic interactions. In contrast, fully atomistic MD simulations can provide a wealth of microscopic and dynamic information about biological systems. They have been used to investigate potential correlations between monovalent cations binding to DNA and structural perturbations and have shed new light on nucleic acid stability and nucleic acid-counterion interactions.^23–27 Within MD simulations, macromolecules, ions, and water are described by force fields based on empirical data and ab initio calculations, and results from MD simulations are limited by the accuracy of these force fields. Additionally, MD simulations model ions as point charges while ignoring electronic effects, such as solvent polarization triggered by Mg²⁺ ions. Despite these limitations, MD simulations have successfully reproduced crystallographic binding sites, sequence-specific binding behavior, and experimental ion distributions.^{13,15,25,26,28}

Recently, several experimental techniques have begun to deconvolute the ion atmosphere and more fully investigate nucleic acid-counterion interactions. One of the first techniques that was used to probe the ion atmosphere was anomalous small-angle X-ray scattering (ASAXS), with initial experiments comparing the distributions of monovalent and divalent cations around DNA.²⁹ While it has revealed a dependence of ion distribution on topology and that the ion atmosphere created by divalent cations is significantly more compact than that of monovalent cations,^28,30,31 ASAXS experiments have been limited by the method not being sufficiently quantitative and lacking the ability to accurately detect Mg²⁺ and other biologically important cations. Bai et al. quantitatively determined the enrichment of cations and depletion of anions surrounding a short DNA segment using a novel technique called buffer equilibration and atomic emission spectroscopy (BE-AES).¹² They also compared the relative DNA binding affinity of several monovalent and divalent cations and made the important observation that Mg²⁺ ions actively displaced Na⁺ ions near the nucleic acid, a result that has been supported by other experimental methods including Raman spectroscopy and second harmonic generation microscopy.^32,33

While these recent experiments have improved understanding of the ion atmosphere, they are unable to explain many properties that are required for a complete description of the ion atmosphere, including local spatial distributions, dynamics, and atom-specific affinity of counterion-DNA interactions. Therefore, computational techniques, such as the PB equation and atomistic MD simulations that can supplement experimental observations remain crucial to developing a complete understanding of the ion atmosphere. Relatedly, computational results can be compared with experiments and with each other to test and refine the computational methods and maximize their efficacy. For example, Bai et al. compared their BE-AES experimental results with PB calculations and found that PB theory underestimates the concentration of divalent cations near nucleic acids within the ion atmosphere,¹² a result in agreement with a decade old observation by Deserno et al. based on comparisons between PB theory and MD simulations.³⁴ More recently, comparisons between PB theory and experimental or MD simulation results have found that PB theory agrees reasonably well with other methods for monovalent cations and that this agreement improves when using distance-dependent solvent dielectric constants and accounting for ion size.^20,22 However, even when using these modified approaches, PB theory showed significant discrepancies in comparison with other approaches for small, high valence cations, such as Mg²⁺, and also underestimated the experimentally observed ability of Mg²⁺ to outcompete Na⁺ for preferred nucleic acid binding sites.^35,36 In contrast, detailed comparisons between MD simulations and recent experimental results have also been performed and have been shown to largely agree for both mono- and divalent cations. Atomistic MD simulations performed by Yoo et al. were able to reproduce ion-count data and Mg²⁺/Na⁺ competition behavior found in BE-AES experiments,¹⁵ and Kirmizialtin et al. reported good agreement between MD simulations and ASAXS experiments for the number and distribution of Na⁺, Rb⁺, and Sr²⁺ cations surrounding A-form RNA.²⁸ The simulations used in these comparisons were also able to provide detailed information about the radial distribution functions surrounding nucleic acids and binding behavior that are currently inaccessible to experiments.

In the following work, we provide a comprehensive description and comparison of the ion atmosphere surrounding a B-form DNA duplex in the presence of monovalent (Na⁺) or divalent (Mg²⁺) cations using atomistic MD simulations and PB theory. We compare the cation concentration distributions surrounding the DNA axis for each computational method and observe discrepancies between PB theory and MD simulations for both cations, with the Mg²⁺ cation distributions in particular showing little agreement between the two methods. However, when comparing the number of excess ions and net solution charge surrounding the DNA duplex, we observe reasonable agreement between MD simulations and PB theory for monovalent cations and, under certain circumstances, divalent cations. We examine the size of the ion atmosphere around the DNA using the solution’s net charge, and find the ion atmosphere formed by Mg²⁺ to be smaller than a corresponding monovalent atmosphere. We also investigate the effect of ion model on the ion distributions found in MD simulations.

Methods

Atomistic molecular dynamics simulations

To compare ion distributions found in atomistic MD simulations with those predicted by the PB equation, we constructed a 12 bp DNA duplex with a sequence of d(CGCGAATTCGCG)₂ using the nucgen module within the AMBER10 software suite.³⁷ The DNA was immersed in a large periodic box (~100 Å × 100 Å × 100 Å) containing TIP3P water, either 31 or 91 monovalent (Na⁺) or divalent (Mg²⁺) cations, and an appropriate number of monovalent anions (Cl⁻) to neutralize the system (Table 1). To prevent artifacts caused by initially placing cations near the DNA duplex, all cations were randomly placed throughout the simulation box at least 35 Å away from the duplex.¹⁴ In all simulations, the DNA duplex was harmonically restrained to the initial coordinates with a 10 kcal/mol*Ų spring constant.

Table 1.

MD Simulation Conditions

Simulation	Force field	Ion parameters	Number	of Ions	[Cation]Bulk (M)	tMD (ns)*
31Na-A	ff99	ions94	31 Na+	9 Cl−	0.033	50
31Na-B	ff10	ions08	31 Na+	9 Cl−	0.033	150
91Na-A	ff99	ions94	91 Na+	69 Cl−	0.137	50
91Na-B	ff10	ions08	91 Na+	69 Cl−	0.135	150
31Mg-A	ff99	ions94	31 Mg2+	40 Cl−	0.035	50
31Mg-B	ff10	Allńer/ions08	31 Mg2+	40 Cl−	0.038	150
91Mg-A	ff99	ions94	91 Mg2+	160 Cl−	0.141	50
91Mg-B	ff10	Allńer/ions08	91 Mg2+	160 Cl−	0.141	150

^*The t_MD listed includes a 10 ns equilibration period.

To examine the effect of force field parameters on ion distributions, we performed two sets of simulations using different force fields and parameters (Table 1). In “A” type simulations, the DNA and the ions were treated with the ff99 and ions94 force field parameters, respectively.^38–40 The ions94 parameter set has widely cited crystallization problems for high concentrations of KCl and NaCl, but the concentrations employed in this work remain below the anomalous crystallization point.^19,41–43 In type “B” simulations, we used the ff10 force field for DNA atoms, Na⁺ and Cl⁻ ion parameters from the ions08 parameter set, and recently published Mg²⁺ parameters from Allńer et al.^44–48 This second group of simulations were run using the CUDA implementation of AMBER12.^49,50 Lennard-Jones parameters of the ions used in the simulations are located in Table 2. With respect to nucleic acid force field parameters, previous MD simulations have shown nucleic acid description does not influence ion distributions around a fixed duplex.¹⁴ Additionally, Mg²⁺ is represented as a point charge in both parameter sets which does not account for polarization and charge-transfer effects and may lead to an inadequate description of cation behavior for some situations.^51–53 However, multiple groups have reproduced experimental results using MD simulations that effectively model Mg²⁺ ions with fully solvated inner coordination shells.^{13–15,22,33} DFT calculations also predicted fully solvated Mg²⁺ ion binding with dimethyl-phosphate as a mimic of nucleic acid backbones.⁵⁴

Table 2.

Lennard-Jones parameters for different ion models

Ion	Parameter set	ε (kcal/mol)	rii (Å)
Na+	ions94	0.00277	3.7360
	ions08	0.0874393	2.738
Mg2+	ions94	0.8947	1.5852
	Allńer and Villa	0.00295	3.109
Cl−	ions94	0.1	4.94
	ions08	0.0355910	5.026

All MD simulations were first minimized for 6000 total steps (1000 steps with harmonic restraints on the DNA) to remove any bad initial contacts. Next, the systems were heated for 20 ps to an equilibrium temperature of 300 K using the Langevin thermostat with a collision frequency of 1.0 ps⁻¹. A time step of 2 fs was used throughout with SHAKE constraints on all bonds involving hydrogen atoms.^55,56 Long-range electrostatics were treated with the particle mesh Ewald summation with a 10 Å direct space cutoff.⁵⁷ NPT simulations with pressure set to 1 bar were then run for a total of 50 or 150 ns, including an initial 10 ns equilibration period and a 40 or 140 ns production run. This simulation length was judged to be sufficient based on the convergence of the number of ions around the DNA, as described previously¹⁴ and shown in the Supplementary Material (Supporting Figure 1). Trajectory analysis was carried out using the Ptraj program distributed with the AmberTools package as well as some in-house Fortran analysis programs. MD trajectories were visualized with Visual MD (VMD) 1.9.1.⁵⁸

In order to examine the ion distributions obtained during MD simulations with predictions based on the PB equation, the bulk cation concentration for each system was determined. We mapped a histogram of ion spatial locations with a 0.5 Å grid covering the entire simulation box. This histogram, n(x,y,z), was then converted to cation molar concentration, C(x,y,z), as a function of location within the box through Equation 1, below, where t_MD is the production simulation length, V_grid is the grid volume, and N_A is Avogadro’s number

$$C(x,y,z)=\frac{N_A}{t_{MD}{V}_{\mathit{grid}}{10}^{27}}n(x,y,z)$$ (1)

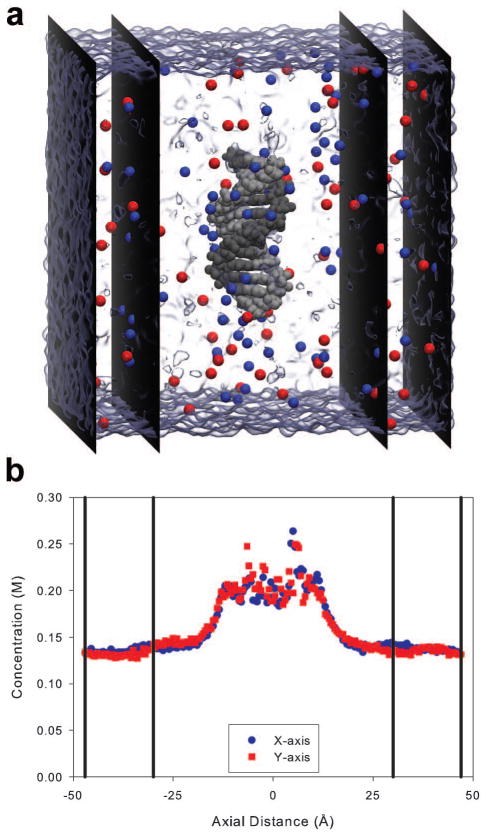
Figure 1a illustrates the volume, separated by black vertical planes, used to determine the bulk ion concentrations during the productions runs. Figure 1b shows a representative concentration profile along the x and y-axis averaged over the entire system box. From approximately −25 to 25 Å, the cation concentration was enhanced due to the nucleic acid’s presence. The bulk cation concentration was, therefore, calculated by averaging over the grid points in regions at least 30 Å away from the center of the helix (the region bordered by vertical lines in Figure 1b).

Figure 1.

Solving the nonlinear Poisson-Boltzmann equation

The nonlinear Poisson-Boltzmann equation that describes the ion distribution around the duplex was solved through the use of the Adaptive Poisson-Boltzmann Solver (APBS) software package.^59–61 The initial DNA structure from the MD simulations was used as the input structure for all of the APBS calculations. An automatically configured sequential focusing multigrid was used to solve the PB equation. The PB equation was solved on a large, coarse grid box with 200 Å dimensions using 161 grid points per axis first, then on a fine grid that matched the periodic box present in the MD simulations. The MD simulations were performed with periodic boundary conditions, while the PB equation was solved using a single Debye-Hückel boundary condition. Artifacts related to boundary conditions were recently investigated by Ye et al.; based on their study and the large size of our system box, these artifacts should be negligible.⁶² We also tested the effect of single vs. multiple Debye-Hückel boundary conditions on the ion distributions and found the effect was insignificant. The solute was treated with a dielectric constant of 2, accounting for the effect of electronic polarizability.^17,63,64 The solvent dielectric was set to 78.4 in agreement with experimental observations for water at 300 K. The ionic radius of Na⁺ was set to 1.16 Å, a value corresponding to its experimental crystal ionic radius,⁶⁵ representing a fully desolvated Na⁺ ion. In comparison with Na⁺ ions which commonly release hydrating water molecules when binding to DNA during MD simulations, Mg²⁺ ions interact more strongly with water molecules and maintain their first solvation shell.^{13,14,32,66–68} Therefore, we modeled Mg²⁺ ions in PB calculations using two atomic radii: 0.86 Å, its experimental ionic radius to represent a desolvated ion, and 3.36 Å, approximating the size of a fully hydrated Mg²⁺ ion, determined from the nearest approach of solvated Mg²⁺ ions to DNA atoms within type B MD simulations (Supporting Figure 3). The large radius is also slightly less than the sum of the desolvated Mg²⁺ radius and approximate diameter of water (2.8 Å). Nucleic acid atomic charges were grouped onto nearest-neighbor grid points and were assigned according to the AMBER ff99 force field.

Results and Discussion

Sensitivity of ion distributions to APBS calculation input parameters

Ion distributions predicted by numerically solving the PB equation are affected by the calculations’ input parameters. To examine the sensitivity of our results to APBS input parameters, we ran a large number of calculations examining the effect of ionic and solvent radius, solute dielectric, and solvent dielectric on the predicted number of cations within 10 Å of the nucleic acid C1′ atoms, N_cat, in solution with a bulk cation concentration of a 0.150 M. C1′ atoms were selected because the atoms are present in every residue and reside near the minor and major groove’s floor. Abbreviated results of these calculations are located in Table 3, while more comprehensive results are provided in Supporting Table 1. The solvent probe radius, r_solv, and the solute dielectric ε_sol, had an insignificant effect on the ion distributions. The solvent dielectric ε_solv had a small influence over the ion atmosphere, with a decrease of approximately one cation over the range investigated. The ion distributions were most sensitive toward changes in the ion probe size, r_Ion, with a decrease of approximately three and two cations for mono- and divalent salts respectively. APBS calculations used in comparisons with MD simulations utilized input parameters (ion size, solute and solvent dielectric constants, etc.) based on reported values whenever possible (see Methods). In the remaining part of the paper, we examine the ion model’s effect on binding and radial distributions, and focus on comparing radial ion concentration profiles, 2D ion concentration contours, number of excess ions, and the net solution charge determined from MD simulations with those predicted by APBS calculations.

Table 3.

Selected APBS results for monovalent and divalent salt

Monovalent								Divalent
rsolv=1.4 Å, εsol=2, εsolv=78.4		rIon=1.5 Å, εsol=2, εsolv=78.4		rIon=1.5 Å, rsolv=1.4 Å, εsolv=78.4		rIon=1.5 Å, rsolv=1.4 Å, εsol=2		rsolv=1.4 Å, εsol=2, εsolv=78.4
rIon (Å)	Ncata	rsolv (Å)	Ncata	εsol	Ncata	εsolv	Ncata	rIon (Å)	Ncata
0.5	12.4	0.0	10.4	2	10.4	70	11.0	0.5	9.8
1.0	11.4	0.5	10.4	4	10.4	74	10.7	1.0	9.1
1.5	10.4	1.0	10.4	8	10.3	78	10.4	1.5	8.5
2.0	9.2	1.5	10.4	10	10.3	82	10.1	2.0	7.7

^aN_cat is the predicted number of cations within 10 Å of the C1′ atoms

Na⁺ ion concentration profiles

We calculated the radial concentration profile of cations around the DNA duplex for each system and method to examine differences in local ion distributions to compare MD simulations with different ion parameters and MD simulations with APBS calculations. For both computational methods, radial profiles were computed by integrating grid-based concentration data within a cylindrical volume surrounding the DNA. The cylindrical volume (Figure 2) considered has an axis that is coincident with the DNA axis and a height of 41 Å (the duplex’s height was ~42 Å), thereby ignoring ions that interact with atoms at the ends of the duplex.

Figure 2.

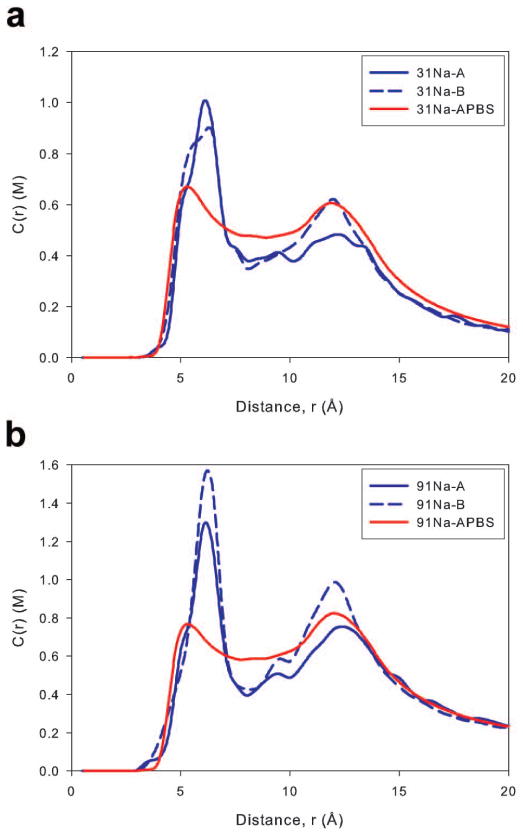
The concentration profiles determined from our MD simulations, along with those predicted by APBS calculations, are located in Figures 3a and 3b. The profiles generated from MD simulations have two main concentration peaks. The first peak (at ~6 Å from the DNA axis) results from interactions with electronegative atoms within the DNA grooves, while the second (at ~13 Å from the DNA axis) indicates interactions with phosphate groups. These profiles agree well with results from similar simulations of ions around DNA and A-RNA, ^13,19,22,69 although topological differences between RNA and DNA shift the position of the peaks. However, they differ from recent profiles of ions surrounding DNA obtained by Yoo et al. which contained only a single large peak.¹⁵ A possible cause of this difference is that, in the simulations described here, the duplex was three dimensionally restrained, while in Yoo et al., the DNA had increased freedom of motion as only its vertical orientation was constrained, which could allow the peaks to broaden and possibly overlap. Our MD simulations show the overall independence of the concentration profiles with respect to the ion parameters, though some peak size dependence was observed. For example groove floor binding (peaks in the 6 Å region) was fairly uniform between the two parameter sets at both concentrations, with 31Na-B having a slightly broader peak than 31Na-A and 91Na-B having a taller peak than 91Na-A. However, both Na-B simulations showed significantly higher backbone binding (peaks in the 13 Å region) than their Na-A counterparts. To explain the differences found in the backbone region, we analyzed Na⁺ ion contacts with all nucleic acid oxygen and nitrogen atoms, and found that both Na-B simulations were located more often within 3 Å of the O3′ sugar atom and the O1P phosphate atom. Contact data for select nucleic acid atoms is located in Supporting Figure 4. The differences between the Na-A and Na-B simulation types are expected based on the parameters used to model the Na⁺ ions (Table 2). The ions08 parameter set used in the Na-B simulations models the Na⁺ ion as smaller than the ions94 parameters in Na-A simulations, allowing ions in the B type simulations to interact more closely with negatively charged groups. Increased short range binding is also supported by the Na⁺-DNA radial distribution function (RDF) where the principal contact peak was approximately twice as high for systems with ions08 parameters (Supporting Figure 2). Whether the enhanced cation binding observed in the 31Na-B and 91Na-B systems better represents experimental results is not clear at the moment. However, Yoo et al. recently found better agreement with experimental osmotic pressure data for cation-acetate and cation-dimethyl-phosphate simulations while using a modified ions08 model.⁷⁰

Figure 3.

To effectively compare the concentration profiles obtained using MD simulations and the PB equation, we matched the bulk cation concentration observed in the MD simulation with the bulk cation concentration used in the subsequent PB calculation. However, as differences in binding to the DNA changed the observed bulk ion concentrations for the A and B type MD simulations, PB calculations were designed to match the bulk concentrations obtained in the B type (ions08) simulation. The first peak for both PB profiles was at approximately 5 Å, in good agreement with the location of the first peak of both simulations, but the peak heights of the PB profiles were significantly lower than observed in corresponding simulation profiles. Between the main peaks of the MD simulations (in the region from 7–10 Å from the DNA axis), PB theory predicted a higher cation concentration than what was observed in the simulations. Previously, it has been suggested that the higher cation concentrations found in PB calculations in the 7–10 Å region was the result of ion-ion correlations within MD simulations that are not considered in the mean-field PB theory.²² Specifically, cation-assisted approach of anions to regions near the nucleic acid have been observed in MD simulations; these anions exclude a certain volume from cations, reducing the observed cation concentration at radial distances containing the anions. However, we found an insignificant difference (less than 1%) in cation concentration once the anionic excluded volume was taken into account. In the region from 10–15 Å, PB theory matched the cation concentration found in the 31Na-B simulation, and it predicted a cation concentration between the two MD simulations for the 91Na systems. At greater distances where the influence of the duplex wanes, the two methods agreed well.

Mg²⁺ ion concentration profiles

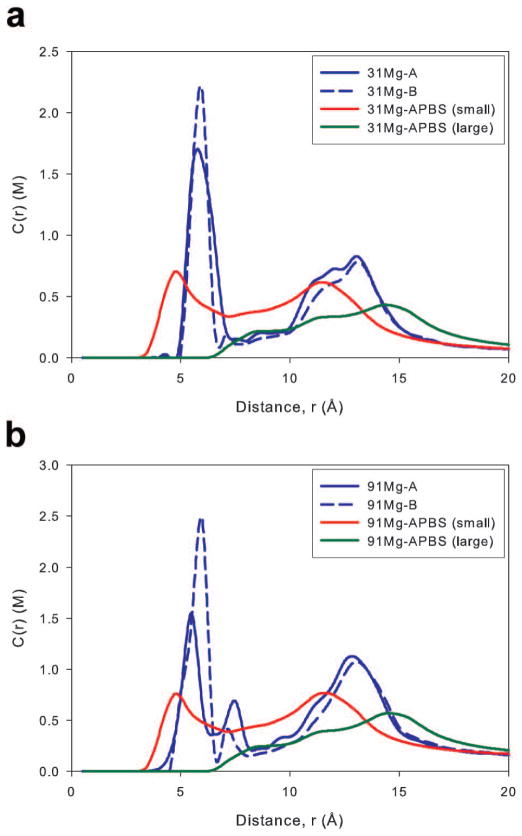
The Mg²⁺ ion concentration profiles obtained from MD simulations and PB calculations are located in Figures 4a and 4b. There were only minor differences between the two Mg MD systems, where both Mg-B simulations had a higher first peak and a slightly smaller peak near the backbone. Cations in both Mg-B systems were found to bind more often with N6 and O4 than cations in the Mg-A systems (Supporting Figure 5). Additionally, both 91Mg systems result in a peak just outside the groove floor region (~7 Å) that was not observed in the 31Mg systems. This peak was caused by cations binding to minor groove atoms near the sugar rings. Interactions in this region, though rare, have the potential for long term binding, with events lasting up to 20 ns.¹⁴ In the 91Mg-A simulation, we observed a single binding event between a Mg²⁺ cation and an O4′ atom that was maintained for 20 ns; this event and increased binding with O3′ and O5′ atoms help explain why the height of the 7 Å peak was higher in the type A simulation. Finally, there is a slight shift and diminished peak height for both Mg-B profiles in the 10–15 Å region caused by diminished O1P and O2P binding that may be due to differences in the cation size between parameter sets. The Mg²⁺ ion model in the ions94 (type A) parameter set is smaller than in the Allńer and Villa parameters (type B simulation), allowing for closer approach of the Mg²⁺ to DNA atoms, as supported by Mg²⁺-DNA radial distribution function (RDF) where the principal contact peak is closer for type A simulations than type B simulations (Supporting Figure 3). Even with this shift, the agreement between the two simulations remained quite good.

Figure 4.

As with Na⁺ ions, we matched the bulk concentration used in the PB calculation with the bulk concentration of the type B simulations. During the PB calculations, we modeled Mg²⁺ ions with probe radii of 0.86 Å, matching the size of a fully desolvated Mg²⁺ ion, or 3.36 Å, to approximate the size of a solvated cation (see Methods). It should also be noted that every Mg²⁺ ion in our MD simulations remained fully solvated. Agreement between the PB calculations and MD simulations was poor for both concentrations. When modeled with a 0.86 Å probe, the PB equation predicted very deep penetration, with cations approaching as close as 2.5 Å from the DNA axis; when a 3.36 Å probe was used, the cations could only approach to within approximately 6 Å of the axis. The PB calculations with both probe sizes did not predict the height and position of the first concentration peaks observed in simulations. In the 7–10 Å region, the 0.86 Å PB calculations resulted in greater cation concentrations than observed in simulations, but good agreement was achieved between both simulations and the 3.36 Å PB calculations. In the backbone region (10–15 Å), the differences between PB and MD simulations were similar to those observed in the groove floor, with PB theory for both probe radii predicting a lower amount of cation binding and different peak positions than MD simulations.

Two dimensional cation concentration plots

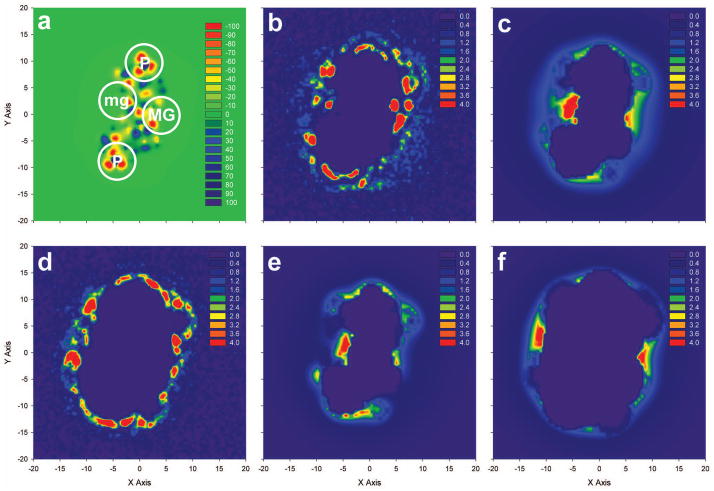
To more fully examine differences in the spatial distributions of cations surrounding DNA predicted by the PB equation and MD simulations, we calculated two dimensional cation concentration plots by integrating grid-based cation concentration and electrostatic potential data within a cubic volume surrounding either a central base-pair or the entire duplex. Figure 5 presents two dimensional cation concentration plots within a rectangular box with a height of 2 Å centered on the A₆-T₁₉ base pair for both 91Na-B and 91Mg-B systems. Peaks in negative electrostatic potential were found primarily near the phosphate backbone and the minor and major grooves (Figure 5a). Binding around the base pair for both 91Na-B and 91Mg-B (Figures 5b and 5d) was intense with the greatest concentration found within the major groove for 91Na-B and near the major groove and backbone for 91Mg-B. Not surprisingly, given that Mg²⁺ remained fully solvated in the simulations and the radial distribution profiles discussed previously, Na⁺ more deeply penetrated both major and minor groove sites than Mg²⁺ in the simulations.

Figure 5.

In general, the 91Na-B two-dimensional plots from the MD simulation (Figure 5b) and PB calculation (Figure 5c) show good qualitative agreement, with cation “hot spots” from both methods near the phosphate backbone and near the major and minor grooves. However, there were some differences between the methods, with the PB equation predicting deeper penetration into the minor groove and lacking some locations of high cation density, such as near (−5, 10), that are observed in MD simulations. Additionally, the magnitudes of the cation density surrounding the base pair did not consistently agree, as peaks in the cation concentration observed in MD simulations were significantly higher than those predicted by the PB equation. To facilitate comparisons in Figure 5, the density cutoffs used to generate the color scheme were identical for all panels and were selected using the concentrations observed in PB calculations. For example, the maximum density observed in the PB equation was located in the minor groove and had a value of 9.3 M, while, the maximum density observed in the MD simulation was 60 M in the major groove, and several locations had cation densities as high as 15 M.

The two-dimensional concentration plot from the 91Mg-B simulation (Figure 5d) was also compared to plots generated from both small and large ion probe PB calculations (Figures 5e and 5f). In general, agreement was poor between the calculation methods for the divalent cation, with the small and large probe PB contour plots bracketing the MD simulation contour. Reasonable agreement was observed for the MD simulation and small probe PB calculation especially near the backbone, but significant discrepancies were found in the minor groove. Groove binding in the large probe contour plot was similar to the binding observed in the MD contour; however, backbone binding was greatly diminished in the large probe contour. As with the Na⁺ ion contours, regions of high cation concentration in the MD simulations had higher magnitudes than corresponding regions in either the small or large probe PB calculation, with the maximum values in MD simulations more than 4 times as large as in PB calculations.

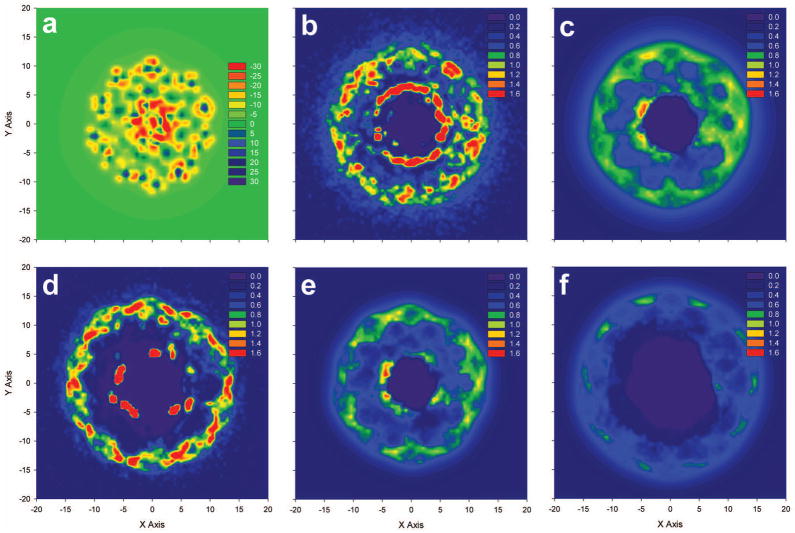
As with the radial concentration profiles, two-dimensional contour plots for the entire duplex (Figure 6) were calculated over a box with a height of 41 Å, ignoring some ions that interacted with the DNA’s termini. Peaks in negative electrostatic potential were roughly symmetric around the duplex due to the phosphate groups in the backbone (Figure 6a), with the largest negative potentials located at the groove floors. Similar to the contour around a single base pair, the binding of the different cations observed in MD simulations (Figure 6b for 91Na-B and Figure 6d for 91Mg-B) was similar around the phosphate groups, but had larger differences near the groove sites. As evidenced by the annulus of concentration approximately 5 Å away from the DNA center axis, Na⁺ was able to consistently penetrate major and minor groove sites, while Mg²⁺ was limited to a smaller number of groove binding sites. Comparison of the densities in the 91Na-B MD simulation (Figure 6b) with those of a corresponding PB calculation (Figure 6c) reveal many of the same features as observed for the plot around a single base pair, with both showing high cation densities at similar locations near the groove sites and phosphates and the PB calculation predicting more diffuse binding in both regions. Again, while the same scale to indicate color cutoff values was used for cation concentrations in all panels of Figure 6, the maximum cation concentrations in the MD simulations were much higher (12 M) than those observed in PB simulations (1.5 M).

Figure 6.

A comparison of the 91Mg MD simulation contour (Figure 6d) with those calculated using the small ion probe APBS calculation (Figure 6e) yielded surprisingly good agreement, as cation “hot spots” isolated from the MD simulation were reproduced fairly well with the PB calculation, although the more diffuse binding predicted by the PB equation was again observed, particularly near the phosphate backbone. While the PB calculation with the small probe radius predicted slightly deeper penetration into the grooves, many of the areas of high cation density near the groove sites, such as near (−4,3) and (5,−2) had corresponding high cation density regions in MD simulations. The MD simulation and the large ion probe PB calculation yielded drastically different contour plots. The large probe PB calculation has an almost complete lack of groove penetration and low backbone binding. Overall, the two dimensional cation concentration contours support the results found with the one dimensional radial concentration plots. The MD simulations produce higher, and more localized, peaks in cation density near groove sites and phosphate groups, while PB calculations have higher concentrations in the region between these peaks, as shown by the areas of green and yellow approximately 7 to 10 Å from the DNA axis in Figures 6c and 6e.

Number of excess ions and net solution charge

Recently, a common method of determining the number of cations bound to a nucleic acid oligomer from computational studies has been to use radial concentration profiles to calculate the number of ions in a volume near the nucleic acid in excess of the number of ions in an identical volume in bulk solution. The number of excess/bound ions calculated in computational studies has been directly compared to, and shown good agreement with, the results of ASAXS and BE-AES experiments.^12,15,28 Specifically, we compute the number of excess ions, N_i(r), of type, i, by integrating over the difference between the radial concentration, C_i(r), and the bulk concentration, C_Bulk, over a cylindrical volume

$$N_i(r)=2\pi h{\int }_0^r[C_i(r)-C_{\mathit{Bulk}}]\mathit{rdr}$$ (2)

where h is the height of the DNA duplex. Results for equation 2 from MD simulations and PB calculations are presented in Figures 7 and 8.

Figure 7.

Figure 8.

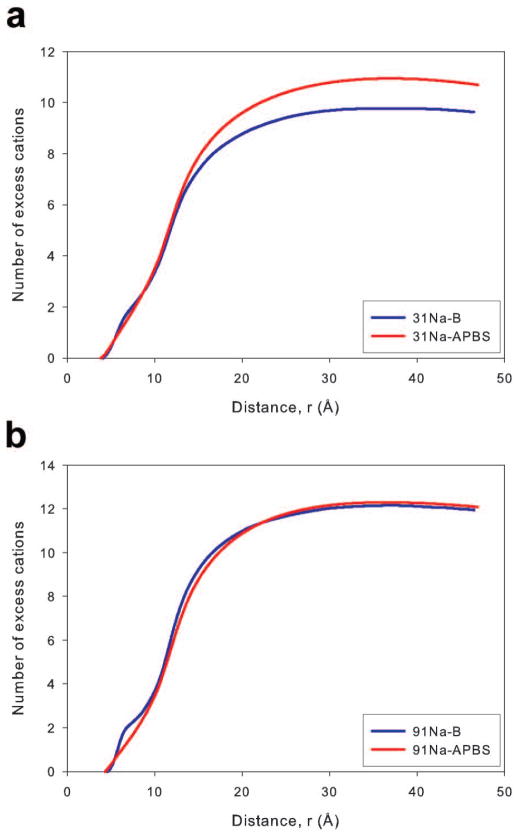
Good agreement between MD simulation and PB calculations was previously reported for the number of bound cations near a RNA duplex.²² However, it should be noted that the results presented in that work provided only the total number of excess ions in the entire simulation box, while the data presented here can be used to compare the development of the ion atmosphere moving away from the nucleic acid axis. The Na⁺ ions plots of equation 2 for both concentrations and theoretical methods are presented in Figure 7. Since the APBS calculations were matched to the type B simulations, only the ion distributions from those simulations will be used for this analysis. For both concentrations, there was good agreement between MD simulation and PB theory, and the overall difference between the methods was less than one Na⁺ ion for both concentrations at all distances from the DNA axis. MD simulations resulted in a slightly higher number of excess ions within 10 Å, a result of increased groove floor binding (Figure 3), while PB theory predicted a larger number of excess Na⁺ ions at radial distances beginning around 15 Å away from the DNA axis for the 31Na system.

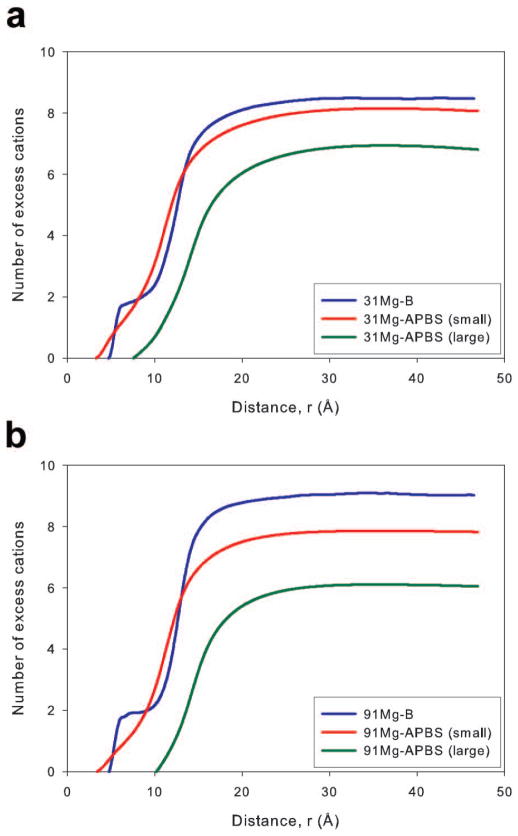
The Mg²⁺ ion plots of equation 2 are found in Figure 8. Type B MD simulations were compared to PB theory using a small and large ion probe (0.86 and 3.36 Å). Agreement between 31Mg-B MD simulation and the 0.86 Å probe APBS calculation was good- the number of excess ions at large radial distances was similar- and better than expected considering the significant discrepancies found in the radial concentration profiles (Figure 4). The good agreement between the small probe PB calculations and MD simulation was not completely repeated at the higher concentration, as the MD simulations predict a greater number of excess Mg²⁺ ions than the small probe PB calculations except in a region from ~8 to 15 Å away from the DNA axis. The PB theory using a large ion probe was not able to satisfactorily reproduce the binding behavior of Mg²⁺ ions at either concentration, failing to match any local features of the ion distributions or the overall number of excess cations.

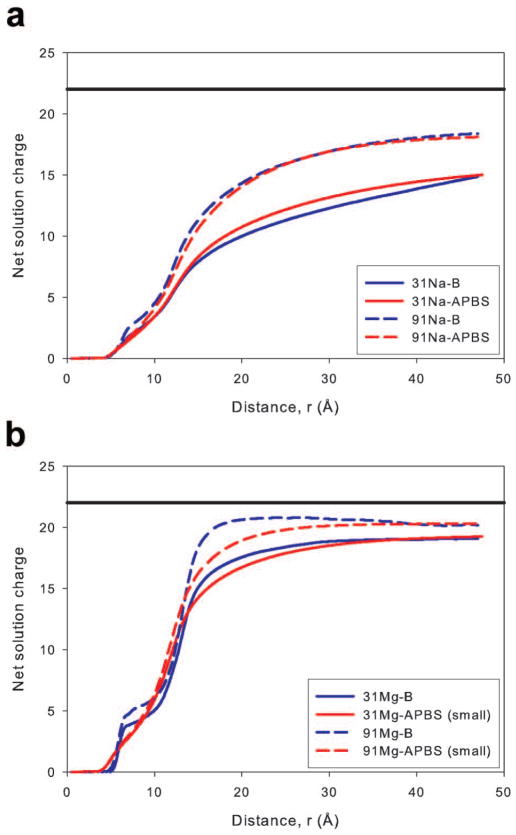
The net solution charge, calculated by considering the total number of cations and anions, as a function of the distance from the DNA axis for the Na and Mg systems is presented in Figure 9. For the Na systems (Figure 9a), the close agreement observed in the bound cation data was repeated. The MD simulations and PB calculations yielded essentially the same net solution charge throughout the radial distance range without reaching total system neutrality (solid black line in Figure 9). The agreement between the Mg²⁺ ion simulations and small ion probe PB calculations improved when comparing the net solution charge. Net charge results for the large ion probe PB calculations are not presented in Figure 9b for clarity, though it should be noted agreement between MD simulations and these PB calculations remained poor. The agreement in the net solution charge for Mg²⁺ systems between the small ion probe PB calculations and MD simulations was surprising based on the cation concentration profiles. However, the agreement can be explained by considering that the closer approach of Mg²⁺ ions to the DNA axis and their higher concentration in the 7–10 Å region while using PB theory counteracts the higher concentrations near groove and phosphate sites observed in MD simulations. Additionally, we note that the net solution charge displayed in Figure 9 did not completely neutralize the DNA for any system. However, this result is due to the fact that the region sampled when calculating the charge included only a cylinder centered on the DNA axis with approximately the same height as the DNA duplex (Figure 2). Cations interacting with the ends of the DNA duplex are often outside of this cylinder and were not included in the calculated net solution charge. We determined the net solution charge while increasing the cylinder height and found that including ions above and below the DNA duplex allowed the net solution charge to more closely approach a value that would neutralize the DNA (Supporting Figure 6). The net solution charge in a cylinder of height 71 Å (approximately 15 Å above and below the end of the DNA) shows similar agreement between predictions of MD simulations and the PB equation (Supplementary Figure 6) as a cylinder with a height equal to the DNA (Figure 9).

Figure 9.

The size of the ion atmosphere is commonly estimated by determining the distance at which charge neutrality occurs. In ASAXS experiments and MD simulations, the ion atmosphere’s size was found to be a function of both the ion’s valence and the bulk ion concentration.^13,15,28 As previously discussed, the calculated net solution charge of the systems did not reach neutrality, but a clear rise in net charge and to shorter distances was observed when the valency and concentration was increased (Figure 9). Although a clear ion atmosphere size could not be obtained, the reported trend was reproduced. To obtain an estimate of the atmosphere size we used the point where the radial cation concentration returned to the bulk ion concentration. Using this definition resulted in ion atmosphere sizes for Na⁺ and Mg²⁺ ions of 25–30 Å and 20 Å, respectively (Figures 7 and 8). These results are in general agreement with previous experimental and theoretical results though direct comparisons are problematic due to the different nucleic acid systems.

Conclusions

In this work, we have examined monovalent and divalent ion distributions around a DNA oligomer with MD simulations and the Poisson-Boltzmann equation. The ion atmosphere was described with radial and two-dimensional concentration profiles within volumes centered and aligned to the duplex’s vertical axis. Our analysis of the ion atmosphere focused on its local and global characteristics, including the number and radial location of ion density peaks, the number of excess cations, and the net solution charge. We also examined the effect of using different ion descriptions on MD-calculated ion distributions. Similarly, a series of calculations were performed to determine the influence of APBS input parameters on predicted ion distributions.

To examine how MD parameters impact the local features of the ion atmosphere and specific interactions that take place within it, we compared radial concentration profiles of Na⁺ and Mg²⁺ around the DNA using MD simulations with two sets of cation parameters (Table 1). For both Na⁺ and Mg²⁺, the general features of the profiles for the different parameter sets were similar, with the concentration profiles for both ions showing peaks located near electronegative atoms within the DNA grooves and near the DNA phosphate groups. However, the different ion parameters did have some impact on both the heights and specific locations of these peaks. Na⁺ ions modeled using the newer parameter set (ions08) bound more readily to backbone sites (Figure 3), while Mg²⁺ binding was more consistent across the different parameter sets, with only slight differences in groove interactions.

While differences between radial concentration profiles surrounding DNA between MD simulations using different ion parameters were modest, differences between the profiles generated using MD simulations and PB theory were more significant. In general, the radial concentration profiles of cations surrounding DNA (Figure 3 and 4) from PB theory had a more diffuse arrangement of cations around the DNA than MD simulations. While MD simulation profiles had peaks at the groove sites and phosphate groups separated by a distinct valley from ~7–10 Å from the DNA central axis, the PB profiles had shorter and broader peaks and a concentration from 7–10 Å that was typically higher than what was observed in corresponding MD simulations. These differences were also observed in two-dimensional plots of the concentration surrounding a DNA base-pair (Figure 5) or the entire DNA axis (Figure 6), where MD simulations predicted higher maximum concentrations and concentration peaks that were localized to specific binding sites in groove regions and near the phosphate backbone in comparison with the more diffuse binding predicted by corresponding PB calculations. To some extent, the higher maximum concentrations observed in MD simulations may be the result of the MD simulations only being averaged over a relatively short time period, while the PB equation is a mean field theory. However, many of the observed differences between the methods, such as differences in the depths of penetration into grooves and in the concentration in the regions between the grooves and phosphates, seem unlikely to be related to the limited sampling of MD simulations.

In agreement with previous studies, we observed much larger discrepancies between the distributions of Mg²⁺ around a nucleic acid oligomer predicted by MD simulations and by PB theory than in corresponding comparisons of Na⁺ distributions. To further investigate these differences, we examined the impact of the probe radius used in PB calculations for Mg²⁺ surrounding DNA by comparing Mg²⁺ modeled as an ion with a radius of 0.86 Å, representing a fully desolvated ion, with Mg²⁺ modeled with a radius of 3.36 Å, the distance of closest approach between Mg²⁺ ions and DNA duplex atoms observed in MD simulations, representing a fully solvated ion. In accord with expectations from previous simulation and experimental results, Mg²⁺ remained fully solvated in all simulations here and was only observed to bind to the DNA through water-mediated interactions, and, therefore, using a large radius probe in PB calculation to represent a solvated Mg²⁺ ion could potentially represent DNA-ion interactions more accurately. However, we found that radial concentration functions around the DNA from PB calculations using the larger radius model had very poor agreement with MD simulations. The distance of closest approach to the DNA axis was ~6 Å using the larger, solvated PB probe radius, compared to ~2.5 Å for the smaller, desolvated probe radius and ~5 Å for MD simulations (Figure 4). Despite Mg²⁺ ions in the MD simulations remaining fully solvated throughout the simulation, they were able to penetrate more deeply into the DNA than the PB probe assuming a solvated ion radius, revealing flexibility in the hydrated Mg²⁺ ions and the DNA duplex that is not reproduced in the PB calculations. Therefore, while Mg²⁺ maintains its 1^st solvation shell, accounting for the impact of these strongly bound waters by using a large probe Mg²⁺radius results in a significant underestimation of the binding between Mg²⁺ and nucleic acids.

Despite differences in the radial concentration profiles, the number of excess cations and net solution charge predicted by MD simulations and PB theory showed good agreement for Na⁺ systems and reasonable agreement for Mg²⁺ when using a 0.86 Å probe radius in the PB equation. The results shown here agree with previous comparisons of PB calculations and MD simulations.^19,22 Kirmizialtin et al. found good agreement for the number of bound ions between PB theory and MD simulations over a large volume.²² Their work used several PB methodologies, an unmodified nonlinear PB, a size-modified PB derived from a lattice gas approach, and a distance-dependent solvent dielectric constant, which improved agreement between MD and PB radial ion concentration profiles, but did not significantly improve agreement in the number of ions bound to the DNA. In this work, we show that not only do the number of excess cations and net solution charge predicted by MD simulations and a standard PB theory treatment agree when considering a large volume surrounding a nucleic acid, but these properties can also show reasonable agreement near the nucleic acid, despite the differences in local binding distributions (i.e., radial and two-dimensional concentration profiles) near the nucleic acid. Our current study, using a widely available, unmodified PB solver without ion size or solvent dielectric corrections, produced very similar results to those produced with heavily customized PB treatments by Kirmizialtin et al. for integrated properties, such as the number of bound ions and net solution charge. To achieve reasonable agreement with MD simulations for these integrated properties, both Na⁺ and Mg²⁺ were modeled in PB theory with probe radii equal to experimentally determined unsolvated ionic radii,⁶⁵ suggesting that using default ion probe sized when solving the PB equation may not always be appropriate. Additionally, we note that agreement between the number of bound ions does not guarantee complete agreement in the local distributions of cations surrounding nucleic acids. For example, while using a PB probe radius corresponding to an unsolvated Mg²⁺ ion predicted a number of Mg²⁺ ions bound to the DNA approaching the value predicted by MD simulations, it did so by predicting deeper penetration of cations into groove sites and closer approach to the DNA center axis during Mg²⁺-phosphate interactions.