Determination of reference values for optical properties of liquid phantoms based on Intralipid and India ink

Abstract

A multi-center study has been set up to accurately characterize the optical properties of diffusive liquid phantoms based on Intralipid and India ink at near-infrared (NIR) wavelengths. Nine research laboratories from six countries adopting different measurement techniques, instrumental set-ups, and data analysis methods determined at their best the optical properties and relative uncertainties of diffusive dilutions prepared with common samples of the two compounds. By exploiting a suitable statistical model, comprehensive reference values at three NIR wavelengths for the intrinsic absorption coefficient of India ink and the intrinsic reduced scattering coefficient of Intralipid-20% were determined with an uncertainty of about 2% or better, depending on the wavelength considered, and 1%, respectively. Even if in this study we focused on particular batches of India ink and Intralipid, the reference values determined here represent a solid and useful starting point for preparing diffusive liquid phantoms with accurately defined optical properties. Furthermore, due to the ready availability, low cost, long-term stability and batch-to-batch reproducibility of these compounds, they provide a unique fundamental tool for the calibration and performance assessment of diffuse optical spectroscopy instrumentation intended to be used in laboratory or clinical environment. Finally, the collaborative work presented here demonstrates that the accuracy level attained in this work for optical properties of diffusive phantoms is reliable.

1. Introduction

Optical measurements at visible and near infrared (NIR) wavelengths are inherently noninvasive, with a potentially high information content. NIR light deeply penetrates into biological tissue, allowing to investigate large tissue volumes and deep biological structures (breast, brain, bone, etc.). Photon propagation through turbid media has been investigated in depth for biomedical applications. Different instrumental techniques have been devised, based on continuous wave (CW), time and frequency domain approaches [1]. The main information recovered by these techniques is related to the optical properties of the tissues explored, that is their absorption and scattering coefficients. Due to the heterogeneity of various biological tissues, a great effort has been devoted to the development of suitable theoretical models for data analysis [2]. The correlation of differences in the retrieved optical properties of investigated tissues to the underlying tissue alterations, both of physiological or pathological origin, is the main target of measurements based on NIR light.

As optical technologies are developing towards clinical applications, the assessment of the reliability of the recovered information is an essential issue that needs to be addressed. Various protocols for the performance assessment of such a kind of instruments have been proposed (in particular, the MEDPHOT and nEUROPt protocols [3, 4]). In addition, there have been recent attempts to establish procedures for quality control of different instruments involved in a multi-center clinical trial [5]. For the implementation of standardized procedures, however, diffusive phantoms, i.e. synthetic media mimicking the optical properties of biological tissues in the visible and NIR wavelength ranges, are needed. In order to be effective in standardized procedures, such phantoms should have accurately determined and stable optical properties, be reproducible, easy to find and, possibly, low-cost. Many diffusive materials have been proposed for preparing diffusive phantoms (for a review see Ref. [6]). However, none of them seems to match all the characteristics mentioned above: in particular, optical properties of none of them have been characterized accurately enough.

Water dilutions of India ink and Intralipid have been widely used to prepare diffusive phantoms for biomedical applications. As a matter of fact, liquid phantoms offer very high flexibility regarding the possibility to gradually change optical properties and to realize various inhomogeneous geometries. Moreover, provided that the mixtures are freshly prepared, with accurate weighing and homogeneous mixing of the components, liquid phantoms can easily be replicated: this can be an advantage in common measurement campaigns.

After pioneering papers characterizing diffusive and absorption properties of Intralipid [7,8], optical properties of India ink and Intralipid have been considered, more recently, for extensive studies [9,10]. Intralipid is a pharmaceutical product used for parenteral nutrition, consisting of small fat droplets suspended in water that make it a highly scattering medium. This compound is inexpensive and readily available on the market. The uniformity among batches is excellent, as was demonstrated by Di Ninni et al. [9]. Batch-to-batch variations of the reduced scattering coefficient of Intralipid were found to be about 2%, while its absorption coefficient is very small and practically equal to absorption of water. Furthermore, it remains stable for a long time (tests have been performed on samples with expiration dates spanning over about 10 years [9]). Finally, in a recent study small variations have been also found between the optical properties of several fat emulsions of different brands having a similar composition to Intralipid [11]. This fact suggests that the characteristics found for Intralipid are also true for other fat emulsions used in parenteral nutrition and can be related to the highly stringent quality control and tight specifications used in the production process of such pharmaceutical products.

As for India ink, it is readily available and inexpensive as well, and consists of insoluble carbon particles suspended in water. It is chemically and spectroscopically stable, nontoxic and non fluorescent. The main drawback is that, being a suspension, particles may sediment over time giving rise to clusters. To obtain reproducible and stable optical properties it is therefore necessary to apply ultrasound for about 30 minutes before using. Furthermore, due to the size of carbon particles, India ink also scatters visible and NIR light, and this complicates the measurements of its absorption coefficient. In Ref. [10] the absorption coefficients of India ink coming from different brands and different batches were systematically studied. Even if large (more than a factor of two) brand-to-brand and batch-to-batch variations were observed for the intrinsic absorption coefficient ε_a,ink and the intrinsic extinction coefficient ε_e,ink, the scattering albedo of the carbon particles showed small variations: the ratio ε_a,ink/ε_e,ink averaged over the different batches and brands was 0.839 at λ = 632.8 nm and 0.885 at λ = 751 nm and 833 nm, and the corresponding maximum deviations from the average were 5.2%, 2.2%, and 3.9%, respectively. Measurements of the extinction coefficient (accurate values are easily obtainable from measurements of collimated transmittance or from spectrophotometric measurements), together with the results of Ref. [10] for the ratio ε_a,ink/ε_e,ink, can be therefore used to predict the absorption coefficient with an uncertainty probably less than 4%. In Ref. [10] it was also demonstrated that the optical properties of diluted India ink are stable for a long time as a monitoring for about one year shows. Finally, it was demonstrated that India ink does not alter the scattering properties of Intralipid when they are mixed together in water. Then, all these properties make India ink and Intralipid promising for becoming reference compounds to prepare diffusive phantoms.

In the framework of the European Project “nEUROPt” (see acknowledgments) a first attempt to accurately characterize optical properties of India ink and Intralipid-20% has been performed by a pilot multi-center study involving 5 research laboratories [12]. The results obtained from different laboratories exploiting different measurement techniques, instrumental set-ups and analysis methods demonstrated the possibility of obtaining a satisfactory agreement among the values of the optical parameters. They also showed that such characterization is not a trivial issue, as substantial uncertainties associated to the obtained values have been found.

In this work, we extend and complete the characterization work started before [12]. Nine research laboratories independently determined the intrinsic absorption coefficient of undiluted India ink, ε_a,ink, and the intrinsic reduced scattering coefficient of Intralipid-20%, ${\epsilon }_{s,\text{il}}^{\prime }$ , at several wavelengths. From the comparison of the different values obtained for ε_a,ink and ${\epsilon }_{s,\text{il}}^{\prime }$, the main result we expect is a cross validation of different instrumentations and methodologies used for measurements of optical properties of diffusive samples, and, in case, the identification of techniques that provide biased results. Furthermore, by analyzing the measurements and their associated uncertainties with a suitable statistical model, we expect to obtain reliable reference values for the optical properties of compounds widely used for liquid tissue phantoms.

2. Materials and methods

2.1. Intrinsic optical properties

To start from the same material, pre-dilutions of India ink (Higgins Waterproof Black India Ink, Sanford, USA) and bags of Intralipid^®-20% (IL, Fresenius Kabi Italia, Italy) from the same production batch were distributed by UNIFI (see affiliation list) to all participating laboratories. A pre-dilution factor of about 7.5 · 10⁻³ for India ink was realized with a relative accuracy better than 0.1%.

As a general procedure, the intrinsic (i.e. for the undiluted compound) optical properties of India ink and IL, ε_a,ink and ${\epsilon }_{s,\text{il}}^{\prime }$ respectively, have been determined by performing measurements of absorption and reduced scattering coefficients on diffusive dilutions prepared with different concentrations of the distributed common samples of the two compounds. If we consider volume concentrations low enough, the absorption coefficient μ_a and the reduced scattering coefficient ${\mu }_s^{\prime }$ of a particular diffusive dilution are linearly related to the volume concentrations of the undiluted compounds. In order to maximize the accuracy in the estimation of the actual concentrations used for the preparation of diffusive dilutions, we considered concentrations in terms of mass. This makes no difference in the case of pre-diluted India ink, while for IL the volume concentration differs from the mass concentration due to the density of IL, which is slightly smaller than that of water: δ_il = 0.988g/cm³ [13]. Then, we assume:

$${\mu }_a={\epsilon }_{a,\text{ink}}{\rho }_{\text{ink}}^{\text{m}}+{\mu }_a^{\text{BKG}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mu }_s^{\prime }={\epsilon }_{s,\text{il}}^{\prime }{\rho }_{\text{il}}^{\text{m}},$$ (1)

where ${\rho }_{\text{ink}}^{\text{m}}=m_{\text{ink}}/m_{\text{dil}}$ and ${\rho }_{\text{il}}^{\text{m}}=m_{\text{il}}/m_{\text{dil}}$ are the mass concentrations of undiluted India ink and IL, respectively, m_dil being the total mass of the mixture of water, ink and IL, while ${\mu }_a^{\text{BKG}}$ is a background contribution to the absorption that does not depend on ${\rho }_{\text{ink}}^{\text{m}}$ and negligibly on ${\rho }_{\text{il}}^{\text{m}}$ [9]. The maximum compound concentrations considered in the measurements are about 10⁻⁵ for ${\rho }_{\text{ink}}^{\text{m}}$ and 0.1 for ${\rho }_{\text{il}}^{\text{m}}$, which guarantee deviations of less than 2% from the linear behavior given in Eq. (1) for the optical properties [14–16].

Furthermore, the assessment of the intrinsic optical properties has been performed at different wavelengths, when possible, in order to also have a spectral characterization of these compounds.

Finally, we would like to stress that the intrinsic values of the optical properties are all that one needs in order to prepare diffusive phantoms with known optical properties.

2.2. Scattering cell

Each laboratory was free to choose the most appropriate measurement geometry and the container for phantom preparation. However, since with time-resolved methodologies the optical properties are usually retrieved from measurements of reflectance or transmittance at several distances from the source (or offsets in case of transmittance), laboratories with a time-resolved instrumentation were provided with a tank designed, replicated and distributed by UNIFI. It consists of a black cell (120 mm × 140 mm lateral dimension and adjustable thickness) with a series of transparent windows on the front and rear walls (see Fig. 1) that guarantees well-defined boundary conditions and prevents internal reflections that might occur with transparent walls, with the risk of substantially compromising the measures.

Fig. 1.

Photo of the scattering cell designed by UNIFI and used for phantom preparation and measurements.

2.3. Instrumental set-ups and data analysis

In the following, we report a short description about the technique and the analysis procedure that each laboratory adopted to characterize at its best the optical properties of supplied India ink dilution and IL. In particular, for each laboratory the wavelengths at which the characterization was performed and the main sources of uncertainty are reported. Each laboratory is referred to with the acronym defined in the affiliations list. A summary of such information is reported in Table 1.

Table 1.

Measurement techniques, wavelengths λ and analysis methods adopted by the laboratories involved in the present study: TR – Time Resolved; IS – Integrating Sphere; DM – Direct Method; CW – Continuous Wave; SR – Spatially Resolved; MC – Monte Carlo; DE – Diffusion Equation. The laboratory identification number ID is used in Fig. 2.

Lab.	ID	Technique	λ (nm)	Analysis method
POLIMI	1	TR	633, 750, 833	Linear time-resolved method [17]
INO	2	TR	633, 750, 830	Non-linear fit, MC simulations [18]
IBIB	3	TR	830	Method of moments [19]
TomOptUS	4	IS + DM	633, 751, 833	Inv. add. doubling + Linear method [20]
UNIFI	5	CW-SR	633, 751, 833	Linear CW method [15, 21]
ICFO	6	TR	687, 785, 830	Non-linear fit, DE model
ILM	7	CW-SR	633, 750, 830	Non-linear fit, MC simulations [22]
PTB	8	TR	750, 830	Linear time-resolved method [17]
ULUND	9	TR	751, 833, 916	Non-linear fit, MC simulations

POLIMI

A time-resolved set-up for NIR spectroscopy based on a supercontinuum laser source (SC450, Fianium, UK) working at 20 MHz repetition rate and a double microchannel plate photomultiplier tube (R1564U, Hamamatsu Photonics, Japan) for detection has been exploited. Time-resolved detection is achieved by means of the time-correlated single-photon counting (TCSPC) technique, implemented with a personal computer board (SPC-130, Becker&Hickl, Germany). Two glass step-index fibers (diameter 1 mm, length 50 cm, NA 0.39) have been used to deliver laser light to and collect diffuse signals from the sample. The diffusive dilutions were placed in the black tank with transparent windows described above (see Fig. 1). The used wavelengths were 633, 750 and 833 nm, while the measurements were performed in reflectance configuration at 20 and 30 mm inter-fiber distances.

Absorption and reduced scattering coefficients were retrieved by exploiting a linear method [17]. As for the absorption coefficient, this method is based on the comparison of two time-resolved measurements at different values of the absorber concentration. In particular, if we denote as μ_a0 the absorption coefficient of the diffusive medium without India ink, and as μ_a the absorption coefficient for the actual India ink concentration, the two corresponding time-resolved reflectance curves R(t, μ_a) and R₀(t, μ_a0) follow, from a general property of the radiative transfer equation [23], the relation:

$$\text{ln}\left(\frac{R_0}{R}\right)=\mathrm{\Delta }{\mu }_{a}vt+\text{ln}\left(\frac{A_0}{A}\right),$$ (2)

where Δμ_a = μ_a − μ_a0 is the increase of the absorption coefficient due to the added absorber; v is the speed of light in the medium; A and A₀ are coefficients that take into account source and detector efficiencies that can vary for the two measurements. Then, by means of a linear fit, we can extract the value of Δμ_a at the particular India ink concentration ${\rho }_{\text{ink}}^{\text{m}}$. By performing this procedure and varying ${\rho }_{\text{ink}}^{\text{m}}$, we can estimate the intrinsic absorption coefficient ε_a,ink of India ink (see Eq. (1)).

As for the reduced scattering coefficient of IL, we assume that in the scattering solution light propagation is described by the diffusion equation. By denoting as r the distance between the injection and detection points, the measured time-resolved reflectance curves R₀(t, r₀) and R(t, r) for two different source-detector distances r₀ and r respectively, satisfy the following relation [17]:

$$\text{ln}\left(\frac{R_0}{R}\right)=\frac{3{\mu }_s^{\prime }(r^2-r_0^2)}{4vt}+\text{ln}\left(\frac{A_0}{A}\right).$$ (3)

From the slope of the linear regression between the independent variable 1/t and the dependent variable ln(R₀/R) one can determine the reduced scattering coefficient ${\mu }_s^{\prime }$ and, then, the intrinsic scattering coefficient ${\epsilon }_{s,\text{il}}^{\prime }$ by repeating the measurements for different ${\rho }_{\text{il}}^{\text{m}}$ (see again Eq. (1)).

Finally, from an accurate analysis of the possible uncertainty sources affecting the measurements, it results that the non-ideal instrumental response function (IRF) of the system set-up is responsible for the major contribution to the uncertainties of ε_a,ink and ${\epsilon }_{s,\text{il}}^{\prime }$.

INO

INO’s time-resolved transmittance (TRT) characterization set-up was used to determine the optical properties of the samples [18]. A supercontinuum laser (SC400, Fianium, UK) generates ≈ 90 ps light pulses at a frequency of 20 MHz. The laser light is filtered with narrow bandpass interference filters. A small fraction of the light is sent to a synchronization detector (PHD-400, Becker&Hickl, Germany). The remaining narrow collimated beam is normally incident on the samples. Since the set-up is optimized for small solid phantoms, the liquid samples were contained in small clear rectangular cell culture bottles with a thickness of about 2 cm. Light exiting the sample on the opposite side is collected with a photon counting micro-channel plate photomultiplier tube (MCP-PMT) (R3809U, Hamamatsu, Japan) located 8 cm from the exit surface. The signals from the PMT and the synchronization detector are sent to the TCSPC computer board (SPC-730, Becker&Hickl, Germany). The optical signal is attenuated to maintain a count rate of about 2 · 10⁴ photons/s in order to avoid the broadening effect that a high count rate has on MCP-PMT instrument response function. The IRF is measured with a piece of thin (< 50 μm) translucent diffuser so that light covers the total area of the MCP-PMT.

After correction for background, sample thickness and IRF, TRT data were compared to a forward model based on the radiative transfer equation solved through Monte Carlo simulations taking into account the finite geometry of the sample [18]. Values of μ_a and ${\mu }_s^{\prime }$ were then extracted with a non-linear optimal fit procedure. In particular, ${\epsilon }_{s,\text{il}}^{\prime }$ was obtained by considering 5 dilutions of IL, with concentrations ranging from 3% to 7%. Moreover, in order to determine ε_a,ink, 7 dilutions of India ink were prepared with concentrations varying from 0% to 1% and 2% of IL added.

Accuracy of the method was estimated through an uncertainty analysis taking into account all possible uncertainty sources [18] (we note that, since [18] was published, some uncertainty contributions have been mitigated). Uncertainty sources are: measurement noise, system repeatability, IRF stability, sample thickness, refractive index, anisotropy factor, TCSPC system time-base and forward model inaccuracies. Since ε_a,ink and ${\epsilon }_{s,\text{il}}^{\prime }$ are slopes, linear regression uncertainties were also included.

IBIB

The phantom experiments were carried out using a time-resolved optical set-up [24]. A MaiTai tunable pulsed laser (Spectra-Physics, USA) was used to generate femtosecond light pulses at 80 MHz repetition rate and at wavelength of 830 nm. The light was delivered to the medium with the use of an optical fiber (length 1 m, diameter 1 mm and NA 0.39, Thorlabs, Sweden). Power of the light delivered to the surface of studied medium was approximately 75 mW. The diffusely reflected photons were collected at 30 mm source-detector separation, using a fiber of the same type. The avalanche photodiode (PDM 50CT, MPD, Italy) was used for detection of the reemitted photons and the single photon pulses were counted with a TCSPC board (SPC-130, Becker&Hickl, Germany). Distributions of times of flight of photons (DTOFs) were acquired. IRF was measured with a sheet of white paper covering the detecting fiber tip in order to fill its numerical aperture [25]. The full width at half maximum (FWHM) of IRF was about 70 ps. The measurements were carried out in reflectance geometry, exploiting the supplied scattering cell (see Fig. 1) with 30 mm thickness.

The optical coefficients of the studied medium μ_a and ${\mu }_s^{\prime }$ were estimated using the method of moments [19] which is based on diffusion theory. The measured DTOFs were preprocessed by background subtraction and analyzed in a range between 10% of maximum number of photons on the rising edge and 1% on the trailing slope of the DTOF. The statistical moments, mean time of flight 〈t〉_m and variance V_m, of the photon DTOFs measured in the medium were calculated and the respective moments of the IRF, 〈t〉_IRF and V_IRF, were subtracted (〈t〉 = 〈t〉_m − 〈t〉_IRF, V = V_m − V_IRF). Finally, the optical properties were obtained from following equations [19]:

$${\mu }_a=\frac{{\langle t\rangle }^4}{2vV\left({\langle t\rangle }^2+V\right)},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mu }_s^{\prime }=\frac{2v\langle t\rangle \hspace{0.17em}\hspace{0.17em}\left({\langle t\rangle }^2+V\right)}{3r^{2}V},$$ (4)

where v is the speed of light in the medium (refractive index was assumed to be n = 1.33) and r is the source-detector separation. Uncertainties of evaluated optical properties were estimated by considering the properties of the method of moments (5% accuracy as reported in [19]) and by analyzing the results of repeated measurements.

TomOptUS

The method used by TomOptUS to determine the properties of Intralipid and India ink is based on the CW measurement of total transmittance T and total reflectance R with an integrating sphere set-up, and ballistic transmission T_b with a direct set-up.

The direct method to measure T_b consists in two power measurements: the incident power P_i and the transmitted ballistic power P_b, using diaphragms as described in Ref. [15] to reduce as much as possible the contribution of scattered light to the measured transmitted light. The extinction coefficient μ_e of a sample of thickness l is obtained using the Beer-Lambert law for T_b:

$$T_{\text{b}}=\frac{P_{\text{b}}}{P_{\text{i}}}=\text{exp}(-{\mu }_{e}l).$$ (5)

The integrating sphere method is used to determine ${\mu }_s^{\prime }$. Compared to the double integrating sphere set-up described in Ref. [26], a single integrating sphere set-up was used here. Both set-ups are equivalent, only that the double-integrating sphere allows measuring the diffuse transmitted and diffuse reflected powers simultaneously without having to move the sample from one port of the sphere to another. Our particular integrating sphere (RT-060-SF sphere with SDA-050-U detector and SC-6000 controller, Labsphere Inc., North Sutton, NH, USA) has an input port and an output port facing the input port on the other side of the sphere.

In the present case, measurement of the diffuse reflected power P_diff,R is made with the sample installed on the output port with the laser beam going through the sphere via the input port. A reference power P_std measurement is made using a reflectance standard R_std installed in the output port and a void power measurement P_void,R is made with a beam passing straight through the sphere as the input and output ports are empty (this is somewhat similar to a dark measurement). As regards the measurements required for obtaining the total transmittance, all are made with the output port filled by a reflectance standard having the same reflectance as the inner wall of the sphere. The diffuse transmitted power P_diff,T is measured with the sample installed on the input port of the sphere and laser light impinging on it. A power measurement P_void,T is made with the input port being empty, and finally a dark measurement P_dark is made with the beam being blocked at the input port. The total reflectance and transmittance are then obtained using the following equations

$$R=R_{\text{std}}\frac{P_{\text{diff},R}-P_{\text{void},R}}{P_{\text{std}}-P_{\text{void},R}},$$ (6)

$$T=\frac{P_{\text{diff},T}-P_{\text{dark}}}{P_{\text{void},T}-P_{\text{dark}}}.$$ (7)

Once the total reflectance and transmittance are measured at a given wavelength, an inverse adding-doubling (IAD) algorithm is ran to determine the corresponding optical properties of the sample at that wavelength. The IAD program used is that of Prahl available on Internet with its documentation [27]. It computes ${\mu }_s^{\prime }$ in an iterative manner. It also provides the anisotropy coefficient g, which allows us calculating μ_s, and then μ_a from μ_e.

We use a 10 mm thick glass cell (Hellma, Müllheim, Germany) to characterize the liquid samples. As light sources, a tunable Ti:Sapphire laser (Tsunami, Spectra-Physics, USA tuned at wavelengths of 751 nm and 833 nm) and a He-Ne laser (633 nm) were used. To obtain the intrinsic coefficients, measurements of ${\mu }_s^{\prime }$ and μ_e are carried out at several concentrations and a linear fit is made. The slope of the line is the corresponding intrinsic coefficient. For the measurements of ${\mu }_s^{\prime }$, 10 different concentrations ${\rho }_{\text{il}}^{\text{m}}$ ranging from 0.001 to 0.041 were used. In such cases, the samples obey the independent scattering approximation. As regards μ_e measurements, 10 different concentrations ${\rho }_{\text{ink}}^{\text{m}}$ were also used ranging from 4.87 · 10⁻⁵ to 8.64 · 10⁻⁴.

Several sources of errors have been identified (sample thickness, refractive index, India ink and IL concentrations, IAD algorithm itself, repeatability). Every contribution has been taken into account to calculate the total error on each measured value. Then the linear fit of the optical properties as a function of the concentration is computed using a linear regression algorithm described in Ref. [28], and taking into account the total maximum statistical error on ${\mu }_s^{\prime }$ or μ_e and on concentrations. The slope of this linear fit (i.e. the intrinsic property) and its error are provided by the linear regression algorithm.

UNIFI

Both ${\epsilon }_{s,\text{il}}^{\prime }$ and ε_a,ink have been obtained from measurements of the effective attenuation coefficient ${\mu }_{\text{eff}}=\sqrt{3{\mu }_a{\mu }_s^{\prime }}$. To measure μ_eff, relative multidistance measurements of the fluence rate ϕ(r) have been carried out for an infinite medium geometry illuminated by a CW point-like isotropic source. For a point source with unit power, the solution of the diffusion equation gives:

$$\varphi (r)=3{\mu }_s^{\prime }/(4\pi r)\text{exp}(-{\mu }_{\text{eff}}r),$$ (8)

and μ_eff is obtained from the slope of the straight line that best fits ln[rϕ(r)] as a function of the source-receiver distance r. Measurements have been carried out at three wavelengths: λ = 632.8 nm, 751 nm, and 833 nm using a He-Ne laser (5 mW) and two laser diodes (3 and 30 mW respectively). Two thin fibers with a small diffusive tip (outer diameter 0.5 mm) having a highly uniform radiation pattern were used to illuminate the medium and to measure the fluence. The inter-fiber distance was varied with a computer controlled translation stage and received photons were measured with a photomultiplier and a lock-in amplifier.

The optical properties of IL at λ = 632.8 nm have been obtained with the method of adding absorption [15]: at a fixed concentration of IL, μ_eff has been measured for different concentrations of an added calibrated absorber, and the optical properties have been obtained from a linear fit of ${\mu }_{\text{eff}}^2$ as a function of the concentration of the added absorber. At NIR wavelengths the method of water absorption has been used [21]: μ_eff has been measured for different concentrations of IL, and the optical properties have been obtained from a linear fit of ${\mu }_{\text{eff}}^2$ as a function of ${\rho }_{\text{il}}^{\text{m}}$ exploiting the knowledge of the absorption coefficient of water. ${\epsilon }_{s,\text{il}}^{\prime }$ has been obtained with an error smaller than 2% (the accuracy of the methods is ultimately limited by the error on the absorption coefficient of the added absorber and of water). As for the specific absorption coefficient of IL, values very close to absorption of water have been obtained [16].

To determine the absorption of India ink, measurements of μ_eff on a dilution of IL with known ${\mu }_s^{\prime }$ have been carried out for different India ink concentrations. ε_a,ink has been obtained again with a linear fit of ${\mu }_{\text{eff}}^2$ as a function of ${\rho }_{\text{ink}}^{\text{m}}$, and the error is mainly determined by the error on ${\mu }_s^{\prime }$ of IL [10]. With measurements of collimated transmittance the extinction coefficient of India ink has also been measured, making possible to determine the single scattering albedo [10].

ICFO

The time-resolved diffuse reflection set-up used by ICFO for the phantom measurements works at three fixed wavelengths (687 nm, 785 nm and 830 nm, BHPL-700 laser modules, 50 MHz repetition rate, typical CW power 1 mW) with a HPM-100-50 hybrid detector and a SPC-130 single photon counting electronics (all components by Becker&Hickl, Germany). Laser light is provided to, as well as collected from the phantom through gradient index fibers (diameter 62.5 μm) which are placed in predefined positions of the scattering cell in reflection geometry. The presently used wavelengths and the four different source-detector inter-fiber distances (15 mm, 20 mm, 25 mm, 30 mm) can be changed by piezoelectric switches. In each of the different configurations, the IRF was measured by aligning source and detector fiber tips head to head with a diffusing thin white paper layer in between (typical FWHM about 300 ps).

Based on the solution of the diffusion equation for a semi-infinite medium with zero boundary conditions [29], the convolution of each IRF was fitted to the measured DTOF with μ_a and ${\mu }_s^{\prime }$ as free parameters. After background subtraction, the curves were fitted starting at 80% of maximum on the rising edge of the phantom response peak down to signal-to-noise dependent values at its falling slope. Typically, fitting extended on the falling slope between 0.1% for a source-detector inter-fiber distance of 15 mm to 3% for a source-detector inter-fiber distance of 30 mm. A linear fit of μ_a in a series of nine different concentrations ${\rho }_{\text{ink}}^{\text{m}}$ provided ε_a,ink, meanwhile a series of four concentrations ${\rho }_{\text{il}}^{\text{m}}$ was measured to determine the value of ${\epsilon }_{s,\text{il}}^{\prime }$.

An accurate analysis of the possible uncertainty sources affecting the evaluated intrinsic optical properties has been performed: the statistical uncertainty is mainly due to both the nonlinear and linear fitting procedures adopted, while the systematic uncertainty is given by the error in the estimation of inter-fiber distances and by the use of the diffusion approximation [30].

ILM

The optical properties were determined with a two step method introduced recently [22]. In the first step, the method of the spatially resolved reflectance was applied. To this end, the turbid medium contained in a vessel of 90 mm diameter and 45 mm height was irradiated with a monochromatic pencil beam (0.5 mm diameter) using a Xenon source and a monochromator [31]. The intensity profile of the reflected light at the surface of the sample was detected up to a distance of 25 mm from the incident source by a 16 bit CCD camera (Pixis 512B, Princeton Instruments, USA). The spatial resolution of the image of the sample surface obtained with the CCD camera was approximately 0.09 mm. The raw data were corrected by the optical transfer function of the system. Then, ${\mu }_s^{\prime }$ was derived by fitting the radially averaged reflectance curve with a solution of the diffusion equation for semi-infinite media using a nonlinear regression routine (Levenberg Marquardt algorithm). The systematic error in the determination of ${\mu }_s^{\prime }$ caused by the use of the diffusion theory was estimated to be approximately 5%. This information was obtained by fitting reflectance curves calculated with the diffusion solution to Monte Carlo simulations, which are, in principle, an exact solution of the radiative transfer theory. The statistical error in the determination of ${\mu }_s^{\prime }$ was determined by calculating the standard deviation of five successive phantom measurements.

The absorption coefficient was determined in the second step of the combined method, namely the measurement of the total reflectance. In this method, the same sample as in step 1 is illuminated with a white light pencil beam of 8 mm diameter. The total reflectance, that is all the light which is scattered from any position of the sample surface into the direction of the detector, was measured with a spectrometer (Ocean Optics, USA). The reflectance measured at the sample was compared to that obtained from a reflectance standard (Spectralon, Lab-sphere, USA) in order to obtain absolute values. With the a priori knowledge of ${\mu }_s^{\prime }$, μ_a was determined exploiting Monte Carlo simulations in which the exact geometry of the set-up was considered. For the analysis, a look-up-table created from Monte Carlo simulations for different combinations of ${\mu }_s^{\prime }$ and μ_a was applied. As a solution of the transfer theory was used for the determination of μ_a, the systematic error caused by theory can be neglected. However, because ${\mu }_s^{\prime }$ was used from the measurement of the first step, we estimated that μ_a has also a systematic error of 5%. The statistical error of each experiment was again estimated by the standard deviation of five measurements.

PTB

PTB performed time-resolved measurements and analyzed them using the linear time-resolved method from Ref. [17]. A dedicated laboratory set-up was based on a SC500-6-custom super-continuum laser (repetition rate 40.5 MHz) with Acousto-Optic Tunable Filter (AOTF, Fianium Ltd., UK), a hybrid PMT detector HPM-100-50 controlled by a DCC-100 card, and a TCSPC board SPC-130 (all Becker&Hickl, Germany). The AOTF was tuned for emission at 750 nm and 830 nm, respectively, with a bandwidth of 7 nm. The output of the AOTF was coupled into a 3.82 m long graded index fiber GIF625 (Thorlabs). The detector fiber was a multimode fiber of 1.30 m length, NA 0.39, core diameter 1 mm. The IRF was measured with the fibers 50 mm apart and paper (2 mm white circles, otherwise black) in front of each fiber to fill the aperture [25]. The IRF had an FWHM of 165 ps and a short tail. Special care was taken to avoid reflections in the optical path, in particular by the optical fibers, in the relevant time range. Time zero was defined as the first moment of the IRF within limits corresponding to 50% of the maximum. Differences in the optical path length between measurements of IRF and sample, including different thickness of filters, were taken into account. Measurements were performed at count rates of about 300 kHz and collection times of 40 s (IL) and 100 s (India ink).

The scattering cell was used with 30 mm thickness and 3 mm diameter Plexiglass windows. The measurement of ${\epsilon }_{s,\text{il}}^{\prime }$ was performed in reflection geometry at source-detector separations of 20 mm, 30 mm and 40 mm. Starting from 400 g of purified water, amounts of about 9 g of IL were added consecutively to reach ${\rho }_{\text{il}}^{\text{m}}\approx 0.1$ in 5 steps. At a given ${\rho }_{\text{il}}^{\text{m}}$, for all pairs of measurements at the three source-detector separations, a linear fit of the logarithmic ratio of time-resolved reflectance vs 1/t was performed in the range 0.3ns⁻¹ ≤ 1/t ≤ 0.7ns⁻¹ to retrieve ${\mu }_s^{\prime }$. The final result ${\epsilon }_{s,\text{il}}^{\prime }$ was obtained by linear regression of ${\mu }_s^{\prime }$ vs ${\rho }_{\text{il}}^{\text{m}}$ for ${\rho }_{\text{il}}^{\text{m}}$ values between 0.04 and 0.1.

The intrinsic absorption of India ink was measured in transmission geometry. Starting from a scattering medium with ${\rho }_{\text{il}}^{\text{m}}\approx 0.1$, amounts of about 220 mg of the pre-diluted India ink provided by UNIFI were added in 8 steps. The maximum ${\rho }_{\text{ink}}^{\text{m}}$ was about 2.5 · 10⁻⁵. Diluted India ink and IL were added by means of syringes, their weight was determined in each step with an accuracy better than 0.1 mg. For each step in absorption, the ratio of time-resolved transmittance with and without added India ink was calculated. A linear fit of the logarithmic ratio was performed in the range 2 ns ≤ t ≤ 4 ns to obtain Δμ_a. Linear regression of all Δμ_a vs ${\rho }_{\text{ink}}^{\text{m}}$ yielded ε_a,ink.

The influence of major sources of uncertainty, i.e. the non-ideal IRF as well as uncertainty of time zero, was estimated by means of simulations. Time-resolved diffuse reflectance and transmittance, respectively, were calculated based on the solutions of the diffusion equation with extrapolated boundary conditions. Geometry, source-detector separations and optical properties as in the experiment were taken into account. The reflectance and transmittance profiles were convolved with the measured IRF. The same algorithms as for the experimental data were applied to the simulated data to obtain ${\epsilon }_{s,\text{il}}^{\prime }$ and ε_a,ink, respectively. The results were compared with the input values of the simulations.

ULUND

The photon time-of-flight measurements of absorption and scattering were performed using our set-up [32,33] at the wavelengths 751 nm, 833 nm and 916 nm. The set-up is based on 80 MHz super continuum source (Model SC500-5, Fianium Ltd, UK) combined with acousto-optical tunable filters, (Fianium Ltd, UK). This provides optical pulses with temporal and spectral width (FWHM) of about 40 ps and 5 nm, respectively. Signal detection is done using silicon single photon counting detector (PD1CTC, MPD, Italy) monitored by TCSPC electronics (SPC-130, Becker&Hickl, Germany) with corresponding software. For signal delivery and collection we utilize 400 μm/600 μm core/cladding custom made multimode gradient-index silica optical fibers (Leoni Fiber Optics, Germany). For evaluation of absorption and reduced scattering coefficients from recorded photon time-of-flight distributions we used original data evaluation algorithm based on White Monte Carlo Simulations [34]. For the evaluation we assumed the following parameters: scattering anisotropy factor g = 0.7 and IL solution refractive index 1.33.

We determine intrinsic reduced scattering coefficient of IL and intrinsic absorption coefficient of India ink by extrapolating absorption/scattering values obtained in added solution series experiments at low IL/ink concentrations. In particular we find ${\epsilon }_{s,\text{il}}^{\prime }$ by extrapolating 11 scattering values obtained on a series with IL volume fractions from 1.3% to 5.3%, then correcting for IL density. ε_a,ink is obtained in similar fashion by extrapolating results of 11 absorption measurements where volume fraction of the supplied ink solution was varied from 0.55% to 2%. In the latter case 3.3% volume fraction of IL solution was added to obtain reduced scattering coefficient of 6.4 cm⁻¹ at 833 nm. All the measurements were performed with fiber separation of 20 mm in a 10 cm diameter cylindrical beaker with total solution volume of 700 ml.

Statistical uncertainties of the present study in the determination of ${\epsilon }_{s,\text{il}}^{\prime }$ and ε_a,ink account for errors due to e.g. uncertainties in added solution volumes and residual fitting uncertainty due to finite signal to noise ratio in acquired time-of-flight characteristics. The statistical uncertainties of ${\epsilon }_{s,\text{il}}^{\prime }$ and ε_a,ink are between 1% and 2% for both parameters for all three measurement wavelengths. The systematic error of the present set-up is caused by uncertainty in the distance between signal delivery and collection fiber. Considering realistic uncertainty of ±0.5 mm we estimate 10% uncertainty in determination of ${\epsilon }_{s,\text{il}}^{\prime }$ and 2.5% uncertainty in determination of ε_a,ink. Systematic errors, due to the data evaluation algorithm employed, are expected to be small compared to the former uncertainty of fiber positioning.

2.4. Statistical analysis

In order to determine a comprehensive reference value for both ε_a,ink and ${\epsilon }_{s,\text{il}}^{\prime }$ starting from the estimates supplied by each laboratory, a statistical analysis on the repeated measurements has been performed. Furthermore, we will see that the presence of some inconsistent measurements has to be faced. A standard statistical model which may account for inconsistency in the dataset when estimating a common mean is the fixed effects model:

$$Y_i=\mu +{\alpha }_i+{\epsilon }_i,\hspace{0.17em}i=1,\dots ,n,$$ (9)

where Y_i represents the measurement of laboratory i at one wavelength, σ_i the uncertainty of this measurement, and ε_i = 𝒩 (0, ${\sigma }_i^2$) a zero mean Gaussian random variable with variance ${\sigma }_i^2$. The aim of this model is to estimate the common mean μ (representing the reference value, RV) as well as the fixed effects α_i (representing the bias) for each laboratory.

For the σ_i we used the combined uncertainties ${\sigma }_i^2={\sigma }_{i,\text{stat}}^2+{\sigma }_{i,\text{syst}}^2$, where σ_i,stat = RU^i,statY_i were reported by the laboratories (see Table 2) and represent uncertainties caused by random errors. The uncertainties caused by systematic errors σ_i,syst were approximated from the maximal limits ±RU^i,syst reported by the laboratories such that ${\sigma }_{i,\text{syst}}={\mathit{RU}}^{i,\text{syst}}{Y}_i/\sqrt{3}$, or were set to zero σ_i,syst = 0 when nothing was reported.

Table 2.

Results of the characterization measurements obtained by different laboratories: the intrinsic absorption coefficient ε_a,ink and the intrinsic reduced scattering coefficient ${\epsilon }_{s,\text{il}}^{\prime }$ with their statistical uncertainties ${\mathit{RU}}_{\text{ink}}^{\text{stat}}$ and ${\mathit{RU}}_{\text{il}}^{\text{stat}}$, and the limits of their relative systematic errors, ${\mathit{RU}}_{\text{ink}}^{\text{syst}}$ and ${\mathit{RU}}_{\text{il}}^{\text{syst}}$, for India ink and IL respectively, are reported at the different wavelengths λ considered.

λ (nm)	εa,ink (mm−1)	${\mathit{RU}}_{\text{ink}}^{\text{stat}}$	${\mathit{RU}}_{\text{ink}}^{\text{syst}}$	${\epsilon }_{s,\text{il}}^{\prime }$ (mm−1)	${\mathit{RU}}_{\text{il}}^{\text{stat}}$	${\mathit{RU}}_{\text{il}}^{\text{syst}}$	Lab.
633	384.3	0.4%		26.6	2.4%		POLIMI
633	354.7	12%		26.5	1.6%		INO
633	393	2%		25.1	3%		TomOptUS
633	375.3	1.6%		26.0	1.8%		UNIFI
633	385.5	6.5%		26.3	0.6%		ILM
687	340	0.9%	3%	23.1	0.8%	5%	ICFO
750	325	1.7%		21.7	2.4%		POLIMI
750	306.5	12.5%		21.6	2%		INO
751	336	2%		26	4%		TomOptUS
751	318.7	1.5%		21.1	1.8%		UNIFI
750	321.8	5.6%		21.3	1.1%		ILM
750	305.4	1.5%		21.4	5%		PTB
751	346.6	0.7%	2.5%	20.5	0.8%	10%	ULUND
785	303	0.7%	3%	19.4	0.9%	5%	ICFO
833	309	3.2%		18.8	3.2%		POLIMI
830	313.5	15%		18.9	2.3%		INO
830	262	1.1%	5%	18.5	2.4%	5%	IBIB
833	302	3%		22.3	3%		TomOptUS
833	288.7	1.6%		18.5	1.6%		UNIFI
830	288	0.7%	3%	17.4	1%	5%	ICFO
830	288.9	5%		18.8	0.7%		ILM
830	277.3	1.5%		18.9	5%		PTB
833	292.0	1.0%	2.5%	17.9	0.9%	10%	ULUND
916	257.3	1.2%	2.5%	16.1	0.9%	10%	ULUND

We note that model (9) cannot be identified without making an additional assumption. To this end we employ the assumption that at least m of the n laboratories measure reliably, where 1 ≤ m ≤ n. This means that for these laboratories the biases are null: α_lk = 0 for l_k ∈ {l₁,...,l_m}, where {l₁,...,l_m} is an unknown set of m (different) indices from 1,...,n; m is called the model order parameter. For further details about this assumption for the statistical model (9) see Ref. [35], where it is discussed in the context of key comparisons in metrology.

3. Results and discussion

Values of the intrinsic absorption coefficient of undiluted India ink ε_a,ink and of the intrinsic reduced scattering coefficient of IL ${\epsilon }_{s,\text{il}}^{\prime }$ as resulting from measurements on Intralipid and India ink dilutions performed by all laboratories are reported in Table 2. Reported values have been corrected for systematic errors if present. Statistical and systematic uncertainties, when available, are also reported. Besides few exceptions, data presented in Table 2 show a promising consistency, although the laboratories involved in the study have used different techniques, instrumental set-ups and data analysis methods.

Next, we applied the procedure described in Sec. 2.4 and fitted the statistical model to the measurements of laboratories. We considered the different wavelengths separately. In particular, the measurements at wavelengths 687 nm, 785 nm, 916 nm have been performed by only one laboratory each. Due to the lack of repetitions, these measurements will not be statistically evaluated. As for the measurements at the other wavelengths, they have been grouped for proximity, by considering the three nominal wavelengths 633 nm, 750 nm and 830 nm, consisting of 5, 7 and 9 repeated measurements, respectively. Furthermore, scattering and absorption measurements have been treated independently.

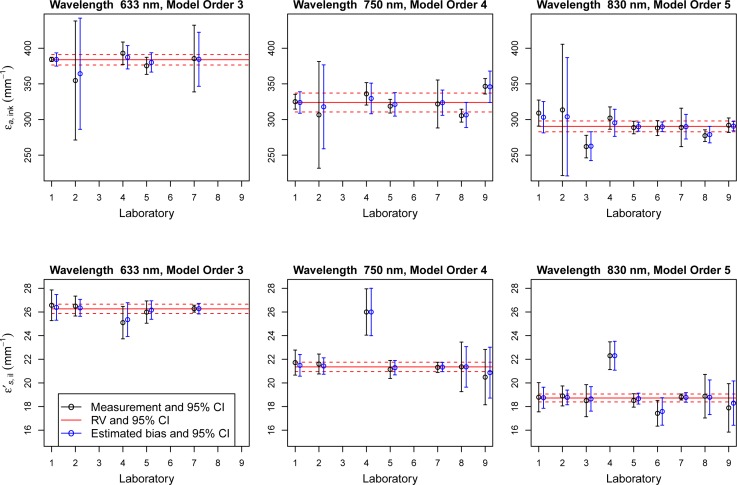
The results of the statistical analysis are displayed in Fig. 2 for ε_a,ink and ${\epsilon }_{s,\text{il}}^{\prime }$ at the three wavelengths considered. The reference values and their 95% credible intervals (CIs) are reported as red lines, while the biases of each laboratory and their symmetric 95% CIs are reported with blue symbols. The laboratory biases are shifted in Fig. 2 by adding the respective reference value, in order to compare them with the respective laboratory measures (reported in black symbols with their CIs) more easily. For each statistical analysis the order parameter m of the model is also reported. By inspecting the estimated biases in this figure, there is evidence that laboratory 4, TomOptUS, has measured the reduced scattering coefficient of IL with a bias at wavelengths 750 nm as well as 830 nm at 95% significance level. However, there is not sufficient evidence in the data to deem other laboratories to have provided biased measurements.

Fig. 2.

Measurements (black symbols) as well as reference values (RV, red lines) and laboratory biases (blue symbols, shifted) and their 95% CIs, estimated by fitting the fixed effect model (see Sec. 2.4) for the intrinsic absorption coefficient of undiluted India ink ε_a,ink (bottom row) and the intrinsic reduced scattering coefficient of IL ${\epsilon }_{s,\text{il}}^{\prime }$ (top row) at 3 different wavelengths. The laboratories are named using the ID number reported in Table 1.

For the sake of clarity, in Table 3 the final and comprehensive reference values for ε_a,ink and ${\epsilon }_{s,\text{il}}^{\prime }$ are reported at the three wavelengths 633 nm, 750 nm and 830 nm, together with the respective standard deviations, both absolute and relative. From the figures reported in this table one can note the high accuracy obtained in this characterization study: in particular, the uncertainty affecting the intrinsic absorption coefficient of the undiluted India ink is 1% or 2%, depending on the wavelength considered, while the intrinsic reduced scattering coefficient of IL has been determined with an uncertainty on the order of 1%.

Table 3.

Final reference values for ε_a,ink and ${\epsilon }_{s,\text{il}}^{\prime }$ with their standard deviations, σ_ink and σ_il, and relative uncertainties, RU_ink and RU_il, at the wavelengths 633, 750 and 830 nm.

λ (nm)	εa,ink (mm−1)	σink (mm−1)	RUink	${\epsilon }_{s,\text{il}}^{\prime }$ (mm−1)	σil (mm−1)	RUil
633	384	4	1.0%	26.3	0.2	0.8%
750	324	7	2.1%	21.4	0.2	1.0%
830	290	4	1.3%	18.7	0.17	0.9%

We now briefly compare the values reported in Table 3 with results recently presented in literature. In particular, the India ink used in this work comes from the same commercial batch of the India ink named “Higgins-A” in Ref. [10]: the intrinsic absorption coefficients determined there, 373 mm⁻¹, 325 mm⁻¹ and 294 mm⁻¹ at 632.8 nm, 751 nm and 833 nm, respectively, with an accuracy of about 2%, are in very good agreement with values reported in Table 3. As for Intralipid, Ref. [9] reports the values of ${\epsilon }_{s,\text{il}}^{\prime }$ averaged over the nine batches: in terms of weight concentrations they read 26.2 mm⁻¹, 21.5 mm⁻¹ and 18.6 mm⁻¹ at 632.8 nm, 751 nm and 833 nm, respectively, again in very good agreement with Table 3.

Finally, we consider previous results obtained by POLIMI and UNIFI for India ink and Intralipid, exploiting the same measurement set-ups and analysis procedures adopted here [17, 21]. As for Intralipid, the values for reduced scattering coefficient ${\epsilon }_{s,\text{il}}^{\prime }$ at 750 nm reported there differ by about 4% from the value showed in Table 3, after having corrected the former because they refer to IL volume concentration. Even if the accuracy level of ${\epsilon }_{s,\text{il}}^{\prime }$ obtained in this work is about 1%, a discrepancy of 4% can be reasonably explained considering the batch-to-batch variability of Intralipid [9], and the uncertainty of the individual measurements and the reference value. It has to be kept in mind that the reported accuracy level of 1% for ${\epsilon }_{s,\text{il}}^{\prime }$ is related to the mean value over many groups and is the result of a comprehensive statistical analysis. As for the India ink, the values for the intrinsic absorption coefficient ε_a,ink at 750 nm reported in [17, 21] are about a factor 2 larger than that showed in Table 3. Again, even if the accuracy obtained here for ε_a,ink is about 2%, one has to keep in mind the very large brand-to-brand variability characterizing ε_a,ink: as a matter of fact the observed discrepancy is just the difference between the intrinsic absorption coefficient of Rotring (Germany) ink used in [17,21] and that of Higgins India ink use in this study, as reported in [10].

4. Conclusions

In conclusion, the work presented here allowed to accurately characterize India ink and IL, in terms of their intrinsic optical properties ε_a,ink and ${\epsilon }_{s,\text{il}}^{\prime }$, respectively.

We note that the reference values determined here for ε_a,ink and ${\epsilon }_{s,\text{il}}^{\prime }$ refer to the batches of India ink and IL used in the present study, where the combination of the results obtained from different laboratories allowed to achieve the accuracy level reported in Table 3. Actually, the batch-to-batch variability of Intralipid is comparable with this accuracy level: in particular, Intralipid^®-20% by Fresenius-Kabi is a medical supply produced in very controlled conditions with tight tolerances on fat droplet size in order to avoid thrombosis in small blood vessels. This explains its stability over time and surprisingly small batch-to-batch variations (about 2% [9]). One could reasonably expect an analogue behavior for the future, as long as the fabrication process remains the same. This is not necessarily true for India ink: its production procedures are not as well controlled as for Intralipid, resulting in larger brand-to-brand and batch-to-batch variations [10]. However, the scattering albedo of India ink remains rather constant, mitigating at least in part this problem: the intrinsic absorption coefficient of a sample of India ink can be determined by a simple extinction measurement with an acceptable accuracy. Then, it can not be straightforwardly assumed that the optical properties of diffusive liquid phantoms calculated using the reference values for ε_a,ink and ${\epsilon }_{s,\text{il}}^{\prime }$ reported in Table 3 have that level of accuracy, if they are prepared with different batches of India ink (even of the same brand) and Intralipid. Nevertheless, one can reasonably expect that the values of μ_a and ${\mu }_s^{\prime }$ obtained in this way are accurate enough for many applications: as a matter of fact, the characterization work for Indian ink and Intralipid performed in Ref. [9, 10] together with this multi-center study for the assessment of their optical properties make the reference values for ε_a,ink and ${\epsilon }_{s,\text{il}}^{\prime }$ reported in Table 3 of general interest. For particular applications where a high level of accuracy is required, the characterization has to be performed for the particular materials used. The comparative study presented here also provided a validation of the measurement and analysis procedures applied, as long as no bias was detected, and also an indication that the accuracy levels reported in Table 2 for the results of the various groups were reasonable.

The level of accuracy for optical properties reported here is not trivially attainable, also considering other kinds of diffusive phantoms mimicking biological tissues (e.g. resin-based solid phantoms or silicone-based flexible phantoms [18]). Then, due to the increasing accuracy requirements for the exploitation of optical techniques in clinical environment, India ink and Intralipid constitute very useful tools for the validation and clinical translation of diffuse optical spectroscopy instrumentation. Taking into account also the temporal stability of India ink [10] and the recently demonstrated thermal stability of Intralipid [36], both these compounds can be considered for becoming reliable materials that can be recommended for tissue phantom preparation at NIR wavelengths.

We add a comment about India ink, the absorber used for this multi-center experiment. As mentioned before, its main drawbacks (it is not a pure absorber, carbon particles may sediment) are related to the large size of suspended particles. A viable alternative could be utilizing nanofluids based on carbon nanohorns. These nanofluids have the same advantages of India ink, but with particles of very small size (around 100 nm): therefore their scattering efficiency is very low and they practically act as pure absorbers. It has been recently shown [37] that their albedo at NIR wavelengths is almost equal to zero, so that their absorption can be measured with high precision with simple measurements of collimated transmittance or with a spectrophotometer. Furthermore, for these small particles Brownian motions are sufficient to prevent sedimentation. Their absorption coefficient remains therefore unchanged over a long time and the application of ultrasound is not necessary.

Finally, we note that in the day-to-day work with optical instruments in clinical environments the use of solid phantoms for calibrating and checking purposes is preferable. Also a participant in this study, INO, is present on the market as a manufacturer of solid phantoms (Biomimic™) with a carefully maintained metrological characterization set-up. Then, an interesting perspective of the successful multi-center calibration work reported here can be its extension and continuation on solids phantoms, even if not all the techniques adopted in this work can be straightforwardly applied to solid phantoms.