Optical coherence micro-elastography: mechanical-contrast imaging of tissue microstructure

Abstract

We present optical coherence micro-elastography, an improved form of compression optical coherence elastography. We demonstrate the capacity of this technique to produce en face images, closely corresponding with histology, that reveal micro-scale mechanical contrast in human breast and lymph node tissues. We use phase-sensitive, three-dimensional optical coherence tomography (OCT) to probe the nanometer-to-micrometer-scale axial displacements in tissues induced by compressive loading. Optical coherence micro-elastography incorporates common-path interferometry, weighted averaging of the complex OCT signal and weighted least-squares regression. Using three-dimensional phase unwrapping, we have increased the maximum detectable strain eleven-fold over no unwrapping and the minimum detectable strain is 2.6 με. We demonstrate the potential of mechanical over optical contrast for visualizing micro-scale tissue structures in human breast cancer pathology and lymph node morphology.

1. Introduction

Key to the advancement of the optical microscopy of tissue has been the exploration of sources of contrast aimed at improving the visualization of structure and providing information on function. On length scales from the molecular (sub-nanometer) to many millimeters, elastic scattering is a source of contrast that provides information on the structure, size and motion of tissue constituents [1], and spectroscopy provides information on molecular composition [2]. Over the same length scales, the mechanical properties of tissue are a rich alternative to optical sources of contrast [3]. Such properties govern the mechanical interactions between cells and their environment, which, in concert with chemical interactions, determine how they grow, differentiate and migrate. The impairment of a cell’s capacity to respond to mechanical forces contributes to the pathogenesis of diseases such as cancer [4], and leads to differences in the mechanical properties of normal and malignant tissue. Tumor cells are known to be commonly softer than their normal counterparts and, at the same time, tumors commonly cause the generation of additional collagen-dense stroma making them feel stiffer on the macro-scale [5]. The result of this innate heterogeneity is that, on the microscopic scale, malignant tissues often have a broader stiffness distribution than normal tissues [5].

The measurement of the mechanical properties of cells and tissues on the nano- and micro-scale, using techniques such as atomic force microscopy [5] and optical tweezers [6], has contributed greatly to our understanding of the role of mechanical interactions in disease. On the macro-scale, physicians have used palpation as a means of diagnosis for centuries. The advent of medical imaging, such as ultrasound and magnetic resonance imaging, has provided the means for elastography, the use of imaging to map mechanical properties [7–9]. In elastography, the tissue is mechanically loaded and imaged to measure its deformation. For the class of methods based on compressive loading, the displacement vector between image acquisitions is used to estimate components of the local strain tensor (change in length per unit length), which are displayed in images (elastograms) that represent relative tissue stiffness [9]. Elastography has a more-than-twenty-year history [10] during which many loading methods and means of extracting mechanical properties have been explored, and clinical applications have emerged, e.g., in breast cancer [11] and liver fibrosis [12].

Amongst optical elastography methods [13–16], the use of optical coherence tomography (OCT) to measure displacement, termed optical coherence elastography (OCE), has been the most prominent [14, 16–26]. Despite much recent progress, optical elastography has not yet demonstrated the required spatial resolution, or mechanical sensitivity and dynamic range, to adequately reveal the micro-scale structure of tissue. In this paper, we aim to address this with optical coherence micro-elastography, which improves on existing compression OCE techniques [22, 26] by incorporating common-path interferometry [27], averaging of the complex OCT signal and three-dimensional phase unwrapping. Additionally, optical coherence micro-elastography is performed using a portable system, facilitating clinical imaging. In en face micro-elastograms compared against en face OCT images and histology, we demonstrate high mechanical contrast maintained over a large dynamic range that is complementary to the optical contrast and reveals additional tissue contrast in human breast cancer and lymph node samples.

2. Methods

2.1 Optical coherence micro-elastography system

Our optical coherence micro-elastography system employs a Fourier-domain OCT system described previously [28]. To perform clinical scanning, the system was housed on a portable trolley with dimensions (height × width × depth) of 1.20 m × 0.7 m × 0.9 m. It uses a superluminescent diode light source with central wavelength of 835 nm and 50 nm bandwidth, and illuminates the sample with 10 mW of optical power. The system was configured in common-path [27], with the reflected beam from the back surface of a 2-mm thick imaging window (IW in Fig. 1(a)) used as a reference. The axial and lateral resolutions (full-width at half-maximum irradiance) were measured to be 7.8 μm (in air) and 11 μm, respectively, and the sensitivity was measured to be 102 dB for an exposure time of 36 μs.

Fig. 1.

Illustration of optical coherence micro-elastography on a structured phantom. (a) Sample arm of the imaging system. RP, rigid plate; SP, structured phantom; IW, imaging window; RA, ring actuator; L, Lens; X-Y GM, xy-scanning galvanometer mirrors. Perspective and side-view illustrations of the phantom are also shown. (b) Displacement of the ring actuator and synchronized x-scanning galvanometer-mirror scan pattern. (c) Illustrations of displacement and local strain at two locations in the phantom.

We used phase-sensitive, three-dimensional OCT to measure the axial displacement of a sample in response to compressive loading. The sample is compressed using a ring actuator, which is rigidly coupled to the imaging window (Fig. 1(a)) [29]. To ensure full contact with the imaging window, the sample was statically preloaded by displacing therigid upper plate after initial contact by a further 0.1-1 mm, corresponding to strain values in the range 0.02-0.2, within the normal range used in compression testing of soft tissue [9]. A 1-minute delay before imaging reduced the effects of viscoelastic creep deformation in the sample [30] to a negligible level. Subsequently, a 5-Hz square-wave loading (Fig. 1b), applied collinearly with the imaging beam [22], was synchronized with the lateral scanning and produced an axial displacement amplitude of up to 2.2 μm in the ring actuator (Fig. 1(b)). At each lateral (xy) position of a three-dimensional complex OCT data set, the phase difference between two A-scans in consecutive B-mode frames reveals the sample’s depth-resolved axial displacement (Fig. 1(c)) [19]. The displacement sensitivity is 0.34 nm, calculated as the standard deviation of 500 displacement measurements acquired from the same position on a stationary adhesive tape phantom with corresponding OCT SNR of 50 dB (Fig. 2(a)) [22, 31]. As shown in Fig. 2(a), this is >40-fold higher displacement sensitivity than achieved using the dual-arm configuration in otherwise the same setup. For each B-mode micro-elastogram, 1000 A-scans were recorded in an acquisition time of 0.1 s. For scanning in the y-direction, oversampling was used to provide phase correlation between consecutive B-mode frames and enabled weighted averaging of the complex OCT signal. (The y-sampling density is four B-mode frames per micrometer for Figs. 3 and 5, and 0.9 B-mode frames per micrometer for Figs. 6-8, corresponding to 3D micro-elastogram acquisition times of 2000 s and 500 s, respectively). Three-dimensional micro-elastograms were generated, wherein each voxel represents the local strain (Fig. 1(c)), i.e., the change in displacement over a specified axial range at each depth position [22]. The chosen axial range,$\Delta z$, lies between 100 μm and 215 μm in the micro-elastograms presented in this paper. The lateral resolution of the micro-elastogram (11 μm here) matches that of the corresponding OCT image.

Fig. 2.

(a) Displacement and (b) strain sensitivity measurements, respectively, for common-path, ${\sigma }_{d,cp}$ and ${\sigma }_{\text{ε},cp}$ (red), and dual-arm, ${\sigma }_{d,da}$ and ${\sigma }_{\text{ε},da}$ (blue), configurations of our portable imaging system determined using (a) an adhesive tape phantom and (b) a scattering silicone sample.

Fig. 3.

Signal processing steps used in optical coherence micro-elastography illustrated with experimental data from a structured phantom. (a) Loaded $(C_L)$ and unloaded $(C_U)$ complex OCT B-mode frame pairs (q) are acquired within a y-range of ~6 μm. (b) The phase difference, $\Delta {\varphi }_k$, and weighting, $W_k$, are calculated for each pair of B-mode scans, for $k=1,3...2q-1$. (c) The weighted-average phase difference, $\Delta {\varphi }_{av}$, is calculated by averaging $q$ complex quotients, $Q_k$. (d) The unwrapped phase difference is calculated using a three-dimensional phase unwrapping algorithm, described in Section 2.5. Negative phase difference indicates decreasing displacement with depth (Fig. 1(c)). (e) A B-mode micro-elastogram is calculated from the rate of change of the unwrapped phase difference with depth, using weighted least-squares linear regression over axial range, $\Delta z$. Increasing negative strain indicates increasing amounts of compression of the sample in response to the load. In the micro-elastogram, the scale is in millistrain, mε. Scales bars, 200 μm.

Strain sensitivity, in common with OCT sensitivity, is a measure of the system sensitivity and not a measure applicable to any given image. Whereas in OCT this sensitivity may be determined by reflection from a mirror: in compression OCE, this measure depends on the sample used to determine it. The system strain sensitivity (Fig. 2(b)) is determined using a method similar to one reported previously [22, 28]. 200 B-mode elastograms acquired at the same y-position in an optically and mechanically homogeneous phantom were averaged. Strain sensitivity is defined as the standard deviation of 100 strain measurements calculated over a lateral range of 100 μm acquired from the central region of the phantom. This provides an estimation of the maximum achievable system strain sensitivity, the strain sensitivity floor, measured to be 2.6 με for our system. This strain sensitivity is >30-fold higher than that achieved using the same method with a dual-arm configuration (Fig. 2(b)). For this measurement, the sample was subjected to a local strain of −0.05 mε, corresponding to the mean strain observed in Fig. 2(b). This approach ensures that all factors influencing the system strain sensitivity, such as actuator response, are included in the sensitivity measurement.

2.2 Phantom fabrication

Heterogeneous tissue-mimicking phantoms with well-determined optical and mechanical properties and structure were fabricated using two-component room-temperature vulcanizing silicone [32, 33]. The optical properties were controlled by adding titanium dioxide particles (refractive index ≈2.5, average diameter 1 μm) to the silicone in concentrations in the range 0.8-2.5 mg/ml. To ensure uniform particle distribution, the mixture was placed in an ultrasonic bath for 25 minutes. Phantoms were then oven-cured at 90°C for ~30 minutes. For each phantom, the Young’s modulus of the soft bulk silicone material, measured using a materials testing system [33], was 20 kPa and that of the inclusion was 850 kPa. The phantom used to generate the images in Fig. 3 has dimensions of 15 × 15 × 1.5 mm. The cubic inclusion in this phantom has approximate dimensions 0.2 × 0.2 × 0.2 mm and was cut by hand using a scalpel. The dimensions of the ‘star’ phantom used to generate the images in Fig. 5 are 15 × 15 × 3 mm. The stiff, star-shaped inclusion was cut from a cube of cured silicone with approximate dimensions 10 × 10 × 2 mm using a femtosecond laser to an equivalent circular diameter of 5 mm and a thickness of 2 mm. To embed the inclusions, we used a procedure described in detail previously [33]. Briefly, a layer of soft silicone was cured in a mold. The thickness of this layer determined the depth of the inclusion from the lower boundary of the phantom and is 1.1 mm and 0.75 mm for the phantoms presented in Figs. 3 and 5, respectively. In both cases, the inclusion was placed on the layer and soft silicone from the same batch as the layer was poured over the inclusion to the desired thickness. Upon curing, this resulted in a soft silicone phantom with a stiff inclusion embedded within.

2.3 Tissue preparation, histology and co-registration

Informed consent was obtained from the patients and the study approved by the Human Research Ethics Committee of Royal Perth Hospital, Perth, Western Australia. In total, 45 samples were excised from 15 patients undergoing mastectomy, or mastectomy with axillary clearance, and were imaged within 2-3 hours of excision. After excision, the fresh tissue was dissected into samples of approximate dimensions 1.5 cm × 1.5 cm × 0.5 cm. The samples were kept hydrated in phosphate-buffered saline prior to imaging. After imaging, each sample was fixed in 10% neutral buffered formalin and then embedded in paraffin and sectioned following the standard histopathology protocols used at Royal Perth Hospital. The haematoxylin and eosin-stained sections were digitally micrographed and co-registered with the corresponding en face OCT images and en face micro-elastograms using a custom three-dimensional visualisation tool [34] that enabled the extraction of arbitrary imaging planes. The planes selected for the micro-elastograms were those determined manually by inspection to correspond most closely to the histological section. The OCT images corresponding most closely were chosen from within the axial range of the corresponding micro-elastogram. A voxel-to-voxel comparison of the en face micro-elastograms and OCT images must take account into account the poorer elastogram axial resolution.

2.4 Signal processing in optical coherence micro-elastography

In Fig. 3, the signal processing chain is illustrated using experimental data acquired from a phantom containing the stiff inclusion, described in Section 2.2. In existing phase-sensitive compression OCE techniques [19, 22], the displacement, d, is determined from the phase difference,$\Delta \varphi$, between loaded and unloaded B-mode pairs, according to: $d=\Delta \varphi {\lambda }_0/4\pi n$ [19], where ${\lambda }_0$ is the central wavelength of the light source and n is the tissue refractive index. In optical coherence micro-elastography, the displacement sensitivity is improved by averaging q complex quotients, $Q_k=W_{\text{k}}exp\left(i\Delta {\varphi }_{\text{k}}\right)$, for k = 1, 3…2q-1, where k is the B-mode index (Figs. 3(a)-3(c)), extracted from a three-dimensional OCT data set [35]. $Q_k$ incorporates weighting by the OCT signal-to-noise ratio (SNR), $W_k$, and the phase difference, $\Delta {\varphi }_k$, (Fig. 3(b)) of the k-th loaded and unloaded B-mode pair. q such pairs acquired within a lateral range (y) of ~6 μm (Fig. 3(a)) are averaged to improve the displacement sensitivity whilst, unlike previous OCE methods [16, 21], retaining the OCT lateral resolution. Additionally, we use a custom three-dimensional phase unwrapping algorithm (Fig. 3(d)), described in detail in Section 2.5. We use the algorithm to correct up to five wrapping discontinuities; thereby, extending the maximum measurable displacement from 0.15 μm to 2.2 μm, representing an eleven-fold improvement on the maximum measurable strain. To calculate local strain from the unwrapped phase difference, we utilize weighted least-squares regression (Fig. 3(e)), assigning a weight to each phase difference based on the OCT SNR, which improves upon ordinary least-squares and gradient methods [22]. Repeating the steps shown in Fig. 3 at ~6-μm intervals in the y-direction provides a three-dimensional micro-elastogram, as presented in Section 3.

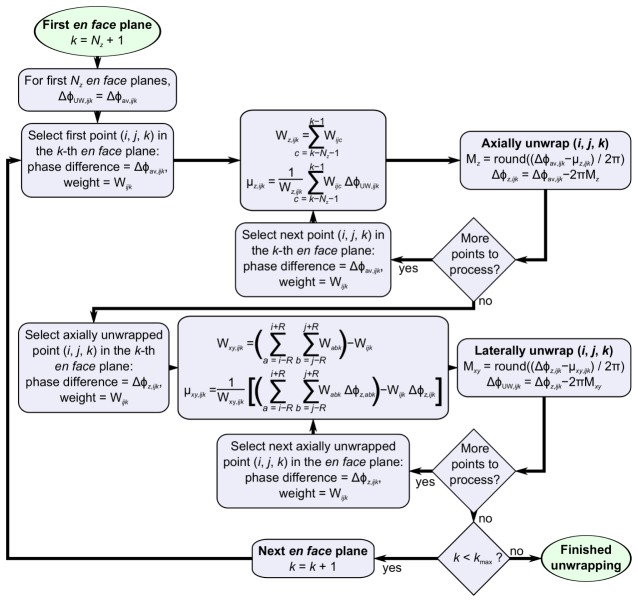
2.5 Phase unwrapping algorithm

As phase is modulo 2π, phase-sensitive OCE techniques have been limited to maximum measurable displacements between two acquisitions of ≈0.3-0.46 μm [16]. To increase the maximum detectable strain, we implemented a custom three-dimensional phase unwrapping algorithm, illustrated using the flowchart in Fig. 4. This algorithm takes advantage of the features of optical coherence micro-elastography as follows. Firstly, the common-path interferometer configuration results in a known phase difference at the initial axial coordinate of a scan, providing a well-defined starting condition. As the sample is physically coupled to the common-path reference reflector at the point corresponding to the first en face plane (z = 0 μm, k = 1), the phase difference at this initial point is known to be 0 radians. Secondly, as the displacement determined with phase-sensitive detection is exclusively in the axial direction [18] and because, for a sample under a compressive load, the magnitude of the phase difference increases with depth, the direction along which phase unwrapping should be performed is always known. Thirdly, the measured phase difference at each voxel is affected by additive Gaussian white noise with variance approximately equal to the inverse of the OCT signal-to-noise ratio (SNR) [31]. This relationship allows the SNR to be used to weight the corresponding phase difference, minimizing the effects of noise on the unwrapped phase (the weight corresponds to $W_{ijk}$ in Fig. 4). Fourthly, the displacement induced by loading is assumed to be uniform over local regions in the acquired data. The phase difference is, thus, unwrapped based on the weighted-average phase difference in local neighborhoods.

Fig. 4.

Flowchart for the three-dimensional phase unwrapping algorithm.

In the flowchart shown in Fig. 4, we index the xyz coordinates of the data volume by $ijk$. The algorithm commences at the en face plane $k=N_z+1$, where $N_z$ is the number of axial voxels used to calculate the axial-weighted mean phase, ${\mu }_{z,ijk}$, which is used to determine if a wrapping discontinuity has occurred. We use $N_z$ = 10, corresponding to ≈14 μm in depth. The phase difference in the first $N_Z$ en face planes is assumed to be free of phase wrapping. For each subsequent en face plane, each voxel is first unwrapped axially (corresponding to $\Delta {\varphi }_{z,ijk}$ in Fig. 4) by subtracting an integer multiple of $2\pi$ to minimize the difference between the phase difference of the voxel, $\Delta {\varphi }_{av,ijk}$, and ${\mu }_{z,ijk}$ of the $N_z$ preceding voxels. After axial unwrapping, every voxel in the en face plane is laterally unwrapped (corresponding to $\Delta {\varphi }_{uw,ijk}$ in Fig. 4) by subtracting a multiple of $2\pi$ to minimize the difference between the phase difference of each axially unwrapped voxel and the lateral-weighted average phase difference,${\mu }_{xy,ijk}$, of the voxels within a $(2R+1)\times (2R+1)$ neighborhood (where we have chosen $R=5$). We have demonstrated that the algorithm can correct up to five wrapping discontinuities. The upper limit on the number of wrapping discontinuities that can be corrected is, in principle, very large, approaching a third of the total number (2048 in our case) of axial voxels [36]. However, for displacements corresponding to more than five wrapping discontinuities, we observed speckle decorrelation artifacts between B-mode acquisitions that reduce the phase sensitivity, setting a practical upper limit on the measurements reported here. The algorithm was tested and validated on both phantoms and tissue. The algorithm was found to perform sub-optimally in areas where the assumption of uniaxial compression did not apply, i.e., close to tissue boundaries and where the tissue was not fully in contact with the compression plate.

3. Results

Figures 5(a) and 5(b) compare a three-dimensional OCT image and an optical coherence micro-elastogram ($\Delta z$ = 100 μm) of an optical and mechanical tissue-mimicking phantom containing a stiff, star-shaped inclusion, described in Section 2.2 and illustrated in Fig. 1(a). Perspective views of the OCT and optical coherence micro-elastography volumes are presented at a depth of ~500 μm. In Fig. 5(b), the star-shaped inclusion is clearly distinguished from the bulk material based on the measured local strain. As observed in this example, optical coherence micro-elastography provides similar spatialresolution in the en face plane to the corresponding OCT image. A cutaway view in Fig. 5(b) reveals the local strain contrast obtained in the xz-plane. The axial strain resolution is lower than the axial OCT resolution as, for each pixel, the local strain is estimated over a depth range of 100 μm. Despite this, high contrast is also observed in this plane between the star and the surrounding bulk material.

Fig. 5.

(a) Three-dimensional OCT perspective view of the phantom obtained from a depth of ~500 μm. (b) Corresponding perspective view of the three-dimensional micro-elastogram displaying the local strain, and a cutaway view revealing a B-mode micro-elastogram through the central region of the inclusion. OCT data are displayed on a log intensity scale and local strain is displayed in millistrain, mε. Scale bars (arrows), 0.5 mm (Media 1 ^{(8.6MB, AVI)} ).

To demonstrate the potential of optical coherence micro-elastography on tissue, in Figs. 6, 7, and 8 we present three representative micro-elastograms co-registered with histology. Figure 6 shows the OCT image (Fig. 6(a)), micro-elastogram ($\Delta z$ = 215 μm, Fig. 6(b)), and histology (Fig. 6(c)) of fresh breast tissue excised from a patient with invasive ductal carcinoma. The micro-elastogram and OCT image are oriented en face and mosaicked from two overlapping data sets, each with xyz dimensions 6 × 6 × 2.25 mm. Observable features of breast microarchitecture in the micro-elastogram include adipose, smooth muscle, ducts, blood vessels and tumor. Ducts and blood vessels appear as regions of high negative strain, indicating that they are more compressible than surrounding tissue. Inverted (positive) strain is observed at feature boundaries, including in each of the labelled ducts (D), and acts to accentuate these features. The magnified inset of Fig. 6 highlights a feature (blood vessel) present in the micro-elastogram but difficult to discern in the OCT image. A region of tumor (T) in the bottom left of the image is distinctive in the micro-elastogram, but difficult to discern in the OCT image. Figure 6 demonstrates that the improvements in spatial resolution, mechanical sensitivity and dynamic range enable optical coherence micro-elastography to reveal contrast in malignant tissue that is complementary and, in some aspects, superior to OCT.

Fig. 6.

Optical coherence micro-elastography of malignant human breast tissue. (a) En face OCT image at a depth of ~100 μm. (b) Corresponding en face micro-elastogram. (c) Histology, co-registered with OCT and micro-elastogram. A, adipose; D, duct; M, smooth muscle; T, region densely permeated with tumor; and V, blood vessel. In the micro-elastogram, the scale is in millistrain, mε. The insets show a 2.5× magnification of the blue-dotted boxes. Scale bars in the inset, 0.25 mm. In the micro-elastogram, the scale is in millistrain, mε.

Fig. 7.

Optical coherence micro-elastography of human breast tissue diagnosed as ductal carcinoma in situ at a depth of ~100 μm. (a) En face OCT image; (b) En face micro-elastogram and; (c) Histology, co-registered with OCT and micro-elastogram. The micro-elastogram presents additional contrast compared to the OCT image. L, lobule; and T, tumor in a duct. In the micro-elastogram, the scale is in millistrain, mε.

Fig. 8.

Optical coherence micro-elastography of human lymph node tissue. (a) En face OCT image at a depth of ~140 μm. (b) Corresponding en face micro-elastogram. (c) Histology, co-registered with OCT and micro-elastogram. C, capsule; F, follicle; M, medulla; and P, paracortex. In the micro-elastogram, the scale is in millistrain, mε.

Figure 7 shows images of tissue excised from a patient with low/intermediate-grade ductal carcinoma in situ. In the micro-elastogram (Fig. 7(b)), there is clear delineation of several ducts infiltrated with malignant cells, labelled T, which appear as focal variations in strain. Additionally, several uninvolved lobules, labelled L, are visible in the micro-elastogram. Each of these features is more clearly visible in the micro-elastogram than in the corresponding OCT image (Fig. 7(a)), and is also visible in the histology (Fig. 7(c)). In comparison, the strain throughout the central region (stroma) presents as more uniform, suggesting that the tissue is more mechanically uniform in these regions.

Figure 8 shows the OCT image (Fig. 8(a)), micro-elastogram ($\Delta z$ = 215 μm, Fig. 8(b)), and histology (Fig. 8(c)) of an uninvolved lymph node excised from a patient undergoing axillary clearance. Observable features of lymph node microstructure in the micro-elastogram include capsule, follicles, medulla and paracortex. Follicles appear in the micro-elastogram as regions of heterogeneous strain. These features are much less apparent in the OCT image. In comparison, the medulla presents as a region of homogeneous strain, indicating that it is a more mechanically uniform structure. The paracortex appears as a smooth texture which transitions between these two regions.

4. Discussion

The results presented in this paper demonstrate the potential of optical coherence micro-elastography in imaging excised breast and lymph node tissue. OCT has previously been proposed as a tool in breast cancer surgery for both intraoperative assessment of tumor margins [37] and lymph nodes [34]. The complementary, and in some cases superior, contrast provided by micro-elastography suggests that it has potential to improve the contrast provided by OCT in these clinical scenarios. Optical coherence micro-elastography could potentially be used to establish margins on excised breast cancer tissues, as has been proposed for OCT [37]. To establish its efficacy in such an application requires further studies aimed at ascertaining its sensitivity and specificity.

In addition to breast cancer, optical coherence micro-elastography has the potential to improve detection of a number of diseases that alter the micro-scale mechanical properties of tissue. Indeed, preliminary measurements in optical elastography have already begun to explore this possibility in areas such as cardiology [38], dermatology [20, 29] and ophthalmology [39]. The clinical application of optical coherence micro-elastography may also be facilitated by translating the developments presented here to needle [40, 41] and endoscopic [42] versions of elastography, potentially providing a pathway to micro-scale mechanical contrast in vivo. The relatively long acquisition times employed here require improvement to make in vivo applications practical. This could be achieved by performing in vivo measurements only in 1D or 2D, thereby, achieving shorter acquisition times. Alternatively, higher speed scanning mechanisms could be implemented to facilitate in vivo 3D application.

Micro-elastograms as presented here employ compression elastography and, thus, rely on relative mechanical contrast provided by strain rather than absolute measurement of a tissue’s elastic modulus, without recourse to inverse methods. By comparison, related optical elastography techniques, e.g., those based on surface acoustic wave [23] and shear wave [43] generation, provide a more direct path to absolute measurements of Young’s modulus. Such quantification of tissue mechanical properties is useful in assessing changes in disease over time and enables comparison of the mechanical properties of different samples. However, using these techniques, it has so far not been possible to resolve the micro-scale structures visible in the results presented here using optical coherence micro-elastography. It may also be possible to quantify tissue elasticity at the spatial resolution provided by optical coherence micro-elastography. For compression elastography, this requires knowledge of both the stress and the strain distributed throughout the tissue. An initial step towards this goal may be possible by coupling optical coherence micro-elastography with optical palpation [44], a technique our group has recently proposed, in which a compliant sensor is used to provide a high-resolution map of the stress distributed across a tissue’s surface.

5. Conclusion

In conclusion, we have demonstrated that optical coherence micro-elastography can reveal the mechanical heterogeneity of tissue at the OCT lateral resolution (11 μm demonstrated here), with microstrain sensitivity and large dynamic range. Through close correspondence with OCT images and histology, we have demonstrated that the mechanical contrast in human malignant breast and non-involved lymph node tissues extends and complements that available from OCT. Beyond the opportunity to expand our understanding of tissue mechanics and the role it plays in biology, optical coherence micro-elastography may enhance the capability to detect a range of diseases, such as cancer, atherosclerosis and glaucoma, by probing tissue mechanical properties on an intermediate scale between nanoscopic and macroscopic methods.