Optimization of camera exposure durations for multi-exposure speckle imaging of the microcirculation

Abstract

Improved Laser Speckle Contrast Imaging (LSCI) blood flow analyses that incorporate inverse models of the underlying laser-tissue interaction have been used to develop more quantitative implementations of speckle flowmetry such as Multi-Exposure Speckle Imaging (MESI). In this paper, we determine the optimal camera exposure durations required for obtaining flow information with comparable accuracy with the prevailing MESI implementation utilized in recent in vivo rodent studies. A looping leave-one-out (LOO) algorithm was used to identify exposure subsets which were analyzed for accuracy against flows obtained from analysis with the original full exposure set over 9 animals comprising n = 314 regional flow measurements. From the 15 original exposures, 6 exposures were found using the LOO process to provide comparable accuracy, defined as being no more than 10% deviant, with the original flow measurements. The optimal subset of exposures provides a basis set of camera durations for speckle flowmetry studies of the microcirculation and confers a two-fold faster acquisition rate and a 28% reduction in processing time without sacrificing accuracy. Additionally, the optimization process can be used to identify further reductions in the exposure subsets for tailoring imaging over less expansive flow distributions to enable even faster imaging.

1. Introduction

Laser speckle contrast imaging (LSCI) is rapidly being adopted by circulation studies for functional information from microvascular beds in exposed or optically accessed tissues. Although initially developed for retinal imaging, LSCI has become predominantly used for neurovascular applications from small animals to humans [1–5]. Given technical and inverse-modeling improvements the technique has increased its quantitative accuracy in observing functional hemodynamics beyond just qualitative angiography. An extension to LSCI, called Multi Exposure Speckle Imaging (MESI), further improves the quantitative accuracy of blood flow changes by enabling better separation of non-flow related contributions to the measured speckle contrast [6,7]. The MESI technique uses an improved mathematical model and instrumentation to more precisely extract the flow related contributions. Beyond bench-side physiological research, there are direct implications for prognostic, diagnostic, and intra-operative imaging applications, as speckle imaging of microcirculatory flows is increasingly becoming applied for gauging local and systemic tissue health [8,9]. Consequently, laser speckle flowmetry studies are expanding in dermatological [10–14], ophthalmological [15–17], and neurosurgical settings [18–20].

Speckle contrast imaging at multiple exposure durations has been shown to improve the quantitative accuracy of flow dynamics in calibrated microfluidic phantoms [6] as well as in vivo in both acute [7] and chronic studies [21]. As a percent of baseline, the in vivo accuracy of the technique was found to be approximately 10 ± 3% deviant with the actual flow dynamics recorded by complementary techniques in single vessels over a wide range of flows, including no flow. The confidence in flow measurements from regions largely sampling single vessels was extended to parenchymal regions as well, which spatially integrate perfusion from a host of unresolvable microvasculature. Particularly, the use of multiple camera exposures spanning nearly three decades of duration has enabled better sampling and mapping of the flow distributions in the specimen. Therefore, MESI is quickly being recognized as a substantial and necessary step in the progression of laser speckle flowmetry [22–26].

In this study, the optimization of which and how many camera exposures are necessary for quantitative speckle flowmetry is driven by the need for imaging flow dynamics over scalable fields-of-view at the level of the microcirculation with sufficient spatial and temporal resolution. Previously, an optimization has been performed for selecting a single camera exposure for fixed exposure LSCI, but confined sensitivity to a smaller range of flow distributions, such as average resting and functional flow dynamics [27], than those encompassed by the in vivo data utilized in this paper. A key conclusion from validation studies of speckle flowmetry is that no single exposure has optimal sensitivity for the range of flows observable in vivo [21]. Hence, multiple exposures are inherently necessary. By identifying the optimal exposures from the current implementation, reductions in both acquisition and processing times can be garnered towards a faster flow imaging system. An optimization process is now posed and utilized from which exposures are systematically analyzed for inclusion or exclusion in arriving at the critical exposures for performing MESI.

2. Methods

2.1 Speckle contrast imaging

When a specimen is illuminated with coherent laser light, a speckle pattern forms at the camera due to the fact that the light reaching each pixel has traveled slightly different pathlengths. Temporal changes in the speckle pattern encode information about the motion of the scattering particles encountered in the sample. When the scattering particles are in motion (e.g. flowing blood cells) the speckle pattern fluctuates in time. Provided that the exposure time of the camera is at least as long than the time scale of the speckle intensity fluctuations (10⁻⁵ to 10⁻¹ seconds for biological tissues), the camera integrates these variations resulting in the appearance of a blurring of the speckle pattern.

The degree of spatial blurring can be quantified by calculating the speckle contrast, K, defined as the ratio of the standard deviation, σ_s, to the mean intensity of pixel values, <I>, in a small region of the image [28]:

$$K\left(T\right)=\frac{{\sigma }_s\left(T\right)}{\langle I\rangle },$$ (1)

where T is the exposure time of the camera. In areas of increased motion there is more blurring of the speckles resulting in a lower contrast value. A spatially resolved map of the local speckle contrast can be calculated by computing this ratio at each point in the image from the pixels in a surrounding NxN region, (typically N = 7) [29].

Over very long exposure times, the speckle intensity fluctuations have sufficient time to blur completely, lowering the measured speckle contrast values. Conversely over very short exposures, the speckles will essentially be frozen and contrast values will be maximized (in theory close to 1). Thus, speckle contrast values are a strong function of the camera exposure duration, T, as illustrated in Fig. 1(b)-1(c).

Fig. 1.

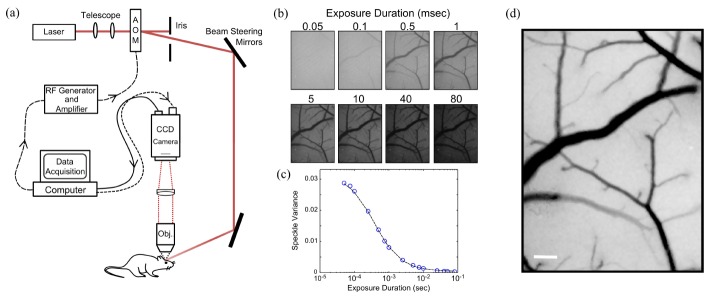
(a) Multi-Exposure Speckle Imaging (MESI) schematic. (b) Representative single exposure speckle contrast images (15 exposures total, 8 shown). (c) Speckle contrast (or variance) dependence on camera exposure duration from a single vascular region of interest. (d) MESI inverse correlation time (ICT) image of flow computed from 15 exposures. Darker pixels are linearly representative of increasing flow. Scale bar = 150 µm.

Alternatively stated, lower flow regions have speckle fluctuations that are slow compared to the camera exposure and therefore result in no appreciable blurring. As the exposure duration is increased, areas with lower flow, such as small vessels, begin to manifest in the speckle contrast image (Fig. 1(b)). Therefore, a close relationship exists between the camera exposure and the underlying perfusion.

To obtain quantitative flow measurements from speckle contrast images, the speckle contrast values are related to the characteristic autocorrelation decay time of the speckles, τ_c, which quantifies the observed rate of dynamic light scattering. Under simplifying assumptions from laser Doppler flowmetry [30], the inverse correlation time (ICT: 1/τ_c) has been posed to be proportional to the speed of the moving particles. Therefore, inverse correlation times (ICTs) in single vessels would correspond to the speed of the moving blood cells. A number of reports have demonstrated strong correlation between speckle ICTs and blood flow dynamics obtained from alternative techniques [7,21,31–33].

2.2 Multi-exposure speckle imaging

The instrumentation for Multi-Exposure Speckle Imaging (MESI) requires control over both the camera exposure duration and the laser intensity. Typically, a laser diode illuminates the sample while the computer triggers 15 camera images spanning nearly 4 decades of exposure while simultaneously adjusting the amplitude of the laser light in each exposure through an acousto-optic modulator (AOM) (Fig. 1(a)). By holding the total amount of laser light in each image constant, the impact of shot noise from illumination variations is mitigated over the multiple exposures. The presented system configuration utilizes an AOM to facilitate fast and automated frame acquisitions, while other implementations adjust intensities manually with the laser drive current or with in-path variable density filters. Table 1 lists the range and number of exposures commonly utilized in various implementations of multi-exposure speckle imaging, with the system configuration presented herein being the most expansive in both range and number.

Table 1. Camera exposure ranges typically adopted for MESI.

Exposure range (msec)	Number of exposures	Reference
0.05 – 80a,b,c	15	[6,7,21]
0.05 – 30d	11	[23]
0.5 – 80e	10	[26]
1 – 100f	7	[22]
1 – 10g	10	[34]

^aOpt. Express 16, 1975–1989 (2008), ^bBiomed. Opt. Express 1, 246–259 (2010), ^cJ Cereb Blood Flow Metab 33, 798–808 (2013), ^dAppl. Opt. 52, C64–C71 (2013), ^eBiomedical Optics Express 4, 2347 (2013), ^fMicrovascular Research 83, 311–317 (2012), ^gJ Biomed Opt 16, 056006 (2011).

In the seminal LSCI studies, Fercher & Briers proposed a simplified model that related the speckle contrast values to the speckle correlation time, τ_c and speed of the scattering particles [35]. The MESI model (Eq. (2) is an extension of that theory and maps the dependence of the speckle contrast, K, on the exposure duration of the camera, T, (Fig. 1(c)) to obtain an estimate of the correlation time of the speckles, τ_c, with the following speckle visibility expression:

$$K(T,{\tau }_c)={\left\{\beta {\rho }^2\frac{e^{-2x}-1+2x}{2x^2}+4\beta \rho \left(1-\rho \right)\frac{e^{-x}-1+x}{x^2}+v_{ne}+v_{noise}\right\}}^{1/2},$$ (2)

where $x=\frac{T}{{\tau }_c}$, ρ is the fraction of light dynamically scattered, β is a normalization factor to account for speckle sampling, ν_ne is a non-ergodic variance due to spatial (e.g. ensemble) sampling of temporal phenomena, and ν_noise accounts for exposure independent instrument noise [6]. The inverse correlation times can be mapped over the entire field of view to generate a MESI flow image (see Fig. 1(d)), where perfusion information is mapped at each pixel.

2.3 Optimization process

In order to determine the optimal set of exposures for performing Multi-Exposure Speckle Imaging, an algorithm was devised (Fig. 2) that systematically finds the minimum combination of exposures that provide comparable accuracy to the flow estimates obtained from the original 15 exposures. Accuracy here is defined by the uncertainty already established for the system, which has previously been evaluated to be at most 10 ± 3% from normalized flow dynamics across 9 animals imaged chronically [21]. Controlled microfluidic [6] and some acute imaging validations [7] have also suggested comparable or better accuracy. The optimization algorithm follows a Leave-One-Out (LOO) process, where flow estimates derived from all 15 exposures (Eq. (2) are considered as the gold standard. Sequentially, a single exposure is removed and new MESI flow estimates (Eq. (2) are obtained from the remaining camera exposures resulting in n-choose-k subsets, where k = n-1 for each iteration. The speckle flow measures from the subsets of exposure are evaluated for deviation with those derived using the full set of 15. The exposure subset that results in the least deviation is retained and the process is rerun to identify the next smaller exposure set (Fig. 2).

Fig. 2.

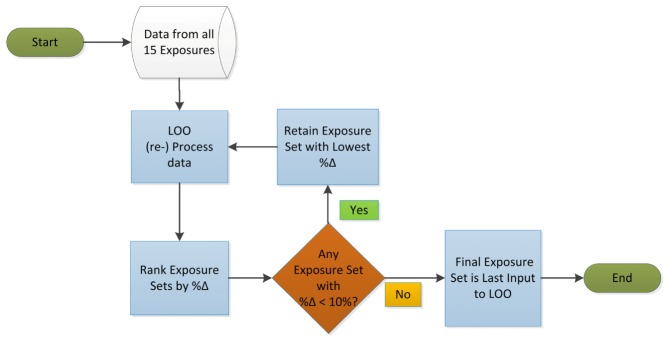
Exposure reduction optimization protocol is shown. Data taken with the full set of exposures is mined to find the minimum number and specific exposures necessary for obtaining quantitative microvascular flow mapping with Multi-Exposure Speckle Imaging.

For example, in the initial iteration, 15 subsets are evaluated each containing 14 total exposures, each missing a different camera exposure. The average percent deviation (%Δ) between the flow related parameter, namely speckle correlation times τ_c, is calculated between each subset and the full set. The subset with the least deviation with the full set is retained, provided that the average %Δ over all measurements in any given animal remains under the pre-established accuracy of 10%. The new subset is again put through the LOO process. Iteratively, the algorithm processes every new subset in this fashion. This process of attrition mines the empirical data in search of the minimum number and optimal combination of exposures from the original 15 that can be used in the design and performance of quantitative microcirculation studies with MESI. Theoretically, a minimum combination of five exposures may be obtained, equal to the number of fitting parameters in the MESI speckle visibility expression (Eq. (2) for full determination.

2.3 Data source

In vivo MESI data was obtained from a previous validation study [21] of the mouse cortical microcirculation with reported red blood cell (RBC) flows ranging from effectively zero, practically on the order of picoliters per minute (speckle 1/τ_c ~10¹ sec⁻¹), to approximately 6 µL/min (speckle 1/τ_c ~10⁴ sec⁻¹) is summarized in Fig. 3(b) and are in keeping with those reported elsewhere [36]. From the 9 mice, a total of n = 314 regions of interest (ROIs) were analyzed using the LOO process, predominantly from single microvessels (n_v = 243) than parenchymal regions (n_p = 71). The frequencies of the speckle inverse correlation times observed across all ROIs are shown in Fig. 3(a). The parenchymal distribution is well encompassed by the range of vascular flows sampled. Single vessel RBC flows were determined by intrinsic green light illuminated RBC tracking as described in detail previously [21].

Fig. 3.

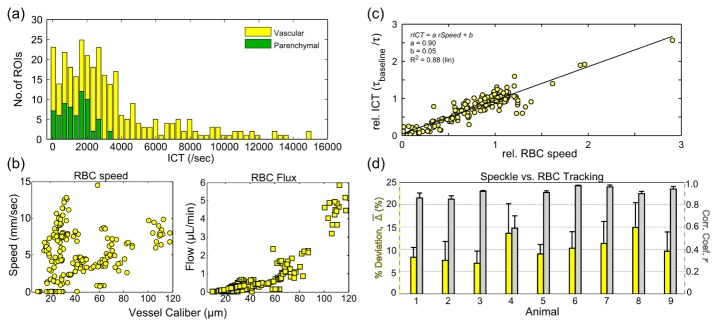
(a) Number of regions of interest (ROIs) with the corresponding inverse correlation times (ICTs) across all animals (n = 314 regions). (b) Red blood cell (RBC) speeds and their corresponding volumetric flux or flow versus vessel caliber. (c) Relative ICTs regressed against relative RBC speeds across all regions and animals. (d) Animal by animal percent deviations (yellow bars) between RBC tracking and MESI flow dynamics along with correlations of their chronic flow dynamics (gray bars). Averages ± std. dev. (errorbars) are across vascular regions.

Briefly, green LED illumination of the cranial window provided absorption contrast for hemoglobin in erythrocytes versus blood plasma. At high frame rates (~500 fps), accomplished by reduced area imaging and high optical magnifications, sufficient spatio-temporal resolution can be achieved to track erythrocytes in planar sections of surface microvasculature [36,37]. RBC speeds can be examined against speckle inverse correlation times, and estimates of flow may be obtained with vessel caliber information [38] as well. Although this technique provides an absolute flow calibration for the surface microcirculation, relative dynamics were used to facilitate cross-modality comparisons with the more spatially integrated speckle perfusion estimates [21]. Flow changes were normalized to baseline and are shown across all animals and vessels in Fig. 3(c) and examined on an animal by animal basis in terms of cross-modality deviations of the relative flows and their correlations in Fig. 3(d). Photothrombotic occlusions were induced in some animals to examine accuracy under large flow redistributions and chronic remodeling phases. Some ROIs with flows near zero can be attributed to these flow alterations as well as those above 5 µL/min, which result from acute flow redistributions (i.e. shunting). Across all animals, MESI estimates of inverse correlate times (ICTs) dynamics are on average 10 ± 3% deviant from the relative RBC speeds. Contributions to speckles from parenchymal regions cannot be decoupled and attributed to single vessels, and inverse correlation times can rather be treated as a regional perfusion index [3,39,40] integrating scattering from unresolvable depth-distributed microvasculature. Therefore, parenchymal measurements are included in the optimization process as well, and the degree of uncertainty or accuracy against RBC flows is extended to these measurements for the purposes of optimization.

Data was obtained from experiments approved by the Institutional Animal Care and Use Committee (IACUC) at The University of Texas at Austin under guidelines and regulations consistent with the Guide for the Care and Use of Laboratory Animals, the Public Health Service Policy on Humane Care and Use of Laboratory Animals (PHS Policy) and the Animal Welfare Act and Animal Welfare Regulations.

3. Results

3.1 Sensitivity and camera exposure duration

The speckle contrast dependence on exposure duration is depicted in the single exposure, K(T), images in Fig. 4(a) and the speckle variance, K²(T), curves in Fig. 4(b). The curves sample the large range of flows observable in vivo and specifically correspond to vascular flows from three animals. Each curve is a result of a different flow rate, highlighting that the shape of the relationship is indicative of the flow magnitude in the region sampled.

Fig. 4.

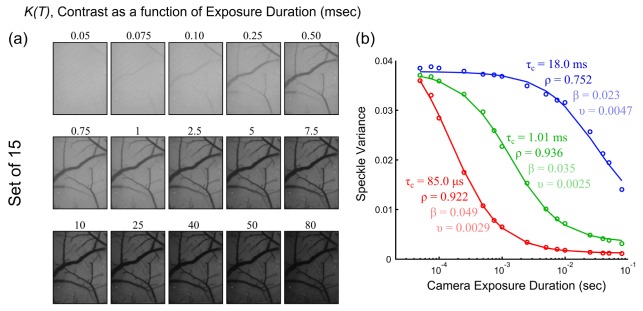
(a) Speckle contrast (K) images at each of the 15 exposure durations (T). (b) Speckle variance curves, K²(T), from mouse cortical microvasculature as a function of exposure duration. Curves were collected from chronic MESI imaging of mice under baseline, occlusion, and vascular remodeling phases. A lumped variance term, υ, which combines the non-ergodic and noise variances from Eq. (2), is shown for simplicity along with the other fit parameters of τ_c, ρ, and β.

Particularly, the speckle variance curves of faster flows decay more quickly with exposure duration (Fig. 4, red curve), while medium flows accentuate the sigmoidal relationship over the exposure range selected. Low to zero flow regions (Fig. 4, blue curve), such as from occluded vessels, typically decay over a decade longer. The speckle contrast sensitivity to the flows, in terms of inverse correlation times, can be theoretically expressed through the following absolute, S_a, and relative, S_r, formulations:

$$\begin{array}{l}{S}_a=\left|\frac{dK}{d(1/{\tau }_c)}\right|\\ =-\frac{\beta {\tau }_c}{2K{x}^2}\left[\rho (8+3\rho x-4x-7\rho )+4\rho (\rho -1)(x+2)\exp (-x)-{\rho }^2(x+1)\exp (-2x)\right],\end{array}$$ (3)

$$\begin{array}{l}{S}_r=\left|\frac{dK/K}{d(1/{\tau }_c)/(1/{\tau }_c)}\right|\\ =-\frac{\beta }{2K^2{x}^2}\left[\rho (8+3\rho x-4x-7\rho )+4\rho (\rho -1)(x+2)\exp (-x)-{\rho }^2(x+1)\exp (-2x)\right].\end{array}$$ (4)

Absolute sensitivity is maximized when the camera exposure duration matches the speckle correlation time (Fig. 5(a)). As the fraction of dynamically scattered light (ρ) increases, the sensitivity also increases expectedly, as more motion related contributions begin to comprise the observed speckle contrast. Correspondingly, the relative sensitivity (Fig. 5(b)) also improves with larger fractions of dynamics scattering. However, the relative sensitivity maximizes when the exposure duration is at least twice the correlation time, highlighting the level of time-integration needed for sensitivity to relative flow dynamics centered about any individual flow. This factor increases by nearly 5 fold as ρ drops to 0.25 highlighting that longer exposures are necessary for improved relative flow sensitivity as the dynamic scattering contributions to the observes speckle contrast reduce.

Fig. 5.

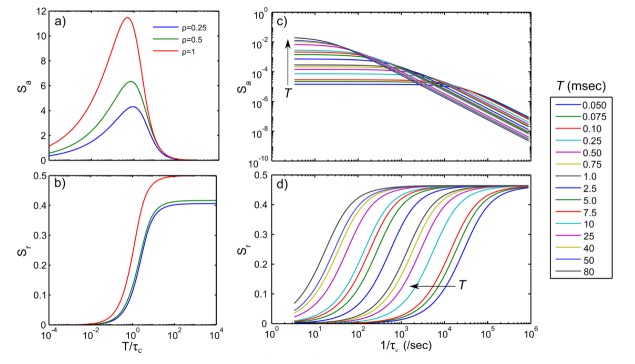
Speckle contrast sensitivities (in arbitrary units) to (a) absolute and (b) relative blood flows, shown as a function of the ratio of camera exposure duration to speckle autocorrelation time for three different fractions of dynamically scattered light, ρ. Alternatively, (c) absolute and (d) relative speckle flow sensitivities at specific exposure durations over 5 orders of inverse correlation times for a typical ρ of 0.9. Individual curves correspond to theoretical formulations in Eqs. (3) and (4) with β = 1, covering the full set of 15 camera exposures, T.

Examining these relationships over individual exposures (Fig. 5(c)), commonly used for MESI at a typical ρ of 0.9, demonstrates that absolute sensitivities 1) generally decrease monotonically with increasing flow at any fixed exposure and 2) can be improved for increasing flows by lowering the exposure duration and vice versa. Additionally, there are transition flows between ICTs of 10² to 10⁵ sec⁻¹ over which individual camera exposures may have comparable absolute sensitivity. Particularly, the empirical flow measurements used in this study also fall within this range, suggesting potential for optimization. Relative sensitivities (Fig. 5(d)) highlight the ability to accentuate the magnitude of flow changes at any given exposure with the maximum change in the normalized speckle contrast being at best close to half of the flow change, depending on ρ. The longest exposures better discriminate flow dynamics over the full range of inverse correlation times (e.g. flows) selected.

3.2 Optimization output

From the LOO process over the flow validated MESI measurements, the deviation in the calculated correlation times from the last three iterations containing 7, 6, and 5 exposures, respectively, with the original 15 are shown in Fig. 6.

Fig. 6.

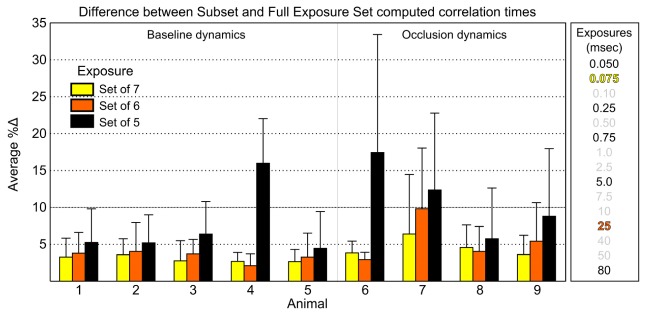
Absolute percent difference in the best subset computed correlation times and those from the full set of 15 exposures, as modeled by Eq. (2), from the last three iterations of the optimization loop. The 10% cutoff accentuates the pre-established uncertainty criterion. Animals 1-5 comprise baseline flows and Animals 6-9 sample substantial periods of flow reductions. Avg. ± std. dev. across ≥ 30 ROIs are shown for each animal. Exposures comprising each subset are listed (right column) beginning with the Set of 5 in black. Table 2’s third column label needs formatting so that the word Regression remains completely on one line, perhaps by removing the starting indentation.

Over all animals, both the 7 and 6 exposure subsets remain within the pre-established uncertainty levels of 10%, while the 5 exposure subset deviates substantially, particularly for the occlusion animals. The optimality of the subset of 6 against the subset of 7, full set of 15, and amongst its alternative subsets of 6 is enumerated in Table 2. The greater variability in the deviations observed in occlusion animals can be attributed to the effects of the exposure selection on the widely disparate flow distributions ranging from baseline to residual, shunted, and reperfused flows and their transients from induced flow alterations. In the absence of induced flow changes, any residual variability across baseline animals may be due to physiological variations such as depth of anesthesia that might vary the cardiac output.

Table 2. Relative optimality of the selected exposure set of 6.

Subset	Deviation with TSet15 (%)	Regression slope, β1	Regression offset, βo (10−2 msec)
TSet7[1]	7.9 ± 11	1.09	2.1
TSet7[2]	4.2 ± 3.5	1.05	2.0
TSet7[3]	11 ± 19	1.10	0.6
TSet7[4]	20 ± 21	1.14	7.0
TSet7[5]	12 ± 11	1.13	7.0
TSet7[6]	7.4 ± 11	0.60	18
TSet7[7]	15 ± 15	0.23	28
TSet7	3.7 ± 2.9	1.03	0.06

The selection process for the removal of an exposure is examined in detail in Fig. 7. Beginning with the optimal 6 exposure set (T_Set6), the deviations resulting from the removal of an exposure are calculated for each animal. The exposure removal having the least impact on the calculated correlation times versus the full exposure set is identified, which in this iteration is the T_Set6[5] = 25 msec exposure. Conversely, the greatest impact results from removal of the first exposure (T_Set6[1] = 0.05 msec) with average deviations over 50%, and then followed more distally by the third (T_Set6[3] = 0.75 msec, %Δ ~16%) and last (T_Set6[6] = 80 msec, %Δ ~15%) exposures. The 0.25, 5, or 80 msec (T_Set6[2/4/6]) exposure could have alternatively been removed for baseline animals alone, given the low subgroup deviation (%Δ_b <10%) on average for each subset. Generally, the observed variation between animals can be attributed to the differences in the sampled flow distributions between baseline flows and occlusion flows as alluded to above. Animals undergoing occlusions typically have slower speckle decorrelations, and consequently lower inverse correlation times, and therefore the speckle variations and sensitivities are better served at longer exposures (T>10msec). The converse is true for faster speckle decorrelations, which is evident in the exposure removals in Fig. 6 and better portrayed in the further absence of exposures redundancies, such as in Fig. 7.

Fig. 7.

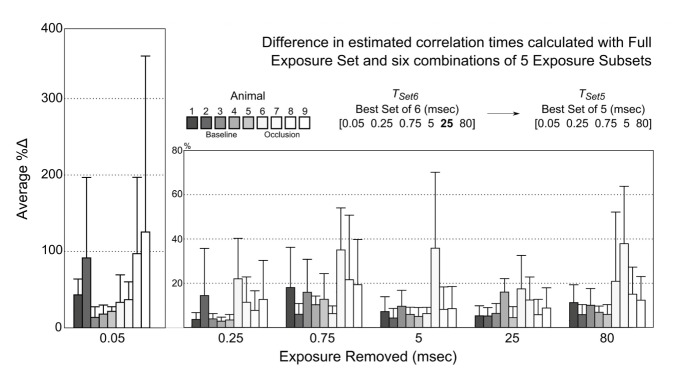
Absolute percent difference in computed correlation times for each subset of 5 exposures and those from the full exposure set. Each subset is identified by the exposure removed. Removal of the 25 msec exposure resulted in the overall lowest deviation across all animals (baseline and occlusion); though omission of the 0.25, 5, or 80 msec exposures also resulted in comparably deviant exposure subsets for animals in the baseline dynamics group (Animals 1-5). Avg. ± std. dev. across at least 30 measurements are shown from each animal.

The correlation times derived from the set of 6 exposures (n = 314 measurements) are regressed with those obtained from all 15 exposures in Fig. 8. Overall, sampled flows resulted in speckle correlation times spanning nearly three decades, while baseline animals predominantly remained under a single decade of correlation times per animal. The coefficients of a linear model,$y={\beta }_O+{\beta }_1{x}_1$, demonstrate a strong one-to-one correspondence given a β₁ value of 1.05 (p = 0), ideally close to unity, and β_o on the order of 10⁻² msec, which is statistically zero (p>0.90). The optimality of 6 exposure subset, denoted as T_Set7[2], versus its alternatives and the best set of 7, T_Set7, is examined in Table 2. The selected 6 exposure subset results in the lowest deviations and highest correlations with speckle flow measures derived with the full set of 15 exposures when compared to the alternative sets of 6 in the optimization loop. The 6 exposure subset is also statistically comparable to the metrics obtained with its progenitor subset of 7.

Fig. 8.

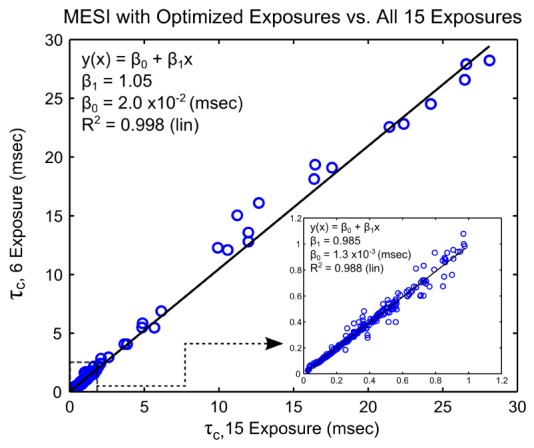
Speckle correlation times obtained with the optimized 6 exposure set regressed with correlation times derived from all 15 original exposures. Speckle correlation times, when expressed inversely, correlate as a flow measure. Coefficients of the regression depict the degree of one-to-one correspondence between correlation times computed from the subset of 6 exposures and the full exposure set over a large range of flows.

The similarity that persists after the reduction to the optimized set of 6 exposures is depicted further in Fig. 9(b). Upon cursory examination, the temporal spacing of the camera exposures captures the inflection points in the speckle visibility curves while also retaining the full dynamic range of the measured speckle contrast by retaining the first and last exposures, 0.050 and 80 msec, respectively. Visibility curves will span this range corresponding to the various perfusion levels and will be reliant on accurate rendering of the contrast relationship with exposure duration. No two sequential images in Fig. 9(a) were retained after optimization from the original set of 15, highlighting the removal of redundant camera exposures with similar local contrast values, as examined over all animals and their flow distributions.

Fig. 9.

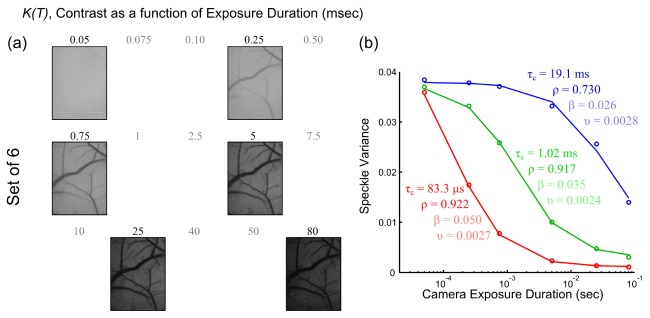
(a) Speckle contrast (K) images at each exposure from the optimal set of 6 exposure durations (T_Set6). Excluded exposures are listed in lighter shade. (b) Speckle variance curves, K²(T_Set6), from microvasculature as a function of the optimized set of exposure durations.

The reduced exposure visibility curves are similar not only in the estimates of the speckle correlation times, τ_c, and but also in the fraction of light dynamically scattered, ρ; both of which constitute parameters relevant to the specimen physiology. Variations in the instrumentation dependent parameters, β and υ, are also listed for completeness (Fig. 9(b), see lighter shaded values) over the selected measurements.

The iterative output of the optimization loop, in terms of relative accuracy, computational complexity, and imaging acquisition speed, is presented for each exposure subset in Table 2. Particularly, the percent deviation of speckle correlations times with those computed from all 15 exposures monotonically increases with exposure reduction. Substantial deviations distributed above 10% are observed by the exposure set of 5, as highlighted in Figs. 6 and 7. Additionally, a relative computational time incorporating average reductions in processing and loading times for performing the nonlinear least squares fitting process by a single processing core are presented for evaluation across all regions. The computational times exhibit a substantial reduction of over 20% beginning with the optimal subset of 9 (Table 3). Thereafter, smaller decrements in the computational complexity are observed until the best subset of 6. However, at the lowest level of determination (exposure set of 5), the number of function evaluations needed for fitting algorithm convergence began to increase for some measurements and thereby increased the computational time from the reduced levels observed in some of the larger subsets. Finally, the acquisition rate increments are substantial upon removal of the relatively longer exposure durations. By the exposure set of 7, the acquisition speed doubles from that of the original set of 15.

Table 3. Best Exposure Subset and Average Computational Complexity.

# of Exposures	Removed Exposure (msec)	Percent Deviation (%)	Comp. Time Reduction (%)	_ x Orig. Acq. Rate
14	10	0.9 ± 0.7	3.9 ± 3.5%	1.0
13	0.1	1.7 ± 2.1	7.4 ± 1.3%	1.1
12	40	1.5 ± 1.8	11 ± 1.7%	1.3
11	11	2.7 ± 3.2	14 ± 1.4%	1.3
10	7.5	3.0 ± 3.1	17 ± 1.1%	1.4
9	0.5	3.1 ± 3.5	21 ± 1.7%	1.4
8	50	3.6 ± 3.5	24 ± 1.8%	1.9
7	2.5	3.7 ± 2.9	26 ± 2.3%	2.0
6	0.075	4.2 ± 3.5	28 ± 3.7%	2.2
5	25	9.1 ± 5.0	23 ± 3.2%	2.7

4. Discussion

4.1 Evaluation of optimization

By removing superfluous exposures the redundancy in the current MESI instrument can be reduced while keeping accuracy with the prevailing system configuration and its validation. The theoretical minimum number of five exposures was untenable given the constraints on the maximum uncertainty with the original computed correlation times. This is likely due a substantial volume of measurements from the extrema of flows observed in vivo from fast arteriole flow to large flow reductions from vascular occlusions. The marked differences in the speckle contrast dependence on camera exposure duration (see curves in Figs. 4 and 9) from these flow conditions resulted in the selection of 6 optimal exposures from the original 15.

Within the optimal set, the 5 millisecond exposure was also preserved by the optimization process, which has previously been demonstrated to be optimal for single or fixed exposure LSCI of functional cortical flows in rodents [27]. By the end of the MESI optimization, the 0.05 millisecond exposure proved to be consistently critical for nearly all animals. This exposure is important for estimating the shape of the speckle visibility relations with exposure duration (e.g. first and second derivatives) for nearly all ROIs, and helps estimate the instrumentation factors that scale the speckle visibility down from unity, as few speckles have decorrelated within this integration time. Therefore, the removal of 0.05 msec exposure, after other nearby redundant exposures are eliminated (Fig. 7), only further imparts increasing criticality to this lowest exposure (%Δ >100%) of the original set. The single exposure sensitivities presented in Fig. 10 fail to emphasize this importance due to assumptions that only a fixed exposure is being used for imaging, when in actuality the fidelity of the shape of the speckle visibility curves with exposure duration is of interest for multi-exposure imaging. In fact, the observed variability across animals can also be explained by variations in the dynamic range of the speckle visibility curves (Fig. 4). The speckle visibility expression’s (Eq. (2)) parameters, derived from fitting over the subset of exposures, will resemble those from the fits to the original set only when the dynamic range of the observed speckle contrast, K(T), is also retained. Therefore, the longer exposures set the other end of this range. However, less consistency is observed in the appropriate long exposure bounding across the animals, which have been more variable for the distribution of flows across baseline, best bounded by T~5 msec (Figs. 4, 6 and 7), versus occlusion animals, which is bounded better by T~80 msec.

Fig. 10.

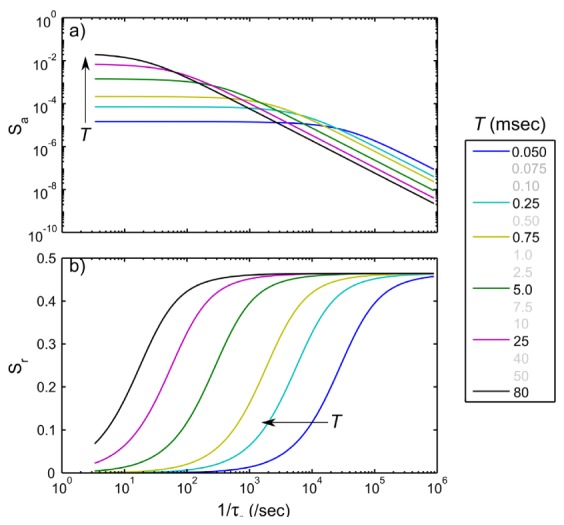
(a) Absolute, Sa, and (b) relative, Sr, speckle contrast sensitivities in arbitrary units to blood flows and flow dynamics, respectively over inverse correlation times encompassing flows observed in vivo. Individual curves correspond to theoretical formulations in Eqs. (2) and (3), assuming fixed camera exposures, T, for a typical ρ of 0.9. The removed exposure durations are listed in lighter shade for comparison.

Consequently for vascular to parenchymal flows, longer or shorter exposures may be excluded for obtaining quantitative flow dynamics over various sub-ranges of flows. However, perfusion levels may vary in vivo due to a number of reasons including physiological variations, both healthy and pathological, as well as from experiment design, anesthesia, and between animals. Therefore, in a full field imaging paradigm the inclusion of at least the optimal 6 exposures enables sampling of the microvascular flows robustly while maintaining a stable level of uncertainty in the predicted flow dynamics throughout the field of view. Ultimately, this accuracy is predicated on treatment of the pre-selected set of 15 exposures as the gold-standard. Therefore, the exposure optimization is limited to exposures explicitly enumerated in the originating set, which albeit its limitations is still relatively expansive (Table 1) and well validated (Fig. 3) [6,21].

Alternatively, by examining the empirical representation (Figs. 8 and 9) of the optimized exposures and the spacing of their theoretical sensitivities (Fig. 10), the reduced exposure set appears sufficient in capturing the dynamic range and shapes of the visibility curves without excessive redundancy. The computationally manageable LOO process tackles the minimization from the least influential of the redundant exposures first. However, the successive iterations are dependent on the preceding best subsets beginning with pre-defined set of 15. The susceptibility of the LOO process in arriving at a local minimum for a given sensitivity range may exist and can only be well-evaluated by examining against all possible combinations of 6 exposures (i.e. 15-choose-6 subsets), which can be computationally taxing. Nevertheless, the swapping of some exposures with others that have comparable sensitivities, or exposures within half a decade of one another, could be evaluated to see if lower deviations and better correlations are achieved. However, these variations will likely be modest and insignificant from the LOO predicted set of 6. Practically, the supervised swapping to the lowest exposure over a given sensitivity range may lower the acquisition time, particularly for exposures longer than the camera read-out time, and therefore be more critical to the optimality than modest improvements in accuracy.

4.2 Implications of optimization

The exposure optimization confers advantages on both the acquisition and processing ends of the Multi-Exposure Speckle Imaging system. First, lowering the number of images needed for quantitative flowmetry improves overall acquisition times by reducing throughput. Frame readout time for the Firewire protocol CMOS camera used in this study is approximately 7.5 milliseconds. The traditional MESI acquisition of 15 exposures is made in approximately 335 milliseconds, which is the sum of all 15 exposure durations and the readout time for each image. The new optimized exposure set of 6 requires 156 milliseconds for acquisition. Alternatively stated, the optimized full frame acquisition rate is at least 6 MESI measurements per second (Table 3), twice that achievable with the original 15 exposures. Functional flow dynamics that occur over a period of seconds, including hyperemia and vasomotion, would be particularly well sampled and spatio-temporally mapped. These faster rates are also sufficient for temporally sampling pulsation dynamics in humans even under tachycardic conditions. For imaging baseline pulsation dynamics in rodents (6-10 Hz), a subset of 5 exposures may be utilized that tolerably omits the longest exposure of 80 msec (Fig. 7), resulting in approximately 15 MESI measurements per second. These faster rates also enable better temporal averaging of any remnant noise. As faster transfer protocols (i.e. Gigabit Ethernet and USB 3.0) facilitate lower camera readout times, MESI acquisition rates with the optimized exposure set may be commensurately improved. Notably the speeds achievable are not limited by the bandwidth for illumination modulation, which is facilitated by using an acoustic optic modulator. On the processing end, fewer images improves overall computational times regardless of the processing power available. The combined processing and data loading times for a typical region of interest reduce by 28% on average by using the optimized subset of 6 exposures. Notably, the computational complexity (Table 3) of the best subset of 7 closely trails that of the best subset of 6 and retains a similar acquisition rate improvement. However, the best subset of 7 comes at the cost of 17% more data storage, which may be a substantial factor over long acquisitions. Percentages are reported as actual computational times will be dependent on the available processing and/or parallel computing power.

5. Conclusions

Overall, the optimal set of 6 exposures comprise those presented in Fig. 9 given by the lowest computational complexity while retaining an approximate deviation of 4.2 ± 3.5% with the flow indices computed from all 15 exposures, which also more than doubles the measurement acquisition rate. This deviation is within the cross-modality accuracy or uncertainty of the MESI flow dynamics with all 15 exposures against RBC tracking, which can be treated as a calibration or gold standard. The optimized exposures presented in this study are relevant for flow dynamics within the microcirculation, typically for vessels under 0.2 mm in diameter in rodents. These bounds on the vessel caliber and the corresponding flows are tailored to the camera exposures and have been validated with calibrated flow measurements in vitro and in vivo. Provided that studies employing MESI are framed within similar specifications, the level of confidence established for the perfusion dynamics should be retained. However if the tolerable uncertainty levels with calibrated flow measures is exceeded, as may be likely for human microcirculatory flows, an extension of the exposure range may be warranted by including appropriately shorter or longer exposures guided by separations seen in the optimized theoretical sensitivities. If a smaller flow range is prevalent, such as for baseline flows, a further reduction in the number and expanse of exposures may be possible. Therefore, the process presented in this paper can be used for optimizing the exposure sets after adaptation and/or extension to various perfusion levels.