Adaptive optics optical coherence tomography with dynamic retinal tracking

Abstract

Adaptive optics optical coherence tomography (AO-OCT) is a highly sensitive and noninvasive method for three dimensional imaging of the microscopic retina. Like all in vivo retinal imaging techniques, however, it suffers the effects of involuntary eye movements that occur even under normal fixation. In this study we investigated dynamic retinal tracking to measure and correct eye motion at KHz rates for AO-OCT imaging. A customized retina tracking module was integrated into the sample arm of the 2nd-generation Indiana AO-OCT system and images were acquired on three subjects. Analyses were developed based on temporal amplitude and spatial power spectra in conjunction with strip-wise registration to independently measure AO-OCT tracking performance. After optimization of the tracker parameters, the system was found to correct eye movements up to 100 Hz and reduce residual motion to 10 µm root mean square. Between session precision was 33 µm. Performance was limited by tracker-generated noise at high temporal frequencies.

1. Introduction

Spectral-domain optical coherence tomography with adaptive optics (AO-OCT) is a highly sensitive in vivo method for three dimensional imaging of the living microscopic retina [1–12]. OCT provides ultrahigh axial resolution using broadband light sources and exquisite sensitivity for detection of faint reflections from essentially any layer in the retina. AO in contrast provides diffraction-limited lateral resolution by correction of ocular aberrations. Together, AO-OCT produces cellular-resolution imaging of retinal structures.

However like all in vivo retinal imaging techniques, and especially those of high magnification, AO-OCT suffers the effects of involuntary eye movements that occur even under normal fixation [13]. Eye movements pose two principal challenges for cellular level imaging: (1) image blur and distortion that diminish the visibility of retinal structures captured in individual images and (2) difficulty to track the same structures across images. The latter is particularly challenging for functional studies in which images are captured over extended time intervals.

Increasing image acquisition speed, by using high speed line-scan cameras in the OCT detection channel [14, 15] or fast swept sources in the source channel [16, 17], reduces motion artifacts within volumes and feature displacement between volumes, but it does not eliminate them. Registration and dewarping algorithms can help further decrease the effects of motion artifacts in the AO-OCT volume videos, but the motion must remain small enough so that the structure of interest stays in the field of view for the entire acquisition [9, 18]. An alternative that has gained interest is active image stabilization in which eye motion is measured and corrected in real time. Two similar but distinct approaches have been pursued for active stabilization: (1) SLO image-based [19–22] and (2) hardware-based retinal tracking [23–29].

SLO image-based retinal tracking was first demonstrated by Wornson et al. in 1987 [30] using SLO images for tracking the centroid of the optic nerve head at 60 Hz. Two decades later, SLO image-based retinal tracking underwent substantive advances with faster and higher resolution SLO systems. This has also included integration into research [21, 22] and commercial (Spectralis, Heidelberg Engineering) spectral domain optical coherence tomography (SD-OCT) systems for stabilization of the OCT beam.

Parallel to these image-based developments has been hardware-based retinal tracking, first demonstrated by Ferguson et al. in 1996 [29] and subsequently re-engineered into a stand-alone prototype by Physical Sciences Inc. (PSI). Unlike the image-based approach, eye motion is sensed via a separate probe beam and servo tracking system that applies phase-sensitive detection to monitor variations in the beam’s fundus reflectance. Tracking in this way has been successfully demonstrated for stabilizing SLO [23, 31], AO-SLO [26, 28, 32], and OCT [24, 25] at tracking closed-loop bandwidths up to 1 KHz. The PSI retina tracker was also demonstrated with a research-grade SD-OCT system that stabilized the image in three dimension [27] and a clinical system investigated for imaging glaucoma patients [33].

In this paper we extend these previous studies by rigorously evaluating performance of a similar, but more advanced hardware-based retina tracker from PSI and customized for AO-OCT. AO-OCT represents a notably more demanding modality for retinal stabilization owing to its cellular 3D resolution and comparatively much slower scan rates compared to SLO. For this study, the tracker was integrated into the sample arm of the 2nd-generation Indiana AO-OCT system. We developed analyses based on temporal amplitude and spatial power spectra in conjunction with a strip-wise registration method to measure and optimize tracker performance for AO-OCT imaging. Evaluation quantified effectiveness to correct inter- and intra-session motion in normal subjects.

2. Materials and methods

Description of methods is divided in five parts. Sections 2.1 and 2.2 describe briefly the key subsystems of the Indiana AO-OCT and the dynamic tracker. The AO-OCT [5, 8, 34] and tracking [24, 25] systems are described in detail elsewhere, but have undergone numerous improvements since, some specific for this study. Section 2.3 presents our approach to integrating the tracker into the AO-OCT system. Experiments to validate tracking AO-OCT performance and methods to process the measurements are described in Sections 2.4 and 2.5, respectively.

2.1 Adaptive optics SD-OCT imager

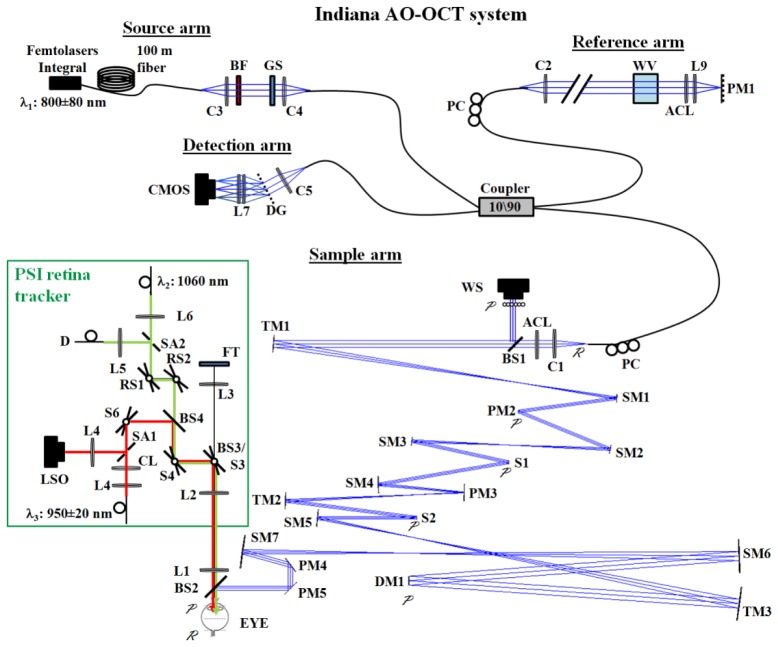
Figure 1 shows a schematic of the Indiana AO-OCT system. The core of the system is the SD-OCT imager. Its four channels (source, sample, reference, and detection) are connected by a 2x2 780HP fiber coupler with 90/10 splitting ratio. The source arm contains a broad band femtosecond laser (Integral OCT, Femto Lasers, Vienna, Austria) with central wavelength at λ_c = 800 nm and bandwidth of Δλ = 160 nm. The 60 mW output of the Integral (full spectrum) provided more power than required for retinal imaging. This allowed us to tailor the spectral bandwidth of the source by insertion of optical bandpass filters of various spectral widths via a fiber optic bench. In this way we traded off axial resolution for acquisition speed by reading out less pixels of the line-scan camera. For cone imaging, we found that the bandpass filter (λ_c = 809 nm, Δλ = 81 nm) provided a good compromise and was used for all imaging in this study. With this filter, nominal axial resolution in retinal tissue (n = 1.38) was 2.6 μm. The detection channel of the SD-OCT system was designed around a Basler Sprint camera whose line rate was maximized for the source spectral bandwidth, in this case achieving an A-line rate of 167 KHz using the central 1,408 pixels.

Fig. 1.

Indiana AO-OCT system with active retina tracker. Schematic of the system is shown with tracker integrated optically via a customized beam splitter (BS2). For illustration purposes, the system is shown flattened to one plane (PM5 folds the beam vertically). Key: blue line, 809 nm AO-OCT beam; red line, 950 nm LSO beam; green line, 1060 nm tracking beam; ACL, custom achromatizing lens; BF, bandpass filter; BS, beam splitter; (C), collimator; CL, cylindrical lens; DG, diffraction grating; DM, deformable mirror; (D), detector; FT, fixation target; GS, glass slide; (L), lens; PC, polarization controller; PM, planar mirror, RS, resonant scanner, (S), scanner; SA, aperture splitting optic; SM, spherical mirror; TM, toroidal mirror; WS, wavefront sensor; WV, water vial.

The sample arm is the most complex of the four arms. Principal components are X and Y galvo scanners, a Shack-Hartman wave front sensor (SHWS), a deformable mirror (DM97, ALPAO, France), and numerous relay optics. Mirror-based telescopes conjugate these four components to the eye pupil. Astigmatism generated at both retinal and pupil conjugate planes due to the off-axis use of spherical mirrors was corrected with three customized toroidal mirrors that were inserted at locations TM1, TM2, and TM3 in Fig. 1. Details of the toroidal mirror design as well as the AO system that dynamically measured and corrected the ocular aberrations (for a 6.7 mm pupil) of the subject can be found in Liu et. al [34].

Custom control software was developed in Matlab (Mathworks, Natick, MA) that incorporated ALPAO Core Engine (ACE) Matlab libraries. Performance of the AO was assessed by monitoring the wavefront root-mean-square (RMS) error and quality of the AO-OCT retinal images during image acquisition. Custom C++ software controlled the SD-OCT imager. This included generating sawtooth waveforms for the XY scanners that were also synced to the Basler Sprint camera, control of and spectra acquisition from the Basler Sprint camera, and finally display and saving of the image data. The datastream from the camera was processed and displayed at 20 fps, and provided visualization of the raw spectrum, A-scan, fast and slow B-scan, and C-scan (en face) projection of the retinal layers of interest.

2.2. Customized tracker module

The self-contained tracker module consisted of three subsystems that performed distinctively different functions: dynamic tracking for retina stabilization, secondary wide field imaging for navigating and monitoring system operation, and a programmable fixation target for controlling subject gaze.

The tracker portion was designed to stabilize the location of the imaging beam relative to a specific retinal landmark, the preferred feature being the optic disc [24, 31] and that used in our study. The tracker focused a near-infrared beam (λ₂, Fig. 1) onto the bright lamina cribrosa of the disc and dithered it in a circular pattern using a pair of resonant scanners (16 KHz). The reflectance was detected by a confocal reflectometer (sampled at 208.3 KHz). The detected signal was processed real-time to generate error signals that were proportional to lateral motion of the optic disc, described in detail below. The error signals were then converted to a voltage bias applied to the AO-OCT galvanometer scanners for correction of the eye motion that would otherwise degrade the AO-OCT image.

Tracker feedback control was based on a standard proportional-integral-derivative (PID) loop. The tracker error signals were generated from the dithered beam by means of dual-channel lock-in amplifier at the resonant scanner frequency implemented in a field programmable gate array (FPGA). P, I, and D control signal parameters were tuned manually with a moving test target whose angular size and brightness approximates those expected of trackable features in the eye (~1deg). The target was driven laterally (by a galvanometer motor) with a square-wave step size approximately twice its diameter simulating expected saccades. The tracking mirror step responses following the target were optimized empirically by adjusting the P, I, and D feedback parameters for speed, accuracy, and minimum overshoot. The resulting tuned PID parameters were particular to these test conditions. In addition, the user-adjustable feedback gain constant, G, linearly scaled each of these parameters (relative to their preset tuned values). This adjustment is necessary to account for the variability in the error signal amplitudes and SNR due to varying brightness of the lamina cribrosa from subject to subject, and to optimize the trade-off between tracking speed and fidelity. G provided smooth control of the tracking bandwidth: too low a gain resulted in “loose” lock and low-bandwidth tracking; too high a gain (in this study typically 1.6) promoted oscillations.

The second subsystem was a wide field line-scan scanning ophthalmoscope (LSO) that provided a 35° × 35° real-time fundus view using a separate near infrared light source (λ₃, Fig. 1). The LSO view facilitated alignment of subject's eye, and monitoring of the AO-OCT and tracking beams during imaging. A small fraction of the AO-OCT beam leaked through BS2 and appeared in the LSO image. In contrast, position of the tracking beam was determined in calibration and marked (in software) on the LSO image.

The final subsystem was the fixation channel, the principal component being a LCD display that was integrated into the tracker module and extended the tracker monitor display. The display (KCD-VDCF-BA, Kopin LCD) had 640 × 480 × 3 active pixels in a compact 9 × 6.8 mm area. It was fully programmable and allowed direct control of the location, size, and shape of the fixation target. As shown in Fig. 1, the tracking, LSO, and fixation subsystems were combined optically with two beam splitters (BS3 and BS4).

2.3 Integration of PSI tracker into AO-OCT sample arm

To adapt the tracker for use with the Indiana AO-OCT system required several key optical and electronic modifications. Optical integration was driven primarily by the spectral transmission window of the eye and the need to preserve the 700-900 nm portion for the Integral Femtolaser for ultrahigh resolution OCT. We adapted the light sources and optics of the tracker module to work around the Integral range. Specifically, the tracker module was integrated into the sample arm of the AO-OCT system using a custom dichroic beam splitter (BS2, Fig. 1) positioned approximately 40 mm in front of the eye pupil plane. The beam splitter reflected 700 nm to 900 nm, which was used for the AO-OCT imaging beam, and transmitted visible wavelengths for the fixation target and above 900 nm for LSO imaging (950 ± 20 nm) and tracking (1060 nm). LSO imaging is sub-optimal at this wavelength from increased ocular absorption and decreased silicon quantum efficiency, though sufficient for global orientation and landmark identification. Ocular absorption could also decrease the retinal tracking signal, but was compensated by an increase in the input power. The entire tracking module (green box in Fig. 1) was mounted above the AO-OCT on a translation stage to correct the subject's refractive error and to focus the LSO and tracker subsystems. Note that L1 and BS2 were not mounted on the translation stage, which assured conjugacy was preserved between the eye's pupil and the front focal plane of L1 regardless of the stage position.

Electronic integration was driven by the fact that the AO-OCT and tracking module were optically separate systems. In some previous tracking systems [24, 28, 31], the primary imaging beam is reflected off of the tracking scanners (in this case S3 and S4) and automatically correcting for eye motion without further signal processing, though full integration is necessary. In this case, the design considerations described above – primarily the need to preserve the AO optical path – proscribed full integration. The open loop nature of this design thus dictated careful attention to the summation and calibration of the tracker signals for use by AO-OCT. Horizontal and vertical error signals generated by the retinal tracker as a result of an eye motion were encoded as two voltage signals. The signals were passed through a custom electronics box that low-pass filtered for noise reduction, scaled to match the volts-to-degree response of the AO-OCT galvo scanners, and finally summed the error signals to the slow- and fast-ramp voltages that control the galvo scanners. The custom box incorporated separate conversion controls (volts to degrees) for each error signal. This allowed fine tuning of the signals for improved stabilization of the AO-OCT image. Prior to subject imaging, the tracker was calibrated by translating the retina of a model eye in horizontal and vertical directions separately while adjusting the conversion controls. The customized box also included control of offsets for centering the summed signals (tracking error signals plus AO-OCT raster scan signals) in the AO-OCT field of view. During subject imaging, adjustments were made to two tracker parameters: (1) cut of the lowpass filter in the custom electronics box and (2) tracker gain (G), which controls the percent error signal applied to the galvo scanners.

2.4 Experiments

Two AO-OCT imaging modes (Table 1) were used to assess tracker performance to stabilize intra- and inter-session motion of AO-OCT volumes. A session is defined as a contiguous set of AO-OCT volumes that form a single video. Intra-session stabilization therefore is the correction of local motion within individual volumes (image warp) as well as bulk motion between volumes (XY image translation) of the same AO-OCT video. Correction of both motions (local and bulk) is required to stabilize the video. In contrast, inter-session stabilization refers to correction of bulk motion between videos (as opposed to between volumes) and reflects the ability of the tracker to lock repeatedly onto the same retinal target.

Table 1. AO-OCT imaging parameters.

Parameters	Mode #1	Mode #2
A-line acquisition rate	166,666 Hz
A-line sampling	1.5 μm/px	1.0 μm/px
# of A-lines per B-scan	300	270
B-scan acquisition rate	546 Hz	606 Hz
# of B-scans per volume	300	216
# of volumes per video (session)	5	13
Volume video duration	2.7 s	4.6 s
AO-OCT image field of view	1.5° × 1.5°	0.9° × 0.72°

Imaging mode #1 was designed to examine stabilization of bulk motion within (intra-) and between (inter-) sessions. A-scan sampling density and volume acquisition rate were traded off for a larger field of view. This facilitated imaging larger (macro-) retinal features, such as blood vessel shadows (~50 μm in diameter), whose overall motion could then be readily tracked between volumes in post processing. Five sessions of volume videos were acquired on two normal subjects (#1 and #2, Table 2) for two stabilization cases: with and without tracking. Each session contained five volumes, thus five en face images. Subjects were removed from the system between sessions. Thus each session began with a realignment of the subject’s pupil to the system, establishment of a new AO correction, and finally engagement of the tracker. All tracking was done on the optic disc. SLO images 35° × 35° degrees using Spectralis (Heidelberg Engineering, Carlsbad, CA) were acquired on the same subjects and used to register the AO-OCT volumes, a post processing step described in Section 2.5.

Table 2. Subject information.

Subject #	Age (y)	Gender	Spherical equiv. refractive error (D)	Axial length (mm)	Imaging mode	Imaged Retinal Eccentricity (from fovea)
1	30	F	0	23.7	#1	5° Nasal
2	47	M	−2.5	25.4	#1, #2	6° Nasal
3	58	M	+ 1.75	23.53	#2	6° Nasal

Imaging mode #2 was similar, but in contrast designed to examine stabilization of local and bulk motion within a session (intra-session), both critical for cellular-resolution imaging. The target retinal structure for this experiment was the cone photoreceptor. The micron-scale size of cones (with row-to-row spacing of ~8 μm at 5°-6° nasal to the fovea) made it a sensitive indicator of uncorrected residual eye motion. Compared to the imaging parameters of imaging mode #1, those of mode #2 were optimized for cone imaging, trading off FOV (3.6 × smaller FOV area) for denser A-scan sampling (2.25 × denser) and increased volume speed (1.53 × faster acquisition). Five sessions of volume videos were acquired on two normal subjects (#2 and #3, Table 2) for two stabilization cases: with and without tracking. Each session contained 13 volumes, thus 13 en face images. This experiment was performed twice. The first pass provided initial performance results that were used to optimize the tracker parameters: (1) cutoff of the electronic lowpass filter and (2) tracker gain. The second pass implemented the optimized parameters and provided final tracker results.

Total light incident on the cornea from the combined imaging systems was the sum of 2.7 mW centered at 950 nm spread over 35° × 35° for LSO imaging, 325 μW at 1060 nm spread over 1.5° diameter circular pattern for tracking at the optic disc, and 400 μW centered at 809 nm spread over 1.5° × 1.5° (Mode #1) and 0.9° × 0.72° (Mode #2) for AO-OCT imaging. The combined light powers were more than an order of magnitude below safe limits defined by ANSI [35]. All procedures on the subjects strictly adhered to the tenets of Helsinki declaration and the Institutional Review Board of Indiana University, and informed consent was obtained from all subjects.

2.5 Post processing: registration and lateral displacement extraction

AO-OCT volume videos were analyzed for uncorrected eye motion based on lateral displacements of blood vessel shadow patterns (imaging mode #1) and cone photoreceptors (imaging mode #2). Volume movies were first axially registered (along the A-scan direction), and the two layers corresponding to inner segment/outer segment junction (IS/OS) and posterior tip of the outer segment (PTOS) of the cone photoreceptors were segmented. Reflections at and between the two segments were projected axially to form a single en face image from which all motion analysis was performed (see Fig. 2).

Fig. 2.

Extraction of the photoreceptor layer from a representative AO-OCT volume acquired using imaging mode #2 (6° nasal to the fovea of Subject #2). Shown is (a) full AO-OCT volume, (b) extracted sub-volume composed primarily of the IS/OS and PTOS reflections, and (c) en face projection of the sub-volume in (b) used for motion analysis. RNFL: retinal nerve fiber layer, GCL: ganglion cell layer, IPL: inner plexiform layer, INL: inner nuclear layer, OPL: outer plxiform layer, ONL: outer nuclear layer, IS/OS: inner segment outer segment junction, PTOS: posterior tips of outer segments.

2.5.1 Imaging mode #1

For imaging mode #1, each AO-OCT en face image was manually registered to the corresponding Spectralis SLO image. This was done by superimposing the AO-OCT image onto the much larger SLO image and then translating pixel by pixel (1.5 µm steps) until the best visual match was obtained for the blood vessels in the two images. The same trained technician registered all images. Alignment repeatability of the technician was 11 µm (RMS), the average RMS for a practice set of five AO-OCT images, each aligned ten times. Displacements between en face AO-OCT frames were measured, corresponding to residual uncorrected eye motion. We also averaged images within each session and compared the resulting visibility of the blood vessel pattern with and without tracking. Using these measurements, we quantified the intra-session effectiveness of the tracker to image the same patch of retina repeatedly. This corresponded to the correction of bulk motion. Next we assessed the effectiveness of the tracker to repeatedly lock on to the same structure on the optic disc between sessions. To do this, we measured displacements between the averaged images, one for each session.

2.5.2 Imaging mode #2

For imaging mode #2, the en face images were processed at much finer spatial and temporal scales to more accurately quantify tracker performance. Processing included temporal amplitude and spatial power analyses that were used to optimize the cutoff of the electronic lowpass filter and gain of the tracker. Performance was assessed for correcting both local and bulk motion (intra-session).

At the core of the temporal analysis was a registration algorithm based on strip-wise cross correlation, an earlier version of which was described by Jonnal et al. (2012) [9]. En face images were divided into thin strips oriented parallel to the fast scan direction and consisted of about 7 contiguous fast B-scans, the width being approximately the cone row spacing at the retinal location imaged. Using the strip-wise algorithm, each strip was cross-correlated with a reference image, establishing a neighborhood of maximum likelihood. Next, the single B-scan at the center of the strip was cross correlated with the reference, and the correlation peak within the maximum likelihood neighborhood was used to register the B-scan. The first step was necessary to avoid spurious maxima that arise when the relatively low correlations of single B-scans are used. The reference image was selected from one of the en face images that exhibited minimal motion artifacts in the same session. This reference image was selected by a human expert following a protocol similar to that commonly used in AO-SLO image registration [19].

Figure 3 illustrates the strip-wise algorithm for determination of X and Y displacements of one strip. Repeated application of the cross-correlation while incrementing the strip location one B-scan at a time resulted in 216 motion measurements per volume and a motion sampling rate of 606 Hz. While this rate was well below that of the tracker (16 KHz), it was sufficient to assess tracker performance across the range of frequencies where the vast majority of eye movements reside (<10Hz) [36, 37]. The rate also covered what we ultimately determined to be the useful range of the tracker. The strip-wise cross-correlation procedure was repeated for all en face images in all sessions.

Fig. 3.

Illustration of the strip-wise cross-correlation method as applied to an AO-OCT en face image. Method determines X and Y displacements of a thin strip (red trace) and its central B-scan (green line) in the target image (left) relative to the reference image (right). Procedure is repeated for each of the 216 B-scans that are applied to the image. The displacements correspond to uncorrected eye motion.

X and Y displacements with a cross-correlation coefficient ≥ 0.7 were considered a strong registration match (reliable) and retained for analysis. Displacements with a coefficient < 0.7 were excluded. Empirically we found low coefficients most often occurred during a microsaccade that severely distorted the AO-OCT image and resulted in a registration for the strip far from the expected location. To illustrate, Fig. 4 shows a representative time trace (black) of the radial displacement $\left(R=\sqrt{X^2+Y^2}\right)$ and associated cross-correlation coefficient (green) for one session. Note the strong overlap of the microsaccades and low correlation values (<0.7). For illustration purposes, the blue trace in the same figure shows only measurements with a coefficient greater than 0.7. Also evident in the figure is a single flat portion of the trace (in this example volume #12) that denotes the reference volume, which was used for strip-wise registration. Because all volumes in the session are registered to the reference volume, the reference must by definition have zero displacements. Taken together, low correlation coefficients due to unregisterable eye motion and the need of a reference volume resulted in a loss of displacement samples. To preserve regular sampling necessary for further processing, we linearly interpolated over the excluded measurements (magenta), a common solution employed in many disciplines when data points are missing [38].

Fig. 4.

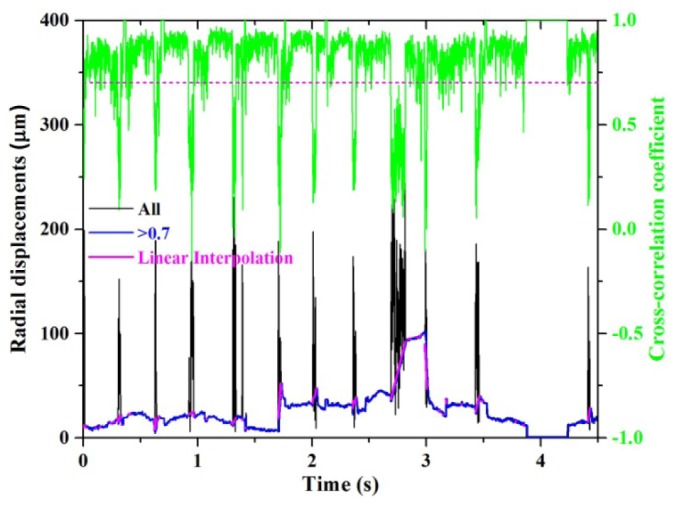
A representative time trace of eye motion as measured with strip-wise registration. Shown is one session without tracking on subject #2. The black trace contains all measured displacements regardless of the cross-correlation coefficient value. The blue trace shows only displacements with a high cross-correlation coefficient (>0.7), indicative of reliable registration. The magenta trace is the linear interpolation used to fill the gaps in the blue trace due to low cross-correlation values (<0.7).

2.5.2.1. Temporal amplitude analysis

This analysis evaluated the temporal spectra of the cross-correlation displacements. It involved Fourier transforming the cross-correlation displacements of individual sessions, as for example the one depicted in Fig. 4 after linear interpolation to replace unreliable data samples. To be consistent with the recent literature [20, 37], temporal spectra were plotted in amplitude (as opposed to power) but in units of microns using the conversion 300 µm/°. Amplitude was averaged across the five sessions, both with and without tracking for comparison. Plotting eye motion in this way elucidated the performance of the tracker to correct motion frequencies up to the Nyquist limit of the cross-correlation registration (303 Hz). To help define the frequency range over which the tracker is beneficial, the amplitude rejection, defined as the ratio of amplitude with and without tracking, was computed. In this way temporal frequencies with a ratio below one are corrected by the system, while those above are amplified.

2.5.2.2. Spatial power analysis

The second power analysis investigated the spatial power of the en face images of cone photoreceptors. This elucidated the ability of the tracker to preserve spatial detail and provided a simple way to determine the optimal gain of the tracker. Two spatial power spectra were computed: (1) power spectrum of the average en face image (PS_of_Avg), determined by averaging all 13 images of the session followed by computing the power spectrum. And (2), average of the power spectra (Avg_of_PS), determined by computing the power spectrum of each of the 13 images of the session followed by averaging the power spectra. Mathematically, these are expressed as:

$$PS\_of\_Avg={\left|ℱ\left\{\langle i\left(\underset{¯}{x}\right)\rangle \right\}\right|}^2\mathrm{and}$$ (1)

$$Avg\_of\_PS=\langle {\left|ℱ\left\{i\left(\underset{¯}{x}\right)\right\}\right|}^2\rangle ,$$ (2)

where $ℱ$ {} denotes the Fourier transform, < > the average over the 13 cone images of the session, and x is the two-dimensional spatial coordinate. i(x) is the acquired AO-OCT image, and is a function of both the object, o(x) and the system point spread function, PSF(x). PSF(x) includes the effects of wavefront aberrations, diffraction, and eye motion, the latter important for this analysis. Eye motion consists of both bulk (XY translation) and local (image warp) effects. To make the model tractable while at the same time capturing overall motion, we approximated the imaging as space invariant by assuming i(x) equals o(x)*PSF(x), where * denotes convolution. This assumption fully captures global motion, but only partly local, which is strictly space variant. However as a performance metric, we were most interested in the two extremes of tracking, perfect and none. Perfect refers to the complete correction of all motion. None refers to when random eye motion remains greater than the granular scale of the spatial frequency examined. At these extremes the space invariant approximation is valid.

To remove the object dependence, which is unknown, we computed the ratio of the two powers, which we term the power ratio metric:

$$\frac{PS\_of\_Avg}{Avg\_of\_PS}=\frac{{\left|ℱ\left\{\langle i\left(\underset{¯}{x}\right)\rangle \right\}\right|}^2}{\langle {\left|ℱ\left\{i\left(\underset{¯}{x}\right)\right\}\right|}^2\rangle }.$$ (3)

The Fourier transform of i(x), which is $ℱ\left(o\left(x\right)*PSF\left(x\right)\right),$ gives O(ν) × OTF(ν). O(ν) and OTF(ν) are the Fourier transforms of the object and point spread function, respectively, and ν the two-dimensional spatial frequency coordinate. Substitution of these variables into Eq. (3) gives

$$\frac{PS\_of\_Avg}{Avg\_of\_PS}=\frac{{\left|\langle OTF\left(\underset{¯}{\nu }\right)\rangle \right|}^2}{\langle {\left|OTF\left(\underset{¯}{\nu }\right)\right|}^2\rangle },$$ (4)

where the object terms cancel at least at the two extremes of tracking: perfect and none. Numerator and denominator depend only on OTF(ν), but differ by a reverse ordering of the average and modulus operations. Because the modulus is computed before the average, <|OTF(ν)|²> is independent of Fourier phase (and therefore insensitive to eye motion) and conversely |<OTF(ν)>|² is dependent on Fourier phase (and therefore sensitive to eye motion). It is well established that the dominant effect of object motion – and object information in general – is encoded in the Fourier phase as opposed to the Fourier modulus [39, 40].

Thus Eq. (4) represents a potentially attractive metric for assessing the tracker’s ability to preserve spatial detail. For perfect tracking |<OTF(ν)>|² converges to <|OTF(ν)|²>, and the metric equals one. At the other extreme of no tracking, the metric approaches the theoretical decrease in contrast predicted for averaging 13 (in this study) statistically independent images (i.e., random intensity). This latter extreme is described in more detail in Section 3.2.2.

In this study, we used the power ratio metric, Eq. (4), to find the optimal tracker gain by systemically measuring performance as a function of gain level (G = 0, 0.1, 0.3, 0.6, 1, 1.3, 1.6). This range covered from no tracking (G = 0) to the maximum gain at which tracking stability was lost (G = 1.6). Gain above 1.6 was observed to generate visible oscillations in the wide-field LSO video as well as degradation of individual cone clarity, indicative of very high frequency noise generated by the tracker and unstable tracking. Note that G is not directly equal to the fraction of the error signal applied to the galvo scanners, but rather a parameter of the PSI tracker system that is roughly proportional to this value.

In order to analyze the 2D power spectra, they were circumferentially averaged. This step takes advantage of the circumferential symmetry of both the cone mosaic power spectrum and eye motion, in order to increase the signal-to-noise ratio by averaging.

3. Results

3.1 Imaging mode #1

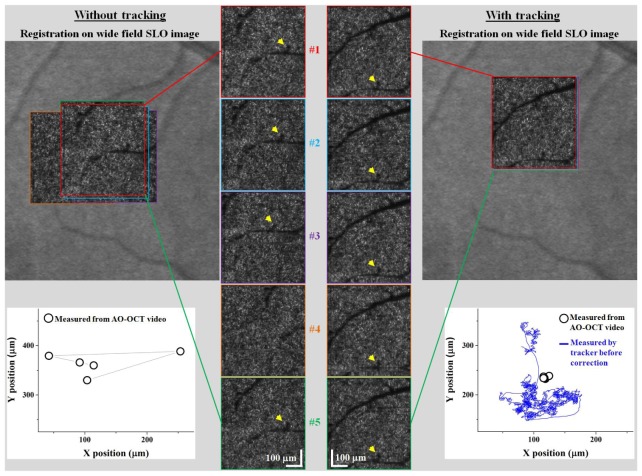
Figure 5 and the corresponding video (Media 1 ^{(178.8KB, AVI)} ) show AO-OCT en face images of the same approximate patch of retina of Subject 1. The two representative sessions depict with and without tracking, and contain similar levels of eye motion (compare open circles in left plot to blue trace in right plot).With tracking, the yellow arrow - pointing to the same location on a vasculature shadow – is present in all frames (never leaves the FOV) and appears visually stationary across images. Without tracking, the arrow is absent in image 4 (leaves FOV) and noticeably shifts between the other images. Measured shifts between the images are plotted in the figure and show that tracking reduced motion by more than 8 times.

Fig. 5.

Intra-session effectiveness of retinal tracking to correct bulk motion in imaging mode #1 (Media 1 ^{(178.8KB, AVI)} ). En face AO-OCT images are shown from the same sessions, (left) without and (right) with active tracking. Images are of the same nominal patch of retina at 5° nasal to the fovea and superimposed on a wide field SLO image of subject #1. In the bottom plots, open circles denote eye motion as determined from the en face frames registered manually to the wide field SLO. Solid blue trace denotes eye motion as measured by the tracker. Tracker gain was 1.3, and no lowpass filtering was applied to tracking signals.

Figure 6 captures the results for all ten sessions of the same subject, five with and five without tracking. Each session is depicted in the figure by a single image, an average of all five images in the session. Therefore contrast of retinal structures in the averaged images indicates effectiveness of the tracker to correct motion between and within volumes of the same session. With tracking, Michelson contrast of the main vasculature shadow is 0.54 ± 0.08 (average ± standard deviation of five measurements along vessel) and is visually similar to that of individual images of Fig. 5, indicating the effectiveness of the tracker to correct intra-session motion. This is particularly apparent when compared to the contrast without tracking for the same vasculature: 0.05 ± 0.02. As evident in the figure, averaged images without tracking show little evidence of the vascular pattern and reveal the severe image degradation caused by eye motion if left uncorrected. Across the ten sessions, tracking was found to improve bulk intra-session stabilization by 3.6 times, reducing radial displacement from 40 ± 33 μm (average ± standard deviation of five sessions' RMS without tracking) to 11 ± 6 μm (with tracking). For the ten sessions on the second subject, bulk intra-session motion was reduced by 6.5 times, from 72 ± 46 μm (without tracking) to 11 ± 6 μm (with tracking). For both subjects, reduction of motion was significant (p = 0.014 and 0.026) and equaled the 11 μm alignment precision measured on the practice image set.

Fig. 6.

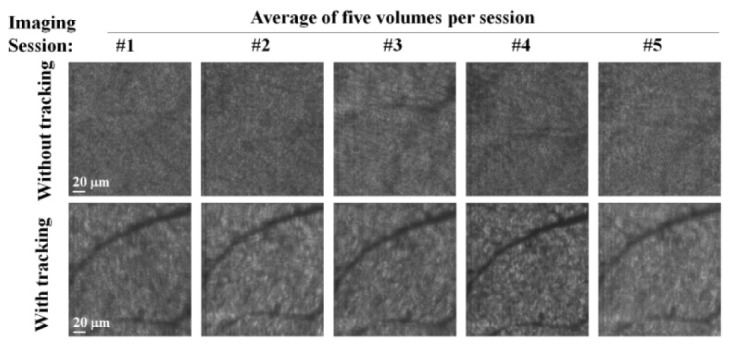
Intra- and inter-session effectiveness of retinal tracking in imaging mode #1. Averaged en face images are shown for all ten sessions, five with and five without tracking. Each session contained five images from subject 1. Images are of the same nominal patch of retina at 5° nasal to the fovea. Tracker gain was 1.3, and no lowpass filtering was applied to tracking signals.

Inter-session imaging also benefited from tracking. Comparing averaged images across the ten sessions in Fig. 6, tracking locked repeatedly onto similar parts of the optic disc, inferred by similar patches of retina being imaged. Locking repeatedly found the same retinal patch to within 23 μm and 42 μm for the two subjects. Without tracking, the large intra-session motion (average RMS = 40 μm and 72 μm for the two subjects) prevented determining inter-session motion, but the latter should be at least as large as the former.

3.2 Imaging mode #2

3.2.1 Initial tracker performance

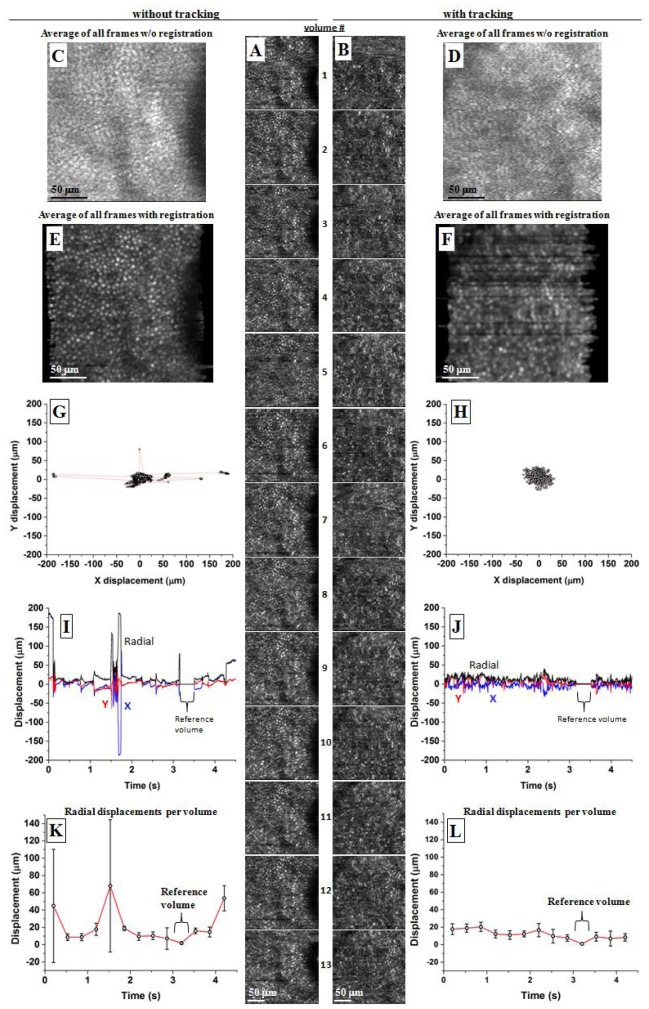
Using imaging mode #2 on the same approximate patch of retina, Fig. 7 and Media 2 ^{(1.2MB, AVI)} illustrate the performance of AO-OCT with and without tracking. The two sessions contain each 13 en face images that are (A,B) vertically displayed down the middle of the figure. Offset to their left and right are the analysis of the images: (C-F) averaged images before and after strip-wise registration and (G-L) plots of X, Y, and radial displacements as determined from strip-wise registration.

Fig. 7.

Initial tracker performance using imaging mode #2 (Media 2 ^{(1.2MB, AVI)} ). Shown are two representative sessions, one with and the other without tracking. Each consists of (A,B) 13 contiguous en face AO-OCT images of the same approximate patch (6° nasal to the fovea) of cones of subject #2. (C,D) Average of all 13 images is shown for the two tracking cases and without registration. (E,F) Average of all 13 images is shown for the two tracking cases and with strip-wise registration applied prior to averaging. Motion displacements were determined from the strip-wise registration and plotted as (G,H) X-Y displacements, (I,J) time traces of the displacements, and (K,L) time traces of the displacements grouped by volume. Tracker gain was 1.3, and no lowpass filtering was applied to tracking signals.

Figure 7(C), 7(D) show the average of all 13 images for the two tracking cases and without the aid of strip-wise registration. Compared to the individual images of (A,B), the averaged images show little evidence of cones, indicating eye motion was much larger than the size of cones (~8 µm), even after motion correction by the tracker. In contrast Fig. 7(E), 7(F) show the average of all 13 images for the two tracking cases and after strip-wise registration was applied. Use of registration noticeably improves clarity of the cone mosaic albeit much less so when tracking is activated. Reduced image quality at the level of individual cones points to high frequency noise (e.g., jitter) generated by the tracker that corrupted the error signals sent to the galvo scanners.

The motion displacement plots in Fig. 7(G)-7(L), measured from the strip-wise registration, substantiate these observations. The X-Y displacements plots (G,H) show that tracking delivered a more uniform clustering of displacements with no outliers as compared to without tracking. X and Y RMS displacements were 8 and 9 μm with tracking compared to 40 and 10 μm without tracking, a factor of four times improvement for X displacements. No improvement was measured for the Y displacements, but this is likely because the displacements were small (9 µm) for this non-tracking trace. Time traces of the same displacements (I,J) reveal the temporal dynamics of the displacements over the duration of the sessions. Without tracking, several large jumps plus smaller, but appreciable, oscillations are present. With tracking, both motion types appear corrected. The tracking session, however, shows small amplitude, high frequency noise on the trace throughout the entire session duration. Similar noise is absent without tracking. The RMS of the radial displacement curves (black traces) are 36 and 12 µm without and with tracking, respectively. Note that the single flat portion of each trace is the reference volume that was used for strip-wise registration. In the figure, the reference volumes are #10.

Finally, the plots in (K,L) group the radial displacement measurements by volume, in this way separating bulk motion from local motion on a per volume basis. In the plot, each point has two numbers, an average (plotted point) and a standard deviation (error bar). The average is the average radial displacement that occurred during the acquisition of that specific volume and thus captured bulk motion of the volume relative to the reference volume. The errors bars represent the standard deviation of the radial displacement across the same volume, thus capturing local motion occurring within the volume. As shown in the figure, tracking reduced both bulk and local motion. Average and standard deviation of radial displacements were 22 ± 16 μm (without tracking) and 12 ± 5 μm (with tracking), respectively.

3.2.2 Frequency analysis to optimize tracker performance

Frequency analysis of the strip-wise registration of AO-OCT images was used to assess the temporal and spatial performance of the tracker and to optimize two key tracker parameters: frequency cutoff of the lowpass filter and gain.

The first analysis looked at temporal amplitude spectra of the strip-wise displacements. Averaged spectra for one of the subjects are shown in Fig. 8, with and without tracking. Plotted on a semilog abscissa, the solid black trace shows eye motion is concentrated at low frequencies with amplitudes approaching 14 µm at the lowest resolved frequency, 0.2 Hz, and less than 2 µm above 10 Hz. Plotted on a linear abscissa (not shown), eye motion drops inversely with frequency. The dashed black trace corresponds to the residual motion after correction with the tracker. Here the tracker effectively suppressed motion, reducing amplitudes to no larger than 2 µm. To further quantify, the ratio of the two curves (with to without tracking) is shown as the blue trace and reveals the frequency range over which the tracker was beneficial (ratio<1). Amplitude was reduced at frequencies up to 240 Hz, where the ratio equaled one. Motion amplitude was reduced by up to 8 times at low frequencies (<10Hz), which improved the overall stability of the cone videos, a result consistent with that observed in the cone imaging sessions of Section 3.2.1. Between 100 to 240 Hz, amplitude reduction was small, no more than 25% improvement.

Fig. 8.

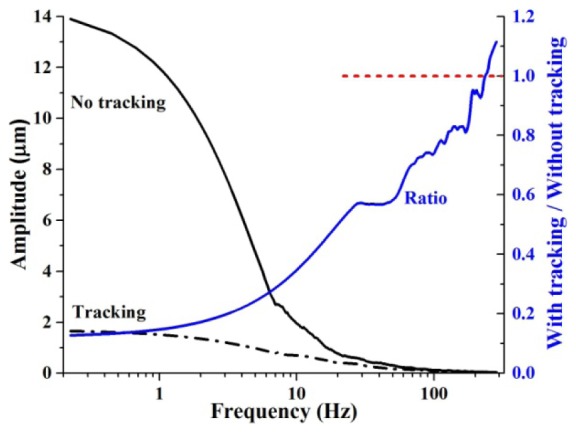
Temporal performance of the combined tracker and AO-OCT system as measured with the strip-wise registration method. (left ordinate) Amplitude of eye motion is plotted as a function of frequency during normal fixation using a semi-log abscissa. Two cases are shown: (solid black) raw motion of the eye with no stablization and (dashed black) residual motion after correction with the PSI tracker and no lowpass filtering. Each amplitude spectra is an average of five sessions from subject #2 (6° nasal to the fovea). (right ordinate) Shown is the amplitude rejection ratio of the amplitude traces in the same plot. A rejection value of unity occurs at 240 Hz, the frequency bandwidth of the tracker AO-OCT system. Tracker gain was 1.3, and no lowpass filtering was applied to tracking signals.

Above 240 Hz, the temporal analysis predicted degraded performance with the tracker imparting more noise on the galvo scanners than what it corrected. Such tracker noise is the likely culprit for the observed poor quality of cones in Section 3.2.1 when the tracker was used, e.g., Fig. 7(F). Certainly degradation at the individual cone level must stem from noise greater than ~100 Hz as each cone is sampled by no more than 7 B-scans (1 µm spacing) that are acquired at 606 Hz, or equivalently a cone spacing rate of 87 Hz. The 240 Hz frequency occurred near the Nyquist sampling limit (303 Hz) of our strip-wise registration, thus limiting our assessment of tracker performance at these high frequencies.

To further substantiate the registration findings, the error signal generated by the retinal tracker was systematically lowpass filtered (1, 18, 30, 60, 70, 100, 200, 500, and 1000 Hz) and AO-OCT images of the same patch of cones acquired with tracking. Visual inspection of the images determined best quality of individual cones occurred with the lowpass filter set at 100 Hz. This setting is consistent with the temporal analysis, which showed little tracking benefit above 100 Hz. Based on these findings, we set the lowpass filter cutoff at 100 Hz and defined this as the optimal cutoff.

The second analysis assessed spatial performance of the tracker system and was used to determine the optimal gain setting of the tracker. Results are shown in Fig. 9 (top), which plots power spectra of en face images of cone photoreceptors for seven gain levels of the tracker and 13 images per session. Traces are shown for PS_of_Avg (Eq. (1)) and Avg_of_PS (Eq. (2)). Both powers have approximately the same DC energy; same shape that decreases monotonically with increasing frequency; and same cusp peaking at 37 cyc/deg, which corresponds to the fundamental frequency of cones at the retinal patch imaged. An obvious difference, however, is the −0.8 dB lower power of PS_of_Avg compared to Avg_of_PS for frequencies above ~10 cyc/deg. The −0.8 dB can be interpreted as a Michelson contrast difference on a per frequency basis. The −0.8 dB approaches the theoretical decrease in contrast predicted for averaging 13 statistically independent images (random intensity). That is, contrast equals (1/√13 = ) 0.277, or equivalently −1.1 dB on the Fig. 9 power scale. Such a difference can occur during AO-OCT imaging if the random eye motion is greater than the granular scale of the frequency examined, e.g., 37 cyc/deg for cones. This scenario reflects the extreme situation of no tracking at the examined frequency. Because our measured 0.8 dB difference falls close to the 1.1 dB theoretical limit, we interpret the 0.8 dB as the empirical threshold for no tracking. Conversely and as discussed in the methods, a 0 dB difference reflects the opposite extreme and corresponds to perfect tracking. Thus 0 to −0.8 dB range for contrast difference corresponds to the full range of tracking, from perfect tracking to none, respectively. This interpretation is applied to our results in the next paragraph.

Fig. 9.

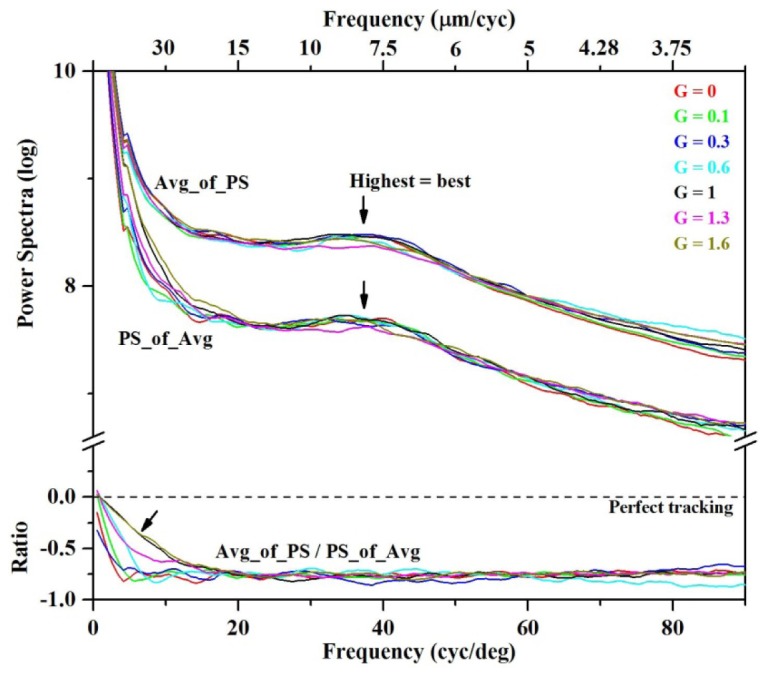
Spatial performance of the tracker system. (top) Average power spectra are plotted for en face images of cone photoreceptors for seven gain levels of the tracker (G = 0, 0.1, 0.3, 0.6, 1, 1.3, 1.6). Images for the seven gains were acquired in consecutive sessions on subject #2 (6° nasal to the fovea). Each average power spectrum was computed from the 13 AO-OCT images that composed the session. Two different average power spectra are shown, PS_of_Avg (Eq. (1) and Avg_of_PS (Eq. (2), the former sensitive to eye motion and the latter insensitive. Spectra were circumferentially averaged. Note the semilog ordinate. No image registration was applied. (bottom) Ratios of PS_of_Avg to Avg_of_PS are shown using the traces in the top plot. Ratios correspond to Eqs. (3) and (4). Because of the semilog ordinate in the top plot, the ratio is equal to the difference between the log traces.

In Fig. 9 (top), Avg_of_PS and PS_of_Avg traces show little apparent dependence on gain, except for PS_of_Avg at frequencies below ~20 cyc/deg. These variations are more evident in the power ratio, PS_of_Avg to Avg_of_PS (Eq. (3)), which is plotted in the bottom of Fig. 9. Here the 0 to −0.8 dB range becomes explicit. The cusp of energy associated with the cones is now absent, which is consistent with Eq. (4). All ratio traces show the same characteristic profile of perfect correction near 0 cyc/deg (0 dB) followed by a monotonic decrease to a cutoff frequency (−0.8 dB) at which correction is lost. As evident in the figure, frequency cutoff varies systematically with gain. For example, gain 0 has a cutoff at 3.5 cyc/deg that corresponds to a spatial period of about 0.28 deg or 85 µm at the retina using a conversion of 300 µm/deg. Stabilization at this gain (G = 0) is determined entirely by the subject’s ability to fixate since none of the error tracking signals were sent to the galvo scanners. Gains of 0.1, 0.3, 0.6, 1.0, 1.3, and 1.6 have cutoffs corresponding to spatial periods of 63 µm, 43 µm, 43 µm, 15 µm, 15 µm, and 15 µm, respectively. Higher gains clearly provided better motion correction with the best settings providing stabilization of image structures as small as about 15 µm. However because performance saturated for gains greater than one (1.0, 1.3, and 1.6) while cone contrast (cusp of energy associated with cones) decreased with gain we selected the lowest of the three, i.e., 1.0.

3.2.3 Optimized tracker performance

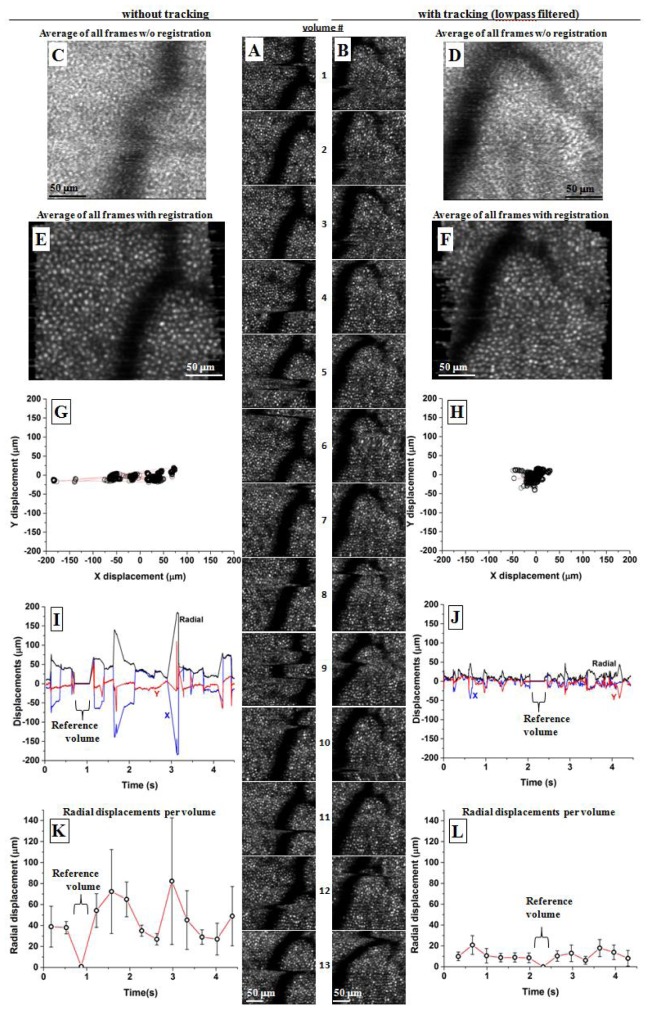
Using imaging mode #2 on the same approximate patch of retina, Fig. 10 and Media 3 ^{(1.4MB, AVI)} illustrate the performance of AO-OCT with and without optimized tracking. Optimization included a 100 Hz low pass filter and a tracker gain of 1.0. The layout of Fig. 10 is identical to that of Fig. 7.

Fig. 10.

Optimized tracker performance using imaging mode #2 (Media 3 ^{(1.4MB, AVI)} ) with a tracker cutoff frequency and gain set at 100 Hz and 1.0, respectively. Shown are two sessions, one without and the other with tracking. Each consists of (A,B) 13 contiguous en face AO-OCT images of the same approximate patch of cones (6° nasal to the fovea) of subject #2. (C,D) Average of all 13 images is shown for the two tracking cases and without registration. (E,F) Average of all 13 images is shown for the two tracking cases and with strip-wise registration applied prior to averaging. Motion displacements were quantified from the strip-wise registration and plotted as (G,H) X-Y displacements, (I,J) time traces of the displacements, and (K,L) time traces of the displacements grouped by volume. See text for additional details.

Figure 10(C), 10(D) show the average image for the two tracking cases, both without the aid of strip-wise registration. As evident in the figure and as expected from the power spectra results of Figs. 8 and 9, tracking remains too coarse to recover the fine granular structure of cones (D). On the other hand, it works well enough even with the 100 Hz lowpass cutoff to preserve macro structures such as the large blood vessel shadow pattern evident in the figure. Of particular interest is the narrow tortuous shadow in the upper right quadrant of the averaged image (D). Its profile is consistent with that in the strip-wise registered, tracked image of (F) indicating that tracking alone can preserve large scale structures in the image.

Most striking is the increased visibility of cones compared to that in the initial tracking experiment. This is evident by comparing the clarity of cones in individual en face images (B) and the averaged images with strip-wise registration (F) of Figs. 7 and 10. While cone visibility with tracking remains reduced from that without tracking (Fig. 10(E), 10(F)), the difference is clearly smaller.

The motion displacement plots in Fig. 10(G)-10(L), measured from the strip-wise registration, provide additional assessment of tracker performance. The X-Y displacements plots (G,H) show that tracking delivers a tighter clustering of displacements with no outliers as compared to without tracking. X and Y RMS displacements are 45 μm and 11 μm without tracking compared to 10 μm and 9 μm with tracking, a factor of ~4 improvement for X displacements and a factor of 2 improvement when compared to the non-tracking X displacements in Fig. 7. Like in Fig. 7, no improvement was measured for the Y displacements and again likely attributed to the small displacements for the non-tracking trace. Tracked time traces of the displacements are similar to the initial time traces of Fig. 7(J), but a couple key differences are apparent. Optimized tracking provided visible reduction of high frequency noise compared to the initial tracking results (compare Figs. 7(J) and 10(J)). But this improvement came at the expense of a more sluggish response. Faster motion correction is evident in Fig. 7(J) compared to Fig. 10(J). The plots in Fig. 10(K), 10(L) separate bulk motion (plotted data points) from local motion (error bars) on a per volume basis. As shown in these plots, tracking reduced bulk and local motion. Average and standard deviation of radial displacements were 43 ± 19 μm (without tracking) and 11 ± 8 μm (with tracking), respectively.

Figure 11 summarizes performance of the optimized tracker for the 20 sessions acquired with imaging mode #2. Plotted on the left are measured RMS displacements without and with tracking on two subjects. Averaged across the two subjects, performance was 26 ± 8 µm (average ± stdev) without and 10 ± 2 µm with tracking, a 2.6 times improvement (two sample t-test, p = 0). For comparison to the literature, superimposed on the Fig. 11 left plot is a semitransparent box that marks the performance range of earlier versions of the PSI tracker reported in the literature. Our tracking AO-OCT clearly performed within this range.

Fig. 11.

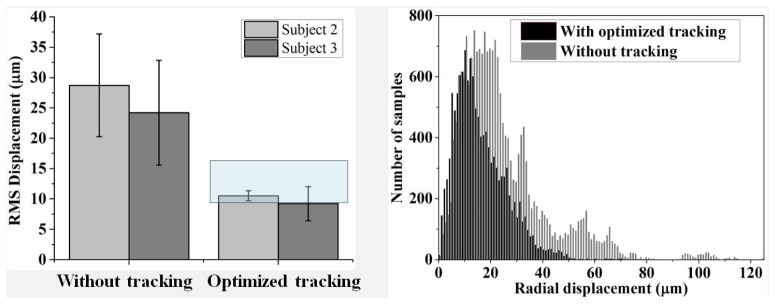
Stabilization of the tracking AO-OCT system over 20 imaging sessions: five imaging sessions per tracking case per subject. Images were acquired with imaging mode #2, and motion displacements measured with strip-wise registration. (left) RMS displacement is across all 13 volumes of the same session and averaged across five sessions. Error bars denote +/− one standard deviation of displacements across the five sessions. Superimposed on the tracking portion of the plot is a semitransparent box that marks the approximate performance range of earlier versions of the PSI tracker reported in the literature [24, 31] (right). Histograms show the radial displacements measured relative to the reference frame of each session. Separate histograms are shown with and without tracking, each combining the measurements from ten sessions, five from subjects 2 and five from subject 3.

Figure 11 (right) shows the histograms of radial displacements for the same 20 sessions. Without tracking, the modal displacement (Gaussian fit) was 14.5 µm, and 50% and 90% of the time the images were within 20 µm and 53 µm, respectively. With tracking, the modal displacement reduced to 9.9 µm, and 50% and 90% of the time the images were within 14 µm and 30 µm, respectively.

4. Discussion

4.1. Stabilizing bulk intra- and inter-session motion

Imaging mode #1 was designed to examine tracker performance for stabilizing bulk intra- and inter-session motion during AO-OCT imaging. Measurements on two normal subjects demonstrated effective stabilization of major retinal structures, namely blood vessel shadow patterns. The representative video of Fig. 4 illustrates the effectiveness of the stabilization. Based on 20 imaging sessions across two subjects and two tracking cases (with and without), tracking reduced bulk intra-session motion by four to seven times. Averaged across the two subjects, the average bulk intra-session motion was reduced from 56 μm to 11 μm, a five-fold improvement.

Tracking was also effective for reducing inter-session bulk motion, thereby improving the precision with which the tracker can repeatedly lock onto the same portion of the optic disc. For the 20 imaging sessions, locking had an average precision of 33 μm. This tracking AO-OCT performance is consistent with earlier reports of hardware-based active tracking combined with conventional OCT systems [24, 25]. Notable weaknesses of this first experiment were its relatively coarse precision (11 μm RMS) and insensitivity to local eye movements.

4.2. Stabilizing local and bulk intra-session motion

The second, more difficult, experiment addressed the weaknesses of the first by using imaging mode #2 in conjunction with temporal and spatial spectral analyses of the images. Tracker performance was quantified for correction of local and bulk intra-session motion. Correction of both is critical for stabilizing the retina down to the level of cells as for example necessary for imaging cone photoreceptors, the target cell of this experiment. As an independent measure of tracker effectiveness, eye movement during the experiment was extracted from the AO-OCT en face images using a custom strip-wise registration method. The two-step process of the method enabled sampling of the eye movements at the fast B-scan rate (606 Hz). While this rate was well below that of the tracker (16 KHz), it was sufficient to assess tracker performance across the range of frequencies where the vast majority of eye movements occur (<10Hz) and the determined useful range of the tracker (less than 100 Hz).

Temporal amplitude and spatial power spectral analyses in conjunction with direct observation of cone quality were used to optimize the lowpass cutoff frequency and gain of the tracker. We found tracker performance was highly sensitive to the cutoff frequency. For example, without filtering tracker noise degraded the clarity of individual cones to the point where the cones were difficult to differentiate in the AO-OCT images (e.g., Fig. 7(E) and (F)). Low pass filtering the tracking error signals of frequencies above 100 Hz removed much of this noise and regained cone clarity, though not quite to the extent of that without tracking (e.g., Fig. 10(E) and 10(F)). Unfortunately low pass filtering was not without penalty. Filtering reduced the response time of the tracker and in doing so nullified a major strength of hardware-based tracking, the ability to track at KHz rates. It is interesting to note that Braaf et al. [22] also needed to lowpass filter the error signals of their image-based tracker as the high frequencies also affected their OCT spot stability. They reported a 10 Hz cutoff frequency, ten times below what we found necessary here. They argued the low cutoff had a minimal effect on tracking quality, although our observations with cutoffs set at 10 and 18 Hz did not support this nor did the findings of Burns et al. [26] who used a 200 Hz cutoff for their hardware-based tracking AO-SLO. In the latter case, however, cone mosaics were not significantly disrupted by tracking noise due the much faster SLO raster. Perhaps these different observations stem from fundamental differences in how hardware-based and image-based systems operate.

We did not find the source of the high frequency noise in our tracker that necessitated the lowpass filter with 100 Hz cutoff. The noise was present in the error signal prior to our customized summation box, which ruled out both the box and galvanometer scanners. This points to the phase-sensitive detection scheme employed in the tracker with the most likely culprit being either optical noise in the 16 KHz dithering signal or electronic noise generated by the two lock-in amplifiers, both realized with a field programmable gate array (FPGA). Confirmation remains, but noise originated at these steps may reflect either implementation issues or a fundamental limit to this tracking approach.

For the spatial power spectral analysis, we used the power ratio metric, Eq. (3), to quantify the tracker’s ability to preserve spatial detail and from which the tracker gain was optimized. As expected, tracker response depended on gain level with the higher gains better preserving high spatial frequencies in the AO-OCT image. However, performance saturated at a spatial frequency corresponding to about 15 µm at the retina. The lack of visibility of cones (8 µm row-to-row spacing) in the averaged intra-session images as for example Fig. 10(D) is consistent with the spectral analysis finding. In general, tracker performance even after optimization fell well short of stabilizing at the scale of individual cone photoreceptors.

The most important tracker results are captured in Fig. 11, which summarizes performance of the optimized tracker for 20 imaging sessions (with and without tracking; two subjects). Tracker reduced eye movements on average by 2.6 times and resulted in a residual RMS motion of 10 ± 2 µm. The latter is consistent with the 11 µm measured in the first experiment and the 15 µm saturation measured in the spatial power spectral analysis. It also falls within the range reported for earlier versions of the PSI tracker that were integrated into other imaging modalities (see Fig. 11). Interestingly, this level of performance is comparable to the lateral resolution (~15 µm) of these other hardware-based tracking OCT systems. Thus for these systems, the ~15 µm of tracker noise was likely of limited consequence. In contrast our tracking AO-OCT system had a lateral resolution of just 2.5 µm, which is six times smaller. For this system, the high frequency noise of the tracker was clearly consequential. It profoundly impacted the quality of individual cones and required electronic filtering of the tracker error signals.

4.3. Key advantages over image-based retinal tracking

Hardware-based retinal tracking has two potential advantages over SLO image-based retinal tracking, the other leading method for active image stabilization. First, the phase-detection scheme of hardware-based retinal tracking provides an absolute measure of retina movement. This is fundamental for accurate representation of the retina anatomy. In contrast SLO image-based tracking relies on a reference frame from which all eye movements are measured relative to and requires a priori knowledge of what the retinal patch should look like in the absence of eye movement. These complications do not arise in hardware-based tracking.

A second advantage of hardware-based tracking is the much higher sampling speeds that can be achieved, currently 208.3 KHz compared to 960 Hz [21, 22]. Higher sampling is particularly beneficial for AO-OCT owing to the combination of its high lateral resolution and slow scan speeds. Its high lateral resolution (~2.5 µm compared to ~15 µm for SLO and OCT) makes it more vulnerable to small amplitude movements, which can occur at high temporal frequencies. As for scan rate, the fastest AO-OCT systems (e.g., this study) generate B-scans up to 50 times slower than AO-SLO systems (600 B-scans/s compared to 30,000 lines/s). In this context, the 217 × speed advantage of hardware-based retinal tracking makes this tracking method an arguably better fit. Unfortunately in this study, we were unable to tap this speed advantage. Much of the tracker bandwidth was found unusable owing to the tracker-generated noise that required lowpass filtering at a 100 Hz cutoff. Addressing this problem is paramount for further development of hardware-based tracking for AO-OCT.

5. Conclusion

We investigated dynamic retinal tracking for stabilization of AO-OCT images. Analyses were developed based on temporal amplitude and spatial power spectra in conjunction with strip-wise registration to independently measure AO-OCT tracking performance. We found the optimized tracker corrected eye movements up to 100 Hz and reduced residual motion to 10 µm root mean square. While this performance failed to stabilize images at the level of individual cones, our study revealed the main culprit to be tracker-generated noise and correction of this may make such performance possible.