Magnetomotive optical coherence elastography using magnetic particles to induce mechanical waves

Abstract

Magnetic particles are versatile imaging agents that have found wide spread applicability in diagnostic, therapeutic, and rheology applications. In this study, we demonstrate that mechanical waves generated by a localized inclusion of magnetic nanoparticles can be used for assessment of the tissue viscoelastic properties using magnetomotive optical coherence elastography. We show these capabilities in tissue mimicking elastic and viscoelastic phantoms and in biological tissues by measuring the shear wave speed under magnetomotive excitation. Furthermore, we demonstrate the extraction of the complex shear modulus by measuring the shear wave speed at different frequencies and fitting to a Kelvin-Voigt model.

1. Introduction

Elastography is the image-based mapping of tissue mechanical properties, which is important in many areas of medicine and biology. Changes in mechanical properties have been shown to be associated with disease progression in several tissues such as in the liver, breast and thyroid [1]. In elastography, the sample is mechanically perturbed and imaging modalities are used to detect the induced displacements, which can subsequently be used to infer the material mechanical properties under certain simplifying assumptions. Elastography techniques differ in the way the sample is mechanically perturbed, how the induced changes are detected, and how the data is processed to assess the material mechanical properties [2].

Ultrasound-based elastography (UE) and magnetic resonance elastography (MRE) are well established modalities undergoing varying stages of commercialization and clinical trials. Elastography based on optical methods such as optical coherence elastography (OCE) has attracted widespread attention in recent years as it can offer much higher spatial resolution and mechanical sensitivity compared to UE and MRE, however with the well-known tradeoff of a shallow imaging depth (~1–2 mm) in highly scattering tissues. OCE has been demonstrated in a number of tissue sites such as the skin, cornea, arteries, etc [3]. In addition, OCE has been demonstrated using needle based configurations that can access deeper underlying structures [4].

Numerous methods for mechanical stimulation have been employed with each having different spatial (internal or external) and temporal (static or dynamic) characteristics. Methods based on static (or quasi-static) excitation subject the sample to static or low frequency loads, and the resulting displacements or strains are measured. Under the assumption that the sample is at mechanical equilibrium during measurements, and the stress is uniform throughout the sample, the measured displacement/strain rate can be used as a substitute for the elastic modulus providing relative mechanical contrast [5]. Elastography techniques utilizing some form of dynamic mechanical stimulus have received considerable attention in recent years, which compared to the static excitation methods, are more quantitative and less dependent on the boundary conditions outside the region of interest [6]. The applied dynamic excitation can be in the form of a short duration (transient) pulse or can be harmonically oscillating at high frequency. Elastography methods that are based on dynamic excitation can be formulated in terms of wave propagation phenomena. The perturbation of a region within the sample results in deformation of the surrounding medium, which can propagate in the form of elastic waves within the sample and be measured using imaging methods such as ultrasound, optical imaging, or MRE [2, 7]. As the characteristics of mechanical wave propagation are dependent on the sample mechanical properties, they can be used to assess the viscoelastic properties.

A wide variety of methods have been utilized to generate mechanical waves within a sample. Excitation methods such as rods [8], needles [9, 10] attached to mechanical/electromechanical actuators, piezo-vibrators, acoustic drivers, etc., or some form of internal excitation such as acoustic radiation force (ARF) [11], have been used. In OCE, mechanical actuators on the surface of the sample [12–15], incident acoustic radiation force [16–19], acoustomotive forces [20], air-puffs [21], and laser induced surface waves [22], among others, have been utilized to mechanically and dynamically stimulate the sample.

Magnetic nanoparticles (MNPs) have been widely used in biomedical applications for enhancing imaging contrast, for treatment in hyperthermia, or for measuring the mechanical properties of cells and tissues [23–25]. In magnetomotive optical coherence tomography (MM-OCT), the magnetic particles which act as force transducers are embedded within the specimen of interest. With the application of the magnetic field, these particles move in the direction of the magnetic field gradient, displacing the surrounding medium [26–29]. The temporal dynamics of this movement has been utilized in magnetomotive optical coherence elastography (MM-OCE) and has been shown to contain valuable information about the tissue viscoelastic properties [30]. In contrast to other elastography techniques, the total force, and hence the magnitude of deformation, depends not only on the material mechanical properties but also on the concentration of the magnetic particles. Therefore, in MM-OCE, the material properties are more readily accessible by analyzing the temporal characteristics of the magnetomotive response rather than the absolute displacement scales. Previous demonstration of MM-OCE has been done in elastically homogenous samples containing uniform distribution of magnetic particles with point-wise measurements typically performed within the magnetic excitation region. These methods utilizing a step or a chirped excitation intrinsically rely on the mechanical resonances of the sample, and hence the sample geometry and boundary conditions need to be taken into account to extract quantitative viscoelastic parameters [30–32].

In this paper, we propose to utilize MNPs as shear wave sources by modulating a localized region containing MNPs within the sample. The magnetic inclusion, when mechanically excited, displaces the surrounding medium, resulting in the generation of mechanical waves. In contrast to previous MM-OCE demonstrations, the measurements are taken at radial distances away from the excitation region to visualize these propagating mechanical waves using phase-resolved OCT. We show the measurement of the shear wave speed under magnetomotive excitation in tissue mimicking elastic and viscoelastic phantoms and in biological tissues. Furthermore, we also demonstrate the extraction of the complex shear modulus by measuring the shear wave speed at different frequencies and fitting data to a Kelvin-Voigt tissue model.

2. Methods

2.1 Experimental setup

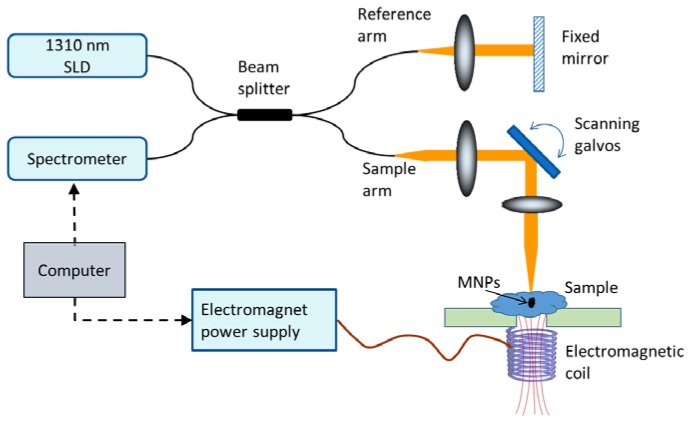
A 1310 nm spectral domain OCT system shown in Fig. 1 was used for the shear wave measurements. The light source was a superluminescent diode (LS2000B, Thorlabs) with 170 nm bandwidth and the measured axial and transverse resolutions (full width at half max) of the system were 6 μm and 16 μm, respectively. A 1024-pixel InGaAs line-scan camera (SU-LDH2, Goodrich) was used in the spectrometer with an optical imaging depth of 2.6 mm. The phase noise of the system was ~20 milli-radians measured at a line-scan rate of 46 kHz with a static sample (IR card) placed in the sample arm. The jitter in the scanning galvanometers was the main contribution to the phase noise which reduces to ~5 milli-radians when the galvanometer scanners are turned off. The coil for generating the magnetic field was placed underneath the sample while the imaging was performed from the top, allowing the coverage of a large field-of-view. The magnetic field strength generated by the coil was measured to be approximately 150 Gauss at the sample surface (~1 cm away from the coil).

Fig. 1.

Spectral domain magnetomotive optical coherence elastography setup.

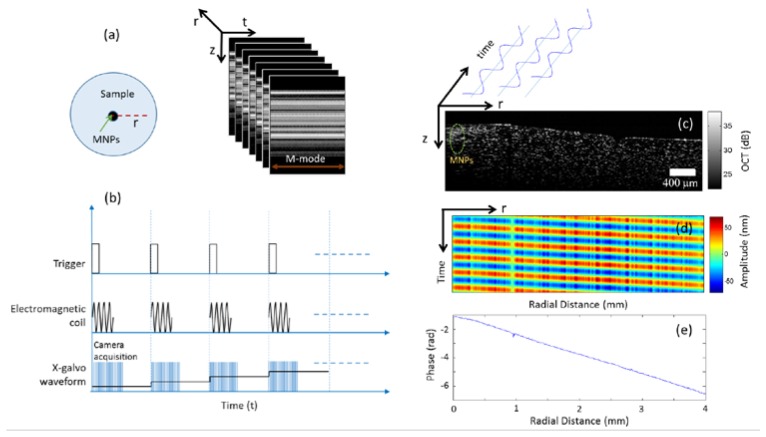
The OCT data is acquired by taking multiple M-mode (A-lines measured as a function of time) measurements at different radial positions away from the MNPs as shown in Fig. 2(a). Typically very high frame rates are needed to image the propagating shear waves, however, these waves can be visualized by a stroboscopic acquisition scheme [18, 33]. A trigger signal is used to synchronize the camera data acquisition with the electromagnetic coil activation and scanning galvanometer (M-B mode scan i.e. M-mode data acquired at different spatial locations) as shown in Fig. 2(b). At the beginning of each M-model data acquisition, the electromagnetic coil is activated to generate a square root sinusoidal waveform of 10-20 cycles at a given frequency f. At each radial position (a single M-mode) 2000 A-lines at a scan rate of ~46 kHz was acquired (unless stated otherwise) and a brief waiting time (~1 sec) was given before subsequent M-mode acquisitions to prevent any heating of the coil. The lateral pixel size was ~8 μm (corresponding to 500 radial locations over a scan range of 4 mm) for shear wave visualization while a lateral pixel size of ~40 μm (100 radial locations) was chosen for the shear wave spectroscopy measurements to minimize the amount of data collected and to reduce the data acquisition time.

Fig. 2.

Data acquisition and processing (a) M-mode scans are taken radially away from the magnetic inclusion. (b) The timing diagram for the scanning protocol (c) Structural OCT image (z, r) showing the location of the MNP inclusion (d) Depth-averaged space-time (t, r) map showing the sinusoidal response at different radial distances. (e) The linear change in phase as the distance from the excitation source increases.

2.2 Data processing

Figure 2(c) shows representative data where MNPs, acting as the shear wave generating source, can be seen in the structural OCT image. Our shear wave excitation source comprising of an inclusion of MNPs is approximately cylindrical in shape, and hence can be considered as generating cylindrical waves. The displacement of the cylindrical shear wave produced by harmonic force with angular frequency $\omega =2\pi f$ acting along the z-axis is given by $u_z(r,t)=\frac{i}{4}{H}_0^{(1)}(kr)\exp (-i\omega t)$where $u_z$is the displacement along the z-axis, $H_0^{(1)}$is the zeroth order Hankel function of the first kind, r is the radial distance and k is the shear wave number given by $k=2\pi /\lambda$with λ being the shear wavelength. If the measurements are made at sufficient distance away from the excitation source ($kr>1$) then it can be shown that the phase of the cylindrical shear wave varies linearly with the radial distance $u_z(r,t)\approx \frac{i}{4}\sqrt{2/(\pi kr)}\exp (i(kr-\omega t+\pi /4))$ [34]. This linear change in phase can be used to calculate the shear wave speed [35].

The M-mode OCT data acquired at different radial positions away from the MNPs was processed by using standard phase-resolved OCT processing (i.e. resampling, Fourier transform and phase extraction) and subsequently the phase values (across time) were bandpass-filtered around the excitation frequency to remove any noise from other frequency bands [36]. These phase values (can also be converted into displacement values based on the system central wavelength and sample refractive index) can then be displayed in the form of a space-time map for any given depth as shown in Fig. 2(d). As expected, there is a phase lag between the measured displacements at different radial positions as we move away from the MNP excitation source. This phase lag for each radial (lateral) location as shown in Fig. 2(e) was computed using a Kalman filter [37], where it can be seen that the phase changes linearly with propagation distance. Although the use of a Kalman filter is not necessary when the shear waves displacement amplitude has sufficiently high signal to noise ratio (SNR), in scenarios where the displacements are small (such as when using high excitation frequencies or in stiffer samples), the use of Kalman filter may provide more robust phase and amplitude estimation as has been shown in the ultrasound literature [37]. The phase gradient $k=\Delta \varphi /\Delta r$ was then estimated by performing a linear fit on the radial phase profile and was used to calculate the shear wave speed $c_s=\omega \Delta r/\Delta \varphi$ at a particular excitation frequency$\omega$ [35]. The first two excitation cycles in each M-mode were excluded from quantitative analysis as these contained a superimposed transient response possibly coming from the settling time of the galvanometer scanners or due to the switching on of the electromagnetic coil. The propagating shear waves can be visualized in the form of a video by playing the phase values in the cross-sectional planes (z, r) across time. In the videos, we applied a binary mask to remove the random phase values in the regions above and below the sample surface. The binary mask was computed by smoothing and thresholding the structural OCT image where the pixels within the sample region were given values of 1 and those outside were assigned a value of 0.

In a viscoelastic medium, the shear modulus is complex and can be quantified by measuring the dispersion of the shear wave speed. The dispersion curves are obtained by measuring the shear wave speed at several different frequencies and can be fitted to tissue rheological models to estimate the complex modulus of the medium [34, 35, 38]. One widely used tissue model is a Kelvin-Voigt model which consists of a spring and dashpot connected in parallel. The shear wave dispersion for this tissue model is given by the expression

$$c_s(\omega )=\sqrt{\frac{2(G^2+{\omega }^2{\eta }^2)}{\rho (G+\sqrt{G^2+{\omega }^2{\eta }^2})}}$$ (1)

where $c_s$is the shear wave speed, G is the real part of the complex shear modulus, $\rho$is the mass density, and$\eta$is the shear viscosity of the material. If a medium is purely elastic i.e. $\eta \approx 0$ or if the shear (storage) modulus is dominant in comparison to the viscosity ($G>>\omega \eta$), the above equation simplifies to $G=\rho c_s^2$ which relates the shear wave speed to the shear modulus for a linear isotropic elastic material [39].

2.3 Tissue mimicking phantom preparation

To demonstrate that a localized inclusion of magnetic particles can generate shear waves, we prepared tissue mimicking phantoms using agar gel. Phantoms with different stiffness were prepared by varying the dry-weight concentration (0.3, 0.5, 0.7 and 1.0%) of agarose gel in distilled water, and the solution was subsequently boiled until it became optically clear. The solution was then allowed to cool at room temperature and titanium dioxide particles (size < 5 μm, 2 mg/ml) were added to increase the optical scattering. Subsequently the solution was poured into cylindrical containers (height 5-10 mm and diameter 35-90 mm) and allowed to congeal at room temperature. A cylindrical mold (~2.5 mm in diameter) was placed in the cylindrical container during the agarose congealing process so that an inclusion containing MNPs (Fe₃O_4, size 50-100 nm) could be placed at that location. The MNPs inclusions were prepared by mixing MNPs (50 mg/ml) in either the same concentration agarose gel or with PDMS gel. The MNP-gel solution was then poured into the center of the cured cylindrical samples. The samples were subsequently allowed to cure at room temperature for 4-6 hours. Although the inclusions did not seem to bond permanently with the surrounding medium, the mechanical coupling between the MNP inclusion and the surrounding medium was sufficient for the generation of shear waves in the medium.

Agar phantoms are known to have an almost purely elastic response [40]. Therefore, to validate our MM-OCE method in viscoelastic samples, we prepared oil-in-gelatin phantoms that have been shown in the literature to exhibit significant viscosity by adding oil in gelatin [41]. A sample of 8% Gelatin (Type B: 225 Bloom) was prepared by dissolving it in de-ionized water and heating the solution at 65° C for approximately one hour until the solution became clear. Titanium dioxide scattering particles (size < 5 μm, 1 mg/ml) were added as scattering particles. To increase the viscosity of the sample, Castor oil was added to the gelatin and the solution was vigorously stirred using a blender after the addition of a surfactant to help in the emulsification [42]. The cylindrical inclusions consisted of MNPs (50 mg/ml) mixed with 8% gelatin. The samples were allowed to cure at room temperature for one hour and then left in the refrigerator for 6 hours before imaging.

3. Results

3.1 Homogeneous tissue phantoms

In Fig. 3, we show representative examples of shear wave propagation in homogenous agarose phantoms of different stiffness. An excitation frequency of 500 Hz was used and the elastic modulus was estimated using a linear elastic model as agarose gel is largely non-dispersive (data shown in Fig. 6(a)). The changes in shear wave wavenumber can be clearly seen where the soft sample (0.3% agarose) exhibits a higher wavenumber (hence steeper phase gradient and lower shear modulus) compared to the stiffer samples (0.5% and 0.7% agarose). In the video (Media 1 ^{(9MB, AVI)} ) the differences in the shear wave speed can be clearly visualized.

Fig. 3.

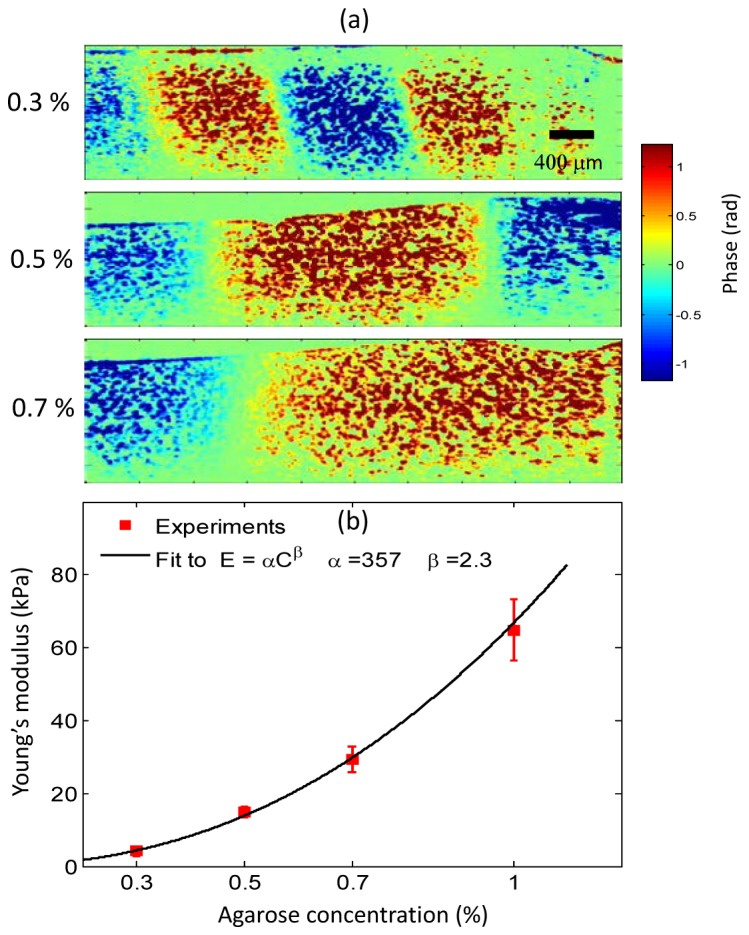
Shear waves in elastically homogeneous phantoms. The MNP inclusions (not shown) are on the right side of the images (a) Visualization of shear waves with phantoms of different agarose concentrations. A line-scan rate of ~92 kHz and 4000 A-lines per M-mode were collected. A sinusoidal excitation at 500 Hz consisting of 20 cycles was used. An increase in the shear wavelength and speed can be seen as the gel stiffness increases (Media 1 ^{(9MB, AVI)} ). (b) Estimated Young’s moduli at different agarose concentrations. A line-scan rate of ~46 kHz, 2000 A-lines per M-mode and 10 cycles at a excitation frequency of 500 Hz was used for these measurements. The error bars correspond to the standard deviation of the measured values at 3 different spatial locations within the same sample (N = 3). The error bars for 0.3% and 0.5% are too small to see, and the values correspond to 4.14 ± 0.25 kPa and 15 ± 1.47 kPa, respectively.

Figure 3(b) shows the measured Young’s modulus (E) for different concentrations of agarose gel, which is related to the shear modulus by the relationship$E=2G(1+\upsilon )$, where the Poisson ratio $\upsilon$ is approximately 0.49 for soft tissues. A different batch of samples with larger dimensions (h = 10 mm and diameter = 90 mm) were prepared for the results shown in Fig. 3(b) to minimize the impact of any boundary reflections. The experimentally determined Young’s moduli exhibit a power law relationship and can be fitted to$E=\alpha C^{\beta }$, where C is the concentration of agar gel (mg/mL) and$\alpha$and$\beta$are the fitting parameters. Our fitting parameters of $\alpha$ = 357 Pa/(mg/mL) and $\beta$ = 2.3 are in agreement with several previous studies using agarose gel samples [32, 40]. In the samples used in these experiments, the shear wavelengths varied from 2 – 9 mm. Hence, the shear wave speed was estimated by selecting regions that were at least r > 1 mm away from the excitation source to satisfy the linear phase requirement, i.e. $kr>1$for cylindrical waves [34].

3.2 Heterogeneous phantoms

Figure 4 shows the shear wave propagation in a heterogeneous agarose gel phantom prepared in a side-by-side configuration with the two sides having different stiffness values. The embedded MNP inclusion can be seen near the middle of the OCT structural image in Fig. 4(a). A relatively high concentration of MNPs was used (250 mg/ml), therefore, only the top part of the inclusion appears in the OCT structural image. A large field-of-view was acquired by translating the sample between acquisitions and stitching three overlapping cross-sectional data sets in post-processing. The phantom was prepared in two steps. In the first step 0.7% agarose was prepared with the magnetic inclusion and allowed to congeal at room temperature. Subsequently, the 0.3% agarose (representing the soft part) was poured in and allowed to cure. The yellow dashed line shows the boundary between the two different concentrations. In Fig. 4(b) and in the corresponding shear wave propagation video (Media 2 ^{(8.7MB, AVI)} ), the two different media can be qualitatively identified. In the softer region we can clearly see the wavelength being shorter and the shear wave propagation speed being slower compared to the stiff portions of the sample.

Fig. 4.

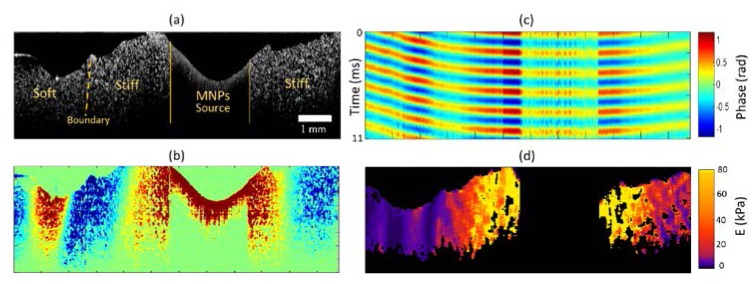
Shear waves in a heterogeneous medium. (a) Structural OCT image. The solid lines delineate the shear wave source boundaries while the dashed line indicates the interface between the stiff and soft regions of the sample. (b) Propagating shear waves (Media 2 ^{(8.7MB, AVI)} ). (c) Depth-averaged space-time map. (d) Young’s modulus map estimated from the localized measurement of the shear wave speed. The black regions correspond to the MNP source location or where the linear fit R² values were less than the threshold. A line-scan rate ~92 kHz with an excitation frequency of 500 Hz was used for these measurements.

In Fig. 4(c), a representative space-time map is shown, after averaging along the depth. As expected, in the region containing the MNP inclusion, no significant phase lag is observed as these regions move in phase with the excitation waveform. However, as we move away from the MNP inclusion, the phase lags become apparent, and clear differences in shear wave speeds can be seen between the stiff and the soft regions.

Space-time maps similar to the one shown in Fig. 4(c) were extracted for each depth and were used to estimate the elastic modulus map shown in Fig. 4(d). A Kalman filter was used to estimate the phase lag at each depth (z) and lateral location (r) within the sample. The estimated phase profile was smoothed by low-pass and median filtering to remove any random fluctuations of the phase within the sample due to low OCT signal. The local shear wave speeds were calculated by performing a linear fit on the smoothed phase profile over a lateral distance of ~300 μm on a pixel-by-pixel basis, and the linear fits that were below a certain R² threshold were discarded. The Young’s moduli were estimated using the relationship$E(r,z)\approx 3\rho c_s^2(r,z)$ where$c_s^{}(r,z)$ is the local speed calculated at each lateral position and depth. In the softer regions of the sample that corresponds to 0.3% agarose gel concentration, the mean value of the estimated Young’s modulus values was ~4.3 kPa, which is in good agreement with the measurements shown in Fig. 3(b). In the stiff regions (0.7% agarose concentration), we note that the mean Young’s modulus in the regions away (> 1 mm) from the location of the MNPs was ~30.2 kPa, which also corresponds well to the previously measured values shown in Fig. 3(b). However, in the regions close to the MNPs, the Young’s modulus values were significantly higher (mean value ~80 kPa) than the values measured in Fig. 3(b). This bias is expected due to the diffraction/near-field effects of the presence of compressional waves, mode coupling, and the breakdown of the assumption of a linear phase gradient [18, 43, 44]. Moreover, these results can also be biased due to the reflections from the internal elastic boundaries. Despite these limitations, differences in elastic contrast between the soft and the stiff regions within the sample can be seen.

3.3 Biological tissues

We used a rat liver (35 x 20 x 4 mm) and chicken muscle (40 x 20 x 6 mm) tissue to demonstrate the technique in biological samples. The tissue samples were prepared by making a 3 mm punch biopsy hole where the MNP-gel solution was added to the tissue. The location of the MNPs can be seen in the rat liver OCT image shown in Fig. 5(a). In the shear wave propagating video (Media 3 ^{(6.3MB, AVI)} ) for the liver, the influence of the geometry of the excitation source (in this case MNPs) can be clearly seen where the wave fronts initially follow the geometric profile of the source and then gradually become planar as they propagate away from the source. In the liver shown in Fig. 5(a), the shear wave speed was measured to be 1.35 ± 0.05 m/s. In Fig. 5(b), the results in a chicken muscle sample are shown, where the propagating waves can be seen travelling at a faster speed than in the liver sample, with a measured shear wave speed of 4.62 ± 0.15 m/s. As biological tissues are known to exhibit viscoelastic behavior, we used a Kelvin-Voigt model to extract the viscoelastic properties (for the liver tissue) as demonstrated in the next section.

Fig. 5.

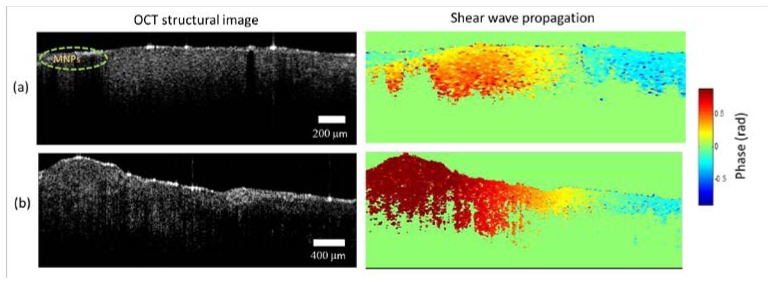
Shear waves in biological tissues. (a) Rat liver tissue. (b) Chicken muscle. OCT structural images (depth range ~1.5 mm) are shown in the first column while the second column shows single frames from the corresponding propagating shear waves videos of rat liver tissue and chicken muscle (Media 3 ^{(6.3MB, AVI)} ). The magnetic particle inclusions are on the left side of these images. A line-scan rate of 46 kHz was used with an excitation frequency of 500 Hz consisting of 10 cycles.

3.4 Dispersion curves

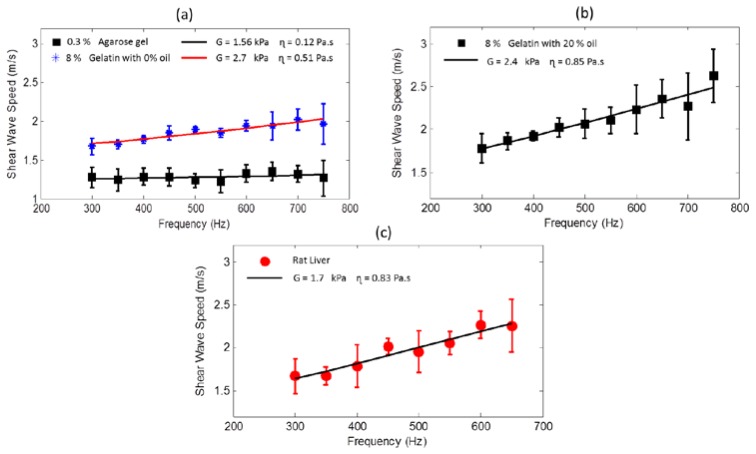
The frequency-dependent shear wave speed (termed as shear wave dispersion curve) can reveal the viscoelastic properties of the material. The slope of the dispersion curve is indicative of the viscosity of the material where a steeper slope implies a higher viscosity. A purely elastic material is characterized by a non-dispersive (no change in shear wave speed with frequency) response. Figure 6(a) shows the dispersion curves of phantoms prepared using agarose and gelatin gels which are known to have a predominately elastic response [34]. The shear wave speeds were measured using an excitation frequency ranging from 300 - 750 Hz. Localized shear wave speed was estimated using a sliding window of length ∆r = 800 μm over a 4 mm scan range. The mean values of these estimates were fitted to the Kelvin-Voigt model given by Eq. (1) while the error bars correspond to the standard deviation of the measurements from the mean shear wave speed at that frequency. The 0.3% agarose phantom gave a shear modulus of G = 1.56 kPa (corresponding to a Young’s modulus of 4.68 kPa) and viscosity of $\eta$ = 0.12 Pa∙s which shows that the response from the agarose sample is largely non-dispersive, hence validating the linear elastic model we have used in the results shown in the previous sections. The measured shear modulus for the 8% gelatin phantom without oil (Fig. 6(a)), was G = 2.7 kPa and the viscosity $\eta$ = 0.51 Pa∙s. However, with the addition of 20% oil (by weight) in the gelatin phantoms (Fig. 6(b)), the shear modulus decreased to G = 2.4 kPa while the viscosity increased to $\eta$ = 0.85 Pa∙s, which is consistent with the trend reported in the literature where the addition of oil increases the viscosity in gelatin phantoms [41]. Similar measurements were performed in a rat liver tissue shown in Fig. 6(c) where the estimated values of G = 1.7 kPa and $\eta$ = 0.83 Pa∙s are consistent with the values reported in previous studies [38]. However, in biological tissues, it is widely acknowledged that the inherent biological variability and the tissue preparation and storage methods can have a significant influence on the measured viscoelastic properties [45].

Fig. 6.

Dispersion curves for agarose, gelatin phantoms and tissue. (a) Gelatin with no oil and 0.3% agarose gel. (b) Gelatin with 20% oil. (c) Rat liver sample. The solid line in each of the plots corresponds to the best fit to the Kelvin-Voigt model while the estimated parameters are given in the legend.

4. Discussion and conclusion

Numerous factors such as boundary effects [46], shear wave patterns [43], diffraction and other near-field effects need to be taken into consideration for accurate estimation of the shear modulus [44]. Measurements need to be performed in the far-field and sufficiently away from the boundaries to minimize the bias caused by the contribution of compression waves and wave coupling at the boundaries. In our experiments with phantoms having large dimensions, the rapid attenuation of the shear waves away from the excitation source resulted in minimal boundary effects. However, this will not be the case in heterogeneous tissues which will have local internal boundaries. To ameliorate this effect, directional filters [47] and transient excitation in the form of short pulses can be used to minimize the impact of the reflected waves from the boundaries [48].

In principle, estimating the shear wave attenuation (amplitude decay) can provide additional information and can be utilized to extract the viscoelastic properties. However, estimating the attenuation is often unreliable and challenging as the amplitude of shear waves is more susceptible to noise especially if the sample is inhomogeneous. Moreover, attenuation due to geometric spreading and diffraction effects also needs to be taken into consideration. Considering these difficulties, we only utilized the shear wave speed to estimate the mechanical properties.

We limited the frequency range used in these experiments to 300-750 Hz. At lower excitation frequencies, the shear wavelengths would be large making the measurements more susceptible to near-field and boundary effects [44] while also increasing the imaging time. On the other hand, at higher excitation frequencies the rapid attenuation of the shear waves and relatively low magnetic field strength from our coil would substantially decrease the SNR of the obtained measurements. The dynamic range of the measured $G$is dependent on the minimum and maximum values of the phase gradient i.e. $k=\Delta \varphi /\Delta r$ that can be reliably measured while the spatial resolution depends on the length scale $\Delta r$ over which the local shear wave speed is estimated. The choice of the length scale $\Delta r$ will be influenced by a number of factors such as the SNR, the displacement amplitudes, excitation frequency and tissue mechanical properties [35, 49]. The accuracy of the phase gradient estimation is fundamentally limited by the SNR of the measurements. The minimum amount of phase shift that can be measured (given sufficient SNR) depends on the number of sampling points per excitation cycle and is given by$\Delta {\varphi }_{\min }=2\pi /(F_s/f)$where F_s is the sampling rate (equivalent to the line-scan rate of the camera in our experiments). Hence, the phase shift $\Delta \varphi$ induced (which depends on$\omega$and the material properties) by the propagating shear waves over a length scale ∆r should be greater than $\Delta {\varphi }_{\min }$and the sampling rate should satisfy$F_s>\omega /\Delta \varphi$.

The shape and characteristics of the propagating wave is influenced by the geometry of the mechanical excitation source [43]. In our experiments, surface (Rayleigh) waves may also be generated as our excitation source (comprising MNPs) extends to the surface of the sample. However, the shear and surface waves are almost identical in speed and hence would not significantly impact our measured values. In these measurements, we have assumed that the propagating shear waves are cylindrical in shape. However, this assumption may not always be valid, especially in tissues where controlling the geometry of the localized MNP inclusions may not be possible. If the sample is uniformly loaded with MNPs, then a focused magnetic field can be used to generate a predictable shear wave shape where the excitation region would be dependent on the magnetic field characteristics of the coil. Another way to have an excitation source (with controlled geometry) that can generate a well-defined wave pattern is by using needle-based magnetic actuation or inserting a metallic rod within the specimen [50]. Due to the high magnetic susceptibility of the metallic (e.g. carbon steel) rod, relatively large localized displacements can be induced in the sample. These large displacements cannot only increase the propagation range of the shear waves, but can also potentially be used to measure the non-linear elastic parameters [51] and the elastic properties in an anisotropic medium by placing the rod at different orientations [52].

Another consideration when using magnetic excitation is the magnetic properties of the tissue itself. Tissues are known to exhibit a weakly diamagnetic response characterized by an out-of-phase response with the applied excitation [36]. However, tissue diamagnetism will not affect our measurements as this response is very weak and the tissue diamagnetic properties are unlikely to change over the phase gradient measurement range.

The generation of shear waves by magnetic particles can potentially explain some of the artifacts seen in MM-OCT and magnetomotive ultrasound [53]. From an imaging perspective, the goal of magnetomotive imaging is to spatially localize magnetic particles within the sample. The propagation of elastic waves induced by the magnetic particles can make this spatial localization challenging. However, due to the relatively low scan rates and small displacement amplitudes used in magnetomotive imaging, shear wave propagation is not directly visualized. These artifacts if present can be minimized by phase gating [53] or filtering the signals that are out of phase with the excitation [36].

Fundamentally, this proposed method is similar to other internal dynamic excitation elastography methods such as ARF elastography. However, ARF-based techniques usually require appropriate acoustic impedance matching between the ultrasound transducer and the sample, have an excitation region that is typically large, and utilize high intensity ultrasound that can potentially damage the areas within the focal regions, making the amplitude of the generated shear waves limited by the local heating effect. Although the proposed method using MNPs is invasive in the sense that it requires the sample to be loaded with magnetic particles, there are current clinical scenarios where these MNPs are already loaded in tissues to serve the purpose of contrast enhancement in MRI or in magnetic hyperthermia applications [54]. Under these scenarios, this requirement may not impose a significant limitation.

An appropriate choice of the rheological model is still an open question and would depend on a number of factors including the frequency range used for excitation and the mechanical properties of the material. Rheological model-free methods have been proposed that estimate the complex shear modulus and wavenumber in a viscoelastic medium without making any assumptions of the underlying mechanical model and could be an interesting area for further exploration [55]. Future work will include the investigation of the influence of stiffness, size and geometry of the MNP source on the shear wave measurements and any bias introduced by these factors. Future studies should validate the estimated viscoelastic parameters with standard rheometry measurements. However, the low frequency range used in rheometery measurements (< 250 Hz) [56] may limit a direct comparison with the current technique. In future applications, the generation of shear waves with a spatially focused magnetic field would be more appropriate, enabling this technique to be used in tissue samples uniformly loaded with MNPs. The possibility of generating shear waves using magnetic particles may also be beneficial for studying cellular mechanics where magnetic beads are already widely used for rheological measurements [24, 25].