Abstract
In order to promote the development of the portable, low-cost and in vivo cancer diagnosis instrument, a miniature laser Raman spectrometer was employed to acquire the conventional Raman spectra for breast cancer detection in this paper. But it is difficult to achieve high discrimination accuracy. Then a novel method of adaptive weight k-local hyperplane (AWKH) is proposed to increase the classification accuracy. AWKH is an extension and improvement of K-local hyperplane distance nearest-neighbor (HKNN). It considers the features weights of the training data in the nearest neighbor selection and local hyperplane construction stage, which resolve the basic shortcoming of HKNN works well only for small values of the nearest-neighbor. Experimental results on Raman spectra of breast tissues in vitro show the proposed method can realize high classification accuracy.
OCIS codes: (170.5660) Raman spectroscopy; (300.6450) Spectroscopy, Raman; (170.6510) Spectroscopy, tissue diagnostics
1. Introduction
Breast cancer is one of the major causes of female death. Data show 20% global increase in breast cancer from 2008 to 2012 [1]. In 2014, about 62570 cases of breast carcinoma in situ will be newly diagnosed in the United States. Breast cancer accounts for 15% of all female cancer deaths, which is second only to lung cancer in the United States [2]. In China, the incidence has also increased significantly in recent years, and ranked first in the female malignant tumors in some large cities, such as Beijing, Shanghai and Tianjin [3].
Since the early diagnosis is the key factor to increase the rate of survival time for the cancer patients, it is important to develop fast, less invasive, objective methods for the diagnosis of breast cancers. Raman spectroscopy, as a molecular spectroscopy, could detect the changes of molecular structure and composition. During the tumor formation, significant changes occurred in the structure and concentration of the main bimolecular, which constitute the cell and tissue, such as carbohydrates, lipids, proteins and nucleic acids. Because these changes occur earlier than the clinical symptoms appearance and tumor medical imaging detection, molecular spectroscopy has the potential to early diagnosis of the tumor [3–7]. Due to the characters such as sharp peaks, freeing from the interference of water, fewer samples required and without sample chemical treatment etc, Raman spectroscopy is promising to realize real-time and noninvasive detection at the molecular level.
Raman spectroscopic diagnosis technology of breast cancers has been developed recently. There are many investigations focus on Fourier Transform Raman spectroscopy (FTRS), Confocal Raman microspectroscopy (CRS), Resonance Raman spectroscopy (RRS) and Surface-enhanced Raman spectroscopy (SERS) for breast cancer diagnosis [8–15]. Using them, the Raman spectra could be acquired with lower fluorescence, higher spatial resolution, but these technologies generally use a large-sized Raman spectrometer or a large desktop microscope, which is also expensive and difficult to achieve clinical portable diagnosis. For Conventional Raman spectroscopy (RS), the Raman spectrometers tend to be small-sized, portable and low cost. Combined with the optical fiber probe, RS has promise for in vivo and in situ cancer detection. While due to the strong fluorescence background interference and low spectral signal-to-noise ratio, it is difficult to achieve high discrimination accuracy by using the miniature Raman spectrometer. Therefore, it is significant to investigate the discrimination analysis method for high classification accuracy. A few studies in [12–14] use the miniature Raman spectrometer to collect the RS spectra to diagnose breast cancers.
In this paper, a novel algorithm of adaptive weight K-local hyperplane (AWKH) is investigated for classification of the acquired Raman spectra from cancerous and normal human breast tissues. It is an extension and improvement of K-local hyperplane distance nearest-neighbor (HKNN) [16]. HKNN performs well only for small values of the number of nearest-neighbor () because it assumes that every single feature of the training data is equally relevant for the nearest neighbors selection [17]. The feature weights measure the importance of each single feature in classification. For AWKH, the feature weight is estimated by using the ratio of the between-group to with-group sums of squares for the data assigned to the given classes. Then the higher weight corresponds to a feature with better class separation capability. In the paper, AWKH realized higher accuracy for the discrimination of the acquired Raman spectra compared to the classifiers support vector machine (SVM) and HKNN.
2. Materials and methods
2.1 Tissue specimens
A total of sixteen breast tissue samples were obtained from female patients in Peking University Third Hospital, including four normal tissues and twelve cancerous tissues. The mean age was 56 years with the oldest 88 years and the youngest 33 years. After the spectra were acquired, the samples were stored in liquid nitrogen and sent for the frozen section pathological diagnosis as the reference in the spectral analysis. The experimental procedures were approved by the Medical Ethics Committee of Peking University Third Hospital and the patients.
2.2 Raman spectral measurements
In order to promote the development of a clinical portable, low-cost and in vivo cancer diagnosis instrument, an Ocean Optics QE65Pro miniature fiber optic Raman spectrometer at a 785nm excitation wavelength was employed to acquire the conventional Raman spectra.
Specimens without any chemical treatment were frozen using liquid nitrogen and maintained until thawed at room temperature. They were placed in the glass slide for Raman spectral measurement. The integration time is 30s. All the spectra were acquired in the wavelength range of interest, from 700 to 2000 cm−1. In the Spectral acquisition process, every sample was measured at different pathology locations, and for every same pathology location three spectra were measured and averaged in order to reduce the noise level. Each Raman spectrum was labeled according to the pathological diagnosis. In order to reflect the experiment results objectively, the sample spectra were collected on the same environmental conditions and the experiments were conducted two days. 75 Raman spectra (16 normal and 59 cancerous) obtained in the first day and 58 Raman spectra (18 normal and 40 cancerous) obtained in the second day.
2.3 Software
All the examined preprocessing and classification algorithms were implemented and tested in Matlab 2009a. In addition, the SVM toolbox was used.
2.4 Preprocessing algorithm
The spectra collected using Ocean Optics QE65Pro Raman spectrometer yielded noise and fluorescence background. The noise was removed by wavelet transform and the fluorescence background was removed by fitting the smoothed spectra to a third-order polynomial function.
The wavelet transform [18, 19] was introduced as follows:The discrete wavelet transform is defined as:
| (1) |
whereis the wavelet basis function, is the J layer approximation coefficient of spectral signal that is also the low frequency coefficient, is the j layer detail coefficient of spectral signal as well as the high frequency coefficient .
The specific process is shown as follows:
Step 1: choose a wavelet function and a decomposition scale.
Step 2: deal with the high frequency coefficients of wavelet decomposition by threshold processing. A soft threshold function is used in this paper:
| (2) |
Step 3: reconstruct the spectrum signal, according to the J layer low frequency coefficient and the high frequency coefficient after threshold processing from 1th to the jth layer.
2.5 AWKH algorithm
Adaptive weight k-local hyperplane (AWKH) algorithm is an improvement and extension of K-local hyperplane distance nearest-neighbor (HKNN) algorithm. HKNN [16] performs well only for small values of, it sufferers from bias for data with high dimensions, AWKH resolves the problem by considering the features weights when calculate the distance between the test set samples and hyperplane. The feature weight is estimated by using the ratio of the between-group to with-group sums of squares. Feature weights are computed such that higher weight corresponds to a feature with better class separation capability. And the bias when HKNN is used in high dimensions is settled by considering the shape of the neighborhood around the test sample. Raman spectra of breast tissues contain some specific peaks which are beneficial to classification but not common exist. Since AWKH only considers the relationship between samples, so when dealing with Raman spectroscopy, AWKH can obtain high accuracy.
The specific process of the AWKH algorithm can be summarized as follows:
Suppose the training set consists of L samples with J classes. Each training sample consists ofinput featureswith known class label .The goal is to predict the class label of a query with input vector.
Step 1: calculate the feature weightof the training sample according to the formula as follows:
| (3) |
wheredenotes the jth component of the grand class centroid anddenotes the jth component of class centroid of class c; denotes the indicator function, it equals1when, otherwise, it equals 0; denotes the jth component of the ith training sample.
Step 2: calculate the weighted Euclidean distance metricbetweenand, the formula is as follows:
| (4) |
Step 3: according to the Euclidean distance, selectnearest neighbors of class c for the given query, then construct the local hyperplane of class c with:
| (5) |
Step 4: calculate the minimum distance betweenand:
| (6) |
where is the regularization parameter, which avoidsbeing too large. Solve the equation, then achievewhere.
Step 5: the class label ofis assigned as: .
3. Results and discussion
133 spectra were obtained by Raman spectroscopic method with the scan region 700 cm−1 to 1800 cm−1. Each Raman spectrum was labeled according to the pathological diagnosis.
3.1 Spectral preprocessing
Symmlet-5 wavelet filter and four-decomposition scale were adopted to reduce noise, and then a third-order polynomial was adopted to remove fluorescence background and baseline corrected. The mean Raman spectra of normal and cancerous tissues before preprocessing and after preprocessing are shown respectively (see Fig. 1, Fig. 2).
Fig. 1.
Typical Raman spectra of breast tissues before preprocessing.
Fig. 2.
Typical Raman spectra of breast tissues after preprocessing.
The raw spectra of normal tissues showed evident peaks (see Fig. 1), while, there are only small peaks in the raw spectra of cancerous tissues because of the effect of the noise and the fluorescent background.
The quality of Raman spectra has improved greatly after data preprocessing (see Fig. 2). The Raman spectra are smoother, the Raman peaks of normal and cancerous tissues are distinguished, and especially the differences between Raman spectra of normal and cancerous tissues are more pronounced after preprocessing.
The essence of the wavelet transform is that project the spectrum signal in the wavelet basis function, decompose the spectrum signal in time domain and frequency domain, get the wavelet approximation coefficients and detail coefficients. Where, the detail signal reflects the local nuances, and most of them are noise in the high frequency region. So wavelet transform could be used to remove the noise of the Raman spectra, and optimize the quality of spectra.
The Raman peaks of normal tissues and cancerous tissues (see Fig. 2) are displayed. The spectral profile of normal tissues is indicative of higher levels of lipids. In comparison, the spectral profile of pathological tissues indicates the presence of more proteins and fewer lipids. The spectral features (1078, 1305, 1447, 1653 and 1747cm−1) of normal tissues indicate a dominance of lipids. The spectral profiles of cancerous tissues (1083, 1278, 1453cm−1) indicate the presence of proteins. The peak intensities of 1305, 1653, 1747 cm−1 in cancerous tissues decrease obviously compared to those in normal tissues. The peak position representing protein molecules appears at 1278 cm−1 in cancerous tissues, while almost disappears in normal tissues. These changes reflect that during tumor formation, the protein, lipid and nucleic acid molecular changed in the configuration, component and quantity, and the proportion of proteins significantly increased against to the greatly reduced lipids proportion. This observation corroborates earlier studies [20, 21]. As is well known, cancerous tissues contain more proteins relative to normal tissues and adipose–rich noncancerous, which is the basis of spectroscopic diagnosis.
Specific assignments of individual peaks could be found in Table 1.
Table 1. Peak positions and assignments of Breast Tissueα.
| Peak position(cm−1) | Major assignment |
|---|---|
| 1078 | C-C or C-O stretch (lipid) |
| 1278 | Amide III(C-N stretch) (protein) |
| 1305/1308 | Amide III, α-helix, C-C str&C-H (protein) |
| 1447 | Scissoring mode of methylene (CH2) (lipid) |
| 1453 | CH2 deformation (protein) |
| 1653 | lipid |
| 1747/1750 | C = O stretch (lipid) |
3.2 Statistical analysis
The whole data set was split into a training set and test set, and each classifier was learned on the training set and applied on the test set.
The 75 Raman spectra (16 normal and 59 cancerous) obtained in the first day after preprocessing were selected as the training set, and the 58 Raman spectra (18 normal and 40 cancerous) obtained in the second day after preprocessing were selected as the test set.
The training set and the test set are normalized to zero mean and unit variance first, then, classify the test set by AWKH、HKNN and SVM classifier respectively. The two parameters andfor AWKH were set as [1:20] and 10 respectively. The parameterfor HKNN in reference [16] was set as [1:20]. Then, select the result with highest testing accuracy as the optimized classification result.
The experimental results are summarized in Table 2 and Table 3. Here, the optimized parameters for AWKH are,, andfor HKNN. Table 2 displays the classification results of test set with AWKH. Table 3 shows the results obtained with three different methods.
Table 2. Classification results of test set with AWKH.
| The predicted cancerous number (T + ) | The predicted normal number (T-) | |
|---|---|---|
| The real cancerous number (D +) | 39 | 1 |
| The real normal number (D-) | 1 | 17 |
Table 3. Comparison of the results for the AWKH, HKNN, SVM.
| Method | Sensitivity (%) | Specificity (%) | Positive* (%) | Negative** (%) | Accuracy (%) |
|---|---|---|---|---|---|
| AWKH | 97.5 | 94.4 | 97.5 | 94.4 | 96.6 |
| SVM | 92.5 | 88.9 | 94.9 | 84.2 | 91.4 |
| HKNN | 92.5 | 77.8 | 90.2 | 82.4 | 87.9 |
* The positive predictive value, ** the negative predictive value
In Table 3, it can be seen that AWKH achieves the highest testing accuracy among three different classifiers. Especially, AWKH is much more accurate than SVM classifier.
The classification accuracy with differentvalue using AWKH and HKNN is shown respectively (see Figs. 3 and 4). In wake of the increase ofvalue, the accuracy with HKNN decreased (see Fig. 4). The accuracy of AWKH stays stable forvalue between 4 and 20 (see Fig. 3).
Fig. 3.

The classification accuracy at different K value for AWKH.
Fig. 4.
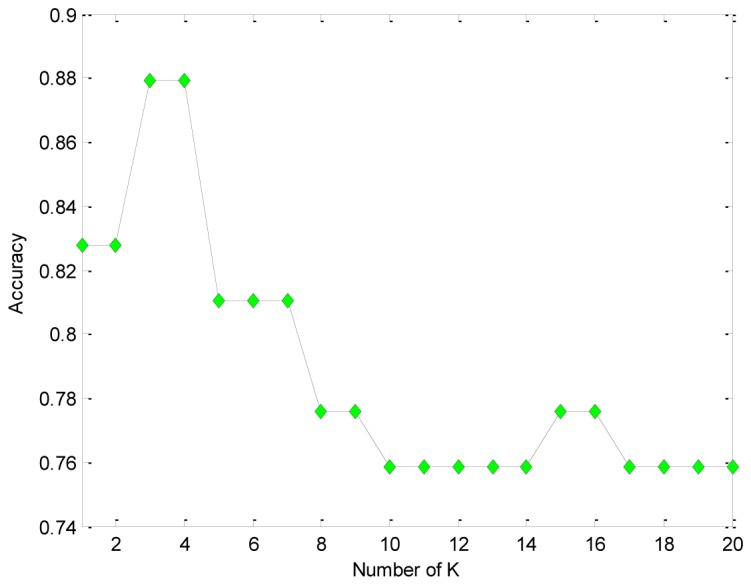
The classification accuracy at different K value for HKNN.
The optimal value of the parameterdepends on. For small, the model can achieve good results without. With larger, the model tends to be various and more complex, so that the regularization can help to improve the performance. In contrast, HKNN does not have the advantage.
The feature weights measure the importance of every single feature of spectral data. HKNN performs well only for small values ofbecause it assumes that every single feature is equally relevant for classification which may yield unsatisfactory performance when data with high dimensions. AWKH computes the ratio of the between class to the within class squared distances to estimate the features weights. The nearest neighbors are selected by the weighted Euclidean distance between the test sample and training set. The resulting nearest neighbors are then associated with the most discriminant feature space. The local hyperplance constructed based on these neighbors is more convincing which leading to the classification result directly. With small, HKNN may be well formulated, but with large, HKNN will suffer the unsatisfactory performance. Moreover, for the higher dimensionality of the extracted features, the more points from each class are needed to accurately estimate the localized model, henceshould be larger. AWKH considers the features weights make it fairly robust on the choice of, which is generally a desirable characteristic of a K-local learning algorithm.
Then the data processing was conducted two more times. The 58 Raman spectra obtained in the second day were selected as the training set, and the other spectra obtained in the first day were selected as the test set. Table 4 shows the results obtained by three different methods with optimal parameters.
Table 4. Comparison of the results for the AWKH, HKNN, SVM.
| Method | Sensitivity (%) | Specificity (%) | Positive* (%) | Negative** (%) | Accuracy (%) |
|---|---|---|---|---|---|
| AWKH | 94.9 | 93.8 | 98.2 | 83.3 | 94.7 |
| SVM | 93.2 | 93.8 | 98.2 | 78.9 | 93.3 |
| HKNN | 88.1 | 87.5 | 96.3 | 66.7 | 90.7 |
* The positive predictive value, ** the negative predictive value
Finally, the total 133 Raman spectra were split into two data sets randomly for ten times, Every time 80 Raman spectra after preprocessing were selected as the training set, and the other 53 Raman spectra after preprocessing were selected as the test set. Then the algorithms were examined. Table 5 shows the average accuracy of the ten experiments using three different methods with optimal parameters.
Table 5. Comparison of the results for the AWKH, HKNN, SVM.
| Method | Accuracy (%) |
|---|---|
| AWKH | 95.8 |
| SVM | 92.4 |
| HKNN | 87.6 |
From the experimental results above, AWKH shows great advantage for the classification of Raman spectra of breast tissues.
Although the two algorithms have similar mechanisms for AWKH and HKNN, AWKH performed better in the experiment. The data sets with irrelevant or redundant features like Raman spectra data can be classified more accurate with AWKH because it considers the features weights. For SVM, kernel function needs to be used for every single sample and the choices of the parameters for the kernel is important, which are complex and unstable. But it is worth noting that, SVM can perform well when the parameters are optimal and it has advantage for the large-scale test set.
4. Conclusions
As evident from the studies conducted so far, it is quite feasible to classify normal and pathological breast tissues optically. The ultimate goal of optical spectroscopy methods is to develop clinical portal, low-cost and in vivo cancer diagnosis instrument. For such applications, a miniature laser Raman spectrometer with a 785nm excitation was employed to acquire the conventional Raman spectra of breast tissues. Then the preprocessing procedures were investigated. At the end of the paper, a novel classification algorithm AWKH is proposed. This novel algorithm improves the HKNN method by stressing the feature weight.
The experimental results show that the proposed classification algorithm is an effective method. AWKH achieved high classification accuracy even when the strong fluorescence background interference and low spectral signal-to-noise ratio were obtained by the miniature laser Raman spectrometer. It is helpful to promote the development of clinical portable diagnosis technology and a desire to apply the technology in vivo breast cancer diagnosis using Raman spectroscopy in the later research.
Acknowledgments
This work is supported by Programs for Changjiang Scholars and Innovative Research Team (PCSIRT) in University of China (IRT0705).
References and links
- 1.Carter D., “New Global Survey Shows an Increasing Cancer Burden,” Am. J. Nurs. 114(3), 17–18 (2014). 10.1097/01.NAJ.0000444482.41467.3a [DOI] [PubMed] [Google Scholar]
- 2.R. Siegel, J. Ma, Z. Zou, and J. Ahmedin, “Cancer statistics, 2014,” CA. 64(1), 9–29 (2014). [DOI] [PubMed]
- 3.Li Q. B., Sun X. J., Xu Y. Z., Yang L. M., Zhang Y. F., Weng S. F., Shi J. S., Wu J. G., “Diagnosis of gastric inflammation and malignancy in endoscopic biopsies based on Fourier transform infrared spectroscopy,” Clin. Chem. 51(2), 346–350 (2005). 10.1373/clinchem.2004.037986 [DOI] [PubMed] [Google Scholar]
- 4.Alfano R. R., Tang G. C., Pradhan A., Lam W., Choy D., Opher E., “Fluorescence spectra from cancerous and normal human breast and lung tissues,” IEEE J. Quantum Electron. 23(10), 1806–1811 (1987). 10.1109/JQE.1987.1073234 [DOI] [Google Scholar]
- 5.Alfano R. R., Liu C. H., Sha W. L., Zhu H. R., Akins D. L., Cleary J., Prudente R., Clemer E., “Human breast tissues studied by IR Fourier transform Raman spectroscopy,” Lasers Life Sci. 4(1), 23–28 (1991). [Google Scholar]
- 6.Pu Y., Wang W. B., Yang Y. L., Alfano R. R., “Native fluorescence spectra of human cancerous and normal breast tissues analyzed with non-negative constraint methods,” Appl. Opt. 52(6), 1293–1301 (2013). 10.1364/AO.52.001293 [DOI] [PubMed] [Google Scholar]
- 7.Teh S. K., Zheng W., Ho K. Y., Teh M., Yeoh K. G., Huang Z., “Near-infrared Raman spectroscopy for early diagnosis and typing of adenocarcinoma in the stomach,” Br. J. Surg. 97(4), 550–557 (2010). 10.1002/bjs.6913 [DOI] [PubMed] [Google Scholar]
- 8.Liu C. H., Zhou Y., Sun Y., Li J. Y., Zhou L. X., Boydston-White S., Masilamani V., Zhu K., Pu Y., Alfano R. R., “Resonance Raman and Raman Spectroscopy for Breast Cancer Detection,” Technol. Cancer Res. Treat. 12(4), 371–382 (2013). [DOI] [PubMed] [Google Scholar]
- 9.García-Flores A. F., Raniero L., Canevari R. A., Jalkanen K. J., Bitar R. A., Martinho H. S., Martin A. A., “High-wavenumber FT-Raman spectroscopy for in vivo and ex vivo measurements of breast cancer,” Theor. Chem. Acc. 130(4–6), 1231–1238 (2011). 10.1007/s00214-011-0925-9 [DOI] [Google Scholar]
- 10.Yu C., Gestl E., Eckert K., Allara D., Irudayaraj J., “Characterization of human breast epithelial cells by confocal Raman microspectroscopy,” Cancer Detect. Prev. 30(6), 515–522 (2006). 10.1016/j.cdp.2006.10.007 [DOI] [PubMed] [Google Scholar]
- 11.Zoladek A., Pascut F. C., Patel P., Notingher I., “Non-invasive time-course imaging of apoptotic cells by confocal Raman micro-spectroscopy,” J. Raman Spectrosc. 42(3), 251–258 (2011). 10.1002/jrs.2707 [DOI] [Google Scholar]
- 12.Haka A. S., Volynskaya Z., Gardecki J. A., Nazemi J., Lyons J., Hicks D., Fitzmaurice M., Dasari R. R., Crowe J. P., Feld M. S., “In vivo Margin Assessment during Partial Mastectomy Breast Surgery Using Raman Spectroscopy,” Cancer Res. 66(6), 3317–3322 (2006). 10.1158/0008-5472.CAN-05-2815 [DOI] [PubMed] [Google Scholar]
- 13.Haka A. S., Volynskaya Z., Gardecki J. A., Nazemi J., Shenk R., Wang N., Dasari R. R., Fitzmaurice M., Feld M. S., “Diagnosing breast cancer using Raman spectroscopy: prospective analysis,” J. Biomed. Opt. 14(5), 054023 (2009). 10.1117/1.3247154 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chowdary M. V. P., Kalyan Kumar K., Mathew S., Rao L., Krishna C. M., Kurien J., “Biochemical correlation of Raman spectra of normal, benign and malignant breast tissues: a spectral deconvolution study,” Biopolymers 91(7), 539–546 (2009). 10.1002/bip.21171 [DOI] [PubMed] [Google Scholar]
- 15.Liu C. H., Wang W. B., Alimova A., Sriramoju V., Kartazayev V., Alfano R. R., “Monitoring changes of proteins and lipids in laser welded aorta tissue using Raman spectroscopy and basis biochemical component analyses,” Proc. SPIE 7175, 717504 (2009). [Google Scholar]
- 16.Okun O. G., “K-local hyperplane distance nearest-neighbor algorithm and protein fold recognition,” Pattern Recognit. Image Anal. 16(1), 19–22 (2006). 10.1134/S1054661806010068 [DOI] [Google Scholar]
- 17.P. Vincent, Y. Bengio, “K-local hyperplane and convex distance nearest neighbor algorithms,” NIPS, 985–992 (2001).
- 18.Feld M. S., Manoharan R., Salenius J., Orenstein-Carndona J., Roemer T. J., Brennan J. F., III, Wang Y., “Detection and characterization of human tissue lesions with near-infrared Raman spectroscopy,” Proc. SPIE 2388, 99–104 (1995). 10.1117/12.208468 [DOI] [Google Scholar]
- 19.Li G., “Removing Background of Raman Spectrum Based on Wavelet Transform,” International Conference on Future Computer and Communication (IEEE, 2009), pp. 198–200 10.1109/FCC.2009.69 [DOI] [Google Scholar]
- 20.Shafer-Peltier K. E., Haka A. S., Fitzmaurice M., Crowe J., Dasari R. R., Feld M. S., “Raman microspectroscopic model of human breast tissue: implications for breast cancer diagnosis in vivo,” J. Raman Spectroscopy 33(7), 552–563 (2002). 10.1002/jrs.877 [DOI] [Google Scholar]
- 21.Haka A. S., Shafer-Peltier K. E., Fitzmaurice M., Crowe J., Dasari R. R., Feld M. S., “Diagnosising breast cancer by using Raman spectroscopy,” Proc. Nat. Acad. Sci. USA 102(35), 12371–12376 (2005). 10.1073/pnas.0501390102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Chowdary M. V. P., Kumar K. K., Kurien J., Mathew S., Krishna C. M., “Discrimination of normal, benign, and malignant breast tissues by Raman spectroscopy,” Biopolymers 83(5), 556–569 (2006). 10.1002/bip.20586 [DOI] [PubMed] [Google Scholar]




