Abstract
Rationale
Organisms emit more responses when food is provided according to random as compared with fixed schedules of reinforcement. Similarly, many human behaviors deemed compulsive are maintained on variable schedules (e.g., gambling). If greater amounts of behavior are maintained by drugs of abuse when earned according to variably-reinforced schedules, this would suggest that excessive drug-taking behavior may be due in part to the nature of drug availability.
Objectives
The aim was to determine whether random schedules of contingent intravenous drug delivery would produce more responding than similarly-priced fixed schedules.
Methods
Six rhesus macaque subjects responded to produce cocaine (0.003–0.03 mg/kg/inj), remifentanil (0.01–1.0 µg/kg/inj), or ketamine (0.01–0.1 mg/kg/inj) according to either fixed- or random-ratio requirements that increased systematically across sessions. Demand curves were generated with the most effective dose of each drug and compared across drug- and schedule-type.
Results
Cocaine and remifentanil maintained higher levels and rates of responding when earned according to random ratio schedules as compared with fixed ratio schedules. This difference was most pronounced when drugs were available at high unit prices. Differences in responding across the schedule types generated by ketamine – a lesser valued reinforcer – were qualitatively similar but smaller in magnitude.
Conclusions
The current study provides a systematic replication across reinforcer-type demonstrating that drugs delivered after a random number of responses generate more behavior than those delivered according to a fixed schedule. The variable nature of the availability of drugs of abuse – particularly those that are scarce or expensive – may be a contributing factor to excessive drug intake by humans. This effect is most likely to be observed when more highly demanded (reinforcing) drugs are being consumed.
Keywords: drug self-administration, rhesus monkeys, cocaine, remifentanil, ketamine, random ratio, fixed ratio, demand curves, response output curves, behavioral economics
Introduction
It has been recognized for some time that variable schedules of reinforcement can maintain relatively high and stable rates of responding as compared to behavior generated by fixed-ratio schedules (Ferster and Skinner 1957). Some forms of high and stable excessive behavior such as pathological gambling may depend heavily on the random delivery of reinforcement. Less is known about the relevance of variable reinforcer deliveries on other types of behavior that can be considered excessive or compulsive, such as drug abuse. Although the variable nature of reinforcer deliveries is less clear with drug abuse than with many gambling games, it is still the case that the amount of behavior required to obtain drugs is not likely to be on a fixed schedule. An important question is what role variably scheduled payoffs may have in the development of excessive drug-taking behavior.
Previous research has assessed nonhuman subjects’ preference for variability in discrete-trial choice assays. In such procedures, subjects make repeated choices between two options – one that is fixed and one that is variable. There are several dimensions that can be manipulated and assessed in this type of procedure, including work requirement, delay to reinforcement, and amount of reinforcement. Several investigators have reported that animal subjects prefer variable over fixed food amounts in discrete choice situations (e.g., Logan 1965; Fantino 1967; Lagorio and Hackenberg 2012). When examining choices between fixed and variable delays to reinforcer delivery, researchers have reported robust preferences for the option that is variable (e.g., Cicerone 1976; Davison 1972; Fantino et al. 1987; Herrnstein 1964; Hursh and Fantino 1973; Lagorio and Hackenberg 2010; Mazur 1984, 2004). And, although not as consistent a finding, there are several reports of preference for variable over fixed ratios, particularly at high ratio requirements (e.g., Ferster and Skinner 1957; Zeiler 1979). Other studies with similar aims have examined free-operant responding when only one schedule type is available. For example,Madden et al. (2005) demonstrated that pigeons responding for food under closed-economic conditions respond at higher rates and consume more food when reinforcers are delivered according to a random ratio (RR) as compared with fixed ratio (FR) schedules, particularly at high unit prices - a quantified relation between work ratio and payoff amount.
To our knowledge, no studies have assessed whether RR and FR schedules engender different performances when subjects are working for reinforcers other than food. The current study was designed to determine whether RR schedules generate more behavior than FR schedules when intravenous (I.V.) drug delivery was used to establish and maintain responding. It was also designed to compare behavior maintained under random and fixed ratio schedule when drugs with different reinforcing effectiveness (Hursh and Winger 1995) were used. It was therefore possible to determine whether differences in behavior generated by FR and RR schedules would emerge only with highly valued reinforcers such as food or cocaine. To accomplish these goals, demand-curve analyses were used to establish relative reinforcing effectiveness among different doses of three drugs: cocaine, remifentanil, and ketamine. Overall responses and response rates produced by each drug under both FR and RR schedules were then compared to assess whether variably delivered drug reinforcers might engender higher rates of responding.
Materials and Methods
Animals
Five adult rhesus monkeys (two females) were subjects in this study. Each subject had a history of drug self-administration under FR schedules of reinforcement. The monkeys were individually housed in stainless steel cages measuring 83.3 cm high×76.2 cm wide×91.4 cm. A metal panel (20 cm high×28 cm wide) was mounted on one side of each cage and contained three response levers with a stimulus light located 5 cm above each lever. Levers were positioned 5 cm above the bottom of the panel and were spaced 2.5 cm apart. The stimulus lights were spaced 5 cm apart and could be independently illuminated red, green, or yellow.
Procedures
Each monkey had an I.V. catheter implanted in an accessible vein under sterile conditions and surgical anesthesia (10 mg/kg ketamine and 2 mg/kg xylazine). The catheter passed subcutaneously to the animal’s back where it exited in the midscapular region and proceeded through a flexible tubular metal tether to the outside rear of the cage. Subjects wore a Teflon jacket (Lomir, Quebec, Canada) that protected the catheter and allowed attachment of the tether to the animal. Located behind each cage was an infusion pump (Watson-Marlow model SCI-Q 400, Wilmington, MA), a failsafe device to stop the pump if a computer malfunction did not stop it automatically at 5 s, and plastic infusion bags containing the drug concentration indicated for the drug dose and weight of the monkey. The catheters were connected to this system by way of a 0.45µm Millipore filter.
Subjects were given access to I.V. drug infusions during twice-daily 2-hr sessions (6am and 12pm). The start of each session was signaled by the onset of a red stimulus light over the right lever. Responses on this lever resulted in a drug infusion after the schedule requirement was completed (described below). Drug infusions always lasted for 5 s and were accompanied by the offset of the right, red stimulus light and the onset of the center, green stimulus light. Following each reinforcer delivery, there was a 10 s timeout period during which all lights were extinguished and responses had no scheduled consequences.
Between three and four subjects were evaluated with each drug: remifentanil (Monkeys MP, AL, FO, DA), cocaine (Monkeys AL, FO, ST), and ketamine (Monkeys AL, FO, ST, DA). Because there was more variability in responding across-subjects when ketamine was the reinforcer, subjects were evaluated twice with this drug. Drug dose order presentation was randomized, and included the following: 0.00001, 0.00003, 0.0001, and 0.0003 mg/kg/inj (remifentanil); 0.003, 0.01, and 0.03 mg/kg/inj (cocaine); and 0.01, 0.03, and 0.1 mg/kg/inj (ketamine). The three drugs were made available according to both fixed- and random-ratio schedules across conditions. Testing of the three drugs was in a consistent order across subjects (remifentanil followed by cocaine and ketamine last). The other manipulations (dose of drug and RR or FR schedule type) were presented in varying orders across subjects. In order to generate demand functions, within each condition the response requirement increased every two sessions in the following ascending order: 10, 32, 100, 320, 560, 1000, and occasionally 1780. For the random ratio schedule, in which each response has an equal probability of producing a reinforcer, the programmed values were generated using a method described by Bancroft and Bourret (2008). This method utilizes a macro (created using Microsoft Excel) to identify a priori how many responses need to be emitted per reinforcer based on the programmed probability. For example, in an RR 10 schedule each response has a 0.1 probability of producing a reinforcer; the macro loops through potential successive responses made (Response 1, Response 2, etc.) to probabilistically determine whether a response meets the 0.1 criteria. When it does, that response number is recorded and subsequent responses continue to be assessed for meeting the next reinforcement criteria based again on the 0.1 probability. The response requirements programmed by the RR schedule were generated in this manner to ensure that the programmed ratio closely approximated the obtained ratio. The maximum obtained values were 46, 334, 586, 1334, 3004, 5534, and 6224 for each ratio, respectively.
Drugs
Lyophilized remifentanil hydrochloride was purchased from the University of Michigan hospital. Cocaine hydrochloride was generously provided by the National Institute on Drug Abuse. Ketamine hydrochloride was purchased from Butler Schein Animal Health (Dublin, OH) as a solution of 100 mg/cc in water. The drug doses were calculated as the salt form of the drugs. All drugs were reconstituted or dissolved in sterile 0.9% sodium chloride solution.
Data analyses
Data are assessed according to unit price (P), which is a quantified relation between the programmed response requirement (R) and amount of reinforcement (A) – in this case, the dose of the drug (Hursh 1980). This equation was modified by Hursh (1988) to account for reinforcers delivered with probability p. According to this basic equation, no differences in responding are predicted for reinforcers produced by fixed- or random-ratio schedules:
| (Equation 1) |
Rates of responding, number of responses, and overall drug consumption were calculated for each ratio and condition. The consumption of each drug was normalized (Hursh and Winger 1995; Hursh and Silberberg 2008) such that the point of origin was set to maximal responding (100%) – the maximum number of injections earned at the lowest cost (FR or RR 10). Consumption was normalized with the equation
| (Equation 2) |
such that normalized consumption (Q) at a specific ratio (Yn) was a function of consumption at the lowest price (Y10). Price (P) was normalized with the equation
| (Equation 3) |
where R is the ratio value (FR or RR). These data were fit to an exponential demand equation (Hursh and Silberberg 2008) using Microsoft Excel’s Solver function:
| (Equation 4) |
Q is the quantity consumed (number of injections multiplied by dose in mg/kg/injection), Qo is the predicted level of consumption when the commodity is freely available (and was set to 100), k indicates the range of the dependent variable in logarithmic units, and α (alpha) is the critical measure reflecting rate of change in consumption with price, or the elasticity of the demand function. This elasticity measure, in turn, indicates the “essential value” of the reinforcer. The alpha parameters were obtained from demand functions that included data from whichever dose generated the highest Pmax (the unit price at which peak levels of responding were maintained) for each of the tested drugs.
Response output functions were determined using Graphpad Prism 5 (La Jolla, CA, USA) in order to compare the amount of behavior generated by the two schedule types. Under ratio schedules, one can calculate response output as the product of reinforcers earned times the cost of those reinforcers (the fixed or random ratio requirement). Using Equation 4 as the expression for the number of reinforcers earned, the equation for total responding is the solution of that expression at any ratio value (C) multiplied by the programmed ratio value, as shown in Equation 5. Separate response functions were generated for each reinforcer type, for the different doses of each drug, and for the schedule arrangement (FR or RR).
| (Equation 5) |
Results
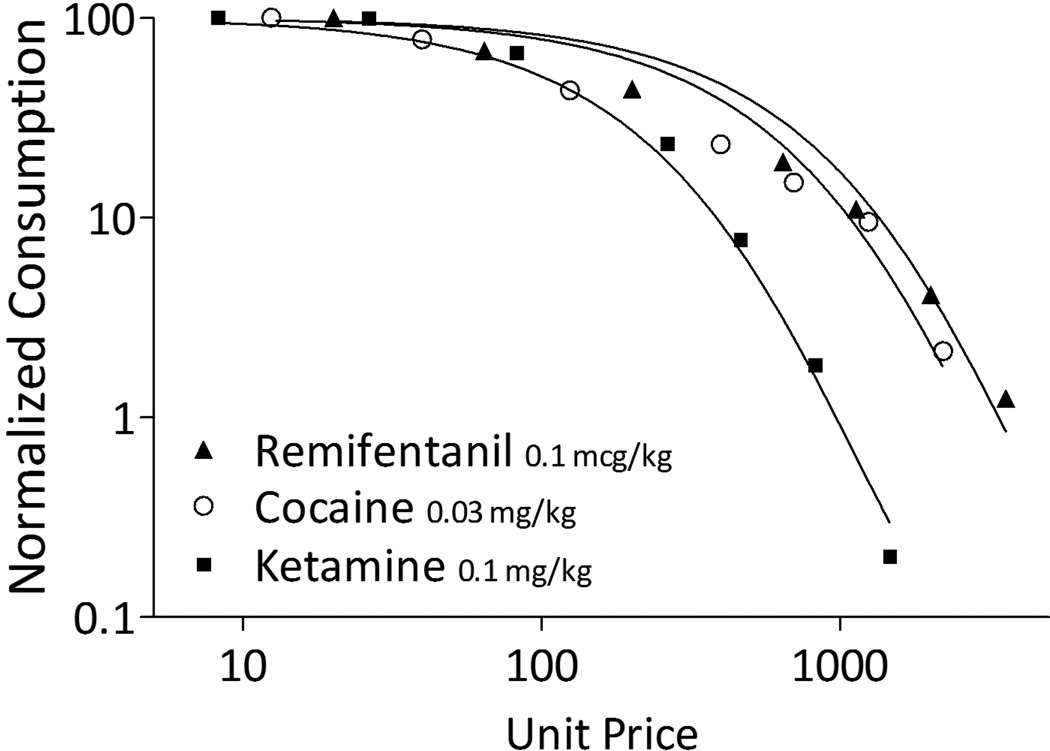
Figure 1 displays a basic comparison of the demand for each of the three tested drugs. Curves were generated using data from the FR schedule condition using the dose that produced the highest Pmax. Data in this figure were normalized across subjects, such that their maximum consumption of each drug was set at 100% with remaining consumption at larger ratios calculated as a percent of maximum. Alpha (α) was free to vary, while k was fixed at 3.495 which was the empirically derived best-fit shared value across the three drugs. Table 1 indicates the elasticity measures of the three drugs, with smaller numbers indicating less elasticity of demand and more reinforcing effectiveness (essential value of the commodity). The relative, rank-order reinforcing value of the three drugs indicated that remifentanil and cocaine were nearly equally valued (remifentanil being somewhat more valuable); and ketamine was less effective in maintaining responding in the face of price increases. Reported R2 values indicate the across-subjects aggregate fit when curves are generated for each subject’s individual-consumption data.
Fig. 1.
Number of injections earned as a function of unit price, normalized to maximum consumption within-subject such that drug intake is calculated as the percent of maximum. Curves are fit to the data using Equation 5
Table 1.
Obtained essential value (α) of remifentanil, cocaine, and ketamine, and average overall variance accounted for (R2) by the exponential demand function
| Drug | alpha (α) FR | R2 |
|---|---|---|
| Remifentanil | 2.50 e-04 | 0.957 |
| Cocaine | 3.14 e-04 | 0.929 |
| Ketamine | 8.77 e-04 | 0.975 |
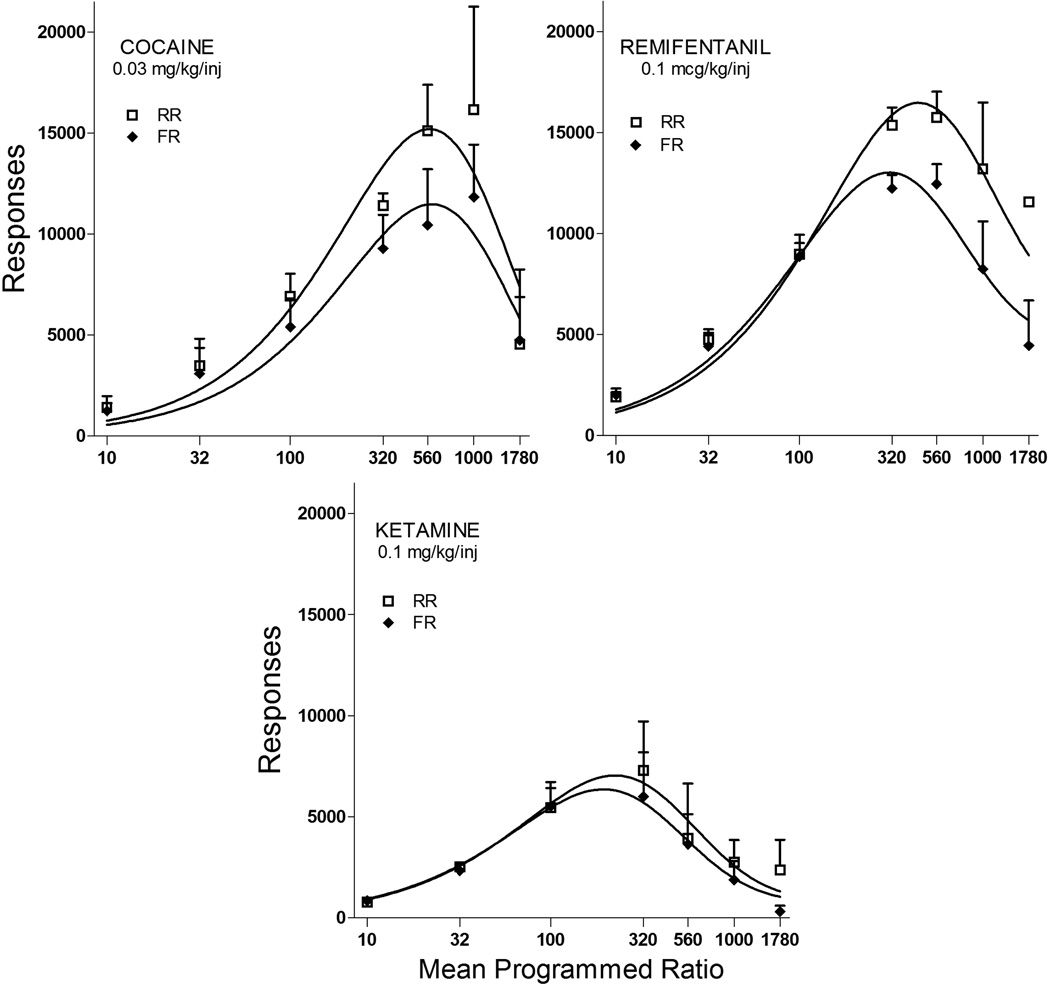
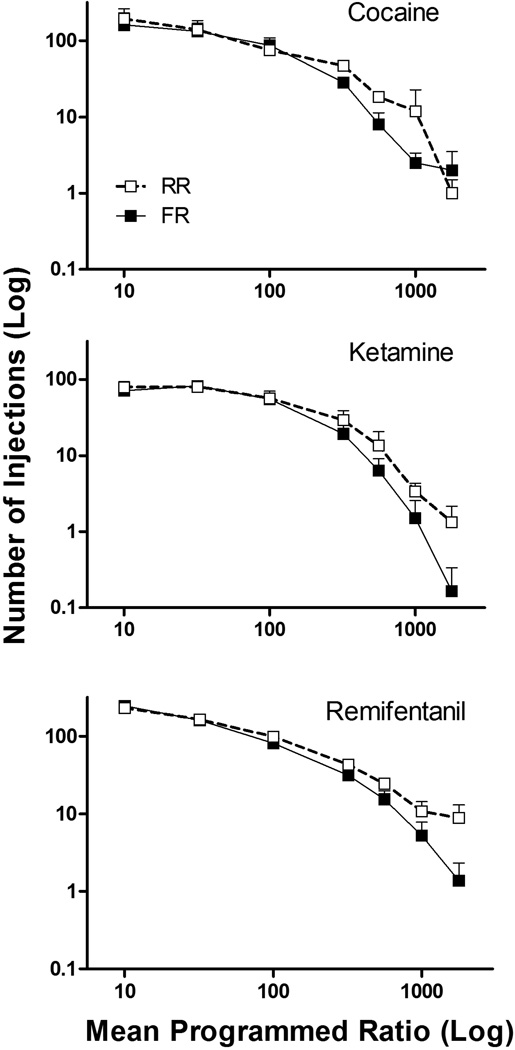
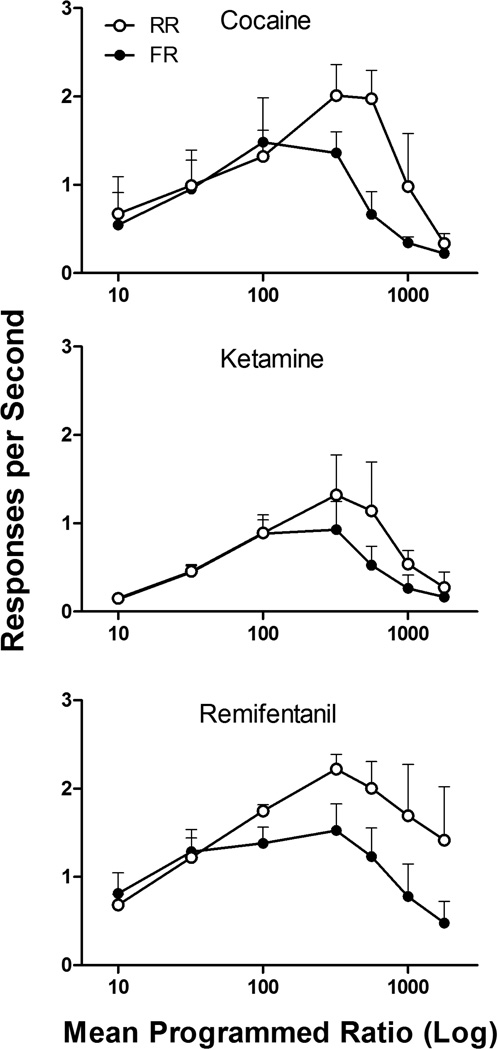
Figure 2 displays response output functions for both the FR and RR conditions when cocaine (upper left), remifentanil (upper right), and ketamine (below) were available. As confirmed by the differences in the elasticities of the demand functions (as shown in Figure 1), remifentanil and cocaine maintained similar maximum response outputs, whereas those produced by ketamine were considerably lower. The variable response requirement produced more responses for all of these drugs; this difference was particularly pronounced when ratio values were higher. With remifentanil and ketamine, differences in FR and RR responding emerged at ratio values of 320; for cocaine, differences were observed at ratio values of 100. At higher ratio values, the two curves diverge with the RR schedule generating substantially more responding and higher levels of consumption (number of injections earned, Figure 3) for each drug. As can be seen, the difference in the amount of behavior controlled by random- as compared with fixed-ratio schedules was more robust in the case of cocaine and remifentanil than with ketamine. In addition, Figure 4 shows the rates of responding (responses per second) produced by the three drugs under the RR and FR schedule requirements. RR schedules generated higher rates of responding, and this effect was particularly pronounced at ratio values above 100.
Fig. 2.
Comparison of responses produced by random (open symbols) and fixed (closed symbols) ratio schedules as a function of the average programmed ratio requirement across the three drugs. Curves are fit to the data based on Equation 5. Error bars display the standard error across subjects
Fig. 3.
Consumption of the three drugs (number of injections earned) as a function of the average programmed ratio requirement under random (open symbols) and fixed (closed symbols) ratio schedules. Error bars display the standard error across subjects
Fig. 4.
Comparison of response rate (responses per second) produced by random (open symbols) and fixed (closed symbols) ratio schedules as a function of the average programmed ratio requirement across the three drugs. Error bars display the standard error across subjects
The ketamine determinations were conducted twice because our initial results did not show a consistent response pattern across subjects (i.e., one subject responded at a much higher rate when reinforcers were delivered on the RR schedule, while response rates for the other subjects were largely undifferentiated). The same pattern emerged upon replication, with one subject (a different monkey from the one showing the anomalous pattern in the first determination) displaying higher rates for ketamine delivered on the RR schedule and others displaying similar response outputs on both FR and RR schedules. Therefore, the data from both conditions are shown in aggregate in Figures 2 – 4. All other results were consistently demonstrated on an individual-subject level; therefore, results are displayed in aggregate with standard error measures presented in Figures 2 – 4.
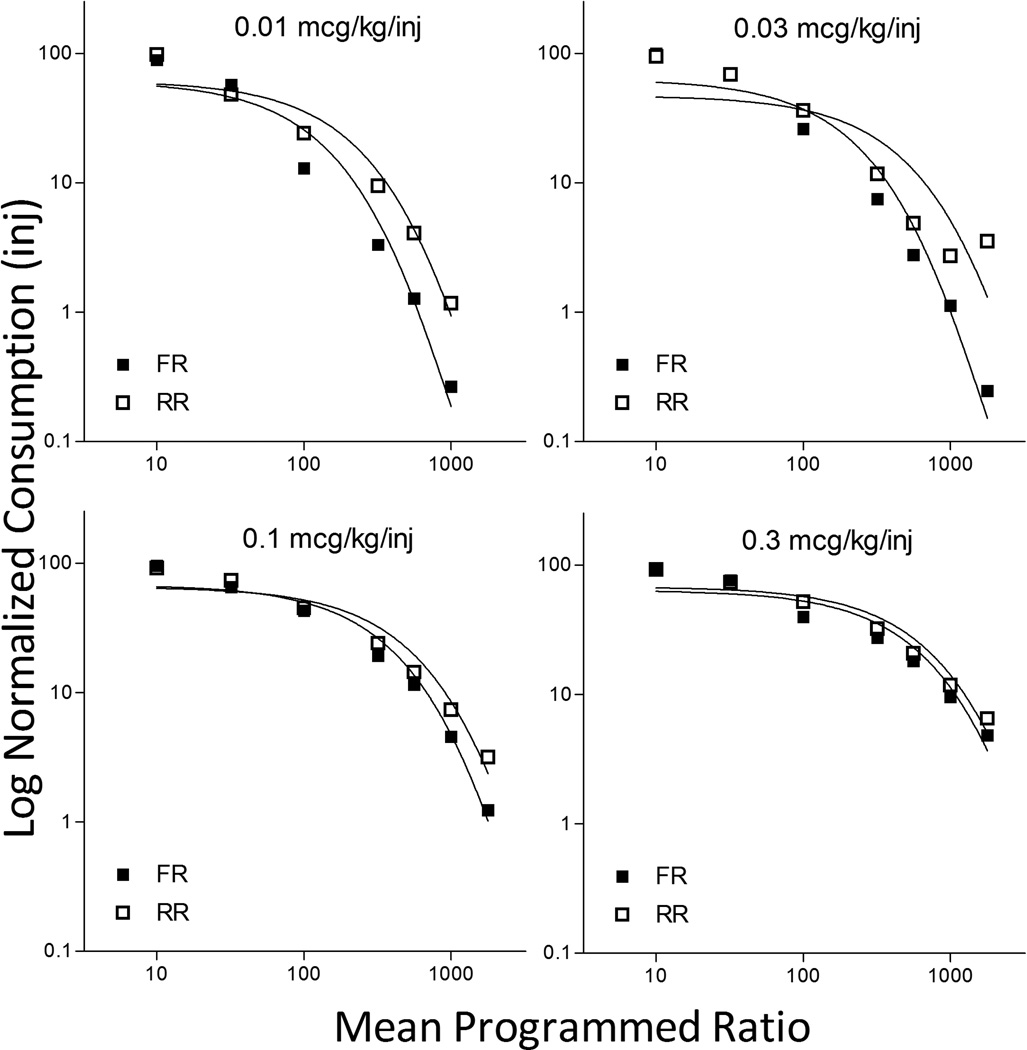
As noted above, differences in responding produced by the two schedule types were more pronounced when the unit price was high (i.e., when more than 100 responses were required to produce one injection). The fact that the current study utilized multiple drug doses permitted a more comprehensive analysis of the effect of unit price on schedule differences. Figure 5 shows this effect in greater detail, displaying the number of drug injections earned as a function of the response requirement during both FR and RR determinations for remifentanil – the drug showing most pronounced schedule differences. Individual panels display the different drug doses examined. The figure represents data from four monkeys, with the RR and FR determinations normalized within-subject such that the maximum number of injections earned by one subject on either schedule is set at 100 (considering that the RR and FR schedules did not induce reliably distinct results at the lowest ratio, normalizing in this fashion did not alter the curves but instead permitted a better way to compare data from several subjects that may have differed in basal rates of drug intake). As can be seen, differences in responding under the FR and RR schedules are not only more pronounced when the ratio value (work requirement) is higher, but also when the drug dose is lower. When the drug was relatively inexpensive (either available at a low ratio requirement or at a higher dose) subjects emitted similar numbers of responses irrespective of the schedule type; however, when drug access was more expensive the random schedule supported higher amounts and rates of behavior. The data displayed in Figure 5 confirm not only that RR schedules generate more responding at high ratio requirements, but also that this effect is influenced by reinforcer quantity such that differences between the schedule types were all but eliminated when the drug dose was high (and, consequently, unit price was lower).
Fig. 5.
Normalized consumption of remifentanil as a function of programmed response ratio (x-axis) and drug dose (different panels). Open squares indicate injections earned under RR conditions; closed under FR conditions. Data are normalized within subject to the maximum number of injections earned when exposed to the lowest ratio (10) in either RR or FR conditions
Discussion
The demand curve analyses of these data support earlier findings that cocaine and remifentanil have nearly equal reinforcing value, which is higher than that of ketamine (Hursh and Winger, 1995). These data also demonstrate that more responses are generated by rhesus monkeys when random-ratio, as compared with fixed-ratio schedules of reinforcement are used to maintain responding, and this difference is greatest when drugs are available at higher unit prices (either at high ratio requirements or low drug doses).
The finding that RR schedules generate greater drug demand at high unit prices expands and generalizes similar results reported byMadden et al. (2005). These investigators used food as a reinforcer in pigeon subjects that were responding under closed-economic conditions (i.e., their entire daily food intake was earned during experimental sessions). They established demand functions for the two schedule types and determined that reinforcers delivered under a variable schedule were more highly valued (i.e., had a lower calculated α value) than reinforcers delivered under a fixed schedule. This preference has been attributed to the fact that reinforcers are occasionally delivered more immediately under variable schedules – there is the possibility of receiving a reinforcer after only a few responses/seconds (Madden et al. 2008). Since it has been readily established that reinforcers lose their value hyperbolically when delayed in the future (e.g., Mazur, 1984), those reinforcers that are delivered after few responses in a variable schedule have considerably more value than those that are delivered after many responses (even when the average payoff is held constant). This hyperbolic discounting of delayed outcomes could account for how the same drugs can maintain higher response rates and higher essential value when delivered after a random number of responses.Madden et al. (2005) extended this analysis and suggested that unit price (when used in obtaining demand functions) may be appropriately modified by dividing it by the value of the reinforcer as obtained by the hyperbolic discounting function (Mazur 1984). When Madden et al. (2005) calculated their demand curves using this measure of price, the difference between consumption under variable and fixed schedules disappeared.
Despite how reinforcer immediacy appears to account for why pigeons in theMadden et al. (2005) study responded faster when reinforcers were presented on a random schedule, not every experiment in the literature confirms reinforcer immediacy as the sole mechanism. For example,Andrzejewski et al. (2005) and Soreth and Hineline (2009) exposed pigeons to choices between random- and fixed-interval schedules, where choosing the random schedule always produced a longer delay to reinforcement than the fixed schedule. They found that the birds did not demonstrate a predicted (and theoretically appropriate) preference for the fixed schedule (with its shorter delay to reinforcement), but responded as much as 50% of the time on the random-interval option. Furthermore, a possible “preference for variability” agrees with neurochemical findings that unpredictable reinforcer deliveries produce greater dopamine release in the ventral striatum than do expected reinforcer deliveries (Schultz 2011). Dopamine release also correlates with delay to reinforcement (Kobayashi and Schultz 2008) suggesting that delays to reinforcer deliveries and unpredictable (variable) reinforcer deliveries are two potentially separable factors that may impact reinforcer value.
In general, ketamine-maintained responding appeared less affected by the RR schedule as compared with behavior maintained by cocaine or remifentanil. However, two monkeys showed instances of extremely high rates of responding on one of two occasions when their behavior was maintained by 0.1 mg/kg/inj ketamine under a high RR schedule (RR 1780). We have not seen any examples of very high rates of ketamine-maintained responding under FR schedules in the years that we have studied this drug (e.g., Winger et al. 2002; Broadbear et al. 2004) This effect mirrors that seen with cocaine and remifentanil when reinforcers were delivered after a random number of responses at high unit prices. With the exception of these observations, however, demand for ketamine was less influenced by the random schedule than was that for cocaine and remifentanil. It is possible that, since demand for ketamine is more elastic (it is a relatively lower-valued commodity), responding is not well-maintained at the high prices necessary for differences between the RR and FR schedules to emerge. Future work could assess how differently-valued reinforcer types may influence the degree of preference for variably arranged outcomes.
Taken as a whole, the experiment described herein indicates that various drugs of abuse will generate more responding when they are delivered on a random as compared to a fixed response schedule. When the amount of responding necessary to produce a valued drug dose is substantial (i.e., the unit price high), the variable nature of the schedule generates considerably more responding. The fact that drugs delivered on variable schedules may periodically be acquired after periods of very brief delays may account for the increase in reinforcer value that is seen. If this information can be translated to the situation of drug abuse-related behavior in humans, it may imply that when an abuser is unsure of some aspects of drug acquisition such as the price required, the quality of the drug purchased, or the amount of time needed to wait before a drug can be used, then drug-procurement behaviors will be increased and occur at a higher rate. The uncertainty is unlikely to account entirely for the excessive nature of drug-associated behavior in addicted individuals, but it may contribute to it.
Acknowledgements
This work was supported by PHS DA023992 to GW and T32 DA007268 to CL. The excellent technical assistance of Angela Lindsey, Matthew Zaks, Kathy Carey Zelenock, and Yong Gong Shi is gratefully acknowledged.
Footnotes
The authors have no conflict of interest to declare.
Contributor Information
Carla H. Lagorio, Department of Psychology, University of Wisconsin-Eau Claire, Eau Claire, WI 54702, USA, lagorich@uwec.edu, Telephone: 715-836-5487, Fax: 715-836-2214
Gail Winger, Department of Pharmacology, University of Michigan, Ann Arbor, MI 48109, USA.
References
- Andrzejewski ME, Cardinal CD, Field DP, Flannery BA, Johnson M, Bailey K, Hineline PN. Pigeons’ choices between fixed and variable interval schedules: Utility of variability. J Exp Anal Behav. 2005;83:129–145. doi: 10.1901/jeab.2005.30-04. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bancroft SL, Bourret JC. Generating variable and random schedules of reinforcement using Microsoft Excel macros. J Appl Behav Anal. 2008;41:227–235. doi: 10.1901/jaba.2008.41-227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Broadbear JH, Winger G, Woods JH. Self-administration of fentanyl, cocaine and ketamine: effects on the pituitary-adrenal axis in rhesus monkeys. Psychopharmacology (Berl) 2004;176:398–406. doi: 10.1007/s00213-004-1891-x. [DOI] [PubMed] [Google Scholar]
- Cicerone RA. Preference for mixed versus constant delay of reinforcement. J Exp Anal Behav. 1976;25:257–261. doi: 10.1901/jeab.1976.25-257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davison MC. Preference for mixed-interval versus fixed-interval schedules: Number of component intervals. J Exp Anal Behav. 1972;17:169–176. doi: 10.1901/jeab.1972.17-169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fantino E. Preference for mixed-versus fixed ratio schedules. J Exp Anal Behav. 1967;10:35–43. doi: 10.1901/jeab.1967.10-35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fantino E, Arbaraca N, Ito M. Choice and optimal foraging: Tests of the delay reduction hypothesis and the optimal diet model. In: Commons ML, Kacelnik A, Shettleworth SJ, editors. Foraging. Quantitative analyses of behavior Erlbaum. Hillsdale, NJ: Lawrence Erlbaum Associates; 1987. [Google Scholar]
- Ferster CB, Skinner BF. Schedules of Reinforcement. Englewood Cliffs, NJ: Prentice-Hall; 1957. [Google Scholar]
- Herrnstein RJ. Aperiodicity as a factor in choice. J Exp Anal Behav. 1964;7:179–182. doi: 10.1901/jeab.1964.7-179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hursh SR. Economic concepts for the analysis of behavior. J Exp Anal Behav. 1980;34:219–238. doi: 10.1901/jeab.1980.34-219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hursh SR. A cost-benefit analysis of demand for food. J Exp Anal Behav. 1988;50:419–440. doi: 10.1901/jeab.1988.50-419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hursh SR, Fantino E. Relative delay of reinforcement and choice. J Exp Anal Behav. 1973;19:437–450. doi: 10.1901/jeab.1973.19-437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hursh SR, Silberberg A. Economic demand and essential value. Psychol Rev. 2008;115:186–198. doi: 10.1037/0033-295X.115.1.186. [DOI] [PubMed] [Google Scholar]
- Hursh SR, Winger G. Normalized demand for drugs and other reinforcers. J Exp Anal Behav. 1995;64:373–384. doi: 10.1901/jeab.1995.64-373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kobayashi S, Schultz W. Influence of reward delays on responses of dopamine neurons. J Neurosci. 2008;28:7837–7846. doi: 10.1523/JNEUROSCI.1600-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lagorio CH, Hackenberg TD. Risky choice in pigeons and humans: A cross species comparison. J Exp Anal Behav. 2010;93:27–44. doi: 10.1901/jeab.2010.93-27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lagorio CH, Hackenberg TD. Risky choice in pigeons: Preference for amount variability using a tokenreinforcement system. J Exp Anal Behav. 2012;98:139–154. doi: 10.1901/jeab.2012.98-139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logan FA. Decision making by rats: uncertain outcome choices. J Comp and Physiol Psych. 1965;59:272–251. doi: 10.1037/h0021850. [DOI] [PubMed] [Google Scholar]
- Madden GJ, Dake JM, Mauel EC, Rowe RR. Labor supply and consumption of food in a closed economy under a range of fixed- and random-ratio schedules: Tests of unit price. J Exp Anal Behav. 2005;83:99–118. doi: 10.1901/jeab.2005.32-04. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madden GJ, Ewan EE, Lagorio CH. Toward an animal model of gambling: Delay discounting and the allure of unpredictable outcomes. J Gambl Stud. 2007;23:63–83. doi: 10.1007/s10899-006-9041-5. [DOI] [PubMed] [Google Scholar]
- Mazur JE. Tests of an equivalence rule for fixed and variable reinforcer delays. J Exp Psych: Animal Behav Pro. 1984;10:426–436. [Google Scholar]
- Mazur JE. Risky choice: Selecting between certain and uncertain outcomes. Behav Anal Today. 2004;5:190–203. [Google Scholar]
- McElroy SL, Keck PE, Jr, Pope HG, Jr, Smith JM, Strakowski SM. Compulsive buying: A report of 20 cases. J Clin Psych. 1994;55:242–248. [PubMed] [Google Scholar]
- Schultz W. Risky dopamine. Biol Psychiatry. 2012;71:180–181. doi: 10.1016/j.biopsych.2011.11.019. [DOI] [PubMed] [Google Scholar]
- Skinner BF. Science and Human Behavior. New York: Macmillan; 1953. [Google Scholar]
- Soreth ME, Hineline PN. The probability of small schedule values and preference for random-interval schedules. J Exp Anal Behav. 2009;91:89–103. doi: 10.1901/jeab.2009.91-89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winger G, Hursh SR, Casey KL, Woods JH. Relative reinforcing strength of three N-methyl-D-aspartate antagonists with different onsets of action. J Pharmacol Exp Ther. 2002;301:690–697. doi: 10.1124/jpet.301.2.690. [DOI] [PubMed] [Google Scholar]
- Zeiler MD. Zeiler MD, Harzem P. Advances in analysis of behaviour: Reinforcement and the organization of behavior. Chichester, England: Wiley; 1979. Output dynamics. [Google Scholar]