Abstract
Purpose
MR histology based on magnetic susceptibility can be used to visualize diamagnetic myelin (and its deterioration) in the central nervous system and is facilitated by the application of high magnetic field strengths and paramagnetic contrast agents. Characterizing the effect of these tools will aid in assessing white matter myelin content and microstructure.
Methods
Image data from six gadolinium-perfused mouse brain specimens were acquired at 2.0, 7.0, and 9.4 Tesla. Magnetic susceptibility contrast was analyzed for its dependence on field strength, gadolinium concentration, and white matter fiber orientation. A model for this contrast is presented based on the three-pool model for white matter.
Results
The specimen data illustrate that white-gray matter susceptibility contrast is field strength independent. White-gray matter contrast improves significantly as a function of gadolinium contrast agent in the tissue—i.e., white matter appears increasingly more diamagnetic relative to gray matter. The simulated data from the model suggest that susceptibility anisotropy of white matter fiber bundles increases nonlinearly as a function of gadolinium concentration due to contrast agent compartmentalization into the extracellular white matter water pool.
Conclusion
Using contrast agents in MR histology facilitates white-gray matter susceptibility contrast modulation and the probing of white matter microstructure and orientation.
Keywords: Anisotropic magnetic susceptibility, Quantitative susceptibility mapping, Tissue compartmentalization, Resonance frequency shift, White matter, Nonlinear contrast enhancement
INTRODUCTION
Tissue-dependent magnetic susceptibility induces resonance frequency shifts that greatly affect gradient-echo MRI and are well defined for many biological substrates. One biological tissue feature of particular interest is the myelin sheath surrounding white matter (WM) axons in the central nervous system. Myelin is a weakly diamagnetic substance and thus experiences a reduced Larmour frequency when placed in an external magnetic field. This frequency shift can be visualized using phase information acquired during gradient-recalled echo MRI. It also aids in the delineation and assessment of myelination in WM brain regions (1–3). However, using the phase of MR images as a contrast mechanism has key limitations that spawn from the fact that image phase is only a convoluted representation of tissue susceptibility differences. For instance, phase contrast is both a non-local and orientation-dependent property—making it very difficult to reliably reproduce.
As a result, much effort has been put into quantitative susceptibility mapping (QSM), which produces a unique form of MRI contrast that directly reflects a scanned tissue’s magnetic susceptibility. Magnetic susceptibility maps have excellent contrast-to-noise ratio, and can be used to visualize para- and diamagnetic tissues better than more traditional MRI contrast mechanisms (4). For example, QSM shows the reduced magnetic susceptibility contrast of demyelinated WM (5), a form of abnormal myelination that is the hallmark of a number of neurodegenerative diseases and developmental disorders (6,7). In the future, QSM may allow radiologists to detect demyelination in the human brain during the early stages of neurodegenerative disease.
Recent discoveries in brain MRI have facilitated using QSM as a tool for probing WM microstructure. First, WM is composed of multiple signal pools, each exhibiting unique relaxation properties that vary according to field strength (8,9) and may have an effect on magnetic susceptibility contrast. Second, lipid chains that form the lipid bilayer of the myelin sheath are magnetically anisotropic, meaning that the orientation of the scanned tissue affects the observed magnetic susceptibility (10). Third, several methods have been applied specifically to susceptibility mapping of the brain to solve the ill-posed problem of inverting the relationship between magnetic susceptibility and image phase (11–14). Fourth, magnetic susceptibility contrast in brain tissue is strongly affected by the presence of iron as well as gadolinium (Gd) and other MR contrast agents, especially at high magnetic field strengths. The effect of Gd perfusion on magnitude images of the mouse brain has been previously explored (15,16), as has the effect of iron and Gd concentrations on R2* contrast at magnetic field strengths up to 7.0 T (17,18). However, far less work has been done to characterize the effect of paramagnetic contrast agents and field strength on the apparent magnetic susceptibility of tissues.
In this study, gradient-recalled echo images were acquired of Gd-perfused mouse brain specimens at multiple field strengths. Despite the field-variant relaxation of multiple WM water pools, it is found that the apparent susceptibility of myelinated WM regions relative to gray matter (GM) in the ex vivo mouse brain remains field invariant as would have been expected for uniform susceptibility materials. However, the nonuniform distribution of Gd within complex WM microstructure enhances susceptibility contrast between WM and GM (hereafter referred to as WM-GM contrast). Counter intuitively, WM becomes significantly more diamagnetic relative to GM with the latter maintaining an apparent magnetic susceptibility value near zero regardless of gadolinium concentration. Finally, an explanatory model is constructed to characterize WM orientation-dependent susceptibility contrast at various concentrations of Gd. These results suggest that WM-GM susceptibility contrast is 1) intrinsically tied to the orientation and compartmental nature of the underlying WM tissue microstructure and 2) substantially enhanced by Gd, making contrast agents critical tools in susceptibility contrast MR histology.
METHODS
Animal Model
All animal preparation protocols were approved by the Duke University Institutional Animal Care and Use Committee. Six adult, male C57BL/6 mice (Charles River Labs, Durham, NC) were anesthetized with Nembutal. The mice were perfused with a peristaltic pump first with 0.9% saline and then a mixture one of six different concentrations (0, 10, 20, 30, 40, and 50 mM) of Gd-HP-DO3A (ProHance; Bracco Diagnostics, Princeton, NJ) in 10% buffered formalin (Buffered Formalde-Fresh; Fisher Scientific, Hampton, NH) according to the “active staining” procedure detailed by Johnson et al. (15). The heads of the mice were removed with the brain intact and stored for 24 hours in 10% buffered formalin. The brain specimens were then washed to remove excess formalin, and stored in one of six different solutions of Gd (0, 0.5, 1.0, 1.5, 2.0, and 2.5 mM) in phosphate-buffered saline, corresponding proportionally to the Gd concentration used during perfusion. The specimens were soaked in these solutions for 60 days prior to scanning. For the diffusion tensor data acquisition, an additional male C57BL/6 mouse brain specimen was prepared using the same protocol (19). Both the perfusion and soaking solutions for this specimen had a Gd-HP-D03A concentration of 50 mM.
MR Microscopy
Each specimen was firmly affixed in an 11-mm polyethylene tube filled with Fomblin (fluoropolyether; Ausimont, Inc., Morristown, NJ) to provide a dark background in the images and mitigate tissue dehydration and susceptibility distortions at the specimen surface. MR experiments were performed using three different magnets: 2T (85 MHz) 30-cm horizontal bore Oxford magnet with shielded gradients of 400 mT/m; 7T (300 MHz) 21-cm horizontal bore Magnex magnet with shielded gradients of 770 mT/m; and 9.4T (400 MHz) 8.9-cm vertical bore Oxford magnet with shielded gradients of 2200 mT/m. All three systems were controlled by GE EXCITE MRI consoles similar to those used in the clinical domain. Data were acquired using three different solenoid coils of the same diameter, each tuned to the frequency of one of the three corresponding magnets.
Specimens were scanned with the long axis of the mouse brain oriented perpendicular to the main magnetic field direction using a 3-D spoiled-gradient-recalled sequence with multi-echo acquisition and the following scan parameters: field of view = 22×11×11 mm3, array = 256×128×128 for 86-μm isotropic resolution, echo train length = 10, first echo time (TE)= 5 ms, echo spacing = 2.9 ms, pulse repetition time (TR) = 500 ms, flip angle = 90°. A sequence with multi-echo acquisition was selected to facilitate the simultaneous acquisition of T2* relaxation data. Total acquisition time for each scan was 136 minutes. Four signal averages were acquired at 2.0 T (compared to only one at 7.0 T and 9.4 T) in order to achieve adequate SNR for comparison with the images acquired at higher fields. The same scan parameters were used for each acquisition to maintain a consistent imaging protocol, even though the field strength and contrast agent concentration varied for each scan. One diffusion tensor image dataset was collected from the additional mouse brain specimen at 9.4 T using the following scan parameters: field of view = 22×11×11 mm3, array = 512×256×256 for 43–μm isotropic resolution, TE= 11.8 ms, TR = 100 ms, one spin-echo scan with b = 0 s/mm2, and 6 diffusion-encoded spin-echo scans with b = 1600 s/mm2. The data were originally acquired during a study by Jiang and Johnson (19).
MR Image Reconstruction and Analysis
All image reconstruction and analytical calculations were performed in Matlab (MathWorks Inc., Natick, MA). The complex-valued image data were used to calculate phase images and a binary mask to extract the brain tissue voxels from the skull. Brain tissue structures were segmented using the three-dimensional region of interest (ROI) labels from the Waxholm Space mouse brain atlas (20). These labels were linearly registered to each data set using FSL-FLIRT (21) and then manually corrected with the ITK-SNAP software (22) using magnitude images. Registering the labels to the image volumes (and not vice versa) ensured that the original data from each specimen did not undergo any interpolation and gave the most accurate voxel-wise representation of the desired brain structures. Only the first echo image (TE = 5 ms) was used to calculate tissue susceptibility due to the time-dependent nature of susceptibility-based contrasts (23). For each data set, the phase image was unwrapped using a Laplacian operator (13). The background phase was then removed using the spherical mean value method with a filter radius of 30 (24). A susceptibility map was then calculated using the “weighted k-space derivative” and “orthogonal and right triangular decomposition” methods (13,25) to invert the susceptibility-frequency relationship (26). Because susceptibility measures are relative, WM susceptibility values are often compared to a reference that is established by the mean susceptibility value of nearby GM (5), cerebrospinal fluid (13), or one or more regions of WM (1,27,28). In the current study, tissue susceptibility values were evaluated relative to GM since the mean susceptibility of GM tissue in each of the 18 datasets was consistently near zero ppb. Additionally, the effective transverse relaxation rate (R2*) was calculated from the multi-echo image data for each concentration and field using a least squares regression model with SNR weighting because the signal of latter echoes diminished to nearly the level of the noise floor due to high relaxation. This calculation used only the odd-numbered images from the echo train to avoid the potential confounding effects between echoes formed by positive and negative read gradients.
Mean magnetic susceptibility and R2* were calculated for three WM structures (anterior commissure, corpus callosum, and hippocampal commissure), two GM structures (neocortex and thalamus), and the ventricles using a fair, voxel-wise comparison between each of the 18 image volumes (6 contrast agent concentrations and 3 field strengths). Linear regression models were fit to the data to model the mean magnetic susceptibility and R2* in each tissue structure as a function of Gd concentration at each field strength (29).
A voxelwise analysis was performed to relate the magnetic susceptibility data to WM fiber angle in the anterior commissure (AC) WM tissue region for each individual specimen. Fiber angle maps were generated by computing the angle between the magnetic field vector and the fiber orientation vector, represented by the major eigenvector of the diffusion tensor image data set. Similar to the Waxholm Space ROI labels, the fiber orientation data were also registered to each individual data set. Only voxels with an effective fractional anisotropy above 0.9 were examined to ensure that the results included data exclusively from myelinated WM. Using linear regression, mean WM-GM susceptibility contrast as a function of WM fiber bundle orientation was calculated for each individual specimen. Finally, a two-parameter linear regression was performed to approximate susceptibility contrast as a function of both WM orientation and Gd concentration.
Model Formulation
Using literature-based values for microstructural properties (Table 1), a model was developed to describe WM-GM susceptibility contrast in the AC of the rodent brain. This model explores the effect of both the contrast agent concentration used during perfusion and WM fiber orientation on the apparent magnetic susceptibility contrast in brain tissue. The WM fiber model adopted here represents the myelin sheath as an infinite hollow cylinder oriented at an angle, θ , to the direction of the static field (Ĥ). The cylinder divides the volume into three distinct water pools, each with its own signal contribution: the myelin-bound water pool, the axon water pool inside the myelin sheath, and the extracellular pool, all of which contribute to a signal magnitude, S, according to the equation,
Table 1.
Properties of white matter microstructure. The model microstructural parameters for predicting white-gray matter susceptibility contrast in the hippocampal commissure of the mouse brain are based on literature values. Standard deviation was provided in only a fraction of the studies referenced.
| Symbol | Definition | Model Values | Literature Values | Ref. |
|---|---|---|---|---|
| g-ratio | Axon-to- fiber ratio | 0.72 | 0.62 | (56)a |
| 0.72 ± 0.01 | (57)b | |||
| 0.80 | (58)b | |||
| FVF | Fiber volume fraction | 0.56 | 0.54 – 0.65 | (59)c |
| 0.59 | (60)d | |||
| 0.66 ± 0.08 | (61)b | |||
| MVF | Myelin volume fraction | 0.27 | 0.17 ± 0.01 | (56)a |
| 0.31 | (60)d | |||
| 0.41 – 0.47 | (61)b | |||
| ρax, ρmy, ρext | Relative spin density of water pools | 1, 0.50, 1 | 1, 0.50, 1 | (23) |
| 1, 0.54, 1 | (31) |
Mouse white matter
Mouse spinal cord
Rat sciatic nerve
Rat hippocampal commissure
| [1] |
where i denotes the index representing one of the three WM water pools. ρi and Vi are the relative spin density and the volume fraction of the ith water pool, respectively. These parameters are derived from literature values describing the geometry and signal contributions of each of these three pools (Table 1). These literature values include the axon-to-fiber ratio (g-ratio), fiber volume fraction (FVF), myelin volume fraction (MVF), and spin density (ρ) of the myelin sheath relative to the other two water pools (23,30,31). Table 2 gives the model relaxation parameters, T1 and T2* for each WM signal pool. These relaxation times were derived from 1) lab measurements, 2) studies examining relaxivity in brain tissues, and 3) the equations describing the linear effect of paramagnetic contrast agent on tissue relaxivity (29). Further details are given in the appendix. For simplicity, the model assumes that the effect of exchange is very small relative to the susceptibility properties of the tissue microstructure because 1) hollow fiber simulations performed by Wharton and Bowtell calculated best-fit exchange values that were relatively very small (23), and 2) slower exchange is expected when scanning specimens ex vivo.
Table 2.
Relaxation values in the three-pool model of white matter at each magnetic field strength. Ranges are given for extracellular white matter, where Gd has its greatest effect on relaxation, and for composite white matter. Each value or range of values represents the relaxation for specimens perfused with contrast agent concentrations ranging from 0 to 50 mM Gd. For the value ranges, longer relaxation rates correspond to the specimen perfused without Gd. The model values were derived from literature values, lab measurements, and relaxation theory. Details on the calculation of these values are in the appendix. Relaxation rates are given in milliseconds.
| B0 (T) | T1,myelin | T1,axon | T1,extracelluar | T1,WM | T2*,myelin | T2*,axon | T2*,extracellular | T2*,WM |
|---|---|---|---|---|---|---|---|---|
| 2.0 | 150 | 1600 | 12 – 646 | 22 – 521 | 10 | 66 | 19 – 54 | 21 – 34 |
| 7.0 | 242 | 2582 | 27 – 1042 | 50 – 840 | 9 | 59 | 7 – 49 | 11 – 31 |
| 9.4 | 271 | 2890 | 33 – 1166 | 60 – 940 | 7 | 45 | 6 – 37 | 8 – 24 |
A single myelinated axon with a fiber diameter of 1.69 μm was simulated in a 2×2×2 μm3 volume. The volume was divided into 128×128×128 voxel array—each voxel being assigned an absolute susceptibility tensor value based on the underlying WM fiber model microstructure:
| [2] |
| [3] |
| [4] |
Here, C is the Gd concentration used at perfusion, DWM,ext is a free parameter representing the fraction of extracellular WM that is occupied by Gd solution, χm,Gd is the molar susceptibility of Gd (32), and I is the identity matrix. The susceptibility tensor representing the magnetically anisotropic lipid chain in myelin, χmy, is the best-fit tensor calculated by Wharton and Bowtell (23) and yields susceptibility anisotropy, χ11 − (χ22 + χ33) / 2 = −180 ppb, which is consistent with the value estimated by Lounila et al. (33) for oriented lipids in lipoprotein shells (−223 ppb).
A frequency map for the model array was calculated using the tensor formulation of the susceptibility-phase equation in the subject frame of reference (34),
| [5] |
where θ is the image phase, γ is the gyromagnetic ratio for water proton, H0 is the amplitude of the applied magnetic field, t is the echo time, μ0 is the permittivity of free space, FT is the Fourier transform, FT-1 is the inverse Fourier transform, Ĥ is the unit vector of the applied magnetic field, T represents the transpose operation, χ is the second-order (rank-2) susceptibility tensor, and k is the spatial frequency vector. The frequency map was then used to generate complex signal data for each voxel. T1, T2*, and pool fraction weighting was applied according to the microstructural component of each voxel in the model. A complex average across the entire array yielded a complex-valued signal representative of the entire volume. Following the complex averaging of the array containing the WM axon model, it is not possible to differentiate the susceptibility contributions to this signal that are either internal or external to the axon, and thus an estimate of the bulk susceptibility of the model voxel is calculated using the theoretical relationship Δf / f0= χ/3 with the correction of spherical inclusion (35,36).
Finally, the following equations were incorporated into the model to simulate WM-GM susceptibility contrast (χWM-GM) and anisotropy (Δχmax):
| [6] |
| [7] |
| [8] |
Here, DGM is a free parameter representing the fraction of GM tissue volume (both intra- and extracellular) that is occupied by Gd solution , and χWM-GM(0°) and χWM-GM(90°) represent WM-GM susceptibility contrast when the voxel’s fiber orientations are parallel and perpendicular, respectively, to the magnetic field. The simulation was repeated for a range of Gd concentrations (0 – 50 mM) and WM fiber orientations (0 – 90°) with respect to Ĥ to produce a model of frequency and susceptibility values that were representative of the entire volume in each scenario.
RESULTS
Susceptibility Mapping of the Image Volumes
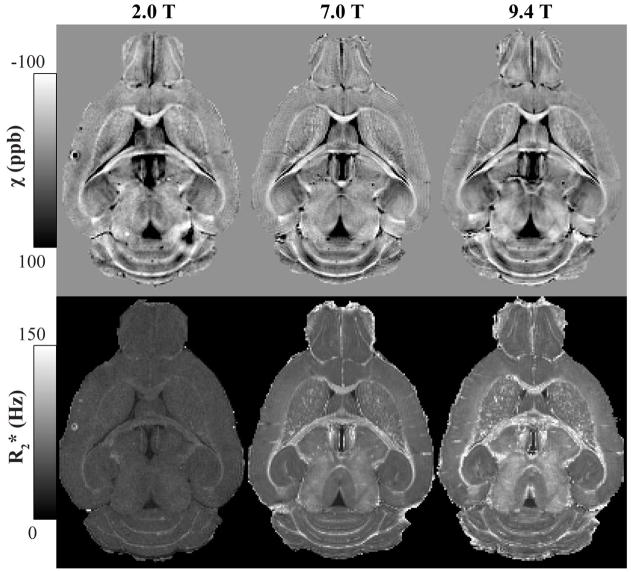
Fig. 1 shows the processed data for a typical image volume in the study (40 mM Gd specimen at 2.0, 7.0 and 9.4 T) from which mean susceptibility and R2* were calculated. Both contrasts effectively delineate WM regions within the brain. Fig. 2 shows the apparent magnetic susceptibility in two WM regions, the anterior commissure and the corpus callosum. The SNR of the averaged 2T image volumes was noticeably lower than the data acquired at high field but was still adequate for the purposes of this study. Though image quality improves with increasing field strength as expected, WM-GM contrast does not increase. There is, however, a clear increase in this contrast as the concentration of Gd in the specimen increases.
Figure 1.
Processed image data representing magnetic susceptibility (top row) and R2* (bottom row) for the mouse brain specimen perfused with 40 mM Gd-HP-DO3A solution and scanned at 2.0, 7.0 and 9.4 T. Image resolution is 3-D isotropic at 86 μm. The intensity scale of the susceptibility maps was inverted to represent diamagnetic regions (such as WM) with bright pixels and paramagnetic regions (such as the Gd-filled ventricles) as dark pixels. Both image contrasts clearly delineate white matter regions at this Gd concentration.
Figure 2.

Apparent magnetic susceptibility maps detailing two white matter brain regions: the A) anterior commissure and B) corpus callosum. Each row represents an individual specimen perfused with one of six concentrations of contrast agent, and each column corresponds to one of the three magnetic field strengths at which the specimens were scanned. White-gray matter susceptibility contrast is significantly enhanced as a function of Gd concentration and is field invariant.
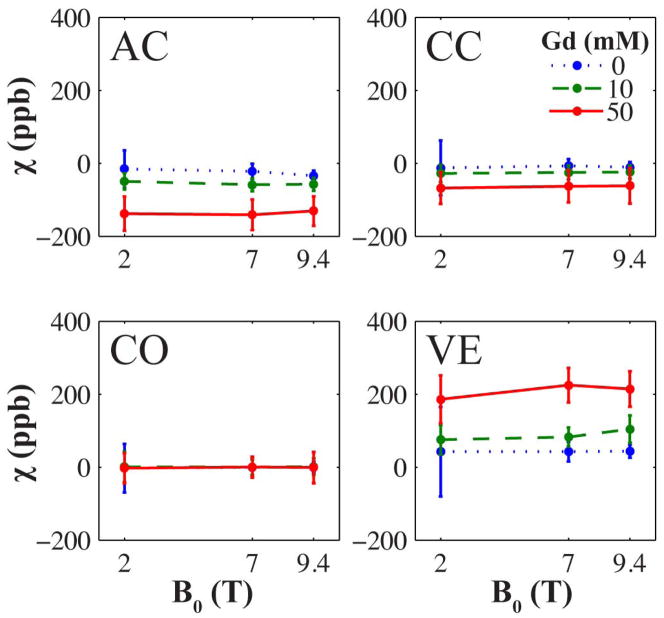
Field Invariance of Susceptibility Contrast
The mean susceptibility values of the six individual brain regions in each specimen were analyzed to verify the theoretical field independence of apparent magnetic susceptibility. Results for three Gd concentrations are displayed for four brain regions in Fig. 3. As H0 increases, the apparent magnetic susceptibility in each of the six brain regions is relatively unaffected. A Pearson linear correlation test revealed that for each of the six specimens, the mean susceptibility value and magnetic field strength are not significantly correlated at the α = 0.05 level of significance, with the exception of the anterior commissure in the specimen perfused with 20 mM Gd solution.
Figure 3.
Mean apparent magnetic susceptibility as a function of magnetic field strength in mouse specimens perfused with three different concentrations of Gd contrast agent (0, 10, and 50 mM). The brain regions shown are the anterior commissure white matter (AC), corpus callosum white matter (CC), cortical gray matter (CO), and ventricles (VE). Error bars represent the standard deviation. The empirical field invariance shown here agrees with magnetic susceptibility imaging theory. Magnetic susceptibility in the cortex appears unaffected by Gd concentration because the radiofrequency pulse is tuned to the frequency of brain specimens composed of mostly gray matter.
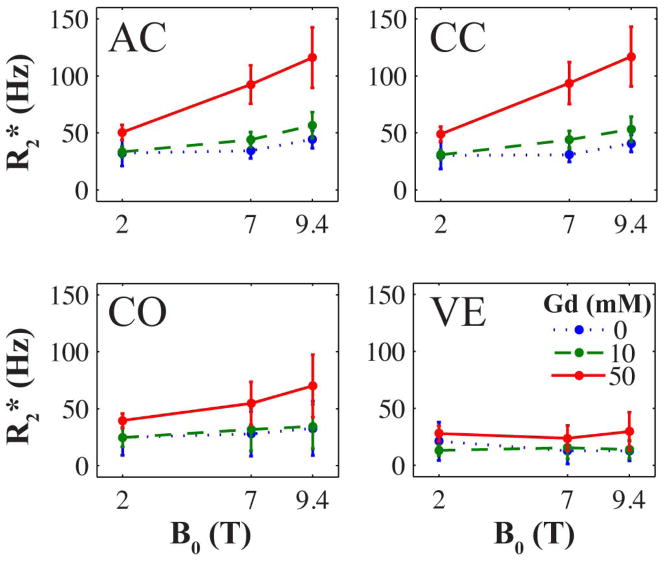
Nonlinear Effect of Magnetic Field Strength on R2*
The mean R2* values from four of the six ROIs are shown in Fig. 4. The field-relaxivity relationships emphasize the super linear increase of R2* as a function of H0. A Pearson test revealed that the linear correlations between relaxivity and field strength in each of the WM and GM regions were positive (β > 0.65). However, this correlation was only significant at the α = 0.05 level in some tissue regions of the 10 mM and 50 mM specimens. Since data was acquired at only three fields strengths— resulting in very few data points for each specimen—a lack of significance is not surprising.
Figure 4.
Mean R2* as a function of magnetic field strength. The brain regions shown are the anterior commissure white matter (AC), corpus callosum white matter (CC), cortical gray matter (CO), and ventricles (VE). Error bars represent the standard deviation. A super-linear increase is most apparent in white matter regions at low concentrations of Gd, which complicates the comparison of R2* contrast between studies performed at different field strengths.
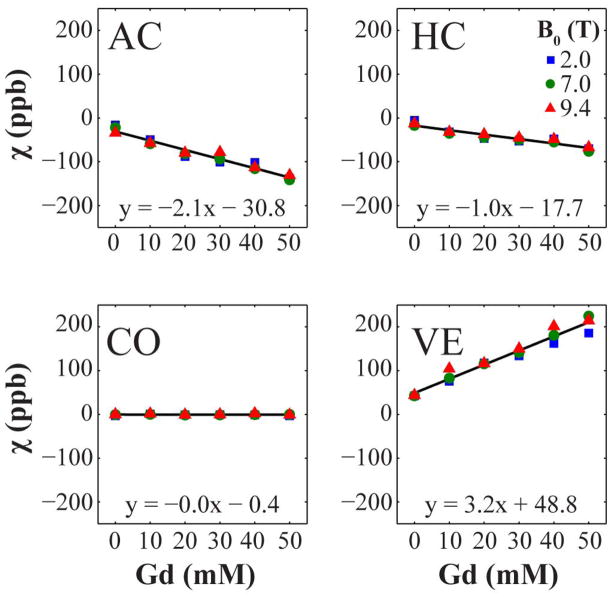
Effect of Contrast Agent on Susceptibility Contrast
Fig. 5 depicts the relationship between mean apparent magnetic susceptibility and Gd concentration in two WM regions, one GM region and the ventricles. With increased Gd staining, WM regions appear more diamagnetic, the ventricles appear more paramagnetic, and GM regions appear unchanged. Equations for the linear regression model are given on each chart to represent the region-wide average susceptibility dependence on Gd concentration.
Figure 5.
Region-wide mean apparent magnetic susceptibility as a function of Gd concentration at 2.0, 7.0, and 9.4 T. The brain regions shown are the anterior commissure white matter (AC), corpus callosum white matter (CC), cortical gray matter (CO), and ventricles (VE). The error bars have been omitted for clarity. The best-fit line and equation were created using least-squares regression on the combined data from all three field strengths. The apparently linear relationship in WM may be the result of averaging susceptibility values from all voxels in each tissue structure regardless of white matter fiber orientation.
Linear Effect of Contrast Agent on Increasing R2*
R2* increases linearly as a function of Gd concentration which is consistent with the observed linear change in apparent magnetic susceptibility contrast. A Pearson test revealed that the linear correlation between relaxivity and Gd is both positive (β > 0.9) and significant (P < 0.05) in all brain regions in this study. The one exception where the data are not significant is the ventricles at 2.0 T, which is the result of a noisy data point representing the specimen perfused without Gd.
Simulating Orientation Dependence Using a Predictive Model
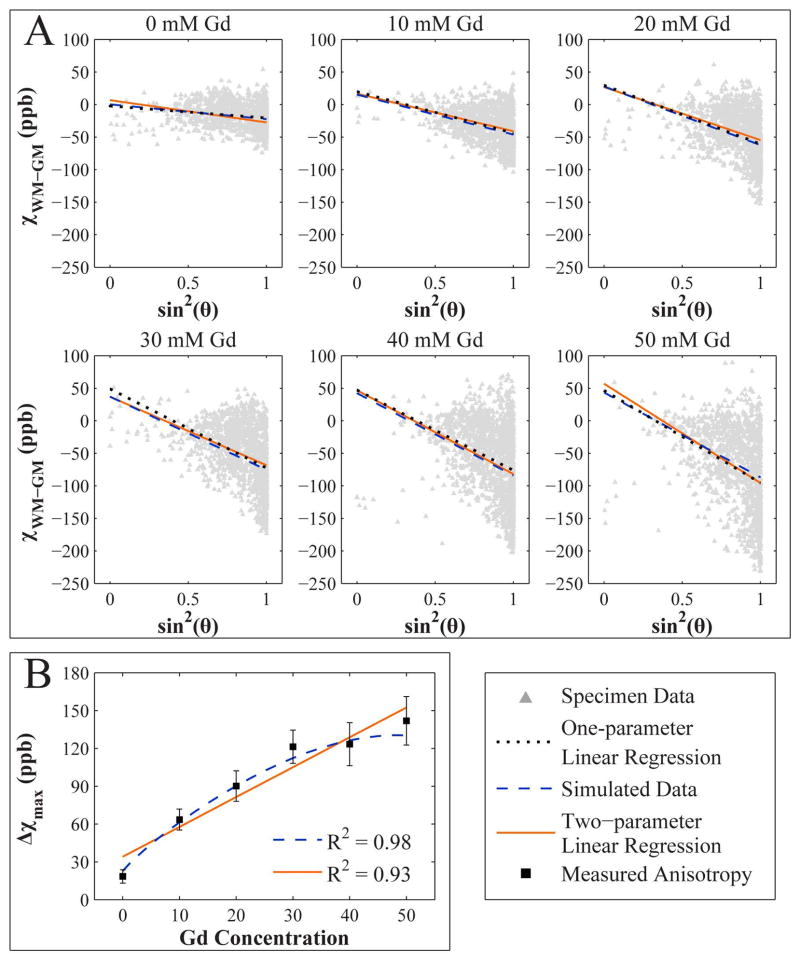
The simulated data from the three-pool WM axon model describing the relationship between WM-GM contrast and fiber orientation at each Gd concentration is shown in Fig. 6A along with the AC data acquired from the six specimens at 7.0 T. At each individual Gd concentration, the data are fit with a one-parameter linear regression model showing the linear relationship between susceptibility and sin2θ, which is in accordance with magnetic susceptibility theory. The variance of the WM-GM contrast as a function of Gd concentration likely increases as a result of the nonuniform distribution of Gd in brain tissue. In fitting the simulated hollow fiber model to the data, the free parameters DWM,ext and DGM were calculated to be 2.0×10−2 and 1.1×10−2 respectively. Fig. 6A also includes the results of the two-parameter linear regression fit, which approximates susceptibility as a function of both fiber angle and Gd concentration. The specimen scan orientation yielded data with a high proportion of WM fiber bundles forming large angles with the magnetic field direction. The data from both the specimen and the model simulation show perpendicular fibers as being more diamagnetic than parallel fibers—a result of the magnetic anisotropy of the lipid chains in the bilayer membrane of the myelin sheath.
Figure 6.
A) WM-GM susceptibility contrast dependence on white matter fiber orientation and Gd concentration at 7.0 T in the anterior commissure. Field-parallel fibers are sparsely represented in the image data due to the scan orientation of the specimens. For each specimen, one-parameter linear regression was used to find the mean susceptibility contrast as a function WM fiber orientation only. A two-parameter regression model was used to find mean susceptibility contrast as a function of both fiber orientation and Gd concentration. The simulated data was generated from the three-pool WM fiber model. B) WM susceptibility anisotropy as a function of Gd concentration in the anterior commissure. Susceptibility anisotropy is increased by more than six-fold at the highest Gd concentration used in this study. Both models are highly correlated with the measured anisotropy.
The susceptibility anisotropies of the specimen data, simulated data, and two-parameter linear regression fit are plotted as a function of Gd concentration in Fig. 6B. Both the simulated data and the linear regression trend are highly correlated with the measured anisotropy from the specimen data (R = 0.98 and 0.93, respectively). The hollow fiber simulation predicts a nonlinear enhancement of anisotropy as a function of Gd concentration and that increasing the Gd concentration eventually leads to less drastic increases in susceptibility anisotropy relative to the linear regression model (Fig. 6B).
DISCUSSION
High magnetic fields and chelated Gd contrast agents improve the effectiveness of susceptibility-based MR histology in both delineating myelinated WM and probing its microstructure. This study has demonstrated through an ex vivo small animal study that the apparent magnetic susceptibility of WM relative to GM is field invariant. Furthermore, Gd enhances WM-GM contrast and susceptibility anisotropy, which is likely due to differences between WM and GM microstructure.
Gd-Enhanced WM-GM Contrast
Magnetic susceptibility is a relative measure with respect to a predetermined frequency—typically the carrier frequency of the RF, which fluctuates due to field shimming, frequency drift, and the concentration of paramagnetic Gd in each specimen. In each of the scans in this study, the radiofrequency pulse was closely tuned to the average GM tissue frequency of each individual specimen. This is not surprising since it is estimated that the mouse brain is roughly three-quarters GM using tissue segmentation data from our lab that was derived from multiple MR image contrasts and a mouse brain atlas prior (20,37). As the Gd concentration in the specimen increases, GM tissue is expected to increase in absolute magnetic susceptibility, i.e., become more paramagnetic. This happens even though the data show that the apparent magnetic susceptibility remains unchanged at approximately 0 ppb (Fig. 5). Thus, this study focuses on susceptibility contrast, i.e., the apparent susceptibility of brain tissues relative to GM. For example, the relative WM-GM contrast is enhanced by the presence of Gd, even though the absolute susceptibility of both tissues should increase in theory.
We propose that the root cause of the increased WM-GM contrast is found in the complex WM tissue structure. Biological membranes, such as the myelin sheath in WM, prevent hydrophilic, high-molecular-weight molecules like Gd chelates (38) from entering the cell (39,40). With this in mind, the relative Gd content of WM and GM was calculated from the model’s fitted parameters, but the exact rate of Gd uptake in each tissue was not determined as has been done in muscle tissue injected intravenously with radiolabeled Gd (41). As a result of the compartmentalization of the contrast agent into extracellular WM, the model predicts that the ratio of Gd solution in WM relative to GM is (DWM,ext × (1 − FVF)) / DGM = 0.80. The relatively lower Gd content per unit volume of tissue and its compartmentalization in WM leads to the observed increased WM-GM susceptibility contrast. It is acknowledged that formalin and other fixatives can have an impact on the integrity of the myelin sheath following prolonged periods of tissue fixation. Though one study suggests that a 24-hour fixation period may be sufficient to compromise the normally Gd-impermeable myelin sheath (42), the chemical modification of lipids, such as those found in the bilayer membrane of myelin, and the formation of cross-links between neighboring proteins, which is the rate-limiting step for fixation, typically requires several weeks (43). After a brief period of immersion fixation, formalin can be effectively removed from tissue by rinsing the specimen (44,45). Due to the short fixation period and the subsequent long immersion in saline buffer of the specimens, this model for WM in the Gd-perfused mouse brain assumes that the myelin sheath remains mostly intact, resulting in contrast agent being compartmentalized into extracellular WM.
Gd-Enhanced Susceptibility Anisotropy
Mean WM-GM susceptibility contrast appears to increase linearly as a function of Gd concentration (Fig. 5). By contrast, when the orientation-dependent effects are isolated by plotting voxel susceptibility as a function of fiber orientation (Fig. 6A), the simulated data predict a nonlinear relationship between susceptibility anisotropy and Gd concentration (Fig. 6B), which appears to be consistent with experimental data. However, we do not have sufficient data to rule out linearity because of the single-orientation experiments we have conducted. As such, a two-parameter linear regression model is also provided for comparison.
The apparent macroscopic susceptibility anisotropy of WM tissue, Δχmax, is calculated from the parallel and perpendicular fiber susceptibility values (Eqn. [8]), that is, the absolute slope against sin2θ. For the specimen perfused without Gd, the macroscopic susceptibility anisotropy values were 18.5 ± 5.3 ppb for the specimen data, 22.7 ppb for the simulated data, and 34.0 ppb for the two-parameter linear regression model. These values agree reasonably with the finding, Δχmax = 26 ppb, by Li et al (10). The simulated data show that susceptibility anisotropy is enhanced roughly six-fold by high (50 mM) perfusion concentrations of Gd (Fig. 6B).
Similar to the nonlinear phase signal evolution of WM tissue as a function of echo time (23,46), nonlinear susceptibility anisotropy modulation as a function of Gd concentration may be due to WM signal contributions arising from multiple, distinct water pools, each with unique relaxation properties (47). Earlier studies have shown that compartmentalization of Gd-DTPA in the extracellular space of muscle tissue both in vivo and in vitro yields a significant T2 reduction in extracellular water but not bound water (41,48). The simulated data from the hollow fiber model suggest that Gd enhances anisotropy by suppressing the isotropic compartments due to the interaction between 1) the increased T2* relaxivity in the extracellular water pool and 2) the complex-valued averaging of the WM water pool signals. Further work in this area may include exploring the time-dependent nature of susceptibility contrast due to Gd contrast agents.
Technical Considerations
The specimen data contain mostly voxels with perpendicular WM fiber orientations due to the scan orientation convention used. This can significantly skew the mean susceptibility measurements as well as the two-parameter regression model. As a result, it is difficult to conclude whether or not the mean susceptibility anisotropy of the data increases nonlinearly. This could potentially be remedied by scanning the specimen at multiple orientations or at higher resolution to increase the number of voxels with more parallel fiber orientations.
The true Gd concentration at the local tissue is presumably much less than the concentration used during perfusion. To define the model WM and GM susceptibility tensors, it was necessary to estimate the extent to which the contrast agent solution was able to penetrate each brain tissue. Hence, both the parameters DGM in Eq. [6] and DWM,ext in Eq. [4] were approximated when fitting the model shape to the scan data and are not based on literature values. In contrast, the selected model parameters for MVF (0.27), FVF (0.56), and g-ratio (0.72) are based on both literature values in the rodent brain (Table 1) and the equation (30). Myelin water fraction is given by MVF × π = 0.135. Under the assumption that myelin water is almost entirely bound water, this calculated parameter is sensible with respect to the average bound water fraction of 0.10 ± 0.01 found by Ou et al. (49,50) in ex vivo mice using quantitative magnetic transfer measurements. This is entirely reasonable considering that formalin fixation has been shown to increase the macromolecular bound water fraction of WM tissue by as much as 50% (51).
An advantage of using QSM over R2* mapping as a susceptibility-based mechanism for WM-GM contrast is that magnetic susceptibility is field independent (Fig. 3), whereas R2* is not (Fig. 4). Earlier studies have shown that the field dependence of R2* in human GM (both in vivo and ex vivo) is approximately linear, but in WM there is evidence of a super-linear increase for magnetic fields ranging from 1.5 to 7.0 T (17,52). In contrast to the super linear increase of R2* as a function of H0, the field invariance of QSM allows for more relevant comparisons among data sets as small animal MRI progresses towards ever-higher field strengths. In the context of the three-pool model of white matter, the field-invariant nature of magnetic susceptibility suggests that the external field alters the relaxivity of one WM water pool in a similar fashion to the other two water pools. This is distinctly different from the changes to relaxivity induced by Gd, which occur almost exclusively in the extracellular water pool.
CONCLUSIONS
Aided by Gd and high magnetic field strengths, susceptibility contrast is extremely effective in visualizing myelinated WM in the brain. Magnetic susceptibility maps of the adult mouse brain verify that WM-GM susceptibility contrast, unlike R2*, is field invariant in spite of the multiple pool structure of WM. This allows for more useful comparisons between QSM studies at different field strengths. Data from both the specimen and the simulated hollow fiber model show that the fiber orientation, contrast agent compartmentalization, and multi-pool relaxation properties of WM produce enhanced WM-GM susceptibility contrast as well as susceptibility anisotropy that, surprisingly, may increase nonlinearly as a function of Gd contrast agent. The proposed model reasonably describes the effect of these microstructural factors on modulating susceptibility contrast. Future work to develop this model, including the analysis of relative signal evolution of WM water pools as a function of echo time, will aid in probing WM microstructural compartments and orientation.
Supplementary Material
Acknowledgments
We are grateful to G. Allan Johnson, PhD and Yi Qi, MD for their assistance in this study. All imaging was carried out at the Center for In Vivo Microscopy of Duke University. This study was supported in part by the National Institutes of Health (NIH) through NIBIB P41 EB015897, R01 MH096979, and NIBIB T32 EB001040, and by the National Multiple Sclerosis Society (RG4723).
APPENDIX
Formulation of model relaxation rates
Limited resources precluded the acquisition of T1 data for every image volume. Instead, previously acquired data from a C57BL/6 mouse brain prepared with a similar protocol (50 mM Gd) revealed WM T1 to be approximately 22 ms, 50 ms, and 60 ms at 2.0, 7.0, and 9.4 T respectively. Empirical T1-field relationships (53) were used to produce ballpark estimates for WM T1 at all field strengths for specimens perfused without Gd. WM T1 values were then estimated for specimens with intermediate Gd concentrations at each field strength, recognizing that Gd has a linearly proportional effect on tissue relaxation rates (29).
Model relaxation values were approximated for each water pool by incorporating the aforementioned whole-tissue relaxation estimates with the microstructure parameters given in Table 1 and tissue relaxation calculations from multi-pool models in the literature (8,9,23,31,47,54,55). This model for tissue relaxation assumes that the relaxation rate of WM is a weighted average of the individual WM water pool relaxation rates. The model T1 and T2* values in each WM water pool are given in the supporting information for each field strength and Gd concentration (Fig. S1 and Fig. S2, respectively).
References
- 1.Deistung A, Schafer A, Schweser F, Sommer K, Turner R. Assessment of brain anatomy with gradient-echo contrasts: a comparison between magnitude, phase, and R2* imaging with quantitative susceptibility mapping (QSM). 20th Annual Meeting of ISMRM; Melbourne, Australia. 2012. p. 416. [Google Scholar]
- 2.Lodygensky GA, Marques JP, Maddage R, Perroud E, Sizonenko SV, Hüppi PS, Gruetter R. In vivo assessment of myelination by phase imaging at high magnetic field. Neuroimage. 2012;59(3):1979–1987. doi: 10.1016/j.neuroimage.2011.09.057. [DOI] [PubMed] [Google Scholar]
- 3.Duyn JH. Study of brain anatomy with high-field MRI: recent progress. Magn Reson Imaging. 2010;28(8):1210–1215. doi: 10.1016/j.mri.2010.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Schafer A, Forstmann BU, Neumann J, Wharton S, Mietke A, Bowtell R, Turner R. Direct visualization of the subthalamic nucleus and its iron distribution using high-resolution susceptibility mapping. Hum Brain Mapp. 2012;33(12):2831–2842. doi: 10.1002/hbm.21404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Liu C, Li W, Johnson GA, Wu B. High-field (9. 4 T) MRI of brain dysmyelination by quantitative mapping of magnetic susceptibility. Neuroimage. 2011;56(3):930–938. doi: 10.1016/j.neuroimage.2011.02.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bitsch A, Schuchardt J, Bunkowski S, Kuhlmann T, Brück W. Acute axonal injury in multiple sclerosis. Correlation with demyelination and inflammation. Brain. 2000;123 ( Pt 6):1174–1183. doi: 10.1093/brain/123.6.1174. [DOI] [PubMed] [Google Scholar]
- 7.Martin R, McFarland HF, McFarlin DE. Immunological aspects of demyelinating diseases. Annu Rev Immunol. 1992;10:153–187. doi: 10.1146/annurev.iy.10.040192.001101. [DOI] [PubMed] [Google Scholar]
- 8.Lancaster JL, Andrews T, Hardies LJ, Dodd S, Fox PT. Three-pool model of white matter. J Magn Reson Imaging. 2003;17(1):1–10. doi: 10.1002/jmri.10230. [DOI] [PubMed] [Google Scholar]
- 9.Andrews T, Lancaster JL, Dodd SJ, Contreras-Sesvold C, Fox PT. Testing the three-pool white matter model adapted for use with T2 relaxometry. Magn Reson Med. 2005;54(2):449–454. doi: 10.1002/mrm.20599. [DOI] [PubMed] [Google Scholar]
- 10.Li W, Wu B, Avram AV, Liu C. Magnetic susceptibility anisotropy of human brain in vivo and its molecular underpinnings. Neuroimage. 2012;59(3):2088–2097. doi: 10.1016/j.neuroimage.2011.10.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Shmueli K, de Zwart JA, van Gelderen P, Li T-Q, Dodd SJ, Duyn JH. Magnetic susceptibility mapping of brain tissue in vivo using MRI phase data. Magn Reson Med. 2009;62(6):1510–1522. doi: 10.1002/mrm.22135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.de Rochefort L, Liu T, Kressler B, Liu J, Spincemaille P, Lebon V, Wu J, Wang Y. Quantitative susceptibility map reconstruction from MR phase data using bayesian regularization: validation and application to brain imaging. Magn Reson Med. 2010;63(1):194–206. doi: 10.1002/mrm.22187. [DOI] [PubMed] [Google Scholar]
- 13.Li W, Wu B, Liu C. Quantitative susceptibility mapping of human brain reflects spatial variation in tissue composition. Neuroimage. 2011;55(4):1645–1656. doi: 10.1016/j.neuroimage.2010.11.088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wu B, Li W, Guidon A, Liu C. Whole brain susceptibility mapping using compressed sensing. Magn Reson Med. 2012;67(1):137–147. doi: 10.1002/mrm.23000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Johnson GA, Cofer GP, Gewalt SL, Hedlund LW. Morphologic phenotyping with MR microscopy: the visible mouse. Radiology. 2002;222(3):789–793. doi: 10.1148/radiol.2223010531. [DOI] [PubMed] [Google Scholar]
- 16.Kim S, Pickup S, Hsu O, Poptani H. Enhanced delineation of white matter structures of the fixed mouse brain using Gd-DTPA in microscopic MRI. NMR Biomed. 2009;22(3):303–309. doi: 10.1002/nbm.1324. [DOI] [PubMed] [Google Scholar]
- 17.Yao B, Li T-Q, Gelderen Pv, Shmueli K, de Zwart JA, Duyn JH. Susceptibility contrast in high field MRI of human brain as a function of tissue iron content. Neuroimage. 2009;44(4):1259–1266. doi: 10.1016/j.neuroimage.2008.10.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Blockley NP, Jiang L, Gardener AG, Ludman CN, Francis ST, Gowland PA. Field strength dependence of R1 and R2* relaxivities of human whole blood to ProHance, Vasovist, and deoxyhemoglobin. Magn Reson Med. 2008;60(6):1313–1320. doi: 10.1002/mrm.21792. [DOI] [PubMed] [Google Scholar]
- 19.Jiang Y, Johnson GA. Microscopic diffusion tensor imaging of the mouse brain. Neuroimage. 2010;50(2):465–471. doi: 10.1016/j.neuroimage.2009.12.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Johnson GA, Badea A, Brandenburg J, Cofer G, Fubara B, Liu S, Nissanov J. Waxholm space: an image-based reference for coordinating mouse brain research. Neuroimage. 2010;53(2):365–372. doi: 10.1016/j.neuroimage.2010.06.067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Jenkinson M, Bannister P, Brady M, Smith S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. Neuroimage. 2002;17(2):825–841. doi: 10.1016/s1053-8119(02)91132-8. [DOI] [PubMed] [Google Scholar]
- 22.Yushkevich PA, Piven J, Hazlett HC, Smith RG, Ho S, Gee JC, Gerig G. User-guided 3D active contour segmentation of anatomical structures: significantly improved efficiency and reliability. Neuroimage. 2006;31(3):1116–1128. doi: 10.1016/j.neuroimage.2006.01.015. [DOI] [PubMed] [Google Scholar]
- 23.Wharton S, Bowtell R. Fiber orientation-dependent white matter contrast in gradient echo MRI. Proceedings of the National Academy of Sciences. 2012;109(45):18559–18564. doi: 10.1073/pnas.1211075109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Schweser F, Deistung A, Lehr BW, Reichenbach JR. Quantitative imaging of intrinsic magnetic tissue properties using MRI signal phase: an approach to in vivo brain iron metabolism? Neuroimage. 2011;54(4):2789–2807. doi: 10.1016/j.neuroimage.2010.10.070. [DOI] [PubMed] [Google Scholar]
- 25.Paige CC, Saunders MA. Algorithm 583: LSQR: Sparse Linear Equations and Least Squares Problems. ACM Trans Math Softw. 1982;8(2):195–209. doi: 10.1145/2527267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Salomir R, de Senneville BD, Moonen CTW. A fast calculation method for magnetic field inhomogeneity due to an arbitrary distribution of bulk susceptibility. Concepts in Magnetic Resonance Part B: Magnetic Resonance Engineering. 2003;19B(1):26–34. [Google Scholar]
- 27.Langkammer C, Krebs N, Goessler W, Scheurer E, Yen K, Fazekas F, Ropele S. Susceptibility induced gray-white matter MRI contrast in the human brain. Neuroimage. 2012;59(2):1413–1419. doi: 10.1016/j.neuroimage.2011.08.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bilgic B, Pfefferbaum A, Rohlfing T, Sullivan EV, Adalsteinsson E. MRI estimates of brain iron concentration in normal aging using quantitative susceptibility mapping. Neuroimage. 2012;59(3):2625–2635. doi: 10.1016/j.neuroimage.2011.08.077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hendrick RE, Haacke EM. Basic physics of MR contrast agents and maximization of image contrast. J Magn Reson Imaging. 1993;3(1):137–148. doi: 10.1002/jmri.1880030126. [DOI] [PubMed] [Google Scholar]
- 30.Stikov N, Perry LM, Mezer A, Rykhlevskaia E, Wandell BA, Pauly JM, Dougherty RF. Bound pool fractions complement diffusion measures to describe white matter micro and macrostructure. Neuroimage. 2011;54(2):1112–1121. doi: 10.1016/j.neuroimage.2010.08.068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Dula AN, Gochberg DF, Valentine HL, Valentine WM, Does MD. Multiexponential T2, magnetization transfer, and quantitative histology in white matter tracts of rat spinal cord. Magn Reson Med. 2010;63(4):902–909. doi: 10.1002/mrm.22267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Deistung A, Reichenbach JR. Susceptibility Weighted Imaging in MRI. John Wiley & Sons, Inc; 2011. Effects of Contrast Agents in Susceptibility Weighted Imaging; pp. 487–515. [Google Scholar]
- 33.Lounila J, Ala-Korpela M, Jokisaari J, Savolainen MJ, Kesäniemi YA. Effects of orientational order and particle size on the NMR line positions of lipoproteins. Phys Rev Lett. 1994;72(25):4049–4052. doi: 10.1103/PhysRevLett.72.4049. [DOI] [PubMed] [Google Scholar]
- 34.Liu C. Susceptibility tensor imaging. Magn Reson Med. 2010;63(6):1471–1477. doi: 10.1002/mrm.22482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Chu SC, Xu Y, Balschi JA, Springer CS. Bulk magnetic susceptibility shifts in NMR studies of compartmentalized samples: use of paramagnetic reagents. Magn Reson Med. 1990;13(2):239–262. doi: 10.1002/mrm.1910130207. [DOI] [PubMed] [Google Scholar]
- 36.Haacke EM, Cheng NYC, House MJ, Liu Q, Neelavalli J, Ogg RJ, Khan A, Ayaz M, Kirsch W, Obenaus A. Imaging iron stores in the brain using magnetic resonance imaging. Magnetic Resonance Imaging. 2005;23(1):1–25. doi: 10.1016/j.mri.2004.10.001. [DOI] [PubMed] [Google Scholar]
- 37.Pokric M, Bromily P, Thacker N, Jackson A. Probabilistic Multi-modality Image Segmentation with Partial Voluming. 10th Annual Meeting of ISMRM; Honolulu, Hawai'i, USA. 2002. p. 356. [Google Scholar]
- 38.Kumar K, Tweedle M, Brittain HG. Analytical profiles of drug substances and excipients. Vol. 24. San Diego: Academic Press; 1992. Analytical profiles of drug substances and excipients; pp. 209–241. [Google Scholar]
- 39.Weinmann HJ, Brasch RC, Press WR, Wesbey GE. Characteristics of gadolinium-DTPA complex: a potential NMR contrast agent. AJR Am J Roentgenol. 1984;142(3):619–624. doi: 10.2214/ajr.142.3.619. [DOI] [PubMed] [Google Scholar]
- 40.Tweedle MF. Physicochemical properties of gadoteridol and other magnetic resonance contrast agents. Invest Radiol. 1992;27 (Suppl 1):2–6. [PubMed] [Google Scholar]
- 41.Adzamli IK, Jolesz FA, Bleier AR, Mulkern RV, Sandor T. The effect of gadolinium DTPA on tissue water compartments in slow- and fast-twitch rabbit muscles. Magn Reson Med. 1989;11(2):172–181. doi: 10.1002/mrm.1910110205. [DOI] [PubMed] [Google Scholar]
- 42.Dortch RD, Apker GA, Valentine WM, Lai B, Does MD. Compartment-specific enhancement of white matter and nerve ex vivo using chromium. Magn Reson Med. 2010;64(3):688–697. doi: 10.1002/mrm.22460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Purea A, Webb AG. Reversible and irreversible effects of chemical fixation on the NMR properties of single cells. Magn Reson Med. 2006;56(4):927–931. doi: 10.1002/mrm.21018. [DOI] [PubMed] [Google Scholar]
- 44.Helander KG. Kinetic studies of formaldehyde binding in tissue. Biotech Histochem. 1994;69(3):177–179. doi: 10.3109/10520299409106282. [DOI] [PubMed] [Google Scholar]
- 45.Helander KG, Widehn S, Helander HF. Kinetic studies of glutaraldehyde binding in liver. Biotech Histochem. 2002;77(4):207–212. [PubMed] [Google Scholar]
- 46.Chen WC, Foxley S, Miller KL. Detecting microstructural properties of white matter based on compartmentalization of magnetic susceptibility. Neuroimage. 2013;70:1–9. doi: 10.1016/j.neuroimage.2012.12.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.van Gelderen P, de Zwart JA, Lee J, Sati P, Reich DS, Duyn JH. Nonexponential T2 decay in white matter. Magn Reson Med. 2012;67(1):110–117. doi: 10.1002/mrm.22990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Gambarota G, Cairns BE, Berde CB, Mulkern RV. Osmotic effects on the T2 relaxation decay of in vivo muscle. Magn Reson Med. 2001;46(3):592–599. doi: 10.1002/mrm.1232. [DOI] [PubMed] [Google Scholar]
- 49.Ou X, Sun S-W, Liang H-F, Song S-K, Gochberg DF. The MT pool size ratio and the DTI radial diffusivity may reflect the myelination in shiverer and control mice. NMR Biomed. 2009;22(5):480–487. doi: 10.1002/nbm.1358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Ou X, Sun S-W, Liang H-F, Song S-K, Gochberg DF. Quantitative magnetization transfer measured pool-size ratio reflects optic nerve myelin content in ex vivo mice. Magn Reson Med. 2009;61(2):364–371. doi: 10.1002/mrm.21850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Schmierer K, Wheeler-Kingshott CAM, Tozer DJ, Boulby PA, Parkes HG, Yousry TA, Scaravilli F, Barker GJ, Tofts PS, Miller DH. Quantitative magnetic resonance of postmortem multiple sclerosis brain before and after fixation. Magn Reson Med. 2008;59(2):268–277. doi: 10.1002/mrm.21487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Peters AM, Brookes MJ, Hoogenraad FG, Gowland PA, Francis ST, Morris PG, Bowtell R. T2* measurements in human brain at 1. 5, 3 and 7 T. Magn Reson Imaging. 2007;25(6):748–753. doi: 10.1016/j.mri.2007.02.014. [DOI] [PubMed] [Google Scholar]
- 53.Rooney WD, Johnson G, Li X, Cohen ER, Kim S-G, Ugurbil K, Springer CS. Magnetic field and tissue dependencies of human brain longitudinal 1H2O relaxation in vivo. Magn Reson Med. 2007;57(2):308–318. doi: 10.1002/mrm.21122. [DOI] [PubMed] [Google Scholar]
- 54.Stanisz GJ, Kecojevic A, Bronskill MJ, Henkelman RM. Characterizing white matter with magnetization transfer and T(2) Magn Reson Med. 1999;42(6):1128–1136. doi: 10.1002/(sici)1522-2594(199912)42:6<1128::aid-mrm18>3.0.co;2-9. [DOI] [PubMed] [Google Scholar]
- 55.Harrison R, Bronskill MJ, Henkelman RM. Magnetization transfer and T2 relaxation components in tissue. Magn Reson Med. 1995;33(4):490–496. doi: 10.1002/mrm.1910330406. [DOI] [PubMed] [Google Scholar]
- 56.Sutor B, Schmolke C, Teubner B, Schirmer C, Willecke K. Myelination defects and neuronal hyperexcitability in the neocortex of connexin 32-deficient mice. Cereb Cortex. 2000;10(7):684–697. doi: 10.1093/cercor/10.7.684. [DOI] [PubMed] [Google Scholar]
- 57.Wong AW, Xiao J, Kemper D, Kilpatrick TJ, Murray SS. Oligodendroglial expression of TrkB independently regulates myelination and progenitor cell proliferation. J Neurosci. 2013;33(11):4947–4957. doi: 10.1523/JNEUROSCI.3990-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Traka M, Arasi K, Avila RL, Podojil JR, Christakos A, Miller SD, Soliven B, Popko B. A genetic mouse model of adult-onset, pervasive central nervous system demyelination with robust remyelination. Brain. 2010;133(10):3017–3029. doi: 10.1093/brain/awq247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Webb S, Munro CA, Midha R, Stanisz GJ. Is multicomponent T2 a good measure of myelin content in peripheral nerve? Magn Reson Med. 2003;49(4):638–645. doi: 10.1002/mrm.10411. [DOI] [PubMed] [Google Scholar]
- 60.Underhill HR, Rostomily RC, Mikheev AM, Yuan C, Yarnykh VL. Fast bound pool fraction imaging of the in vivo rat brain: association with myelin content and validation in the C6 glioma model. Neuroimage. 2011;54(3):2052–2065. doi: 10.1016/j.neuroimage.2010.10.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Ong HH, Wright AC, Wehrli SL, Souza A, Schwartz ED, Hwang SN, Wehrli FW. Indirect measurement of regional axon diameter in excised mouse spinal cord with q-space imaging: simulation and experimental studies. Neuroimage. 2008;40(4):1619–1632. doi: 10.1016/j.neuroimage.2008.01.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.