Fluid flows created by swimming bacteria drive self-organization in confined suspensions

Significance

The collective dynamics of swimming microorganisms exhibits a complex interplay with the surrounding fluid: the motile cells stir the fluid, which in turn can reorient and advect them. This feedback loop can result in long-range interactions between the cells, an effect whose significance remains controversial. We present a computational model that takes into account these cell–fluid interactions and cell–cell forces and that predicts counterintuitive cellular order driven by long-range flows. This prediction is confirmed with experimental studies that track the orientation of cells in a confined, dense bacterial suspension.

Abstract

Concentrated suspensions of swimming microorganisms and other forms of active matter are known to display complex, self-organized spatiotemporal patterns on scales that are large compared with those of the individual motile units. Despite intensive experimental and theoretical study, it has remained unclear the extent to which the hydrodynamic flows generated by swimming cells, rather than purely steric interactions between them, drive the self-organization. Here we use the recent discovery of a spiral-vortex state in confined suspensions of Bacillus subtilis to study this issue in detail. Those experiments showed that if the radius of confinement in a thin cylindrical chamber is below a critical value, the suspension will spontaneously form a steady single-vortex state encircled by a counter-rotating cell boundary layer, with spiral cell orientation within the vortex. Left unclear, however, was the flagellar orientation, and hence the cell swimming direction, within the spiral vortex. Here, using a fast simulation method that captures oriented cell–cell and cell–fluid interactions in a minimal model of discrete particle systems, we predict the striking, counterintuitive result that in the presence of collectively generated fluid motion, the cells within the spiral vortex actually swim upstream against those flows. This prediction is then confirmed by the experiments reported here, which include measurements of flagella bundle orientation and cell tracking in the self-organized state. These results highlight the complex interplay between cell orientation and hydrodynamic flows in concentrated suspensions of microorganisms.

In the wide variety of systems termed “active matter” (1, 2), one finds the spontaneous appearance of coherent dynamic structures on scales that are large compared with the individual motile units. Examples range from polar gels (3, 4), bacterial suspensions (5–10), and microtubule bundles (11) to cytoplasmic streaming (12, 13). At high concentrations, suspensions of rod-like bacteria are known to arrange at the cellular scale with parallel alignment as in nematic liquid crystals (5, 14), but with local order that is polar, driven by motility (15, 16). At meso- and macroscopic scales, coherent structures such as swirls, jets, and vortices at scales 10 μm to 1 mm have been experimentally observed (5–10). Many studies have focused on how complex cell interactions can give rise to macroscopic organization and ordering, and the role of self-generated fluid flows in the dynamics of dense suspensions is still under debate (8, 10, 17–21). This controversy is due in part to the inherent complexity of the systems under investigation and the difficulty in making faithful mathematical models.

Microswimmers such as Escherichia coli, Bacillus subtilis, and Chlamydomonas rheinhardtii produce dipolar fluid flows through the combined action of their flagella and cell body on the fluid. In the far field, they are well described as “pusher” or “puller” stresslets (22–24), corresponding to the case of flagella behind or in front of the cell body. These fluid flows affect passive tracers (25, 26), as well as swimmers: their motion is subject to convection and shear reorientation induced by neighboring organisms, which can lead to complex collective organization. Macroscopic fluid flows emerge from the collective motion of a colony of motile bacteria, and the suspension can exhibit a quasi-turbulent dynamics (5). Microorganisms like B. subtilis live in porous environments, such as soil, where contact with surfaces is inevitable as mesoscale obstacles and confinement are the norm. Recent experiments give insight into the interactions of single microorganisms with surfaces (24, 27–29), yet suspension dynamics in confinement has only begun to be investigated (30), and the role of the collectively generated fluid flows in the macroscopic organization has yet to be fully understood.

Recently, Wioland et al. (30) showed that a dense suspension of B. subtilis, confined into a flattened drop, can self-organize into a spiral vortex, in which a boundary layer of cells at the drop edge moves in the opposite direction to the bulk circulation. This spatiotemporal organization is driven by the presence of the circular boundary and the interactions of bacteria with it. At the interface, the packed cells move at an angle to the tangential that is dictated by the drop curvature, swimmer size, and shape. This macroscopic nonequilibrium pattern and double circulation were not anticipated by theory and have not been seen in any simulations of discrete particle systems due to the computational difficulty of capturing both confinement and complex interactions between elongated swimmers. Although previous simulations have demonstrated the importance of hydrodynamics in populations of spherical squirmers (31) and rod-shaped swimmers (32), they do not consider boundary effects and the elongated shape of the swimmers in the steric interactions. On the other hand, continuum models of motile suspensions that include fluid dynamics and have been successful in explaining large-scale patterns (32, 33), have either ignored confinement or interactions with surfaces, or, if addressing confinement (34), have imposed boundary conditions that generally do not resolve the orientations of the bacteria at the interface. Thus, the conditions at boundaries and microscopic interactions between cells warrant careful consideration in the modeling of these suspensions so that the macroscopic dynamics and organization are correctly captured.

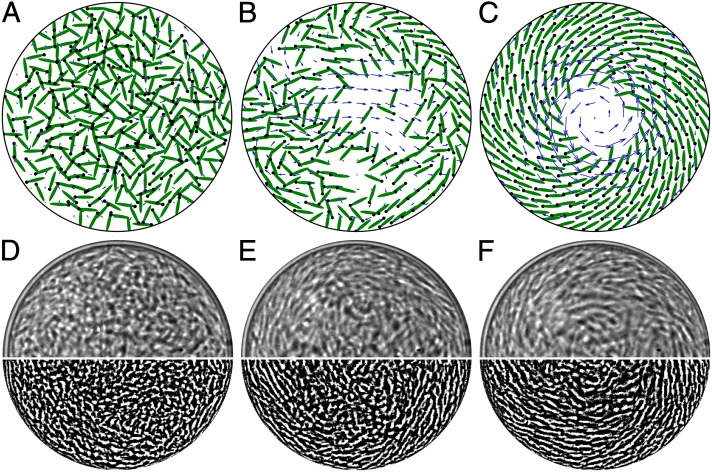
Here, we elucidate the origin and nature of the spontaneous emergence of the spiral vortex and cellular organization in a confined motile suspension. A computational model is described for bacterial suspensions in which the direct and hydrodynamic interactions between the swimmers and the confining circular interface can be tuned. The cells are represented as oriented circles or ellipses subject to cell–cell and cell–fluid interaction, whereas the fluid flow is the total of the pusher dipolar fluid flows produced by each swimmer’s locomotion. It is shown that, although some circulation under conditions of confinement may arise with direct interactions only, hydrodynamics are necessary and crucial to reproduce and explain the double circulation that is observed experimentally. Simulations (Fig. 1 A–C) are able to reproduce the emergence of the spiral vortex from an isotropic state (Fig. 1 D–F) and give insights into the origin of the microscopic organization of the bacteria in the drop. The computational results show the remarkable feature that cells in the bulk of the drop swim against the stronger colony-generated fluid flow and thus have a net backward motion. We confirm this observation by measuring the orientation of the cells and of their flagella through suitable fluorescent labeling methods.

Fig. 1.

Snapshots of the bacterial suspension self-organization from simulations (A–C) and experiments (D–F). (A–C) An initially isotropic suspension of microswimmers inside a circle with diameter 12ℓ (ℓ = individual swimmer length). Black dots indicate the swimming direction. The swimmer-generated fluid flow is shown superimposed in each plot (blue arrows). (D–F) A dense suspension of B. subtilis in a drop, 70 μm in diameter. (Upper) Bright field. (Lower) Images processed by edge-detection filtering. Initial disordered state is obtained by shining a blue laser that causes cells to tumble. In both simulations and experiments, the suspension organization initiates at the boundary, as seen in B and E. See also Movie S1.

Model and Simulations

Because no vertical motion of the swimmers was observed experimentally (30), we assume the dynamics is confined to a plane and the simulations are therefore implemented in 2D domains to increase the computational speed. We consider M pusher swimmers immersed in a fluid contained inside a circle. Each swimmer is modeled as a slender ellipse with length ℓ = 1 and width w = ℓ/6 (or w = ℓ for disks) that propels itself along its main axis. The dynamics of each is expressed in terms of its center of mass position X_i and orientation P_i (35)

$${\partial }_t{\mathbf{X}}_i=V{\mathbf{P}}_i+\mathbf{u}+{\Xi }_i^{-1}{\displaystyle \sum _{j\ne i}{\mathbf{F}}_{ij}^e},$$ [1]

$${\partial }_t{\mathbf{P}}_i=\left(\mathbf{I}-{\mathbf{P}}_i{\mathbf{P}}_i^T\right)\left(\gamma \mathbf{E}+\mathbf{W}\right){\mathbf{P}}_i+k{\displaystyle \sum _{j\ne i}{\mathbf{T}}_{ij}^e\times {\mathbf{P}}_i}.$$ [2]

Eq. 1 describes self-propulsion with constant speed (chosen as V = 1 without loss of generality) along the cell direction P_i, advection by the fluid velocity u, and pairwise repulsion with force ${\mathbf{F}}_{ij}^e$ between swimmers. Here, $\Xi =m_{\mathrm{\parallel }}{\mathbf{P}}_i{\mathbf{P}}_i^T+m_{\perp }\left(\mathbf{I}-{\mathbf{P}}_i{\mathbf{P}}_i^T\right)$ with m_⊥ = 2m_∥ = 2 for elongated ellipses and m_⊥ = m_∥ = 1 for disks (36). The first term of Eq. 2 describes rotation of the particle by the fluid flow u with 2E = ∇u + ∇u^T, 2W = ∇u − ∇u^T; γ ∼ 0.95 for ellipses with aspect ratio 6 and γ = 0 for disks. The last term of Eq. 2 describes swimmer rotations due to torques from direct interactions with neighbors: k = 6 for elongated ellipses and k = 0 for disks. The purely repulsive steric forces ${\mathbf{F}}_{ij}^e$ and torques ${\mathbf{T}}_{ij}^e$ are obtained using methods described elsewhere (37). Each swimmer is discretized into n_b beads (n_b = 6 for ellipses, n_b = 1 for disks). Beads from different swimmers interact by with a soft capped Lennard-Jones potential; this allows some overlaps. Noise terms are not included.

The swimmer-driven fluid velocity u is governed by the (nondimensional) 2D Stokes equations with an extra stress

$$-{\nabla }^2\mathbf{u}+\nabla q=\nabla \cdot {\displaystyle \sum _i{\mathbf{S}}_i^a\delta \left(\mathbf{x}-{\mathbf{X}}_i\right)},\hspace{1em}\nabla \cdot \mathbf{u}=0.$$ [3]

Here q is the fluid pressure to account for the fluid incompressibility and ${\mathbf{S}}_i^a=\alpha \mathbf{P}{\mathbf{P}}_i^T$ denotes the active stress tensor resulting from the swimmer locomotion in 2D with nondimensional stresslet strength α ∼ −1 for a pusher swimmer with length ℓ = 1 and speed V = 1. Eqs. 1 and 2 are integrated in time, and the instantaneous fluid flow that swimmers collectively generate is obtained by solving Eq. 3 on an underlying uniform Eulerian grid (35). The interpolation of the fluid velocity u to the swimmers’ positions X_i, and the extrapolation of the active stresses ${\mathbf{S}}_i^a$ onto the Eulerian grid x are done using an Immersed Boundary method framework (38) with a discretized delta function δ(x − X_i). Essentially, the fluid velocity u is the superposition of the pusher-like dipolar flows generated by each swimmer.

We use the method of images for swimmers at the drop boundary (39), which in experiments is an oil–water interface. In a circle of radius R, at each time step, if a swimmer i is within 3ℓ of the surface, then an approximate mirror swimmer is placed outside the circle at R²/∥X_i − X_center∥, with mirror orientation P_i − 2(X_i − X_center)/∥X_i − X_center∥. The steric forces, torques, and fluid velocity u are calculated for the swimmers and their images, whereas Eqs. 1 and 2 are integrated in time only for the actual swimmers. This approach approximates simultaneously and at low computational cost an effective confinement and a no-stress condition at the drop boundary. This boundary condition is appropriate, as we observed that the surrounding oil in experiments was set in motion by the drops of bacterial suspension.

Simulation Results

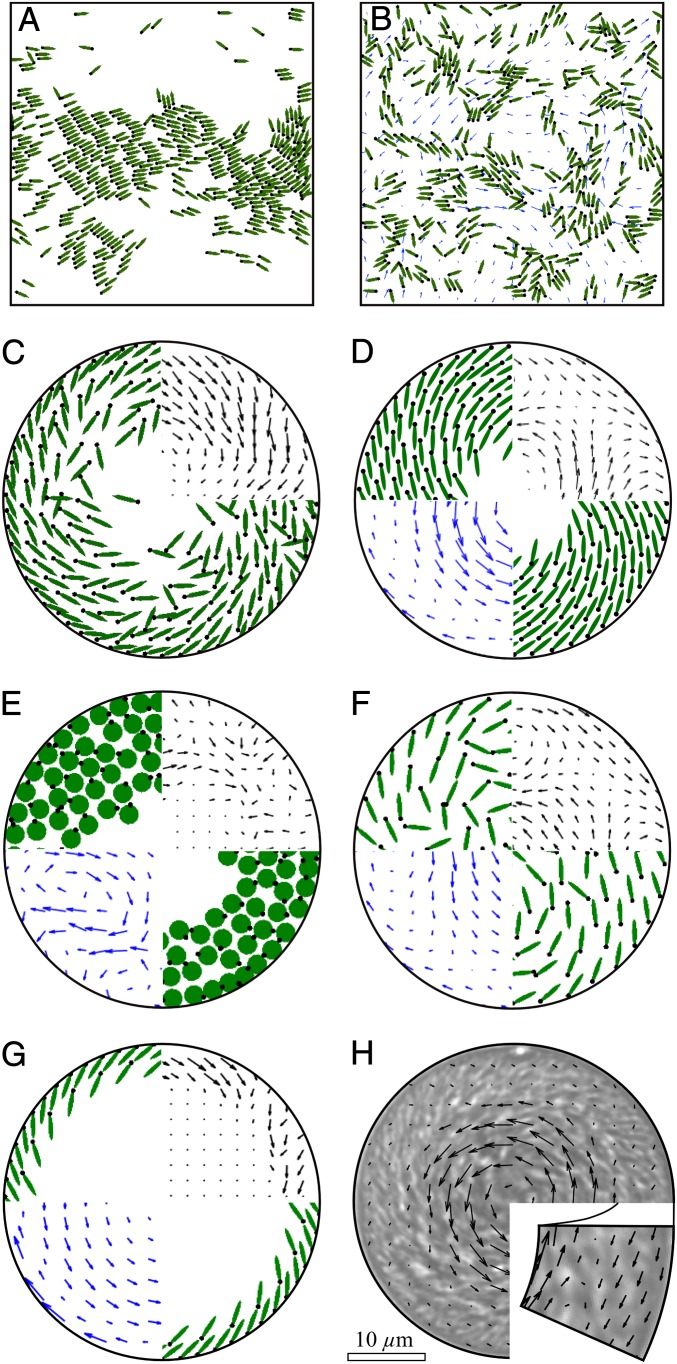
We first describe computational results in an unconfined periodic domain. With neglect of hydrodynamics (α = 0 = u), the suspension exhibits swarming at low concentration (Fig. 2A and Movie S2) or a stable “bionematic” state (5) at higher concentration, as classified by ref. 16 and seen in swarming colonies on surfaces (40). Introducing hydrodynamics (Fig. 2B and Movie S2) destabilizes these two states to generate a turbulent dynamics qualitatively similar to experimental observation (5, 8). Remarkably, hydrodynamics disrupts bacterial clusters, as also suggested by a squirmer model (18). This disruption of long-range polar order is a consequence of an instability that has been previously analyzed (17, 32, 33).

Fig. 2.

Suspension organization in periodic domains and inside circular confinement. (A) Self-propelled ellipses interacting without hydrodynamics achieve a swarming or bionematic state when in a periodic domain. (B) Pusher swimmers in a periodic domain exhibit a turbulent dynamics and are less clustered. (C) Self-propelled ellipses interacting sterically without any hydrodynamics. (D) Self-propelled ellipses interacting sterically with hydrodynamics. (E) Circular pusher swimmers. (F) Pusher swimmers with isotropic steric repulsions but alignment with fluid flow (γ ∼ 1, k = 0, T = 0). (G) Dilute suspension of ellipsoid pusher swimmers. (H) Bacterial flow measured in experiments by PIV (30). The Upper Right Insets in C–G indicate the swimmer net circulation direction and plot the mean swimmer motion with arrows magnified by 4, 1, 13, 1, and 2, respectively. Lower Left Insets in D–G show the fluid flow velocity arrows magnified by 1, 5, 1, and 2, respectively. See Movies S1–S7.

Next, consider the case of confined suspensions. Without fluid interactions (α = 0 = u), Fig. 2C (Movie S3) shows cells concentrating or jamming at the drop boundary with small unidirectional circulation. With more realistic conditions (ellipses, direct, and hydrodynamic interactions), we observe in Fig. 2D (Movie S4) a spiral vortex similar in form and dynamics to that of experiments (Fig. 2H). For disk-shaped pusher swimmers (γ = 0, α = −1, ${\mathbf{T}}_{ij}^e=\mathbf{0}$) subject to reorientation and advection by the fluid flows they create, Fig. 2E (Movie S5) shows that, although the alignment between neighboring cells is lost, swimmers form unstable layers with very small transient circulation. These three configurations show that, although steric interactions force local alignment of ellipsoidal swimmers, it is the collectively generated fluid flow that produces the large-scale organization and double circulation. In fact, in simulations where alignment with the flow but not through steric interaction was considered (i.e., setting γ ∼ 1 but k = 0, ${\mathbf{T}}_{ij}^e=\mathbf{0}$), the spiral organization and double circulation are still obtained (Fig. 2F and Movie S6, cells are spaced further apart due to isotropic steric repulsions with a larger radius). These model parameters would be appropriate to the description of spherical bacteria, whose collective behavior has recently been studied in the absence of confinement (41). In Fig. 2G (Movie S7), we show that a dilute suspension of ellipse-shaped swimmers also orders into a spiral vortex and self-generates bidirectional fluid flows. As an aside, we note that circulation has been observed in confined systems of self-propelling disks with prescribed alignment interactions and possibly noise terms (42) but that circulation is unidirectional, as in Fig. 2C.

Emergence of Organization

Bacteria move by swimming and through advection by the local fluid flow; the balance between the two yields the observed direction of motion. In drops of bacterial suspension, particle image velocimetry (PIV) measurements reported previously (30) showed that a boundary layer circulates in a direction opposite to that of the bulk, but it was not possible to resolve whether swimming or advection dominates the overall motion and, in particular, in which direction cells point.

To understand how the spiral order and double circulation arise, we consider suspensions of increasing density. When a few cells are trapped in a drop, they swim to the oil interface and slide along it at a small angle, as in Fig. 2G. With more cells added, they form clusters sliding along the boundary [akin to those seen with self-propelling rods in channels (43)]. The clusters finally merge to form the circulating outer boundary layer, as seen in Fig. 2G. (In the images of Fig. 1 B and E, we note that this layer is the first to form.) Bacteria point outward with an angle characteristic of the spiral pattern. As pusher swimmers, they push fluid backward, and the added effect produces the drop bulk fluid flow that is in the opposite direction to the swimmer circulation.

On increasing the concentration to the dense regime, additional cells arrange into more layers with an angle dictated by steric interactions, thus reproducing the spiral arrangement. Although bulk cells were first proposed to be pointing inward (30), simulations show instead that almost all cells point outward and swim in the same direction (clockwise in Fig. 2D). Moreover, the fluid flow is in the opposite direction to the bulk swimmers’ orientation and, in the inner part of the drop, is strong enough to counterbalance the swimming speed. This phenomenon is illustrated in Fig. 1, where central cells point clockwise but overall move counterclockwise. Although the macroscopic suspension dynamics is in agreement with experiments (Fig. 2H), new experiments are required to determine the actual cell orientation and to test the predicted arrangement.

Experiments

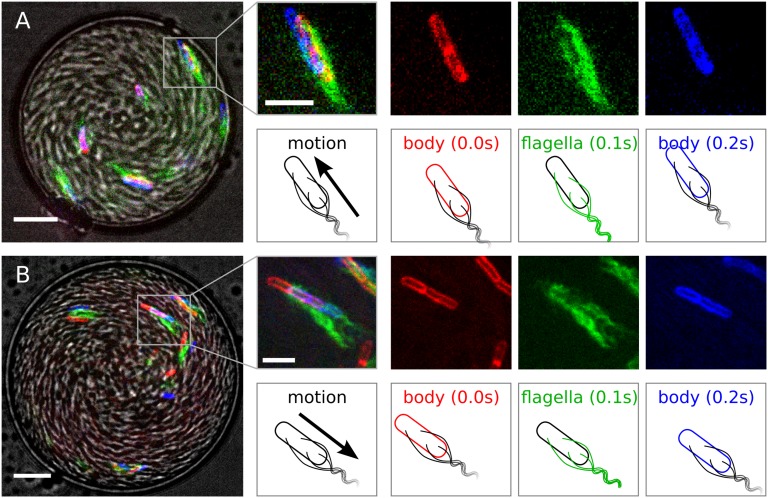
To determine precisely the cell configuration and orientation in the spiral vortex state, we used a mutant of B. subtilis [DS1919 3610, a generous gift of H. C. Berg (Harvard University, Cambridge, MA) (44)], labeled with Alexa Fluor 488 C5 maleimide on the flagella and FM4-64 on the cell membrane, following the protocol of Guttenplan et al. (45). From these two-colored bacteria, mixed with a large amount of WT cells (strain 168), we form numerous drops 10–100 μm in diameter and ∼ 25 μm in height in an emulsion, the background liquid of which is mineral oil (30). A sequence of four images was taken: (i) in bright field to determine the spatial organization (gray scale in Fig. 3 A and B), (ii) of the membrane (FM4-64, false colored red), (iii) of the flagella (Alexa-488, false colored green), and (iv) again of the membrane (FM4-64, false colored blue). From these we determine the cell position, overall motion, and swimming direction.

Fig. 3.

Drop overview in gray scale: bright field image. Positions of the membrane (false colored red at time t = 0, blue at t = 0.2 s) and flagella (false colored green at t = 0.1 s) dyes help determine the cell orientation. (A) Forward motion: cell at the oil interface both point and move to the top left corner. (B) Backward motion: the cell is pointing to the top left corner while moving overall in the opposite direction. (Scale bars: at the drop images, 10 μm; at the individual bacterium images, 5 μm.)

Fig. 3A highlights a cell at the oil interface. Both the cell motion and swimming direction are toward the upper-left corner. Fig. 3B highlights a bacterium in the bulk. The two images of the membrane indicate that the cell is moving toward the lower right corner. However, the relation between the flagella position and the mean membrane position and the flagella bundling at the rear of the bacteria reveal that the cell is pointing to the upper-left corner, in a direction opposite to its motion. These results, consistently found by sampling over 20 cells, confirm the prediction from simulations: although all of the bacteria point in the same direction (outward), the bulk microswimmers move overall in a backward fashion, opposite to the boundary layer motion.

Quantification of Spatial Order

As shown in previous sections, experiments and simulations with both steric and hydrodynamical interactions are in qualitative agreement on both micro- and macroscopic scales. In this section, we consider quantitative measures of the spatial order in the numerical studies and compare them to the experimental results reported previously (30). In experiments, drops show stable circulation when the confining chamber is 30–70 μm in diameter. To quantify the order in simulations, we introduce the vortex order parameter

$$\mathrm{\Phi }=\frac{1}{1-2/\pi }\left(\frac{{\displaystyle {\sum }_i\left|{\mathbf{v}}_i\cdot {\mathbf{t}}_i\right|}}{{\displaystyle {\sum }_j\Vert {\mathbf{v}}_j\Vert }}-\frac{2}{\pi }\right),$$ [4]

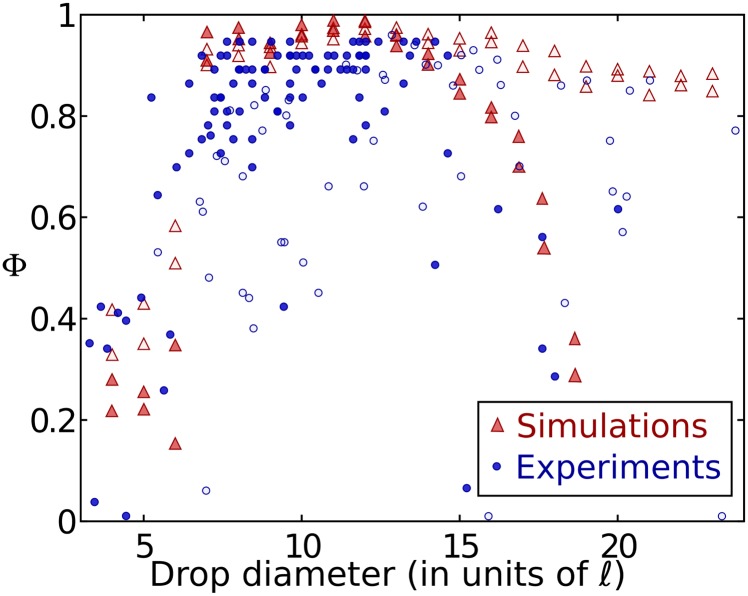
where v_i is the bacterial overall motion and t_i is the azimuthal unit vector. Φ = 1 for purely azimuthal flows, Φ = 0 for disordered chaotic flows, and Φ < 0 for mostly radial flows. Φ is computed for drops with diameters between 4ℓ ∼ 20 μm and 25ℓ ∼ 125 μm for dense (area fraction ∼25%) and semidilute suspensions (area fraction ∼ 10%).

Fig. 4 shows a first transition from random to vortex state around d = 7ℓ. For dense suspensions, the plot reveals that a highly ordered single-vortex state with Φ > 0.7 is achieved in drops with diameter d = 7 − 16ℓ (vs. 30–70 μm, ∼ 6–14ℓ in experiments). In experiments and simulations, we observe that turbulence arises in the center of the largest drops. In the case of dilute or semidilute suspensions (Fig. 2G), this center is depleted in cells, thus leading to ordered states even for d > 14ℓ.

Fig. 4.

A stable vortex forms for a range of drop diameters. The vortex order parameter Φ for dense (solid color) or dilute (faded color) suspensions in drops with various diameters for both simulations (triangles) and experiments (circles).

As seen in Fig. 1, in both simulations and experiments, the cell orientation is not parallel to the direction of the fluid circulation. We examine the azimuthally averaged swimmer orientation angle θ_m for the layer of cells at the boundary. Not surprisingly, the effect of the surface curvature makes this angle higher for smaller drops and smaller for larger drops. In experiments, it ranges from θ_m ≃ 35° for drop diameters d = 30 μm to θ_m ≃ 10° for d = 70 μm (30). In simulations, it ranges from θ_m ≃ 42° for circle drops with diameter d = 7ℓ to θ_m ≃ 36° for d = 16ℓ. Although the boundary behavior and swimmer angles are qualitatively similar to the experiments, they do not match quantitatively due to simplifications in the model. Including short-range hydrodynamics between the cells would likely remedy this discrepancy.

Discussion

We presented a minimal model and simulation method for microswimmer suspensions that includes direct cell–cell, cell–fluid interactions, and swimmer-generated flows. The method, although minimal and in two dimensions, captures the dynamics seen in experiments on confined bacterial suspensions. In agreement with previous simulations, we show here that the long-range hydrodynamic interactions are crucial to reproduce the organization and circulation that are observed in experiments. In periodic domains, the swarming states predicted by active matter theories are disrupted by hydrodynamics, resulting in a more turbulent suspension behavior. Under circular confinement, although direct cell interactions lead to local cell alignment, large-scale order appears only when the swimmer motion is coupled to the fluid dynamics. Simulation results not only agree qualitatively with the experiments but they also highlight the microscopic bacterial organization. In particular, the cells in the bulk are shown to swim against the collectively generated fluid flow, a result that was not foreseen in previous publications. We confirmed that prediction by experimentally recording both motion and swimming directions, which to our knowledge has never been done in dense bacterial suspensions. To do so, we tagged and tracked the relative positions of the cells body and flagella.

These results emphasize the necessity to include more realistic hydrodynamic interactions in active fluid particle simulations and also continuum theories (17, 33). Ultimately, a closer comparison with experiments requires 3D particle simulations, more accurate descriptions of the fluid flows generated by the swimmers in the bulk and near boundaries, and possibly an accounting of the swimmers’ geometry and flagella. This model could be adapted to a 3D domain, changing the packing of the cells but also the fluid flow they generate: in 2D domains, a swimmer dipolar flow decays with distance from the cell as 1/r instead of the 1/r² decay in 3D, which is more appropriate for the experimental situation. The present model does not account for close-range and lubrication hydrodynamics or Brownian noise effects. Recent simulations of spherical squirmers at high packing fractions (18, 21) show that including close-range hydrodynamics significantly affects the suspension behavior. Although simplified, the model described here has been shown to give good insights into the dynamics of microswimmer suspensions and could be applied to more complex geometries to study microscopic interactions and ordering that are difficult to visualize experimentally.

Materials and Methods

Experimental Protocol.

We use two B. subtilis strains: the WT 168 strain and the mutant amyE::hag(T204C) DS1919 3610 [generous gift of H. C. Berg (Harvard University, Cambridge, MA)], both grown in standard Terrific Broth (TB; Sigma) at 35 °C on a shaker. An overnight culture was diluted 200× and grown for 5 h until the end of exponential growth when the proportion of motile cells is maximal (46).

To label mutant bacteria, we followed the protocol of Guttenplan et al. (45). One milliliter of the suspension was centrifuged (1,000 × g, 2 min) and resuspended in 50 μL of PBS containing 5 μg/mL Alexa Fluor 488 C5 Maleimide (Molecular Probes) and incubated at room temperature for 5 min to stain the flagella. Bacteria were then washed in 1 mL PBS and resuspended in PBS containing 5 μg/mL FM4-64 (Molecular Probes) for membrane staining. The suspension was washed one final time and resuspended in 50 μL PBS.

A dense suspension of bacteria was prepared by centrifuging 10 mL of WT B. subtilis (1,500 × g for 10 min). If necessary, a small volume of stained bacteria was added to the pellet, which was then mixed into four volumes of mineral oil containing 10 mg/mL diphytanoyl phosphatidylcholine (DiPhyPC; Avanti) to prevent drops from coalescing. The emulsion was then created by gently pipetting the suspension and placing it between two silane-coated coverslips, creating numerous flattened drops, ∼25 μm in height and 10–100 μm in diameter.

Bright field movies were acquired at 125 fps with a high-speed camera (Fastcam; Photron) on an inverted microscope (Cell Observer; Zeiss), using a 100× oil immersion objective and analyzed with Matlab mPIV algorithm (47). To observe the emergence of order (Fig. 1 and Movies S1 and S2), we shined blue light on the drop for a few seconds. Bacteria naturally react by tumbling (48), thus disorganizing the drop.

To measure the swimming and motion directions of the cells, we imaged stained mutant B. subtilis on a confocal spinning disk microscope. To increase the resolution, images were taken at the bottom of the drop. We excited both fluorophores with a 488-nm laser and filtered the emission with a GFP filter cube (barrier filter 500–550 nm; Zeiss) for Alexa Fluor 488 C5 Maleimide and DsRed filter cube (barrier filter 570–640 nm; Zeiss) for FM4-64. Images were taken every 0.1 s (limited by the acquisition rate), filtering first for the membrane (false colored red), flagella (false colored green), and again membrane (false colored blue; Fig. 3). The direction of bacterial motion was determined from the membrane displacement and the swimming direction from the relative position of the flagella to the average membrane position.

Simulations.

To calculate the repulsive forces and torques between neighboring swimmers, we use the method of Constanzo et. al. (37) and discretize each swimmer into n_b beads of diameter ℓ/n_b. Beads of different swimmers interact with each other via a capped Lennard-Jones potential

$${\mathrm{\Psi }}_{LJ}^{\alpha }\left(r\right)=\{\begin{array}{ll}8\mathit{ϵ}\left[\frac{2r_c^{12}}{{\left(r^2+{\alpha }^2\right)}^6}-\frac{r_c^6}{{\left(r^2+{\alpha }^2\right)}^3}\right]\hfill & \text{if}\hspace{0.5em}r\le r_c\hfill \\ 0\hfill & \text{if}\hspace{0.5em}r>r_c\hfill \end{array},$$ [5]

where r is the distance between the bead centers, r_c = 2r_b is the cutoff distance, r_b is the bead radius, and α = r_c[(1/2)^1/3 − 1]^1/2 is the capping or smoothing factor. The smoothing of the potential allows for larger time steps when integrating Eqs. 1 and 2, but it comes at the expense of the swimmers overlapping or possibly escaping the confinement. The effective bead radius is then ∼ r_c/2, giving the swimmer an effective thickness of r_c and effective aspect ratio of ℓ/r_c.