Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2014 Apr 9;30(15):2219–2220. doi: 10.1093/bioinformatics/btu166

relax: the analysis of biomolecular kinetics and thermodynamics using NMR relaxation dispersion data

Sébastien Morin 1,2, Troels E Linnet 3, Mathilde Lescanne 4, Paul Schanda 4, Gary S Thompson 5, Martin Tollinger 6, Kaare Teilum 3, Stéphane Gagné 1, Dominique Marion 4, Christian Griesinger 7, Martin Blackledge 4, Edward J d’Auvergne 4,7,*
PMCID: PMC4103588  PMID: 24764461

Abstract

Nuclear magnetic resonance (NMR) is a powerful tool for observing the motion of biomolecules at the atomic level. One technique, the analysis of relaxation dispersion phenomenon, is highly suited for studying the kinetics and thermodynamics of biological processes. Built on top of the relax computational environment for NMR dynamics is a new dispersion analysis designed to be comprehensive, accurate and easy-to-use. The software supports more models, both numeric and analytic, than current solutions. An automated protocol, available for scripting and driving the graphical user interface (GUI), is designed to simplify the analysis of dispersion data for NMR spectroscopists. Decreases in optimization time are granted by parallelization for running on computer clusters and by skipping an initial grid search by using parameters from one solution as the starting point for another —using analytic model results for the numeric models, taking advantage of model nesting, and using averaged non-clustered results for the clustered analysis.

Availability and implementation: The software relax is written in Python with C modules and is released under the GPLv3+ license. Source code and precompiled binaries for all major operating systems are available from http://www.nmr-relax.com.

Contact: edward@nmr-relax.com

Biological macromolecules are intricate machines, and their functions are closely related to their motions. These motions can be studied experimentally at the atomic level by nuclear magnetic resonance (NMR) spectroscopy. Many important biological processes occur on the Inline graphics to ms time scale, and for atoms exchanging between different states, NMR relaxation dispersion can be observed. By studying this exchange process, kinetic and thermodynamic information can be obtained.

For exchanging atoms, their nuclear spin magnetization is described by the Bloch–McConnell equations (McConnell, 1958). Using experimental data, the solution to these equations reveals both populations of the molecular states (thermodynamics) and rates of exchange between them (kinetics). Though the general solution valid for all motions remains intractable, analytic solutions with restricted motions are available and are frequently used. The equations can also be solved numerically.

Two NMR dispersion methods are used for analysing motions: Single, Zero, Double or Multiple Quantum (SQ, ZQ, DQ, MQ) CPMG (Carr and Purcell, 1954; Meiboom and Gill, 1958); or 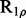Inline graphic (Deverell et al., 1970). Combined SQ, ZQ, DQ and MQ data will be labelled as Multiple-MQ (MMQ) data. Various models are used to analyse different data and motions. The simplest one is that of no motion (No Rex). For SQ CPMG-type experiments, analytic models include the original Luz and Meiboom (1963) multiple-site fast exchange models (LM63), the Carver and Richards (1972) and population-skewed Ishima and Torchia (1999) 2-site models for most time scales (CR72, IT99) and the Tollinger et al. (2001) 2-site very slow exchange model (TSMFK01). The CR72 model has been extended by Korzhnev et al. (2004) for MMQ data. For 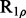Inline graphic-type data, analytic equations include the Meiboom (1961) 2-site fast exchange model for on-resonance data (M61), extended by Davis et al. (1994) to off-resonance data (DPL94), and the Trott and Palmer (2002) and Miloushev and Palmer (2005) 2-site models for non-fast and all time scales (TP02, MP05). Different numeric solutions (NS) can be designed for SQ or MMQ data.

Diverse software solutions exist for analysing relaxation dispersion data including CPMGFit (http://www.palmer.hs.columbia.edu/software/cpmgfit.html), cpmg_fit (available on request from Dmitry Korzhnev), CATIA (Hansen et al., 2008), NESSY (Bieri and Gooley, 2011), GUARDD (Kleckner and Foster, 2012), ShereKhan (Mazur et al., 2013) and GLOVE (Sugase et al., 2013). The software relax (d’Auvergne and Gooley, 2008) is a platform for studying molecular dynamics using experimental NMR data, and can be used as a numerical computing environment. Herein, support for relaxation dispersion within relax is presented. Distributed as part of relax, this is the most comprehensive dispersion package supporting the greatest number of dispersion models and NMR data types.

The number of dispersion models supported by relax is extensive (Table 1). This allows for detailed comparisons between modern numeric and traditional analytic approaches. Different user interfaces (UIs) can be used to analyse dispersion data including the prompt, scripting and graphical user interface (GUI). The scripting UI enables the greatest flexibility and allows for most analysis protocols to be replicated. By implementing a novel automated analysis and providing an easy-to-use GUI based on this auto-analysis, the study of dispersion data is much simplified.

Table 1.

Comparison of model support for different dispersion software

Software CPMG-type
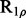 Inline graphic-type
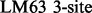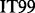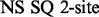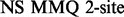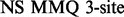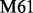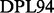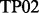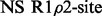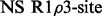Inline graphic Inline graphic Inline graphic Inline graphic Inline graphic Inline graphic Inline graphic Inline graphic Inline graphic Inline graphic Inline graphic Inline graphic Inline graphic Inline graphic Inline graphic Inline graphic
CPMGFit ✓ ✓ ✓ ✓
cpmg_fit ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓
CATIA ✓
NESSY ✓ ✓ ✓ ✓
GUARDD ✓ ✓
ShereKhan ✓ ✓ ✓
GLOVE ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓
relax ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓
Open in a new tab

The set-up of the auto-analysis includes defining the molecular system, loading the dispersion data directly from peak lists, clustering atoms with the same kinetics, modifying the list of dispersion models and setting up Monte Carlo (MC) simulations for error propagation. Execution involves sequential optimization of the models, fixed model elimination rules to remove failed models and failed MC simulations increasing both parameter reliability and accuracy (d’Auvergne and Gooley, 2006) and a final run whereby Akaike's Information Criterion (AIC) model selection is used to judge statistical significance (Akaike, 1973; d’Auvergne and Gooley, 2003). The optimization is designed for absolute accuracy and robustness, but, as this can take time, it has been parallelized at the spin cluster and the MC simulation level to run on computer clusters using OpenMPI. Three additional methods are used to speed up calculations, all designed to skip the computationally expensive grid search. The first is model nesting—the more complex model starts with the optimized parameters of the simpler. The second is model equivalence—when two models have the same parameters. For example, the CR72 model parameters are used as the starting point for the CPMG numeric models, resulting in a huge computational win. The third is for spin clustering—the analysis starts with the averaged parameter values from a completed non-clustered analysis.

The dispersion analysis in relax is implemented in Python using NumPy and the GUI using wxPython. Optimization using the Nelder–Mead simplex and log-barrier constraint algorithms from the minfx library (https://gna.org/projects/minfx/) removes the need for numerical gradient approximations, which add a second numeric layer to the NS models. Data visualization is via the software Grace.

ACKNOWLEDGEMENTS

The authors thank Nikolai Skrynnikov for his generous feedback and code contributions for implementing many of the numeric models, and Flemming Hansen and Dmitry Korzhnev for kindly providing their software and published dispersion data.

Conflict of Interest: none declared.

REFERENCES

  1. Akaike H. Information theory and an extension of the maximum likelihood principle. In: Petrov BN, Csaki F, editors. Proceedings of the 2nd International Symposium on Information Theory. Budapest: Akademia Kiado; 1973. pp. 267–281. [Google Scholar]
  2. Bieri M, Gooley PR. Automated NMR relaxation dispersion data analysis using NESSY. BMC Bioinformatics. 2011;12:421. doi: 10.1186/1471-2105-12-421. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Carr HY, Purcell EM. Effects of diffusion on free precession in nuclear magnetic resonance experiments. Phys. Rev. 1954;94:630–638. [Google Scholar]
  4. Carver J, Richards R. General 2-site solution for chemical exchange produced dependence of T2 upon Carr-Purcell pulse separation. J. Magn. Reson. 1972;6:89–105. [Google Scholar]
  5. Davis D, et al. Direct measurements of the dissociation-rate constant for inhibitor-enzyme complexes via the T1rho and T2 (CPMG) methods. J. Magn. Reson. B. 1994;104:266–275. doi: 10.1006/jmrb.1994.1084. [DOI] [PubMed] [Google Scholar]
  6. d’Auvergne EJ, Gooley PR. The use of model selection in the model-free analysis of protein dynamics. J. Biomol. NMR. 2003;25:25–39. doi: 10.1023/a:1021902006114. [DOI] [PubMed] [Google Scholar]
  7. d’Auvergne EJ, Gooley PR. Model-free model elimination: a new step in the model-free dynamic analysis of NMR relaxation data. J. Biomol. NMR. 2006;35:117–135. doi: 10.1007/s10858-006-9007-z. [DOI] [PubMed] [Google Scholar]
  8. d’Auvergne EJ, Gooley PR. Optimisation of NMR dynamic models. J. Biomol. NMR. 2008;40:107–133. doi: 10.1007/s10858-007-9214-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Deverell C, et al. Studies of chemical exchange by nuclear magnetic relaxation in rotating frame. Mol. Phys. 1970;18:553–559. [Google Scholar]
  10. Hansen DF, et al. Probing chemical shifts of invisible states of proteins with relaxation dispersion NMR spectroscopy: how well can we do? J. Am. Chem. Soc. 2008;130:2667–2675. doi: 10.1021/ja078337p. [DOI] [PubMed] [Google Scholar]
  11. Ishima R, Torchia D. Estimating the time scale of chemical exchange of proteins from measurements of transverse relaxation rates in solution. J. Biomol. NMR. 1999;14:369–372. doi: 10.1023/a:1008324025406. [DOI] [PubMed] [Google Scholar]
  12. Kleckner IR, Foster MP. GUARDD: user-friendly MATLAB software for rigorous analysis of CPMG RD NMR data. J. Biomol. NMR. 2012;52:11–22. doi: 10.1007/s10858-011-9589-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Korzhnev DM, et al. Probing slow dynamics in high molecular weight proteins by methyl-TROSY NMR spectroscopy: application to a 723-residue enzyme. J. Am. Chem. Soc. 2004;126:3964–3973. doi: 10.1021/ja039587i. [DOI] [PubMed] [Google Scholar]
  14. Luz Z, Meiboom S. Nuclear magnetic resonance study of protolysis of trimethylammonium ion in aqueous solution—order of reaction with respect to solvent. J. Chem. Phys. 1963;39:366–370. [Google Scholar]
  15. Mazur A, et al. ShereKhan–calculating exchange parameters in relaxation dispersion data from CPMG experiments. Bioinformatics. 2013;29:1819–1820. doi: 10.1093/bioinformatics/btt286. [DOI] [PubMed] [Google Scholar]
  16. McConnell H. Reaction rates by nuclear magnetic resonance. J. Chem. Phys. 1958;28:430–431. [Google Scholar]
  17. Meiboom S. Nuclear magnetic resonance study of proton transfer in water. J. Chem. Phys. 1961;34:375–388. [Google Scholar]
  18. Meiboom S, Gill D. Modified spin-echo method for measuring nuclear relaxation times. Rev. Sci. Instrum. 1958;29:688–691. [Google Scholar]
  19. Miloushev VZ, Palmer AG., III R(1rho) relaxation for two-site chemical exchange: general approximations and some exact solutions. J. Magn. Reson. 2005;177:221–227. doi: 10.1016/j.jmr.2005.07.023. [DOI] [PubMed] [Google Scholar]
  20. Sugase K, et al. Fast and accurate fitting of relaxation dispersion data using the flexible software package GLOVE. J. Biomol. NMR. 2013;56:275–283. doi: 10.1007/s10858-013-9747-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Tollinger M, et al. Slow dynamics in folded and unfolded states of an SH3 domain. J. Am. Chem. Soc. 2001;123:11341–11352. doi: 10.1021/ja011300z. [DOI] [PubMed] [Google Scholar]
  22. Trott O, Palmer AG., III R1rho relaxation outside of the fast-exchange limit. J. Magn. Reson. 2002;154:157–160. doi: 10.1006/jmre.2001.2466. [DOI] [PubMed] [Google Scholar]

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES