Multicenter trials using FDG PET to predict chemotherapy response : Effects of differential measurement error and bias on power calculations for unselected and enrichment designs

Introduction

Predictive biomarkers have great potential to personalize cancer therapies, but their clinical validation may be complicated and resource-intensive [1]. Retrospective analysis of banked samples from randomized clinical trials are an ideal setting for timely and cost-effective assessment of potential predictive biomarkers identified in smaller studies [2, 3]. However, unlike novel assays performed on formalin-fixed tissue samples, molecular imaging biomarkers cannot be derived from banked samples. Without access to retrospective analysis of large datasets, functional imaging biomarkers and biomarkers requiring fresh blood or tissue must be developed in a more incremental fashion. A prospective multicenter observational study is a sensible step in order to reproduce earlier findings in a multicenter setting, and design considerations for these studies are the focus of this manuscript.

A multicenter replication study may be used to evaluate potential cutpoints for the predictive biomarker for use in guiding therapy, and in general will inform the design of future studies. However, the principal analytic goal is merely to show a relationship between the predictive biomarker and the clinical endpoint. Since this is only a small step toward marker validation, investigators will want to conduct the trial quickly and efficiently. If new targeted therapies emerge or the standard of care changes, development of a biomarker may be stunted [2], even if the marker still has potential under the new treatment paradigm. Enrolling from a large number of centers can speed accrual, but adds startup costs at each center, and may introduce bias or increased variability (error).

Enriched samples are used to speed early drug testing by including only patients who are most likely to benefit [2, 4, 5]. Later trials may test the therapy in an unselected patient population, to prevent bias introduced by the selection process, especially in case the mechanism of action is different from expected [6, 7].

Rapid enrollment (with many study sites) and enrichment designs are both strategies that may facilitate development of a predictive biomarker. The objective of this manuscript is to demonstrate the use of simulation studies to select a design that will optimize study power, under realistic scenarios derived from the substantive literature. The case study for illustration is a multicenter study using ¹⁸F-fluorodeoxyglucose (FDG) PET to monitor response to breast cancer neoadjuvant chemotherapy. Our prior work demonstrated that PET measurement error and quantification methods may have a great impact on study power [8]. This simulation study extends that work by examining bias and measurement error for individual measurements. Under this realistic scenario for generation of study data, we can examine the study power implications for different trial designs: recruitment from primary sites versus accelerating enrollment with secondary sites, and unselected designs versus enrichment for patients considered more likely to show an association between the biomarker and clinical response.

Case study: Early FDG PET response as a predictive biomarker for response to breast cancer neoadjuvant chemotherapy

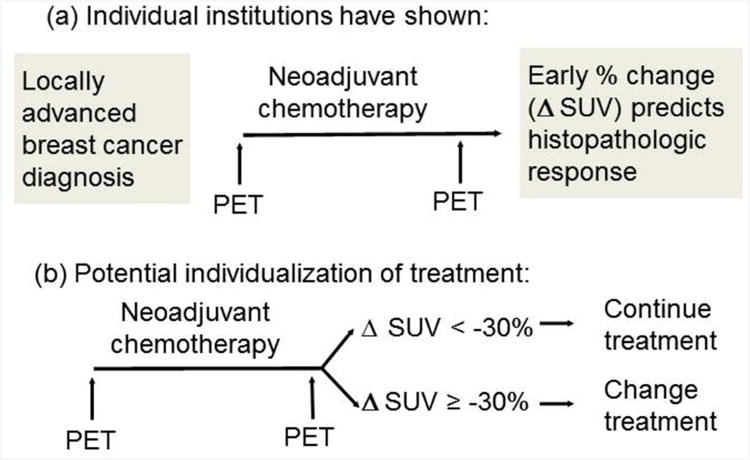
Several studies have shown that early metabolic response measured by FDG PET after 1-4 cycles of neoadjuvant chemotherapy for locally advanced breast cancer (LABC) predicts subsequent histopathologic response (Figure 1(a)) [9-13]. These results suggest that early changes in FDG uptake could be used as a predictive biomarker, with potential to direct therapy by discontinuing ineffective therapies and continuing effective therapies (Figure 1(b)). Testing of this treatment paradigm could be accomplished using a marker-based strategy design [14]. However, while published evaluations of FDG PET response were relatively consistent in demonstrating an association between early metabolic response and histopathologic response, most were single-center observational studies. Breast cancer patient populations and neoadjuvant chemotherapy regimens varied, as did FDG PET patient preparation, scanning protocol, and quantification of FDG uptake. Since FDG PET scans must be performed prospectively, this is a scenario where a multicenter observational study is a viable intermediate step toward validation of serial FDG PET as a predictive biomarker.

Figure 1.

Schemas for using quantitative FDG PET imaging as a predictive biomarker. (a) Design for single-institution observational studies, and for proposed multicenter replication. (b) Potential clinical application of marker-driven therapy.

The most common method of quantifying FDG uptake is the standardized uptake value (SUV), which normalizes the measured tissue activity in a region of interest (identified within a tumor site) by injected dose and patient mass. Following the observation that cell kill by cytotoxic chemotherapy is expected to occur as a percentage of tumor cells rather than absolute numbers [15], metabolic response (decrease in FDG uptake as a result of effective therapy) is measured as the percentage change in FDG SUV:

$$\mathit{\text{SUV}}\mathit{\text{change}}=100\ast \frac{({\text{SUV}}_1-{\text{SUV}}_0)}{{\mathit{\text{SUV}}}_0}$$

where SUV₀ is baseline (pre-therapy) FDG SUV, and SUV₁ is follow-up (i.e., after 2 cycles of neoadjuvant chemotherapy) FDG SUV. Several percentage change thresholds have been proposed as reflecting a minimal clinically meaningful metabolic response, or a response that is unlikely to be due to chance [16-18]. However, factors affecting the apparent change in FDG SUV for breast cancer treatment response may limit the utility of standardized criteria. Perhaps most important is that untreated breast tumors may have lower FDG uptake than other cancers routinely imaged with FDG PET, but are still detectable due to the low average uptake of normal breast tissue [19]. For low-uptake tumors, circulating FDG in the bloodstream and uptake by surrounding normal tissue may account for a relatively large fraction of the measured SUV; since these fluctuating background levels are not expected to change predictably with treatment, they may obscure decreases in tumor FDG metabolism that could accompany treatment response. Prior studies have shown that FDG PET SUV is not effective in measuring response when pre-therapy SUV is < 3 [10, 20, 21], and that dynamic PET imaging provides superior precision in measuring response in low-uptake breast tumors [12]. While results from dynamic PET imaging inform our simulation design, this multicenter study will only examine the standardized uptake value (SUV), which requires less scanner time, is measured by clinical scanner software, and is more well-developed toward broad use in clinical trials [17].

Response to pre-surgical breast cancer chemotherapy is evaluated by pathologic complete response (pCR) at surgery, which has a strong association with long-term clinical prognosis [22]. As assessed by the local imaging study used for data simulation, pCR has occurred when no invasive tumor is seen by microscopic inspection of post-therapy surgical breast tissue specimens. The primary analysis will be logistic regression, with percent change in SUV predicting pCR and the C-statistic examined as a preliminary measure of classification accuracy. Known clinical predictors of pCR should be included as covariates in logistic regression models evaluating SUVchange [23] but are omitted here for simplicity of presentation.

The goal of these studies is to optimize use of resources for a prospective multicenter observational study as an intermediate step for validation of SUVchange as a predictive biomarker for breast cancer neoadjuvant therapy response. Therefore, the focus of simulations is on study power for combinations of design strategies (limited versus broad recruitment of sites; unselected versus enrichment design). To represent variability associated with inexperienced sites performing PET for quantitative analysis, we assume two classes of sites: experienced (primary) sites that are likely to produce SUVs with lower measurement error, and secondary sites expected to yield SUVs with higher measurement error due to past performance, limited experience, and/or higher staff turnover. We estimate the loss of power expected when accrual is accelerated through increasing reliance on secondary sites. In the ideal scenario, all sites could achieve the performance of primary sites. However, this expectation is unrealistic; generalizability and practical considerations require the inclusion of secondary sites as well as sites with greater experience and demonstrated measurement precision. We therefore consider the impact on power when a study with a fixed sample size varies in the proportion from primary and secondary sites.

In the unselected design, all enrolled patients are followed for early response by FDG PET SUV and pathologic complete response. In the enrichment design, patients with SUV < 3 at baseline are not be assessed for metabolic or histopathologic response, but are instead replaced by patients with higher baseline FDG uptake. For a prospective observational study with patients receiving standard therapy, patient scans are the greatest contributor to study costs. To keep total costs consistent, for every two patients with SUV < 3, an additional patient is recruited, and assessed for response if baseline SUV ≥ 3. In this way, we can compare the study power for the unselected design and the enrichment design, for the same total study cost.

Results for both design strategies rely heavily on the measurement error scenarios for individual SUV values. Simulation results will only be valuable if the input variables are based on relevant empirical data. The simulation parameters and their rationale are described below.

Simulation parameters

Key parameters for the simulation are described in Table 1. We assumed that the true distribution of FDG SUV in patients with LABC was similar to that observed in our local imaging study [12]. SUV data for the simulation were generated by sampling from the pairs of SUV values (SUV at baseline and mid-therapy), with replacement [24]. Response data were simulated by random sampling from a binomial distribution with probability estimated by logistic regression models fitted to our local LABC study. Separate logistic regression models were fitted for baseline SUV ≥ 3 (N=50) and baseline SUV < 3 (N=25):

Table 1.

Key parameters in the simulation of power calculations for a multicenter trial estimating the association between percent change in FDG PET SUV and pathologic response to neoadjuvant chemotherapy for patients with locally advanced breast cancer.

Simulation input	Description	Values explored Primary sites	Values: explored: Secondary sites
Reference SUV data	Baseline and mid-therapy SUV values were sampled together from the University of Washington locally advanced breast cancer (LABC) dataset (N=75), with replacement, to form simulation datasets.
Response data	1 = pathologic complete response 0 = other than pathologic complete response Response (0/1) was generated from a binomial distribution with the response probability modeled by logistic regression for percentage change in true SUV.	See equation 1
Sample size	Sample size for hypothetical study (all centers combined, without exclusions based on baseline SUV)	N=100
Percent secondary	Percent of SUV measurements taken from sites expected to have higher measurement error	25% 50% 75%
Percent error (V%)	Random noise (with mean 0 and standard deviation V% of the reference SUV value) added to reference SUV values	20%	40%
Percent bias (B%)	Random noise (with mean B% of the true SUV value, and standard deviation V% of the true SUV value) added to the reference SUV values	20% -20%	40% -40%
Absolute error (V)	Random noise (with mean 0 and standard deviation V) added to the reference log(SUV) values	0.25	0.50
Absolute bias (B)	Set of observed SUV values are generated by adding random noise (with mean B and standard deviation V) to the reference log(SUV) values	0.25 -0.25	0.50 -0.50
Correlation (ρ)	Correlation of noise added to baseline and mid-therapy reference SUV values for the same person to create observed values. Random noise is generated by a bivariate normal distribution.	0.1	0.1

$$\begin{array}{l}\text{baseline}\text{SUV}\ge 3:\mathit{\text{logit}}(\mathit{\text{pCR}})=-3.13-0.039\ast \mathit{\text{SUV}}\mathit{\text{change}}\\ \text{baseline}\text{SUV}<3:\mathit{\text{logit}}(\mathit{\text{pCR}})=-2.29-0.015\ast \mathit{\text{SUV}}\mathit{\text{change}}.\end{array}$$ Equation(1)

For example, simulated pCR for a patient with true baseline SUV ≥ 3 and 10% decline would have a 0.06 probability of pCR, in contrast to a 0.49 probability of pCR with 80% decline. For patients with true baseline SUV < 3, estimated pCR probabilities were 0.11 and 0.25 for 10% and 80% decline, respectively.

The sample size of N=100 was chosen as an incremental increase in size over the single center study, and a reasonable moderate size for a multicenter study. As described in the Introduction, rapid multicenter replication of single-center associations is the goal, rather than specific effect sizes or biomarker cutpoint refinement. For an enrichment design, more than 100 patients would have a first scan, but fewer than 100 would have a second scan and be used for analysis. “Percent secondary” refers to the percentage of patients who would be recruited from sites with less experience in monitoring breast cancer chemotherapy using FDG PET.

While simulated response data were generated from the reference SUV data, power under scenarios for measurement error and study design were based on “observed” SUV data generated by adding error to the reference values:

$$\left(\begin{array}{c}\text{SUV}{o}_{ij0}\\ \text{SUV}{o}_{ij1}\end{array}\right)=\left(\begin{array}{c}\text{SUV}{r}_{ij0}\\ \text{SUV}{r}_{ij1}\end{array}\right)+\left(\begin{array}{c}{e}_{ij0}\\ e_{ij1}\end{array}\right).$$

In this equation, SUVo_ij0 is the observed baseline SUV for the jth patient at center i, SUVo_ij1 is the follow-up measurement for the same patient, SUVr_ij0 and SUVr_ij0 are the reference SUV values for the same patient (the values sampled with replacement from the N=75 LABC dataset), and e_ij0 and e_ij1 are measurement error.

We next describe the measurement error scenarios examined (Table 1). “Percent error” refers to SUV measurement error as it has been described in much of the test-retest repeatability data to date. While the widely accepted measurement error standard deviation from test-retest studies is 10% [25], the average is higher for multicenter studies [26], even for multicenter studies of pseudo-patient phantoms, in which biologic variability does not occur [27, 28]. Based on these and other repeatability and reproducibility studies we chose representative values of 20% error for primary sites and 40% error for secondary sites. We also examined systematic bias, in which observed SUV values are not only more variable than the reference data, but have an expected value (mean) different from that of the reference data. Positive and negative 20% bias were considered for primary sites, and positive and negative 40% bias were considered for secondary sites.

Although PET measurement error is usually described as a percentage, the seminal work of Weber [25] provided evidence to support describing errors in individual PET SUV measurements in terms of absolute values of SUV units. Therefore, we also examined a range of simulations with absolute error and bias. However, since we made the common assumption of a normal (Gaussian) distribution for the measurement error, we used as a starting point the approximately normal distribution of log-transformed SUVs [29]. Values for log(SUV) of 0.25 and 0.5, approximately 1/4 and 1/2 of the pooled standard deviation of baseline and follow-up reference values, were used as values for absolute bias and standard deviation of error for primary and secondary sites respectively. Due to the log-transformation of SUV for absolute error/bias, we expected the distributions of simulated data with percentage error/bias and absolute error/bias to be similar. For simplicity of presentation, we assumed the bias and/or error distribution was the same for all primary sites and for all secondary sites.

With i taking the value 0 for primary sites and 1 for secondary sites, the error terms for the “percent bias” scenario have the distribution

$$\left(\begin{array}{c}{e}_{ij0}\\ e_{ij1}\end{array}\right)~N\left(\right(\begin{array}{c}{\mathrm{B}}_i\times \text{SUV}{r}_{ij0}\\ {\mathrm{B}}_i\times \text{SUV}{r}_{ij1}\end{array}),(\begin{array}{cc}{({\mathrm{V}}_i\times \text{SUV}{r}_{ij0})}^2& \rho \times {\mathrm{V}}_i\times \text{SUV}{r}_{ij0}\times {\mathrm{V}}_i\times \text{SUV}{r}_{ij0}\\ \rho \times {\mathrm{V}}_i\times \text{SUV}{r}_{ij0}\times {\mathrm{V}}_i\times \text{SUV}{r}_{ij0}& {({\mathrm{V}}_i\times \text{SUV}{r}_{ij1})}^2\end{array}\left)\right),$$

with B, V, and ρ as described in Table 1. The calculations for absolute error and bias are similar, but are applied to log-transformed reference values.

The error and bias models can result in observed SUV data that would likely not be analyzed as observed in the hypothetical trial under consideration. For example, a mass with an SUV of 0.8 at baseline would be unlikely to be identified as a malignancy. Therefore, ceiling and floor values were established for simulated SUV values, with a minimum of 1.3 for baseline and normal breast average of 0.5 [19] for follow-up, and a maximum of 20 for both.

Power is the probability of rejecting the null hypothesis of no relationship in a logistic regression model predicting pathologic complete response (pCR) by percent change in SUV, with a two-sided Type I error rate of α = 0.05.

Results

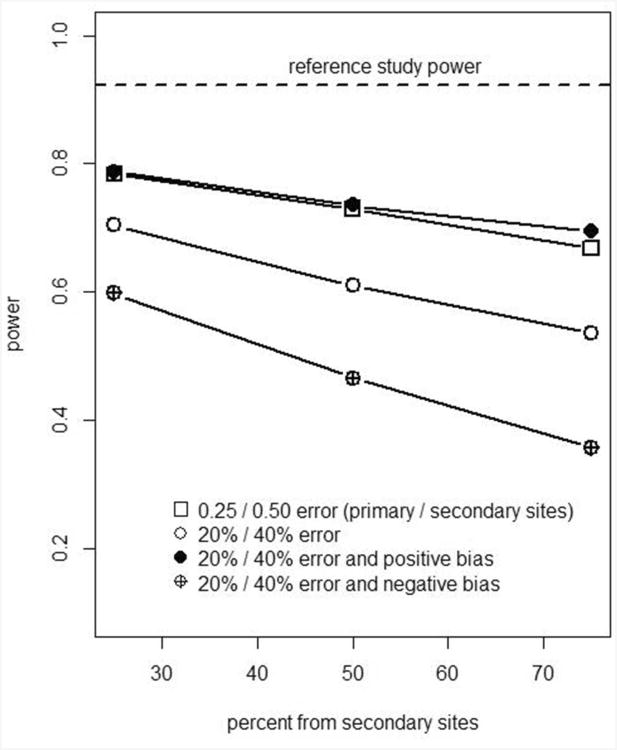
Results for simulations with 10,000 iterations each are presented in Figures 2 and 3, and Table 2. Figure 2 shows power for recruitment strategies in which 25%-75% of patients are from secondary sites, under different scenarios for bias and error in measuring FDG PET SUV. Table 2, column 1 is the power based on “reference” SUV values and responses. Without additional measurement error, the power for finding an association between SUV change and pCR was 0.92 for the unselected design (Figure 2, horizontal line).

Figure 2.

Graphical presentation of Table 2 error conditions 1-5: impact of recruitment strategy (balance of primary and secondary sites) on study power, N=100 patients (200 scans).

Figure 3.

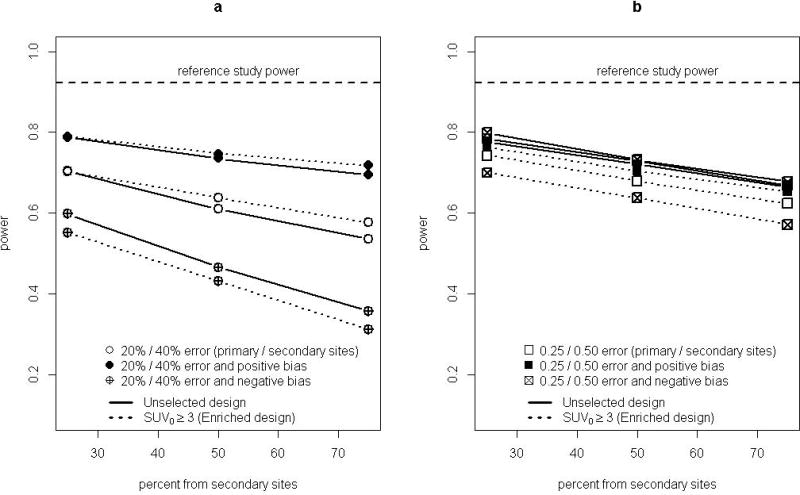
Graphical presentation of relative power for unselected design (solid lines) and enrichment design (dashed lines), for a study with N=200 scans. (a) error and/or bias as a percentage of reference values. (b) error and/or bias in absolute log(SUV) units.

Table 2.

Power calculations for a multicenter trial estimating the association between percent change in FDG PET SUV and pathologic response to neoadjuvant chemotherapy for patients with locally advanced breast cancer, calculated by simulation of 10,000 datasets with characteristics described in Table 1.

Error conditions for each scenario:	1	2	3	4	5	6	7
	Ref. power	20%/40%	20%/40%	−20%/−40%	0.25/0.50	0.25/0.50	−0.25/−0.50
Simulation scenarios:		pct error	pct bias	pct bias	abs error	abs bias	abs bias
75% from primary sites
- all data analyzed (no selection by SUV0)	0.92	0.71	0.78	0.60	0.78	0.78	0.79
- enriched sample (observed SUV0 ≥ 3)	0.87	0.70	0.79	0.54	0.73	0.76	0.70
25% from primary sites
- all data analyzed (no selection by SUV0)	0.92	0.54	0.69	0.36	0.67	0.66	0.68
- enriched sample (observed SUV0 ≥ 3)	0.87	0.57	0.71	0.32	0.62	0.65	0.57

SUV0 is SUV of first scan

N=100 for unselected design (200 scans), N < 100 for enrichment design (200 scans)

Impact of recruitment strategy

Power for the unselected design was substantially reduced (lower than the reference line in Figure 2) under all bias and/or measurement error scenarios examined. When most additional error was of modest size (for example, when 75% of simulated patients were from primary sites with lower additional measurement error), the power was about 10-30 percentage points lower than for the reference sample. The lowest power was for the scenario with negative bias as a percentage of the reference SUV. This was not due to a weaker true relationship between SUVchange and pCR, since for all scenarios the response values were simulated from reference data, rather than simulated “observed” data with additional measurement error. With negative bias it is likely that percent change was attenuated by simulated “observed” data hitting the floor values of 1.3 for baseline and 0.5 for follow-up SUV. Accelerating study enrollment by recruiting 75% of patients rather than 25% from sites expected to have greater measurement error (moving along the X axis in Figure 2) led to an additional decrease in power of 10-30 percentage points.

For the unselected design, scenarios with absolute measurement error and bias resulted in the same power as for absolute measurement error alone (Table 2, columns 5-7). Absolute bias largely cancelled when calculating percentage change in SUV, as would occur if a scanner were miscalibrated but did not drift or undergo further calibration between scans. This presumed cancellation of bias for serial scans may not apply if a patient is not imaged on the same PET/CT scanner each time. Bias as a percentage of baseline SUV and follow-up SUV did not generally cancel when calculating percentage change.

Impact of unselected vs. enrichment design

Approximately 1/3 of the baseline scans (33/100) sampled from the reference data had SUV1 (baseline SUV) less than 3. Not performing follow-up scans for those patients would free funds for recruitment of approximately 16 additional patients, of whom about 11 would have SUV1 ≥ 3, for a final average sample size of N=77. The greater effect size for detecting an association between SUVchange and pCR for patient scans with SUV1 ≥ 3 was offset by the smaller sample size, resulting in lower power (0.87) for the enrichment design using reference data (Table 2, column 1).

Power for the enrichment design (dashed lines in Figure 3) ranged from substantially lower than to slightly higher than for the unselected design (solid lines in Figure 3) for the error and bias scenarios examined. Figure 3(a) shows scenarios with error and/or bias as a percentage of SUV values (columns 2-4 of Table 2). Figure 3(b) shows scenarios with absolute error and/or bias (columns 5-7 of Table 2). For error as a percentage of SUV and no systematic bias, power was similar for unselected and enrichment designs (Table 2, column 2). Under absolute error (column 5) the percentage differential between power of unselected and enriched designs was similar to that for reference data. Power for enrichment designs compared to unselected designs was low under negative bias, especially for absolute bias (column 7). Both scenarios for positive bias (columns 3, 6) had power similar to that of the unselected design. These scenarios did not have higher power (relative to other enrichment design scenarios) because more of the data were generated under the larger SUV1 ≥ 3 model effect size, since the additional bias and/or measurement error does not affect the underlying model for generating response values in the simulation. (Equation 1 always used reference data without additional error.) However, the positive bias did lead to fewer excluded patients under the enriched design: the average sample size was close to 90 for all positive bias scenarios. This was likely the reason that power could be approximately the same as for the unselected design for these scenarios, but never substantially higher. The C-statistic was examined as a preliminary measure of classification accuracy, in anticipation of cutpoint selection for future marker-directed therapy (Figure 1(b)). The average C-statistic for reference data was 0.71 for both unselected and enrichment designs, and was 0.63-0.69 for all measurement error scenarios examined.

Discussion

Power calculations from simulation studies may be used to inform the efficient design of a multicenter study to replicate single-institution findings. This scenario is a common-sense step toward clinical validation of predictive biomarkers when the biomarker cannot be assessed retrospectively in archived data from large clinical trials. As a case study, we examined serial FDG PET to predict early response to breast cancer neoadjuvant chemotherapy, using both unselected designs and enrichment designs assessing only patients with high initial FDG uptake. The number of total scans was held fixed since the cost of scans is a limiting factor for studies involving quantitative imaging. Reference power (from source data with no added error) was 0.92 for N=100 to detect an association between percentage change in SUV and response. With moderate (20%) simulated measurement error for 3/4, 1/2, and 1/4 of measurements and 40% for the remainder, power was 0.70, 0.61, and 0.53 respectively. Reduction of study power was similar for other manifestations of measurement error (bias as a percentage of true value, absolute error, and absolute bias). Any increased power by enriching the sample for patients with initial SUV ≥ 3 was offset by the smaller analysis sample size due to the cost of initial scans for patients who were not assessed for response. The simulations demonstrated that different assumptions about measurement error (drawn from observations from test-retest studies in both patients and pseudo-patient phantoms) had a substantial impact on study power.

In addition to addressing design considerations for a specific scenario, this case study is intended as a template for future simulation studies to design clinical trials involving quantitative imaging. It demonstrates the value of simulation studies in situations where different study designs are under consideration, and where preliminary data are available from complementary sources (breast cancer response to therapy; measurement error parameters for FDG PET). The magnitude of effect of PET measurement error on study power supports the need for cross-calibration of PET scanners, and for thorough understanding of PET measurement error. For example, it is unclear whether PET measurement error manifests in SUV units, log(SUV) units, or as a percentage of true SUV. Results from a reproducibility study with 26 patients suggest that mean-variance relationships between measurement error and SUV magnitude could be avoided by modeling error as a percentage for SUVmax (based on the pixel with maximum uptake – the measure used for clinical reports and for the reference data study) or by absolute SUV units for SUVmean (the average within a region of interest of fixed size, favored for research due to superior reproducibility) [30].

Additional future work may address how to incorporate site-specific calibration results into study analysis. If calibration errors are detected during site initiation they are corrected, but similar errors may be likely to occur at that site in the future. While incorporation of audit results into measurement of study effects [31] does not apply directly in a setting in which error comes from primary data acquisition rather than abstraction errors, errors in variables methods will be applicable for later-stage studies for biomarker refinement.

The primary limitation of this approach to study design is that the simulation parameters could be incorrect, or not generalizable. For example, pCR was simulated without consideration for uncertainty in measuring logistic regression model parameters (Equation 1). Rather than a true modest effect without power to find significance, the observed association between percent change in SUV and pCR when SUV1 < 3 could have been random fluctuation from a truth of no relationship. When the power for the enrichment design is calculated under the assumption of no association between SUVchange and pCR when SUV1 < 3, we find scenarios that would favor the enrichment design (Supplementary Table), including the reference data without additional measurement error. Additionally, there have been changes in chemotherapy regimens and in patient selection (and tumor subtype) for neoadjuvant chemotherapy since the reference study accrued patients (1995-2007) [32].

In summary, the characteristics of measurement error and bias (percentage versus absolute), and the magnitude of error and bias, can have great impact on power and sample size. As study reliance on secondary sites increased to 75%, power was up to 24 percentage points lower than for studies with 25% of subjects from secondary sites, and up to 56 percentage points lower than the reference power with no additional measurement error. Enrichment designs could result in modest increases in power, but for most scenarios had power slightly lower than for an unselected design. Ongoing quantitative characterizations of PET imaging data and sources of measurement error will allow refinement of methods to inform planning of multicenter clinical trials involving quantitative imaging.

Supplementary Material

supp table

Supplementary Table. Power calculations for a multicenter trial estimating the association between percent change in FDG PET SUV and pathologic response to neoadjuvant chemotherapy for patients with locally advanced breast cancer, calculated by simulation of 10,000 datasets with characteristics described in Table 1. Unlike in Table 2 (which uses equation 1), the probability of pathologic response is 0.20 for all SUV1 < 3. SUV1 is SUV of first scan, N=100 for unselected design (200 scans), N < 100 for enrichment design (200 scans)