Physical Stature Decline and the Health Status of the Elderly Population in England

Abstract

Few research papers in economics have examined the extent, causes or consequences of physical stature decline in aging populations. Using repeated observations on objectively measured data from the English Longitudinal Study of Ageing (ELSA), we document that reduction in height is an important phenomenon among older individuals. On average, physical stature decline amongst older individuals occurs at an annual rate of between 0.08% and 0.10% for males, and 0.12% and 0.14% for females—which approximately translates into a 2cm to 4cm reduction in height over the life course. Since height is commonly used as a measure of long-run health, our results demonstrate that failing to take age-related height loss into account substantially overstates the health disadvantage of older birth cohorts relative to their younger counterparts. We also show that there is an absence of consistent predictors of physical stature decline at the individual level. However, we demonstrate how deteriorating health and reductions in height occur simultaneously. We document that declines in muscle mass and bone density are likely to be the mechanism through which these effects are operating. This has potential implications for the existing literature because if this decline is determined by deteriorating health in adulthood, the coefficient on a measured height when used as an input in a typical empirical health production function will be affected by reverse causality. While our analysis details the inherent difficulties associated with measuring height in older populations, we do not find that significant bias arises in typical empirical health production functions from the use of height which has not been adjusted for physical stature decline. Therefore, our results validate the use of height among the population over 50.

1 Introduction

Height is widely used as an objective measure of health status, for example it is commonly used in the large body of research evaluating welfare trends in historic populations and the long-run impacts of childhood environment. To address the lack of good quality data on other more direct measures, researchers have routinely used height as an indicator for both population health and early life conditions. Apart from the advantage that height is often available when other indicators are not, it also has several other useful properties. It is relatively easy to measure, it has an objective scale, and it is generally assumed to be fixed in late adolescence. Hence, it is seen as a useful proxy for childhood nutritional status and disease environment, and a potential complement to other indicators of health and welfare such as life expectancy and GDP. The presence of information on height thus allows researchers to investigate these topics in circumstances where lack of data would otherwise prevent it.

Given that height is regularly substituted as a measure for health status or early-life conditions, understanding the relationship between the height and health of individuals or societies is of obvious importance. Not surprisingly, a large literature exploring this relationship exists, including numerous articles in the most prominent economics journals. However, one aspect of the height-health nexus has been somewhat overlooked: physical stature decline associated with aging. The goal of this paper is to address this issue, which has a number of potential implications for the existing literature. Firstly, if age is an important determinant of height, then it is important not to confound the effects of age and cohort when comparing the physical stature of different birth cohorts. Secondly, if height is affected by some adult characteristic, such as health, then it is important not to confound the effects of height with the effects of the adult characteristic when estimating empirical models. For examples of papers in the economics literature which treat height as fixed, and do not adjust for age effects among older respondents by restricting analysis to those under 50 or otherwise, see Bozzoli et al. (2009), Case and Paxson (2008), and Smith et al. (2012). Therefore, although our findings focus on physical stature, our results also shed light on the validity of the use of height in previous research.

We begin by illustrating how reductions in height amongst older individuals represents an important phenomenon. To the best of our knowledge, this paper is the first to document the relationship between age and reductions in physical stature using longitudinal data on measured height in a large-scale nationally representative sample. We use predictions from a linear regression model estimated on the same individuals over time from the ELSA survey to determine the magnitude of physical stature declines. This analysis suggests that the height of both men and women falls by as much as 2 cm to 4 cm on average across the adult life course. We test whether age-related height reduction amongst the population is random, or whether it is predicted by either current or early-life environment.

To examine the determinants of physical stature decline, and following from our motivation which discussed the use of height in empirical research, we estimate a series of empirical models. Firstly, we model changes in height on a number of time-invariant, or fixed, variables and find little consistent evidence linking physical stature decline to adverse conditions in adulthood or early-life. Secondly, we utilize the panel dimension of the ELSA dataset and analyze how reductions in height are affected by changes in health status (measured using either grip strength or peak respiratory flow). Thus, we are effectively estimating a fixed effects regression model that accounts for unobserved heterogeneity by controlling for all time-invariant factors. Our results show how deteriorating health status contributes to physical stature decline for both males and females. These results are robust to a number of model specifications, changes in survey wave, and placebo regressions wherein we model earlier reductions in height as a function of later health changes. In addition, we are able to investigate one potential mechanism through which these effects are operating. We show that among women, physical stature decline is associated with reductions in body mass, which suggests that changes in bone density and muscle mass may be the relevant channels of interest.

The body of evidence we present clearly illustrates how physical stature decline is of a nontrivial magnitude, and also how it is correlated with deterioration in health. The implication of these findings is that the naïve inclusion of height which is not adjusted for physical stature decline as an additional explanatory variable in a model with health as the outcome could lead to biased results in the context of regression modeling as it is correlated with declining health. The coefficient on height could be affected by reverse causality, or omitted variable bias if physical stature decline and the outcome are both caused by some third confounding factor. Given that height is frequently used in this way, our findings may have important implications for the economics literature on the subject. We investigate the extent of this possible bias by estimating a number of health production functions wherein physical stature is included as an input. To measure the consequences of using height that has not been adjusted to account for physical stature declines over the life course (henceforth referred to as unadjusted height), we compare the coefficients produced via the inclusion of unadjusted height with those resulting from a standardized measure of physical stature that is not known to change over the life course: demispan. Despite the relatively large changes in height, the results in this section do not support the hypothesis that using unadjusted height will lead to substantially biased coefficients in similar applications. This pattern is also observed when we use unadjusted height from earlier waves.

2 Existing Research

The relationship between height and economic welfare is a popular research topic. A summary of the growth in this literature is provided by Steckel (2009), who listed 325 studies on physical stature published between 1995 and 2009. This literature has led to the reconsideration of living standards during the Industrial Revolution (Voth, 2003), and the status of the Native Americans (Steckel and Prince, 2001). Data have often been gathered from innovative sources, such as prison and army records (Mokyr and Ó Gráda, 1996) and skeletons (Steckel, 2005). Easterlin (2000) and Cutler et al. (2006) reference the use of height to document improvements in living conditions over time. Fogel (2004a; 2004b) linked nutritional gains to economic growth via height, and physical stature has also been used to compare sub-groups of individuals (Subramanian et al., 2011 and Bodenhorn et al., 2012).

At the individual level, height has been shown to be related to childhood disease environment in developed countries (Alderman et al., 2011; Bozzoli et al., 2009), including historical populations (Peracchi and Arcaleni, 2011; Young et al., 2008), although the relationship is not as clear for developing nations (Akachi and Canning, 2010; Deaton, 2007). The economics literature has noted the association between height and a number of adult outcomes, including cognitive ability, labor market status, and health (Case and Paxson, 2008; Deaton and Arora, 2009; Denny, 2010), and at least part of this relationship is believed to be due to the aforementioned association with early environment (Case and Paxson, 2010). Interestingly, Mankiw and Weinzierl (2010) have argued that the above properties encapsulated by human height should be used as an efficient alternative to income based tax policy.

Many of the papers discussed in Steckel (2009) use self-reported height, which has the potential to be affected by various types of measurement error (Engstrom et al., 2003; Rowland, 1990). Depending on the application, the issue is most serious when the reporting bias is systematically correlated with some characteristic of the individual. Using objectively measured height does not solve this issue if physical stature decline occurs. To the best of our knowledge there are very few papers in the economics literature which identify the consequences of this potential measurement error in height. This issue of potential bias is raised, but not investigated in Leon et al. (1995), Case and Paxson (2008) and Smith et al. (2012). Mokyr and Ó Gráda (1996) adjust for the age profile in prison records, while more recently Huang et al. (2013) examined this issue with Chinese data.¹

Clearly, all of these papers rely on the assumption that height is positively correlated with health, or some other measure of wellbeing. There is substantial empirical evidence that height is indeed associated with a wide range of outcomes (as we note in the references above). For both the anthropometric and early life conditions literature, this requires the assumption that height is fixed in early adulthood. For the former this is the case because cohort comparisons are generally based on cross sectional comparisons, and it is not possible to distinguish the effects of age and cohort without longitudinal data. For the latter, if height changes during adulthood then this could induce spurious findings. For example, individuals may have low height, not because of early environmental effects, but due to some other factor such as age, adult health or adult socioeconomic status. This is particularly important if physical stature decline itself is a function of early environment, or the outcome of interest is also a function of reductions in height.

There is some existing evidence that height declines with age in the anthropometric literature, but this generally comes from surveys with relatively small samples which are not nationally representative. The data requirements to establish physical stature decline are quite burdensome, as rigorously testing the existence of shrinking ideally requires longitudinal data with height measured repeatedly, and objectively, not just self-reported. Using data from Western Australia, Chandler and Bock (1992) found evidence of physical stature decline after the age of 40, as did Cline et al. (1989). Their analysis suggested that up to 55% of the difference between birth cohorts can be attributed to age effects, and that the cumulative effect does not become significant until age 60. Galloway et al. (1990) found that physical stature decline is related to maximum height and bone density, although they rely on self-reports for estimating maximum height. A related study highlighted the fact that individuals are not aware of physical stature decline (Galloway, 1988).

The consequences of physical stature decline have been noted to some extent in the clinical and anthropometric literatures, but not in economics (with one notable exception). The proposed solution has been to use arm or leg length to substitute for measured or reported height (Raxter et al., 2006; Sethi et al., 1995; Webb et al., 2008; Whitley et al., 2012). Recently, Hirani and Mindell (2008), and Hirani et al. (2010) developed an updated correction procedure using arm length. Maurer (2010) instrumented for height using limb length. However, this may not be valid if physical stature decline is correlated with maximum height (a feature we have confirmed in these data). The one exception to the absence of evidence on physical stature decline in the economics literature is Huang et al. (2013). These authors used data from the Chinese Health and Retirement Longitudinal Study (CHARLS) and estimated the extent of changes in height in this population, the association between physical stature decline and socioeconomic variables, and how this impacts on estimates of the effects of height and various adult outcomes. It is not clear whether their results are generalizable from the specific Chinese context to more developed countries, especially given the type of environments faced by the individuals in their data, which are not necessarily comparable to those faced by individuals in Western societies. In addition, as they only have a single cross-section of data, they rely on estimating pre-shrinkage height by predicting the relationship between limb length and height in a separate sample.

The main contribution of this paper is that we focus on nationally representative data which contains multiple observations for each individual over time. Therefore, we are able to directly measure physical stature decline using objective measured height across four waves and 10 years. We are also able to determine the relevance of limb length by comparing results where we substitute demispan (arm length) measurement for height. We establish that there is surprisingly little consistent association between physical stature decline and time invariant individual characteristics. However, as we have longitudinal data, we are able to demonstrate that the extent of height change is predicted by deterioration in health, as well as discuss a potential mechanism for these effects. In the final section we discuss the implications of physical stature decline for the existing economics literature.

3 Data

3.1 Sample

The English Longitudinal Study of Ageing (ELSA) is a nationally representative panel of individuals aged over 50 in England.² The first round of data recruitment (Wave 0) occurred separately in 1998, 2000, and 2001 from the Health Survey for England (HSE).³ Respondents were re-interviewed in 2002–2003 for the first wave. The second wave took place in 2004–2005, the third wave in 2006–2007, and Wave 4 in 2008–2009. Detailed health exams (which included nurse measured height) were conducted in Wave 0, Wave 2, and Wave 4. As well as providing demographic and socioeconomic information in each round, Wave 3 additionally included a retrospective life history wave, which has been shown to be an effective measure of early life conditions (Smith, 2009).

The sample size for analysis is presented in Table 1. Firstly, we focus on estimating actual physical stature decline as the difference in measured height between Wave 0 and Wave 2, giving a total of 6,981 observations with valid height. Of these individuals 5,168 are also present in Wave 3 to answer the module on childhood conditions. We also measure reductions in height between Wave 0 and Wave 4, which results in a sample of 4,625. Finally, in Wave 0 demispan measurement was taken from individuals aged 65 and over who also have height data, giving 4,654 observations. Because not all of these individuals were re-contacted for Wave 2, this represents a separate analysis sample. In all of our analysis we consider males and females separately. We are able to make use of differences in the length of time since the first interview to determine age effects when estimating physical stature decline between Wave 0 and Wave 2, as individuals in Wave 0 were recruited from different years of the HSE.

Table 1.

Analysis Sample

	Men	Women	Total
Measured Height in Wave 0 and Wave 2	3,135	3,846	6,981
Measured Height in Wave 0 and Wave 2 and Childhood Variables in Wave 3	2,303	2,865	5,168
Measured Height in Wave 0, Wave 2 and Wave 4	2,051	2,574	4,625
Demispan Sample (65+ in W0)	2,098	2,556	4,654

Note: Data from the English Logitudinal Study of Ageing is publically available from the UK data service http://discover.ukdataservice.ac.uk/catalogue?sn=5050

Table 2 gives descriptive statistics for variables in the regression models presented in Section 4 and Section 5 for the sample with measured height in Wave 0 and Wave 2, and the demispan sample. Initial baseline (Wave 0) measurements were taken under the auspices of the Health Survey for England. Demispan was recorded by nurses from individuals aged 65 years or over who were able to straighten their arms, while height was recorded during the main interview. The survey manual (HSE 1999) defines the demispan measurement as the distance between the sternal notch and the finger roots with arm out-stretched laterally. The measurement occurs by using a modified tape measure which hooks onto the gap between middle and ring fingers and then extends to measure the distance to the middle of the respondent’s back.⁴ For measuring height in the HSE interviewers were provided with a portable stadiometer, a device which consists of a sliding bar on a height scale which rests on top of the respondent’s head.⁵ Height was recorded without shoes, and to the nearest even millimetre.

Table 2.

Variables For Regression Models

Sample With Measured Height in W0 and W2
	Mean	Median	SD	N
Year of Birth	1935.69	1939	66.48	6981
Age Wave 0	60.98	60	9.46	6981
Age Wave 2	66.09	65	9.54	6981
Age Wave 4	67.84	68	13.31	5309
HSE Start Year 1998	0.44	0	0.5	6981
HSE Start Year 1999	0.17	0	0.38	6981
HSE Start Year 2001	0.39	0	0.49	6981
Male	0.45	0	0.5	6981
Excellent Childhood Health	0.33	0	0.47	5168
Left School Before 16	0.55	1	0.5	6981
Has a Degree	0.12	0	0.33	6981
5 Quantiles of Equivalised Household Income (W0)	3.15	3	1.4	6101
Bedrooms in Childhood Residence	2.93	3	0.91	4981
Number of Facilities in Childhood Residence	2.86	4	1.44	4994
Grip Strength W2	29.51	28	11.39	6862
Grip Strength W4	28.15	26	11.32	4677
Peak Flow W2	339.35	325	137.92	6303
Peak Flow W4	320.85	310	142.31	4379
Measured Height in Wave 0 (CM)	165.89	166	9.33	6981
Measured Height in Wave 2 (CM)	165.3	165	9.52	6981
Measured Height in Wave 4 (CM)	165.02	165	9.68	4625
Height Difference W0–W2	−0.59	−1	1.73	6981
Height Difference W0–W4	−1.19	−1	2.58	4625
Self Rated Health W2 (1=Excellent, 5=Poor)	2.76	3	1.09	6975
Self Rated Health W4 (1=Excellent, 5=Poor)	2.81	3	1.06	5204
Sample With Measured Demispan (65+ in W0)
	Mean	Median	SD	N
Self Rated Health W0 (1=Excellent, 5=Poor)	2.27	2	0.97	4653
Demispan (cm)	76.81	77	5.31	4654

For Wave 2 and Wave 4, all core members of the survey who had completed the previous interview in person were eligible for a nurse visit, where height was recorded. A similar procedure to the HSE was used for recording height.⁶ Where the nurse was unable to measure standing height the respondent was asked to estimate their own height.⁷ If the nurse believed that this guess was more than 2 cm off, the measure was recorded as unreliable. The nurse was unable to measure height in relatively few cases (for example, less than 5% of individuals in Wave 2).

Attrition is a feature of these data, and we carefully consider the consequences of attrition for our results throughout the analysis. There are a number of important points to note on this issue. 911 men and 990 women drop out of the sample between Wave 2 and Wave 4, and thus the power of our statistical tests will decrease as a result of this decrease in sample size. Attrition may have other effects. We have compared the mean values for respondents who remain in the sample, relative to those who leave the survey, and find only relatively small differences. Nevertheless, attrition does differentially affect older individuals, so the analysis sample in Wave 4 is younger than would be expected without attrition. Additionally, these respondents are less well educated. Our analysis later presents evidence showing a link that connects aging, ill-health, and height loss. If those who leave our panel are older and less educated, it is likely that these individuals would have experienced a greater deterioration in both health and stature, compared to those who remained in the survey. Thus, if our results are affected by attrition bias, this bias would underplay the links between aging, stature loss and ill health.

We also take a number of steps to specifically account for loss to follow up in our analysis. Firstly, we are using height differences generated by subtracting measured height in Wave 0 with measured height in Wave 2 and Wave 4. Tracing and comparing the birth cohort height trajectories (using levels) over multiple waves would be problematic, and is therefore avoided. Secondly, we use the fact that we have multiple waves of data to perform sensitivity analyses. Our expectation is that some common element generating attrition exists. If attrition is biasing our results, then we would expect to see a difference in the analysis where we use the height difference between Wave 0 and Wave 2 and Wave 0 and Wave 4 as the outcome. Therefore this approach provides a sensitivity analysis for determining whether the missing data are affecting the estimates in this paper.

3.2 Physical Stature Decline

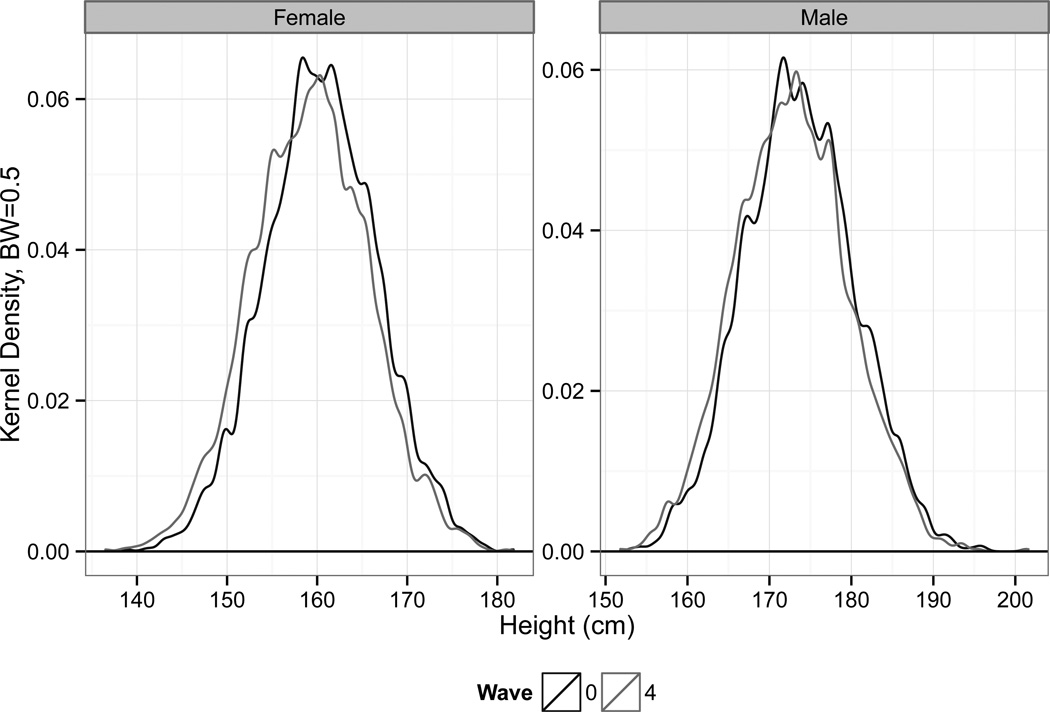
We present initial evidence on the extent of physical stature decline based on the actual observed change in measured height across waves. All of our analysis concerns the change in height for the same individual, and not estimated using separate cohorts or samples. As outlined in Table 2, on average respondents lost 0.6 cm between Wave 0 and Wave 2, compared to the overall mean of 166 cm. Consistently, the mean reduction from Wave 0 to Wave 4 was twice this. Figure 1 shows the distribution of height for men and women in both waves. Interpreting the raw descriptive statistics is complicated by the fact that baseline height was collected in three different years depending on the initial HSE year, but on average this translates into a reduction of 0.1 cm per year. In all our analyses we consider men and women separately, as previous research has established that women are more likely to be affected by physical stature decline (Huang et al., 2013). This is confirmed in our data.

Figure 1.

Height Distribution of Men and Women

Source: ELSA Sample. Note: Note: Initial intake for Wave 0 of the survey occurred at three different years: 1998, 1999 and 2001. Wave 4 was conducted in 2008–2009. On average, for the sample as a whole, 5 years pass between Waves 0 and Wave 2 and 9 for Wave 0 and Wave 4. Estimates shown are kernal density estimates using a bandwidth of 0.5.

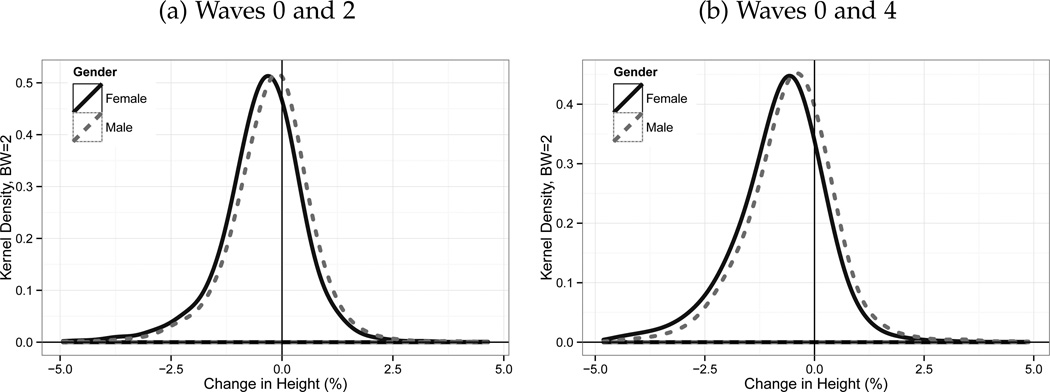
Figure 2 presents kernel density estimation plots of the percentage change in height. Panel (a) displays the difference between Wave 0 and Wave 2. Both men and women exhibit distributions where the mean is negative, and this is particularly evident for women. Panel (b) shows the corresponding density plot for the change in heights between Wave 0 and Wave 4. The physical stature decrease is even more pronounced over this longer time period. We focus on the percentage change rather than the absolute change in order to capture the fact that the rate of shrinking is greater for taller individuals (which is also confirmed in the data).

Figure 2.

Changes in Height Between Waves.

Source: ELSA Sample. Note:Note: Initial intake for Wave 0 of the survey occurred at three different years: 1998, 1999 and 2001. Wave 4 was conducted in 2008–2009. On average, for the sample as a whole, 5 years pass between Waves 0 and Wave 2 and 9 for Wave 0 and Wave 4. Estimates shown are kernal density estimates using a bandwidth of 2.

While the mean of each height distribution in Figure 2 is evidently less than zero, a considerable portion of individuals appear to increase in height.⁸ We believe that this variation stems from two sources, measurement error on the part of the interviewer and diurnal fluctuations due to spinal compression. It is well established in the biology literature that height varies quite considerably over the day (Tillmann and Clayton, 2001). It is important to consider how this error will impact our results. For the tracing of the average height loss function and the average physical stature decline by birth cohort, this type of classical measurement error will serve to increase the associated standard errors, although we note that all our results indicate that shrinkage is important at all conventional statistical significance levels. We believe that this mismeasurement can be legitimately be viewed as random. Firstly, since height is measured objectively by interviewers, there is little reason to believe that the potential for reading or assessing the height value (as performed by the interviewer) would differ by height (except for perhaps the extremely tall). Secondly, there is no reason to suspect that the time of day that each measurement took place at was systematically biased. Finally, our analysis deliberately uses percentage change in height (as opposed to the absolute change in height) as the measure of shrinking in order to account for this issue. Thus, if measurement error was systematically related to the level of height, this would be eliminated by making our outcome of interest the proportionate change.

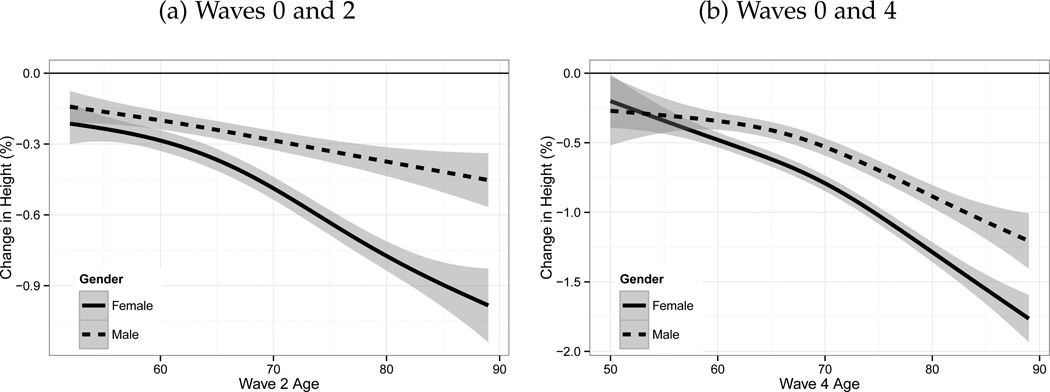
Figure 3 plots the relationship between physical stature decline and age using semi-parametric generalized additive models. In panel (a), for individuals under 60, the loss is less than a third of a percentage point. However, for those aged over 60 the loss is up to a percentage point for both men and women. Panel (b) demonstrates the equivalent change between Wave 0 and Wave 4. The effect is much larger for both men and women, with the average reduction in physical stature over the time period approaching 2 percentage points for the oldest women. On the basis of these results, there is evidence that physical stature decline is most important after the age of 60.

Figure 3.

Age Related Changes in Height Between Waves.

Source: ELSA Sample. +/− 1 SD Shaded. Note: Initial intake for Wave 0 of the survey occurred at three different years: 1998, 1999 and 2001. Wave 4 was conducted in 2008–2009. On average, for the sample as a whole, 5 years pass between Waves 0 and Wave 2 and 9 for Wave 0 and Wave 4. The relationship between physical stature decline and age is estimated using semiparametric Generalized Additive Models.

4 Comparing Cohorts in the Presence of Physical Stature Decline

As outlined in the introduction, a common means of comparing the welfare of populations has been to evaluate their heights, particularly, but not exclusively, in the absence of any other health related data. Generally these papers compare different groups within populations, or within the same population over time. However, these comparisons almost always involve the use of a single cross section, or occasionally repeated cross sections, and to the best of our knowledge few studies have adjusted their data to take account of physical stature decline, although some do restrict attention to individuals aged under 50.

Given our findings in the previous section, ignoring this problem has the potential to provide very misleading results. The worst case scenario involves using a single cross section of data, comparing the height of the elderly to the height of the young, and ascribing any difference to birth cohort effects. Figure 3 shows that there are substantial age effects. In what follows, we use the observed change in measured height for each individual. This allows us to separate out the cohort and age effects, and demonstrate the extent of the bias that reductions in height causes in these comparisons.

We correct the birth cohort height trajectory with the following procedure. Firstly, we fit the following linear regression models using the specification from columns 1 and 4 in Table 3 (for men), and columns 1 and 4 in Table 4 (for women):

$$\frac{({\mathbf{h}}_{it}-{\mathbf{h}}_{i0})}{{\mathbf{h}}_{i0}}=\eta +\tau {\mathbf{\text{age}}}_{it}+({\mathbf{\text{year}}}_{it}-{\mathbf{\text{year}}}_{i0})\mathit{\rho }+{\mathit{\nu }}_{\mathit{i}\mathit{t}},t\in \{2,4\}$$ (1)

separately for both men and women, where t indicates the terminal wave, the dependent variable represents the percentage change for individual i’s height between waves, and the regressors are age in terminal wave and the difference in years between waves (as a categorical variable). Eq. (1) is a simple representation of how physical stature change is related to both age and time. In the following section, we add explanatory variables. While we have adopted a basic linear functional form in eq. (1), we also estimated this relationship via nonparametric regression, and found that the results were almost identical.⁹ As discussed above, we use the percentage change in height to account for the potential for measurement error to be correlated with initial height, and as we find that physical stature decline is positively correlated with initial height, indicating that taller individuals have the capacity to shrink more.

Table 3.

Modeling Percentage Changes in Height Between Waves: Male Sample.

	Wave 0 and Wave 2			Wave 0 and Wave 4
	(1)	(2)	(3)	(4)	(5)	(6)
Intercept	0.89***	0.86***	0.88**	2.04***	1.91***	1.95***
Age W2	−0.02***	−0.02***	−0.01***
Age W4				−0.04***	−0.04***	−0.04***
4 Years Between Waves	−0.11	−0.07	−0.09
5 Years Between Waves	−0.48***	−0.43***	−0.44***
6 Years Between Waves	−0.49***	−0.53***	−0.55***
7 Years Between Waves	−0.51***	−0.48***	−0.56***	0.43	0.49*	0.42
8 Years Between Waves				0.28	0.32	0.24
9 Years Between Waves				−0.05	−0.03	−0.04
10 Years Between Waves				−0.05	−0.02	−0.03
11 Years Between Waves				−0.24	−0.20	−0.27
Excellent Childhood Health		0.14**	0.15**		0.10	0.13
Facilities in Childhood Home			0.05*			0.04
# Bedrooms in Childhood Home			−0.07*			−0.11**
Left School Before 16			0.02			0.14
Has a Degree			−0.01			−0.05
Equivalised Income Quintile: 2			0.09			0.08
Equivalised Income Quintile: 3			−0.02			0.06
Equivalised Income Quintile: 4			−0.11			0.01
Equivalised Income Quintile: 5			0.05			0.10
R2	0.03	0.03	0.04	0.06	0.07	0.07
Adj. R2	0.03	0.03	0.03	0.06	0.06	0.06
Num. obs.	3098	2282	1949	2187	1963	1693

^***p < 0.01,

^**p < 0.05,

^*p < 0.1

Table 4.

Modeling Percentage Changes in Height Between Waves: Female Sample.

	Wave 0 and Wave 2			Wave 0 and Wave 4
	(1)	(2)	(3)	(4)	(5)	(6)
Intercept	1.76***	1.56***	1.38***	3.32***	3.24***	1.95***
Age W2	−0.03***	−0.03***	−0.03***
Age W4				−0.06***	−0.06***	−0.04***
4 Years Between Waves	0.02	0.09	0.07
5 Years Between Waves	−0.58***	−0.46***	−0.48***
6 Years Between Waves	−0.47***	−0.42***	−0.47***
7 Years Between Waves	−0.44***	−0.28***	−0.33***	−0.07	0.03	0.42
8 Years Between Waves				−0.01	0.09	0.24
9 Years Between Waves				−0.47*	−0.33	−0.04
10 Years Between Waves				−0.46*	−0.36	−0.03
11 Years Between Waves				−0.44*	−0.32	−0.27
Excellent Childhood Health		−0.01	0.00		0.08	0.13
Facilities in Childhood Home			0.03			0.04
# Bedrooms in Childhood Home			−0.02			−0.11**
Left School Before 16			0.00			0.14
Has a Degree			0.06			−0.05
Equivalised Income Quintile: 2			−0.10			0.08
Equivalised Income Quintile: 3			−0.08			0.06
Equivalised Income Quintile: 4			−0.16			0.01
Equivalised Income Quintile: 5			−0.07			0.10
R2	0.07	0.06	0.06	0.12	0.13	0.07
Adj. R2	0.07	0.06	0.05	0.12	0.13	0.06
Num. obs.	3765	2817	2355	2775	2481	1693

^***p < 0.01,

^**p < 0.05,

^*p < 0.1.

Standard errors and p-values in columns (1)–(5) adjusted for heteroscedasticity.

The coefficient estimates of eq. (1) are listed in Table 3 and Table 4 (included in Section 5). We use these estimates to correct for age related height reduction by predicting the percentage height change for each individual depending on their age, and then calculating the cumulative height reduction by projecting these in reverse until the individual’s age in the initial wave is 50.¹⁰

Panel (a) in Figure 4 gives results of this analysis based on our aforementioned correction procedure for Wave 0 and Wave 2. This graphic demonstrates the magnitude of the bias which arises from ignoring the effects of physical stature decline when comparing populations on the basis of height. In a single cross section, the researcher would conclude that the female cohort born around 1940 was approximately 5.4 cm taller than the female cohort born around 1920. In reality, once the fact that those born in the 1920s are older in the data and reductions in height are accounted for, the difference is closer to 1 cm. For men, this difference is also evident. For example, the difference in raw height between those born in the 1920 and those born in the 1940 is approximately 5 cm in the data, but is 2.6 cm when adjusted for age effects. This difference is somewhat smaller for males, reflecting the fact that females are more prone to age-related physical stature decrease. We also find similar results when we estimate the model using changes in height between Wave 0 and Wave 4, as displayed in panel (b).¹¹ This analysis demonstrates that cohort comparisons on the basis of height data which is not adjusted for age structure can provide highly misleading results. In particular, the use of unadjusted height will dramatically understate the pre-shrinkage stature of the older population. In the following section, we consider the implications of physical stature decline for the existing economics literature in light of these findings.

Figure 4.

Measured and Corrected Heights Comparison.

Source: ELSA Sample. Note: Initial intake for Wave 0 of the survey occurred at three different years: 1998, 1999 and 2001. Wave 4 was conducted in 2008–2009. On average, for the sample as a whole, 5 years pass between Waves 0 and Wave 2 and 9 for Wave 0 and Wave 4. Corrected height refers to the estimated maximum height of the birth cohort, and is obtained from the model described in eq. 1. Age related height reduction is calculated by predicting the percentage height change for each individual depending on their age, and then calculating the cumulative height reduction by projecting these in reverse until the individual’s age in the initial wave is 50.

5 Characteristics and Consequences of Physical Stature Decline

Thus far we have presented evidence that clearly shows how physical stature decline affects older populations. In this section, we further our analysis by exploring whether there is individual-level heterogeneity in terms of the predictors of height change.

5.1 Physical Stature Decline and Early Environment

Both Table 3 and Table 4 display our linear regression results when we model changes in height as a function of observable fixed characteristics. Columns (1) and (6) of both tables correspond to the regression model in eq. (1). The other columns display the results for additional regression models wherein we introduce additional variables that measure childhood conditions, education, and current income. We have also estimated models where we include height in Wave 0 as a covariate. We find that this variable is negatively correlated with changes in height, so that taller individuals experience a proportionally larger amount of stature loss. However, the other coefficients in the regression are relatively unaffected by the inclusion of height in Wave 0.

The results exhibited in Table 3 provide mixed evidence for the hypothesis that childhood conditions play an important role in physical stature decline for the male population. The self-reported measure of childhood health is positively correlated with physical stature change from Wave 0 to Wave 2, indicating that those with better childhood health—defining themselves either excellent, or very good and excellent—experienced a lower degree of physical stature decrease. Columns (3) and (6) include further measures that account for childhood environment: facilities in the childhood home and number of bedrooms in this home. Household facilities also appear to be protective. This holds only for physical stature decline between Wave 0 and Wave 2. However, these results show the existence of a negative conditional relationship between the number of bedrooms in childhood home and physical stature change for Wave 0 to Wave 4. If we use number of bedrooms as an indicator of childhood family income, these results indicate that greater childhood family wealth is associated with reductions in height. Alternatively, this variable could be a proxy for family size. However, it is difficult to separate whether or not this variable is contaminated by urban-rural differences. Unfortunately the data do not contain information on the location of birth or childhood residence. In columns (3) and (6) we also add further explanatory variables measuring educational attainment and income. Interestingly, these variables do not appear to predict physical stature decline.

Table 4 reports the results for women in an equivalent format to those displayed for men. To an even greater extent than for men, there is no consistent predictor of physical stature decline.

It is important to note that most of our sample (69%) are at least 55 when the survey begins, and that 82% are at least 55 when the survey ends. Therefore, our estimates are mainly driven by this age group. Additionally, our empirical models all control for age, thus capturing any confounding due to this variable. Finally, as we describe above, when we estimate fully nonparametic models that allow for a fully flexible relationship between age and stature loss, we found that our estimates for the extent of stature loss were almost exactly the same as those currently in the paper. Another issue is that there are missing values for some variables in the data, and this could potentially be affecting the results in Table 3 and Table 4. However, we have conducted sensitivity analyses by running the models for different samples and found that the estimates are unchanged. Therefore, it seems unlikely that this is having an impact on results.

5.2 Changing Health Status and Physical Stature Decline

The previous section tested for predictors of reductions in height in terms of time invariant characteristics. In this section, we expand our analysis to examine the dynamic relationship connecting height and health status. To do this, we use the panel dimension of our data and estimate the following linear regression model:

$$\mathrm{\Delta }{\mathbf{h}}_{it}=\alpha +\mathrm{\Delta }{\mathbf{\text{health}}}_{it}\beta +\mathrm{\Delta }{\mathbf{\text{year}}}_{it}\mathit{\gamma }+{\mathit{\epsilon }}_{\mathit{i}}$$ (2)

where changes in height (Δh_it) are regressed on changes in health (Δhealth_it) and the number of years between waves, which we model as a fixed effect. Since we are using a first differences approach, we can rule out the influence of fixed factors, or individual heterogeneity that does not change over time, which may simultaneously influence physical stature decline and changes in health status.

To model the effect of changing health status, we use two well-known indicators: peak flow and grip strength. Both are known to predict worsening physical health, including markers of frailty and mortality (Rantanen et al., 1999; Sharp et al., 1997; Syddall et al., 2003). Since these health variables were not measured in the baseline interview, we model changes between Wave 2 and Wave 4. In addition, we also consider the association between weight and physical stature decline. If reductions in bone density and muscle mass are responsible, then we would expect changes in these two measures to be positively correlated.

Our results are presented in Table 5. Once again, we split our sample based on gender. Overall, the coefficients reported in this table are consistent with the hypothesis that physical stature decline is a function of worsening health. Each of the coefficients on either peak flow or grip strength is positive, and all the two-sided t-tests have p-values, at most, below 0.1. Interestingly, none of the coefficients included to measure time between the surveys appears to be important in the model, as all of these coefficients are small in magnitude and have t-test p-values above any conventional statistical significance level. This finding suggests that, conditional on the inclusion of health changes, time, or change in age, does not matter for reductions in height. In other words, physical stature decline is mediated through deteriorating health status (which obviously is a function of age), but age itself does not appear to have an independent effect on changes in height in this population. In addition, Table 5 shows that reductions in weight are associated with increased physical stature loss, although the associated p-value for the male weight coefficient is above 0.1.

Table 5.

Panel Regressions, Change in Height Waves 2 and 4 (Z-Scores).

	Male Sample			Female Sample
	(1)	(2)	(3)	(4)	(5)	(6)
Intercept	0.11*	0.11*	0.11*	−0.06	−0.06	−0.06
Change in Peak Flow (Z-Score)	0.05**			0.09***
Change in Grip Strength (Z-Score)		0.07***			0.05*
Change in Weigth (Z-Score)			0.03			0.08***
4 Years between Waves 2 and 4	−0.08	−0.08	−0.08	0.02	0.02	0.03
5 Years between Waves 2 and 4	−0.01	−0.03	−0.02	0.04	0.05	0.05
R2	0.00	0.01	0.00	0.01	0.00	0.01
Adj. R2	0.00	0.00	0.00	0.00	0.00	0.00
Num. obs.	1670	1670	1670	1996	1996	1996

^***p < 0.01,

^**p < 0.05,

^*p < 0.1

To examine the robustness of our findings in Table 5, we conduct a placebo test. One concern with Table 5 is that a simultaneity exists between height and health differences, so that our results may simply reflect a path dependence between these two elements. Our placebo analysis represents an attempt to allay this concern by modeling height change between Wave 0 and Wave 2 as a function of later changes in health status. If a path dependence exists, then we would expect to find a relationship between previous physical stature decline and later health change. However, Table 6, which is presented in an identical format to Table 5, does not support such a relationship. All of the health variable coefficients are insignificant. Furthermore, the time effect that was absent from Table 5 appears to be present in these models.

Table 6.

Panel Regressions, Change in Height Waves 0 and 2 (Z-Scores).

	Male Sample			Female Sample
	(1)	(2)	(3)	(4)	(5)	(6)
Intercept	0.29***	0.29***	0.29***	0.09**	0.09**	0.09**
Change in Peak Flow (Z-Score)	0.01			−0.01
Change in Grip Strength (Z-Score)		−0.01			0.01
Change in Weigth (Z-Score)			0.00			0.00
4 Years between Waves 0 and 2	−0.08	−0.08	−0.08	0.10	0.10	0.10
5 Years between Waves 0 and 2	−0.21**	−0.21**	−0.22**	−0.31***	−0.31***	−0.31***
6 Years between Waves 0 and 2	−0.39***	−0.39***	−0.39***	−0.29***	−0.29***	−0.29***
7 Years between Waves 0 and 2	−0.33***	−0.33***	−0.33***	−0.19***	−0.19***	−0.19***
R2	0.02	0.02	0.02	0.03	0.03	0.03
Adj. R2	0.02	0.02	0.02	0.03	0.03	0.03
Num. obs.	1685	1685	1685	2022	2022	2022

^***p < 0.01,

^**p < 0.05,

^*p < 0.1

5.3 Consequences of Physical Stature Decline For Health Production Function Estimation

In the previous sections we demonstrated how physical stature decline is both symptomatic of poor health, and can dramatically overstate birth cohort comparisons in cross-sectional data. In this section we extend this line of investigation, and analyze the importance of using a measure of physical stature that is not subject to change over the life course. To the best of our knowledge there is no existing evidence on the extent to which the use of raw height measurements (which are not adjusted for physical stature decline) results in bias when applied to health production function type regressions. Given the magnitude of physical stature decline we find, it seems ex ante important to test for these potential effects. These results will have important implications for both the existing literature and future research, as we provide validation of existing results and demonstrate that it may be acceptable to use height which has not been adjusted for stature loss.

In order to examine this issue, we being by estimating the following prototypical health production function:

$${\mathbf{\text{health}}}_i=\theta +{\mathbf{\text{height}}}_i\delta +{\mathbf{X}}_i\mathit{\lambda }+{\mathit{\mu }}_i$$ (3)

where we measure health as a function of height and other factors (X_i). As previously discussed, height is commonly used as a control variable to capture net nutrition in early life and genetic factors. Estimating eq. (3) is potentially problematic in cases where health status is correlated with unadjusted height, causing δ̂ to be greater than its true value. Although the control variables (X_i) may be the same as eq. (2), our models are intended to be descriptive, and we do not claim that they are structural and identify specific causal parameters. Nevertheless, we argue that the coefficient values that we do estimate are informative about physical stature decline and its relationship to both aging and deterioration in physical health.

Huang et al. (2013) used an adjusted measure of height, via a two-step procedure, whereby arm and leg lengths of a younger cohort are used to predict height an older cohort. The rationale underlining this methodology assumes that arm and leg length do not change over the life course of an individual, so in effect they are just substituting the unadjusted height for arm and leg lengths. We follow a similar methodology here, and use the demispan measurement that was collected in the baseline survey. There is a substantial literature demonstrating that demispan produces a valid estimate for pre-shrinkage height (for discussion of this relationship in ELSA, see Hirani and Mindell, 2008, and Hirani et al., 2010). Unlike Huang et al., we do not use a two-step procedure. Instead we include the demispan variable as a substitute for unadjusted height and standardize both measures into z-scores so that we can directly compare the coefficients. In our case there is no advantage to using the Huang et al. method, and replicating it would only result in larger standard errors on the corrected height coefficient due to the addition of regression parameter uncertainty (Murphy and Topel, 2002).

Table 7 details the health production function regression results. Once again, we stratify our results based on gender, and within this we perform two analyses. In the first case—columns (1) and (2), and columns (5) and (6)—we do not include any additional control variables. Column (1) shows the coefficient results when unadjusted height is included as a regressor, whereas column (2) includes demispan, instead of unadjusted height, as the regressor of interest. The format is identical for the female sample, shown in columns (5) and (6). Columns (3), (4), (7), and (8) show results for equivalent models that include control variables for educational attainment. Overall, the results in Table 7 show that the naïve use of non-physical stature adjusted height does not lead to substantial biases in empirical health production functions. Columns (2), (4), (6), and (8) all include p-values from t-tests examining if the height coefficient from the previous column is equal to the demispan coefficient. All of these tests fail to reject the null hypothesis that the two physical stature measures are equal.

Table 7.

Health Production Functions, Linear Probability Models: Self-Rated Health is Excellent or Very Good in Wave 0

	Male Sample				Female Sample
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
Intercept	0.83***	0.86***	0.93***	0.93***	0.86***	0.89***	0.93***	0.95***
Age W0	0.00	0.00*	0.00	0.00	0.00**	0.00**	0.00**	0.00**
Height W0 (Z-Score)	0.03***		0.02*		0.04***		0.03***
Demispan W0 (Z-Score)		0.03***		0.03**		0.04***		0.03***
Left School Before 16			−0.16***	−0.16***			−0.13***	−0.13***
Has a Degree			0.08**	0.08**			0.14***	0.14***
R2	0.01	0.01	0.04	0.04	0.01	0.01	0.03	0.03
Adj. R2	0.01	0.01	0.03	0.04	0.01	0.01	0.03	0.03
t-test of Height=Demispan P-value		0.90		0.71		0.93		0.83
Num. obs.	2097	2097	2094	2094	2556	2556	2554	2554

^***p < 0.01,

^**p < 0.05,

^*p < 0.1.

Standard errors and p-values in Models 1–8 adjusted for heteroscedasticity.

It is important to note the consequences of measurement error for this regression, which are distinct to the case in the previous analysis as height now appears as an explanatory variable as opposed to an outcome. In this case random measurement error is expected to bias the coefficient on height towards 0, therefore that we still find results consistent with our prior beliefs about ill-health and shrinking is encouraging and indicates that the signal to noise ratio is sufficiently strong for us to be able to detect the effects of interest, even if they are underestimated.

Tables 8 and 9 further our analysis into the potential biases introduced from using unadjusted height. These tables make use of the fact that our data is in longitudinal form, so we have repeated height measurements. Table 8 presents the results obtained via the male only sample, and Table 9 is the equivalent table for the female sample. In all of these regressions we use unadjusted height, however we allow unadjusted height to vary based on the sample wave. For example, columns (1)–(4) in both tables display results obtained using a sample of individuals interviewed in both Wave 0 and Wave 2, whereas (5)–(8) shows individuals interviewed in Wave 0 and Wave 4.

Table 8.

Health Production Functions, Linear Probability Models: Self-Rated Health is Excellent or Very Good, Male Sample.

	SRH Wave 2				SRH Wave 4
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
Intercept	0.91***	0.91***	0.87***	0.87***	0.84***	0.86***	0.78***	0.79***
Age W2	−0.01***	−0.01***	−0.01***	−0.01***
Age W4					−0.01***	−0.01***	0.00***	0.00***
Height W0 (Z-Score)		0.03***		0.02**		0.02**		0.01
Height W2 (Z-Score)	0.03***		0.02**
Height W4 (Z-Score)					0.03**		0.02
Left School Before 16			−0.10***	−0.10***			−0.10***	−0.10***
Has a Degree			0.10***	0.10***			0.09***	0.09***
R2	0.03	0.03	0.05	0.05	0.02	0.02	0.04	0.04
Adj. R2	0.03	0.03	0.05	0.05	0.02	0.01	0.04	0.04
t-test of Later=Earlier Height P-value		0.83		0.82		0.71		0.66
Num. obs.	3093	3093	3093	3093	2187	2187	2187	2187

^***p < 0.01,

^**p < 0.05,

^*p < 0.1.

Standard errors and p-values in Models 1–8 adjusted for heteroscedasticity.

Table 9.

Health Production Functions, Linear Probability Models: Self-Rated Health is Excellent or Very Good, Female Sample.

	SRH Wave 2				SRH Wave 4
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
Intercept	0.84***	0.86***	0.84***	0.85***	0.91***	0.94***	0.84***	0.86***
Age W2	−0.01***	−0.01***	−0.01***	−0.01***
Age W4					−0.01***	−0.01***	−0.01***	−0.01***
Height W0 (Z-Score)		0.02**		0.01		0.02**		0.01
Height W2 (Z-Score)	0.02***		0.01
Height W4 (Z-Score)					0.03***		0.01
Left School Before 16			−0.13***	−0.13***			−0.14***	−0.14***
Has a Degree			0.07**	0.07**			0.12***	0.12***
R2	0.02	0.02	0.04	0.04	0.03	0.02	0.05	0.05
Adj. R2	0.02	0.02	0.04	0.04	0.02	0.02	0.05	0.05
t-test of Later=Earlier Height P-value		0.53		0.51		0.44		0.39
Num. obs.	3764	3764	3764	3764	2774	2774	2774	2774

^***p < 0.01,

^**p < 0.05,

^*p < 0.1.

Standard errors and p-values in Models 1–8 adjusted for heteroscedasticity.

The assumption underlining the analysis here is that height measured at Wave 0 is less subject to physical stature decline than the heights measured in the later waves. Thus, physical stature decreases should bias the later wave height coefficients away from the null. The results reported in Tables 8 and 9, show that this occurs to a certain extent. The coefficients on height from wave 2 and wave 4 are typically greater than those from Wave 0 to Wave 4. Furthermore, the disparity between these is greater when the comparison is made between Wave 4 and Wave 0, as opposed to between Wave 2 and Wave 0, which we would expect as physical stature decline increases over time. However, as in Table 7, all of the p-values on t-tests examining the equality of the coefficients cannot reject the null hypothesis, at any conventional significance level. In summary, it appears that while the height coefficients in health production functions may be biased, the extent of this bias does not appear to be substantial, although further research is required to establish whether our results generalize fully to other settings.

Although height at Wave 0 is not a perfect measure of pre-shrinkage height, we are able to test its validity to a certain extent in the comparison with measured height in Wave 2 and Wave 4. Height at Wave 0 should be less influenced by prior stature loss than measured height in Wave 2 and Wave 4, especially given that our sample period spans up to 11 years, and thus if shrinkage was causing a bias in the height coefficient we would expect to see evidence of this in that comparison. In addition, we do have access to data on a proxy for pre-shrinkage height: demispan. Reassuringly, as we note above in reference to Table 8, we find the same result: the consequence of using a measured height measurement subjected to shrinkage as a regressor in a common empirical health economics model is minimal.

6 Conclusion

This paper documents the extent of reductions in height in an elderly population. We find substantial amounts of physical stature decline, which increase in age. Ignoring the life course trajectory associated with height will dramatically overstate cohort differences when viewed in terms of a cross section due to confounding with age effects. At the same time, we find a lack of consistent predictors of physical stature decline in terms of fixed characteristics such as education, childhood environment, or adult household income. However, we demonstrate that height loss occurs in conjunction with worsening health. Although this potentially introduces bias from reverse causality in the context of health production function models, when we test for how this form of measurement error affects this typical regression analysis involving height, we find that, qualitatively, results are not affected. We shed light on a potential mechanism linking physical stature decline and health. The association with weight that we show in the data supports the hypothesis that changes in muscle mass and bone density are the channel through which these effects are operating, at least for women. However, we are careful to interpret the coefficient in this instance, as weight gain associated with increases of body-fat beyond an acceptable level may indicate worsening physical health. Nevertheless, these findings indicate potentially important avenues for future work.

Our results have a number of consequences for the extensive economics and demographic literature on height. To the best of our knowledge, this paper is the first to provide evidence on the extent of physical stature decline in a nationally representative sample with longitudinal objective measurements. We are therefore able to validate the use of height in previous research, where concerns about shrinking have been raised, but not tested (Case and Paxson, 2008; Smith et al., 2012). While our results indicate no significant differences in the effects of adjusted and unadjusted height for health models, future research should investigate further whether these findings hold in other contexts beyond the health production function regressions we present in this paper. Although our findings suggest that the consequences of physical stature decline for individual level analysis may not be too adverse, this is not that case at cohort level. We show that age structure must be accounted for when comparing height across groups.

Finally, we found no clear relationship between reductions in height and measures of childhood SES or childhood health. This is perhaps somewhat surprising, given the literature on the consequences of these variables for health. Instead, our results are more consistent with the view that shrinking is affected by deteriorating health, as opposed to the health stock of an individual. It will take further research to establish whether there are any causal determinants of physical stature decline.

Research Highlights.

Physical stature decline results in a 2cm to 4cm reduction in heightover the life course, relative to maximum height.

Comparisons of average height across cohorts comprising individuals over 50 must adjust for age structure to be valid.

Deteriorating health and stature loss occur simultaneously.

For women, physical stature decline and health are likely to be associated via reductions in muscle mass and bone density.

We validate the inclusion of height which has not been adjusted for stature loss in health production function models.