Hierarchical Cascades of Instability Govern the Mechanics of Coiled Coils: Helix Unfolding Precedes Coil Unzipping

Abstract

Coiled coils are a fundamental emergent motif in proteins found in structural biomaterials, consisting of α-helical secondary structures wrapped in a supercoil. A fundamental question regarding the thermal and mechanical stability of coiled coils in extreme environments is the sequence of events leading to the disassembly of individual oligomers from the universal coiled-coil motifs. To shed light on this phenomenon, here we report atomistic simulations of a trimeric coiled coil in an explicit water solvent and investigate the mechanisms underlying helix unfolding and coil unzipping in the assembly. We employ advanced sampling techniques involving steered molecular dynamics and metadynamics simulations to obtain the free-energy landscapes of single-strand unfolding and unzipping in a three-stranded assembly. Our comparative analysis of the free-energy landscapes of instability pathways shows that coil unzipping is a sequential process involving multiple intermediates. At each intermediate state, one heptad repeat of the coiled coil first unfolds and then unzips due to the loss of contacts with the hydrophobic core. This observation suggests that helix unfolding facilitates the initiation of coiled-coil disassembly, which is confirmed by our 2D metadynamics simulations showing that unzipping of one strand requires less energy in the unfolded state compared with the folded state. Our results explain recent experimental findings and lay the groundwork for studying the hierarchical molecular mechanisms that underpin the thermomechanical stability/instability of coiled coils and similar protein assemblies.

Introduction

Coiled coils are one of the most common protein motifs known, existing in over 200 natural proteins (1,2), including structural fibrous protein materials such as vimentin, fibrin, myosin, keratin, and epidermin. Coiled coils serve various biological and mechanochemical functions, playing a key role in transcription, muscle contraction, gene regulation, transmembrane protein channels, chromosome segregation, and blood clotting (3–11). This universal motif is characterized by two or more α-helical protein secondary structures wrapped around each other to form a superhelical assembly. A typical coiled-coil sequence has a characteristic pattern of seven-residue repeats called a heptad, denoted as (abcdefg)_n, where positions a and d are often occupied by nonpolar residues forming an interior hydrophobic core, and amino acids e and g are often oppositely charged residues forming salt links (9). The conserved nature of this sequential distribution provides direct evidence for the exceptional stability of this fundamental protein motif. This is further supported by studies on de novo coiled coils, helix bundles, and protein assemblies that preserve stability and functionality (12–19,75) in a myriad of applications related to imaging (20), biosensors and affinity chromatography (21,22), and electronic or optical materials (23–25), among others.

The ability to use coiled coils in engineered systems such as hybrid block copolymers, polymeric membranes, or drug-delivery vehicles (2,26–36,76) while preserving their structural and biomechanical functions requires an in-depth understanding of the kinetics and thermodynamics of their assembly, as well as the mechanisms of disassembly under extreme environments such as elevated temperatures and pressures. Recent investigations have focused on understanding the thermodynamics and kinetics of coiled-coil folding/unfolding using various experimental methods, including fluorescence techniques (37–39) and NMR (40,41), as well as single-molecule techniques such as atomic force microscopy (AFM) (42–45). Studies thus far have marked a dichotomy in our understanding of the coiled-coil formation and disassembly mechanisms, which cannot easily be resolved with the current limited spatiotemporal resolution of experiments. Although some studies have suggested that the equilibrium unfolding of coiled coils follows a two-state transition in which the protein can only assume two thermodynamic conformations (native coiled coil and unfolded monomers (37,40,41,46–48)), other studies (49–52) have suggested that two-state equilibrium models cannot accurately describe the kinetics of coiled-coil unfolding. Additionally, computer simulations utilizing enhanced sampling techniques have been used to characterize coiled-coil structural parameters such as twist angle and side-chain conformations, as well as helix packing geometries (53–56). A key assumption of these studies is that the backbone Cα atoms preserve the α-helical conformation in the assembly process (54), which implies that helix folding is a precursor to coiled-coil packing—an assumption that needs to be validated. Steered molecular dynamics (SMD) studies on helix unfolding revealed that coiled coils are superelastic, highly dissipative protein bundles (57–60). However, the separate contributions of helix extension and coil unzipping to the total free energy of disassembly remains to be established. Metadynamics (MetaD) simulations on helix unfolding in the stutter region of the dimeric coiled-coil segment of vimentin (61) support the hypothesis that local helix unfolding is a precursor instability mechanism for coiled-coil bundle disassembly, at least under particular mechanical loading scenarios. However, further studies are needed before this observation can be generalized to isotropic loading conditions such as thermal denaturing or melting experiments.

Despite advances in our understanding of coiled coils, whether unfolding of helices is a precursor to coiled-coil disassembly needs further investigation, and the relative energetics of unfolding and disassembly in coiled coils and their underlying mechanisms remain to be fully characterized. The coupling between these two phenomena makes it challenging to discern their individual contributions to the coiled-coil stability/instability in experiments. As a step toward uncoupling the physics of the onset of instabilities in coiled coils, we report all-atomistic simulations of a trimeric coiled coil in an explicit solvent using enhanced sampling techniques, including SMD and MetaD. We base our study on a three-helix coiled coil because dimers and trimers are the most frequently occurring types of coiled coil; however, the mechanical stability of trimers are generally less investigated in the literature compared with dimers. Additionally, according to some studies (62,63), trimers are the default coiled-coil state, while specific sequence interactions are required to trigger formation of coiled coils with other oligomeric states, namely, dimer, tetramer, and higher orders. In this regard, the trimer is a suitable model for capturing basic common features of coiled coils, whereas other orders of aggregation may have more variability arising from how the sequence biases supramolecular conformation. Since unfolding and disassembly of coiled coils occur over relatively long time scales with regards to current atomistic simulation capabilities, it is a challenge to come up with reliable modeling techniques to sample these phenomena accurately using reasonable computational resources. Here, to accelerate these processes in atomistic simulations, we employ SMD and MetaD simulation techniques that enhance sampling through the use of a bias in force and potential, respectively. First, we present SMD simulations that explain the mechanisms of helix unfolding and coil unzipping under applied forces, where unzipping involves detachment of one strand from the assembly. The obtained energy-extension curves enable us to correlate the geometric features of the coiled-coil motif with its anisotropic mechanical stability. Next, MetaD simulations are utilized to reveal the free-energy landscapes of helix unfolding, coil unzipping, and the coupling between these two processes as quantified through 2D sampling.

Materials and Methods

Materials

In this study, we use as a representative model for coiled coils a molecular structure that has been well-characterized by NMR (64) and other experimental techniques (65). The coiled-coil structure (Fig. 1 a) was built based on the crystalline structure of a trimeric coiled coil with 29 amino acids in each α-helical strand (Protein Data Bank ID 1COI (64)). The structure of this three-helix coiled coil is stabilized by hydrophobic valines and leucines located at positions a and d, respectively, as well as salt bridges formed by glutamic acids and lysines at positions e and g, respectively.

Figure 1.

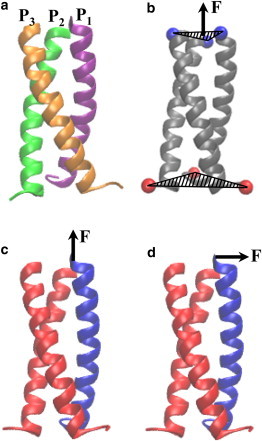
(a) Schematic of the coiled coil used in the simulations consisting of three homo helical strands, denoted by P₁, P₂, and P₃, each having a sequence of Ac-EVEALEKKVAALESKVQALEKKVEALEHG-CONH₂. (b–d) Schematics of SMD simulations illustrating (b) pulling the Cα atoms of one end of the coiled coil while fixing the Cα atoms of the other end, and fixing all of the atoms on the two strands of the coiled coil while pulling the tip of the third strand in a direction (c) along the helix axis and (d) normal to the helix axis. The red and blue colors denote, respectively, the fixed and pulled segments of the coiled coil. To see this figure in color, go online.

MD simulations

All of the MD simulations were performed using NAMD (66). The coiled coil was solvated in a water box using the TIP3P water model (67), and periodic boundary conditions were applied to the box in three dimensions. The velocity Verlet algorithm with a time step of 1 fs was used to solve the equations of motion. The NPT ensemble with constant pressure of 1 atm and constant temperature of 300 K was adopted for the simulations. Bonded interactions of the coiled coil were modeled using the CHARMM (77) force field, and long-range interactions were computed using standard Lennard-Jones potentials and the particle-mesh Ewald technique for electrostatics. The initial structure was minimized for 50,000 steps followed by a 5 ns equilibration simulation. Production SMD or MetaD simulations were then performed. Since the coiled-coil structure was initially taken from its NMR crystalline structure, a short simulation was sufficient to ensure water equilibration of the solvated coiled coil.

SMD simulations

To study the coiled-coil response under deformation, we employed the SMD method (68). To unfold the helical structure of the helices under tensile loading, Cα atoms at one end of the coiled coil were fixed and the Cα atoms of the other end were attached to a fictitious harmonic spring, with spring constant k, which was pulled with constant velocity (Fig. 1 b). Thus, the SMD technique mimics an AFM experiment in which an AFM cantilever tip is used to pull the molecule. The force applied to the SMD (or pulled) atom, F, can be calculated as

$$F=k\left(v.t-x\right),$$ (1)

where v is the pulling velocity, t is the time step, and x is the displacement of the pulled atom. A preliminary study was carried out to investigate the effect of different pulling velocities, including 1, 5, 10, 50, and 80 m/s, on the unfolding response of the system and select an appropriate velocity value for SMD simulations. The obtained results, which for brevity are not presented here, displayed a clear rate-dependent behavior that was diminished for pulling velocities <5 m/s. Therefore, for the tensile loading simulations, a pulling velocity of 1 m/s and a spring constant of 10 kcal/mol/Ų were employed. This value of spring constant was chosen to achieve a stiff spring approximation (69), as much softer spring constants (∼2 orders of magnitude lower) would give rise to large fluctuations in force measurements. The SMD simulation ran for ∼9 ns to reach the complete unfolding of helical strands. The second set of SMD simulations was aimed at characterizing the unzipping of one strand from the coiled coil. For this purpose, all of the atoms on the two strands of the three-helix coiled coil were fixed and the Cα atom located at tip of the third strand was pulled in two directions: parallel to the helix axis (Fig. 1 c) or normal to the helix axis (Fig. 1 d). For both cases, $v=2\mathrm{m}/\mathrm{s}$ and the simulations ran for ∼5 ns to capture the complete detachment of one strand from the trimer assembly.

MetaD simulations

In the MetaD method, a history-dependent bias potential is added to the system along a few selected reaction coordinates or collective variables (CVs) (70,71). This allows for an enhanced sampling of the configuration space and a more accurate free-energy estimation. The height of bias Gaussians and the bias deposition strides are two main input parameters of MetaD simulations, which should be tuned to optimize the sampling accuracy and the computational cost. We performed the MetaD simulations using the PLUMED (72) plugin implemented in NAMD, at a temperature of 300 K. To obtain the free-energy landscape of helix unfolding, we defined the CV, denoted by d₁, as the distance between the first and last Cα atoms of one helical strand of the trimeric coiled coil (say, strand P₁). Next, to investigate the unzipping of one coil (say, strand P₁) from the bundle, we selected the CV, denoted by d₂, as the distance between the backbone center of mass (COM) of P₁ and the backbone COM of the remaining two strands, P₂ and P₃. Finally, to compare the energy required for unfolding with the energy required for unzipping, we explored the 2D free-energy landscape of the coiled coil using two CVs: d₁ and d₂. It should be noted that as the simulation progresses, the position of the atoms changes, and so does the position of their COM. Thus, the position of the COM is dynamically readjusted during simulations. For the CV d₁, the lower and upper boundaries of the sampling region were selected as 36 Å and 60 Å, respectively, and the corresponding values for the reaction coordinate d₂ were 7 Å and 30 Å. Both CVs had a width of 0.1 Å. A parametric sweep was performed to determine the appropriate input parameters for MetaD simulations, and, accordingly, the parameters that led to the most accurate and reproducible energy landscapes within a reasonable computational time were selected. For 1D MetaD simulations, bias Gaussian functions with a hill height of h = 0.01 kcal/mol and a hill width of w = 0.3 Å were added to the system every f = 100 steps (0.1 ps). The corresponding parameters for the 2D MetaD simulation were selected as h = 0.1 kcal/mol, w = 0.3 Å, and f = 200 steps. The 1D and 2D MetaD simulations ran for ∼40 ns and 170 ns, respectively.

Results and Discussion

Here, we present the results of atomistic simulations of a trimeric coiled coil solvated in explicit water. First, we present SMD simulations that employ constant-velocity pulling to apply tensile forces to all three strands (Fig. 1 b) to drive the unfolding process (Movie S1 in the Supporting Material). The obtained unfolding energy landscape as a function of extension of pulled atoms in the direction of loading is shown in Fig. 2. Pulling one end of the coiled coil along its axis while fixing its other end leads to simultaneous unfolding of all three helices without other types of deformations such as bending and unzipping. Thus, for this loading condition, the applied force is mainly used for backbone hydrogen-bond breaking and backbone stretching, and these deformation mechanisms take almost the same amount of force (or energy) for all three homo helices. Therefore, to estimate the energy required for unfolding of a single strand of the trimer (Fig. 2), we divided the obtained SMD results for all strands by the number of strands, i.e., three. Clearly, the coiled-coil structure undergoes large deformations before failure occurs due to sequential breaking of backbone hydrogen bonds, which leads to helix unfolding. Also, Fig. 2 shows the free energy of helix unfolding obtained by MetaD simulations. Unlike the SMD method, where one end of the coiled coil is fixed, no constraints are imposed on the coiled-coil structure in MetaD unfolding simulations, which gives rise to additional deformation mechanisms such as unzipping of the unfolded segment. Furthermore, the SMD loading rate (associated with the pulling velocity and spring constant) is not exactly the same as the MetaD loading rate (associated with height and deposition stride of the bias potential). Thus, it is expected that the dynamics and energy of unfolding obtained from SMD and MetaD simulations are different. For small deformations, i.e., extensions <5 Å, the energy difference from the two methods is ∼10%; however, it increases with an increase in the extension (∼25% at the extension of 17 Å).

Figure 2.

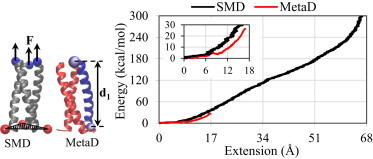
Comparison of the SMD and MetaD simulation results for the free-energy landscape of unfolding of a single helix in the trimeric coiled coil. The SMD results were obtained by fixing the Cα atoms of one end of the coiled coil while pulling the Cα atoms of the other end of three helices and eventually partitioning the forces to the number of helices. The MetaD results were predicted along a reaction coordinate d₁, defined as the distance between the Cα atoms of the first and last residues of a single strand. To see this figure in color, go online.

We performed additional SMD simulations to study the unzipping of a single coil from the bundle by pulling its tip in two directions: 1) along the coiled-coil axis (Fig. 1 c); and 2) normal to the coiled-coil axis (Fig. 1 d). The unzipping energy landscapes as a function of the extension of the pulled atoms in the direction of loading are shown in Fig. 3, a and c, respectively for cases 1 and 2. A video of the unzipping simulation in the transverse (normal) direction is provided in the Supporting Material (Movie S2). While the tip is being pulled, unzipping occurs in a slow, sequential fashion such that segments of the pulled strand first unfold and then unzip from the coiled-coil hydrophobic core in a row, as depicted by the snapshots of coiled coil in Fig. 3, b and d. This observed mechanism is also confirmed by a decrease in the number of backbone hydrogen bonds of the pulled strand (secondary axes of Fig. 3, a and c) with progression of the unzipping process, reinforcing the notion that unzipping is accompanied by unfolding of the helical structure. Also, the relation between the unzipping energy and the number of hydrogen bonds (Fig. 3, a and c) highlights the significance of the coiled-coil’s structural features for its mechanical stability. Additionally, the obtained results show that the complete unzipping of one strand in the transverse direction (Fig. 3 c) requires less energy compared with the longitudinal direction (Fig. 3 a), suggesting that the transverse direction is a weaker path for coiled-coil dissociation.

Figure 3.

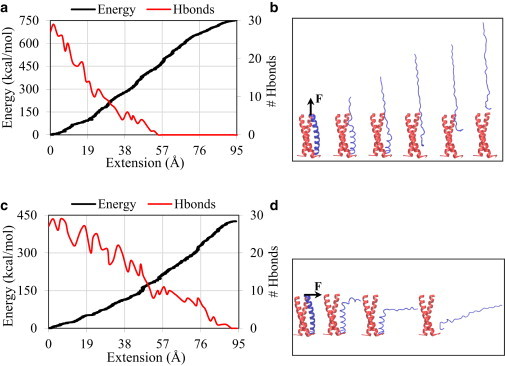
(a–d) Results of SMD simulations showing the free-energy landscape of unzipping obtained by pulling the tip of a single strand (a and b) along the helix axis and (c and d) normal to the helix axis. The primary axes of plots a and c depict the energy, and the secondary axes illustrate the number of backbone hydrogen bonds (Hbonds) of the pulled strand. Panels b and d show snapshots of the coiled coil throughout the simulations. To see this figure in color, go online.

Fig. 3, a and c, illustrate the mechanisms underlying the unzipping of a single strand in a prespecified direction, either longitudinal or transverse. Although projections of the energy landscape to prescribed directions are useful, they do not show the free, unconstrained path of coil unzipping in the coiled coil. To gain a deeper insight into this issue, we performed MetaD simulations of coil unzipping with the reaction coordinate defined as the distance of the backbone COM of one strand, P₁, from that of the two other strands, P₂ and P₃ (Movie S3). The obtained free-energy landscape illustrated in Fig. 4 a shows a global minimum and a few local minima before the energy value levels off. Each minimum point observed in the energy curve corresponds to an event in which the amino acids valine and leucine located at positions a and d of one heptad repeat lose hydrophobic contacts with their counterpart amino acids in the hydrophobic core, and thus one heptad repeat starts to get unzipped from the assembly. This indicates the significant contribution of the hydrophobic core to the stability of coiled coils. Fig. 4 b shows the distance between the COMs of each heptad of strand P₁ from that of strands P₂ and P₃. Clearly, not all of the coiled-coil heptads unzip at the same time, but unzipping happens in a step-by-step, sequential manner such that approximately one heptad gets detached from the coiled-coil assembly at each step, in agreement with the dips observed in the free-energy landscape (Fig. 4 a). These findings suggest that the loss of hydrophobic contact occurs in a noncollective manner in the assembly, so that the relatively high energy barrier of collective unzipping can be overcome more easily. An interesting observation is that each segment is detached only after it becomes unfolded due to breaking of the backbone hydrogen bonds, as can be seen in the snapshots of the coiled coil in Fig. 4 a. Once a segment of the strand unfolds and detaches from the coiled-coil core, it can fluctuate more freely and thus repeatedly gets closer to and farther away from the other two strands, before it completely unzips. These fluctuations give rise to local decreases in the distances between heptads as observed in Fig. 4 b. This hierarchical cascade of instability mechanisms, namely, sequential unfolding of helical segments followed by their unzipping, was also observed experimentally by AFM (44,45) and is clearly seen in our simulations. In addition, the snapshots of the unzipping process demonstrate that the transverse direction, a direction normal to the helix axis, is the path of unzipping even without constraints, in agreement with our SMD observations. Another remarkable feature is that as one strand is being unzipped from the three-helix bundle, the other two strands undergo slight conformational changes, yet they still preserve their helical structure and remain assembled together. This implies that under an anisotropic loading condition, a trimeric coiled coil may transform into an unfolded monomer together with a folded dimer, which is an intermediate state before the trimeric coiled coil transitions to three unfolded monomers. This observation from our simulations supports previous results from time-resolved fluorescence change experiments on a three-stranded coiled coil (52), suggesting that a two-state model is not adequate to fully explain the kinetics of coiled-coil unfolding. It should also be noted that helix unfolding is a reversible process in which the unfolded strand may refold after it detaches from the assembly, as shown in the snapshots of the coiled coil in Fig. 4 a. However, no recoiling of the unzipped strand was observed during the course of the simulation.

Figure 4.

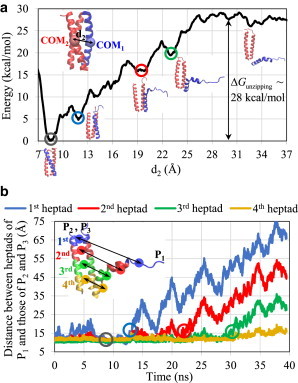
(a) Free-energy landscape of coil unzipping obtained by MetaD simulation of the coiled coil, with the CV d₂ defined as the distance between the backbone COM of one strand (say, P₁) from the backbone COM of the two other strands (say, P₂ and P₃). (b) The distance between the COMs of each heptad repeat of strand P₁ from the corresponding heptads of strands P₂ and P₃ as a function of simulation time. To see this figure in color, go online.

To compare the relative energies of unfolding and unzipping in the coiled coil, we performed 2D MetaD simulations with two reaction coordinates, d₁ and d₂, as described in Materials and Methods, and obtained the free-energy landscape of helix unfolding and unzipping (Fig. 5 a). Starting from a region of minimum energy on the landscape it takes less energy to move along the energy paths in the d₁ direction compared with the d₂ direction, and consequently the molecular instability of the coiled coil starts with local helix unfolding and progresses with disassembly of unfolded segments. Additionally, Fig. 5, b and c, illustrates the cross sections of the energy surface at minimum d₁ and d₂, respectively, including the best-fit curves to a small region around the energy minimum. We selected a quadratic function for fitting the energy landscapes based on the simplifying assumption that the strand behaves like a spring with two vibrational modes along d₁ and d₂ coordinates. A comparison of the stiffness constants obtained from fitting along the two reaction coordinates indicates that local unzipping of a strand in the coiled-coil assembly is energetically more costly compared with local unfolding. This conclusion is not limited to small deformations and can also be extended to large deformations, where the 2D energy surface confirms that more energy is required to unzip a strand in a folded state compared with a partially unfolded state. In fact, Fig. 5 d indicates that once the energy barrier of unfolding is overcome and a segment is unfolded, the extra energy required for its unzipping is relatively very low, resulting in an almost unforced unzipping of the unfolded segment. Finally, the free energy of disassembly of a single coil from the trimeric coiled coil can be estimated as ∼28 kcal/mol from the MetaD results shown in Fig. 4 a. This result agrees reasonably with the known experimental unfolding free energy of a similar three-stranded coiled coil, ∼18.4 kcal/mol per helix (73).

Figure 5.

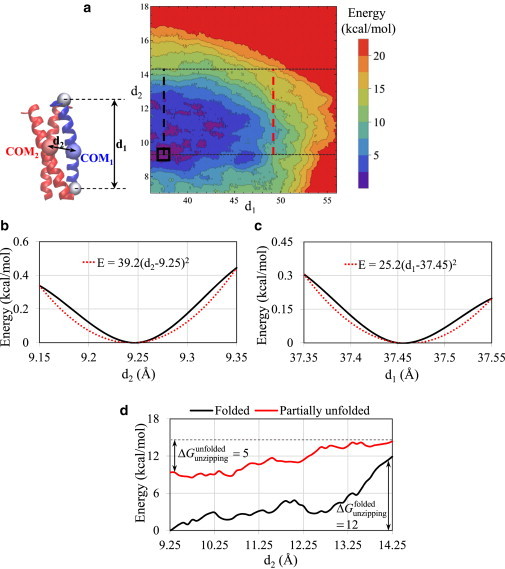
(a) Free-energy landscape of helix unfolding and unzipping obtained from the 2D MetaD simulation of the coiled coil with two CVs: d₁ (the distance between the Cα atoms of the first and last residues of one strand) and d₂ (the distance between the backbone COM of one strand from the COM of the two other strands). (b and c) Cross sections of the energy surface at (b) minimum d₁ and (c) minimum d₂, with a focus on a small deformation region (shown by the square box in a) around the energy dips. (d) Cross sections of the energy surface (along the dashed black and red lines illustrated in a) comparing the free energy required for partial unzipping of a single strand in a folded state versus a partially unfolded state. To see this figure in color, go online.

It is worth mentioning that all of the energy values reported here pertain to the specific coiled coil of this study, and they may vary if the sequence, length, or oligomeric state of the coiled coil changes. In particular, the stability of coiled coils generally increases with an increase in length (74), and thus more energy will be required for deformation (unfolding or unzipping) of longer coiled coils. Additionally, disassembly of coiled coils of higher aggregation number is energetically more costly compared with that of coiled coils with a lower degree of oligomerization. Boice et al. (73) showed experimentally that the free energy of unfolding for a coiled coil with similar sequence and length as the one investigated in this study is higher in the trimeric state than in the dimeric state. Regardless of possible differences in the values of dissociation energy for different coiled coils, the mechanisms of instability unraveled in this study are universally relevant for all coiled coils.

Conclusions

In this study, we performed atomistic simulations of a trimeric coiled coil using enhanced sampling techniques, providing new insight (to our knowledge) into the molecular mechanisms that underpin the instability of α-helical coiled coils. We were able to uncouple the contributions of unfolding and disassembly to coiled-coil dissociation by employing SMD and MetaD techniques, which yield key features of the free-energy landscapes of single-helix unfolding and unzipping processes pertaining to the supercoil structure. The MetaD results for unzipping of a single strand from the assembly establish that unzipping occurs in a sequential fashion, such that heptad repeats of the strand lose their hydrophobic contacts with the coiled-coil hydrophobic core and consequently get detached sequentially. Additionally, these results illustrate that unfolding of a helical segment of the coiled coil is a prerequisite to its detachment from the assembly. 2D MetaD simulations reveal the complete picture of unfolding and unzipping landscapes and validate these observations. The obtained results indicate that unzipping of a strand in the folded state is an energetically costly process with a high energy barrier, which becomes significantly smaller once the strand unfolds. This finding clearly explains the hierarchical cascades of instability mechanisms observed in the simulations, i.e., helix unfolding followed by coil unzipping.

The trajectories of the MetaD simulations show that after the detachment of one strand from the trimer assembly, the two other strands remain folded and assembled, possibly because their hydrophobic amino acids can still form an interior hydrophobic core, in accordance with a dimeric structure. This implies that the induction of instability in one strand of the trimeric coiled coil does not necessarily affect the stability of the two other helices. Thus, under an anisotropic loading condition, the trimeric coiled coil can assume two possible thermodynamic states: a folded dimer together with a monomer or three monomers. The formation of a dimer and a monomer can be deemed to be a transition state while going from the native coiled-coil state to the unfolded monomers state.

Our simulations unravel the underlying universal mechanisms of coiled-coil dissociation and identify the energetically weak processes and pathways of coiled-coil instability. One can readily apply the methodology presented here to other proteins and soft materials with hierarchical structures and assembly processes to better understand their stability/instability mechanisms. Furthermore, the knowledge gained from our studies paves the way for the design and synthesis of novel coiled coils, protein bundles, and hierarchical assemblies with stable structures and preserved functionalities under different loading and environmental conditions.