Abstract
Long-range directional transport in cells is facilitated by microtubule-based motor proteins. One example is transport in a nerve cell, where small groups of motor proteins, such as kinesins and cytoplasmic dynein, work together to ensure the supply and clearance of cellular material along the axon. Defects in axonal transport have been linked to Alzheimer’s and other neurodegenerative diseases. However, it is not known in detail how multimotor-based cargo transport is impaired if a fraction of the motors are defective. To mimic impaired multimotor transport in vitro, we performed gliding motility assays with varying fractions of active kinesin-1 motors and inactive kinesin-1 motor mutants. We found that impaired transport manifests in multiple motility regimes: 1), a fast-motility regime characterized by gliding at velocities close to the single-molecule velocity of the active motors; 2), a slow-motility regime characterized by gliding at close-to zero velocity or full stopping; and 3), a regime in which fast and slow motilities coexist. Notably, the transition from the fast to the slow regime occurred sharply at a threshold fraction of active motors. Based on single-motor parameters, we developed a stochastic model and a mean-field theoretical description that explain our experimental findings. Our results demonstrate that impaired multimotor transport mostly occurs in an either/or fashion: depending on the ratio of active to inactive motors, transport is either performed at close to full speed or is out of action.
Introduction
Intracellular transport is essential for the maintenance of cellular function. Newly synthesized proteins and cellular material are transported by motor proteins along cytoskeletal filaments to their target destinations. Cargo transport is often performed by the collective operation of multiple molecular motors, leading to effects such as increased run length and increased force (1). Notably, collective effects in transport arise both with motors of the same type and with motors of different types that vary in speed or directionality (2,3). As an example, collective cargo transport is essential for the cellular function of polarized cells, such as the neuron, where many proteins are synthesized in the cell body and need to be transported to their destinations over long distances. As a consequence, defects in axonal transport in motor and sensory neurons have been linked to Alzheimer’s and other neurodegenerative diseases (4,5). In particular, two diseases, hereditary spastic paraplegia (HSP) and Charcot-Marie-Tooth type 2A neuropathy (CMT2A), are connected to mutations that affect the ATPase activity of the motor domains of kinesin-1 and kinesin-3 (6–8). These mutations impact the anterograde axonal transport, leading to degeneration or damage of nerves (neuropathy) (5). Thus, it is important to understand how cargo transport is impaired by such defectively mutated motors.
To study multimotor transport in the presence of defective motors, we performed in vitro microtubule gliding assays on surfaces coated with mixtures of active and inactive kinesin-1 motors (Fig. 1 A). Inactive motors were obtained by a point mutation in the kinesin-1 motor domain, which hindered ATP binding (9,10). Caught in the nucleotide-free state, the inactive motors are associated with the microtubules in a strongly bound (rigor) state and thus cannot move on the microtubules as do the active motors. To identify the key mechanisms underlying impaired transport, we developed a theory based on the physical properties of individual motors. The almost identical structure of active and inactive motors allowed us to model the collective motor behavior by using, to a large extent, the same parameter set to describe both motor types.
Figure 1.
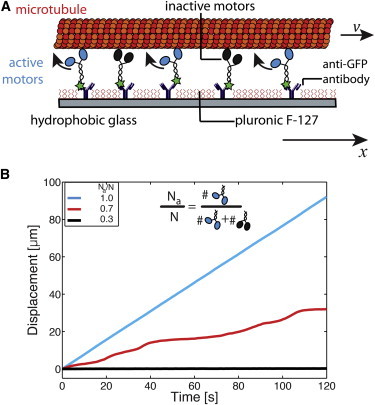
Experimental setup. (A) Schematic diagram of the gliding motility assay. Active motors (rKin430-EGFP) and inactive motors (rKin430-EGFP[T93N]) were bound to the surface of a flow cell via antibodies. The surface was blocked by F127 to prevent unspecific attachment of proteins. Gliding of the fluorescently labeled microtubules with (positive) gliding velocity v was observed by fluorescence microscopy. The arrow indicates the positive x direction. (B) Time-distance plot of gliding microtubules at three ratios of the number of active motors (Na) to the total number of motors (N). The examples show fast gliding at maximum velocity (for Na/N = 1), stopping (for Na/N = 0.3), and bistable movement with phases of fast or slow motility (for Na/N = 0.7). See also Movies S1, S2, and S3 for videos of the corresponding gliding assays.
Materials and Methods
Flow cells
Experiments were performed in 1.5- to 3-mm-wide flow channels made from two silanized glass coverslips (22 × 22 mm2 and 18 × 18 mm2; Corning) glued together by strips of double-sided adhesive tape (11). Before silanization, the coverslips were cleaned by the following washing steps: 1), 30 min immersion in acetone followed by 20 min of sonication; 2), rinsing with deionized water; 3), incubation in piranha solution for 60 min at 60°C; 4), rinsing with water; and 5), incubation for 15 min in 0.1 M KOH followed by rinsing with water and blow-drying with nitrogen. For silanization, coverslips were incubated in 125 μl of dichlorodimethylsilane diluted in 250 ml trichloroethylene for 60 min. Finally, the coverslips were sonicated in methanol twice for 15 min and washed with filtered water (MilliQ) followed by blow-drying with nitrogen.
Preparation of kinesin motors and microtubules
All experiments were performed with truncated, enhanced green fluorescent protein (EGFP)-labeled kinesin-1 constructs (rKin430-EGFP), which contained the first 430 aa of kinesin-1 fused to a EGFP and a His tag at the tail-domain (12). For the inactive motor, a T93N substitution (threonine exchanged for asparagine) was introduced into the P-loop of rkin430 EGFP, leading to rigor binding of the inactive motor to the microtubule (9,10). A kinesin solution containing 50 μg/ml active motor in a dilution buffer (1% Tween 20, 10 mM dithiothreitol (DTT) and 1 mM MgATP in BRB80T) and a solution containing 50 μg/ml inactive motor in dilution buffer were prepared. The relative concentrations of active motor and inactive motor were estimated using SDS-PAGE. Double-stabilized microtubules were prepared by polymerization of partially rhodamine-labeled tubulin (in-house-prepared porcine brain tubulin, 4.6 mg/ml final concentration, labeling ratio 0.67) in BRB80 buffer with 1 mM MgCl2, 1 mM guanylyl 5′-α,β-methylenediphosphonate at 37°C for 2 h. The microtubules were spun down in an ultracentrifuge for 5 min at ≈120,000 g (room temperature) to remove free tubulin. The microtubules were resuspended and stabilized in BRB80 containing 10 μM taxol (BRB80T).
Gliding motility assays
After the inner parts of the flow-cell channels were washed with BRB80, an anti-GFP antibody solution (20 μg/ml in BRB80) was perfused into the channels and incubated for 10 min. The channels were washed with BRB80 again. F127 (1% in BRB80) was incubated for 30 min for surface blocking. The channels were then washed with BRB80T. Various ratios of active motor to inactive motor were mixed to a total kinesin concentration of 50 μg/ml. The mixed motor solution was perfused into the channels and allowed to bind to the antibodies for 5 min. The channels were washed with dilution buffer. A motility solution (10 mM DDT, 40 mM D-glucose, 124 μg/ml glucose oxidase, 22 μg/ml catalase in dilution buffer) containing the double-stabilized microtubules was applied (see Table S1 in the Supporting Material for information on the average lengths). Finally, a motility solution without microtubules was applied. Based on the lengths of the shortest microtubules reliably gliding on the surface, we estimated the total kinesin density to be on the order of 100 μm−2. This density roughly translates into motor numbers between 10 and 100 for microtubules with lengths between 1 and 10 μm.
Imaging
Gliding microtubule motility was imaged using an inverted fluorescence microscope (Axiovert 200M; Zeiss) with a 40× oil immersion objective (NA 1.3). Illumination was achieved by means of a metal arc lamp (Lumen 200; Prior Scientific) and filter sets for rhodamine were used (exc: 535/50, dichroic: LP 565, em: 610/75). An EMCCD camera (Andor) was used for image acquisition, and time-lapse movies of 200 frames with a 100 ms exposure time at a frame rate of 1.1 Hz were acquired using MetaMorph software (Universal Imaging). Five time-lapse movies from different fields of view per experimental condition (i.e., per ratio of active to inactive motors) were collected and the respective data are presented. Experiments were repeated in several independent sets of gliding assays (more than three) and similar results were obtained.
Data analysis
For filament tracking and path statistics, the Fluorescence Image Evaluation Software for Tracking and Analysis (FIESTA) software package was used (13). FIESTA uses Gaussian models to find and track the filaments. Tracks of every microtubule were checked and data points were filtered out, at which point the length of the microtubule changed greatly compared with adjacent frames. Instantaneous velocities were determined by calculating 1D velocities using the difference quotient of the distance along the path and the time between consecutive frames for each microtubule in the field of view at each point of time. Average velocities were determined by calculating the arithmetic mean of the instantaneous velocities at a given Na/N. Gaussian fits (single and double) of the instantaneous velocities collected in the histograms were performed using MATLAB (The MathWorks, Natick, MA). Details on the Gaussian fitting, the mean velocities, and the number of data points are summarized in Table S1.
Monte Carlo simulation
We recorded each active and inactive motor by its state and length yi. At each iteration step of duration Δt, an attached motor detached if λ < ω(yi)Δt, where λ is a uniformly distributed random number on the interval (0, 1), and ω denotes the detachment rate, which depends on the linker extension yi. A detached motor attached with an initial length obeying the normal distribution g(y) if λ < μΔt, where μ denotes the attachment rate. We then calculated the total force Fa + Fp acting on the microtubule by summing up all the elastic forces. From Eq. 4, we obtained the instantaneous velocity of the microtubule v. The linker length of active and inactive motors then evolved according to Eqs. 1 and 2, respectively. Instantaneous velocities were extracted similarly to the data analysis for the experimental data. In a given simulation run, the total number N of motors was fixed. To mimic the effects of motor number variations in the experiments, we averaged the simulation results over runs with different numbers N, varying from 10 to 100 in increments of 10. This corresponds to a motor number distribution with 〈N〉 = 55 and .
Mean-field approach and phase behavior
We analyzed the phase behavior of microtubule motility using a mean-field approach in which we introduced a function ϕa/p(y,t) to describe the length distribution of the linkers associated with the microtubule-attached motors. This approach becomes exact in the limit of large N where velocity fluctuations of the microtubules can be ignored. To find the stable solutions in the region of coexistence of fast and slow motility regimes for the mean field approach, we extracted the solutions from the force-balance equation in this region for different detachment rates. The coexistence regions found in the simulation were determined using Hartigan’s dip test (14).
Results
In this work, we characterized motor mixtures by the ratio of the number Na of active motors to the total number N of active and inactive (or passive, hence the index p) motors N = Na + Np, with the ratio Na/N being 1 when all motors are active and 0 when all motors are inactive. Experimentally, we varied the ratio Na/N by incubating the substrate surfaces with solutions that contained different concentrations of active and inactive kinesin-1 motors. To allow for comparable measurements at equal motor density, we kept the total concentration of motors in the incubation solutions constant (see Materials and Methods). When we systematically analyzed the motility of gliding microtubules for 0.3 ≤ Na/N ≤ 1 (where Na and N can be considered as the number of active and total motors per filament, respectively), we observed multiple regimes of movement: 1), a fast-motility regime at high Na/N, characterized by gliding at velocities close to the single-molecule velocity of the active motors; 2), a slow-motility regime at low Na/N, characterized by gliding at close-to zero velocity or full stopping; and 3), a bistable regime at intermediate Na/N, characterized by switches between fast and slow motility (Fig. 1 B). By plotting histograms of the instantaneous velocities (Fig. 2 A), i.e., the velocities derived from the distances that individual microtubules moved between two consecutive frames of image capture, we observed the corresponding velocity distributions: a single peak with vcenter > 500 nm/s (fast-motility regime), a single peak around vcenter ≈ 0 nm/s (slow-motility regime), and a dual-peak velocity distribution with vcenter ≈ 500 nm/s and vcenter ≈ 0 nm/s (bistable regime). We observed a sharp transition from the fast to the slow regime around Na/N = 0.7, the point at which the movement was bistable and both regimes of fast and slow motility coexisted.
Figure 2.
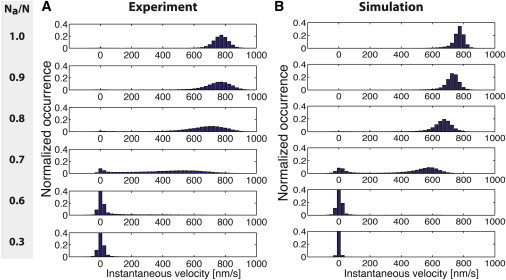
Normalized histograms (bin size 25 nm/s) of gliding microtubules for different ratios of Na/N. Both the experimental data (A) and simulated data (B) display a clear shift in the velocity distributions from fast motility (at high Na/N) to slow motility (at low Na/N), notably with a bimodal distribution at approximately Na/N = 0.7. To keep the y axis equal in all panels, the actual peaks are not visible in all graphs. The peak amplitudes of the normalized occurrence at the given bin width for Na/N = 0.6 are 0.52 in the experiment and 0.62 in the simulation. Similarly, for Na/N = 0.3, the peak values are 0.65 in the experiment and 0.96 in the simulation. Negative velocities were due to the finite tracking error of ≈ 20 nm for the microtubule positions. For the numbers of microtubules and the coefficients of the Gaussian fitting to the histograms, see Table S1. In the simulation, the total motor number was varied from N = 10 to N = 100 in increments of 10 and the results were combined in a single histogram. The following parameter values were used: κ = 1 pN/nm, fc = 3 pN, μ = 5 s−1, fs = 7 pN, Da = 1000 nm2/s, , , v0 = 830 nm/s and ξ/L = 10 Ns/m2. To see this figure in color, go online.
To quantitatively understand the underlying principles of our experimental results, we developed a theoretical description of the microtubule movement based on single-motor properties. Active motors and inactive motors (subscripts a and p, respectively) are connected to the substrate by elastic linkers of stiffness κa/p (motor stiffness). The force of the elastic linkers exerted on the microtubule is fa/p = −κa/py, where y is the linker extension (with y being positive for linker extensions in the positive x direction; see Fig. 1 A). The motion of an active motor on the microtubule is defined by the force velocity relationship, which describes the velocity va of an active motor as function of the load force κay. For simplicity, we used a linear relationship va = −v0(1 + κay/fs), where v0 > 0 denotes the magnitude of the velocity of an active motor in the absence of a load force and fs > 0 denotes the magnitude of the stall force. The minus sign implies that active motors move in the negative x direction and stall at the negative linker extension ya = −fs/κa. If the microtubule moves relative to the substrate with velocity v, the linker extension of active motors changes as
| (1) |
Here the effective diffusion constant Da describes the stochasticity of motion of individual motors and Γ(t) denotes a white noise with zero average 〈Γ(t)〉 = 0 and correlation 〈Γ(t)Γ(t′)〉 = δ(t − t′). In contrast, an inactive motor is carried with the microtubule it is attached to, and thus the extension changes as
| (2) |
In addition, active and inactive motors attach to or detach from the microtubules. The attachment rate is denoted by μa/p. The detachment rate is denoted by ωa/p, which depends on the load force . These force-dependent detachment rates are described by
| (3) |
Here, denotes the detachment rate in the absence of a load force, denotes the characteristic force of detachment (an approximation for the more detailed description presented in Parmeggiani et al. (15)). Because the rate of linker relaxation after detachment is fast compared with the rate of attachment, the distributions of the linker extensions of detached active and inactive motors are described by equilibrium distributions , where are the normalization constants (16).
We consider the 1D movement of microtubules on active and inactive motors distributed on a substrate with a total linear density ρ. The total number of motors N = Na + Np is then defined by N = ρL, where L is the length of the microtubule. The force generated by all active and inactive motors onto one microtubule is , where is the number of attached motors. The velocity of a microtubule is determined by the force balance equation
| (4) |
where ξ is the friction coefficient of the microtubule, which is proportional to its length L.
Active and inactive motors only differ in a single amino acid. Therefore, in our theory we use the same values for both active and inactive motors for the following parameters: motor stiffness κ = κa/p, characteristic force and attachment rate μ = μa/p. In addition, we describe the active motors by an effective diffusion constant Da, the stall force fs, the force-free velocity v0, and the force-free detachment rate . For inactive motors, we use the force-free detachment rate . The friction coefficient of the microtubule per unit length is ξ/L.
We performed Monte Carlo simulations to determine the instantaneous velocities in dependence of Na/N from Eq. 4. The number of total motors per microtubule was varied between 10 ≤ N ≤ 100 to mimic the variance in microtubule length. Histograms of the instantaneous velocities are shown in Fig. 2 B. In agreement with the experimental results, we found a fast- and a slow-motility regime, as well as a regime in which fast and slow motilities coexisted (at approximately Na/N = 0.7). To quantitatively match the experimental velocity histograms in Fig. 2 A, we optimized the values of the force-free detachment rate of inactive motors, the motor stiffness κ, the effective diffusion constant Da, and the force-free velocity v0 of active motors (see caption of Fig. 2 B for the parameters used in the simulation).
When we analyzed the simulated movement of individual filaments in the coexistence region, we observed bistable motility with frequent switches between fast and slow movements (Fig. 3). The shapes of the simulated position-time curves were similar to the experimental data, although the switches appeared more abrupt in the simulated curves (see Discussion). When we plotted the average velocities of the microtubules in dependence of Na/N, we detected a sharp transition from slow to fast motility between Na/N = 0.6 and 0.8 (Fig. 4). This demonstrates the sensitivity of the transport system to the amount of inactive motors.
Figure 3.
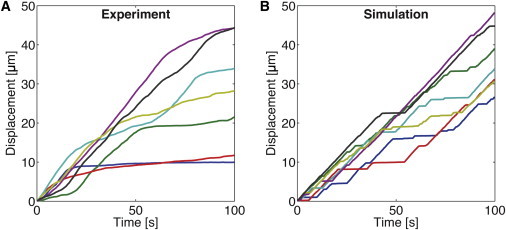
Trajectories of gliding microtubules at Na/N = 0.7 for experiment (A) and simulation (B). Microtubules show a bistable movement with frequent transitions between fast and slow motility. The parameter values for the simulation are the same as described in Fig. 2B. To see this figure in color, go online.
Figure 4.
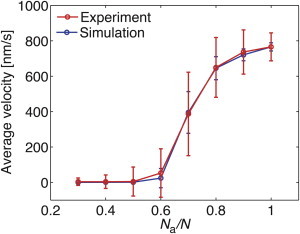
Average velocities of gliding microtubules in dependence of Na/N. The average velocity shows a sharp transition from slow to fast motility between Na/N = 0.6 to 0.8 for both experimental and simulated data. The broad error bars during the transition represent the presence of different velocities in this region. The parameter values for the simulation are the same as in Fig. 2B. Experimental and simulation results for microtubule velocities as a function of microtubule length, as well as simulation results for motor numbers as low as 2 and 3, are presented in Figs. S1 and S2, respectively. To see this figure in color, go online.
The threshold behavior and the observed region of coexistence between fast and slow motilities are signatures of a first-order phase transition. To gain further insight into this phase behavior, we developed a mean-field approach. This approach becomes exact in the limit of large N, where velocity fluctuations of the microtubules can be ignored. We introduced a function ϕa/p(y,t) for the length distribution of the linkers associated with the microtubule-attached motors. The dynamical processes described above can be characterized by two equations that govern the evolution of ϕa/p(y,t):
| (5) |
| (6) |
Here is the fraction of bound active or inactive motors within their own population. The two equations are coupled by the force balance equation
| (7) |
in which is the average force generated by a single active or inactive motor. At steady state, ∂tϕa = 0, ∂tϕp = 0, the microtubule velocity is constant. Solving Eqs. 5 and 6 gives the average force fa/p(v) per motor at a given velocity. By inserting fa/p(v) into the right side of Eq. 7, we obtain the force-velocity relationship for the ensemble of motors in dependence of Na/N (Fig. 5 A, colored lines). The intersections of these force-velocity curves with the curve of friction forces (Fig. 5 A, black line) yield the steady-state solutions to Eq. 7.
Figure 5.
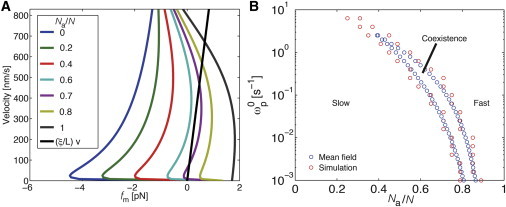
Mean-field results. (A) Force-velocity relationship in dependence of Na/N. The black line indicates microtubule gliding under friction. The force-velocity curves for Na/N < 0.7 lead to negative forces (i.e., toward the negative x direction in Fig. 1A), as inactive motors dominate, resulting in stopping of the microtubule. For Na/N = 0.7, both positive and negative forces are possible and two stable solutions exist. For Na/N > 0.7, microtubules are under positive forces, leading to gliding with positive velocities. (B) Phase diagram parameterized with Na/N and the detachment rate of the inactive motor in the absence of forces for the mean-field approach (blue circles) and the simulation (red circles). Symbols represent the lower and upper critical ratios, which confine the region of coexistence of fast and slow motilities. We note that even for motor numbers as small as N = 20 (red circles), the simulation results agree well with the mean-field approach. The parameter values are the same as those used for the simulation results in Fig. 2B.
We found that one stable solution exists for regimes with Na/N ≥ 0.8 and Na/N ≤ 0.6. For Na/N = 0.7, the force-balance equation has three solutions: one at low velocities, one at high velocities, and one at intermediate velocities. It can be proved that only the solutions at low and high velocities are stable. This corresponds to the coexistence of slow- and fast-motility regimes at intermediate Na/N. We interpret the bimodal behavior as follows: If microtubules move toward the positive x direction (see Fig. 1 A), inactive motors will follow the movement of the microtubules. Hence, the inactive motors get positively stretched (i.e., in the positive x direction) and thus generate negative forces on the microtubule. As the velocity of microtubules increases, the average extension yp becomes longer and consequently the fraction of attached motors Qp becomes smaller due to the force-dependent detachment rate. In contrast, active motors are able to step in the negative x direction on the microtubule. If the positive velocity of the microtubule is slower than the motion of active motors, the active motors will be on average negatively stretched. At Na/N = 0.7, the low-velocity solution represents a state in which inactive motors dominate, whereas the higher-velocity solution represents a state in which the active motors dominate. The noise caused by stochastic binding and unbinding of motors induces the transitions between these two states.
Motivated by experimental observations that inactive motors hardly detach from microtubules (9,10), we theoretically studied the influence of the detachment rate of the inactive motors on the phase behavior and on the region of coexistence. We obtained a phase diagram showing the three motility regimes as a function of Na/N and the detachment rate of the inactive motors in the absence of force (Fig. 5 B, red circles for simulation, blue circles for mean field). We find good agreement between the regime boundaries obtained in the mean-field theory and the simulation. The phase diagram shows the region of coexistence of slow and fast motilities confined by an upper and lower critical ratio at which the mean-field theory shows a pitchfork bifurcation. As increases, the coexistence region shifts to smaller Na/N, because for larger , inactive motors are more likely to detach. At a critical value , the coexistence region disappears.
Discussion
Our experimental and theoretical results show that impaired transport manifests in multiple motility regimes: 1), a fast-motility regime; 2), a slow-motility regime; and 3), a bistable regime with coexistence of fast and slow motilities. With respect to our numerical simulation, the obtained histograms agree well with the experimental data regarding their general shape and dependency on the fraction of active motors Na/N (Fig. 2). We note, however, that compared with the experimental data, the velocity distributions appeared narrower in the numerical simulations. As a result, the transitions between high and low velocity in the time-distance plots of individual microtubules appear more abrupt (Fig. 3). The differences in the width of the velocity distributions presumably arose from the fact that in the simulation, all motors of one kind were treated equally, i.e., using equal parameters for stiffness, stall force, attachment rate, unloaded detachment rate, etc. In the experiment, however, these parameters might have varied, for example, because each motor interacted with the microtubule in a particular geometry (e.g., a sideways-stretched motor may not be able to apply the full stall force). During simulations for different motor stiffnesses, the peaks of the velocity distributions do shift (Fig. S3). Thus, stiffness variations can indeed explain (in part) the broader velocity distributions in the experiment. Furthermore, we found that allowing fluctuations in both the total number of motors N and the number of active motors Na by randomly distributing both types of motors along a 1D geometry also slightly shifted the velocity peaks and increased their widths (Fig. S4). Thus, variations in motor stiffness, motor density, and motor ratio are likely to contribute to the observed differences between experiments and simulations.
We used previously measured parameters for the active motors, i.e., attachment rate μa = 5 s−1 (17) force-free detachment rate (18), stall force fs = 7 pN (19), and characteristic detachment force (18). By comparing our theory with the experimental data, we obtained estimates for the force-free detachment rate of inactive motors, the force-free velocity of active motors v0 = 830 nm/s, the effective diffusion constant Da = 1000 nm/s, and the motor stiffness κ = 1 pN/nm. Interestingly, the estimated value for the force-free detachment rate of inactive motors is larger than the value measured in single-molecule experiments (our unpublished data). This difference might arise from the fact that in single-molecule experiments the motors are under zero load, whereas in gliding assays the motors, being attached to both the substrate and the microtubule, are presumably always slightly stretched sideways even when no force in the x direction is present. The value for the effective diffusion constant Da = 1000 nm/s is smaller than the value Da = 1500 nm/s that corresponds to r = 0.5 (randomness parameter r = 2Da/(v0d) with d = 8 nm (20)) reported in the absence of force for full-length kinesin-1. When we performed simulations using Da = 1500 nm/s, we found that the coexistence region of fast and slow motilities vanished and only the transition remained (Fig. S5). Thus, the observed coexistence range suggests that the effective diffusion coefficient in our system is indeed slightly smaller than previously estimated. The smaller diffusion coefficient may result from the collective effects of multiple motors or from the shorter lengths of the truncated kinesins used in our experiments. The value of the motor stiffness κ = 1 pN/nm is higher than the value κ = 0.5 pN/nm obtained by optical force-clamp assays (21). When we performed simulations for κ = 0.5 pN/nm, we found that the coexistence of fast and slow motilities was still present, although less pronounced compared with the case of κ = 1 pN/nm (Fig. S3). Our results from the simulations and the mean-field approach show that values of κ lower than 0.1 pN/nm or higher than 10 pN/nm result in loss of bimodal behavior (Figs. S3 and S6). These results could possibly be tested using truncated kinesins of different lengths.
The coexistence of fast and slow motilities and the sharp transition between the two motility regimes are the results of collective motor effects. These collective effects result from a mechanical coupling between motors mediated by the force-dependent detachment rate. This force-dependent detachment rate leads to motors suddenly detaching in a group, thus generating dynamic transitions and bistable behavior. The collective effects of motors were predicted theoretically (22–25) and first found experimentally in actin-myosin motility assays (26). In kinesin-microtubule systems, the collective effects of identical motors working antagonistically (27) and motors with different force-free velocity relations (3,28,29) were recently studied experimentally. For a system of fast and slow motors, different observations were reported for a changing fraction of fast motors. On one hand, a smooth change between fast and slow velocity was observed using Osm-3/Kin-2 motors (29) and Xklp1/Xkid motors (3). On the other hand, Larson et al. (28) found a sharp transition between fast and slow motility in regular kinesin-1 and slow kinesin-1 mutants. An analysis of the average velocities reveals that only 15% of fast motors were needed to reach half-maximal velocity in the study by Larson et al. (28), whereas 70% of active motors were required in our experiments (Fig. 4). This difference might be due to our use of inactive motors, which are more strongly bound to the microtubule than the slow but active motors used by Larson et al. (28).
The situation studied in this work is similar to previous theoretical studies of antagonistic motors (27) and motors with different force-free velocities (30). However, we note that the model developed by Li et al. (30) (describing previous experimental results (3,28,29)) cannot be applied to our system of active and inactive motors, because in that model the microtubule velocity already vanishes if at least one attached motor is inactive. In the system studied here, we observed that the microtubule can move if a small fraction of inactive motors is attached. This behavior cannot be captured by the model of Li et al. (30). The vanishing velocity in the presence of inactive motors in their study results from two properties of their model: 1), the velocity of the microtubule depends only on the motor number and linker extensions are not considered; and 2), the velocity of motors with zero force-free velocity always vanishes.
Conclusions
To mimic impaired multimotor transport, we performed in vitro gliding motility assays with mixtures of active and inactive motors. Our work shows that impaired multimotor transport can act in a bimodal either/or fashion with sharp threshold behavior. In a strongly impaired transport system (e.g., with more than four nonworking motors out of 10 motors) transport may stop completely and pathological effects are expected in vivo. However, in a slightly impaired system (e.g., with roughly only one in 10 nonworking motors), transport is only marginally impacted. This finding, namely, that a small backward strain (applied by a small number of inactive motors) is not a hindrance for cargo transport, is in agreement with the observation that dynein might still be attached during anterograde transport performed by kinesins (31). A multimotor system of kinesin-1 is thus able to work at close to full speed even under adverse conditions.
Acknowledgments
We thank Wilhelm Walter for preparation of the inactive kinesin-1 motor and for fruitful discussions, and Corina Bräuer and Cornelia Thodte for technical support.
This work was supported by the European Research Council (ERC starting grant to S.D.), the Deutsche Forschungsgemeinschaft (Heisenberg Programme and Research Unit SFG 877), and the Max Planck Society.
Footnotes
Lara Scharrel and Rui Ma contributed equally to this work.
René Schneider’s present address is Max Planck Institute of Molecular Plant Physiology, Potsdam-Golm, Germany.
Contributor Information
Frank Jülicher, Email: julicher@pks.mpg.de.
Stefan Diez, Email: diez@bcube-dresden.de.
Supporting Material
References
- 1.Gross S.P., Vershinin M., Shubeita G.T. Cargo transport: two motors are sometimes better than one. Curr. Biol. 2007;17:R478–R486. doi: 10.1016/j.cub.2007.04.025. [DOI] [PubMed] [Google Scholar]
- 2.Snow J.J., Ou G., Scholey J.M. Two anterograde intraflagellar transport motors cooperate to build sensory cilia on C. elegans neurons. Nat. Cell Biol. 2004;6:1109–1113. doi: 10.1038/ncb1186. [DOI] [PubMed] [Google Scholar]
- 3.Bieling P., Kronja I., Surrey T. Microtubule motility on reconstituted meiotic chromatin. Curr. Biol. 2010;20:763–769. doi: 10.1016/j.cub.2010.02.067. [DOI] [PubMed] [Google Scholar]
- 4.De Vos K.J., Grierson A.J., Miller C.C. Role of axonal transport in neurodegenerative diseases. Annu. Rev. Neurosci. 2008;31:151–173. doi: 10.1146/annurev.neuro.31.061307.090711. [DOI] [PubMed] [Google Scholar]
- 5.Chevalier-Larsen E., Holzbaur E.L. Axonal transport and neurodegenerative disease. Biochim. Biophys. Acta. 2006;1762:1094–1108. doi: 10.1016/j.bbadis.2006.04.002. [DOI] [PubMed] [Google Scholar]
- 6.Caballero Oteyza A., Battaloğlu E., Schüle R. Motor protein mutations cause a new form of hereditary spastic paraplegia. Neurology. 2014;82:2007–2016. doi: 10.1212/WNL.0000000000000479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Reid E., Kloos M., Marchuk D.A. A kinesin heavy chain (KIF5A) mutation in hereditary spastic paraplegia (SPG10) Am. J. Hum. Genet. 2002;71:1189–1194. doi: 10.1086/344210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zhao C., Takita J., Hirokawa N. Charcot-Marie-Tooth disease type 2A caused by mutation in a microtubule motor KIF1Bbeta. Cell. 2001;105:587–597. doi: 10.1016/s0092-8674(01)00363-4. [DOI] [PubMed] [Google Scholar]
- 9.Crevel I.M.T.C., Nyitrai M., Cross R.A. What kinesin does at roadblocks: the coordination mechanism for molecular walking. EMBO J. 2004;23:23–32. doi: 10.1038/sj.emboj.7600042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Telley I.A., Bieling P., Surrey T. Obstacles on the microtubule reduce the processivity of Kinesin-1 in a minimal in vitro system and in cell extract. Biophys. J. 2009;96:3341–3353. doi: 10.1016/j.bpj.2009.01.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gell C., Bormuth V., Howard J. Microtubule dynamics reconstituted in vitro and imaged by single-molecule fluorescence microscopy. Methods Cell Biol. 2010;95:221–245. doi: 10.1016/S0091-679X(10)95013-9. [DOI] [PubMed] [Google Scholar]
- 12.Piperno G., Fuller M.T. Monoclonal antibodies specific for an acetylated form of alpha-tubulin recognize the antigen in cilia and flagella from a variety of organisms. J. Cell Biol. 1985;101:2085–2094. doi: 10.1083/jcb.101.6.2085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ruhnow F., Zwicker D., Diez S. Tracking single particles and elongated filaments with nanometer precision. Biophys. J. 2011;100:2820–2828. doi: 10.1016/j.bpj.2011.04.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hartigan J.A., Hartigan P.M. The dip test of unimodality. Ann. Stat. 1985;13:70–84. [Google Scholar]
- 15.Parmeggiani A., Julicher F., Peliti L., Prost J. Detachment of molecular motors under tangential loading. Europhys. Lett. 2001;56:603–609. [Google Scholar]
- 16.Grill S.W., Kruse K., Jülicher F. Theory of mitotic spindle oscillations. Phys. Rev. Lett. 2005;94:108104. doi: 10.1103/PhysRevLett.94.108104. [DOI] [PubMed] [Google Scholar]
- 17.Leduc C., Campàs O., Prost J. Cooperative extraction of membrane nanotubes by molecular motors. Proc. Natl. Acad. Sci. USA. 2004;101:17096–17101. doi: 10.1073/pnas.0406598101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Schnitzer M.J., Visscher K., Block S.M. Force production by single kinesin motors. Nat. Cell Biol. 2000;2:718–723. doi: 10.1038/35036345. [DOI] [PubMed] [Google Scholar]
- 19.Visscher K., Schnitzer M.J., Block S.M. Single kinesin molecules studied with a molecular force clamp. Nature. 1999;400:184–189. doi: 10.1038/22146. [DOI] [PubMed] [Google Scholar]
- 20.Svoboda K., Mitra P.P., Block S.M. Fluctuation analysis of motor protein movement and single enzyme kinetics. Proc. Natl. Acad. Sci. USA. 1994;91:11782–11786. doi: 10.1073/pnas.91.25.11782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kawaguchi K., Ishiwata S. Nucleotide-dependent single- to double-headed binding of kinesin. Science. 2001;291:667–669. doi: 10.1126/science.291.5504.667. [DOI] [PubMed] [Google Scholar]
- 22.Jülicher F., Prost J. Cooperative molecular motors. Phys. Rev. Lett. 1995;75:2618–2621. doi: 10.1103/PhysRevLett.75.2618. [DOI] [PubMed] [Google Scholar]
- 23.Jülicher F., Ajdari A., Prost J. Modeling molecular motors. Rev. Mod. Phys. 1997;69:1269–1282. [Google Scholar]
- 24.Badoual M., Jülicher F., Prost J. Bidirectional cooperative motion of molecular motors. Proc. Natl. Acad. Sci. USA. 2002;99:6696–6701. doi: 10.1073/pnas.102692399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Müller M.J.I., Klumpp S., Lipowsky R. Tug-of-war as a cooperative mechanism for bidirectional cargo transport by molecular motors. Proc. Natl. Acad. Sci. USA. 2008;105:4609–4614. doi: 10.1073/pnas.0706825105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Riveline D., Ott A., Prost J. Acting on actin: the electric motility assay. Eur. Biophys. J. 1998;27:403–408. doi: 10.1007/s002490050147. [DOI] [PubMed] [Google Scholar]
- 27.Leduc C., Pavin N., Diez S. Collective behavior of antagonistically acting kinesin-1 motors. Phys. Rev. Lett. 2010;105:128103. doi: 10.1103/PhysRevLett.105.128103. [DOI] [PubMed] [Google Scholar]
- 28.Larson A.G., Landahl E.C., Rice S.E. Mechanism of cooperative behaviour in systems of slow and fast molecular motors. Phys. Chem. Chem. Phys. 2009;11:4890–4898. doi: 10.1039/b900968j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Pan X., Ou G., Scholey J.M. Mechanism of transport of IFT particles in C. elegans cilia by the concerted action of kinesin-II and OSM-3 motors. J. Cell Biol. 2006;174:1035–1045. doi: 10.1083/jcb.200606003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Li X., Lipowsky R., Kierfeld J. Bifurcation of velocity distributions in cooperative transport of filaments by fast and slow motors. Biophys. J. 2013;104:666–676. doi: 10.1016/j.bpj.2012.11.3834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hendricks A.G., Perlson E., Holzbaur E.L. Motor coordination via a tug-of-war mechanism drives bidirectional vesicle transport. Curr. Biol. 2010;20:697–702. doi: 10.1016/j.cub.2010.02.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


