Mechanical Checkpoint For Persistent Cell Polarization In Adhesion-Naive Fibroblasts

Abstract

Cell polarization is a fundamental biological process implicated in nearly every aspect of multicellular development. The role of cell-extracellular matrix contacts in the establishment and the orientation of cell polarity have been extensively studied. However, the respective contributions of substrate mechanics and biochemistry remain unclear. Here we propose a believed novel single-cell approach to assess the minimal polarization trigger. Using nonadhered round fibroblast cells, we show that stiffness sensing through single localized integrin-mediated cues are necessary and sufficient to trigger and direct a shape polarization. In addition, the traction force developed by cells has to reach a minimal threshold of 56 ± 1.6 pN for persistent polarization. The polarization kinetics increases with the stiffness of the cue. The polarized state is characterized by cortical actomyosin redistribution together with cell shape change. We develop a physical model supporting the idea that a local and persistent inhibition of actin polymerization and/or myosin activity is sufficient to trigger and sustain the polarized state. Finally, the cortical polarity propagates to an intracellular polarity, evidenced by the reorientation of the centrosome. Our results define the minimal adhesive requirements and quantify the mechanical checkpoint for persistent cell shape and organelle polarization, which are critical regulators of tissue and cell development.

Introduction

Polarity encompasses essentially every aspect of cell and developmental biology. Cell polarity is defined by a morphological and functional asymmetry of cellular components that are oriented along a well-defined intracellular axis (1–3). Although spontaneous cell polarization can occur in eukaryotic cells (4–6), cells have the ability to interpret asymmetrical extracellular cues and transmit signals to generate intracellular asymmetries (7–12). Cell-extracellular matrix (ECM) interactions, mediated by the family of integrin receptors, provide spatial cues for orienting cell polarity (9,11,13,14). Specifically, single adherent cells feel and respond to stiffness gradients during durotaxis (9,15,16) through mechanosensory adhesion sites to the ECM, cytoskeletal proteins, and signaling molecules (14,17–20). The molecular role of cell-ECM contacts on the establishment of cell polarity has been well characterized for cells spread on two-dimensional substrates (14). The nature of engaged adhesion molecules, as well as the mechanical tension developed on the ECM, instruct and guide mechanotransduction of external physical cues into intracellular signaling. The degree of cell spreading, however, affects many cellular functions (21–23), and the mechanotransduction within a three-dimensional topology is poorly understood. In addition, nascent adhesions formation and their maturation proceed in various steps involving different force-bearing proteins (24). Therefore, a high number of entangled processes, coupling mechanics to biochemical signaling on preestablished adhesion sites, are at work in experiments carried out on cells spread in two-dimensional surfaces. The respective contributions of substrate mechanics and biochemistry for cell polarization process remain unknown, as well as the minimal trigger of ECM cues for the establishment of cell polarity.

Here, we develop a believed-novel and well-controlled single-cell approach to assess the minimal trigger for the establishment of cell polarity in adhesion-naive NIH 3T3 fibroblast cells (called hereafter “3T3 cells”). We combine, in a dual-objective system, three-dimensional fluorescent microscopy with an optical tweezers setup for controlled mechanical nanomanipulation of chemically coated beads, mimicking extracellular matrix adhesion sites of weak rigidity. This system enables us to monitor and quantify the early cell responses to single mechano-chemical cues in real-time over one hour’s time. Thank to simultaneous measurements, at the single cell level, of force and cell shape change, we unveil the existence of a mechanical checkpoint for a persistent cell polarization.

Materials and Methods

Pll-PEG-coated coverslips

The surface treatment was prepared as follows: Pll-PEG (poly(L-lysine)-graft-poly(ethylene glycol)) copolymer (SUSOS, Dübendorf, Switzerland) at 0.1 mg.mL⁻¹ was prepared in 10 mM HEPES (pH 7.2). Glass coverslips were sonicated in a solution of ethanol 70%, rinsed twice with ultra-pure water, and air-dried. The coverslips were then incubated for 1 h with Pll-PEG solution. As the final step, the coverslips were washed twice with phosphate-buffered saline (pH 7.2) and used the same day.

Bead preparation

A quantity of 1.7-μm diameter carboxylated polystyrene beads (Polysciences, Eppelheim, Germany) were coated with the entire fibronectin protein from bovine plasma (F1141; Sigma-Aldrich, St. Louis, MO) according to the method described by Felsenfeld et al. (25). Briefly, beads were coated with biotinylated BSA (bovine serum albumin) using a carbodiimide linkage (E7750; Sigma-Aldrich). Beads were then incubated with avidin and finally with biotinylated fibronectin at a concentration of 0.6 μg.mL⁻¹. To ensure maximum functionality, beads were used within 12 h from the time of preparation. Coating thickness was checked by slot-blot. Coated beads, in a calibrated amount, were loaded on a nitrocellulose membrane (Schleicher & Schuell Bioscience, Bath, UK), and detected using anti-fibronectin primary antibody (gift from F. Coussen, Institut Interdisciplinaire des Neurosciences, Bordeaux, France) and anti-rabbit-HRP second antibody (Sigma-Aldrich). Immunoreactive bands were visualized using enhanced chemoluminescence detection (Pierce Biotechnology, Rockford, IL). We ensured that the density of fibronectin proteins on each bead was reproducible.

Cell culture and drug treatments

NIH 3T3 mouse fibroblasts were grown in DMEM (GIBCO, Life Technologies, Carlsbad, CA) supplemented with 10% fetal calf serum (GE Healthcare, San Diego, CA) at 37°C in a 5% CO₂ atmosphere. Plasmid transfection was carried out using Nanofectin (GE Healthcare). Transfected cells were selected with geneticin (350 μg.mL⁻¹, Life Technologies) and then sorted by FACS (ImagoSeine facility, Institut Jacques Monod, Université Paris Diderot/Centre National de la Recherche Scientifique, Paris, France). Experiments were carried out in 3T3 cells stably expressing eGFP-actin (gift of C. Ballestrem), eGFP-myosin-IIA (gift of M. Sheetz), eGFP-tau-cod-H (hereafter called “eGFP-Tau”, provided by L. Behar), α5-integrin-eGFP (Addgene plasmid 15238; https://www.addgene.org/), paxillin-eGFP (Addgene plasmid 15233; https://www.addgene.org/), and eGFP-vinculin (gift of B. Geiger). Adherent 3T3 cells were incubated with 5 μM of nocodazole (NZ; Sigma-Aldrich) and 5 mM of EDTA (ethylenediaminetetraacetic acid; Sigma-Aldrich) for 1 h, or 50 μM of BB (blebbistatin; Calbiochem, Darmstadt, Germany) for 30 min before suspension in Pll-PEG glass coverslips.

Cell synchronization

Experiments on centrosome positioning were performed on 3T3 cells stably expressing eGFP-Tau synchronized in G1 phase by mitotic shake. Cells were grown to 75% confluence on a collagen-fibronectin coated 150-cm² culture flask (Techno Plastic Products, Trasadingen, Switzerland). One hour before the mitotic shake itself, the flask was slightly shaken to remove less adherent cells. Mitotic cells were then collected by a strong shake-off, harvested, and plated on a 25-cm² flask to allow them to undergo cytokinesis and used 2 h later.

Assays on round nonadherent 3T3 cells

Cells were detached with trypsin (GIBCO, Life Technologies), harvested, and resuspended in DMEM F12 medium without phenol Red, with riboflavin, without B12 vitamin, with 20 mM HEPES (pH 7.2; GE Healthcare), and plated on Pll-PEG-coated glass coverslips mounted on a customized microscopy chamber The chamber was then incubated at 37°C in 5% CO₂ atmosphere for 30 min before experiments.

Live-cell imaging

Oscillating cell recordings were done using a model No. CSU22 spinning head (Yokogawa Engineering, Tokyo, Japan) mounted on a DMI6000 inverted microscope (Leica, Solms, Germany) for high-resolution imaging (×40 objective, 1.4 optovar). The microscope was equipped with a Coolsnap HQ camera (Photometrics Roper Scientific, Tucson, AZ) and was controlled by the software METAMORPH (Universal Imaging, Burbank, CA). The chamber was maintained at 37°C in a 5% CO₂ atmosphere by a stage incubator (Life Image Services, Basel, Switzerland). Differential interference contrast and fluorescent images were successively acquired every 15 s.

Laser ablation

Laser ablation experiments were performed on an inverted scanning confocal microscope (TCS SP2 AOBS MP; Leica) coupled with a 80-MHz laser head (MaiTai DeepSee; Spectraphysics, Evry, France) delivering infrared (IR) femtosecond pulses. To perform local ablation, the pulsed laser beam was focused on the cell membrane with a microscope objective (1.4 NA, 63×, HCX PL APO; Leica) which transmits 85% of the incoming near-IR light. The focused beam was set at 860 nm and was targeted on cell membrane during 40 ms with an average power of 330 mW measured at the entrance of the scanning head. The ablation spot was ∼250 nm in diameter and 1-μm high. The microscope system was controlled by LAS AF Lite (Leica). Single fluorescent images were acquired typically every 5 s before and after performing laser ablation.

Optical tweezers assay

Experiments were performed using the dual objective system described in Fig. S1 in the Supporting Material. Calibration of optical tweezers was done using the drag force method (26) from which the relative displacement of the trapped object from the equilibrium trap position was retrieved to estimate the optical trap stiffness relative to the IR laser power (see Fig. S1 C). Briefly, the chamber containing trapped beads was mounted on an X-piezo-driven stage. A controlled oscillating movement was applied to the chamber, and trapped bead movement was recorded using a fast camera. Upon correction with the drag coefficient, the bead displacement generated by the known drag-force gave access to the optical force, and thus to the optical tweezers stiffness. The stiffness variation depends on the total laser power.

Before experiments, the laser power was measured before entering the trapping objective, and adjusted to generate optical trap of defined stiffness. To avoid evaporation, a thin film of paraffin was added to cover the microscopy chamber, which was maintained at 37°C using a thermostated holder. Coated beads were trapped and positioned using either the driving software AOD (AOD Software, Coral Springs, FL) or the motorized sample stage controller. The optical trap remains fixed during the assay. Cell shape as well as fluorescence signals were retrieved taking successively one stack of transmitted light images followed by one stack of fluorescence images every 30 s or 2 min (for experiments on microtubule-organizing centers) during 30 or 40 min. For some experiments, only images of a single plane of either fluorescence or transmitted light were acquired. To rule out the possibility of laser heating artifacts, we targeted 3T3 cells with the IR laser. No protein recruitment, cell damage, or other events were observed.

Image processing and data analysis

Images were processed by using the software IMARIS (BITPLANE, Zurich, Switzerland) for three-dimensional reconstruction or the software FIJI (IMAGEJ, National Institutes of Health, Bethesda, MD) in which they were cropped, rotated, and manually adjusted for contrast and brightness. Fluorescent images, except those that concerned centrosome positioning assays, were registered using the IMAGEJ plugin STACKREG (Biomedical Imaging Group, http://bigwww.epfl.ch/thevenaz/stackreg/).

Cell shape polarization

To determine the cell centroid, the thresholded fluorescence signal from the cell contour was fitted by an ellipse defining major and minor axes. Cell orientation was then given by the orientation of the major axis. In the absence of beads, cell orientation was defined by the angle formed between the major axis and a horizontal axis, which is arbitrarily fixed by the software FIJI (IMAGEJ, National Institutes of Health). Cell protrusion growth was quantified by fitting three-dimensional reconstructions with prolate spheroids to extract the ellipticity parameter using the software IMARIS (BITPLANE).

Generation of kymographs

To follow the cortical distribution of actin and myosin-II, we wrote a FIJI macro to extract the fluorescence intensity of the cell contour over time using mathematical morphology operators. We first roughly thresholded the cell contour using a combination of implemented image processing functions such as “Find” edges, “Gray Morphology”, and the “Smooth” filter to yield a cortical mask. The mask was then successively dilated and skeletonized as needed to ensure complete and homogeneous cortex coverage. Finally, an XOR operation was carried out with the original mask to create a cortex mask. Once the cortex masks were generated, 72 line profiles (5° clockwise angular step) were generated from the center of the cell, allowing nonzero values in the cortical masked regions. Generation of kymographs was typically averaged over a width of five pixels to portray representative cortical behavior. Kymographs were then normalized with the overall GFP intensity of the cell at each time point.

Oscillation frequency

We applied the temporal image correlation spectroscopy method (27) on kymographs. Briefly, the method consists of a temporal correlation of the cell contour series. Fast Fourier transform was next applied to extract the main frequency peak (see Fig. S1 E).

Force measurement

To evaluate the force exerted by cells, we recorded the bead XYZ displacements over time. Bead positions were retrieved from a Z-stack of transmitted light images using a custom MATLAB (The MathWorks, Natick, MA) program. We first applied an inverted look-up table to transmitted light images to properly fit a two-dimensional Gaussian intensity function. We then extracted XYZ bead positions over time.

Centrosome positioning

Centrosome positions were retrieved from fluorescent images of cells stably expressing eGFP-Tau, using the plugin developed by F. Cordelieres (Institut Curie, Paris, France) called MANUAL TRACKING. Briefly, the position of the centrosome is manually tracked, and automatically corrected (barycenter correction) depending on the fluorescence intensity of the tracked object. The imaging plane containing the brightest spot was considered the centrosome plane.

Statistics

Statistical significance was determined using a two-tailed Mann-Whitney test or a Kruskal-Wallis test, as appropriate. Post-hoc testing was done with Tukey HSD or Dunnett’s test as indicated in Results and Discussion. Calculations were performed with the software MATLAB (The MathWorks).

Results and Discussion

A single local, stiff, and specific adhesion cue triggers cell shape polarization in detached and round fibroblasts

Numbers of studies have examined the role of the ECM interactions as spatial cues for polarized cells adhered on substrates (9,11,13,14,28). The minimal mechanical and biochemical requirements for an ECM cue to trigger polarization in cells not previously exposed to ECM signals are, however, unknown. To address this issue, we develop a dual-objective microscopy system combining an optical tweezers setup for quantitative nanomanipulation and force measurements with three-dimensional fluorescence imaging. This allows for the application of a single local adhesion cue using ECM-coated beads on 3T3 cells while monitoring intracellular dynamics (see Fig. S1 A). Specific cell adhesion and spreading on the substrate is fully prevented using Pll-PEG-treated glass coverslips (see Fig. S1 A). Specific cell adhesion then only occurs with the bead coated with ECM proteins and optically trapped (see Fig. S1 B). Cells are allowed to bind single beads for 30 s. The attached beads are then either released (untrapped condition) or maintained (trapped condition) within the optical trap. This experimental setup allows setting precisely the starting time of the adhesion trigger and the stiffness of the ECM-adhesion site given by the stiffness of the optical trap (see Fig. S1, A and C).

We first observe the behavior of detached 3T3 cells in the absence of cell-bead contact. 3T3 cells remain spherical without developing any active adhesion sites on the coverslip for at least 1 h. A continuous oscillatory shape is observed for 79% of the cells (N = 88; Fig. 1 A; see Fig. S1, D and E, and Movie S1 in the Supporting Material). Spontaneous shape oscillations of single cells have already been described for nonadhering cells and have been proposed to arise from a loss of cell-substrate adhesions (29).

Figure 1.

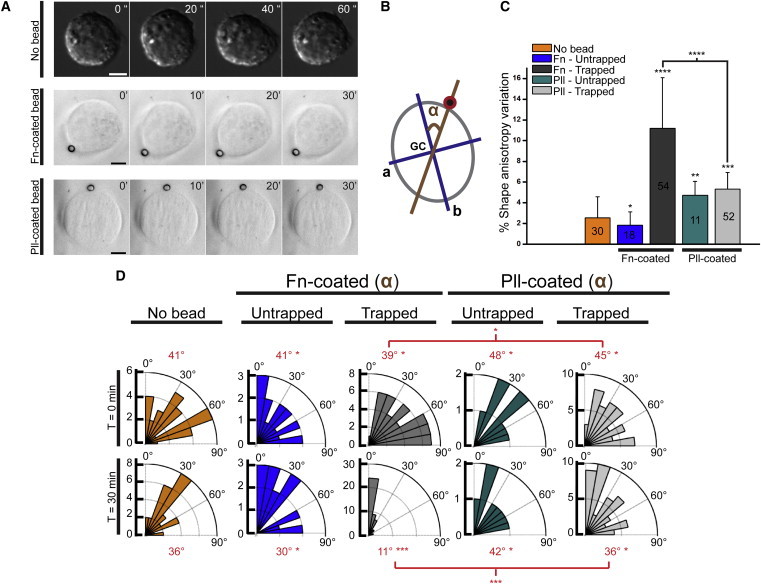
Application of a single trapped Fn-coated bead triggers polarization of adhesion-naive 3T3 cells. (A) Still images from differential interference contrast in a time-lapse movie (see Movie S1 in the Supporting Material) of single oscillating 3T3 cells plated on Pll-PEG coated glass coverslips; and still transmitted-light images from a time-lapse movie (see Movie S2) of single cells plated on Pll-PEG coated glass coverslips and with Pll-coated (middle) and Fn-coated (bottom) bead applied on the cell cortex. (B) Schematics defining the two measured parameters: shape anisotropy of a cell fitted with an ellipse defined by major b and minor a axes, and cell orientation corresponding to the angle α (in degrees) between the major axis b and the cell geometrical center (GC)-bead axis (brown line). (C) Percentage of shape anisotropy variations for each assay conditions. The variation is calculated with respect to the initial cell shape at time 0. The number of analyzed cells is indicated on the histogram. (D) Rose diagrams indicate the proportion of cells for each angular sector under different assay conditions. (Red) Median angle. Statistical differences are indicated (Dunnett’s test: ^∗, P < 1; ^∗∗, P < 0.4; ^∗∗∗, P < 0.006; ^∗∗∗∗, P < 0.0001). All scale bars, 5 μm. Times shown in seconds (A, upper row) and minutes (A, middle and lower row).

Application of a fibronectin (Fn)-coated bead on the cortex of individual oscillating 3T3 cells readily abolishes these oscillations (Fig. 1 A; see Fig. S1 D). After 30 s of contact, we quantitatively analyze the shape anisotropy obtained by fitting the cell with an ellipse and measuring the ratio between the two principal axes (a and b) and the orientation of cell shape deformation (Fig. 1 B). Optical trapping of the Fn-coated bead induces a cell shape deformation along the geometrical cell center (GC)-bead axis, whereas the untrapped Fn-coated bead does not (Fig. 1, C and D; see Movie S2). Cell shape deformation in the presence of a single Fn-coated bead trapped at 120 pN.μm⁻¹ increases during the first 20 ± 6 min (mean ± SD, N = 54). The deformation does not show any reversibility during the duration of our experiments.

To discriminate between the mechanical and the biochemical contributions of the trapped Fn-coated bead contact to the cell response, we replace Fn proteins with nonspecific adhesive poly-lysine molecules (Pll-coated beads). The contact with Pll-coated beads, either trapped or not, is sufficient to suppress cell-shape oscillations (Fig. 1 A; see also Fig. S1 D). However, this response does not lead to persistent cell shape deformation and polarization along the GC-bead axis, as was observed with trapped Fn-coated beads (Fig. 1; see Movie S2). This result shows that a specific adhesion to fibronectin, in addition to contact stiffness (trapped bead), is required for persistent cell shape polarization.

Taken together, our findings demonstrate that a single, stiff adhesion-specific signaling cue (here a trapped Fn-coated bead) is necessary and sufficient to induce a transition from an oscillatory cell shape toward a global and persistent cell shape polarization along the GC-bead axis.

Cell shape polarization and traction force respond to a stiff adhesion cue in a dose-dependent manner

To further characterize the cell shape polarization in response to the stiffness of a single adhesion site, we record simultaneously the Fn-coated bead displacements (i.e., indicator of the force exerted by cells) and the cell shape changes, over time, for a range of optical trap stiffness. One to two minutes after contact, the cells develop a growing force on the bead, reminiscent of the traction forces exerted by cells on a two-dimensional substrate (9,16,30–33) (Fig. 2 A). By modulating the trap stiffness from 60 to 270 pN.μm⁻¹, we notice that the cells respond to higher stiffness with a faster increase of traction force (Fig. 2 A). The traction force reaches the maximum trapping force, so that the beads escape the optical trap 5.7 ± 1.5 min (270 pN.μm⁻¹, N = 9) to 24 ± 3.0 min (60 pN.μm⁻¹, orange curve, N = 3 out of nine cells) after contact (Fig. 2 A). This, however, does not affect cell shape polarization, which continues to build up along the GC-bead axis, indicating that adhesion rigidity is not required to maintain cell shape polarization (Figs. 1 B and 2 B). Similarly, the rate of variation of cell anisotropy increases with trap stiffness (Fig. 2 B). This implies that the amplitudes and rates of cell shape changes correlate with that of the traction force exerted on the bead before escape. Both shape changes and traction forces quantitatively depend on adhesion stiffness.

Figure 2.

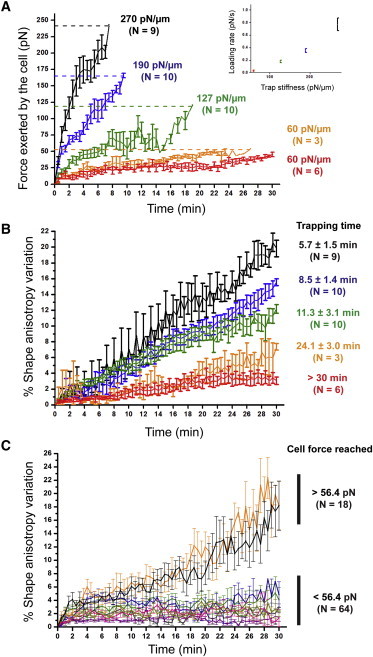
Generation of a threshold traction force is required for persistent shape polarization. (A) Plots depict traction forces exerted by single nonadherent 3T3 cells in response to an Fn-coated bead trapped with different stiffness as a function of time. (Colored curves) Corresponding trap stiffness. (Dashed lines) Maximum trapping force, and thus the maximum cellular traction force that can be measured before bead escape. (Inset) Force loading rate represented as a function of trap stiffness. Number of analyzed cells is indicated. Data are represented as mean ± SE (in pN.μm⁻¹). (B) Monitoring the corresponding cell shape polarization in each condition depicted in panel A. We measure the percentage of variation in shape anisotropy up to 30 min after bead application for different trap stiffness conditions (colored curves). The variation is calculated with respect to the initial cell shape at time 0. The trapping time of the Fn-coated bead (in minutes) is indicated for each trap stiffness condition. Data are represented as mean ± SE. Number of analyzed cells is indicated. (C) Plots depict the percentage of variation in cellular shape anisotropy as a function of time for ranges of traction force exerted on beads (colored curves). According to panel A, the bead was released at specific time points so that cells exert traction forces either lower or higher than 56.4 pN. μm⁻¹. The colored curves correspond to specific cellular forces (purple, 5.71 pN; green, 14.1 pN; blue, 22.8 pN; pink, 31.7 pN; beige, 44.2 pN; orange, 56.4 pN; black, >60 pN). Results from different trap stiffness are pooled together. The cellular shape anisotropy is monitored during the time course of the experiment. The variation is calculated with respect to the initial cell shape at time 0. Number of analyzed cells is indicated.

A minimal threshold of cell traction force has to be exerted to sustain polarization

We next ask whether a minimal threshold of traction force is required to sustain cell shape polarization. Indeed, we observe that six out of nine cells exposed to a trap stiffness of 60 pN.μm⁻¹ do not polarize, as evidenced by the variation of shape anisotropy statistically similar to the untrapped-bead condition (Fig. 1 C). Moreover, these cells exert a traction force that remains below the maximum trapping force fixed at 53.6 pN (red curve, Fig. 2, A and B). In contrast, the three other cells that polarize, exert traction forces exceeding 53.6 pN (orange curve, Fig. 2 A). Additionally, at higher stiffness, the force exerted by cells reach 53.6 pN within a few minutes and these cells always polarized (Fig. 2 A). These observations suggest that a threshold force of ∼53.6 pN has to be exerted by cells for triggering a self-sustaining polarization process after the bead escape.

To test this hypothesis, we release the trapped Fn-coated bead by tuning off the laser at different time points, so that cells can exert traction forces ranging from 5.71 ± 0.50 pN to 96.3 ± 8.28 pN (Fig. 2, A and C). Typically, Fn-coated beads are transiently held for 30 s to 20 min, depending on the optical trap stiffness (Fig. 2 A). In addition, we monitor the cell shape changes over time. We find that the cells able to exert traction forces higher than 56.4 ± 1.62 pN do exhibit a significant shape polarization (black and orange curves, Fig. 2 C). In contrast, the cells exerting forces below this threshold do not sustain polarization independently of the trap stiffness (Fig. 2 C). Interestingly, the value of this force threshold compares to the force generated by a few tens of actin-bound myosin-II motors together (34).

Taken together, our findings demonstrate the existence of a well-defined mechanical checkpoint, beyond which cell polarization can self-sustain in the absence of the initial stiff and specific adhesion cue.

Cell shape polarization and redistribution of cortical actomyosin depend on myosin activity

Dynamic instabilities of the cortical actomyosin distribution have been previously suggested to be involved in cell shape oscillations (29,35). Therefore, we monitor the cortical distribution of eGFP-myosin-IIA and eGFP-actin proteins over time. In oscillating cells, both cortical distributions are spatially and temporally heterogeneous along the cortex (Fig. 3 A; see Fig. S2 A). The temporal fluctuations of cortical actomyosin distribution show periodical changes at a frequency of 0.013 ± 0.003 Hz (N = 22; see Fig. S1 E). Decreasing myosin-II ATPase activity with blebbistatin (BB) treatment stalls cell shape oscillations together with fluctuations of cortical actomyosin distribution. In contrast, disruption of microtubules (MTs) with NZ does not significantly perturb the fluctuations of cortical actomyosin distribution (0.014 ± 0.004 Hz, N = 7; P < 0.2) or the proportion of oscillating cells (Fig. 4 A; and see Fig. S1, D and E). These results show that cell shape oscillations and spatio-temporal fluctuations of the cortical actomyosin distribution depend on myosin activity.

Figure 3.

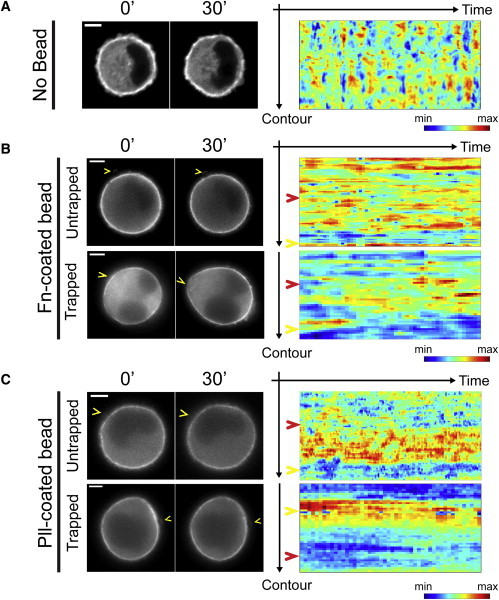
Cell shape polarization is sustained by a polarized cortical myosin distribution. Monitoring of the cortical dynamics of myosin-IIA. (Left) Fluorescence images of single nonadherent 3T3 cells expressing eGFP-myosin-IIA from time-lapse movies acquired in different mechanical and adhesive conditions: in the absence of any trapped adhesive cue (A); in the presence of a single Fn-coated bead (B); and Pll-coated bead (C) (see Movie S3). (Arrowheads) Position of the inductive trigger. (Right) Cell contour kymographs show the evolution of fluorescence intensity of cortical myosin-IIA over time. Representative contour kymographs are displayed for each condition. (Yellow arrowheads) Cortical angular position of the trigger; (red arrowheads) opposite pole. All scale bars, 5 μm.

Figure 4.

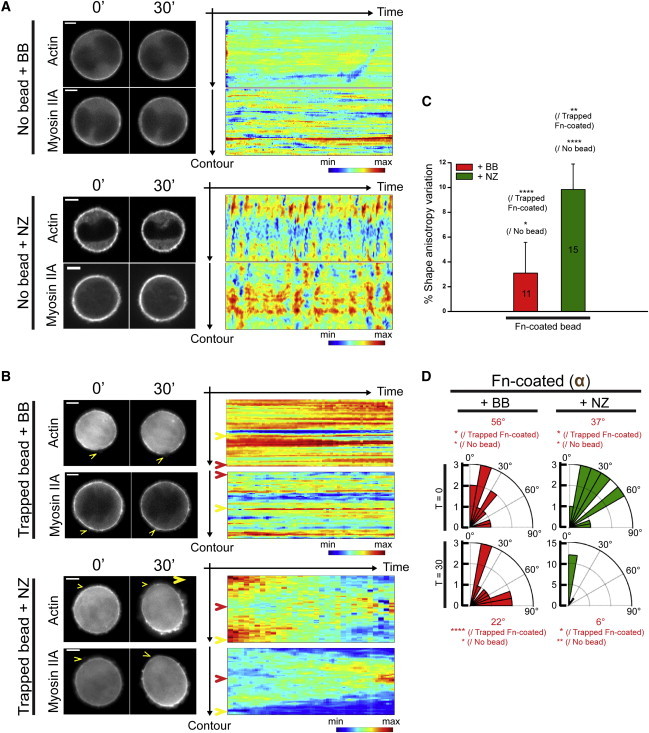
The dynamics of cortical actomyosin drive myosin-II-dependent cell-shape behaviors. Fluorescence images of single nonadherent cells expressing eGFP-actin and eGFP-myosin-IIA treated with chemical perturbants. (A) Cell-shape oscillation. Cell-contour kymographs exhibit fluctuation of cortical actomyosin when cells are treated with nocodazole (NZ), whereas the cortical distribution of actomyosin is frozen in the presence of blebbistatin (BB). (B–D) The application of a single Fn-coated bead does not induce cell shape polarization in the presence of BB. (B) The kymograph highlights a frozen cortical distribution of actomyosin. Depolymerizing the MTs does not impair the polarized redistribution of cortical actomyosin. (Yellow arrowheads) Cortical angular position of the trigger; (red arrowheads) opposite pole. Representative contour kymographs are displayed for each condition. All scale bars, 5 μm. (C) The shape anisotropy variation of nonadherent 3T3 cells is monitored while triggering cell shape polarization in the presence of BB or NZ. (D) Rose diagrams indicate the proportion of cells for each angular sector upon addition of BB or NZ. (Red) Median angle. Statistical differences are indicated (Dunnett’s test: P < 1; ^∗∗, P < 0.5; ^∗∗∗, P < 0.02; ^∗∗∗∗, P < 0.0001).

We next investigate the effect of trapped Fn-coated bead contacts on this cortical actomyosin distribution. Live imaging of eGFP-actin and eGFP-myosin-IIA shows a local decrease in fluorescence intensities at the point of adhesion, and conversely an increase at the opposite cell pole (Fig. 3 B; see Fig. S2 B). This recruitment is similar to that observed in previous studies despite the differences in topological and mechanical environments (5,36,37). Additionally, cell shape polarization occurs only in cells that exhibit a polarized redistribution of cortical actomyosin (Figs. 3 B and 4, A and B; and see Fig. S2 and Movie S3). For the 20% of cells (i.e., nonoscillating cells) that do not polarize in the presence of the cue, the actomyosin cortex remains frozen without any visible redistribution. Moreover, inhibition of myosin-II ATPase activity prevents both the redistribution of cortical actomyosin and cell shape polarization (Fig. 4, B–D). In contrast, nocodazole treatment does not perturb the cell shape and cortical actomyosin polarization (Fig. 4, B–D).

Altogether, these results show that redistribution of cortical actin and cell shape polarization are myosin-dependent processes.

Persistent cell shape polarization requires a persistent and local depletion of cortical actomyosin

The depletion of cortical actomyosin observed for several minutes at the contact point between the trapped Fn-coated bead and the cell (Figs. 3 B and 4 B; and see Fig. S2 B) contrasts with the actin recruitment at focal adhesion sites in cells spread on two-dimensional surfaces (38,39). This effect suggests that cell cortical tension locally decreases at the adhesion site. Similar to the effect of sperm entry in Caenorhabditis elegans oocyte (7), we hypothesize that this local tension decrease triggers an asymmetric redistribution of cortical actomyosin, leading then to cell shape polarization.

To test this idea, we locally ablate the cell cortex using a femtosecond-pulsed infrared laser (see Movie S4). Immediately after ablation, a cytoplasmic-pressure-driven bleb grows from the site of cortex disruption and retracts within 1 min. Concomitantly to bleb retraction, myosin-II proteins are progressively recruited to the site of ablation with levels similar to the pre-ablation level. This behavior indicates that laser ablation causes only a local and transient depletion of cortical actomyosin. In contrast to the effect of stiff ECM bead adhesion, cortical actomyosin does not polarize toward the opposite pole of the laser ablation site. This result supports the idea that local and sustained depletion of actomyosin, which is induced by the trigger of a stiff and adhesion-specific signaling cue, is required for persistent cell shape and cortical actomyosin polarization. We conclude that biochemical signaling downstream of ECM adhesion may persist after stiff ECM bead contact to maintain actomyosin polarization even after bead escape from the trap.

To account for this observation, we develop an active membrane shell model of the cell cortex ((40); see the Supporting Material). The description of the cortical actomyosin by the active gel theory (41) has already proven to reproduce accurately distinct complex behaviors of the cell cortex, such as cell shape oscillations (29,42,43). An actomyosin gel develops internal contractile stresses due to myosin activity. Integrated over the cortical layer, this active stress (σ^a) creates a local active tension τ^a (= ςΔμe/2) proportional to the myosin-II activity ςΔμ and to the cortical actomyosin thickness e (Fig. 5; see Fig. S3) (44). The active tension is isotropic (i.e., identical in both tangential and azimuthal directions of the surface), whereas the passive viscous tension, that opposes cell deformations and cortical flows, may be anisotropic. We also include explicitly in the theory the turnover dynamics of the cortex components (k_d). Starting from a spherical cell shape of radius R₀ at mechanical equilibrium (satisfying Laplace’s law ΔP = 2τ^a/ R₀), we propose that a single trapped Fn-coated bead induces a local decrease of the active tension τ^a. The decrease in active tension is triggered by a local decrease in the myosin activity ςΔμ and/or in the actin polymerization velocity v_p (= k_de₀) (Fig. 5; see Fig. S3). We study the response of the cell cortex to a local and weak decrease in active tension by using a perturbation theory similar to the work of Salbreux et al. (29).

Figure 5.

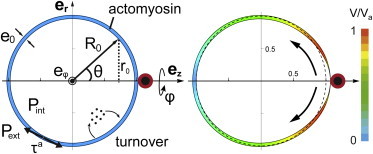
Active viscous membrane shell model for cortical polarization. (Left) Schematics of the mechanical parameters involved in the model depicted on the initial spherical state of the cell: the myosin activity (ςΔμ) generates an active tension τ^a = ςΔμe₀/2 in the viscous cortex of thickness e₀ and viscosity η under permanent actomyosin turnover. The cortical tension balances the pressure difference across the cell according to Laplace’s law: P_int-P_ext = 2 τ^a/R₀. (Right) Result of the numerical simulation is represented here. Stationary polarized state of the cell is obtained numerically by locally weakening the active tension at the bead location. The perturbation generates a cortical flow toward the opposite pole, whose normalized amplitude V is rendered using a color gradient. The cortical flow perturbs the cortical actomyosin thickness, as evidenced by the variation in the shell thickness, and polarizes the cell shape.

Solving the mechanical equations lead to the following results (Fig. 5; see Fig. S3, B–D).

• 1.A local but sustained decrease of myosin activity (see Fig. S3 B) and/or actin polymerization (Fig. 4; see Fig. S3, B and C) is sufficient to trigger a polarized cortical flow toward the pole opposite to the weakened region;
• 2.The cortical flow propagates alongside the cell surface and tends to increase the cortex thickness as it moves away from the weakened region, while competing with actomyosin turnover which, on the contrary, tends to maintain a uniform thickness;
• 3.The polarized cortical flow results in anisotropic viscous contributions to the cortex tension;
• 4.The resulting anisotropic cortical tension leads to stationary polarized cell shapes similar to those observed experimentally.

Therefore, the active shell model supports the idea that cortical actomyosin redistribution and polarized cell shape arise from a local depletion or decrease in contractile activity of the cortex. Furthermore, the model requires that the local depletion or decrease in contractile activity of the actomyosin gel be maintained for driving persistent cell shape polarization and actomyosin redistribution. The mechano-chemical cue provided by the trapped Fn-coated bead is essential for triggering the locally depleted (or inactivated) actomyosin, and thus the cell shape polarization. However, because cell shape polarization continues after the Fn-coated bead release from the trap, we conclude that the persistence of this depletion likely requires subcellular chemical signaling but not substrate stiffness.

Myosin-dependent cortical polarity propagates to a microtubule-dependent intracellular polarity

We then ask whether the cell shape and cortical actomyosin polarization is followed by an intracellular polarization. As a mark of internal polarity, we consider the location of the centrosome with respect to the cell GC of the centrosome-containing cell section (45). The centrosome location is essential in polarized cells, because it determines the position of different organelles, and reorients during neural (46) and epithelial differentiation (47) and cell migration (48–50). In oscillating cells, before Fn-coated bead contact, the centrosome is positioned at 3.4 ± 1.5 μm away from the cell GC (N = 49), and its position exhibits small oscillations (displacement amplitude of 0.16 ± 0.05 μm, N = 19). The existence of a finite distance between the centrosome and the cell GC reveals an intrinsic intracellular polarity in round nonadherent 3T3 cells, also displayed by a bean-shaped, off-centered nucleus.

However, the centrosome-GC axis does not significantly reorient along the cell major axis in oscillating cells, suggesting that this stable internal polarity is disconnected from the unstable cell periphery (Fig. 6). While triggering cell shape polarization, the distance between the centrosome and the Fn-coated bead remains constant whereas the centrosome-GC axis aligns along the orientation of cell shape polarization in 10 out of 12 cells. The median angular repositioning of the centrosome decreases from 67 to 29° (N = 12) (Fig. 6; see Movie S5). This effect occurs simultaneously to cell shape polarization within 8–14 min after bead contact (optical trap fixed at 120 pN.μm⁻¹) in 10 out of 12 cells (the two cells that did not polarize were not oscillating before the cue application). Therefore, we hypothesize that the centrosome relocation relies on cortical actomyosin activity.

Figure 6.

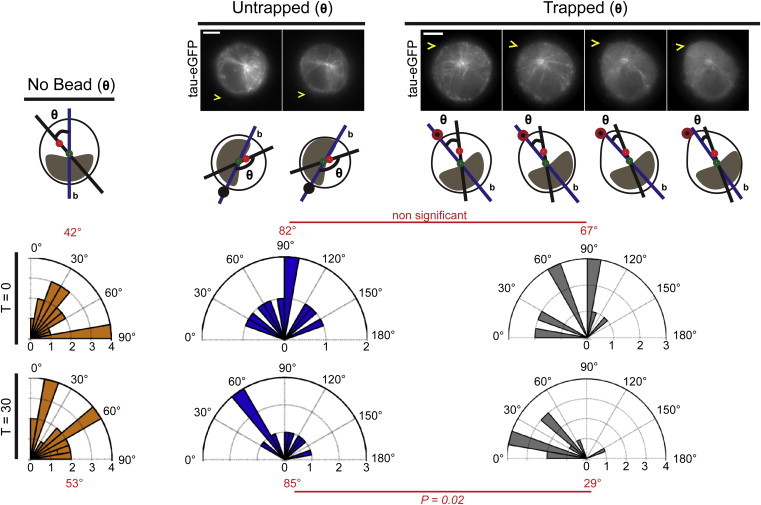
Cortical polarity propagates to an MT-dependent intracellular polarity. Centrosome angular repositioning along the polarization axis. Distribution of the angle θ between the centrosome-GC axis (black line) and the cell major axis b. The intracellular organization of the cell (green dot, cell center; red dot, centrosome; black dot, untrapped bead; black dot with red donut, trapped bead; yellow arrowheads indicate bead position) in each condition is depicted above the rose diagrams (top, time T = 0 min; bottom, time T = 30 min after bead contact). (Red) Median angle. Statistical differences are mentioned (Mann-Whitney test). All scale bars, 5 μm.

To test this idea, we treated unadhered 3T3 cells with BB before the application of a trapped Fn-coated bead. Centrosome movements (0.15 ± 0.14 μm, N = 6) as well as the angular repositioning (no significant change of the median angle θ from 63 to 67°, N = 6) are abolished. Several mechanisms have been proposed to explain the centrosome positioning, implying motor-mediated peripheral MT capture at the cortex (13,51–54) or a retrograde actomyosin flow-based nucleus relocation (45). In our experimental approach, the nucleus is always positioned close to the cell side in contact with the side, likely due to gravitational forces and the absence of a surrounding actin-enriched cage. Because of the nucleus geometry (vertical bean-shaped), the quantification of the position as well as the displacement of the nucleus cannot be precisely carried out. Having not observed transmembrane actin-associated nuclear lines as well as actin cables, we cannot totally exclude the possible role of nucleus relocation. Finally, we suggest that the centrosome relocation may result from the myosin-II-mediated pulling activity on MT plus-ends at the cell cortex, as previously suggested in other biological contexts (13,51–53).

Eventually, to investigate later stages of cell polarization, we performed three-dimensional monitoring of cell shape changes up to 40 min after Fn-coated bead contact. We observed that a large protrusion eventually grows below the bead, dragging the bead far away from the trap, and the three-dimensional cell shape deforms from a quasi-spherical to a pearlike shape (see Fig. S4 A). Examination of the cell protrusion with fluorescently tagged-proteins evidenced a strong actin and α5-integrin recruitment at the Fn-coated bead contact ∼12–18 min after contact (optical trap fixed at 120 pN.μm⁻¹), concomitant with the centrosome angular repositioning (Fig. 6; see Fig. S4 B). In NZ-treated cells, however, no such protrusion occurred after initial cell shape polarization (see Fig. S4 A). We conclude that while MTs are not necessary during the early stages of cell shape and cortical actomyosin polarization (Figs. 1, C and D, and 4), they are required for the generation of later-stage cell protrusion at the point of contact. The generation of this protrusion may involve MT-dependent molecular mechanisms previously evidenced in polarizing cells (55,56).

Conclusions

We have presented a minimal and well-controlled experimental system to study cell polarization upon adhesion signaling. This allowed us to distinguish the respective biochemical and mechanical minimal contributions of ECM adhesion that induce polarization in cells naïve for ECM adhesion cues.

We report direct evidence that the application of a local adhesion-specific signaling cue, through stiffness sensing, is necessary and sufficient to induce a transition from a randomly polarized cell shape, characterized by oscillating cortical actomyosin, to a persistent polarized shape where actomyosin is depleted at the contact site and enriched at the opposite pole of the cell. A physical model for the cell cortex supports the idea that a sustained decrease of actomyosin cortical tension is sufficient to induce persistent cortical polarization. Additionally, we reveal the existence of a well-defined traction force threshold, above which cell polarization is self-sustaining, even in the absence of the initial mechanochemical cue.

Finally, we show that cortical polarity further propagates to an intracellular and persistent cell polarization, characterized by a myosin-II-dependent centrosome reorientation and the growth of an MT-dependent protrusion at the site of adhesion. Our work defines minimal adhesive requirements and quantifies the mechanical checkpoint for cell shape and organelle polarizations, which are critical regulators of tissue and cell development.

Supporting Citations

References (57–59) appear in the Supporting Material.