Abstract
Collective cell movement is a crucial component of embryonic development. Intercellular interactions regulate collective cell movement by allowing cells to transfer information. A key question is how collective cell movement itself influences information flow produced in tissues by intercellular interactions. Here, we study the effect of collective cell movement on the synchronization of locally coupled genetic oscillators. This study is motivated by the segmentation clock in zebrafish somitogenesis, where short-range correlated movement of cells has been observed. We describe the segmentation clock tissue by a Voronoi diagram, cell movement by the force balance of self-propelled and repulsive forces between cells, the dynamics of the direction of self-propelled motion, and the synchronization of genetic oscillators by locally coupled phase oscillators. We find that movement with a correlation length of about 2 ∼ 3 cell diameters is optimal for the synchronization of coupled oscillators. Quantification of cell mixing reveals that this short-range correlation of cell movement allows cells to exchange neighbors most efficiently. Moreover, short-range correlated movement strongly destabilizes nonuniform spatial phase patterns, further promoting global synchronization. Our theoretical results suggest that collective cell movement may enhance the synchronization of the segmentation clock in zebrafish somitogenesis. More generally, collective cell movement may promote information flow in tissues by enhancing cell mixing and destabilizing spurious patterns.
Introduction
Collective cell movement is widely observed during embryonic development (1–4). In some situations, for example the lateral line primordium of zebrafish, moving cells are physically connected by tight cell-cell junctions (1,5). In other situations, such as the streaming of the neural crest cell population, cells lack tight cell-cell junctions (6–8). In general, the organization of collective cell movements requires mechanisms to share information across tissues, and intercellular signaling provides a way to transmit information for collective cellular behaviors.
A key question is how collective cell movement in turn influences the flow of information across a cell population. Vertebrate somitogenesis may provide a model system to address this question. It features both collective cell movement and intercellular signaling, and allows the outcome of information sharing to be visualized as the synchronization of coupled genetic oscillators, the segmentation clock. Somites, the precursor of segmental structures of the adult body, segregate sequentially from an unsegmented tissue called presomitic mesoderm (PSM), see reviews (9–11). Segregation of somites occurs rhythmically, for example, roughly every 30 min in zebrafish embryos (12). Somitogenesis period and somite length are thought to be determined by cyclic gene expression observed in the PSM (13,14). Cells in the PSM have a genetic oscillator composed of negative feedback loops (15–20). Cells communicate with each other through membrane proteins, Notch and Delta, to synchronize the phase of their genetic oscillations (21–28). Binding of Delta to Notch induces the cleavage of Notch intracellular domain, which activates cyclic genes in the cell nucleus. The genetic oscillator regulates the production of Delta, causing oscillatory intercellular signals. Because the disruption of synchronization leads to defected somite boundary formation (23–25), the mechanism for synchronization is a fundamental element in vertebrate somitogenesis.
Posterior to the PSM, in the tailbud, the phase of cyclic gene expression is spatially synchronized across the region. It has been shown that cells move around in the tailbud, exchanging neighbors frequently (24,29–32). Cell movement in the PSM during somitogenesis has been experimentally studied for its potential relevance to axis elongation in vertebrate embryos (30–34). In chick embryos, cells perform a random walk movement in the posterior PSM (30,31). In the zebrafish PSM, a recent experimental study observed collective cell movement during somitogenesis (32). The study reported positively correlated cell movement in the ventral side of the tailbud, with a correlation length of 20 ∼ 100 μm, corresponding to roughly 2 ∼ 10 cell diameters (32).
Previous theoretical studies indicated that synchronization of genetic oscillators is enhanced when the movement pattern of cells is random (35,36). Random movement of oscillators effectively extends their interaction range, accelerating the realization of synchronization (37). However, if cells tend to move coherently, relative position exchanges will hardly occur, impeding the effect of cell movement on synchronization. The observation of coherent movement (32) raises the question whether collective cell movement can still enhance the synchronization of the segmentation clock. In addition, previous studies on the synchronization of mobile coupled oscillators used simple descriptions for their movement, such as random exchange of locations between oscillators in the lattice (35–37), and random walk movement in a continuous domain without volume exclusion (38–41). These simplifications allow many formulae for synchronization dynamics to be analytically derived, but in reality cells with finite volume move in a space under intercellular physical forces. The contact surface area between two cells gradually increases as they come close to each other. The time evolution of network topology for intercellular interactions, that is which cell interacts with which, is influenced by the mechanical processes of cell movement. Thus, it is necessary to develop a general physical model to study the effect of cell movement on synchronization dynamics of the segmentation clock.
To address these points, here we develop a physical model for collective cell movement and the phase dynamics of the segmentation clock. We use numerical simulations to show that a movement pattern with a short-range velocity correlation is optimal for synchronization across a population. The mean squared difference of the displacement between pairs of cells shows that this optimal collective movement maximizes cell mixing. These theoretical results indicate that a detailed quantification of relative cell movement is key to understanding synchronization dynamics of the segmentation clock.
Materials and Methods
Theory
In this work, we examine whether cell movement patterns with velocity correlations affect the synchronization dynamics of coupled oscillators across a field of cells. The theory introduced below describes cells in the tailbud of a zebrafish embryo, where coherent cell movement and phase synchronization of cyclic gene expression have been reported. The theory consists of four key elements: 1), a description of the tissue and cell shapes; 2), a balance of forces describing the movement of cells as particles; 3), the alignment dynamics of self-propelled motility; and 4), the synchronization dynamics of coupled oscillators. Below we introduce dimensionless equations for cellular mobility and the phase dynamics of the segmentation clock. In the Appendix, we derive these dimensionless equations from a fully dimensional theory.
For a clear presentation of the effects of correlated movement, we adopt a simple description of the tissue. In a two-dimensional continuous space of size L × L, we locate N cells. The dimensionless length L is expressed in units of the lengthscale given by the isolated cell diameter r0, which we use as a characteristic lengthscale throughout this work, see Eq. 16 in the Appendix. To exclude boundary effects, we adopt periodic boundary conditions in space. We do not consider cell division and cell apoptosis in the theory for simplicity, so the total number of cells N is fixed in simulations. The cell density is ρ = N/L2. In most of the PSM, cells are densely packed. Although in the tailbud they appear to be less tightly packed (31), this condition enhances cellular mobility so the small gaps between cells are very short lived. For this reason, in this work we choose a cell density ρ such that the distance between the centers of nearest cells is approximately equal to the diameter of an isolated cell r0. In the dimensionless model this distance is equal to 1.
Let xi(t) = (xi(t), yi(t)) be the position of the center of cell i (i = 1,2,…,N) at dimensionless time t in the two-dimensional space. We use the timescale of phase dynamics as the characteristic timescale in this work, see Eq. 17 in the Appendix. To determine cellular shapes and the neighboring relation of cells, we use a two-dimensional Voronoi tessellation based on these cell centers, Fig. 1 A. This approach has been used to describe various tissues including the neurogenic region of insect ectoderms (42), the intestinal crypt (43), and the chick limb bud (44). We assume here that the shape of the Voronoi region for the cell center xi represents the shape of cell i. The contact length between cells i and j is then determined by the boundary between the two corresponding Voronoi regions, Fig. 1 B. In a Voronoi diagram there is no gap space between cells. This tessellation provides a good approximation for cell shapes, given the cell density observed in the tissue. In Text S1 in the Supporting Material we analyze an alternative description, in which cells are represented by soft discs allowing for gaps between them, Fig. S1. We obtain the same qualitative results as with the Voronoi tessellation, showing that our results are not sensitive to the choice of cell shape and packing.
Figure 1.
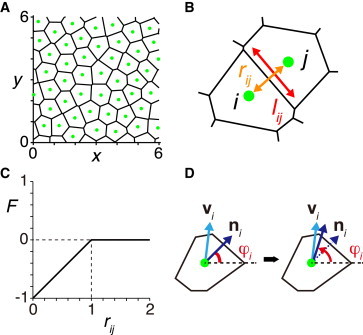
Theoretical description of collective cell movement in the zebrafish tailbud. (A) Two-dimensional Voronoi tessellation represents cell shape. The green dots indicate cell centers. (B) Contact length lij (red) and intercellular distance rij (orange) between cells i and j. (C) Repulsive force F is a function of the distance rij between cells i and j, see Eq. 2. (D) Polarity ni aligns toward instantaneous velocity vi, see Eq. 3. To see this figure in color, go online.
Collective movement of cells and animals has been extensively studied in the context of statistical physics because of the occurrence of phase transitions (45,46), and the interesting dynamic properties of active matter (47). Because the mechanism for generating collective cell movement in the zebrafish tailbud has not been established yet, here we adopt a phenomenological description of cell movement that can reproduce the movement patterns observed in this tissue (32). We describe cell movement by a dimensionless overdamped equation derived from Newton’s second law in the presence of self-propelled cellular motion and intercellular forces (see the Appendix (48)):
| (1) |
where v0 is the modulus of self-propulsion velocity, ni = (cosφi,sinφi) is a unit vector pointing at an angle φi(t) representing the polarity of self-propelled motion, μ is the coefficient of intercellular force strength. The summation is carried over the Voronoi neighbors of cell i denoted as Vi(t), and F(xi,xj) represents the physical force between cells i and j. For simplicity, we consider repulsive central forces representing the volume exclusion interaction between neighboring cells, F(xi,xj) = F(xi,xj)eij, with eij = (xj−xi)/|xj−xi|. We describe the magnitude of this force as a linear function of the dimensionless distance between cells i and j, rij = |xj−xi| with a distance cut-off at the diameter of isolated cells:
| (2) |
see Fig. 1, B and C. Because we set the diameter of isolated cells as the lengthscale of our model (see the Appendix), the distance cut-off is 1 in dimensionless Eq. 2. We confirm qualitatively the same results in the presence of an adhesive force between cells (see Text S1 and Fig. S2).
The time evolution of the angle φi(t) of the polarity vector ni(t) is described as (32,48)
| (3) |
where κφ is the polarity alignment strength, vi(t) = dxi(t)/dt, ez = (0,0,1) is the unit vector pointing out of the plane where cells move, Dφ is the polarity noise intensity, and ηi(t) represents white Gaussian noise of 〈ηi(t)〉 = 0 and 〈ηi(t)ηj(t′)〉 = δi,jδ(t − t′). Angular brackets 〈⋅〉 denote ensemble averages.
Eq. 3 describes a situation where each cell tends to align its direction of self-propelled motion ni along its current direction of motion vi/|vi|, with a characteristic timescale 1/κφ, Fig. 1 D. Velocity correlations between neighboring cells arise through the alignment of ni along the direction of the net force fi = ∑j∈ViF(xi,xj) that cells sense, as ni(t) × vi = μni(t) × fi. For instance, if a cell is pushed by other surrounding cells to move in a particular direction, the cell aligns its self-propulsion velocity to match the local direction of motion. We also consider a different equation for polarity alignment below to show that our results do not depend on the description of polarity alignment dynamics.
To describe the dynamics of the segmentation clock, we use locally coupled identical phase oscillators in the presence of noise (36,49). Previous studies on the segmentation clock showed that phase oscillators can explain quantitative experimental data (23,26). The time evolution of the phase of each oscillator is given by
| (4) |
where θi(t) is the phase of cell i at time t, ω is the autonomous frequency of oscillations, κij is the coupling strength between cells i and j, Dθ is the phase noise intensity and ξi(t) is a white Gaussian noise of 〈ξi(t)〉 = 0 and 〈ξi(t)ξj(t′)〉 = δi,jδ(t − t′). The summation is over the Voronoi neighbors Vi(t) of cell i. All parameters in Eq. 4 are dimensionless.
Cells in the zebrafish tailbud interact with their neighbors through Delta and Notch proteins on their membranes. Here, we assume that these proteins are uniformly distributed on cell membranes. Under this assumption the contact surface area between two cells determines the strength of interaction between them. We define the relative coupling strength κij(t) between cells i and j as
| (5) |
where lij is the length of the edge between cells i and j, Fig. 1 B, and is the perimeter of cell i. The coupling strength between cells i and j is larger when cell i has a longer contact length to cell j. In reality, the association of these membrane proteins between two contacting cells may require some time to be accomplished after movement (36). For simplicity however, here we assume that it occurs instantaneously in Eq. 5. Note that a coupling strength constant does not appear in Eq. 4 due to nondimensionalization, see Eq. 17 in the Appendix.
In Eq. 4 we do not consider time delays in coupling. Previous studies showed that time delays in coupling affect the collective period of the segmentation clock in zebrafish (26,50). In the current study, however, we adopt a simpler theory without time delays in coupling for clear illustration of the effects of collective cell movement on the synchronization of coupled oscillators.
To set the initial cellular positions and the initial degree of collective cell movement, we simulate the system from t = −tp (tp > 0) to t = 0 without considering phase dynamics, Eq. 4. Typically, we have set tp = 200 in this work. We first randomly put cell centers in the two-dimensional space L × L at t = −tp. The initial velocity angles φi(−tp) are chosen randomly from a uniform distribution between 0 and 2π. We simulate cell movement according to Eqs. 1–3, to realize a steady-state collective movement with a given parameter set. After preparing the system in this way, we assign random phases for each cell θi(0), chosen from the uniform distribution between 0 and 2π unless noted otherwise.
Quantification of movement and synchronization
To quantify the degree of collective cell movement we introduce a global velocity order parameter (46,48):
| (6) |
If cells in the system move with a similar direction, Φ ∼ 1. Instead, if they move in different directions, Φ ∼ 0. We also consider the ensemble average of the velocity order parameter 〈Φ(t)〉 over 200 different realizations of movement and initial conditions.
To further characterize cell movement in simulations, we calculate the velocity autocorrelation Ca(t) defined as
| (7) |
where t0 is the reference time, which we set t0 = 0 without loss of generality in this work.
We also consider the velocity cross correlation C(r,t) between two cells at a distance r. We compute an average of the inner product of velocity vectors over all pairs of cells for which the distance is in the shell between r − Δr and r + Δr:
| (8) |
In this work, we set Δr = 0.2. If C(r,t) ∼ 1, the direction of motion between two cells with distance r is highly correlated, and they move almost in the same direction. In contrast, C(r,t) ∼ −1 indicates that two cells with distance r move in opposite directions. If there is no correlation of direction of motion, C(r,t) ∼ 0. In this work, we measure and plot the steady state of C(r) after transients elapsed.
To quantify the timescale of neighbor exchange between cells, we introduce the mean squared difference of displacement vectors (51,52):
| (9) |
where 〈⋅〉ij represents an average over all the N(N − 1)/2 possible pairs of cells in a system. Because we do not know in advance the lengthscale of velocity correlations, we perform an average over all pairs of cells to avoid introducing a spurious intermediate lengthscale for averaging. For instance, in the presence of short-range velocity correlations, an average over initially neighboring cells would fail to capture mixing because these cells would remain neighbors for some time.
Because m(t) quantify how rapidly two cells disperse, the rapid increase of m(t) is a signature of extensive cell mixing. Because we set the diameter of isolated cells r0 as the lengthscale of the system, the cellular diameter is ≈1 in our dimensionless model. Therefore, the time te, where m(te) = 1, is an average waiting time for a pair of cells to move apart from each other one cell diameter. We define λ ≡ 1/te as a mixing rate. A larger λ indicates more extensive cell mixing.
In addition, m(t) is expected to increase as a power law, m(t) ∼ tγ. The exponent γ determines the type of cell movement. When cells perform directed ballistic movement, m(t) ∼ t2. In contrast, m(t) ∼ t for random movement. When cells are constrained, for example by strong physical forces, the exponent of m(t) can be less than one. Because we consider a finite domain L × L, m(t) saturates to a finite value L2/6 for t ≫ 1. This saturation value can be derived from the steady-state distribution of the distance between two cells in a periodic domain for large time.
To measure the degree of global phase synchronization, we use the Kuramoto phase order parameter (53):
| (10) |
where . If cells are synchronized, Z is close to unity, while if cells are not synchronized, the phase order parameter Z is close to zero. Similar to the velocity order parameter, we also consider the ensemble average of the phase order parameter 〈Z(t)〉 over 200 different realizations of simulations.
Results
We study the synchronization of coupled oscillators under steady-state movement patterns characterized by a steady-state velocity distribution and a velocity order parameter Φ fluctuating around a constant value. Movement patterns are determined by the ratios v0/μ in Eq. 1 and κφ/Dφ in Eq. 3. We first analyze synchronization in the presence of uncorrelated movement patterns that arise for κφ/Dφ = 0 and different values of the ratio v0/μ. Next, we study synchronization under collective motions arising for different values of the ratio κφ/Dφ at constant v0/μ. The timescale for neighbor exchange 1/λ and that of phase dynamics are the most relevant timescales for synchronization of coupled genetic oscillators (37). Here, we ask how collective motions of cells change the timescale of neighbor exchange between cells. Finally, we study the stability of a spatial phase pattern that develops from particular initial conditions against collective cell movement. In this work we do not aim at a complete characterization of all the possible dynamical regimes in the theory. We rather focus on regimes where collective cell movement arises and oscillators sustain local synchronization even in the presence of phase noise, conditioned by 1/Dθ > 1/2 (39).
Cell movement without spatial velocity correlations
We first ask whether cell movement without spatial velocity correlations enhances synchronization in our current physical description, as reported previously by other studies (35–37,39,40). We consider the situation in which there is no active mechanism for polarity alignment, described by the polarity alignment strength κφ = 0 in Eq. 3. In this situation, the mean velocity modulus 〈v〉i = 〈|dxi/dt|〉i of a cell population depends on the value of the ratio v0/μ as indicated in Fig. 2 A. Even though the velocity modulus for self-propelled motion v0 is constant, the instantaneous velocity modulus vi = |dxi/dt| in simulations distributes around its population average 〈v〉i due to the effect of intercellular repulsive forces, Fig. 2, B–D. Because the value of the coefficient of intercellular force strength μ has not been experimentally determined yet, in Fig. 2 we change its value and fix v0 = 1.2, which is close to previously reported values (31,32) (see the Appendix). The ratio v0/μ describes the tissue softness, Fig. 2 A. If v0/μ ≪ 1 cells cannot move freely due to strong repulsive forces between them. In the intermediate regime of v0/μ, cells can change their relative positions, subject to a volume exclusion effect. If v0/μ ≫ 1, the effect of volume exclusion is negligible compared to self-propelled motion, and each cell moves at the roughly constant velocity modulus v0. There is a value of v0/μ above which 〈v〉i remarkably increases with the increase in v0/μ. For Fig. 2 A this value is v0/μ ≈ 0.04.
Figure 2.
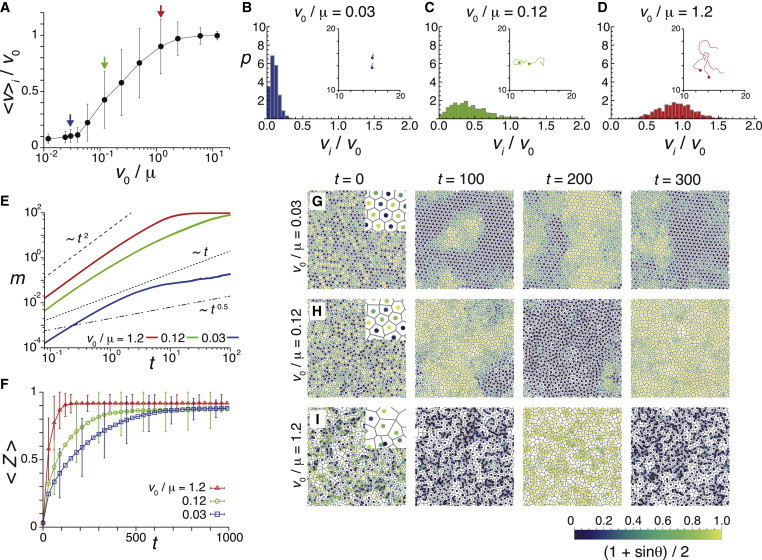
Uncorrelated movement of cells enhances synchronization, as shown by numerical simulations of Eqs. 1–5 with κφ = 0 in Eq. 3. (A) Dependence of the average velocity modulus over a cell population 〈v〉i on the ratio of self-propulsion speed to the coefficient of intercellular force strength v0/μ. The arrows point to v0/μ = 0.03 (blue), 0.12 (green), and 1.2 (red). (B–D) Probability density of |vi| for (B) v0/μ = 0.03, (C) v0/μ = 0.12, and (D) v0/μ = 1.2. Insets show trajectories of two cells for 0 ≤ t ≤ 10, with dots indicating cell positions at t = 0. (E) Time evolution of m(t) defined in Eq. 9. (F) Time evolution of the average phase order parameter 〈Z(t)〉 defined in Eq. 10. (G–I) Phase profiles for (G) v0/μ = 0.03, (H) v0/μ = 0.12, and (I) v0/μ = 1.2. The color indicates the intensity determined by (1 + sinθi)/2, see color code bar. Error bars in (A) and (F) indicate standard deviation (SD). In all panels: L = 24, N = 800, v0 = 1.2, κφ = 0, ω = 2.1, Dθ = 0.1, and Dφ = 0.5. To see this figure in color, go online.
Below this value of v0/μ, for example for v0/μ = 0.03, cells can hardly move as indicated by the very small value of the mean velocity modulus 〈v〉i/v0 ≈ 0.1. The shape of the probability density function for vi is quite different from that of a normal distribution, Fig. 2 B. The mean squared difference of displacement vectors m(t) increases as m(t) ∼ t1.63 at very short timescales, Fig. 2 E. This behavior is the result of a wiggling motion at a subcellular lengthscale of about 10−1r0, Fig. 2 B inset and Movie S1. However, because of strong repulsive forces between cells, a cross over occurs and m(t) ∼ t0.5 at longer timescales, indicating that movement is slower than normal diffusion. m(t) does not exceed 1 even at t = 100 (i.e., te > 100). This indicates that these cells do not change their relative positions within a timescale comparable with that of phase dynamics. In this regime, the Voronoi regions tend to be hexagonal and the tissue is similar to a rigid hexagonal lattice with a few defects, Fig. 2 G.
In this slow mobility regime (v0/μ = 0.03), the average phase order parameter 〈Z(t)〉 slowly increases over time and reaches the steady-state 〈Z〉 ∼ 0.88, Fig. 2 F (see also Movie S1). Most of the individual trajectories of the order parameter Z(t) reach and fluctuate around the mean value after a transient, indicating that cells attain global phase order. However, in a few cases, roughly 1.5% of the initial conditions for this parameter setting, the phase order parameter Z remains <0.3 even after long time t = 1000. In such cases, kinematic spatial phase waves with a wavelength comparable to the domain length L persist and prevent the population from attaining global phase order (39).
When v0/μ becomes larger than v0/μ ≈ 0.04, cells can move around subject to intercellular forces, Fig. 2, A and C. Because there is no polarity alignment, that is κφ = 0 in Eq. 3, the velocity order parameter is very low 〈Φ〉 < 0.15, indicating a movement pattern without spatial velocity correlations. For v0/μ = 0.12, m(t) ∼ t2 for short timescales, whereas m(t) ∼ t1.4 for long timescales, Fig. 2 E. This indicates that these cells exchange neighbors more frequently than in the previous case v0/μ = 0.03. Note that offsets of m(t) in Fig. 2 E are different among different values of v0/μ. This is because the average velocity modulus 〈v〉i differs for different values of v0/μ, Fig. 2 A.
In this regime of faster mobility (v0/μ = 0.12), even though spatial phase waves emerge for a few initial conditions, the average phase order parameter increases more rapidly than in the case of slower mobility (v0/μ = 0.03), Fig. 2, F and H (see also Movie S2). This result indicates that the self-propelled motion in the theory enhances synchronization, as previous lattice (35–37) and off-lattice models (39,40) suggested.
As we further increase v0/μ to v0/μ = 1.2, self-propelled motion dominates the movement pattern and 〈v〉i/v0 ≈ 1, Fig. 2, A and D. The shape of the velocity probability density becomes closer to that of a normal distribution, Fig. 2 D. m(t) ∼ t2, which indicates ballistic cell movement, before it saturates due to the finite size of the system, Fig. 2 E. The exchange of neighboring cells occurs more quickly. As a result, the phase order parameter increases much more rapidly over time, Fig. 2, F and I (see also Movie S3). After transients elapse, individual trajectories of the phase order parameter Z(t) fluctuate around Z ∼ 0.92, which is slightly higher than the case of slower mobility. We could interpret this result in terms of an increasing effective interaction range, similar to what has been observed for random movement (37). There are two ways in which the ratio v0/μ can become large. In the limit μ → 0, cells behave as self-propelled particles without volume exclusion as in (39,40). In the other limit v0 → ∞, the system behaves as a mean-field system, studied in (37,40). In both cases movement promotes synchronization of oscillators. Taken together, cellular mobility enhances synchronization in the physical model including intercellular forces and self-propelled motion.
Next, we study the dependence of the phase order parameter on the polarity noise intensity Dφ describing polarity fluctuations in Eq. 3, while fixing v0/μ = 0.12, Fig. 3. The average phase order parameter 〈Z(t)〉 increases more rapidly when polarity fluctuations are smaller, Fig. 3 A. To see why this happens, we compute the velocity autocorrelation Ca(t) defined by Eq. 7. The autocorrelation Ca(t) decreases rapidly over short timescales t < 2, due to intercellular forces randomly exerted from neighboring cells, Fig. 3 B. Over long timescales, the decay rate of Ca(t) is determined solely by the polarity noise intensity Dφ. In the presence of stronger polarity fluctuations, the persistence time of cells quantified by the inverse decay rate of Ca becomes shorter, Fig. 3 B. The net displacement tends to be small because cells frequently change the direction of motion. As a result, the mean squared difference of displacement vectors m(t) increases slowly, Fig. 3 C, indicating that it takes a longer time for these cells to exchange neighbors. As polarity fluctuations become weaker the persistence time gets longer, allowing cells to exchange neighbors more efficiently. Thus, longer persistence time can enhance the synchronization of coupled genetic oscillators when cells move without spatial velocity correlations.
Figure 3.
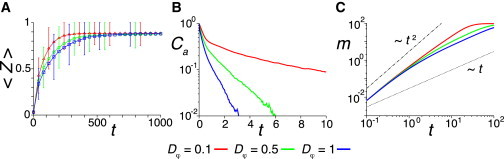
Persistent cell movement enhances synchronization in the absence of spatial velocity correlations. (A) Time evolution of average phase order parameter 〈Z(t)〉 for different values of polarity noise intensities Dφ. Error bars indicate the SD. (B) Velocity autocorrelation Ca(t) defined by Eq. 7 for different values of Dφ. (C) Time evolution of m(t) for different values of Dφ. In all panels, L = 24, N = 800, v0 = 1.2, μ = 10, κφ = 0, ω = 2.1, and Dθ = 0.1 in Eqs. 1–5. To see this figure in color, go online.
Cell movement with spatial velocity correlations
To study the effect of collective cell movement on the synchronization of coupled genetic oscillators, we examine the dependence of the phase order parameter Z on the polarity alignment strength κφ in Eq. 3. We confirm that our model generates collective cell movement as κφ increases, Fig. 4. When the ratio of the polarity alignment strength to the noise κφ/Dφ is small, cells do not develop spatial velocity correlations, Fig. 4, A and D. The average velocity order parameter is low 〈Φ〉 ≈ 0.1, indicating no collective cell movement, Fig. 4 E. The small but finite value of 〈Φ〉 is due to a finite size effect of the spatial domain and physical repulsive forces that can cause small nearest-neighbor velocity correlations, Fig. 4 D. As the value of κφ increases, the system undergoes a transition around κφ/Dφ ≈ 1.5 for the parameter set used here, Fig. 4 E. Slightly above this transition point, cells develop short-range velocity correlations, Fig. 4, B and D. Neighboring cells move in a similar direction, but distant cells move in different directions. As κφ increases, the correlation length extends. When the ratio κφ/Dφ is much larger than the transition point, most of the cells move in almost the same direction, Fig. 4, C and D. The average velocity order parameter is almost one, indicating highly collective cell movement, Fig. 4 E.
Figure 4.
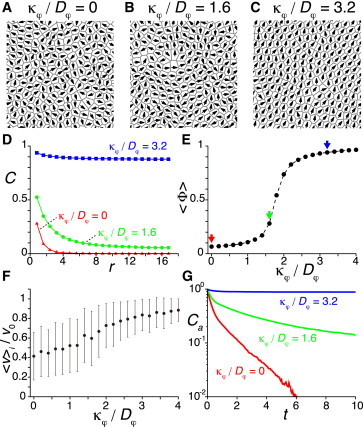
Correlation of direction of motion between cells. (A–C) Direction of velocity vector vi/|vi| for each cell represented by arrows for different ratios of the polarity alignment strength to the polarity noise intensity κφ/Dφ. For illustration, small square domains (12 × 12) of a system are shown. (D) Dependence of the cross correlation C of unit velocity vector vi/|vi| defined by Eq. 8 on the distance between cells r for the different values of κφ/Dφ. (E) Dependence of the average velocity order parameter 〈Φ〉 in Eq. 6 on the ratio κφ/Dφ. Arrows point to κφ/Dφ = 0 (red), 1.6 (green), and 3.2 (blue). The solid circles indicate the steady-state values of 〈Φ〉. (F) Dependence of the average velocity modulus 〈v〉i on κφ/Dφ. Error bars indicate the SD. (G) Velocity autocorrelation Ca for different values of κφ/Dφ. In all panels, L = 24, N = 800, v0 = 1.2, μ = 10, and Dφ = 0.5 in Eqs. 1–3. To see this figure in color, go online.
Below, we change the value of κφ to control the degree of collective cell movement. In principle, one could alternatively change the polarity noise intensity Dφ while fixing κφ to alter the degree of collective movement. However, as we already showed in Fig. 3, Dφ itself can affect phase synchronization by extending persistence time, so we choose here to tune κφ.
Fig. 5 A shows the time evolution of the average phase order parameter 〈Z(t)〉 for different ratios of polarity alignment strength to noise intensity κφ/Dφ. For much stronger polarity alignment than the critical polarity alignment strength, for example κφ/Dφ = 3.2, cell movement is highly collective 〈Φ〉 ≈ 0.94 and the average phase order parameter 〈Z(t)〉 increases slower than without polarity alignment κφ/Dφ = 0 (see also Movie S4). After a longer transient, 〈Z(t)〉 reaches a steady state that is close to the steady state for κφ/Dφ = 0. Due to strong polarity alignment among cells, the exchanges of relative positions between two neighboring cells hardly occurs, as shown by the slow increase in m(t), Fig. 5 B. Therefore, the time evolution of the phase order parameter 〈Z(t)〉 is similar to that of a population of nonmobile cells. Thus, strong polarity alignment reduces the effect of cell movement on the synchronization of coupled oscillators.
Figure 5.
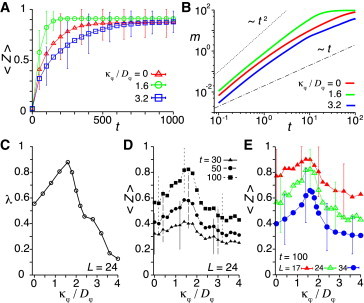
Optimal polarity alignment strength for synchronization. Time evolution of (A) the average phase order parameter 〈Z(t)〉 and (B) the mean squared difference of displacement vectors m(t) for the different ratios of the polarity alignment strength to the polarity noise intensity κφ/Dφ. (C) Dependence of the mixing rate λ on κφ/Dφ. (D) Dependence of 〈Z〉 on κφ/Dφ. 〈Z〉 at several time points is plotted. (E) Dependence of 〈Z〉 at t = 100 on κφ/Dφ for different domain lengths L. In all panels, v0 = 1.2, μ = 10, Dφ = 0.5, ω = 2.1, and Dθ = 0.1 in Eqs. 1–5. Error bars in (A, D, and E) indicate the SD. In (A–D), L = 24 and N = 800. In (E), N = 400,800,1600 for L = 17,24,34, respectively. To see this figure in color, go online.
However, cell movement with an intermediate polarity alignment can enhance phase synchronization more than cell movement without alignment, Fig. 5 A (see also Movie S5). For κφ/Dφ = 1.6, the polarity alignment strength is slightly above the transition point for collective cell movement, 〈Φ〉 ≈ 0.28. The average phase order parameter increases much more rapidly than in the case without alignment κφ/Dφ = 0. Moreover, it reaches a steady-state value that is larger than in the case of κφ/Dφ = 0. This happens because no spatial phase wave appears from random initial conditions in simulations. The faster increase of m(t) indicates that these cells can efficiently exchange neighbors, Fig. 5 B, leading to quicker synchronization.
These findings suggest the existence of an optimal polarity alignment strength for cell mixing, Fig. 5 C, and consequently for synchronization, Fig. 5 D. For the parameter set used here, the optimal polarity alignment strength is about κφ/Dφ ≈ 1.6. We study the dependence of the optimal polarity alignment strength for synchronization on the domain length L, Fig. 5 E. To this end, we increase the domain length L and increase the number of cells N maintaining a fixed cellular density ρ. The optimal polarity alignment strength is almost the same for L = 17 (N = 400), L = 24 (N = 800), and L = 34 (N = 1600), indicating that it is not sensitive to the domain length. This is because the mixing rate λ does not depend on the domain length L.
The mechanism for the existence of an optimal polarity alignment strength can be explained as follows. Without correlated movement, the individual velocities tend to be slow because neighboring cells moving in a different direction are more likely to be an obstacle due to volume exclusion. Moving together with surrounding cells by aligning polarity, each individual cell can efficiently migrate through longer lengthscales in the tissue, so its velocity becomes higher, Fig. 4 F. This enhances cell mixing, as in Fig. 2 E. Moreover, velocity alignment among neighbors increases the velocity autocorrelation, Fig. 4 G. As in Fig. 3, longer persistence time of cell movement enhances cell mixing. However, as the polarity alignment strength further increases, cells start moving more coherently, Fig. 4 C, and do not exchange their relative positions. The balance between these opposing effects sets the optimal polarity alignment strength for cell mixing, Fig. 5 C. More extensive cell mixing better enhances synchronization, as previous theoretical studies have shown (35–37,39,40). Hence, an optimal polarity alignment strength for the synchronization of coupled oscillators arises.
Optimal short-range velocity correlation for synchronization
To show that the previous results do not depend on the particular form of polarity alignment dynamics, we consider here a different mechanism of polarity alignment. In the mechanism considered so far in Eq. 3, polarity alignment occurs due to the effect of mechanical forces. We now assume instead that cells sense the polarity of neighboring cells directly by biochemical signals, such as proteins with a polarized pattern on the cell membrane, and respond by aligning their own polarity as
| (11) |
where κij is given by Eq. 5. We adopt a sinusoidal function for polarity alignment in Eq. 11 because of its simplicity and an analogy with coupled phase oscillators described as in Eq. 4. Note that intercellular forces have no influence on the dynamics of polarity alignment in Eq. 11. Polarity alignment dynamics Eq. 11 generates cell movement with spatial velocity correlations of a lengthscale that depends on the ratio κφ/Dφ (54).
We obtain an optimal polarity alignment strength for synchronization and cell mixing for Eq. 11, Fig. 6, A and B. The optimal value of polarity alignment strength κφ in Eq. 11 is different from the one in Eq. 3, but this is because κφ describes different things in the two mechanisms. Of importance, however, these two different optimal values of polarity alignment strength generate quantitatively the same short-range velocity correlation, Fig. 6 C. We can fit an exponential decay to the velocity cross correlation C(r) to estimate the decay length rc for short lengthscales, Fig. 6 C inset. We obtain rc ≈ 2.65 with the optimal polarity alignment strength in Eq. 3 and rc ≈ 2.27 for Eq. 11. In addition, we find that the optimal values of rc in the disk model and the Voronoi model including cell adhesion are quite similar to the previous values (Text S1). These results suggest that a spatial velocity correlation with a lengthscale of around 2 ∼ 3 cell diameters is optimal for the synchronization of coupled phase oscillators, regardless of the particular form of polarity alignment dynamics.
Figure 6.
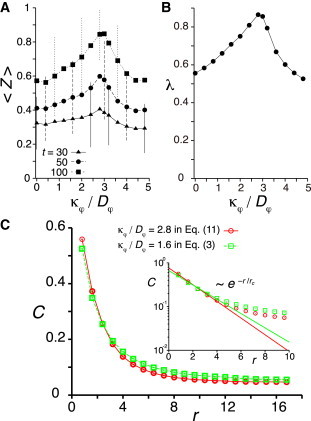
Optimal short-range velocity correlation for synchronization of coupled oscillators. (A) Dependence of average phase order parameter 〈Z〉 on the ratio of the polarity alignment strength κφ to the polarity noise intensity Dφ in Eq. 11. Error bars indicate the SD. (B) Dependence of cell mixing rate λ on κφ/Dφ in Eq. 11. (C) Velocity cross correlation generated with the optimal values of κφ/Dφ for synchronization in two different polarity alignment rules, Eq. 3 and Eq. 11. The curved lines are visual guides. Inset: Log-linear plot of the velocity cross correlation. An exponential function is fitted for short lengthscales (first five data points) to obtain the correlation length rc. In all panels, L = 24, N = 800, v0 = 1.2, μ = 10, Dφ = 0.5, ω = 2.1, and Dθ = 0.1 in Eqs. 1, 2, 4, 5, and 11. To see this figure in color, go online.
Destabilization of spatial phase waves by a short-range velocity correlation
To further examine the mechanism by which collective cell movement enhances global synchronization, we study whether collective cell movement influences the stability of spatial phase waves. To this end, we set a spatial phase gradient as an initial condition for simulations. The phase gradient can travel across the system as a kinematic spatial phase wave due to the periodic boundary condition. We examine whether the spatial phase wave is destabilized by correlated cell movement in Eqs. 1–5.
The initial phase for cell i at position xi = (xi,yi) is
| (12) |
setting a spatial phase wave with the longest wavelength, Fig. 7 A. A previous study indicates that the spatial phase wave with the longest wavelength is the most stable against the random movement of oscillators (39). The phase order parameter Z(t) is almost zero when such spatial phase wave exists in the system, Fig. 7 B.
Figure 7.
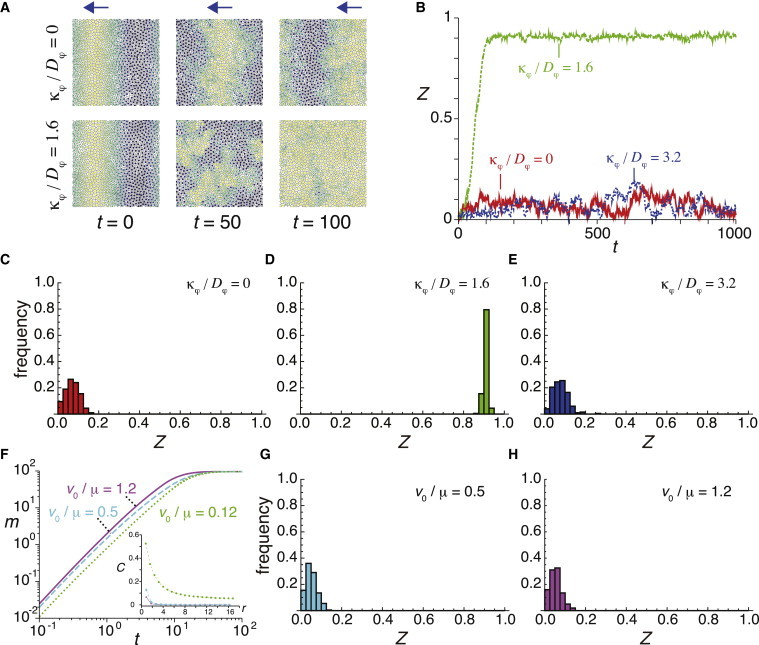
A short-range velocity correlation disturbs spatial phase waves and leads to global synchronization. (A) Kinematic phase wave for κφ/Dφ = 0 (top) and its destabilization for κφ/Dφ = 1.6 (bottom). The blue arrows indicate the direction of motion of the phase wave. The color indicates the intensity determined by (1 + sin θi)/2 as in Fig. 2. (B) Time evolution of the phase order parameter Z(t) for different values of κφ/Dφ, starting from an initial condition with a phase gradient Eq. 12. A single realization for each κφ/Dφ is plotted. (C–E) Histogram of the order parameter Z at t = 1000 for (C) κφ/Dφ = 0, (D) κφ/Dφ = 1.6, and (E) κφ/Dφ = 3.2 when the initial condition of the simulations is a phase gradient Eq. 12. (F) Time evolution of m(t) for different values of v0/μ. Inset: velocity cross correlation C(r) for corresponding v0/μ. (G and H) Histogram of the order parameter Z at t = 1000 for (G) v0/μ = 0.5, and (H) v0/μ = 1.2. In all panels, L = 24, N = 800, v0 = 1.2, Dφ = 0.5, ω = 2.1, and Dθ = 0.1 in Eqs. 1–5. For (A–E) μ = 10. For (F–H) κφ = 0.8. In (C–E, G, and H), the results of 200 different realizations are used for each histogram. To see this figure in color, go online.
When there is no spatial velocity correlation between cells (κφ/Dφ = 0), the phase order parameter Z(t) remains small even after long times (t = 1000), indicating that spatial phase waves persist in the system, Fig. 7, A–C and Movie S6. In contrast, when there is a short-range velocity correlation (κφ/Dφ = 1.6), Z(t) grows to a higher value, Fig. 7, A, B, and D, and Movie S7, indicating that spatial phase waves disappear and cells attain global synchronization of coupled oscillators. As κφ increases further and cell movement becomes highly collective (κφ/Dφ = 3.2), phase waves recover persistence, Fig. 7, B and E. These observations suggest that cell movement with a short-range velocity correlation strongly disturbs spatial phase waves, thereby enhancing global synchronization.
Cell movement with short-range velocity correlations also enhances cell mixing, Fig. 5 C, so it may be that it is this stronger mixing that perturbs spatial phase waves. An alternative possibility is that the correlated movement of neighboring cells itself disturbs phase waves.
To elucidate which of these two effects are important, we compare the result of a cell population with a short-range velocity correlation in Fig. 7 D with that of a cell population without spatial velocity correlation but higher mobility, Fig. 7 F. As the ratio v0/μ increases with fixing κφ/Dφ and all the other parameters, the velocity of movement becomes higher while the velocity cross correlation between neighboring cells is lost, Fig. 7 F inset. This faster movement without spatial velocity correlations induces more extensive cell mixing, Fig. 7 F, compared to the case of slower movement with a short-range velocity correlation, Fig. 7 D. If the degree of cell mixing is important for disturbing the spatial phase waves, this higher mobility without correlation is expected to disturb spatial phase waves. However, this higher mobility without correlation cannot disturb spatial phase waves, Fig. 7, G and H, and Movie S8. We conclude that the short-range velocity correlation disturbs spatial phase waves.
We emphasize that stronger cell mixing realizes the synchronization of coupled oscillators for most of the initial conditions quicker than weaker cell mixing, regardless of the presence of spatial velocity correlations. For particular sets of initial conditions that develop long wavelength patterns such as the spatial phase wave in Fig. 7 A, movement with short-range velocity correlations outcompetes the movement without correlation.
In summary, we showed two different mechanisms for a short-range correlation of cell movement to enhance synchronization of coupled oscillators. It both increases cell mixing and disturbs persistent spatial phase patterns in the system.
Discussion
In this work, we developed a physical model for mobile coupled oscillators including forces and alignment dynamics to study the effect of collective movement on their synchronization. We explicitly considered cell shapes and gradual contact processes between two cells by two-dimensional Voronoi tessellation, Fig. 1. We generated positively correlated cell movement with polarity alignment dynamics, Fig. 4, and showed that cell movement with a short-range velocity correlation is optimal for synchronization, Figs. 5 and 6. This short-range correlated movement realizes intense cell mixing, Fig. 5 D, and strongly destabilizes spatial phase patterns in a domain, Fig. 7. Thus, our theory indicates that collective cell movement can promote information flow across a cell population.
Here, we described a tissue with a two-dimensional Voronoi diagram with periodic boundary to focus on the fundamental effect of collective movement on the synchronization of coupled phase oscillators. Other ways to describe the tissue and coupled genetic oscillators may be to use a Cellular Potts model (51,55,56), a continuous reaction-advection-diffusion equation (57), or a Vertex dynamics model (58–61). In our description, cells are represented as particles and cell shapes in the Voronoi tessellation are determined solely by the positions of cell centers. This simpler approach may be suited to describe the movement of mesenchymal cells that are easily deformable, as observed in the zebrafish tailbud, whereas Vertex dynamics models are suitable descriptions of epithelial tissues where cells have an active elastic apical cortex. In Vertex models, cells require an energy influx to exchange neighbors within a packed tissue (58). The energy for tissue remodeling is usually provided by cell divisions (59,61) and active cortical tension (60). In the theory we use here the energy influx is provided by the self-propulsion speed v0. Cells can exchange neighbors when v0 is large enough for them to surpass an energy barrier, which is determined indirectly by the central forces due to volume exclusion, Fig. 2 A.
In reality, the zebrafish tailbud has a complex tissue geometry. Swirls of cell flow can be observed in the tailbud (32). The boundary condition of the tissue may additionally influence movement patterns (48). Furthermore, ∼10–15% of cells in the posterior PSM appear to be in the mitotic phase during one cycle of oscillation (22). The phases of oscillation of cells immediately after cell division are delayed compared to neighboring cells (28). In this work we chose a simple description of the tissue that neglects cell proliferation, to allow for a clear illustration of the effects of collective cell movement. Future effort describing the complex tissue geometry and cell divisions will reveal to what extent they affect synchronization of the segmentation clock.
We described collective movement in phenomenological ways using Eqs. 3 and 11, because its molecular mechanism in the zebrafish tailbud has not been determined yet. Of importance, however, our results for the synchronization of phase oscillators do not depend on the underlying mechanism for collective cell movement, Fig. 6. Future experimental studies will reveal the molecular mechanism for collective cell movement in the tailbud, allowing the theory to be constrained.
We used the mean squared difference of displacement vectors between pairs of cells to quantify cell mixing in simulations. Previous experimental studies quantified cellular movement in the PSM during somitogenesis to understand the axis elongation of vertebrate embryos (30–34). These studies focused on single cell movement rather than the relative movement of cells, which is more relevant to the synchronization of the segmentation clock as the current study indicates. Calculating the mean squared difference of displacement vectors in living tissues will determine whether relative cell movement observed in the tailbud could improve synchronization of the segmentation clock. In addition, a difficulty to measure cell movement in living tissues is how to eliminate the contribution of tissue movement to cell displacement. A previous study observed cell movement relative to extracellular matrix in the chick PSM (31) to distinguish cell movement from tissue movement. The mean squared difference of displacement vectors used here eliminates the contribution of tissue movement to cell movement.
Recent progresses of live imaging techniques in vertebrate somitogenesis allows simultaneous monitoring of cell movement and cyclic gene expression in single cells in living tissues (28). Combined with quantitative measurement and experimental perturbations of cell movement (32), these imaging data will test the theory of mobile coupled genetic oscillators. The current model indicates that cell movement with a velocity correlation length of about 2 ∼ 3 cell diameter is optimal for synchronization of coupled oscillators, Figs. 5 and 6. A previous measurement of cell movement in the zebrafish tailbud revealed a positive correlation with a lengthscale of 2 ∼ 10 cell diameters (32). Thus, our current study predicts that collective cell movement reported in the zebrafish tailbud may enhance synchronization of the segmentation clock in the living tissue.
Many morphogenetic processes during embryonic development include collective cell movement. Our study suggests that the degree of collective movement changes information flow across a cell population. Therefore, a detailed analysis of cell movement is required to understand collective cellular behaviors during embryonic development.
Acknowledgments
We thank the members of the Theoretical Biology Laboratory at RIKEN for helpful discussion. We thank the hospitality of Max Planck Institute for the Physics of Complex Systems.
K.U. was supported by the fellowship for young scientists from the Japan Society for the Promotion of Science. This research was partially supported by the RIKEN iTHES Project. L.G.M. acknowledges support from FONCyT through PICT 2012-1954.
Contributor Information
Koichiro Uriu, Email: k.uriu@riken.jp.
Luis G. Morelli, Email: morelli@df.uba.ar.
Appendix: Derivation of the Overdamped Equation of Motion
We derive Eq. 1 as an overdamped limit of a force balance equation, Newton’s second law for self-propelled cells in a tissue. We describe cell movement by a force balance (46):
| (13) |
where χi is the position of cell center i in arbitrary units of length, dχi/dτ is cell velocity, and d2χi/dτ2 is acceleration. mc represents the mass of a cell. The first term of the right-hand side describes self-propulsion and dissipation, with a stable velocity V0 in the absence of external forces, and relaxation constant γ. The unit vector ni with an angle φi describes the polarity of self-propelled motion for cell i. The external forces exerted by other cells is described by the last term, which has a characteristic force scale f0. The brackets {χ} simply denote that the force depends on the positions of all cells.
For the intercellular force, we choose harmonic repulsion when cells get closer than a characteristic length scale r0, which we call the diameter of isolated cells, for simplicity. Introducing the distance between cells i and j as dij = |χj − χi| and the central direction of the force eij = (χj − χi)/|χj − χi|, we can write the force as fi(χi,χj) = fi(χi,χj) eij, where
The dynamics of the polarity angle φi is given by
| (14) |
where Vi = dχi/dτ, kφ and Cφ are the polarity alignment strength and the polarity noise intensity with unit, respectively.
The phase dynamics of oscillators reads
| (15) |
where Ω, kθ, and Cθ are the autonomous frequency, the coupling strength, and the phase noise intensity with unit, respectively. represents the neighborhood of cell i defined by a tissue description. κij is a weight for the coupling strength between cells i and j.
We introduce dimensionless variables x and t by choosing r0 as a lengthscale, and 1/kθ as a timescale in the system:
| (16) |
| (17) |
In terms of the dimensionless variables the equations of motion are
| (18) |
with . We choose the force scale γr0kθ, and divide the force balance Eq. 18,
| (19) |
where we set ɛ ≡ mckθ/γ. The overdamped limit ɛ ≪ 1 is
| (20) |
where v0 = V0/(r0kθ) and μ = f0/(γr0kθ).
We introduce κφ = kφ/kθ, and Dφ = Cφ/kθ, and obtain Eq. 3 from Eq. 14. Similarly, we obtain Eq. 4 from Eq. 15 by introducing ω = Ω/kθ, and Dθ = Cθ/kθ.
We set r0 = 10 μ m and kθ = 0.1 min−1 (23,26), V0 = 1.2 μm min−1 (31,32) and Ω = 0.21 min−1 (12), based on previous experimental studies. Because the values of all the other parameters have not been determined for zebrafish yet, we study the behavior of the system as we change them in the main text.
We used a custom code written in the C language for our numerical simulations. Eqs. 1–4 are numerically solved by the Euler method. We compute the Voronoi tessellation (62) at every time point when solving Eqs. 1–4. The time step used in the Euler method is 0.01. The code is available upon request.
Supporting Material
The color indicates the intensity determined by (1 + sinθi)/2 as in Fig. 2. For clear visualization, we ran a simulation in a domain 12 × 12. Other parameters are N = 200, v0 = 1.2, Dφ = 0.5, ω = 2.1, and Dθ = 0.1.
The domain size and other parameters are the same as in Movie S1.
The domain size and other parameters are the same as in Movie S1.
The domain size and other parameters are the same as in Movie S1.
The domain size and other parameters are the same as in Movie S1.
Other parameters are L = 24, N = 800, v0 = 1.2, Dφ = 0.5, ω = 2.1, and Dθ = 0.1.
Other parameters are the same as in Movie S6.
Other parameters are the same as in Movie S6.
References
- 1.Friedl P., Gilmour D. Collective cell migration in morphogenesis, regeneration and cancer. Nat. Rev. Mol. Cell Biol. 2009;10:445–457. doi: 10.1038/nrm2720. [DOI] [PubMed] [Google Scholar]
- 2.Rørth P. Collective cell migration. Annu. Rev. Cell Dev. Biol. 2009;25:407–429. doi: 10.1146/annurev.cellbio.042308.113231. [DOI] [PubMed] [Google Scholar]
- 3.Montell D.J., Yoon W.H., Starz-Gaiano M. Group choreography: mechanisms orchestrating the collective movement of border cells. Nat. Rev. Mol. Cell Biol. 2012;13:631–645. doi: 10.1038/nrm3433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Tada M., Heisenberg C.P. Convergent extension: using collective cell migration and cell intercalation to shape embryos. Development. 2012;139:3897–3904. doi: 10.1242/dev.073007. [DOI] [PubMed] [Google Scholar]
- 5.Aman A., Piotrowski T. Cell-cell signaling interactions coordinate multiple cell behaviors that drive morphogenesis of the lateral line. Cell Adhes. Migr. 2011;5:499–508. doi: 10.4161/cam.5.6.19113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Teddy J.M., Kulesa P.M. In vivo evidence for short- and long-range cell communication in cranial neural crest cells. Development. 2004;131:6141–6151. doi: 10.1242/dev.01534. [DOI] [PubMed] [Google Scholar]
- 7.Carmona-Fontaine C., Matthews H.K., Mayor R. Contact inhibition of locomotion in vivo controls neural crest directional migration. Nature. 2008;456:957–961. doi: 10.1038/nature07441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Coburn L., Cerone L., Neufeld Z. Tactile interactions lead to coherent motion and enhanced chemotaxis of migrating cells. Phys. Biol. 2013;10:046002. doi: 10.1088/1478-3975/10/4/046002. [DOI] [PubMed] [Google Scholar]
- 9.Roellig D., Morelli L.G., Oates A.C. SnapShot: the segmentation clock. Cell. 2011;145:800–800.e1. doi: 10.1016/j.cell.2011.05.007. [DOI] [PubMed] [Google Scholar]
- 10.Pourquié O. Vertebrate segmentation: from cyclic gene networks to scoliosis. Cell. 2011;145:650–663. doi: 10.1016/j.cell.2011.05.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Oates A.C., Morelli L.G., Ares S. Patterning embryos with oscillations: structure, function and dynamics of the vertebrate segmentation clock. Development. 2012;139:625–639. doi: 10.1242/dev.063735. [DOI] [PubMed] [Google Scholar]
- 12.Schröter C., Herrgen L., Oates A.C. Dynamics of zebrafish somitogenesis. Dev. Dyn. 2008;237:545–553. doi: 10.1002/dvdy.21458. [DOI] [PubMed] [Google Scholar]
- 13.Schröter C., Oates A.C. Segment number and axial identity in a segmentation clock period mutant. Curr. Biol. 2010;20:1254–1258. doi: 10.1016/j.cub.2010.05.071. [DOI] [PubMed] [Google Scholar]
- 14.Harima Y., Takashima Y., Kageyama R. Accelerating the tempo of the segmentation clock by reducing the number of introns in the Hes7 gene. Cell Reports. 2013;3:1–7. doi: 10.1016/j.celrep.2012.11.012. [DOI] [PubMed] [Google Scholar]
- 15.Hirata H., Yoshiura S., Kageyama R. Oscillatory expression of the bHLH factor Hes1 regulated by a negative feedback loop. Science. 2002;298:840–843. doi: 10.1126/science.1074560. [DOI] [PubMed] [Google Scholar]
- 16.Holley S.A., Jülich D., Nüsslein-Volhard C. her1 and the notch pathway function within the oscillator mechanism that regulates zebrafish somitogenesis. Development. 2002;129:1175–1183. doi: 10.1242/dev.129.5.1175. [DOI] [PubMed] [Google Scholar]
- 17.Oates A.C., Ho R.K. Hairy/E(spl)-related (Her) genes are central components of the segmentation oscillator and display redundancy with the Delta/Notch signaling pathway in the formation of anterior segmental boundaries in the zebrafish. Development. 2002;129:2929–2946. doi: 10.1242/dev.129.12.2929. [DOI] [PubMed] [Google Scholar]
- 18.Lewis J. Autoinhibition with transcriptional delay: a simple mechanism for the zebrafish somitogenesis oscillator. Curr. Biol. 2003;13:1398–1408. doi: 10.1016/s0960-9822(03)00534-7. [DOI] [PubMed] [Google Scholar]
- 19.Takashima Y., Ohtsuka T., Kageyama R. Intronic delay is essential for oscillatory expression in the segmentation clock. Proc. Natl. Acad. Sci. USA. 2011;108:3300–3305. doi: 10.1073/pnas.1014418108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Schröter C., Ares S., Oates A.C. Topology and dynamics of the zebrafish segmentation clock core circuit. PLoS Biol. 2012;10:e1001364. doi: 10.1371/journal.pbio.1001364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Jiang Y.-J., Aerne B.L., Lewis J. Notch signalling and the synchronization of the somite segmentation clock. Nature. 2000;408:475–479. doi: 10.1038/35044091. [DOI] [PubMed] [Google Scholar]
- 22.Horikawa K., Ishimatsu K., Takeda H. Noise-resistant and synchronized oscillation of the segmentation clock. Nature. 2006;441:719–723. doi: 10.1038/nature04861. [DOI] [PubMed] [Google Scholar]
- 23.Riedel-Kruse I.H., Müller C., Oates A.C. Synchrony dynamics during initiation, failure, and rescue of the segmentation clock. Science. 2007;317:1911–1915. doi: 10.1126/science.1142538. [DOI] [PubMed] [Google Scholar]
- 24.Mara A., Schroeder J., Holley S.A. Priming, initiation and synchronization of the segmentation clock by deltaD and deltaC. Nat. Cell Biol. 2007;9:523–530. doi: 10.1038/ncb1578. [DOI] [PubMed] [Google Scholar]
- 25.Özbudak E.M., Lewis J. Notch signalling synchronizes the zebrafish segmentation clock but is not needed to create somite boundaries. PLoS Genet. 2008;4:e15. doi: 10.1371/journal.pgen.0040015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Herrgen L., Ares S., Oates A.C. Intercellular coupling regulates the period of the segmentation clock. Curr. Biol. 2010;20:1244–1253. doi: 10.1016/j.cub.2010.06.034. [DOI] [PubMed] [Google Scholar]
- 27.Okubo Y., Sugawara T., Saga Y. Lfng regulates the synchronized oscillation of the mouse segmentation clock via trans-repression of Notch signalling. Nat. Commun. 2012;3:1141. doi: 10.1038/ncomms2133. [DOI] [PubMed] [Google Scholar]
- 28.Delaune E.A., François P., Amacher S.L. Single-cell-resolution imaging of the impact of Notch signaling and mitosis on segmentation clock dynamics. Dev. Cell. 2012;23:995–1005. doi: 10.1016/j.devcel.2012.09.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kulesa P.M., Fraser S.E. Cell dynamics during somite boundary formation revealed by time-lapse analysis. Science. 2002;298:991–995. doi: 10.1126/science.1075544. [DOI] [PubMed] [Google Scholar]
- 30.Delfini M.C., Dubrulle J., Pourquié O. Control of the segmentation process by graded MAPK/ERK activation in the chick embryo. Proc. Natl. Acad. Sci. USA. 2005;102:11343–11348. doi: 10.1073/pnas.0502933102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bénazéraf B., Francois P., Pourquié O. A random cell motility gradient downstream of FGF controls elongation of an amniote embryo. Nature. 2010;466:248–252. doi: 10.1038/nature09151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lawton A.K., Nandi A., Holley S.A. Regulated tissue fluidity steers zebrafish body elongation. Development. 2013;140:573–582. doi: 10.1242/dev.090381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Fior R., Maxwell A.A., Saúde L. The differentiation and movement of presomitic mesoderm progenitor cells are controlled by Mesogenin 1. Development. 2012;139:4656–4665. doi: 10.1242/dev.078923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Dray N., Lawton A., Holley S.A. Cell-fibronectin interactions propel vertebrate trunk elongation via tissue mechanics. Curr. Biol. 2013;23:1335–1341. doi: 10.1016/j.cub.2013.05.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Uriu K., Morishita Y., Iwasa Y. Random cell movement promotes synchronization of the segmentation clock. Proc. Natl. Acad. Sci. USA. 2010;107:4979–4984. doi: 10.1073/pnas.0907122107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Uriu K., Ares S., Morelli L.G. Optimal cellular mobility for synchronization arising from the gradual recovery of intercellular interactions. Phys. Biol. 2012;9:036006. doi: 10.1088/1478-3975/9/3/036006. [DOI] [PubMed] [Google Scholar]
- 37.Uriu K., Ares S., Morelli L.G. Dynamics of mobile coupled phase oscillators. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2013;87:032911. [Google Scholar]
- 38.Frasca M., Buscarino A., Boccaletti S. Synchronization of moving chaotic agents. Phys. Rev. Lett. 2008;100:044102. doi: 10.1103/PhysRevLett.100.044102. [DOI] [PubMed] [Google Scholar]
- 39.Peruani F., Nicola E.M., Morelli L.G. Mobility induces global synchronization of oscillators in periodic extended systems. New J. Phys. 2010;12:093029. [Google Scholar]
- 40.Fujiwara N., Kurths J., Díaz-Guilera A. Synchronization in networks of mobile oscillators. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2011;83:025101. doi: 10.1103/PhysRevE.83.025101. [DOI] [PubMed] [Google Scholar]
- 41.Frasca M., Buscarino A., Fortuna L. Spatial pinning control. Phys. Rev. Lett. 2012;108:204102. doi: 10.1103/PhysRevLett.108.204102. [DOI] [PubMed] [Google Scholar]
- 42.Honda H., Tanemura M., Yoshida A. Estimation of neuroblast numbers in insect neurogenesis using the lateral inhibition hypothesis of cell differentiation. Development. 1990;110:1349–1352. doi: 10.1242/dev.110.4.1349. [DOI] [PubMed] [Google Scholar]
- 43.Meineke F.A., Potten C.S., Loeffler M. Cell migration and organization in the intestinal crypt using a lattice-free model. Cell Prolif. 2001;34:253–266. doi: 10.1046/j.0960-7722.2001.00216.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Morishita Y., Iwasa Y. Growth based morphogenesis of vertebrate limb bud. Bull. Math. Biol. 2008;70:1957–1978. doi: 10.1007/s11538-008-9334-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Toner J., Tu Y., Ramaswamy S. Hydrodynamics and phases of flocks. Ann. Phys. 2005;318:170–244. [Google Scholar]
- 46.Vicsek T., Zafeiris A. Collective motion. Phys. Rep. 2012;517:71–140. [Google Scholar]
- 47.Ramaswamy S. The mechanics and statistics of active matter. Annu. Rev. Condens. Matter Phys. 2010;1:323–345. [Google Scholar]
- 48.Szabó B., Szöllösi G.J., Vicsek T. Phase transition in the collective migration of tissue cells: experiment and model. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2006;74:061908. doi: 10.1103/PhysRevE.74.061908. [DOI] [PubMed] [Google Scholar]
- 49.Sakaguchi H., Shinomoto S., Kuramoto Y. Local and global self-entrainments in oscillator lattice. Prog. Theor. Phys. 1987;77:1005–1010. [Google Scholar]
- 50.Morelli L.G., Ares S., Oates A.C. Delayed coupling theory of vertebrate segmentation. HFSP J. 2009;3:55–66. doi: 10.2976/1.3027088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Szabó A., Ünnep R., Czirók A. Collective cell motion in endothelial monolayers. Phys. Biol. 2010;7:046007. doi: 10.1088/1478-3975/7/4/046007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Rafelski S.M., Keller L.C., Marshall W.F. Apparent diffusive motion of centrin foci in living cells: implications for diffusion-based motion in centriole duplication. Phys. Biol. 2011;8:026010. doi: 10.1088/1478-3975/8/2/026010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Kuramoto Y. Springer; Berlin: 1984. Chemical Oscillations, Waves, and Turbulence. [Google Scholar]
- 54.Farrell F.D.C., Marchetti M.C., Tailleur J. Pattern formation in self-propelled particles with density-dependent motility. Phys. Rev. Lett. 2012;108:248101. doi: 10.1103/PhysRevLett.108.248101. [DOI] [PubMed] [Google Scholar]
- 55.Hester S.D., Belmonte J.M., Glazier J.A. A multi-cell, multi-scale model of vertebrate segmentation and somite formation. PLOS Comput. Biol. 2011;7:e1002155. doi: 10.1371/journal.pcbi.1002155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Kabla A.J. Collective cell migration: leadership, invasion and segregation. J. R. Soc. Interface. 2012;9:3268–3278. doi: 10.1098/rsif.2012.0448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Zhou C., Kurths J. Noise-sustained and controlled synchronization of stirred excitable media by external forcing. New J. Phys. 2005;7:18. [Google Scholar]
- 58.Bi D., Lopez J.H., Manning M.L. Energy barriers and cell migration in densely packed tissues. Soft Matter. 2014;10:1885–1890. doi: 10.1039/c3sm52893f. [DOI] [PubMed] [Google Scholar]
- 59.Farhadifar R., Röper J.C., Jülicher F. The influence of cell mechanics, cell-cell interactions, and proliferation on epithelial packing. Curr. Biol. 2007;17:2095–2104. doi: 10.1016/j.cub.2007.11.049. [DOI] [PubMed] [Google Scholar]
- 60.Rauzi M., Verant P., Lenne P.F. Nature and anisotropy of cortical forces orienting Drosophila tissue morphogenesis. Nat. Cell Biol. 2008;10:1401–1410. doi: 10.1038/ncb1798. [DOI] [PubMed] [Google Scholar]
- 61.Staple D.B., Farhadifar R., Jülicher F. Mechanics and remodelling of cell packings in epithelia. Eur. Phys. J. E. Soft Matter. 2010;33:117–127. doi: 10.1140/epje/i2010-10677-0. [DOI] [PubMed] [Google Scholar]
- 62.Sloan S.W. A fast algorithm for constructing Delaunay triangulations in the plane. Adv. Eng. Software. 1987;9:34–55. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The color indicates the intensity determined by (1 + sinθi)/2 as in Fig. 2. For clear visualization, we ran a simulation in a domain 12 × 12. Other parameters are N = 200, v0 = 1.2, Dφ = 0.5, ω = 2.1, and Dθ = 0.1.
The domain size and other parameters are the same as in Movie S1.
The domain size and other parameters are the same as in Movie S1.
The domain size and other parameters are the same as in Movie S1.
The domain size and other parameters are the same as in Movie S1.
Other parameters are L = 24, N = 800, v0 = 1.2, Dφ = 0.5, ω = 2.1, and Dθ = 0.1.
Other parameters are the same as in Movie S6.
Other parameters are the same as in Movie S6.


