Statistical methods for the assessment of EQAPOL proficiency testing: ELISpot, Luminex, and Flow Cytometry

Abstract

In September 2011 Duke University was awarded a contract to develop the National Institutes of Health/National Institute of Allergy and Infectious Diseases (NIH/NIAID) External Quality Assurance Program Oversight Laboratory (EQAPOL). Through EQAPOL, proficiency testing programs are administered for Interferon-γ (IFN-γ) Enzyme-linked immunosorbent spot (ELISpot), Intracellular Cytokine Staining Flow Cytometry (ICS) and Luminex-based cytokine assays. One of the charges of the EQAPOL program was to apply statistical methods to determine overall site performance. We utilized various statistical methods for each program to find the most appropriate for assessing laboratory performance using the consensus average as the target value. Accuracy ranges were calculated based on Wald-type confidence intervals, exact Poisson confidence intervals, or via simulations. Given the nature of proficiency testing data, which has repeated measures within donor/sample made across several laboratories; the use of mixed effects models with alpha adjustments for multiple comparisons was also explored. Mixed effects models were found to be the most useful method to assess laboratory performance with respect to accuracy to the consensus. Model based approaches to the proficiency testing data in EQAPOL will continue to be utilized. Mixed effects models also provided a means of performing more complex analyses that would address secondary research questions regarding within and between laboratory variability as well as longitudinal analyses.

1. Introduction

External Quality Assessment (EQA) or proficiency testing (PT) has played a role in laboratory medicine for over 65 years (Belk and Sunderman, 1947; Wootton and King, 1953). In the late 1980s, EQA was introduced to HIV clinical laboratories for antibody detection (Taylor and Przybyszewski, 1988; Polesky and Hanson, 1990) and Flow Cytometry (Paxton et al., 1989). As technologies for HIV detection and clinical monitoring have changed, new EQA programs have been added as evidenced by the articles in this special issue. The application of EQA programs helps to assure that independent laboratories testing the same sample will yield comparable results. They also help to identify technical areas of potential weakness, problems with instrumentation and/or reagents, as well as determine areas for assay protocol harmonization. In order for an EQA program to meet these goals, statistical methodologies must be applied to identify underperforming laboratories.

In September 2011, Duke University Human Vaccine Institute (DHVI) became home to the National Institute of Health/National Institute of Allergy and Infectious Diseases (NIH/NIAID) External Quality Assurance Program Oversight Laboratory (EQAPOL) through a Department of Health and Human Services contract. EQAPOL develops and runs PT programs for Interferon-γ (IFN-γ) Enzyme-linked immunosorbent spot (ELISpot), Intracellular Cytokine Staining (ICS) Flow Cytometry and Luminex bead-based multiplex cytokine assays. One of the charges of the EQAPOL program was to apply statistical methods to assess proficiency for these three assays and define assay acceptability (pass/fail criteria) for overall site performance.

Both the ELISpot and ICS Flow Cytometry programs were a continuation of PT programs previously administered by another contractor, although the ELISpot program did not grade sites on assays performance (Jaimes et al., 2011). The Luminex program was newly-created for EQAPOL. Only the Flow Cytometry program had existing methods for proficiency assessment; therefore statisticians at DHVI worked with leaders in EQAPOL, as well as with an external overall EQAPOL Scientific Advisory Board (SAB) and Program-specific Advisory Committees, to define grading criteria schemes for each program with an emphasis on having synergy between programs. The criteria developed for each program include evaluations of timely data reporting and protocol adherence. However, the majority of the assessment criteria for each program were designed to grade accuracy and precision for their specific assay.

In order to determine proficiency for these parameters an expected target must be established as well as an accuracy range. Laboratory assays have inherent variability (e.g., technician to technician, day to day, peptides) and thus knowing the true response rate for a donor/sample by peptide/stimulation is essentially impossible. Without a known concentration or outcome to use as a benchmark, the consensus to the average was considered the most reasonable value to use. After defining the consensus average as the target value, we reviewed various statistical methods for each program in an attempt to have as uniform an approach as possible for analysis and grading purposes.

Using all laboratory data for reference estimation provides a process for making a fair assessment, since all laboratories have a contribution to the estimate. Only laboratory data with extreme outliers, obvious plate or assay issues such as no response for a high responder or vice versa, were removed. This avoided the use of a particular reference lab, which could be difficult to justify should the reference laboratory be quite different from the other participating labs.

This paper will describe various statistical methods used for assessing laboratory performance, particularly in regard to accuracy, for each program. These methods were assessed in terms of utility (i.e., how reasonable are the grades provided) and functionality in association with the respective steering committees. The goal was to use a statistical methodology that detects relevant differences and expand upon the methods used in previous programs as well as have similar analyses across programs.

2. ELISpot program

The EQAPOL ELISpot EQA program has assessed the proficiency of NIAID/Division of AIDS (DAIDS)-supported laboratories at performing an IFN-γ ELISpot assay through four completed PTrounds;a fifth round is ongoing with two PT rounds being completed each year. For each PT round, sites run the IFN-γ ELISpot assay normally used by their laboratory (termed the in-house assay) using EQAPOL-provided peripheral blood mononuclear cells (PBMCs) and standardized peptide pools. PMBCs from HIV-negative, healthy donors were collected by leukapheresis and cryopreserved at the EQAPOL Central Laboratory, which acts as a repository for all EQAPOL reagents and specimens (see Garcia et al. in this issue). Prior to leukapheresis, all donors were properly consented according to Duke University IRB, Federal and State regulations. The cryopreserved PMBCs selected for each PT round were selected based on varying reactivities to the provided peptides, and all PBMCs were screened by the EQAPOL ELISpot Laboratory.

Two peptide pools were included in the PT send-out: one represents the Cytomegalovirus pp65 protein (CMVpp65, JPT Peptide Technologies, Berlin, Germany) and the other a combination of peptides representing selected class I-restricted epitopes within the Cytomegalovirus, Epstein–Barr, and influenza virus antigens (CEF pool, JPT Peptide Technologies, Berlin, Germany). A negative control (Dimethyl sulfoxide — DMSO plus culture medium) was also provided. Both PBMCs and peptides were provided in a blinded fashion as sample 1, 2 or 3 and reagent A, B or C, respectively. The blinding scheme was changed for each PT round.

In addition to these standardized peptides, the materials to run an IFN-γ ELISpot assay were provided in each PT send-out: IFN-γ capture-Ab coated 96-well plates, biotinylated secondary anti-human IFN-γ, Streptavidin-HRP (all MAbTech, Mariemont, OH) and a detection substrate (NovaRED substrate, Vector, Burlingame, CA). This EQAPOL-provided kit was termed the EQAPOL assay. Sites were required to run both the EQAPOL assay and their in-house assay using the provided PBMCs and reagents. A protocol was provided for the EQAPOL assay, and sites were instructed to perform their in-house assay according to their normal protocol. The EQAPOL assay is used to assist in site remediation.

There were three donor samples sent per PT round with nine replicate wells per donor for each of the three peptides. Sites ran two assay plates per assay type (EQAPOL and in-house) and were allotted wells to run their own in-house cellular controls. Sites reported the number of spot forming cells (SFC) per well, and all sites were instructed to plate cells at 2 × 10⁵ cells/well. Analyses were performed on background (the negative control, DMSO) subtracted SFC for the CMV and CEF peptides. These were calculated by subtracting the average of the nine DMSO wells from each CMV or CEF well.

2.1. ELISpot: statistical approach

There have been earlier attempts at evaluating ELISpot proficiency panels and assay equivalence (Cox et al., 2005; Boaz et al., 2009; Gill et al., 2010), which focused primarily on positive or negative responses and concordance among labs. The EQAPOL ELISpot program does not have criteria for defining positive or negative responses, rather the goal is to assess how accurate to the consensus average and precise laboratories are using their own in-house assay given standard peptides and samples.

If we assume that there is no well-to-well variability, then these data are counts of spot forming cells per well with a common denominator of 2 × 10⁵ cells per well and should follow a Poisson distribution. Various research articles have described ELISpot data as following a Poisson distribution and have developed methods for positivity criteria (Hudgens et al., 2004; Moodie et al., 2006; Moodie et al., 2010). Three approaches for assay acceptability based on a Poisson distributional assumption for ELISpot data are described. These approaches were evaluated to determine which one produced the most reasonable boundaries for grading.

2.1.1. Simulation of Poisson spot forming cell data

One approach to determining laboratory assay performance was based on the simulation of ELISpot data. Given a true average SFC and a known dispersion factor ϕ (σ²/μ — the variance divided by the mean), 500 simulations were run to generate nine wells per simulation. This mimics the data that are collected in the ELISpot program. For each simulation, the nine wells were averaged and an exact Poisson 95% confidence interval (CI) was calculated (Garwood, 1936).

The minimum lower CI and maximum upper CI for each of the 500 nine well SFC averages was used to estimate an accuracy range. If a laboratory’s nine well average SFC was within the accuracy range, they were considered to have passed (i.e., were included in the accuracy range).

Also, a per-well range for each of the nine wells was estimated based on a negative binomial 95% CI (Hoffman, 2003). The dispersion factor ϕ for generating the negative binomial data was the average ϕ from all donors by stimulation data. The minimum lower CI and maximum upper CI on the negative binomial simulated data were used to calculate the per-well range. These confidence boundaries were calculated using the same data generated in 500 simulations for accuracy in SAS (Cary, NC) via the RAND Function for Poisson and Negative Binomial distributions (Rodríguez, 2007).

2.1.2. Poisson confidence intervals

Another way to address laboratory accuracy to the consensus average was to use 95% exact Poisson CIs for the basis of comparison. The laboratory average and consensus average were compared via overlapping CIs. If the laboratory CI did not overlap with the consensus average CI then the laboratory assessment for that donor by stimulation would not pass. This method does not account for the correlation between measures in a laboratory; however the goal was to have liberal boundaries and these are not derived from statistically rigorous methods. The average of the nine wells for each laboratory was used as the laboratory count, and the 95% exact Poisson CI was calculated. All participating laboratory data for that donor by stimulation were averaged for the consensus mean and associated 95% exact Poisson CI.

2.1.3. Mixed effects Poisson model

A generalized linear mixed effects model based on a Poisson distribution was also used for accuracy comparisons to the consensus average of all participating laboratories. This model accounts for the within and between lab variability (Zeng et al., 2005). It is a means model with random lab effects:

$$Y_{\mathit{ij}}=\mu +{\alpha }_{\mathrm{i}}+{\mathrm{\epsilon }}_{\mathrm{ij}}$$

where i = laboratory and j = well.

This model, which also accounts for over dispersion in these data, was run in SAS 9.2 using PROC GLIMMIX. In this model, we had a random effect for each laboratory.

The null hypothesis tested for each laboratory was that the laboratory’s nine well average is not different from the model based consensus average. For grading purposes, a False Discovery Rate (FDR) (Benjamini and Hochberg, 1995) and Bonferroni correction were assessed to account for multiple comparisons of each site to the consensus average. An FDR correction was used to determine which sites are significantly different from the consensus average while maintaining an adjusted alpha = 0.05 significance level. The Bonferroni correction was considered too conservative for these data.

2.1.4. Precision based on dispersion

Precision, or repeatability, was evaluated based on the dispersion factor ϕ for all donor by stimulation (excluding DMSO) combinations within each laboratory. An upper bound for pass/fail criteria was calculated using a 95% Wald-type confidence interval. To remove extreme values, the 90th percentile of ϕ for the six donor by stimulation conditions was calculated and used as a cutoff. Using the remaining 90% of these data the mean and standard deviation was calculated and the upper bound of a 95% CI was considered the dispersion limit.

2.2. ELISpot: results

The previous ELISpot program did not have defined performance criteria, and thus we developed criteria for EQAPOL. The first three PTs were utilized to determine how best to create grading criteria. The grading criteria were introduced in PT4. For accuracy to the consensus assessment three methods were examined for their utility in providing reasonable boundaries: simulation of data, Poisson CIs, and mixed effects modeling.

The simulation of ELISpot data for the purpose of generating accuracy ranges allowed for the calculation of power given various scenarios (Table 1). An example with a low response: If the true mean SFC of the sample was 21 then the accuracy range is 12–32 and per-well range is 5–44. Therefore, if a participating laboratory has a true mean SFC of 30, for that sample, with a dispersion factor of 5, then there is 68% power to find that at least one of the nine wells outside the per-well range. However, there is only 30% power that the laboratory’s mean of the nine replicate wells is outside the accuracy range.

Table 1.

Power Calculations Based on Simulated ELISpot Data.

True Mean SFC	Accuracy Range for Mean SFC	Dispersion Factor	Precision Range for each Well	Lab True Mean SFC	Lab Dispersion Factor	Power 1+ Wells outside Range	Power Mean SFC outside Range
21	(12, 32)	2	(5, 44)	14	5	74	39
				17	5	55	9
				21	10	80	5
				30	5	68	30
				40	5	98	96
615	(540, 691)	2	(503, 721)	560	4	72	11
				560	8	90	19
				615	12	88	0
				700	4	98	66
				700	8	99	65

For a high response sample with a true mean SFC of 615, the accuracy range is 540–691 and per-well range is 503–721. If the true mean SFC of the sample for a participating laboratory was 700 with a dispersion factor of 8, there is 99% power to find at least one of the nine wells outside the per-well range. There is only 65% power that the laboratory’s mean of the nine replicate wells is outside the accuracy range.

The use of exact Poisson 95% CIs for assessing laboratory accuracy does not take into account the correlation of the nine replicate wells. This approach also provides liberal boundaries of acceptability for accuracy with only 13 of the 66 (19.7%) laboratory attempts falling outside the accuracy range. In Fig. 1A with Donor A and Reagent 1, we find that all the laboratory’s CIs overlap with the consensus CI.

Fig. 1.

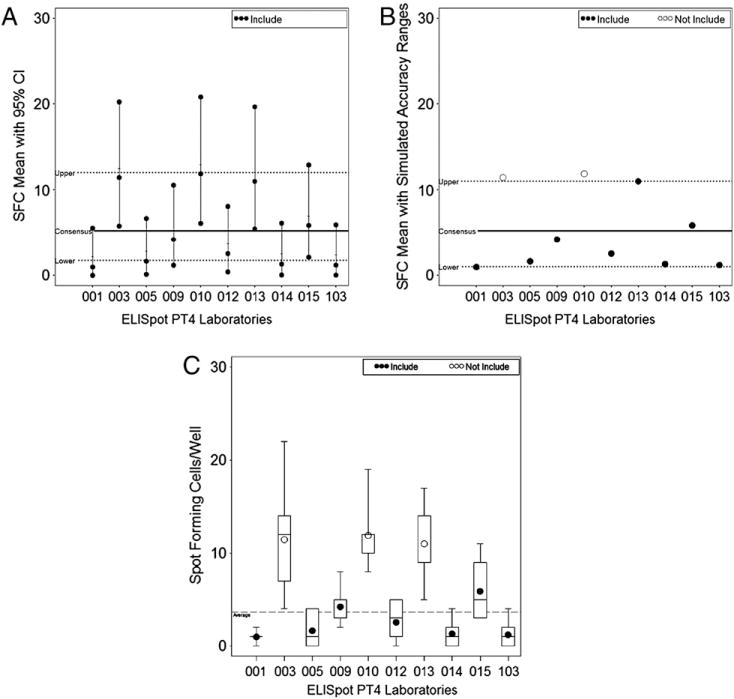
ELISpot graphs for donor 1 reagent A. A) All exact 95% CIs overlap and no laboratories were considered outside the acceptability range for this donor by stimulation. B) Using an acceptability range created using simulations, laboratories 003 and 010 are considered outside the acceptability range for this donor by stimulation. C) Laboratories 003, 010, and 013 are outside the acceptability range using a mixed effects model.

Boundaries calculated using simulations provided less liberal boundaries than the exact Poisson 95% CIs with overlap. The Poisson boundaries are based on the min lower 95% CI and max upper 95% CI values generated in 500 simulations. In Fig. 1B, with the same donor and reagent as Fig. 1A, there are two laboratories outside the boundary, which is 11 SFC. Overall, this approach had 22 of the 66 (33.3%) laboratory attempts falling outside the accuracy range.

The mixed effects models, which accounted for within and between laboratory variability, used for grading had 20 of the 66 (30.3%) laboratory attempts considered significantly different from the consensus average. This method and the simulation method provide very similar grading with only two of the six donor by stimulations having any difference. One of these is seen in Fig. 1B and C where laboratory 013 in the simulation graph is not outside the boundary (the average is the same as the boundary of 11 SFC), but laboratory 013 is significantly different using the mixed effects model. The other donor by stimulation discrepancy had three more labs outside the accuracy range for the simulation method, which had 6 of the 11 not included in the accuracy range.

The use of simulations and the various power calculations were presented to the ELISpot Steering Committee. This method for generating an accuracy range and 95% CI comparisons was not accepted for grading purposes because this method would be too restrictive for labs with poor accuracy. Such a lab would be penalized for both accuracy and precision if only the accuracy was poor. It was decided to use the mixed effects model for accuracy grading purposes. Grading was initiated in PT round 4, and grading outcomes were compared using the three methods previously discussed. In Sanchez et al. in this issue, accuracy to the consensus and precision scores are calculated for PT rounds conducted by the previous contractor, as well as from the EQAPOL PT rounds to show the robustness of this analysis.

The precision boundary for the ELISpot program was based on an upper threshold for the dispersion factor ϕ, which was 2.75 for PT round 4. Two laboratories had one of the six donor by stimulations over the precision boundary, along with one laboratory each that had two, three, and five donor by stimulations over the precision boundary.

3. Luminex program

The EQAPOL Luminex EQA program has assessed the proficiency of NIAID/DAIDS and Cancer Immunotherapy Consortium (CIC) supported laboratories at performing a Luminex-based cytokine assays through four completed PT rounds; a fifth round is ongoing with two PT rounds being completed each year (see Lynch et al. in this issue). For each PT round, the Luminex program participating laboratories received a de-identified commercial 5-plex Luminex-bead assay kit, which includes all necessary reagents to run the assay; the vendor is blinded since the study is not intended to be a vendor comparison. In addition to these kits, labs received test samples of Human AB serum containing known amounts of the five human cytokines measured by the kit (interleukin-2 (IL-2), interleukin-6 (IL-6), interleukin-10 (IL-10), IFN-γ, Tumor Necrosis Factor alpha (TNF-α)). For PT round 1, one test sample was culture supernatant from PMA/Ionomycin-stimulated human PBMCs, and the other was human AB serum (Gemini Bio-products, West Sacramento, CA) spiked with known concentrations of recombinant cytokines (all R&D Systems, Minneapolis, MN). For subsequent PT rounds, labs received only the human AB serum matrix samples.

Laboratories received instructions for the Luminex assay and the plate layout for the 21 blinded samples. Each of the 21 samples was run in triplicate. Within the 21 samples, there were seven sample types provided as three blinded replicates. Therefore, each sample type was run a total of nine replicates. Each sample type contained varying concentrations of the five cytokines within the range of quantification for the assay. Assuming no well-to-well variability inherent in the plate (Clarke et al., 2013), a total of nine replicates for five separate analytes (IL-2, IL-6, IL-10, IFN-γ, TNF-α) were measured for each sample. Sites reported both their raw Median Fluorescence Intensity (MFI) data and calculated/observed concentrations in pg/mL for each sample by analyte.

The first PT round was designed to assess each laboratory’s ability to run a standard curve and only the average of the triplicate wells was reported for several different sample types. The second PT round again focused on the standard curve as well as high, medium, and low spiked serum samples with only the average of the triplicate wells reported. For subsequent PT rounds, there were seven serum samples sent for analyses to focus on laboratory accuracy and precision.

3.1. Luminex: statistical approach

The goal of the EQAPOL Luminex program is to determine how accurate to the consensus average and precise laboratories are given a standard protocol, reagents, and samples. Since there have not been previously described proficiency testing standards for Luminex, PT round 1 was an initial assessment of standard curve generation by the participating laboratories. The deviation (number of standard deviations) from the consensus average was presented. PT round 2 also evaluated the standard curve and concentrations in pg/mL for a low, medium, and high serum sample. These first two PTs were used to setup the panel moving forward with the program. For PT rounds 3 and 4 there were seven concentrations provided that cover the concentration range (low to high) and five analytes (IL-2, IL-6, IL-10, IFN-γ, TNF-α).

The laboratory-reported background subtracted MFI (MFI-Bkg) data were used to generate an EQAPOL-calculated standard curve for each analyte. A four-parameter logistic (4PL) function was fit in SAS using PROC NLIN with the laboratory-reported data and expected concentrations. The fit probability was calculated using the weighted sum of squared errors (SSE). The SSE follows a chi-square distribution with 2 degrees of freedom (number of curve points [6] minus the number of parameters [4]) and a p-value was obtained to assess fit (Gottschalk and Dunn, 2005). The alpha level was set at 0.05, and no adjustment was made for multiple comparisons.

The estimated 4PL equation was used to calculate the observed concentrations in pg/mL for the laboratory-provided MFI-Bkg data for each analyte and sample. We defined a 4PL with the following: MFI is MFI-Bkg, a is the minimum, b is the slope factor, c is the EC50/inflection point, d is the maximum, and x is the concentration in pg/mL. The 4PL equation is:

$$\mathrm{MFI}=\left(\frac{\mathrm{a}-\mathrm{d}}{1+\left({\left(\frac{\mathrm{X}}{\mathrm{C}}\right)}^{\mathrm{b}}\right)}\right)+\mathrm{d}.$$

To get estimates of the concentration (x) in pg/mL we used the following equation and plugged in the estimates from the standard curve:

$$\mathrm{x}=\mathrm{c}\ast {\left(\right(\frac{\mathrm{a}-\mathrm{d}}{\mathrm{MFI}-\mathrm{d}})-1)}^{\frac{1}{\mathrm{b}}}.$$

3.1.1. Consensus average with a 95% CI

Initially accuracy was assessed using laboratory-reported and EQAPOL-calculated estimates to determine if labs could correctly identify the concentration of an analyte in a sample. The accuracy range was based on a Wald-type 95% CI. The deviation from the mean along with the number within the accuracy range was reported. Outlier laboratory-reported data (per analyte and sample) were removed from the estimate of the consensus mean and 95% CI using an iterative application of the Kolmogorov–Smirnov test. Specifically, the Kolmogorov–Smirnov test was performed on the full set of data (per analyte and sample) at the alpha 0.05 level. If the test failed, then the lab with the greatest outlier was removed, and the test was reapplied to the remaining data. This process was repeated until the remaining data passed at the alpha 0.05 level.

3.1.2. Mixed effects model

Given the nine replicates per sample type, accuracy was assessed using laboratory-reported data that were natural log transformed for analysis. A mixed effects model (Wong et al., 2008; Dossus et al., 2009; Gu et al., 2009) was used to estimate whether a laboratory-reported mean estimate was significantly different from the model based consensus average. The means model with random lab effects was:

$${\mathrm{Y}}_{\mathrm{ij}}=\mu +{\alpha }_{\mathrm{i}}+{\mathrm{\epsilon }}_{\mathrm{ij}}$$

where i = laboratory and j = well.

The model was run using PROC MIXED in SAS 9.2. For grading purposes, an FDR and Bonferroni correction were assessed to account for multiple comparisons of each site to the consensus average. For each laboratory, the null hypothesis tested was that the laboratory’s nine well average was not different from the model based consensus average. The significance level was adjusted using a Bonferroni correction while maintaining an adjusted alpha = 0.05 significance level. The FDR correction was anti-conservative for these data.

3.1.3. Precision based on CV and ICC

The average coefficient of variation (CV) and a 1SD range, for the nine laboratory-reported replicates for each of the seven samples, was presented. The precision limit was the upper bound of the 1SD range around the mean within sample CV.

A separate measure of variability/reliability used was the intraclass correlation (ICC), which is an estimate based on the within and between laboratory variability (Sang-Ah et al., 2007; Chaturvedi et al., 2011; Scott et al., 2011). The ICC can easily be calculated from the mixed effects model run for each donor by sample combination. Calculation of the ICC is as follows:

$$\mathrm{\sigma }2b/(\mathrm{\sigma }2b+\mathrm{\sigma }2w).$$

• σ2b between site variance

• σ2w within site variance

This is the ratio of the between site variability to the total variability. The higher the ICC the more between site variability exists (i.e., σ2w is smaller relative to σ2b). The ICC provides a metric to compare the within and between lab variability and can help answer whether differing cytokine concentrations along the 4 or 5 PL function have more within or between lab variation.

3.2. Luminex: results

A Wald-type 95% CI was calculated using the laboratory-reported pg/mL data to estimate the accuracy range for the Luminex data. This was done when there were only three replicates per each sample. In PT round 3 there were nine replicates per each sample, and a mixed effects model was used for grading purposes. The concentrations in pg/mL were natural log transformed for use in the mixed effects model. We compared the number of samples by analyte that were considered outside the accuracy range by the Wald-type 95% CI method and mixed effects model (Fig. 2). Using the Wald-type 95% CI method there were 135 out of the 840 (16.1%) measures that were outside the accuracy range, compared with 164 out of 840 (19.5%) using the mixed effects modeling.

Fig. 2.

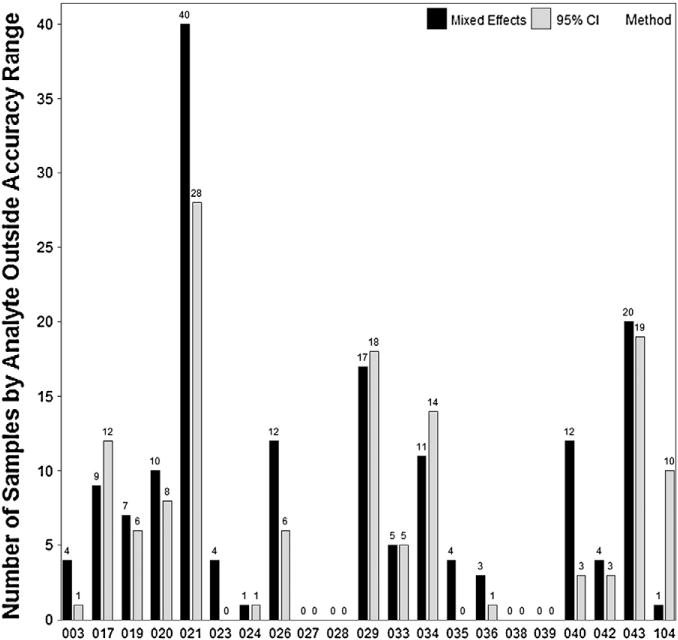
Luminex comparison of Wald-type 95% CI method versus mixed effects model. The Wald-type 95% CI method had 29 measures less outside the accuracy range compared with the mixed effects model method.

Fig. 3A shows the graphical representation for the Waldtype 95% CI method, which has the accuracy range, consensus average, and the site concentration as well as the concentration determined by the 4PL re-analysis of the MFI data. This allows laboratories to see the difference between their estimates and the EQAPOL-calculated estimates, as well as if their data were within the accuracy range. Fig. 3B is a graphical representation of the mixed effects model natural log transformed outcomes with average concentrations. The laboratory concentrations represented with a white circle were significantly different from the consensus average. This graph allows a site to see their model-based average compared to the consensus and the range of reported model based average concentrations. The examples in Fig. 3A and B are from PT round 3 and show the same sample type with IL-10 as the analyte.

Fig. 3.

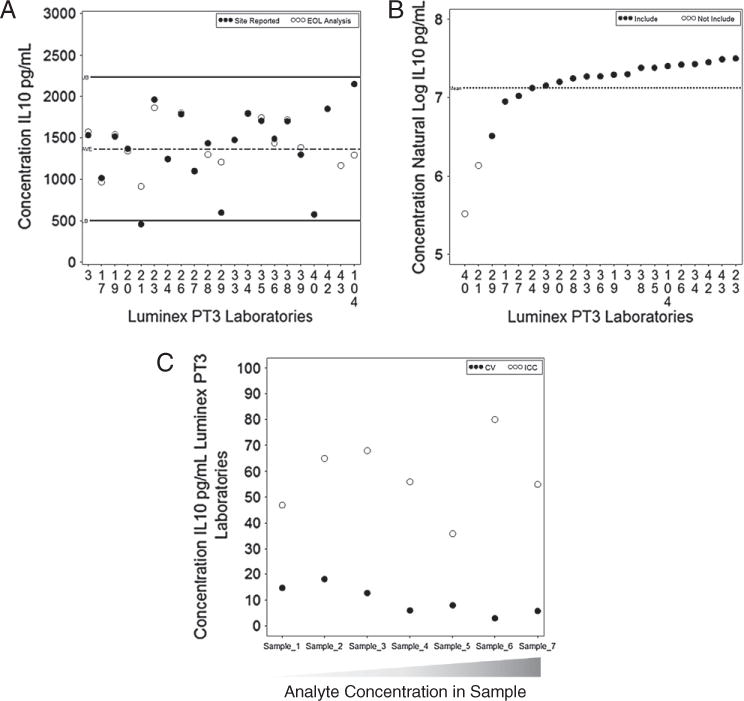
Luminex graphs for accuracy and precision. A) Example of the Wald-type 95% CI method graphed for one sample type included in the PT round 3 with analyte IL-10. B) The mixed effects model method graphed for the same sample type as in 3a for analyte IL-10. The two laboratories (unfilled circles) are not included in the accuracy range. C) The CVs and ICCs graphed for all samples with analyte IL-10. The samples are ordered from the lowest concentration to the highest concentration of the analyte present in the panel.

Another issue was the amount of variability at various concentrations along the standard curve. A primary question was the amount of variability at the tail ends of the curve; are really high or very low sample concentrations less precise? Generally CVs are used to assess this question, and the CVs are generally higher at the low end, which is in part due to the calculation of CVs (σ/μ — the standard deviation divided by the mean). As the mean (denominator) increases it is more likely that the CV will decrease. Also, the comparisons of CVs across the standard curve may not be entirely reasonable since different concentrations will not give ratio values, rather they are interval scaled. The use of a mixed effects model allows the calculation of the ICC, and we calculated bootstrapped 95% confidence intervals for each analyte by sample combination. There was no evidence (data not shown) that the ICCs differ in any systematic way across the standard curve since a majority of the confidence intervals overlapped and samples had ICCs ranges that were not related to their concentration (e.g., a medium-high sample generally had the lowest ICC whereas other medium-high to high concentration samples did not).

The precision boundary for the Luminex program was based on the upper bound of 1 SD interval of the CV for each of the 40 sample by analyte combinations. Six of the 21 laboratories did not have any exclusions from the precision boundary. There were nine laboratories with one to ten exclusions from the precision boundary, three laboratories with 11–20 exclusions, two laboratories with 21–30 exclusions, and one with more than 30 exclusions. Fig. 3C shows the CVs and ICCs for all samples included in PT round 3 for the analyte IL-10. The CVs are higher at lower concentrations, and the ICCs vary across the curve.

4. Flow Cytometry (ICS) program

The EQAPOL Flow Cytometry program assessed proficiency of NIAID/DAIDS-supported laboratories in the performance of multiple Flow Cytometry protocols in three PT rounds; a fourth round is ongoing (see Staats, et al. in this issue). In particular, the program has assessed site ability to run a 4-color Intracellular Cytokine Staining (ICS) assay that measures CD4 and CD8 T cell production of IFN-γ and IL-2 simultaneously in response to specific antigen stimulation. The 7-color ICS assay measures CD4 and CD8 T cell production of IFN-γ, IL-2 and TNF-α in response to specific antigen stimulation. Lastly, the 8-color ICS assay measures these same cytokines as well as expression of CD107a. This program is a continuation of a previously described Flow Cytometry ICS PT effort (Jaimes et al., 2011).

EQAPOL provided all of the reagents to run ICS assays including, donor PBMCs selected based on cytokine production following stimulation with lyophilized peptide pools (15-mers overlapping by 11aa): Cytomegalovirus (CMV); Cytomegalovirus, Epstein–Barr, Influenza virus (CEF) pool and a no peptide control. Cryopreserved PBMCs come from the repository of PBMCs described for the ELISpot program, see Garcia et al. in this issue. Lyophilized stimulation and staining plates were custom made by BD Biosciences. All other necessary staining and instrument set-up reagents were provided. Laboratories were required to run the assay using the EQAPOL-provided kit and protocol. Laboratories provided both analyzed results and raw Flow Cytometry Standard (FCS) data files.

There have been three PTs run for the Flow Cytometry program. PT rounds 1 and 2 were 4-color panels, PT round 3 had a 4-color and 7-color panel, and PT round 4 will have an 8-color panel. The data reported were triplicates for each of three donors by peptide.

4.1. Flow Cytometry: statistical approach

The goal of the Flow Cytometry program was to assess laboratories performing clinical Flow Cytometry. Accuracy to the consensus average was measured based on the EQAPOL Flow Cytometry Oversight Lab manual re-analysis (termed EOLm) of the participating laboratories’ FCS files. Statistical analyses were performed on the final proportions for the CD4+ or CD8+ T cells by CMV, CEF, and the no peptide control. In PT rounds 1 and 2 outlier laboratory-reported data (per cytokine and donor) were removed from the estimate of the consensusmean and 95% CI using aniterative application of the Kolmogorov–Smirnov test. Specifically, the Kolmogorov–Smirnov test was performed on the full set of data (per cytokine and donor) at the alpha 0.05 level. If the test failed, then the lab with the greatest outlier was removed, and the test was reapplied to the remaining data. This process was repeated until the remaining data passed at the alpha 0.05 level. In PT round 3, as we were moving to the 7 and 8-color panels, we used externalized student’s residuals greater than two to remove individual data points from the consensus mean calculation. These analyses were performed using PROC MIXED in SAS. Similar type of modeling has been used for other Flow Cytometry proficiency testing (Hultin et al., 2007).

The accuracy assessment was made with a Wald-type 95% CI, calculated using the EOLm data for each donor by peptide response. Individual laboratory estimates that fell outside of this accuracy range were considered failures.

We also assessed deviations from each laboratory analysis and the EOLm analysis. The deviations were calculated by taking the average of the three replicates, from each analysis, and subtracting the laboratory’s average from the EOLm average. A Wald-type 95% CI was calculated to produce the acceptability range. Deviations that fell outside of this acceptability range were considered failures. This analysis was done to assess how well laboratories perform gating in Flow Cytometry.

4.2. Flow Cytometry: results

The accuracy grading for the Flow Cytometry program is based on a Wald-type 95% CI that determines the accuracy range. There were 60 of the 594 (10.1%) estimates outside of the EOLm accuracy range for PT round 3 4C ICS. The Flow Team wanted to grade each individual laboratory estimate, thus a model based approach used for ELISpot and Luminex was not implemented. Fig. 4 gives an example of the graphical representation that laboratories receive regarding accuracy grading. The acceptability range, deviations from each laboratory estimate and the EOLm analysis, had 26 of the 198 (13.1%) ruled out for the deviation from EOLm. A regression model was used to remove outliers from the accuracy and acceptability range calculations based on externalized student’s residuals greater than two.

Fig. 4.

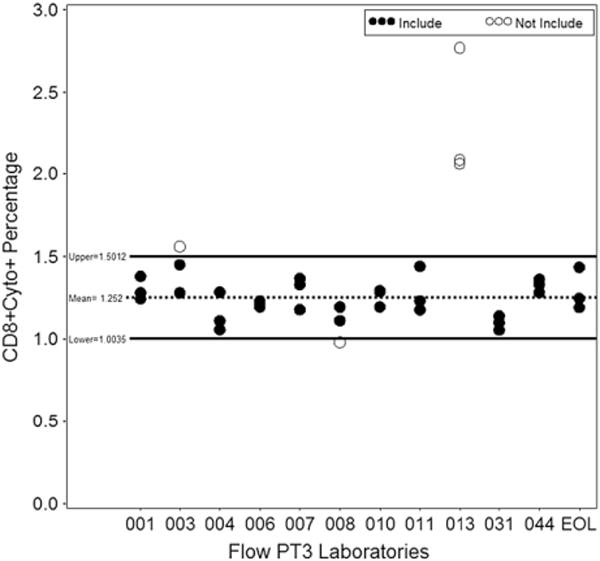
Flow cytometry graph of Wald-type 95% CI method. The Wald-type 95% CI method graphed for CD8+ with CEF, the open circles represent laboratories outside the accuracy range.

5. Discussion

A variety of statistical methods have been assessed for the EQAPOL ELISpot, Luminex, and Flow Cytometry EQA programs. The participating EQAPOL laboratories were statistically evaluated on accuracy to the consensus average and precision, as well as other non-statistical components. The previous proficiency programs were useful starting points for development of these grading criteria and statistical methods.

The use of the consensus average to assess accuracy is most appropriate given there is not a known target value. However, it is not possible to determine which of the methods is correct due to the lack of a target value. Given this caveat, we had to balance the use of statistical methodology and biologic relevance to establish reasonable grading methods. It was also of importance to have a uniform approach for the statistical methodologies and grading across all EQAPOL programs.

The mixed effects models for the ELISpot and Luminex programs provide a legitimate grading approach compared with the other methods; the laboratories that deviate from the consensus average are detected with this method without apparent misclassifications. Our use of mixed effects models with alpha adjustments for these proficiency testing data might not be considered a standard or typical statistical application. Regardless, these models function well for these proficiency data and provide a useful means of grading laboratory performance. Efforts have been made to educate sites about the benefits of statistical modeling for performance assessment, and site-specific reports include graphs clearly showing sites that are outside of the acceptability criteria (see Figs. 1c, 3b and 4).

A particularly important aspect of these statistical models is they allow for the incorporation of covariates, as well as longitudinal analyses as these programs move forward (see Bainbridge et al. in this issue). We can also model these data as multivariate since there are five analytes in Luminex and three peptides in ELISpot. This would allow the use a more complex model with the entire PT or multiple PT data at once instead of the simple models currently used for grading purposes. Furthermore, these models provided a different means of assessing precision that could be used for future PTs or for secondary analyses. The current precision metrics are based on the CV or dispersion, which are both metrics that describe the rate of variability divided by the mean.

Mixed effects models are a useful tool for performing grading and provide a means to answer a variety of research questions. These models can be used to address secondary issues such as laboratory variability over time, the stability of samples over time, as well as direct comparison of laboratories or machine differences. Proficiency testing data are well suited for these models because there are several replicates of a sample across multiple laboratories. The usefulness of mixed effects models will be further explored as we acquire more data in each of the EQAPOL programs.