A conceptual and methodological framework for investigating etiologic heterogeneity

Abstract

Cancer has traditionally been studied using the disease site of origin as the organizing framework. However, recent advances in molecular genetics have begun to challenge this taxonomy, as detailed molecular profiling of tumors has led to discoveries of subsets of tumors that have profiles that possess distinct clinical and biological characteristics. This is increasingly leading to research that seeks to investigate whether these subtypes of tumors have distinct etiologies. However, research in this field has been opportunistic and anecdotal, typically involving the comparison of distributions of individual risk factors between tumors classified on the basis of candidate tumor characteristics. The purpose of this article is to place this area of investigation within a more general conceptual and analytic framework, with a view to providing more efficient and practical strategies for designing and analyzing epidemiologic studies to investigate etiologic heterogeneity. We propose a formal definition of etiologic heterogeneity and show how classifications of tumor subtypes with larger etiologic heterogeneities inevitably possess greater disease risk predictability overall. We outline analytic strategies for estimating the degree of etiologic heterogeneity among a set of subtypes and for choosing subtypes that optimize the heterogeneity, and we discuss technical challenges that require further methodologic research. We illustrate the ideas by using a pooled case-control study of breast cancer classified by expression patterns of genes known to define distinct tumor subtypes.

1. Introduction

In the past decade, a lot of attention has focused increasingly on the goal of classifying cancers into distinct molecular subtypes, using extensive genomic data that distinguish the somatic characteristics of these subtypes [1]. It is anticipated that subclassifications based on molecular characteristics will lead to a greater understanding of cancer biology, and avenues for determining appropriate targeted therapies [2, 3]. Efforts to validate the relevance of candidate subtypes have usually focused on establishing their clinical distinctiveness by comparing subtype specific survival patterns, or by showing that genomically defined subtypes differ systematically with respect to conventional pathologic criteria. Parallel to this research, epidemiologists have been actively searching for new genetic risk factors, using modern tools such as genome-wide association studies [4, 5]. These two strands of research have been, for the most part, carried out in isolation. It is reasonable to speculate, however, that subtypes that are genuinely biologically distinct may also possess distinct etiologies. Thus, knowledge about tumor subtyping could inform the design and interpretation of epidemiological studies.

Conventionally, epidemiologists have examined the potential etiologic heterogeneity of cancer subtypes by comparing the candidate subtypes with respect to the presence of known risk factors for the cancer in question [6]. Prior to the molecular genetic era, studies of this nature would involve classifications of tumors on the basis of histologic or other pathologic features available in the medical records. Early studies of etiologic heterogeneity using genetic tumor characteristics linked environmental exposures to candidate somatic mutations, such as the relation of cancers characterized by specific TP53 mutations with smoking, exposures to infectious agents or exposure to other known carcinogens [7–9]. Recently, some investigators have explored the extent to which etiologic heterogeneity is reflected by distinctive epigenetic profiles in a variety of cancer sites (e.g., [10]), although more commonly the focus has been on expression levels of candidate genes, especially in breast cancer [11]. An example is a large study that showed that nulliparity and obesity at a young age are more frequently associated with tumors exhibiting positive expression of the estrogen receptor gene (ER+) versus tumors with negative expression (ER−), while early age at menarche is associated with tumors expressing progestin receptor (PR) [12]. Studies have also examined the association of known risk factors in relation to molecular subtypes of breast cancer defined on the basis of four tumor subtypes characterized by expression of ER, PR and human epidermal growth factor receptor (HER2) (e.g., [13]). Also, large consortia and case-control studies have shown that susceptibility loci identified from genome-wide association studies have different risks for ER+ versus ER− breast cancers (e.g., [14]). Combined, these findings indicate support for the presence of multiple etiologic pathways in breast carcinogenesis [15].

Because of technological advances and the onslaught of genomics research, it is highly likely that this recent literature is a prelude to an intensive period of epidemiological research into the etiologic heterogeneity of many different cancer types. Yet the methodology to date has been hampered by the absence of a conceptual framework for conducting these studies. A typical study will be framed in the context of a candidate subclassification, such as the comparison of breast cancers on the basis of ER+ versus ER− tumors. Tumors classified on this basis are then compared statistically with respect to the distributions of individual risk factors or with respect to estimated relative risks if a control group is available. Such a strategy can confirm that the subtypes differ etiologically, but it does not provide a unitary quantitative measure of the extent to which the groups differ based on the entire collection of risk factors. It is important to have a suitable measure that can be applied when the goal is to distinguish the merits of alternative candidate subclassification systems or when we wish to explore other subclassifications to determine an optimal subclassification. We further believe that increasingly, investigators will examine the etiologic heterogeneity of tumors using extensive molecular data based on expression arrays, methylation arrays, profiles of somatic DNA mutations and other global tumor profiles. A major goal will be to determine the clusters of cases that best characterize the etiologic heterogeneity of the disease.

In Section 2, we create the conceptual and methodological framework for investigating etiologic heterogeneity and show how this relates to the overall risk predictability of the disease. In Section 3, we outline formal analytic strategies for identifying the optimal tumor subclassification system, that is, the set of disease subtypes that are optimally etiologically heterogeneous. We then illustrate the approach using data from two historical breast cancer case-control studies in Section 4.

2. Conceptual framework

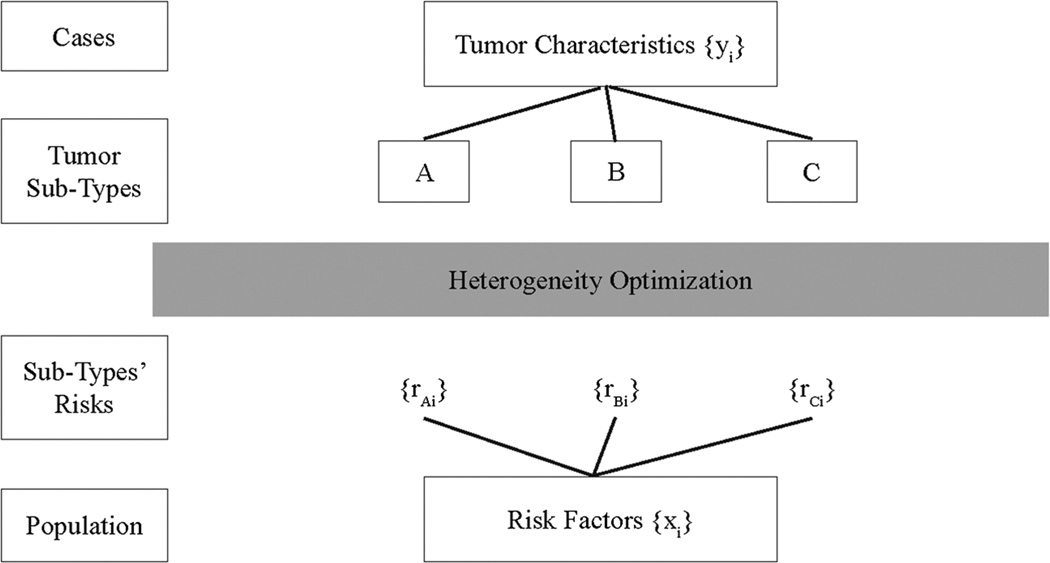
We display the framework for our strategy schematically in Figure 1, along with some of the general notation that we use. Cases of cancer are defined by tumor characteristics, such as traditional pathologic characteristics in addition to genomic features of the tumor such as somatic mutations, copy number changes, methylation profiles and so on. We denote such tumor characteristics that are available to us for analysis by {y_i} where the subscript denotes the individual case. We seek to use these characteristics to define subtypes, denoted A, B, C and so on. Conversely, we have information from epidemiologic studies of cancer risk concerning a constellation of risk factors denoted by {x_i}. We can use the data from case-control or cohort studies to predict the risks of the distinct subtypes under investigation for individual subjects, denoted {r_Ai}{r_Bi}{r_Ci} and so on. Our goal is to determine how to find the subtypes that are genuinely etiologically distinct. More specifically, we seek the set of subtypes that best explains the etiological heterogeneity in the cancer under investigation. In order to perform this ‘heterogeneity optimization’, we need a precise quantitative definition of etiologic heterogeneity, ideally in the form of a scalar measure that best captures the degree of heterogeneity exhibited by a set of subtypes.

Figure 1.

The figure displays conceptually the interplay of genetic and pathologic tumor characteristics (denoted by {y_i}) and risk profiles (denoted by {x_i}) that are used interactively to determine the set of subtypes that best characterize etiologic heterogeneity.

Etiologic heterogeneity is based necessarily on the concept of risk heterogeneity because risks must vary among different members of the population in order for the risk profiles of distinct tumor subtypes to differ. In the following, we define risk heterogeneity and then use this concept to define etiologic heterogeneity. We note that these entities are dependent on the sampled population, and thus rely on the definition of the population at risk. Consequently, the measures we utilize are not inherent entities but may differ depending on the geographic or ethnic population in which the study is conducted. This entire section addresses the relationships between these parametric entities. We will discuss estimation later in Section 3.

2.1. Population risk heterogeneity

Consider a population in which every individual has a distinct risk of the disease, denoted r_i for the i^th individual, i = 1, …, n. Risk heterogeneity represents the extent to which this risk varies from person to person in the population. The conventional measure of variation is the variance, but we need a measure that is scale invariant, and because risks cannot be negative, a natural measure of risk heterogeneity is the coefficient of variation of risks, which we denote by K. Thus, K² = v/μ², where μ = n⁻¹ ∑ r_i and $\upsilon =n^{-1}\sum r_i^2-{\mu }^2$.

2.2. Etiologic heterogeneity

Consider any two disease subtypes, A and B. The risk profiles of these two subtypes are homogeneous to the extent that the risks are aligned for individuals in the population, with etiologic heterogeneity representing the converse of this, that is, discordant risk profiles. Thus, the subtypes are etiologically homogeneous if a person with a high risk of subtype A typically also has a high risk of subtype B, and vice versa. In other words, etiologic heterogeneity is embedded in the correlations of the risk profiles of the subtypes across individuals. Let r_Ai and r_Bi be the mutually exclusive risks of the subtypes for the i^th individual, where r_i = r_Ai + r_Bi, and where μ_A = n⁻¹ ∑ r_Ai, μ_B = n⁻¹ ∑ r_Bi, ${\upsilon }_A=n^{-1}\sum r_{Ai}^2-{\mu }_A^2$, and ${\upsilon }_B=n^{-1}\sum r_{Bi}^2-{\mu }_B^2$. We define ${\mathrm{K}}_A={\upsilon }_A^{1/2}/{\mu }_A$ to be the population coefficient of risk variation for tumor subtype A; we define ${\mathrm{K}}_B={\upsilon }_B^{1/2}/{\mu }_B$ to be the coefficient of risk variation for tumor subtype B, and we define a corresponding standardized term for the risk covariance, the degree to which the risks of A and B are aligned from person to person, using K_AB = c/μ_Aμ_B, where c = n⁻¹ ∑ r_Air_Bi − μ_Aμ_B. Etiologic heterogeneity is inversely related to K_AB. Note that the corresponding correlation coefficient of the risk profiles is ρ_AB = K_AB/K_AK_B.

2.3. Etiologic heterogeneity and incremental explained variation

We presume now that multiple subtypes may exist. For simplicity in the following, we consider three subtypes, A, B and C, but all subsequent results are easily generalizable. The total coefficient of variation can be decomposed in the following way:-

$${\mathrm{K}}^2={\pi }_A^2{\mathrm{K}}_A^2+{\pi }_B^2{\mathrm{K}}_B^2+{\pi }_C^2{\mathrm{K}}_C^2+2{\pi }_A{\pi }_B{\mathrm{K}}_{AB}+2{\pi }_A{\pi }_C{\mathrm{K}}_{AC}+2{\pi }_B{\pi }_C{\mathrm{K}}_{BC},$$ (1)

where π_j is the proportion of cases with subtype j, that is, π_j = μ_j / (μ_A + μ_B + μ_C). This formula bears a superficial resemblance to a conventional analysis of variance, but it differs because the subtypes represent a partitioning of total risk and the K terms are coefficients of variation. The crucial insight from (1) is that the left-hand side of the equation K² is a constant regardless of how the subtypes are formulated. This represents the total risk variation on the basis of the disease as an aggregate entity. Thus, a subtyping scheme that increases etiologic heterogeneity, by virtue of reducing the aggregate of the three covariance terms, necessarily must increase the aggregate of the three variance terms. In other words, subtypes with larger etiologic heterogeneity will have larger risk predictability in aggregate. This is more easily observed by constructing a term that represents the incremental explained risk variation:

$$D=({\pi }_A{\mathrm{K}}_A^2+{\pi }_B{\mathrm{K}}_B^2+{\pi }_C{\mathrm{K}}_C^2)-{\mathrm{K}}^2.$$ (2)

This is the difference between the mean explainable risk variation in the subtypes (in parentheses) and the overall risk variation K². We note that in general, D ≥ 0, with D = 0 occurring when the risks of all of the subtypes are perfectly correlated in the population; that is, there is no risk heterogeneity. It is easily shown that D can be re-expressed as

$$D={\pi }_A{\pi }_B({\mathrm{K}}_A^2+{\mathrm{K}}_B^2-2{\mathrm{K}}_{AB})+{\pi }_A{\pi }_C({\mathrm{K}}_A^2+{\mathrm{K}}_C^2-2{\mathrm{K}}_{AC})+{\pi }_B{\pi }_C({\mathrm{K}}_B^2+{\mathrm{K}}_C^2-2{\mathrm{K}}_{BC}).$$ (3)

Equation (3) shows more clearly how smaller values of the risk covariances lead individually to larger values of D.

3. Analysis methods

A major premise of our strategy is that a goal of epidemiologic investigation, rather than relying on hypothesis-driven investigations into whether a particular classification is heterogeneous, is to find the set of subtypes that best explain etiologic heterogeneity. We may have several tumor features that need to be combined to define the subtypes that are the most clearly heterogeneous. This could include features of tumor histology, more detailed somatic mutations, copy number changes, methylation or other genomic events. Indeed, as molecular genotyping becomes more extensive, we are likely in the future to have countless features that are candidates for defining these etiologically heterogeneous subtypes. Our goal will be to find the classification that optimizes the observed heterogeneity. That is, we wish to find the set of subtypes that maximizes D. This requires novel approaches to clustering that seek to optimize D. In the following, we describe how to combine the estimation of risk profiles from case-control data with a novel clustering strategy to identify the etiologically heterogeneous subtypes.

3.1. Risk estimation

Our analytic strategy for estimating individual risks is conceptually straightforward. We use logistic regression of cases and controls to determine the independent contributions of the risk factors, and then obtain risk predictions for each individual control participant. These are then used to calculate directly the coefficient of risk variation K². We note that in obtaining this estimate, we use only the controls in the formula because K² is a population-based measure of variation, calculated with respect to the population at risk, that is, the controls. Specifically, if there are n controls and the risk factor data for these controls are denoted x_i = (1, x_i1, x_i2, …), i = 1, …, n, and if we define our logistic regression as log (p_i / (1 − p_i) = α′x_i), then we set ${\mathrm{K̂}}^2=n^{-1}\sum {\mathrm{p̂}}_i^2/{(n^{-1}\sum {\mathrm{p̂}}_i)}^2-1$, where p̂_i = exp(α̂′x_i) / (1 + exp(α̂′x_i). We clarify that n indexes the number of controls and K̂ is estimated using only the p̂_i s from controls, although both cases and controls are used in estimating the model parameters α̂. We also note that we have used {p̂_i} rather than {r̂_i} because the risk predictions from a case-control study do not represent the set of absolute risks as these cannot be estimated from a case-control study. However, it is easily shown that all of the coefficient of variance and covariance terms can be estimated from any set of relative risks because these terms are invariant to the choice of baseline risk employed. Recognizing that these risk predictors are aggregates of the risks of the subtypes, that is, p_i = p_Ai + p_Bi + p_Ci + …, we can estimate the coefficients of variation and covariation correspondingly from a polytomous logistic regression model. That is, given a candidate set of subtypes A,B,C… and setting $\text{log}(p_{ki}/p_{0i})={\beta }_k^{\prime }{x}_i$ for k = A, B, C… and so on where p_0i = 1 − p_Ai − p_Bi − p_Ci …, we can derive the subtype risk predictors using ${\mathrm{p̂}}_{ki}=\text{exp}({\mathrm{\beta ̂}}_k^{\prime }{x}_i)/(1+\text{exp}({\mathrm{\beta ̂}}_A^{\prime }{x}_i)+\text{exp}({\mathrm{\beta ̂}}_B^{\prime }{x}_i)+\text{exp}({\mathrm{\beta ̂}}_C^{\prime }{x}_i)\dots )$. Estimators of the individual coefficients of variation and covariation can then be obtained using ${\mathrm{K̂}}_k^2=n^{-1}\sum {\mathrm{p̂}}_{ki}^2/{(n^{-1}\sum {\mathrm{p̂}}_{ki})}^2-1$ and K̂_kl = n⁻¹ ∑ p̂_ki p̂_li / ((n⁻¹ ∑ p̂_ki)(n⁻¹ ∑ p̂_li)) − 1. We then use these estimates to calculate the extent of heterogeneity (D) exhibited by any candidate subtypes defined by the tumor characteristics. For any pre-specified candidate classifications, we can test whether a particular set of subtypes exhibits statistically significant etiologic heterogeneity by performing a simultaneous test of the hypothesis that the relative risks for each of the risk factors are identical in each of the subtypes (excluding the intercepts). We can accomplish this in SAS PROC-LOGISTIC (SAS Institute, Cary, NC.) using the ‘TEST’ statement, a Wald test of the hypothesis that all subtypes share the same odds ratios for each risk factor. For examining in more detail which risk factors influence observed heterogeneity between subtypes, one can use the same command to perform a Wald test of the hypothesis that the odds ratios of a specific risk factor are identical for each of the subtypes while allowing the other risk factors to exhibit heterogeneity.

3.2. Identifying optimal subtypes using hierarchical clustering

Our goal is to identify the ‘optimal’ set of subtypes from the perspective of etiological heterogeneity. To obtain reproducible subtypes (i.e., clusters), these must be defined in terms of the tumor characteristics. Thus, we first need to identify candidate clusters defined by the tumor characteristics using some suitable selection method, and then find the set of clusters from among these candidates that maximizes D. Finding the best way to select candidate clusters is a topic for future research. For this article, we have adopted an agnostic strategy that makes use of k-means clustering to identify candidate sets of clusters. This method is structured to create clusters that minimize the intra-cluster variation with respect to the inter-cluster variation. Logic suggests that clusters that exhibit multidimensional separation of this nature are more credibly etiologically heterogeneous than clusters that do not exhibit such separation. This method produces a variety of solutions at local maxima of the clustering criterion. It also has the benefit of giving lower weight to clusters that are easier to form by chance, that is, those based on very few patients.

The k-means clustering algorithm is based solely on the somatic tumor characteristics of the cases, that is, {y_i}. We emphasize that these are characteristics of the tumor as opposed to risk factors and are thus entirely different from the features {x_i} used in the previous section. Suppose that there are k clusters with cluster means of these tumor characteristics denoted θ₁, θ₂, …θ_k, with overall mean θ, and let the cluster membership be denoted by the term d_ik for the i^th case, where d_ik = 1 if the tumor of case i belongs to cluster k and d_ik = 0 otherwise. The k-means criterion is the inter-cluster dissimilarity G = (S_T − S_I) / S_T, where $S_I=\sum _{i,d_{ik}=1}\left\{\right(y_i-{\mathrm{\theta ̂}}_j)\prime (y_i-{\mathrm{\theta ̂}}_j\left)\right\}$ is the intra-cluster sum of squares and $S_T=\sum _i\left\{\right(y_i-\mathrm{\theta ̂})\prime (y_i-\mathrm{\theta ̂}\left)\right\}$ is the total sum of squares [16, 17]. We generate an initial set of clusters randomly and reassign the observations to the closest cluster mean. We recalculate the means, and the process iterates to a local solution. This will not typically produce a global solution, so we repeat the entire process with a new random seed multiple times. In our application, we used k-means clustering in this way repeatedly for a predetermined number of clusters to generate candidate sets of subtypes, and then performed polytomous logistic regressions using the disease risk factors in order to calculate D for the selected clusters and thus determine the maximum D overall.

4. Example – etiologically heterogeneous subtypes of breast cancer

In Section 1, we summarized briefly the literature on breast cancer. Various studies have provided evidence that for some risk factors, the relative risks for ER+ tumors differ from ER− tumors. In the clinical research arena, hierarchical clustering of expression arrays led to the identification of four breast cancer subtypes with distinct clinical characteristics, and it was shown that these subtypes can be approximated on the basis of ER, PR and HER2 expression as follows: luminal A (ER+ or PR+ and HER-2/neu−), luminal B (ER+ or PR+, HER-2/neu+), HER2-enriched (ER−, PR− and HER-2/neu+), and triple negative (ER−, PR− and HER-2/neu−) [18]. Subsequent investigations have provided evidence that these subtypes are also etiologically heterogeneous (see [13]). We have examined two archival case-control studies that contributed to this literature with a view to exploring the ‘optimal’ subtype classifications of breast cancer based on these tumor characteristics. In these studies, information on P53 expression is available in addition to ER, PR and HER2.

4.1. Data

We have combined data from the two studies. The Cancer and Steroid Hormone (CASH) Study, led by the CDC in the early 1980s made use of the SEER registries for identification of incident cases of breast cancer [19, 20]. The cases were women aged 20 to 56 with primary breast cancer diagnosed between 1980 and 1982. Controls were ascertained through random digit dialing in the geographic areas served by the study registries. In a later study, tumor tissue was successfully obtained for a subset of cases and evaluated for expression of ER, PR, HER2 and P53. The Womens’ Contraceptive and Reproductive Experiences (CARE) Study is a population-based case-control study of invasive breast cancer in women aged 35 to 64, diagnosed between 1994 and 1998, who resided in one of the five geographical areas [21]. Tumor tissue was sought subsequently for cases registered from two of the study sites, and these were successfully analyzed for expression levels of ER, PR, HER2 and P53. These markers are considered positive or negative using the identical criteria employed by both Ma et al. [22] and Gaudet et al. [24] in their analyses of the CARE and CASH studies, respectively. Gaudet et al. analyzed a total of 890 cases and 3432 controls from CASH while Ma et al. analyzed a total of 1197 cases and 2015 controls from CARE to explore etiological heterogeneity. Our analysis employs the risk factors published previously by Gaudet et al. [24]: age at diagnosis, age at menarche, nulliparity, age at first birth, months of breastfeeding, body mass index (separately for premenopausal and postmenopausal participants), ever use of oral contraceptives, menopausal status and family history of breast cancer. We have combined participants from CASH and CARE who have complete data on this set of risk factors and tumor markers, resulting in a total of 1752 cases and 4581 controls.

In their evaluation of the CASH Study, Gaudet et al. [24] examined various configurations of risk factors and subtypes. Their primary conclusions, among others, were that triple negative tumors are associated with breast feeding, increasing Body Mass Index (BMI) is associated with luminal B and triple negative subtypes in premenopausal women and family history is more strongly associated with triple negative tumors in younger women than in older women. In the analysis of the CARE Study, use of Oral Contraceptives (OCs) was solely associated with triple negative tumors, while the influence of parity was observed to be limited to the other three subtypes [22]. The authors also concluded that P53 expression did not contribute to the etiologic heterogeneity observed. The purposes of our analyses in the subsequent sections are first to provide quantitative summaries of the extent to which the expression markers contribute broadly to etiologic heterogeneity based on all of the risk factors collectively, and then to provide an exposition of how to adapt available hierarchical clustering techniques to the search for a classification system that optimizes the explainable etiologic heterogeneity. We conducted this latter analysis recognizing the fact that we only have four tumor characteristics at our disposal: ER, PR, HER2 and P53. However, we really design the analytic strategy for future studies in which tumors have been profiled for numerous molecular characteristics.

4.2. Results – candidate subtypes

In all of our analyses, we treat the four tumor markers as binary, consistent with the original reports of the CASH and CARE studies. We examine initially the results for each of the tumor markers and for the standard four-cluster classification system, focusing on the extent to which the expression levels of ER, PR, HER2 and P53 distinguish etiologically distinct subtypes on an individual basis, using a model that includes all of the risk factors listed in Section 4.1 in addition to study center. We provide the results in Table I. We note first that the total coefficient of risk variation was estimated to be 0.176 (footnote) using a logistic regression in which breast cancer was considered to be a single disease entity. This is a relatively small degree of risk variation, and it reflects the fact that the extent to which we can predict breast cancer risk overall is relatively weak. For benchmarking purposes, this corresponds to an Area Under the (receiver operating characteristic) Curve (AUC) of 0.66. We estimated the risk variation coefficient to be 0.295 for ER+ cases and 0.160 for ER− cases, leading to an incremental explained risk variation estimate D = 0.057(p < 0.001). We observed the corresponding incremental risk variation to be 0.032 for PR (p < 0.001), 0.014 for HER2 (p = 0.04) and 0.027 for P53 (p < 0.001), suggesting that ER status provides more evidence of etiologic heterogeneity than the other expression markers. In fact, the evidence that HER2 contributes to etiologic heterogeneity is only marginally significant. The higher etiologic heterogeneity for ER is reflected by the substantially lower correlation between the ER+ and the ER− risk profiles than the corresponding correlations for the other classifications (Table I). When we study the widely used four-category system for classifying breast cancers, the incremental risk variation increases to 0.083. The luminal B subtype appears to exhibit the most risk variation among these subtypes, although this is the most infrequent of the subtypes, and risk variation estimates are likely to be inflated for small subtypes.

Table I.

Results for candidate subtypes¹.

Subtypes	N	π̂j	${\mathrm{K̂}}_j^2$	K̂ij	ρ̂ij	D	p-value4
ER+	981	0.58	0.295	0.109	0.50	0.057	< 0.001
ER−	771	0.42	0.160
PR+	924	0.55	0.287	0.141	0.75	0.032	< 0.001
PR−	828	0.45	0.122
Her2+	354	0.19	0.134	0.125	0.75	0.014	0.04
Her2−	1398	0.81	0.205
P53+	528	0.28	0.205	0.138	0.67	0.027	< 0.001
P53−	1224	0.72	0.204
Luminal A	912	0.53	0.289	Note2	Note3	0.083	< 0.001
Luminal B	168	0.11	0.381
HER2-enriched	186	0.08	0.098
Triple negative	486	0.28	0.240

¹The total coefficient of risk variation (K²) is estimated to be 0.176.

²The six coefficients of covariance are 0.198, 0.057, 0.119, 0.052, 0.236 and 0.038.

³The six correlation coefficients are 0.60, 0.34, 0.45, 0.27, 0.78 and 0.25.

⁴Corresponds to the test of the hypothesis of no etiologic heterogeneity between the subtypes.

4.3. Results – optimal subtypes

We next sought to use our optimization methods to identify the subtyping systems that provide the greatest degree of etiologic heterogeneity on the basis of these risk factors. We evaluated this by repeatedly conducting k-means clustering (1000 times) with random starting classifications and selecting the optimal D from among the k-means solutions. [Recall from Section 3.2 that the k-means algorithm finds a local maximum for the inter-cluster dissimilarity G at each run.] We see in Table II that the optimal two-class system identified by the methodology outlined in Section 3.2 (D = 0.055) is actually lower than the configuration that simply uses ER+ versus ER− as the two subtypes. This occurs because the ER+/ER− configuration does not represent a k-means local maximum. By an exhaustive search of all possible two-class subtypes, we discover that the true maximum is D = 0.063. We will discuss the implications of this issue in more detail in Section 5.1. However, what is clear from our analysis is that ER status carries most of the signal in the two-class framework. Moving to the four-class options, the optimal solution is D = 0.095. This compares with D = 0.083 for the commonly used four-category system derived from expression profiling. Later, in Section 5.2, we discuss validation strategies to address the concern that our supervised strategy for identifying subtypes is certain to identify apparent heterogeneity. Thus, we need to be confident that a true heterogeneity signal exists. Similarly, we address the issue of how to best choose the number of clusters.

Table II.

Optimal subtypes.

Subtypes	Heterogeneity (D)
ER+ versus ER−	0.057
Four-category system	0.085
Optimal two-class (complete enumeration)	0.063
Optimal two-class1	0.055
Optimal three-class1	0.073
Optimal four-class1	0.095
Optimal five-class1	0.114

¹These optima represent the maxima over 1000 random starts rather than the true maxima over an exhaustive search of all possible classification systems.

An interesting and unexpected finding is that the ‘optimal’ four-class system involves only ER and P53. That is, the optimal four-class system is defined by (ER+, P53+), (ER+, P53−), (ER−, P53+) and (ER−, P53−) with no involvement of either PR or HER2. This result is driven by the fact that HER2 appears to provide very little contribution to heterogeneity (Table I) and presumably, the contribution of PR must be subsumed by ER because the markers are strongly correlated. This simple classification allows us to examine the key distinctions in the risk factor profiles of these four subtypes on the basis of the risk factors that were used in the analysis. In Table III, we display the relative risks for each risk factor for the four subtypes. In this table, we report only the relative risk estimates to one significant figure after the decimal so that we are not distracted by small differences that are likely to be insignificant.

Table III.

Odds ratios from logistic regressions for ER/P53 subtypes.

	Tumor characteristics1
	ER+		ER−
Risk factor2	P53+ n = 205	P53− n = 776	P53+ n = 323	P53− n = 448	Test for heterogeneity
Age at diagnosis (×10 years)	2.1 (1.4–3.2)	1.9 (1.6–2.4)	0.8 (0.7–1.0)	1.2 (1.0–1.5)	< 0.001
Age at menarche (×2 years)	1.0 (0.8–1.2)	0.9 (0.8–1.0)	1.0 (0.9–1.2)	1.0 (0.9–1.2)	0.04
Nulliparous	1.9 (1.3–2.6)	1.4 (1.1–1.7)	0.7 (0.5–1.0)	1.2 (0.9–1.5)	0.001
Age at 1st Birth (×5 years)	1.2 (1.0–1.4)	0.9 (0.8–1.0)	1.1 (0.9–1.2)	1.1 (1.0–1.2)	0.67
Breastfeeding (×6 months)	1.0 (0.9–1.1)	0.9 (0.9–1.0)	0.8 (0.7–0.9)	0.9 (0.9–1.0)	0.12
Postmenopausal	0.4 (0.3–0.6)	0.6 (0.4–0.7)	0.9 (0.6–1.3)	0.6 (0.4–0.8)	0.01
BMI (premenopausal ×20 units)	1.1 (0.5–2.3)	0.7 (0.4–1.0)	1.2 (0.7–2.2)	1.9 (1.2–3.0)	0.01
BMI (postmenopausal ×20 units)	0.9 (0.4–2.0)	0.8 (0.5–1.3)	1.0 (0.5–1.9)	0.8 (0.4–1.4)	0.96
Ever use of OCs	1.0 (0.7–1.4)	0.9 (0.8–1.1)	1.0 (0.8–1.3)	1.1 (0.8–1.3)	0.82
Family history of BC	2.2 (1.5–3.3)	2.1 (1.7–2.7)	2.0 (1.4–2.8)	1.6 (1.2–2.2)	0.44

¹In all four columns, the entries are the relative risks, versus controls, of tumors characterized by the combination of markers: (ER+,P53+), (ER+,P53−), (ER−,P53−) and (ER−,P53−), respectively.

²All analyses are adjusted for study center in addition to the factors in the table. For variables involving structural exclusions such as age at first birth for women with no children, we assigned the mean age at first birth among parous women (22.8) to the women with no children. Similarly, we assigned 5.3 months of breast feeding to nulliparous women, a postmenopausal BMI of 23.9 for premenopausal women and a premenopausal BMI of 24.8 for postmenopausal women. We recommend this strategy for structural exclusions of this nature [23]. It ensures that the influence of these structurally excluded subjects is minimized with respect to the estimation of the odds ratios for these factors.

For each risk factor, we performed a test of heterogeneity to determine which of the risk factors appear to explain the observed heterogeneity. Given that our search algorithm sought to identify subtypes with distinct odds ratios, we cannot interpret the ‘significance’ of these tests at face value. We use them here solely as a tool to identify the most influential risk factors in explaining the apparent heterogeneity. The results, in the last column of the table, appear to indicate that the factors that are driving the heterogeneity are age at diagnosis, parity, menopausal status and premenopausal BMI. The first two columns correspond to the subtypes defined by ER+ tumors. Comparing these two columns with the last two columns (corresponding to ER−), we observe that the risk factors that seem to most clearly distinguish ER+ from ER− tumors are later age at diagnosis, nulliparity and possibly low premenopausal BMI. Comparing the two P53+ columns with the two P53− columns does not provide any obvious contrasts. However, the influence of P53 may occur within ER categories, and indeed, the ER−/P53+ subtype appears to be distinctively characterized (relative to the other subtypes) by early age at onset, parity and postmenopausal status. We emphasize that these observations are speculative.

5. Methodological issues

5.1. Methodologic challenges and limitations

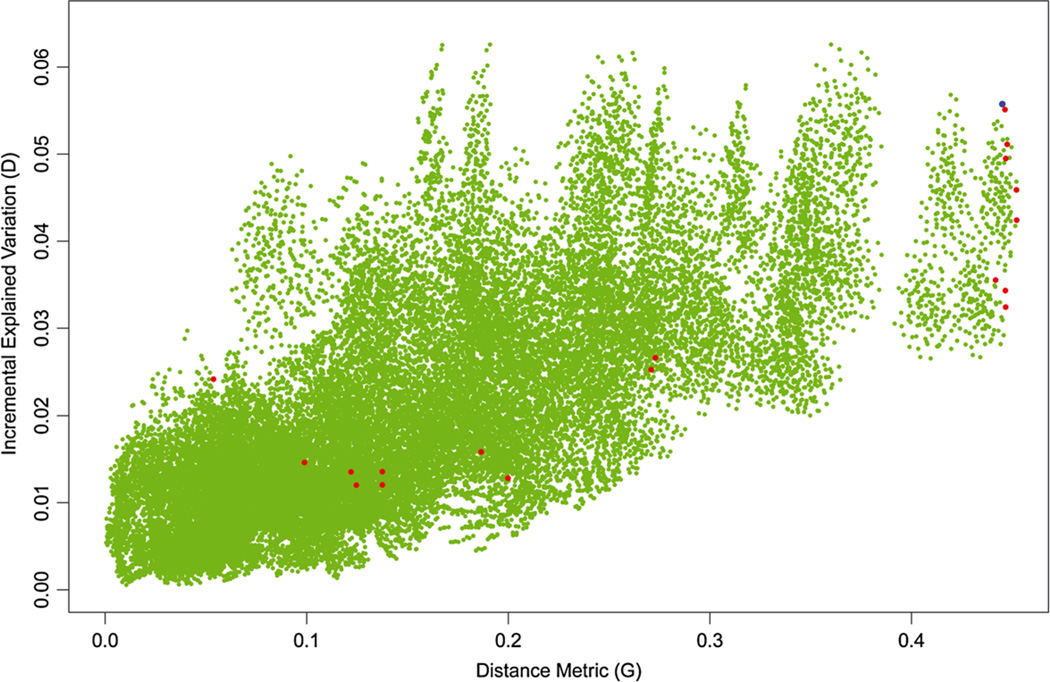
A key feature of our analytic strategy is the combined use of k-means clustering and optimization of the incremental explained variation metric, D. We can shed light on the possible limitations of the hybrid strategy of using k-means clustering to identify local maxima and then selecting the one with the largest value of D by examining the optimal two-class system where it is computationally feasible to perform logistic regressions and evaluate D for all of the 32,767 possible two-class systems created by our 2⁴ distinct combinations of ER/PR/HER2/P32. In Figure 2, we plot the distance metric G on the X-axis against the incremental explained variation metric D on the Y-axis. The green dots represent the complete set of admissible candidate systems, excluding arbitrarily any system in which one of the subtypes identified contained less than 5% of the cases. The red dots represent the local maxima that were observed as solutions to the k-means algorithm. The blue dot corresponds to the ER+ versus ER− classification. The figure shows a modest though pronounced positive correlation between G and D, indicating that configurations that are geometrically distinct (higher G) are more likely to exhibit higher values of D, reflecting the fact that classification systems that are very similar in terms of allocation of cases will tend to have similar values of both D and G. This would suggest that in practice, the k-means hybrid strategy will be likely to reach a solution that is reasonably close to the optimal solution; that is, it will be close to the top right-hand corner of the figure, with both high D and high G. However, it is noticeable that a strong logical candidate, the ER+ versus ER− classification (denoted by the blue dot), is not situated at a local k-means solution despite the fact that its incremental explained variation (D) is actually slightly higher than the maximum among classifications with the highest distance measure (red dots, see also Table II). There are, however, a number of configurations that are not k-means solutions that produce higher values of D at considerably lower values of G, reaching a maximum of D = 0.063. A further concern from Figure 2 is the fact that several k-means solutions have low value of both D and G, raising the possibility that this strategy might fail to identify a solution at or close to the optimal one if these low G/D values occur with high relative frequency. However, an examination of the relative frequencies of solutions at each of the local maxima indicates that the local maximum with the highest value of D occurs in 68 (6.8%) of the random starts, ensuring that this solution would be almost certain to be observed even if we had only 100 random starts.

Figure 2.

The incremental explained variation is plotted against the distance metric for every possible two-class configuration of the 16 distinct permutations of the four binary markers, excluding only configurations in which one subtype contains fewer than 5% of the cases (green dots). The red dots represent local maxima obtained from k-means clustering. The blue dot corresponds to the classification ER+ versus ER−.

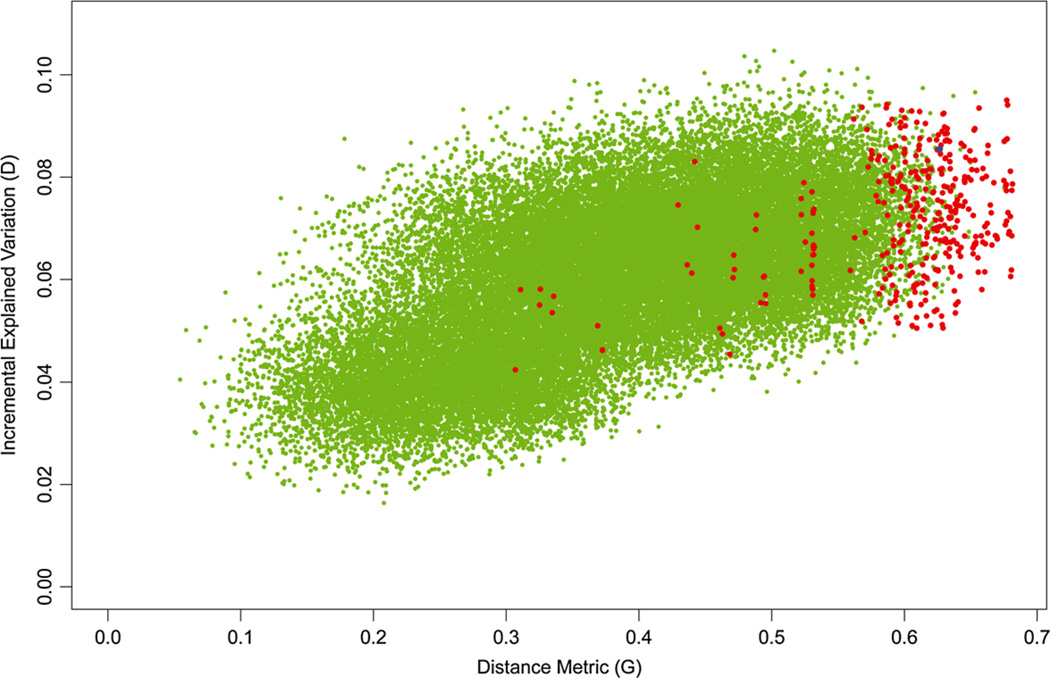
We display a similar plot of four-class systems in Figure 3. In this figure, the green dots represent a random sample of 50,000 candidate configurations rather than an exhaustive search of all configurations as in Figure 2. It can be seen that the k-means solutions in red are much more concentrated at higher values of the distance metric G than in the two-class setting in Figure 1. The optimal solution produces values of both D and G that are somewhat higher than for the familiar candidate system (luminal A, luminal B, HER2-enriched, triple negative) denoted by the blue dot, although again there are clearly a few configurations that possess higher values of D than our optimal hybrid solution.

Figure 3.

This figure is similar to Figure 2, except that the green dots represent a random sample of 50,000 candidate configurations. The blue dot corresponds to the widely used four-class system: luminal A, luminal B, HER2-enriched and triple negative.

5.2. Validation strategy

In our example, we have elected to use all of the data to obtain the most precise estimates. However, the overall strategy clearly involves a high degree of selection and thus would appear to be highly susceptible to overconfidence with respect to the apparent heterogeneity effects that might be detected. Given that our goal is to optimize the heterogeneity observed in the dataset, it is inevitable that subtypes with apparent heterogeneity will be identified. In the following, we seek a validation strategy to provide reassurance about whether or not we can be confident that there is truly any etiologic heterogeneity present. We accomplish this by creating a reference distribution for D under the scenario where there is no underlying heterogeneity signal. The observed value of D can then be compared with this reference distribution to determine whether or not the magnitude of heterogeneity observed is sufficiently large to be convincing. To obtain the reference distribution, we simply permute the cases with respect to the tumor characteristics. That is, we reassign {y_i} randomly to the cases but retain the risk factors {x_i} with the cases to which they belong. This ensures that there is no heterogeneity signal. Because the set of k-means solutions does not depend on {x_i}, we simply calculate D for each k-means solution, select the one with the largest value of D and then re-permute {y_i} a large number of times to obtain the null distribution of D. We display the results in the top half of Table IV for each of the analyses with fixed numbers of subtypes. In effect, the same hypothesis is being tested in each case: Is there a heterogeneity signal? Clearly in each setting, the observed D is much higher than the reference distribution.

Table IV.

Validation.

	Configuration	Mean	Maximum1	Observed	p-value
			D
Test for signal	2	0.014	0.031	0.055	< 0.001
	3	0.028	0.052	0.073	< 0.001
	4	0.040	0.065	0.095	< 0.001
	5	0.051	0.081	0.114	< 0.001
			ΔD
Test for increment	2 versus 3	0.014	0.030	0.017	0.12
	2 versus 4	0.026	0.048	0.040	0.01
	2 versus 5	0.037	0.065	0.059	0.001
	3 versus 4	0.012	0.025	0.022	0.003
	3 versus 5	0.023	0.043	0.042	0.001
	4 versus 5	0.011	0.024	0.019	0.006

¹Maximum over 2000 simulations.

A related challenge is to determine the appropriate number of subtypes. We can shed light on this by testing whether an increase in the number of subtypes leads to an incremental increase in D that is significant. To accomplish this, we adopted the following strategy. Consider as an example the test of whether the use of four subtypes provides significantly more heterogeneity than the use of three subtypes. The test statistic is the increment in the optimal value of D for these two settings, that is, 0.095–0.073 (Table II). To obtain a reference distribution for this increment, we again make use of the fact that the sets of k-means solutions are fixed for each setting. That is, we can simply permute {y_i} and calculate D for all of the three-class and four-class k-means solutions and subtract the maximum three-class solution from the maximum four-class solution. We then re-permute {y_i} and repeat this process multiple times to obtain the reference distribution. We display the results of this strategy in the lower half of Table IV. Unfortunately, the results are not mutually consistent in this example. All of the tests are highly significant except for the transition from two classes to three classes, leaving no clear evidence for the most appropriate number of subtypes in this example.

We note that regardless of the number of subtypes selected, the observed heterogeneity measure D is inevitably inflated and the degree of heterogeneity in the estimated odds ratios, as in Table III, will be inflated also. The ideal way to correct the optimistic biases in these estimates would be to apply the new subtypes to an independent dataset in order to re-estimate D and the profiles of odds ratios of the risk factors.

6. Discussion

Our purpose in this article has been to map out a conceptual framework for the quantitative evaluation of etiologic heterogeneity and to outline ideas for specific statistical methods that can be used for approaching the issue. Traditionally, the evaluation of etiologic heterogeneity by epidemiologists has been anecdotal, in the sense that candidate subtypes have been compared on the basis of individual risk factors. The candidate subtypes themselves have been based typically on widely observable tumor characteristics, such as the histology or anatomic location of the tumor. However, as we move into the era of genomic evaluation of tumor specimens, whereby tumors can be characterized on the basis of thousands of markers, there is a need for new, more comprehensive strategies for evaluating etiologic heterogeneity that are computationally and interpretably feasible. Etiologic heterogeneity is increasingly being recognized by epidemiologists as an important avenue of investigation, and it is likely that there will be many studies over the next few years that seek to define etiologically distinct tumor subtypes using genomic data. Thus, there is a strong need for an accepted, comprehensive framework for evaluating this issue.

We acknowledge that the future of this line of research is likely to involve classification of tumors into etiologically distinct subtypes on the basis of genome-wide arrays that characterize broadly the somatic features of the tumors. The examples used in this article involved only four expression markers, but future studies may involve thousands of such markers. These could include somatic mutational profiles of the tumors rather than expression arrays. In either case, we will require large-scale hierarchical clustering to identify the subtypes. In this article, we outlined in general terms how this might be accomplished. The pivotal feature of our analysis is the interactive use of an unsupervised strategy for obtaining candidate sets of subtypes using the k-means algorithm and then selecting the optimal set of subtypes by maximizing D over this set of candidates. However, this strategy is likely to be robust only if the distance measure used in the k-means approach is positively associated with the measure of etiologic heterogeneity we seek to optimize. A strong positive correlation will occur if, in general, clusters (subtypes) that are genuinely etiologically distinct are also genomically distinct with respect to the distance measure that we employ. We can only address this speculation empirically by conducting real investigations with much more complete genomic information on the tumors than we have at our disposal, and investigating whether or not the plots of D versus G exhibit the strong positive correlation that we expect to observe.

How does our strategy differ from the conventional modus operandi of epidemiologists conducting studies of etiologic heterogeneity? Typically, epidemiologists will identify candidate tumor classifications, such as ER+ versus ER−, and examine individual risk factors to look for differences in the relative risks. If there is more than one tumor marker, this approach is applied to selected combinations of the markers. Clearly, as the number of markers increases, the strategy becomes rapidly unmanageable, as the opportunities for subclassification mushroom exponentially, as does the number of comparisons of risk factors. Our proposed methodology provides an organizing framework for examining etiologic heterogeneity in this context. By defining a theoretically derived metric to characterize heterogeneity, D, we eliminate the initial search among risk factors. By creating a clustering strategy based on D, we focus the analysis on identifying the most promising classification system. We can then interpret this optimal classification by using comparisons of the relative risks of individual risk factors, as before.

We chose an optimization strategy that relies on unsupervised clustering to identify candidate sets of subtypes, with D being used as a criterion to identify the optimal set of subtypes from among these candidates. Thus, our method differs from conventional ‘supervised’ clustering methods proposed by others. For example, Bair and Tibshirani [25], in the context of identifying prognostic clusters, have proposed first ranking the markers individually on the basis of their degrees of association with the optimization criterion, in their setting case survival, and then performing unsupervised clustering on the reduced set of markers. This strategy is not pertinent to our example, which consisted of only four markers. Also, our criterion, D, is an entity that is defined by a specific set of clusters and thus cannot be correlated with individual markers. However, one could apply a strategy in which a reduced set of markers is identified based on high correlation with one or more of the risk factors prior to clustering in future settings where the tumor genotyping is more elaborate. Our strategy is proposed merely as one of many possible ways to identify an optimal subtyping system, and future research will be needed to examine the comparative merits of alternative strategies.

Our analysis of the breast cancer data using these methods supports the general conclusion that amongst the four expression markers studied, ER status carries considerably more of the heterogeneity signal than the other three markers, a result that conforms with current thinking in pathology [26]. Perhaps more interestingly our analysis of four-class systems (Table III and Figure 3) suggests that P53 expression may be more important in refining subtypes defined by ER than either PR or HER2 or both. The appropriate pathological subtyping of breast cancer is currently a fluid topic as data emerge from the explosion of information on genotyped tumor samples. In particular, the triple negative subtype overlaps with a category known as ‘basal-like’, characterized using a 50-gene expression panel [27], so named because the tumor cells express genes and proteins normally found in basal/myoepithelial cells of the normal breast [26]. Interestingly, the recent publication of results from the National Cancer Institute’s Cancer Genome Atlas project showed that luminal A and B tumors are characterized by frequent mutations in several commonly mutated cancer genes, but only infrequently TP53, while most ER− tumors have mutations in TP53 [28]. Truncating mutations are especially common in the basal-like subtype. In short, it is plausible that the influence of TP53, as measured by P53 expression, is a more important marker of heterogeneity than PR and/or HER2 expression. The results in Table III confirm the observations of other studies that women diagnosed with ER+ tumors have on average a later age at diagnosis [29], are more likely to be nulliparous [12, 30] and are less likely to have elevated premenopausal BMI [12]. Interestingly, the influence of P53 on the odds ratios in Table III seems to show distinctive nonproportional effects on each of these three factors, rather than an independent effect on any specific risk factor. The few studies that have examined risk factor differences between cases classified by P53 expression have found only modest and inconsistent evidence of any differences [31–33]. Our study, like all others in the literature, is limited by the non-exhaustive set of risk factors available and by the fact that the tumors are profiled solely on the basis of four expression markers. Modern genomic tools have the potential to define tumors on a vastly greater array of genomic features.

We note an important aspect of the central use of risk variation in our formulation of the concept of etiologic heterogeneity. Risk variation depends on the population from which the study sample was obtained. For example, a case-control study from a specialist referral center may have a preponderance of cases with clinically aggressive subtypes compared to, say, a community hospital. Likewise, risk variation depends on the distribution of risk factors in the population, so this could also vary even among population-based studies. Consequently, our framework for evaluating etiologic heterogeneity is dependent on the sampled population. Also, our formulas for the various coefficients of risk variance and covariance use estimated risk predictors for each control patient in the dataset. These estimates are necessarily correlated, in some cases highly correlated [34]. Although we use these items as data for calculating our measures of heterogeneity and incremental explained variation, we need to recognize this dependence in any methods one might use to characterize the statistical properties of final estimates of explained variation. Another critical conceptual issue is the fact that the analyses are based on a specific set of observed risk factors. Thus, a study that has data on an extensive set of known risk factors is better than one with limited risk factor data. Just like the preceding issue concerning population-based sampling, our method is defined by the set of risk factors included in the analysis. As more risk factors become known, knowledge about etiologic heterogeneity becomes more refined, and additional or more appropriate subtypes may emerge. In the limit, we would strive to define etiologically heterogeneous subtypes based on all risk factors for the disease. In related work, it has been shown that this problem can in principle be addressed using population-based studies of independent double primary malignancies in which correlations between the somatic tumor profiles of tumor pairs from the same patient become the focus of the analysis [35].

In summary, a major focus of contemporary cancer research is the overhaul of disease taxonomy from one based on general, visible characteristics of the cancer cell and the anatomic site of origin to one in which the classification is based on genome-wide molecular characterization of the tumor [1] To date, such classifications have been constructed using hierarchical clustering, with validation of clusters being based on establishing that the subtypes have distinct clinical characteristics. An important parallel challenge is to evaluate subtypes of tumors from the perspective of etiologic distinctiveness. We have laid out a framework for evaluating etiological heterogeneity of this nature, providing guidelines for how to establish etiologically distinct subtypes. We have shown that the establishment of etiological heterogeneity improves the risk predictability of the disease overall. It has also been shown to increase the statistical power to detect new risk factors [36]. However, many technical challenges remain, and we view this as a new line of research that requires further study.