Relaxor-based ferroelectric single crystals: growth, domain engineering, characterization and applications

Abstract

In the past decade, domain engineered relaxor-PT ferroelectric single crystals, including (1-x)Pb(Mg_1/3Nb_2/3)O₃-xPbTiO₃ (PMN-PT), (1-x)Pb(Zn_1/3Nb_2/3)O₃-xPbTiO₃ (PZN-PT) and (1-x-y)Pb(In_1/2Nb_1/2)O₃-yPb(Mg_1/3Nb_2/3)O₃-xPbTiO₃ (PIN-PMN-PT), with compositions near the morphotropic phase boundary (MPB) have triggered a revolution in electromechanical devices owing to their giant piezoelectric properties and ultra-high electromechanical coupling factors. Compared to traditional PbZr_1-xTi_xO₃ (PZT) ceramics, the piezoelectric coefficient d₃₃ is increased by a factor of 5 and the electromechanical coupling factor k₃₃ is increased from < 70% to > 90%. Many emerging rich physical phenomena, such as charged domain walls, multi-phase coexistence, domain pattern symmetries, etc., have posed challenging fundamental questions for scientists. The superior electromechanical properties of these domain engineered single crystals have prompted the design of a new generation electromechanical devices, including sensors, transducers, actuators and other electromechanical devices, with greatly improved performance. It took less than 7 years from the discovery of larger size PMN-PT single crystals to the commercial production of the high-end ultrasonic imaging probe “PureWave”. The speed of development is unprecedented, and the research collaboration between academia and industrial engineers on this topic is truly intriguing. It is also exciting to see that these relaxor-PT single crystals are being used to replace traditional PZT piezoceramics in many new fields outside of medical imaging. The new ternary PIN-PMN-PT single crystals, particularly the ones with Mn-doping, have laid a solid foundation for innovations in high power acoustic projectors and ultrasonic motors, hinting another revolution in underwater SONARs and miniature actuation devices. This article intends to provide a comprehensive review on the development of relaxor-PT single crystals, spanning material discovery, crystal growth techniques, domain engineering concept, and full-matrix property characterization all the way to device innovations. It outlines a truly encouraging story in materials science in the modern era. All key references are provided and 30 complete sets of material parameters for different types of relaxor-PT single crystals are listed in the Appendix. It is the intension of this review article to serve as a resource for those who are interested in basic research and practical applications of these relaxor-PT single crystals. In addition, possible mechanisms of giant piezoelectric properties in these domain-engineered relaxor-PT systems will be discussed based on contributions from polarization rotation and charged domain walls.

Introduction

1.1. Piezoelectric and ferroelectric materials

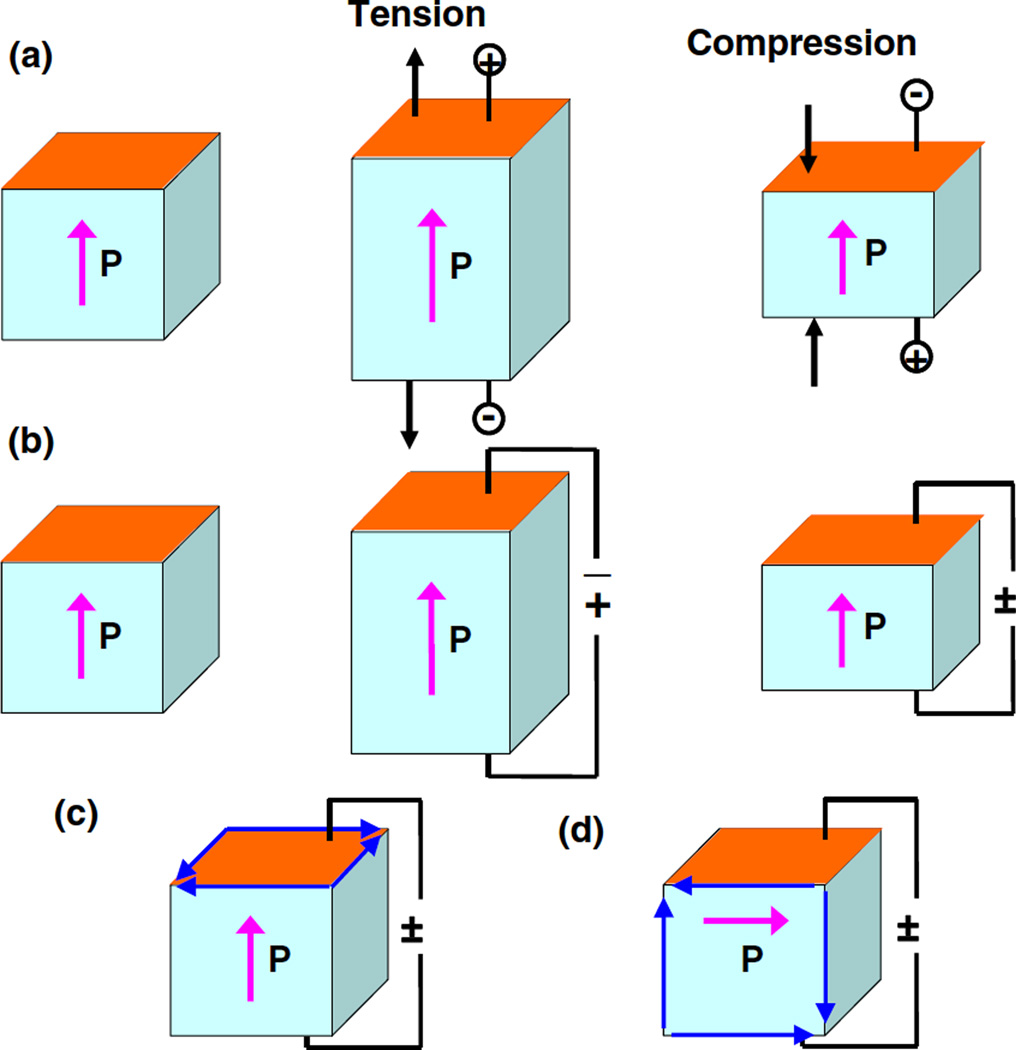
Piezoelectric phenomena were discovered by the Pierre and Jacques Curie brothers in early 1880s on α-quartz crystals [1,2]. Since then, piezoelectricity is commonly used to describe the ability of a material to develop electric displacement D that is linearly proportional to an applied mechanical stress T, i.e., the ability to convert mechanical energy into electrical energy (direct piezoelectric effect) or vice versa [3]. Electrical polarity of the material will reverse if applied mechanical stress is changed from tensile to compressive, as shown in Fig. 1(a). Based on thermodynamics, all piezoelectric materials will deform under an applied electric field, i.e., possess a converse piezoelectric effect. The sign of the strain S will reverse if the direction of the electric field E is reversed, as shown in Fig. 1(b). The shear piezoelectric effect refers to the linear coupling between shear mechanical stress (or strain) to the longitudinal electric field, as shown in Fig. 1(c) and Fig. 1(d).

Fig. 1.

Schematic of (a) longitudinal direct, (b) converse, (c) face-shear, and (d) thickness-shear piezoelectric effects.

According to the point group symmetry of lattices, crystals can be classified into seven crystal systems: triclinic, monoclinic, orthorhombic, tetragonal, rhombohedral, hexagonal and cubic. These systems can again be subdivided into 32 point groups according to their lattice symmetries. 11 of them possess a center of symmetry, and are non-piezoelectric. In the remaining 21 noncentro-symmetric crystallographic classes, piezoelectricity exists in all but cubic class 432, for which the piezoelectric charges developed along the <111> polar axes and cancel each other [3]. Of the 20 piezoelectric crystal classes, 10 (1, 2, m, mm2, 4, 4mm, 3, 3m, 6, 6mm) have a unique polar axis with a spontaneous polarization. Generally speaking, the spontaneous polarization is temperature dependent and can be detected by observing the flow of charges to and from the material surfaces with a change of temperature. This effect is known as the pyroelectric effect, and these 10 polar classes are regarded as pyroelectric classes [4]. If polarization can be reversed by the application of an electric field, the material is called ferroelectric. Table 1 lists those point groups that permit piezoelectricity among crystallographic systems.

Table 1.

Centro-symmetric and noncentro-symmetric point groups in crystals with different symmetries [3].

Crystal system	Symmetry elements	Centro-symmetric	Noncentro-symmetric
Triclinic	Center	1̱	1
Monoclinic	Center, axis, plane	2/m	2, m
Orthorhombic	Center, axis, plane	mmm	222, mm2
Tetragonal	Center, axis, plane	4/m, 4/mmm	4, 4̱, 422, 4mm, 42m
Trigonal	Center, axis, plane	3̱, 3̱m	3, 32, 3m
Hexagonal	Center, axis, plane	6/m, 6/mmm	6, 6̱, 622, 6mm, 6̱m2
Cubic	Center, axis, plane	m3, m3m	23, 4̱3m, 432

Nowadays, most electromechanical devices are made of piezoelectric materials, particularly high frequency and miniaturized ones like transducers, sensors and actuators. They are widely used in nondestructive evaluation (NDE) [5,6,7,8], medical diagnoses and therapy [9,10,11], communications [12,13,14], and underwater acoustics [15,16]. The electromechanical properties of the piezoelectric material are the determining factors for the performance of these electromechanical devices. Therefore, better piezoelectric materials are always needed for the advancement of electromechanical devices, particularly high-frequency ultrasonic imaging transducers and miniature piezoelectric actuators. Common piezoelectric materials include piezoelectric crystals (such as quartz, LiNbO₃, and LiTaO₃ [17,18]), piezoelectric ceramics (such as PZT system [19,20]), and organic piezoelectric materials (such as polyvinylidene fluoride (PVDF) [21]). In addition, piezoelectric films have recently attracted considerable attention in the development of various high frequency ultrasonic transducers, sensors and MEMS devices [22,23,24].

Quartz crystal is a typical piezoelectric material with point group symmetry 32, which has been widely used for making electrical oscillators [25,26] and high-frequency radio transmitters [27,28]. However, the piezoelectric constants and electromechanical coupling factors of quartz crystal are too low for making broadband ultrasound transducers [29]. Ferroelectric materials have large piezoelectric effects because their polarization can be easily changed by applying external electric fields [30]. Ferroelectric crystals are characterized by a spontaneous polarization in the absence of an electric field below the ferroelectric phase transition temperature T_C, and for ferroelectric materials, the spontaneous polarization must be reversible when subjected to an external electric field [31].

The ferroelectric phenomenon was first discovered in Rochelle salt in 1920 by Valasek [32], who also studied electric hysteresis and the piezoelectric response [33]. It was not until the 1940s discovery of ferroelectricity in barium titanate (BaTiO₃), which has ABO₃ perovskite structure, that interest in ferroelectricity developed beyond a pure scientific curiosity [34]. BaTiO₃ ceramic has a much stronger piezoelectric effect than quartz crystal, after being poled by an external electric field [35,36]. But BaTiO₃ is not an ideal piezoelectric material for device applications because of its relatively poor temperature stability. The Curie temperature T_c of BaTiO₃ is 120 °C, below which the crystal transforms from paraelectric cubic m3̄m to a ferroelectric tetragonal 4mm phase, then transforms to a ferroelectric orthorhombic mm2 phase with further cooling below 0 °C, and finally transforms to a ferroelectric rhombohedral 3m phase at −90 °C [37]. Lithium niobate (LiNbO₃) and lithium tantalite (LiTaO₃) single crystals have stable ferroelectric single domain structure (3m point group symmetry) after being poled and possess excellent temperature stability because of their high Curie temperatures (1210 °C for LiNbO₃ and 630 °C for LiTaO₃) [38,39]. Therefore, they have been widely used for surface acoustic wave (SAW) devices [40,41]. However, their piezoelectric constants and electromechanical coupling factors are much lower than those of BaTiO₃ materials [42,43].

An important advance in piezoelectric and ferroelectric materials is the discovery of lead zirconate titanate [Pb(Zr_1-xTi_x)O₃, PZT for short] piezoelectric ceramic in 1954 [44]. PZT is a solid solution of PbZrO₃ (PZ) and PbTiO₃ (PT), which has a large piezoelectric effect near the morphotropic phase boundary (MPB) composition (Zr/Ti=52/48 at room temperature) [45]. The MPB marks the compositional driven phase transition between the rhombohedral and tetragonal ferroelectric phases. PZT piezoelectric ceramics have been the dominant piezoelectric material for electromechanical devices for more than fifty years. Unfortunately, PZT cannot be grown into a large single crystal form, which prevents further improvement of its piezoelectric properties using the “domain engineering method”. But the discovery of PZT ceramics with excellent piezoelectric properties near the MPB composition stimulated further searches for other ferroelectrics with better piezoelectric properties through chemical doping, such as ternary piezoelectric ceramics and other modified systems [19,20].

In 1997, ultrahigh electric-field-induced strain and superior electromechanical coupling properties were reported in relaxor-based ferroelectric single crystal systems: (1-x)Pb(Mg_1/3Nb_2/3)O₃-xPbTiO₃ (PMN-PT) and (1-x)Pb(Zn_1/3Nb_2/3)O₃-xPbTiO₃ (PZN-PT) [46]. The large piezoelectric constant (d₃₃ > 2500 pC/N) of [001]_c poled rhombohedral single crystals is 5 times that of the best modified PZT ceramics (d₃₃~500 pC/N), where the subscript “c” indicates that the crystallographic orientation refers to the cubic crystal structure. The electromechanical coupling factor k₃₃ is more than 90%, and the dielectric loss is less than 1%. For the first time in history, the field induced strain has reached the level of 1.7%, spurring expectations that these relaxor-PT single crystals would spawn new generations of high performance electromechanical devices, including transducers, sensors, and actuators [47]. For comparison, the piezoelectric constants and electromechanical coupling factors of some typical piezoelectric and ferroelectric materials are summarized in Table 2.

Table 2.

Comparison of piezoelectric constants and electromechanical coupling factors of typical piezoelectric and ferroelectric materials.

Materials	Point group symmetries	Piezoelectric constants	Electromechanical coupling factors
Alpha-quartz crystal [29]	32	d11=2.31 pC/N d14=0.727 pC/N	k11=10%
BaTiO3 ceramic [35]	6mm	d31=−79 pC/N d33=191 pC/N	k31=21%, k33=50%
BaTiO3 single crystal [36]	4mm	d31=−32.5 pC/N d33=90 pC/N	k31=32%, k33=55%
LiNbO3 single crystal [48]	3m	d31=−0.85 pC/N d33=6 pC/N	k31=2%, k33=17%
LiTaO3 single crystal [48]	3m	d31=−3 pC/N d33=5.7 pC/N	k31=7%, k33=14%
Pb(Zr0.52Ti0.48)O3 ceramic [45]	6mm	d31=−93.5 pC/N d33=223 pC/N	k31=31%, k33=67%
[001]c poled PMN-33%PT single crystal [49]	4mm	d31=−1330 pC/N d33=2820 pC/N	k31=59%, k33=94%
[001]c poled PZN-8%PT single crystal [50]	4mm	d31=−1455 pC/N d33=2890 pC/N	k31=60%, k33=94%

1.2. A little history about relaxor-based ferroelectric single crystals

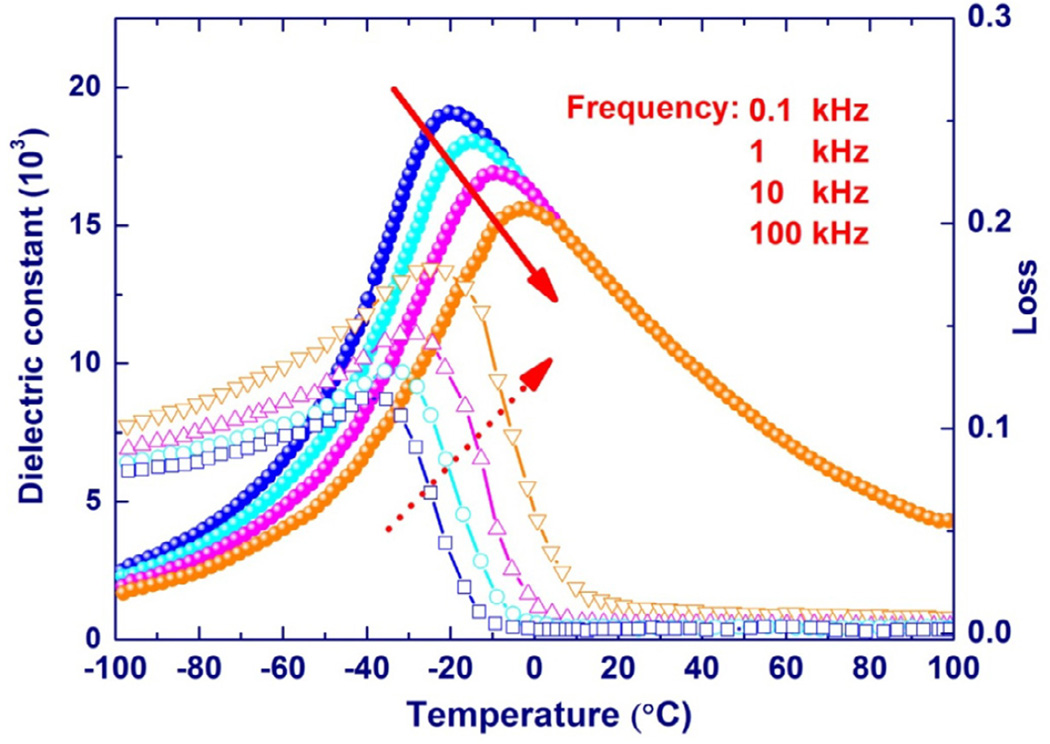
Relaxor ferroelectric phenomena were first found in the lead magnesium niobate [Pb(Mg_1/3Nb_2/3)O₃, PMN] solid solution system in 1958 [51]. As shown in Fig. 2, relaxor ferroelectrics have the features of a diffuse maximum of the dielectric constant at T_max associated with a strong frequency dispersion, which is in contrast to the sharp dielectric peak and insensitivity to frequency found in normal ferroelectrics, such as BaTiO₃ and PbTiO₃ [52]. The dielectric constant shifts to lower values and higher temperatures as frequency increases. Moreover, the maximum in the dielectric constant and dielectric loss under the same frequency do not coincide at the same temperature. It is noteworthy to mention that the dielectric maximum does not mark a phase change into a ferroelectric phase since the maximum temperature increases with frequency. Compared with normal ferroelectrics, which follow the Curie-Weiss law, the relaxation process in relaxor ferroelectrics is reasonably described by the Vogel-Fulcher relation [53,54]

$$\frac{1}{\omega }={\tau }_0\text{exp}\left[\frac{U_{\mathrm{a}}}{k_{\mathrm{B}}(T_{\text{max}}-T_{\mathrm{f}})}\right]$$ (1)

where τ₀, U_a, and T_f are parameters, and k_B is the Boltzmann constant. For a relaxor PMN system, τ₀ is 10⁻¹¹ s, the freezing temperature T_f is about 225 K, and the activation energy U_a/k_B is about 750 K.

Fig. 2.

Dependence of dielectric properties on temperature and frequency for the relaxor ferroelectric PMN solid solution [69].

As for the origin of relaxor behavior, some researchers believe it is due to the formation of polar micro-regions (PMRs) or nano-regions (PNRs) [55,56,57,58]. The dynamics of PMRs or PNRs causes a diffuse and frequency-dependent broad dielectric maximum, a broad distribution of relaxation times, and aging behaviors at low temperatures. Other researchers attribute the diffuse phase transition (DFT) to micro-compositional heterogeneity, which leads to different ferroelectric transition temperatures and broadens the dielectric peak [59,60]. Various physical models have been proposed to explain the origin of the relaxor behavior in relaxor ferroelectrics, such as the dipolar glass model [61,62,63,64], the random-field (RF) model [65,66], and the spherical random-bond-random-field (SRBRF) model [67,68].

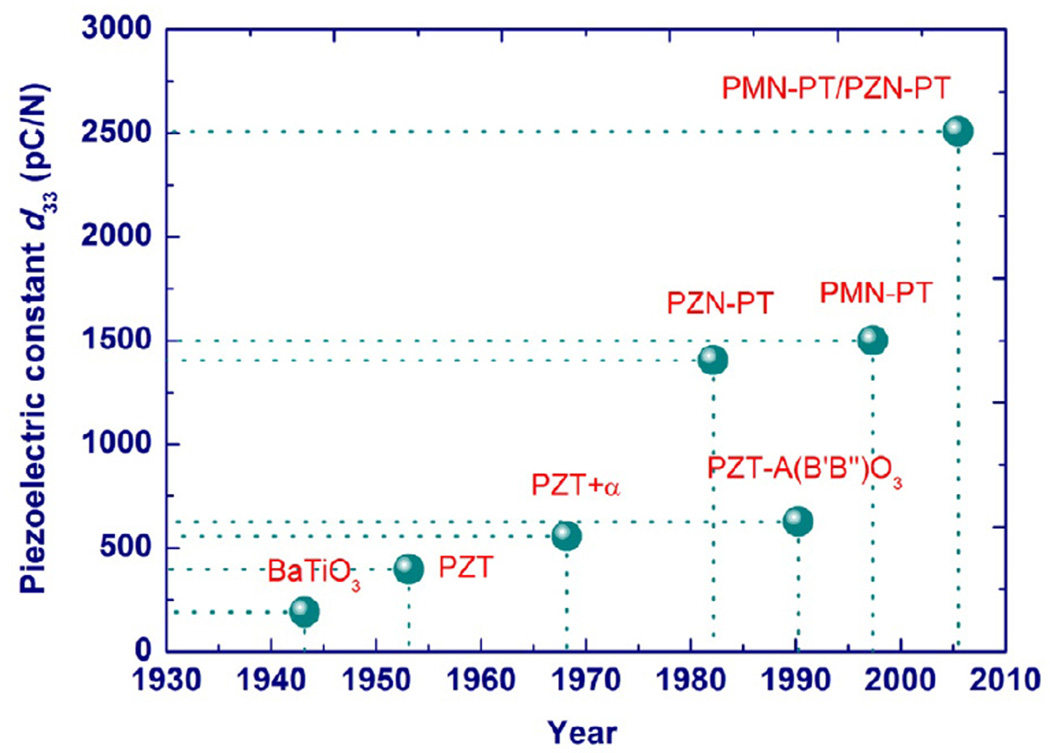
Relaxor-based ferroelectric materials are generally solid solutions of a relaxor with PbTiO₃, which are also represented by “relaxor-PT” for short. The basic crystal structure is the perovskite structure (ABO₃) and the molecular formula is given by Pb(B₁B₂)O₃ (B₁=Mg²⁺, Zn²⁺, Ni²⁺, Sc³⁺, Co³⁺, Fe³⁺, Yb³⁺, In³⁺, …; B₂=Nb⁵⁺, Ta⁵⁺, W⁶⁺, …) [70]. The useful properties of relaxor-based ferroelectric single crystals were first reported in the (1-x)Pb(Zn_1/3Nb_2/3)O₃-xPbTiO₃ (PZN-PT) solid-solution system in 1969 [71]. Pb(Zn_1/3Nb_2/3)O₃ (PZN) is a typical relaxor ferroelectric material, which has rhombohedral symmetry 3m at room temperature and exhibits a diffuse phase transition around 140 °C. The Zn²⁺ and Nb⁵⁺ cations are randomly arranged at the B-sites [72,73]. On the other hand, PbTiO₃ (PT) is a normal ferroelectric material, which shows typical long-range ordering and has tetragonal symmetry 4mm below 490 °C. The solid solution PZN-PT single crystals of ferroelectric compounds PT and relaxor ferroelectric compounds PZN exhibit more advantages due to their special compositions and symmetry structures. It is believed that the PT compound changes the short-range ordering of PZN, and reduces its phase transition diffuseness and dielectric relaxation. In other words, upon the addition of ferroelectric PT to relaxor PZN, there is a transition from short-range ordered relaxor behavior at low PT content, to long-range ordered normal ferroelectric behavior at higher PT content. Besides the characteristic frequency dispersion of their dielectric constants, millimeter size PZN-PT single crystals show remarkable piezoelectric and electromechanical properties as reported in 1982 [74]. In 1997, giant piezoelectric constants and super high electromechanical coupling properties were reported in centimeter size PMN-PT and PZN-PT single crystals [46]. Nowadays, crystals can be grown to tens of centimeters. Through domain engineering, the [001]_c poled PMN-PT or PZN-PT can generate an extremely large electric-field-induced strain (>1%) and a superior high electromechanical coupling factor k₃₃ (>90%). Due to their extremely large piezoelectric properties, extensive studies had been carried out on these relaxor-based ferroelectric single crystal systems in the past decade, including fundamental research on the mechanism of the giant piezoelectric effect (Sec. 2), crystal growth techniques (Sec. 3), characterization of material properties (Sec. 4–7), and innovative electromechanical device applications (Sec. 8) using these crystals. Fig. 3 depicts the history of the development of piezoelectric materials in terms of piezoelectric coefficient d₃₃ [75].

Fig. 3.

Historical development of perovskite-based piezoelectric materials in terms of piezoelectric coefficient d₃₃ [75].

1.3. Domain engineering and domain pattern symmetries

Ferroelectric materials generally consist of small uniform regions with aligned polarization, called “domains”. Within each domain, dipoles in each unit cell have the same orientation. Different domains in a crystal are separated by interfaces, called “domain walls”. For example, the walls separating domains with oppositely oriented polarization are called “180° walls” and those separate regions with mutually perpendicular polarizations are called “90° walls” [76]. Domain patterns, which occur when the crystal goes through the paraelectric-ferroelectric phase transition, are generated due to the degeneracy of those domain states and are regulated by electric and mechanical boundary conditions. The polarization direction of each domain is determined by the crystal symmetry while the types of domain patterns generated at the phase transition depend on the symmetry relation between the parent and product phases as well as boundary conditions. The process of applying an electric field larger than the coercive field to switch domains and align dipoles towards the applied field direction is termed “poling”.

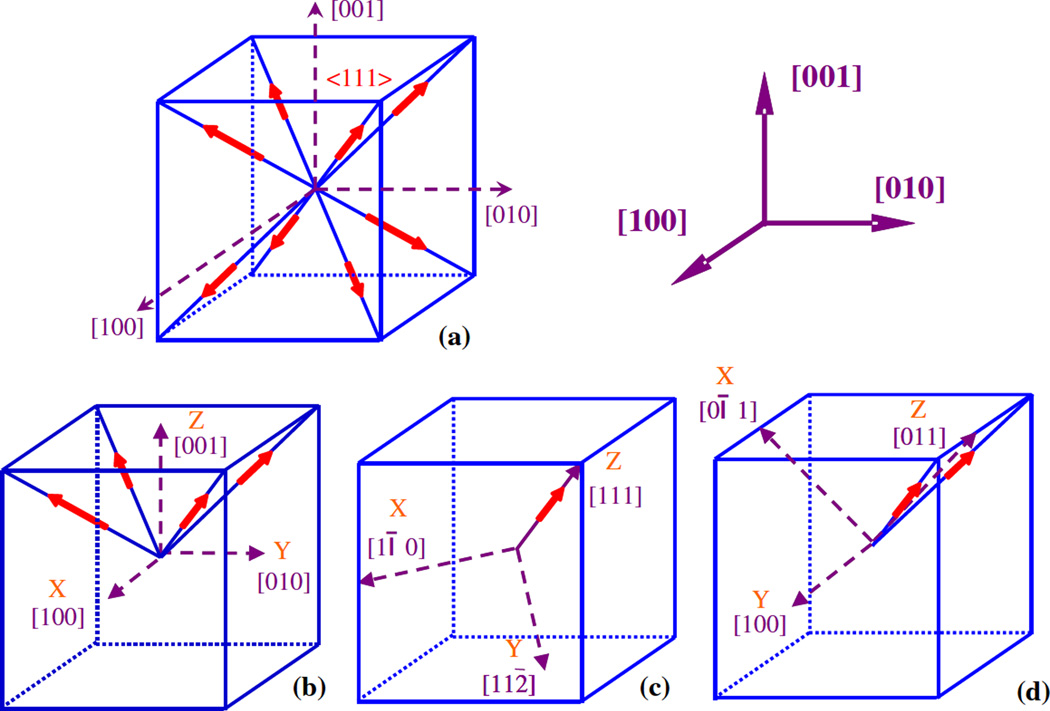
For relaxor-based ferroelectric PMN-PT and PZN-PT single crystals, domain pattern symmetries are more complicated than in normal ferroelectrics. Their domain structures are sensitive to composition, poling condition, and temperature [77,78,79]. The effective macroscopic symmetry is a key issue for the characterization of domain engineered single crystals. Generally, for rhombohedral phase crystals, poling along [001]_c direction induces 4mm macroscopic domain pattern symmetry, poling along [011]_c direction induces mm2 macroscopic domain pattern symmetry, and poling along [111]_c direction induces 3m symmetry of the single domain state. It is well known now that the superior longitudinal piezoelectric constants and excellent electromechanical coupling factors appear only in the [001]_c poled rhombohedral PMN-PT and PZN-PT single crystals. The single crystals in the rhombohedral phase have eight possible spontaneous polarization directions along <111>_c, as shown in Fig. 4(a). When an electric field is applied along [111]_c, only one spontaneous polarization orientation remains to form a single domain state, as shown in Fig. 4(c). The [111]_c poled rhombohedral crystal with single domain structure shows excellent shear piezoelectric coefficient d₁₅ and high electromechanical coupling factor k₁₅, but the d₃₃ becomes very small [80,81]. In addition, experiments showed that the single domain state is not stable due to poling induced strain [82]. When an electric field is applied along [001]_c of the pseudo-cubic coordinates, a multidomain configuration is produced [83], which consists of four degenerate domain states. These domain states can form either charged or neutral domain walls [84,85], as shown in Fig. 4(b). Note that this multidomain state is induced by an electric field larger than the coercive field, but not excessively large. If the electric field is too large, a [001]_c single domain state can be induced by a field induced structural transformation from rhombohedral 3m phase to tetragonal 4mm phase as discussed in Sec. 2.3. Statistically, the [001]_c poled multidomain single crystal has a tetragonal 4mm macroscopic symmetry, although the microscopic crystal symmetry of the system is rhombohedral 3m [86]. The [001]_c poled rhombohedral multidomain single crystals show large longitudinal piezoelectric and electromechanical properties, i.e., giant d₃₃ and high k₃₃. Besides the [001]_c direction, [011]_c is another popular poling direction in domain engineering process. The [011]_c poled domain engineered single crystal shows a macroscopic mm2 symmetry with a multidomain configuration consisting of two degenerate domain states, as shown in Fig. 4(d). The [011]_c poled rhombohedral multidomain single crystals show large transverse and shear piezoelectric and electromechanical properties, i.e., giant d₃₂, k₃₂, d₁₅, and k₁₅. Simlarization directions before poling for a tetragonal phase single crystal. Only one polarization orientation remains after being poled along [001]_c, three orientations remain after being poled along [111]_c, and two orientations remain after being poled along [011]_c.

Fig. 4.

(a) Eight possible spontaneous polarization directions before poling for a rhombohedral single crystal. (b) Four orientations remain after being poled along [001]_c. (b) one orientation remains after being poled along [111]_c. (b) Two orientations remain after being poled along [011]_c.

Domain engineering is an important technique for obtaining enhanced piezoelectric properties in ferroelectric materials. In 2004, the dependence of the piezoelectric properties of domain engineered BaTiO₃ single crystals as a function of domain size was studied [87]. It was revealed that piezoelectricity is enhanced for domain engineered crystals with smaller domain sizes or higher domain wall densities. Thus, domain wall density strongly influences the piezoelectric properties of the final product. There have been some theoretical studies on the electromechanical properties of single domain ferroelectric BaTiO₃, such as first-principle’s calculations [88] and continuum Landau theory to study the electromechanical properties as a function of temperature and electric field direction [89,90]. Recently, the piezoelectric properties of domain-engineered ferroelectrics were also studied using a two-dimensional (2D) time-dependent Ginzburg Landau (TDGL) [91], which provides an explanation to the origin of domain size dependence. Lattice distortions inside domain walls make the system less stable, thus increasing the responsiveness of the multidomain system to external stimuli, such as an electric field. This results in an enhancement of the piezoelectric properties. But it comes at a cost; the critical field for field induced phase transition is reduced so that the systems cannot sustain a large field drive. The 2-D TDGL model was also used to investigate the dependence of piezoelectricity on the size of 90° domains on BaTiO₃, to understand piezoelectric property enhancement at small domain sizes [92,93]. The piezoelectric coefficients can be enhanced by a factor of 3 when the domain size is reduced from 22 microns to 6.5 microns [94,95]. Hence, piezoelectric properties can be regulated by controlling domain configurations.

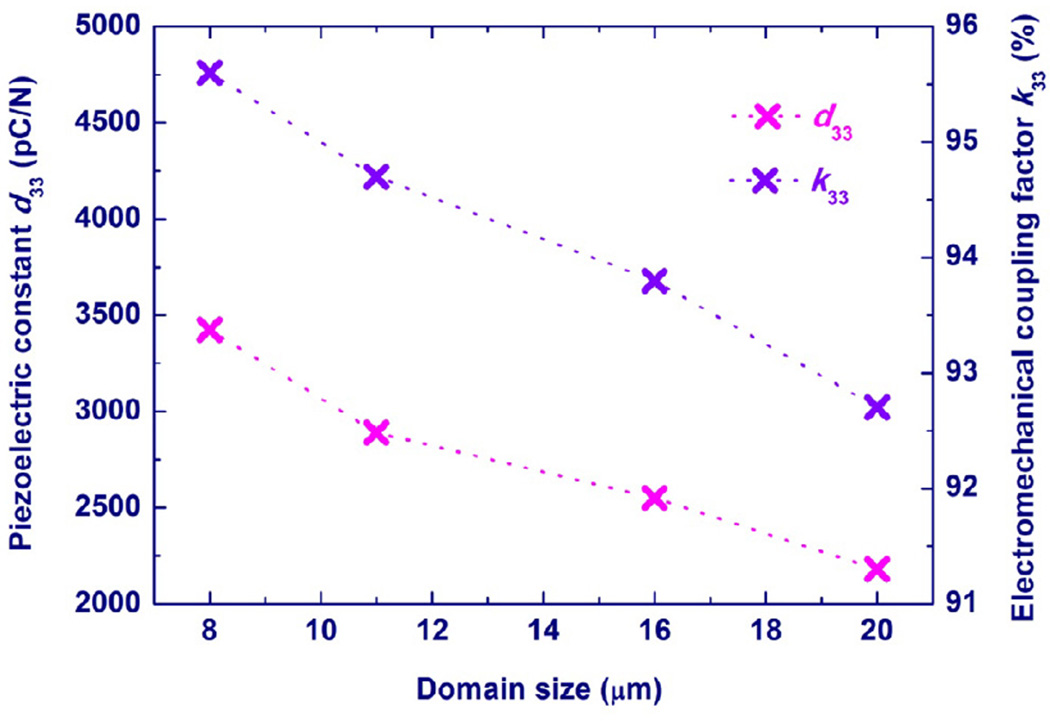
More recently, different poling procedures were performed on a k₃₃ resonator of [001]_c-oriented PZN-6%PT single crystal [96]. The experiments showed that piezoelectric properties can be greatly enhanced by reducing the domain size. Upon decreasing the domain size from 20 µm to 8 µm, d₃₃ increases rapidly from 2180 to 3425 pC/N and k₃₃ increases from 92.7% to 95.6% for [001]_c poled PZN-6%PT single crystal, which indicates that domain walls contribute significantly to the piezoelectric effect. The domain patterns formed in [001]_c poled PZN-6%PT single crystal and the measured properties are shown in Fig. 5 and Fig. 6, respectively.

Fig. 5.

Domain structures observed on (100) surface of [001]_c-poled PZN-6%PT single crystal poled by different procedures. The domain sizes of (a), (b), (c), and (d) are 20, 16, 11, and 8 µm, respectively [96].

Fig. 6.

Measured piezoelectric properties in different domain sizes [001]_c-poled PZN-6%PT single crystals [96].

2. Mechanisms of enhanced piezoelectric response

2.1. Morphotropic phase boundary

The morphotropic phase boundary (MPB) is a compositional boundary of two different structural phases. Near the MPB composition, the structure is relatively less stable, which will produce larger responses under external stimuli, including temperature, electric field and stress. Consequently, the piezoelectric coefficients and dielectric constants become very large. This advantage of MPB had been fully explored in the PbZr_1-xTi_xO₃ (PZT) solid-solution piezoelectric ceramics. PZT has a paraelectric cubic phase above the Curie temperature and its ferroelectric phase is divided into two regions with different crystal symmetries. For Zr-rich compositions, the low temperature ferroelectric phase is rhombohedral, while for the Ti-rich compositions, the low temperature ferroelectric phase is tetragonal. The best piezoelectric and electromechanical coupling properties occur near the MPB composition at x≈0.48 [45]. The term “morphotropic” literally means “the boundary between two forms”. PZT piezoelectric ceramics with MPB compositions have very high dielectric and piezoelectric properties as the result of enhanced polarizability arising from the coexistence of two energetically equivalent phases, i.e., the rhombohedral and tetragonal phases [97].

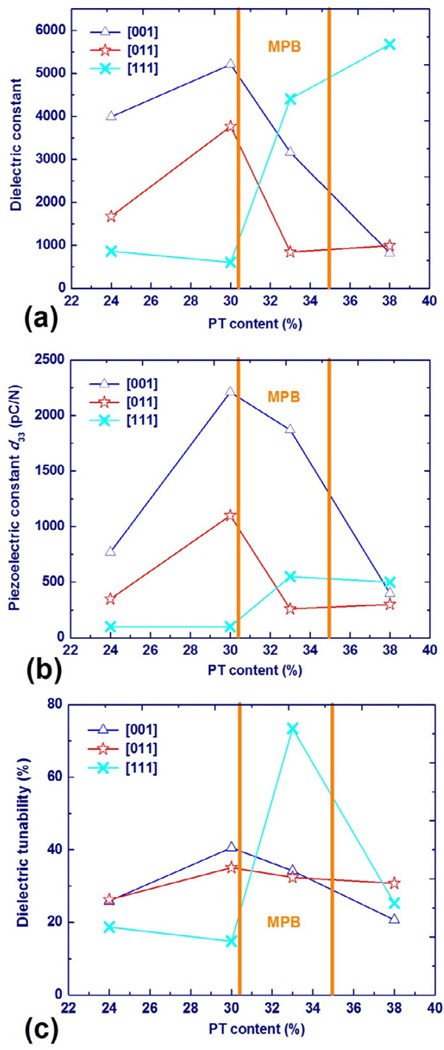
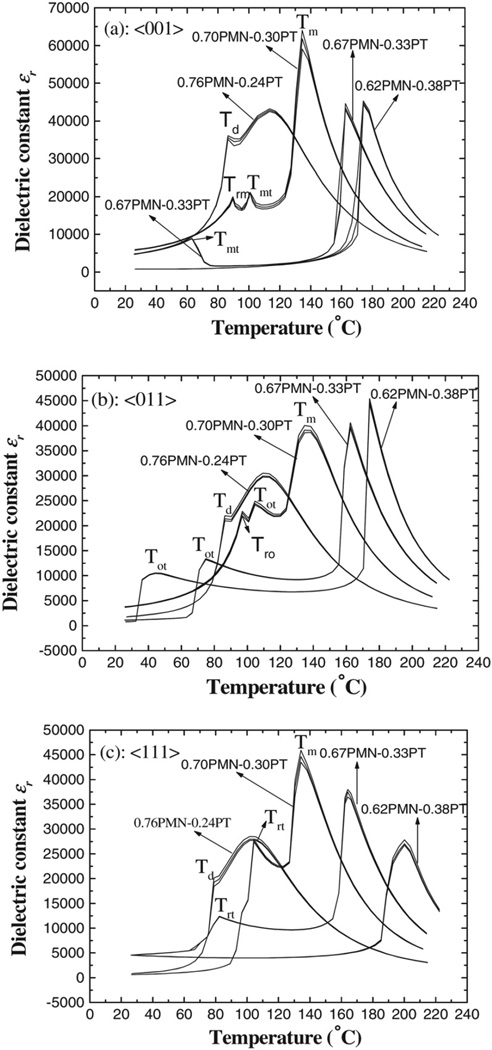
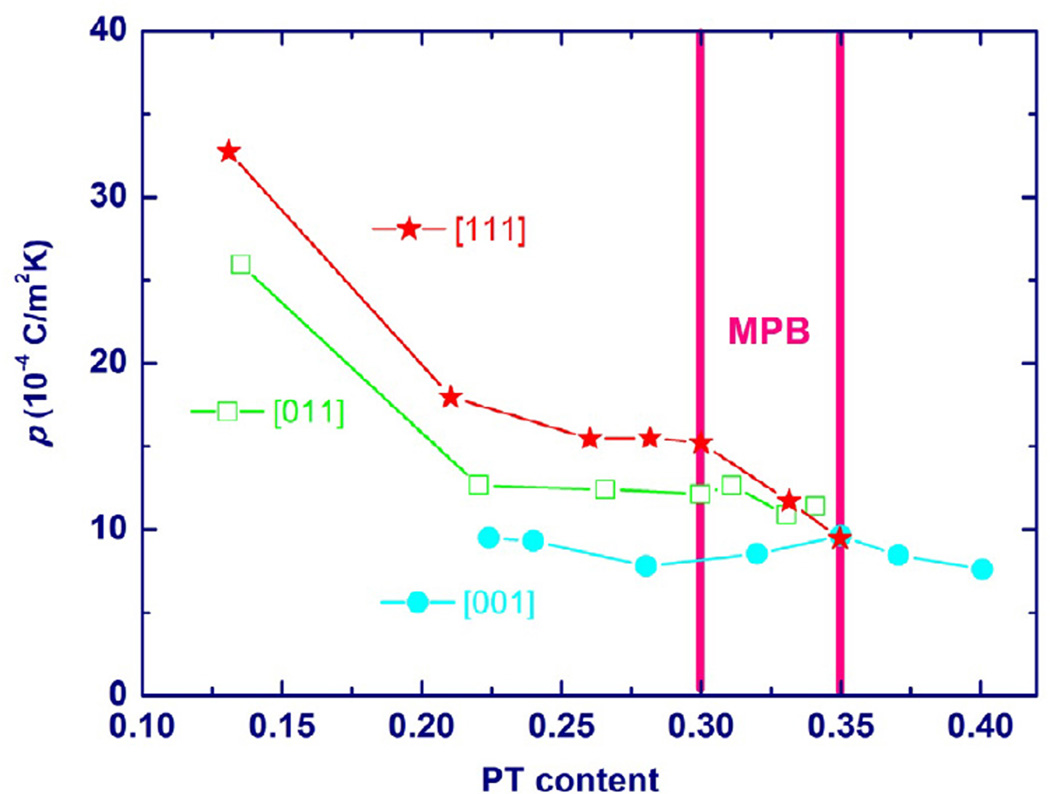
For PZN-xPT single crystals, the largest piezoelectric constants and electromechanical coupling factors were observed in the MPB composition near x=0.09 [98]. There are other reports of the MPB of PZN-xPT single crystal systems between rhombohedral and tetragonal phases the range of x=0.08–0.105 [99]. In 1989, the dielectric and pyroelectric properties of the PMN-xPT solid solution across the MPB compositions, x=0.275–0.4, were studied as a function of temperature. The MPB was found in the vicinity of x≈0.3 with a small curvature with increasing temperature [100]. The temperature vs. dielectric constant behaviors of the [001]_c and [011]_c oriented PMN-PT single crystals in the rhombohedral phase with compositions near the MPB showed that dielectric and piezoelectric properties strongly depend on the PbTiO₃ content in a narrow composition region of x=0.30–0.35 [101]. The largest piezoelectric properties appear at the MPB composition for PMN-PT single crystals. More recently, x-ray diffraction results indicated that the “flat” MPB of PIN-PMN-PT polycrystalline ceramics was located around PT=0.33–0.36, which was also confirmed by the measurements on dielectric, piezoelectric and electromechanical properties [102]. The MPBs of several relaxor-based ferroelectric (1-x)Pb(B₁B₂)O₃-xPT solid-solution systems are summarized in Table 3 together with their Curie temperature T_C. In PZT ceramics, the MPB is relatively insensitive to temperature. But MPB compositions are strongly temperature dependent in relaxor-PT single crystals, i.e., the MPB boundary is severely curved.

Table 3.

Morphotropic phase boundaries of relaoxr-based ferroelectric (1-x)Pb(B₁B₂)O₃-xPT solid-solution systems [103].

(1-x)Pb(B1B2)O3-xPT system	PT content on MPB	TC
(1-x)PbZrO3-xPbTiO3 (PZT) [45]	x≈0.48	~360 °C
(1-x)Pb(Zn1/3Nb2/3)O3-xPbTiO3 (PZN-PT) [98]	x≈0.09	~180 °C
(1-x)Pb(Mg1/3Nb2/3)O3-xPbTiO3 (PMN-PT) [104]	x≈0.33	~150 °C
(1-x)Pb(Mg1/3Ta2/3)O3-xPbTiO3 (PMT-PT) [105]	x≈0.38	~80 °C
(1-x)Pb(Ni1/3Nb2/3)O3-xPbTiO3 (PNN-PT) [106]	x≈0.40	~170 °C
(1-x)Pb(Co1/3Nb2/3)O3-xPbTiO3 (PCN-PT) [107]	x≈0.38	~250 °C
(1-x)Pb(Sc1/2Ta1/2)O3-xPbTiO3 (PST-PT) [108]	x≈0.45	~205 °C
(1-x)Pb(Sc1/2Nb1/2)O3-xPbTiO3 (PSN-PT) [109,110]	x≈0.43	~250 °C
(1-x)Pb(Fe1/2Nb1/2)O3-xPbTiO3 (PFN-PT) [103]	x≈0.07	~140 °C
(1-x)Pb(Yb1/2Nb1/2)O3-xPbTiO3 (PYN-PT) [111]	x≈0.50	~360 °C
(1-x)Pb(In1/2Nb1/2)O3-xPbTiO3 (PIN-PT) [112]	x≈0.37	~320 °C
(1-x)Pb(Mg1/2W1/2)O3-xPbTiO3 (PMW-PT) [113]	x≈0.55	~60 °C
(1-x)Pb(Co1/2W1/2)O3-xPbTiO3 (PCW-PT) [114]	x≈0.45	~310 °C

2.2. Phase diagrams of PMN-PT and PZN-PT single crystals

PMN-xPT or PZN-xPT single crystals are typical solid solutions of relaxor ferroelectric PMN or PZN with normal ferroelectric PT. Their phase structures at room temperature strongly depend on the composition x. The traditional phase diagrams of PZT, PZN-PT, and PMN-PT solid solutions are shown in Fig. 7.

Fig. 7.

The traditional phase diagrams of (a) PZT ceramics, (b) PZN-PT single crystals, and (c) PMN-PT single crystals [115].

However, the MPB composition x is given in a range of 0.30<x<0.35 in the literature for PMN-xPT single crystals (PZN-xPT single crystals are similar with 0.08<x<0.105), which means that the MPB is not a single line but a composition range [116,117]. The exceptional piezoelectric and electromechanical coupling behavior of these single crystals were believed to be the result of ferroelectric rhombohedral and tetragonal phases coexisting [118], or a field-induced phase transition between these two phases [119]. However, further investigations showed that there are monoclinic and/or orthorhombic phases in the MPB region as well, which appear as an intermediate phase structure with and without biasing the electric field, depending on the composition and temperature [120,121].

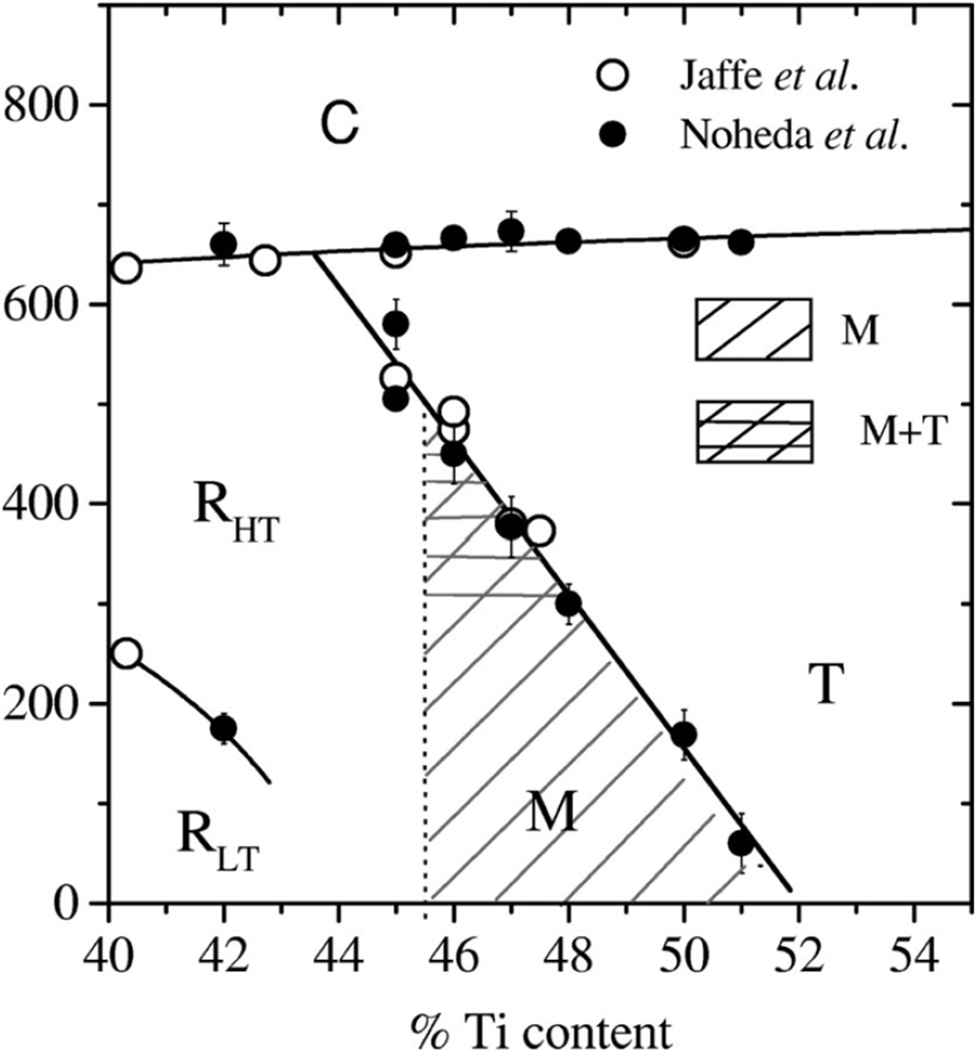
The monoclinic phase was first discovered in the PbZr_0.52Ti_0.48O₃ ceramic below ~250 K using high-resolution synchrotron x-ray powder diffraction [122]. It is known that the space group of the tetragonal phase is P4mm with the polar axis along <001>_c. In the rhombohedral phase, the space group is R3m and the polar axis is along the body diagonal of the pseudocubic structure <111>_c. The space group of the monoclinic phase is Cm, which is a subgroup of P4mm and R3m. The polar axis lies in the monoclinic ac plane close to the pseudocubic <111>_c direction [122]. The phase diagram of a PZT system around a nearly vertical MPB was modified as shown in Fig. 8 [123]. The monoclinic region is shaded with diagonal lines. Horizontal lines are superimposed in the region of tetragonal-monoclinic phase coexistence. For x=0.45, the solid symbols represent the limits of the tetragonal-rhombohedral coexistence region. It was proposed that the ultrahigh electromechanical response in PZT ceramics with MPB compositions is directly related to the existence of the low symmetry monoclinic phases in the range of x=0.46–0.51 [124,125].

Fig. 8.

The modified phase diagram of PZT ceramics around the MPB [123]. The solid symbols are the results reported by Noheda et al. [126,127]. Data from Jaffe et al. [45] and Amin et al. [128] are represented by open circles.

The existence of this monoclinic ferroelectric phase was not considered before because the sixth-order free energy by Devonshire could successfully describe ferroelectric perovskites [129], in particular for the PZT ceramics without the monoclinic phase [130,131]. PZT could have ferroelectric monoclinic phases first predicted in 1970 with polarization components P_x=P_y≠P_z [132]. The monoclinic phase in PZT ceramics had been observed by Raman spectroscopy [133,134], x-ray diffraction, dielectric measurements [135], and neutron diffraction [136]. In theory, calculations showed that an eighth-order Devonshire-type expansion can generate three possible M phases (M_A, M_B, and M_C) between the R and T phases and orthorhombic phases in perovskites [137]. In fact, even triclinic phases can be generated by a 12^th-order expansion of the free energy.

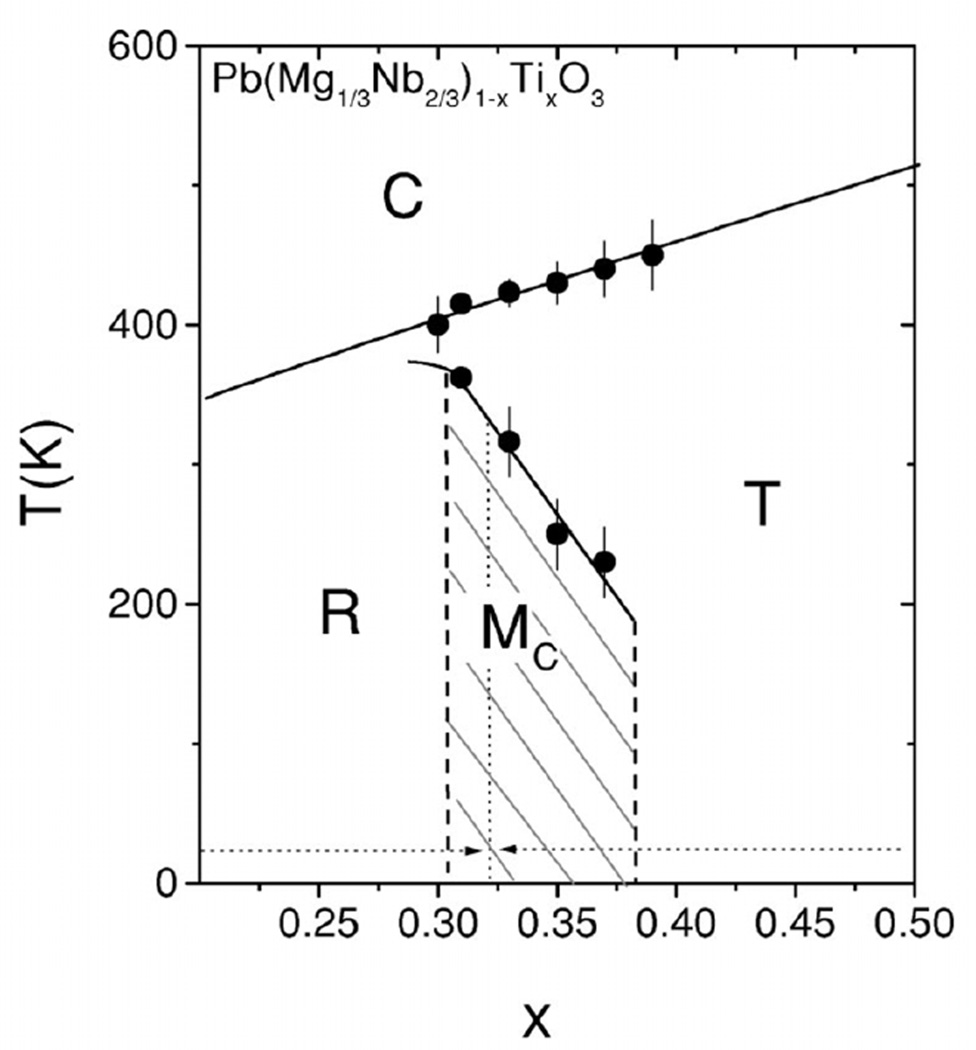
A monoclinic phase with various angles of polarization rotation was observed in the PMN-0.33PT single crystal at room temperature together with the rhombohedral and tetragonal phases [138]. The phase structures were confirmed through the observation of ferroelectric domain configurations using polarized optical microscopy. The polarization rotation can be easily induced by external electric fields, showing that the origin of the ultrahigh piezoelectric performance of PMN-0.33PT single crystal is from the polarization rotation induced structural deformation. In 2002, a new phase diagram of PMN-PT single crystal was modified, as shown in Fig. 9 [139]. The MPB separating the rhombohedral from tetragonal phases is in a range of x=0.30–0.38, in which the monoclinic phase exists. The existence of the monoclinic phase is also regarded as the main cause of the high piezoelectric properties of PMN-PT single crystals because the polarization vector of this phase can undergo continuous rotation in response to the poling field [140,141,142,143]. In addition, the orthorhombic phase was also observed in the PMN-PT single crystals poled along the [001]_c in a narrow composition region. It was also found that monoclinic/orthorhombic phases always present in ternary PIN-PMN-PT single crystals with MPB compositions based on the elastic hysteretic measurements [144,145].

Fig. 9.

The modified phase diagram of PMN-PT single crystals around the MPB [139]. The solid line indicating the transition to the cubic phase is the average of the two temperatures reported by Noblanc et al. [146]. The symbols separating the M_C and T phases represent the temperatures at which the M_C-T phase transition begins to take place.

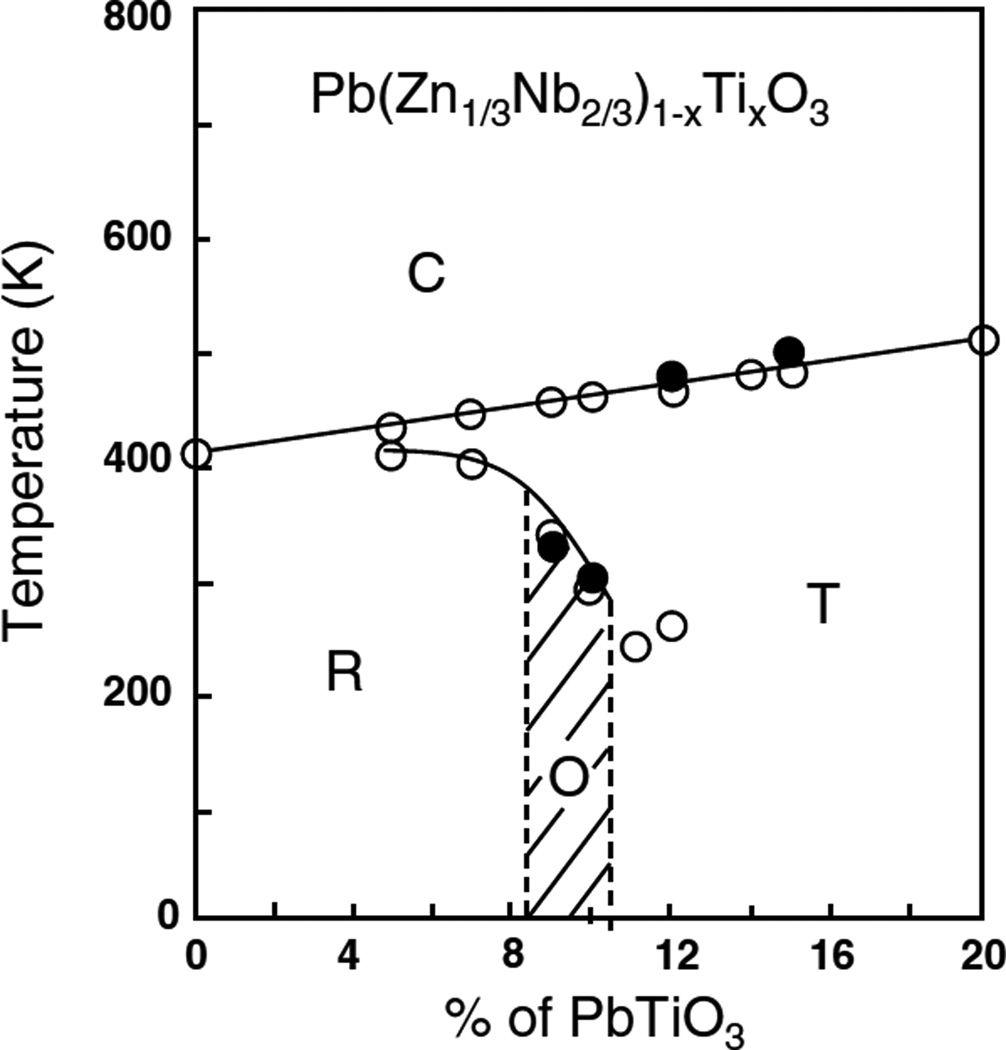
PZN-0.08PT single crystal shows a rhombohedral symmetry before poling, but an orthorhombic phase can be irreversibly induced by an external electric field [147,148]. This orthorhombic phase is the limiting case of a monoclinic M_C-type phase when the lattice parameters a=c. For PZN-0.09PT, a true M_C phase was observed in unpoled and poled single crystals using optical second harmonic generation microscopy [149]. The orthorhombic phase was observed for compositions of x=0.08–0.10, but for x > 0.11 only tetragonal phase was found down to 20 K [150]. Thus, the orthorhombic phase exists only in a narrow composition range with near-vertical phase boundaries, i.e., a narrow “chimney like” shape for the intermediate orthorhombic region. The modified phase diagram of a PZN-xPT single crystal is shown in Fig. 10. The orthorhombic phase in PZN-PT single crystals had also been observed by optical methods [151,152]. Phenomenological models showed that an intermediate metastable orthorhombic state (F_O) can present in a narrow composition range between the ferroelectric rhombohedral (F_R) and tetragonal (F_T) phases, but is relatively unstable compared to the F_R-F_T states for perovskite A(B1B2)O3 ferroelectrics. There are some conditions for stabilizing the nearly degenerate F_R, F_T and F_O states in the Pb(B₁B₂)O₃-PbTiO₃ single crystals in terms of the expansion coefficients of the energy function [153].

Fig. 10.

The modified phase diagram of a PZN-PT single crystal around the MPB [150]. The new orthorhombic phase is represented by the shaded area. The open circles and solid lines represent the phase diagram reported by Kuwata et al. [98]. Solid circles are the results reported by Noheda et al. [150,154].

Although we can use a phase diagram to show the phase structure of these relaxor-based ferroelectric solid solutions, their true symmetry structures are more complicated than the descriptions in the phase diagram. It is worth pointing out that the phase diagrams presented by different researchers are not fully consistent, especially near the MPB. In addition, many complicated phenomena cannot be displayed in the phase diagram. Thus, the phase diagram of relaxor-based ferroelectric system describes only a macrostructure in terms of either symmetry structures or material compositions, and shows the equilibrium conditions between two thermodynamically distinct phases.

2.3. Polarization rotation and orientation effect

2.3.1 Polarization rotation mechanism

As mentioned above, the [001]_c poled rhombohedral PMN-PT and PZN-PT single crystals with spontaneous polarization along the <111>_c direction show ultrahigh longitudinal piezoelectric constants d₃₃ and electromechanical coupling factors k₃₃. An acceptable explanation for this giant piezoelectric response is the polarization rotation mechanism induced by external electric fields along certain paths that generate large strains through polarization-strain coupling, which was found previously to occur in BaTiO₃ single crystals [155]. In addition, the ultrahigh strain was also attributed to an electric-field-induced rhombohedral-to-tetragonal phase transformation [156,157]. This phase transformation can in fact be explained as a result of the polarization rotation. However, it becomes more complicated since the monoclinic/orthorhombic phases have been found in both PMN-PT and PZN-PT single crystals with MPB compositions. It was believed that the polarization rotation through monoclinic distortions plays an important role in high piezoelectric performance in these systems. In the monoclinic phases, the polarization direction can easily adjust to the applied electric field, thus naturally giving a large piezoelectric response.

Based on first principles calculations, the polarization rotation mechanism was proposed [158] to explain the giant piezoelectric response in PZN-PT systems at an atomistic level using BaTiO₃ single crystals as a model system. This was done because the complex mesoscopic ordering in PZN-PT or PMN-PT single crystals greatly complicated the studies using the first principles method [159,160]. It is well known that the BaTiO₃ single crystal, which was found to have large piezoelectric enhancements induced by a <001>_c electric field in the rhombohedral phase at −90 °C (d₃₃=400 pC/N, k₃₃=79%) or a <111>_c electric field below 6 kV/cm in the tetragonal phase at room temperature (d₃₃=203 pC/N) [161,162], is similar to PMN-PT and PZN-PT single crystals, but is a much simpler system to analyze.

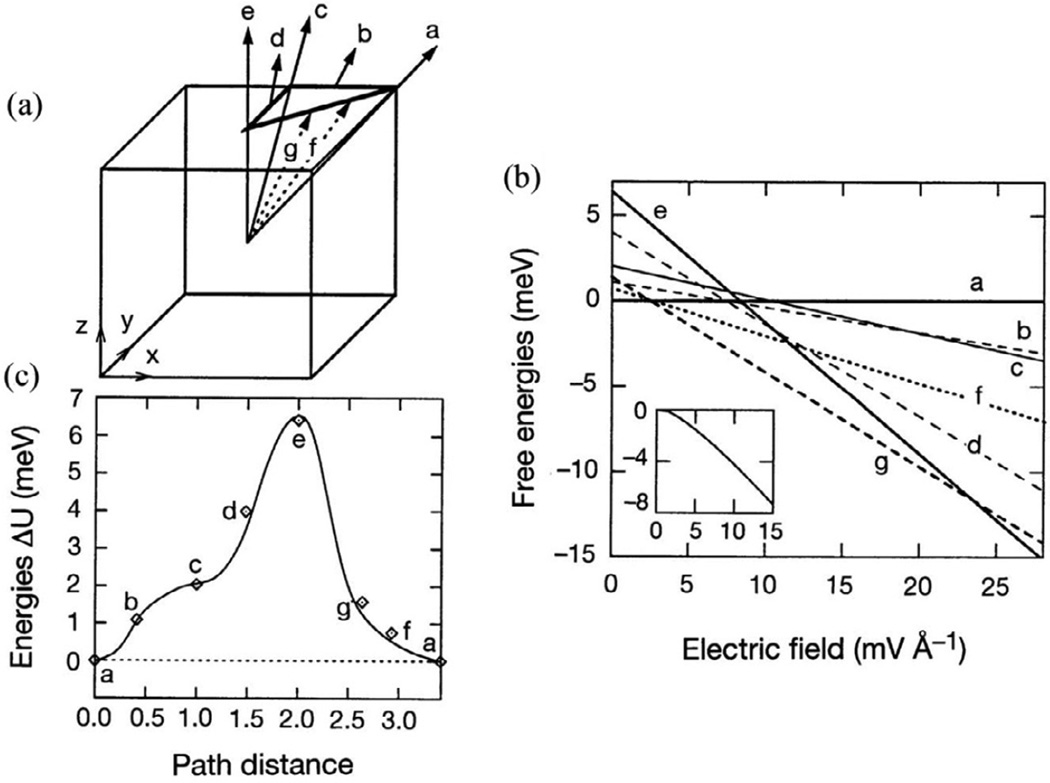
In the computations, the phase stability under electric field E was studied using free energy F=U-P·E, where U is the internal energy under zero field and P is the polarization per unit volume. The internal energies of different polarization directions were calculated by using the first-principles linearized augmented plane wave (LAPW) method with the local density-functional approximation (LDA) [163,164]. The polarization direction is controlled by constraining the direction of movement of the Ti atom, and other degrees of freedom of atomic positions, with unit cell shape optimized. The final polarization P is computed from the optimized geometric structure using Berry's phase approach [165,166]. The calculated internal energies and polarization magnitudes showed increasing phase stability in the order of tetragonal-orthorhombic-rhombohedral without a field. The calculated spontaneous polarizations for these three phases agree well with pseudopotential results [167]. The polarization directions are shown in Fig. 11(a). The free energies as a function of field strength are shown in Fig. 11(b). The minimum energy path is found to be directly from the <111>_c to <001>_c directions (that is, the path a→f→g→e). The strain increases rapidly in the low-field region, and a small electric field will induce a large strain level. It was also found that if the rotation path a→b→c→d→e is possible, the piezoelectric coefficient d₃₃ of this path will be 5 times as small as that of the path a→f→g→e in the low-field region. The internal energies for the considered polarizations are shown in Fig. 11(c), which showed a rather flat internal energy surface along the path a→f→g. Furthermore, along this path there is a large increase of the c-axis polarization P_z, thus, there is a large coupling between the polarization and the electric field. The flat internal energy surface and the large c-axis polarization variation facilitate polarization rotation, and cause the peculiarly large piezoelectric response along this path.

Fig. 11.

(a) Schematic illustration of the polarization directions, (b) free energies as a function of field strength for different polarization directions, and (c) the internal energies relative to the rhombohedral phase [158].

For PZT solid solutions near the MPB, first-principles calculations showed the existence of three ferroelectric phases at low temperatures, i.e., a tetragonal phase for larger x compositions, a rhombohedral phase for smaller x compositions, and a monoclinic phase in between. In the monoclinic phase, the polarization associated with the Zr atoms behaves differently than the polarization associated with the Ti atoms. As the composition x decreases, the former rotates more quickly towards the pseudo-cubic [111]_c direction and grows in magnitude, while the latter lags in its rotation and its magnitude shrinks. The local microscopic structure is found to deviate significantly from the average structure in the PZT phases as a result of fluctuations in directions and magnitudes of local polarizations. The monoclinic phase is characterized by a very large piezoelectric and dielectric response [168,169,170]. Moreover, the first-principles atomistic modeling showed that when a small amount of Ti is added into PMN, a weak polar state develops, but structural disorder dominates, and the symmetry is rhombohedral. As more Ti is added, the ground state becomes clearly polar, but with easy rotation of the polarization direction. In the high Ti content region, the solid solution adopts ferroelectric behavior similar to PT, with tetragonal symmetry. The ground state sequence with increasing Ti content is R-M_B-O-M_C-T. The high-temperature phase is paraelectric cubic for all compositions [171]. A number of experimental studies (x-ray diffraction, neutron diffraction, and polarized light microscopy) have focused on the loading (electric field, temperature, and stress) induced behaviors (phase transitions and accompanying polarization rotation paths) of PMN-PT and PZN-PT single crystals [172,173,174,175,176,177,178,179,180,181,182,183,184]. It was shown that polarization rotation could occur quite easily in response to electric field, temperature and stress, and could occur in either direction in the permissible planes, but the polarization rotation paths depend on the compositions and crystallographic orientations, as well as the measurement conditions. Two different homogeneous polarization rotation pathways are present between R and T phases under an electric field, and three kinds of M phases are associated with the two pathways. When an electric field is applied along the [001]_c of PZN-PT and PMN-PT single crystals, polarization rotation occurs from [111]_c towards [001]_c via either M_A or M_C or both depending on the composition and measurement conditions. For [011]_c oriented single crystals, polarization rotates from [111]_c to [011]_c via M_B phase when the electric field is along [011]_c, and ends with an O phase when the electric field exceeds a critical value [185], but the O phase is usually unstable; its free energy balance between R and T phases depends on the electric and mechanical loading history [186]. Under an electric field along the [111]_c direction, a R phase single crystal can be polarized into a single domain state, and this single domain state may not be stable due to polarization switching-induced strain.

2.3.2 Orientation effect and directions of optimum cut

PMN-PT and PZN-PT single crystals with rhombohedral phase give a superior longitudinal piezoelectric strain constant d₃₃ (2000–3000 pC/N) and an excellent electromechanical coupling factor k₃₃ (>90%) under [001]_c-poling, while [111]_c poled rhombohedral single crystals with single domain structure show excellent shear piezoelectric strain coefficient d₁₅ (2000–4000 pC/N) and high electromechanical coupling factor k₁₅ (>80%). For example, the [111]_c poled PMN-0.31PT single crystal with Cu electrodes showed a d₁₅ of 5980 pC/N and k₁₅ of 97% [187]. Moreover, [011]_c poled rhombohedral multidomain single crystals showed large transverse and shear piezoelectric properties (large d₃₂, k₃₂, d₁₅, and k₁₅) [188]. Since these results are obtained at a low electric field, crystal orientation dependence of the coupling factor and piezoelectric coefficient may play a more important role than domain reorientation, which contributes substantially to the high strain level at a high electric field. It is noted that this large property enhancement exists not only in relaxor ferroelectrics, but also in normal ferroelectrics, such as BaTiO₃ single crystals [189,190,191]. The orientation dependence of the piezoelectric properties of [111]_c poled single domain PMN-0.33PT single crystals was calculated based on the standard matrix transformation using a complete set of single domain material constants [192], and the effective material properties under differently defined coordinates were calculated [193]. The results showed that the shear piezoelectric constant d₁₅ of the single domain PMN-0.33PT is very large (d₁₅=4100 pC/N, under a bias), but the piezoelectric constant d₃₃ is only 190 pC/N. The rotated properties along [001]_c are: d₃₃=2316 pC/N and k₃₃=93%, respectively, which are comparable to the measured [001]_c poled multidomain properties (d₃₃=2820 pC/N, k₃₃=94%) [49]. It can be seen that the superior longitudinal electromechanical properties in [001]_c poled PMN-33%PT multidomain crystals come from the contribution of large d₁₅ of the single domain state. In other words, large shear properties were converted to longitudinal properties through the re-orientation effect. More recently, a complete set of material coefficients of ternary 0.24PIN-0.49PMN-0.27PT single-domain single crystal without bias were measured [194]. The orientation dependence of piezoelectric strain constant d₃₃, elastic compliance constant $s_{33}^E$, dielectric constant ${\epsilon }_{33}^T$, and electromechanical coupling factor k₃₃ of [111]_c poled single-domain 0.24PIN-0.49PMN-0.27PT single crystal in the [111]_c–[112̄]_c plane are shown in Fig. 12. The comparison between the rotated single domain properties in the [001]_c direction and the measured data for the [001]_c poled multidomain state is given in Table 4. One could conclude from the results in Table 4 that the orientation effect plays a dominant role in the multidomain material properties of this relaxor-based ferroelectric single crystal, particularly for longitudinal properties. Similar results have been found in [001]_c poled rhombohedral PZN-PT single crystals with 4mm macroscopic symmetry [195]. Generally speaking, the maximum longitudinal piezoelectric responses of single domain crystals are along their nonpolar directions, including rhombohedral, tetragonal, and orthorhombic phase single crystals [196,197,198,199].

Fig. 12.

Orientation dependence of (a) piezoelectric strain constant d₃₃, (b) elastic compliance constant $s_{33}^E$, (c) dielectric constant ${\epsilon }_{33}^T$, and (d) electromechanical coupling factor k₃₃ of [111]_c poled single domain 24%PIN-49%PMN-27%PT single crystal in the [111]_c-[112̅]_c plane [194].

Table 4.

Comparison between rotated single domain properties along [001]_c and the directly measured [001]_c poled multidomain crystal properties for the 24%PIN-49%PMN-27%PT single crystal [194].

	Rotated single-domain properties along [001]c	Measured constants for [001]c poled multi-domain crystal	Ratio of rotated constant to measured constant
d33	1048	1109	95%
$s_{33}^E$	40.03	43.48	92%
${\epsilon }_{33}^T$	4080	4222	97%
k33	0.87	0.87	100%
$s_{33}^D$	9.60	10.53	91%
g33	29.03	29.68	98%

Besides the poling orientation effect, coordinate rotations may also be used to find the optimum cut directions of piezoelectric crystals after poling [200]. It was assumed that the elasto-piezo-dielectric matrices are applicable not only to the 3m single-domain crystal but also to the domain engineered crystals with 4mm or mm2 symmetry multidomain configurations. The maximum piezoelectric coefficients can be determined based on the measured independent matrix values in the original coordinates. Coordinate rotations showed that the rhombohedral PZT exhibits maximum piezoelectric response under an electric field along the [001]_c direction, but not along the polar [111]_c direction [201]. Recently, it was discovered that the largest d₁₅ of the [111]_c poled single-domain single crystal occurred in the zxt-22.5° cut (22.5° clockwise rotation about the x axis). The maximum d₁₅ value in the rotated coordinates is approximately 1.1 times of the original d₁₅ [202].

When the crystal is poled along [011]_c, a multidomain configuration is formed with a macroscopic orthorhombic symmetry mm2. The piezoelectric matrix of ferroelectric crystals with orthorhombic symmetry has five independent piezoelectric coefficients: d₁₅, d₂₄, d₃₁, d₃₂, and d₃₃. It has been mentioned above that [011]_c poling induces large transverse and shear piezoelectric coefficients d₃₂ and d₁₅. Recently, a new mode, k₃₆ face shear mode, was studied in the [011]_c poled PMN-PT single crystal [202]. The shear piezoelectric coefficient d₃₆ is a derived tensor component and is zero in the original coordinates. The maximum d₃₆ (±2600 pC/N) was obtained in the direction of θ =0° and φ =±45° (zxt±45°) or ±225°. The d₃₆ rotated about the z axis can be expressed by the following expression:

$$d_{36}=-2d_{31}\text{sin}\phi \text{cos}\phi +2d_{32}\text{sin}\phi \text{cos}\phi$$ (2)

The maximum amplitude of d₃₆ equals ±(d₃₂-d₃₁) at φ =±45° or ±225°. From the application point of view, it is very exciting that the k₃₆ longitudinal shear mode can be used because the field direction to operate the k₃₆ mode is the same as the poling direction, while the field direction to operate k₁₅ mode is perpendicular to the poling direction, which often causes de-poling because large fields could re-orient domains to align polarization to the field direction. The maximum value of d₃₆ from theoretical calculations has been verified by a quasi-static method using a Berlincourt meter [203]. Large piezoelectric d₃₆ coefficients (2000–2500 pC/N) and a high electromechanical coupling factor k₃₆ (0.80–0.83) were also determined by the resonance method in ternary PIN-PMN-PT single crystals [204,205]. Recently, an electroacoustic transducer based on the d₃₆ mode was designed, and published as a patent [206].

3. Growth of relaxor-based ferroelectric single crystals

3.1. Growth of PZN-PT single crystals

PZN-PT single crystals were first grown from PbO flux by the slow cooling technique in 1969 [71]. The starting materials were PbO, ZnO, TiO₂, and Nb₂O₅, and the mole ratio of the flux to the composition was 2 to 1. The reagents were mixed and charged in a platinum crucible. The crucible was heated up to 1100–1200 °C and held at this soak temperature for 5 hr, then the melt was cooled slowly at the rate of 5–10 deg/hr. Crystals with the composition rich in PZN were obtained in an arrowhead form stretched along the pseudo-cubic <111> direction (~10 mm), and crystals rich in PT were obtained in the form of cubes (~3 mm) [71]. About ten years later, PZN-PT single crystals with MPB compositions were grown by the same method in 1981 [98], and anomalously large piezoelectric and electromechanical properties were observed. However, the size of the obtained crystal was very small until 1996, when a systematic study of the high-temperature flux-solution growth of PZN-PT single crystals was performed [207,208]. The high purity (>99.9%) powders used in the crystal growth were PbO, Pb₃O₄, TiO₂, ZnO, and Nb₂O₅, while PbO and Pb₃O₄ were used as the flux. The raw powders were loaded into a Pt crucible and re-charged several times at 900 °C until the crucible was full. The Pt crucible was covered with a platinum lid and placed in an alumina crucible. The alumina crucible was sealed with an alumina lid using alumina cement to minimize PbO volatilization, and then placed in the bottom loading furnace. The typical crystal size ranged from 3 to 15 mm [207].

In 2002, large PZN-8%PT single crystals were grown by the high temperature top seeded solution method [209]. The powders used were high-purity ZnO, Nb₂O₅, TiO₂, and PbO or Pb₃O₄. PbO and Pb₃O₄ were used as the flux. Composition of the flux ratio was 60%. Raw powders were loaded into a platinum crucible by melting the starting materials twice within 4 hr at 1000 °C. The platinum crucible was placed into a furnace. The perovskite phase PZN-PT solution was formed at about 1250 °C. In order to obtain pure perovskite phase single crystals, the furnace must be cooled at a fast rate to room temperature, after cooling the system from 1250 °C to 850 °C at a slow rate to avoid the crystal turning into the pyrochlore phase at about 850 °C. The slow cooling rate varied from 1.5 to 1.8 °C per hour, while the fast cooling rate was about 50 °C per hour. A cooling well at the bottom and center of the platinum crucible was introduced to induce concentrated nucleation at that position and to enlarge the size by providing a large temperature gradient. The as-grown PZN-8%PT crystals were transparent with their color varying from pale-yellow to brown. The largest crystal had a dimension of 26×20×16 mm³ [209].

In order to reduce the number of nuclei, the temperature gradient of the crucible was optimized as following: the bottom of the crucible was made >50 °C cooler than the top during the cooling process [210]. PZN-PT with dimensions of 43×42×40 mm³ and weighing 415 g were grown using this improved flux method [210]. Fig. 13 shows two types of crucible cooling arrangements designed to induce concentrated nucleation at the bottom of the crucible and to enlarge the crystals by providing a large temperature gradient. One is an alumina rod cooling structure, as shown in Fig. 13(a), and the other is an oxygen gas cooling structure, as shown in Fig. 13(b).

Fig. 13.

Two crucible cooling arrangements for PZN-PT single crystal growth, (a) alumina rod cooling and (b) oxygen gas cooling [210].

Another crystal growth technique for PZN-PT is the Bridgman method [211]. PZN-9%PT single crystals with a diameter of 2 inches and length of 0.5 inches was grown from solution by the Bridgman method with a PbO flux supported on the bottom of the crucible. The growth speed was 0.2–0.5 mm/h. This type of Bridgman method is more suitable for growing large/heavy crystals than the suspended type of Bridgman method [211]. In 2002, PZN-9%PT single crystals with a 28 mm diameter and 30 mm length were grown by the modified Bridgman technique with PbO flux using an allometric seed crystal [99]. The crystals were grown at about 1250 °C, which was higher than that of the supported Bridgman method [212]. The temperature gradient is around 30–50 °C/cm at the solid-liquid interface, which was ideal for crystal growth. In addition, PZN-PT single crystals were also successfully grown by the vertical Bridgman method [213,214] and the top seeded solution growth (TSSG) technique [215,216].

The electromechanical coupling factor k₃₃ of [001]_c poled PZN-9%PT single crystal is about 92%, and its Curie temperature is 178 °C. However, its piezoelectric properties degrade at temperatures higher than its rhombohedral-tetragonal phase transition temperature T_RT. The Ti component must be decreased for obtaining PZN-PT single crystals with higher T_RT. In 2003, PZN-7%PT single crystals with dimensions up to Φ33mm×28mm were successfully grown by the flux Bridgman method [217]. The Curie temperature T_C and the rhombohedral/tetragonal transition temperature T_RT were 179 °C and 120 °C, respectively. The T_RT of PZN-7%PT single crystals was much higher than that of PMN-30%PT (~50 °C) and PZN-9%PT (~68 °C) [217]. In 2004, homogeneous high-performance PZN-xPT single crystals of a range of compositions with x=0.045–0.09 and edge length greater than 35mm were grown from PbO flux with local point cooling and by engineering the isotherms of the solution to promote controlled (001) layer growth of the crystals [218]. It was found that the PZN-(6–7)%PT single crystals exhibited high homogeneity in composition and superior electromechanical properties compared to those grown by conventional flux growth techniques. By this time, the qualities of the crystals were good enough for practical devices. Fig. 14 shows a crystal growth facility, as-grown crystals, and the processed crystals [219].

Fig. 14.

Crystal growth facility, as-grown crystals, and processed crystals [219].

3.2. Growth of PMN-PT single crystals

In 1990, PMN-PT single crystals were grown from PbO-B₂O₃ flux using the flux growth technique [220,221]. The reagents were mixed and put into a platinum crucible and heated to the melting point ~1150 °C. After maintaining at this temperature for about 10 hrs, the melt was slowly cooled at a rate of 3 °C/hr to ~950 °C, then to 800 °C at 5 °C/hr and finally to down to room temperature at a much faster rate. The flux was removed by dissolving in a dilute nitric acid solution. The crystals grown by this method ranged from a few millimeters up to ~1 cm on the side dimension [220]. Later, it was found that the optimum flux composition and concentration was 49 wt% PbO + 1 wt% B₂O₃, which led to the stabilization of the perovskite crystals against the pyrochlore phase, and to the growth of high-quality PMN-PT crystals [222]. The B₂O₃ additive plays an important role in improving the effectiveness of the PbO solvent by promoting optimum complex phase formation and adequate viscosity. In addition, the top seeding technique can substantially modify the nucleation kinetics [222]. However, it is difficult to grow large-size single crystals required for commercial devices using the flux method. Besides size and orientation restrictions, the loss of material due to the high volatility of PbO containing melts is also a major concern when choosing an appropriate growth technique for this system.

PMN-PT solid solution crystals were also grown by a top-seeded solution growth (TSSG) method that can prevent phase segregation and promote [001]_c direction growth. The TSSG technique offers some advantages in growing single crystals of good quality, high compositional homogeneity and controlled morphology, thanks to its unique temperature field design and slow growth process [223]. The weighed chemicals were thoroughly mixed and loaded into a platinum crucible, which were then placed into a vertical tubular furnace to melt. A small PMN single crystal was used as seed and the saturation temperature of the solution was determined accurately by repeated seeding trials. The crystal growth took place upon cooling from 1180 °C to 1100 °C at a rate of 0.2 °C/h. At the end of a slow cooling process, the grown crystal was pulled out of the melt surface and cooled to room temperature at a rate of 15 °C/h. A brown quadrate single crystal with dimensions of 17×17×15 mm³ was obtained in 2007, as shown in Fig 15 [223]. However, this technique cannot grow long boules. The crystals have a large area but thin layer only.

Fig. 15.

As-grown PMN-PT single crystal and a polished [001] platelet (scale in mm) [223].

The solid state crystal growth (SSCG) technique is another method to grow PMN-PT single crystals, and its principle is the following: let an external single crystal seed grow by consuming the fine matrix grains without melting the major constituents. Since this process is quite cost-effective and also good for mass production of large single crystals, many researchers have tried to grow single crystals by the SSCG method [224,225,226,227]. Fig. 16 shows the PMN-PT single crystal blocks. The disadvantage of this technique is the production of porosity in the final single crystal products.

Fig. 16.

PMN-PT single crystal blocks grown by the solid state crystal growth (SSCG) method [228].

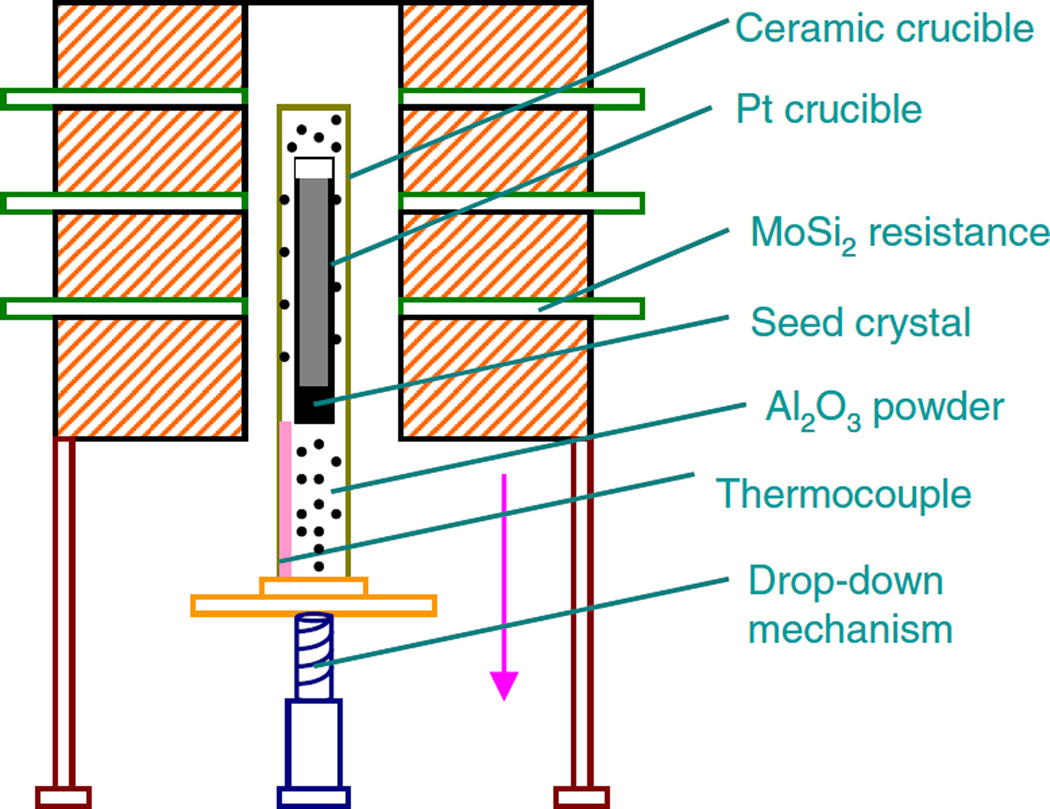
In 1997, a modified Bridgman method developed by the Shanghai Institute of Ceramics was used to grow the PMN-PT single crystals [229]; crystal boules larger than 25 mm in diameter and 50 mm long were obtained [230,231,232]. PMN-PT single crystals were grown directly from its melt at high temperature in an isolated Pt crucible, and a PMN-PT single crystal seed was adopted during the crystal growth. A schematic of the furnace for crystal growth is given in Fig. 17. Raw powders of PbO, MgO, Nb₂O₅, and TiO₂ with a purity of more than 99.99% were used as the starting materials. The furnace was maintained at about 1380 °C, which is 100 °C higher than the melting point during crystal growth. After soaking about 10 h, the crucible was pulled down at the rate of 0.1–1.0 mm/h, and the temperature gradient was controlled to be about 40–100 °C/cm at the solid-liquid interface. At the end of the crystal growth, the furnace temperature was dropped down to room temperature. The as-grown PMN-PT single crystals with a size of Φ50×80 mm³ were obtained [233]. The easily grown direction is [111]_c, but nowadays, PMN-PT single crystals can also be grown along the [001]_c, [011]_c, which are more useful for practical applications.

Fig. 17.

Schematic of furnace for crystal growth using modified Bridgman method [233].

PMN-PT single crystals were also grown using the vertical Bridgman method, and the boules were 50 mm in diameter and 70 mm in length [234,235,236]. Recently, large size PMN-PT single crystals (up to 100 mm in diameter) were grown using a modified Bridgman method [237,238]. The maximum temperature in the furnace was 1395 °C and the crystal growth rate was controlled at 0.4 mm/h at a temperature gradient of 20 °C/h, which appears to give the optimum results for growing this type of relaxor ferroelectric. Fig. 18 shows the PMN-PT single crystals grown using the modified Bridgman technique by H.C. Materials Inc., USA [239].

Fig. 18.

PMN-PT single crystals grown by the modified Bridgman technique [239].

3.3. Higher Curie temperature single crystals and ternary systems

PZT piezoelectric ceramics have high Curie temperature T_C ~350 °C, but it is very difficult to grow PZT single crystals with a large size and desired composition. As mentioned above, PMN-PT and PZN-PT single crystals have super large piezoelectric and electromechanical properties and can be grown relatively easily, but they also have some disadvantages, such as low thermal stability (low rhombohedral to tetragonal phase transition temperature, T_RT ~ 50–75 °C) and relatively low Curie temperature (T_C ~ 150–170 °C), which restrict them from some applications that require better thermal stability. A broader temperature operating range would allow for greater device design flexibility and therefore a wider range of potential applications. Therefore, improved relaxor-based ferroelectric single crystals with higher T_RT/T_C and better thermal stability are much needed.

3.3.1 PSN-PT single crystal

One of the higher Curie temperature solid solutions is the (1-x)Pb(Sc_1/2Nb_1/2)O₃-xPbTiO₃ (PSN-PT) system [240]. In 1997, PSN-PT single crystals were successfully grown by the flux method, which has higher T_C (206 °C for [001]_c poling) and good thermal stability [241]. The single crystal has a remnant polarization of P_r =26 µC/cm², a coercive field of E_C=6 kV/cm, a room temperature dielectric constant ${\epsilon }_{33}^T=960$ after poling, a dielectric loss of 0.5%, and an electromechanical coupling factor k₃₃=72%. But there are two major shortcomings in this system: a high melting point of 1420 °C and a high cost of raw-materials. Later, ternary systems xPb(Sc_1/2Nb_1/2)O₃-yPb(Zn_1/3Nb_2/3)O₃-(1-x-y)PbTiO₃ (PSN-PZN-PT) and xPb(Sc_1/2Nb_1/2)O₃-yPb(Mg_1/3Nb_2/3)O₃-(1-x-y)PbTiO₃ (PSN-PMN-PT) were found to be more attractive [242,243]. In 2000, PSN-PMN-PT single crystals were grown by the flux method [244], but the crystal size was very small (2–3 mm in length). In 2001, larger size PSN-PMN-PT single crystals that were 15 mm in diameter and 20 mm in length were grown by a modified Bridgman technique [245]. Their dielectric constant peaks were in the range of 162 °C to 180 °C and the PSN-PMN-PT single crystals cut from the seed end had the piezoelectric constant of d₃₃ =1200 pC/N. The thickness coupling factor was relatively high with k_t = 60%.

3.3.2 PYN-PT single crystal

In 2001, (1-x)Pb(Yb_1/2Nb_1/2)O₃-xPbTiO₃ (PYN-PT) binary single crystals near the MPB composition with the [100] orientation and 1–2 mm in length were successfully grown by the flux method using PbO-PbF₂-B₂O₃ flux [246]. In 2002, PYN-PT single crystals were grown using the high temperature solution method [247,248]. The Curie temperature of PYN-40%PT ranges from 244 °C to 268 °C. The piezoelectric constant d₃₃ of the [001]_c poled single crystal was ~1200 pC/N, with a strain reaching 0.54% at 100 kV/cm. The large piezoelectric constant, high coercive field, and high Curie temperature (>250 °C) makes PYN-PT single crystals promising candidates for applications of high temperature and high performance solid-state actuators and transducers [249, 250]. Recently, Pb(Yb_1/2Nb_1/2)O₃-Pb(Mg_1/3Nb_2/3)O₃-PbTiO₃ (PYN-PMN-PT) ternary solid solution systems with the dimensions of 30×30×12 mm³ were successfully grown by the top-seeded solution growth method [251].

3.3.3 PIN-PT single crystal

Perovskite Pb(In_1/2Nb_1/2)O₃ (PIN) is a typical relaxor ferroelectric material with a T_C ~ 90 °C, higher than that of Pb(Mg_1/3Nb_2/3)O₃ (PMN) (−10 °C) [252]. The solid solution of the (1-x)Pb(In_1/2Nb_1/2)O₃-xPbTiO₃ (PIN-PT) binary system exhibits a MPB near 37 mol% PT, where high piezoelectric and dielectric properties can be obtained. The Curie temperature of PIN-PT is about 320 °C, much higher than that of PMN-PT [253]. Consequently, it is very promising by adding the PIN component to improve the T_C and T_R-T of PMN-PT systems. PIN-PT single crystals were grown by the flux method in 2000, but the crystal size was small and the composition was not uniform. The piezoelectric constant d₃₃ was only about 700 pC/N [254]. In 2002, PIN-PT single crystals near the MPB were grown directly from the melt by the modified Bridgman technique [255]. Curie temperature of PIN-PT was higher than 200 °C, with a piezoelectric constant d₃₃ > 2000 pC/N, and electromechanical coupling factor k₃₃~92% when poled along [001]_c direction in the rhombohedral phase [256].

3.3.4 PIN-PMN-PT single crystal

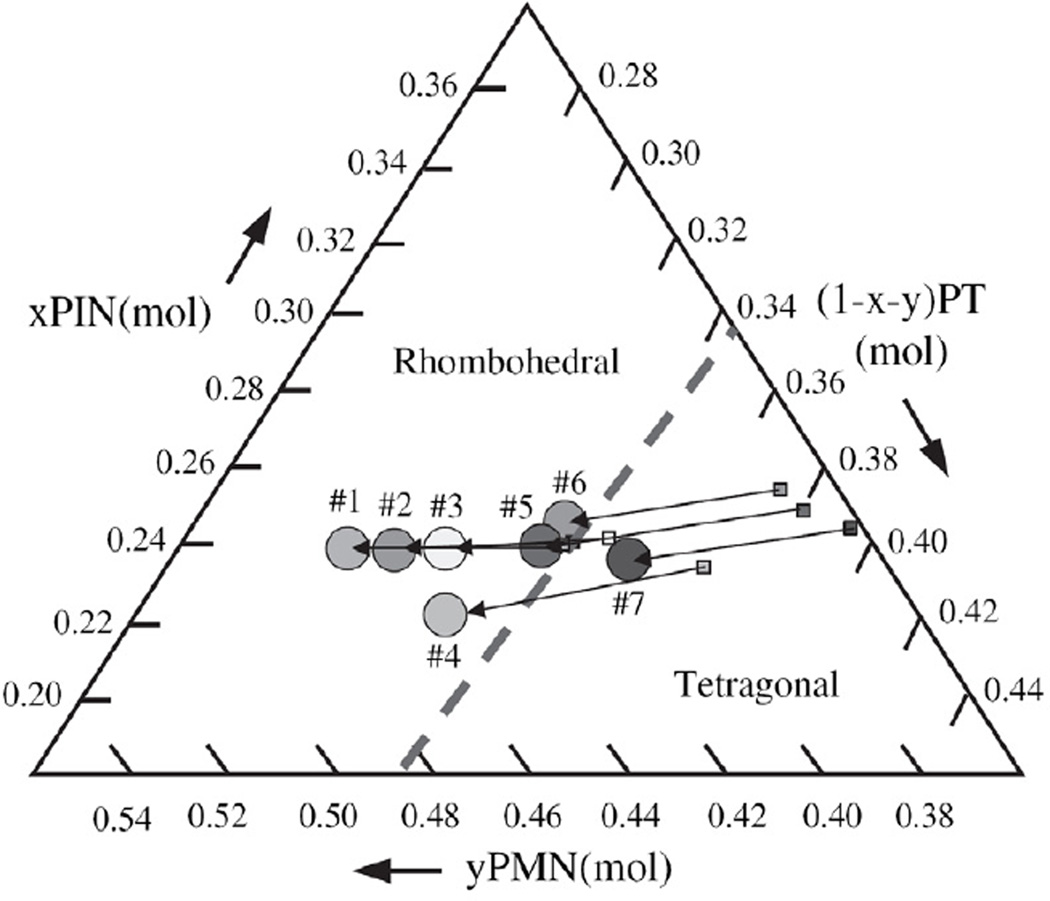
In 2002, the ternary (1-x-y)Pb(In_1/2Nb_1/2)O₃-yPb(Mg_1/3Nb_2/3)O₃-xPbTiO₃ (PIN-PMN-PT) single crystals were successfully grown by a conventional flux method using PbO-B₂O₃ flux [257]. The crystals were grown in a platinum crucible by mass crystallization achieved through slow cooling of a 50PIMNT 16/51/33: 40PbO: 10B₂O₃ (mol%) molten solution from 1230 °C down to 850 °C at 1.2 °C/h. The largest crystal had the dimensions of 20×10×5 mm³. The Curie temperature was 187 °C and the piezoelectric constant d₃₃=2200 pC/N, which was the highest value so far reported for piezoelectric materials with T_C >185 °C [258]. PIN-PMN-PT single crystals were also grown by using the top-seeded solution growth (TSSG) method. The crystal with a composition of PIN-43%PMN-33%PT showed the Curie temperature T_C at 208 °C and rhombohedral to tetragonal phase transition temperature T_RT at 120 °C. A phase diagram for this ternary crystal system near the MPB is shown in Fig. 19 [259]. Compared with other growth methods, the TSSG technique offers some advantages in growing single crystals of good quality and high compositional homogeneity but with small crystal size [260].

Fig. 19.

Phase diagram for the ternary PIN-PMN-PT single crystal system near the MPB. The concentration of PIN was chosen to be 24% mole [259].

PIN-PMN-PT single crystals have also been grown by the Bridgman method [261]. In 2007, PIN-PMN-PT single crystals with a [011]_c seeding was grown by a modified Bridgman method [262]. High-purity (99.99%) oxide powders of PbO, In₂O₃, Nb₂O₅, MgO, and TiO₂ were mixed stoichiometrically and ground using an attrition mill to reduce particle size. The resulting powder was pressed and sintered into ceramic forms before loading into a platinum crucible with a [011]_c oriented seed crystal affixed in the base. The crucible was sealed and packed within an alumina tube and placed inside a furnace. The charge was heated up to 1370 °C and the melt was equilibrated for 10 h before the crucible was lowered at 0.3–0.8 mm/h for seeded crystal growth. Compared with binary PMN-PT crystals, the corresponding ternary PIN-PMN-PT crystals have more than twice the coercive field (E_C~6.0 kV/cm), and about a 20 °C higher depoling temperature T_RT (100–117 °C). Other properties, such as dielectric constants, piezoelectric strain constants, and electromechanical coupling factors are slightly reduced, but the elastic stiffness coefficients show some increase at room temperature. PIN-PMN-PT single crystals can be grown in large sizes, just like PMN-PT single crystals. Their functional properties are similar to that of PMN-PT single crystals, but the much higher coercive field and depoling temperature gives them advantages for greater stability in terms of applied electric field and the variation of temperature, which are important for many piezoelectric devices, particularly when the device is used in high-drive and higher-temperature conditions. Fig. 20 shows the as-grown PIN-PMN-PT (21/49/30) single crystal with 50 mm diameter [263], and the as-grown PIN-PMN-PT (29/44/27) single crystal and wafer by the Shanghai Institute of Ceramics, China [233].

Fig. 20.

(a) As-grown PIN-PMN-PT (21/49/30) single crystal with 50 mm diameter [263], and (b) as-grown PIN-PMN-PT (29/44/27) single crystal and wafer [233].

3.4. Doped single crystals

PZT piezoelectric ceramics doped with aliovalent substitutions have much superior functional properties and hence more applications [76]. Dopants are usually added in concentrations at ≤ 3% [264]. Two different groups of ions have been identified for doping: ions with higher valences as donors, and lower valences as acceptors. Donors and acceptors influence PZT ceramics antagonistically and are called “softeners” or “hardeners”, respectively. The antagonism can be understood considering the fact that vacancies in general are the mediators. The violation of neutrality by the substitution of ions with deviating valences is compensated in PZT by the creation of charged lead or oxygen vacancies. Generally speaking, lower valent substitutents (such as Fe, Mn, Ni, Co) in PZT ceramics produce the following results: (i) decreased dielectric constant, (ii) increased frequency constant, (iii) large increase in mechanical quality factor, and (iv) larger aging effect. In contrast, higher valence substituents (such as La, Sb, Bi, W) result in: (i) increased dielectric constant, (ii) increased electromechanical coupling factor, (iii) decreased mechanical quality factor, and (iv) smaller aging effect [265]. A typical set of dielectric and piezoelectric data is given in Table 5.

Table 5.

Modification of PZT ceramic with donor and acceptor dopants [264].

Dopant	Materials	TC (°C)	${\epsilon }_{33}^T$	tanδ (10−3)	kp	d33 (pC/N)	Qm
Soft
Nb5+	Pb0.98(Zr0.52Ti0.48Nb0.024)O3	365	1700	15	0.60	374	85
Sb5+	Pb0.96Sr0.05(Zr0.52Ti0.46Sb0.02)O3	>350	1510	15	0.46	410	95
Nd3+	Pb0.97Nd0.02(Zr0.54Ti0.46)O3	330	1600	20	0.60	355	100
Hard
Fe3+	Pb(Zr0.525Ti0.472Fe0.003)]O3	300	820	4	0.59	240	500
Ni3+	Pb0.95Sr0.05[(Zr0.52Ti0.44)Ni0.04)]O3	330	1000	8	0.50	200	350

For relaxor-PT systems, it was reported that doping effects are significantly different from that of PZT ceramics. Mn doping in PMN-PT ceramics resulted in improved Q_m while Fe doping had almost no effect on the Q_m value. Thus, Mn was generally selected as a substituent in relaxor-PT single crystals for improving the mechanical quality factor to meet the need of high power applications [266].

3.4.1 Mn-doped single crystals

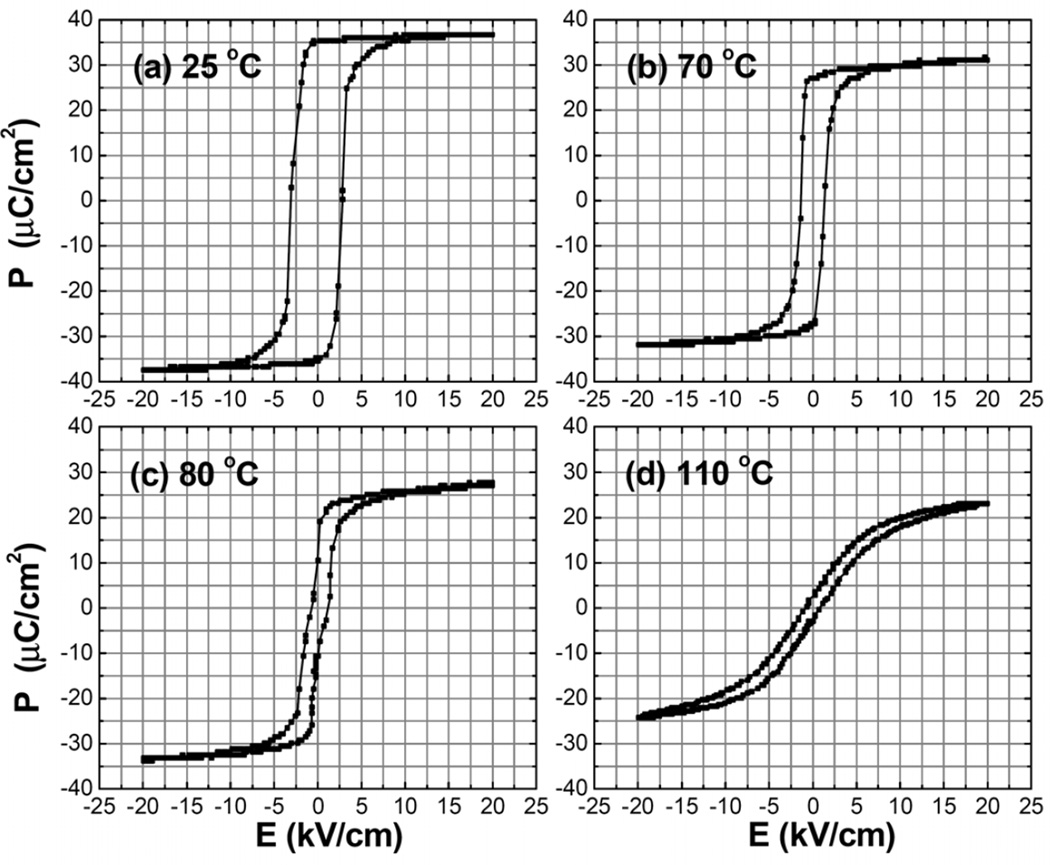
Though PIN-PMN-PT single crystals have improved mechanical quality factors (Q_m~100) compared to PMN-PT crystals (Q_m<80), their Q_m are still much lower than that of high-power piezoelectric ceramics (Q_m>800), which significantly hampered their application potential for high-power or resonant-based devices. Mn substitution resulted in enhanced mechanical quality factor Q_m and a moderate increment in the rhombohedral to tetragonal phase transition temperature with increasing Mn composition [267]. The mechanical quality factor Q_m ~1000 of Mn doped PIN-PMN-PT single crystals was reported recently, which is comparable to “hard” PZT8 ceramics [268,269,270]. In Mn-doped PZN-PT single crystals, the improved Q_m was due to the induction of “hard” characteristics into the single crystal [271]. In addition, it was found that the production rate of PZN-PT single crystals was increased and no pyrochlore crystals were produced with 0.9 mol% of MnO additive, and the manganese substitutes for Zn at the B-site in the perovskite structure [272]. In 2006, 3 mol% Mn-doped PMN-29PT% single crystals were grown by a modified Bridgman technique [273]. Mn substitution resulted in an enhanced pyroelectric coefficient and a lower dielectric loss, which led to the improvement of the detectivity figure of merit by about a factor of 4 at 50 Hz compared with that of undoped crystals. Moreover, thermal stability was enhanced by Mn substitution. The mechanism of the doping effect is due to domain walls pinning by the dopant dipolar defects [273]. In 2007, it was reported that 3 at.% Mn substitution results in (i) large increment of coercive field at the cost of reduced piezoelectric response, (ii) increased Curie temperature and enhanced stability of the ferroelectric rhombohedral phase, which enables a wider operation temperature range, and (iii) enhanced linearity in electric field induced strain with lower hysteresis [274]. X-ray rocking curves (XRC) indicated that the quality of single crystals could be significantly improved for Mn-doped PMN-28%PT single crystals by appropriate annealing. The dielectric loss of annealed samples decreased about 50% compared to the unannealed ones, which should be attributed to the reduction of oxygen vacancies. The domain wall pinning effect caused by oxygen vacancies was enhanced through nitrogen annealing [275]. In addition, it was found that aging induced a double ferroelectric hysteresis loop and a giant recoverable electrostrain of 0.8% at an electric field of 1.2 kV/mm in the [001]-oriented 0.2 mol % Fe-doped PMN-38%PT crystal. This result is much higher than the strain obtained in undoped crystals near the MPB composition under the same field level. Such aging effects are attributed to a point-defect-mediated reversible domain-switching mechanism [276]. Fig. 21 shows pure PMN-PT, PIN-PMN-PT, and Mn-doped single crystals [277].

Fig. 21.

(a) Pure PMNT crystal, (b) a wafer of pure PMNT,(c) Mn-doped PMNT crystal, (d) a wafers of Mn-doped PMNT, (e) PIMNT crystal, and (f) a wafer of PIMNT [277].

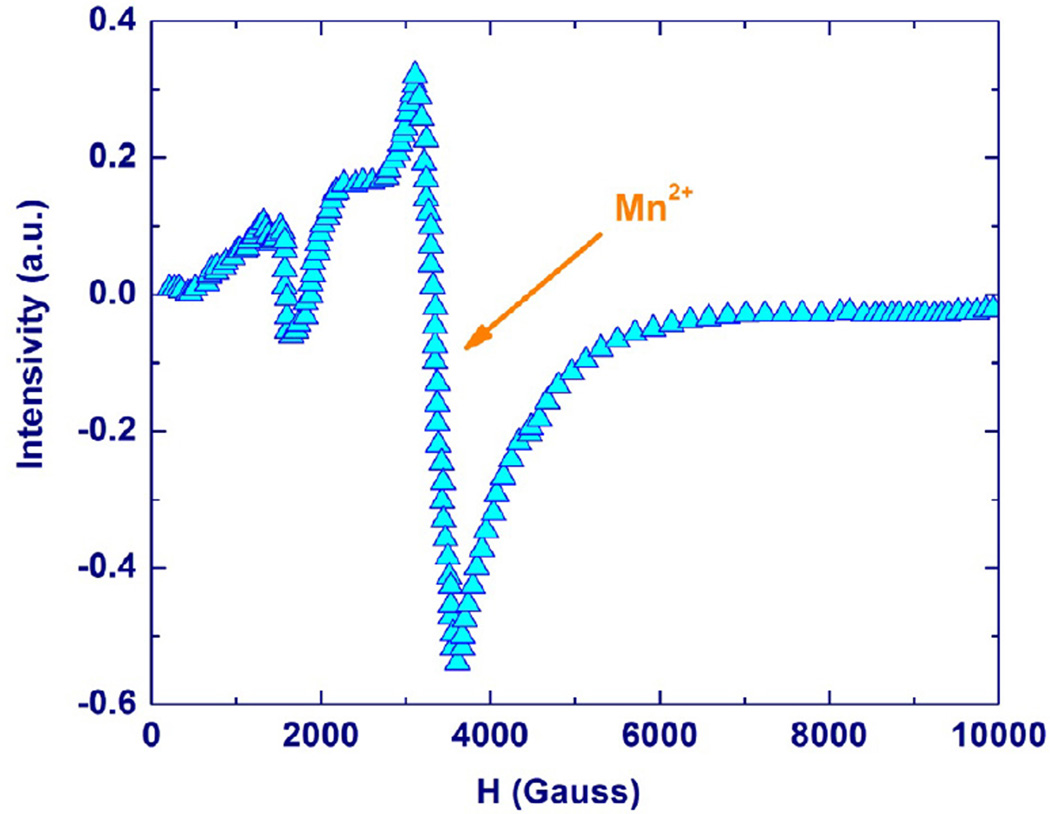
(Mn,F) co-doped PZN-PT single crystals were reported with typical crystal size up to 30 mm with a dark brown color [278]. Crystal lattice parameters of doped PZN-PT crystals are slightly decreased compared to undoped ones. The room temperature dielectric permittivity of Mn doped PZN-8%PT single crystals along the [001]_c direction is lower than that of undoped ones. The Curie temperature and ferroelectric phase transition temperature of the doped crystal are increased. The valence state of the manganese dopant was determined by electron spin resonance, indicating no Mn⁴⁺ in the crystals and suggesting that the valence of manganese ions in PZN-PT crystals to be 2⁺, which acts as a hardener to stabilize domain walls and pin the domain wall motion. On the other hand, the dopant will enter the Ti⁴⁺ position, shifting the crystal composition to higher PT content. Fig. 22 shows the electron spin resonance (ESR) spectrum of (Mn,F) doped crystals, in which a broad peak around 3400 G was observed, attributed to Mn²⁺, and there was no Mn⁴⁺ characteristic peak in the spectra. Mn²⁺ ions can easily enter the Ti⁴⁺ ion position, producing oxygen vacancies to form defect dipoles which align themselves in the polarization direction. The fluorine ion creates immobile defect dipoles with the Mn ion that can influence the domain pattern by stabilizing the polarization in their direction. The main consequence of the presence of these defect dipoles is the decrease of domain wall mobility, which produces the hardening effect. On the other hand, owing to the dopant of manganese ions at the Ti⁴⁺ position in the crystal lattice, Pb(TiMn_x)O_3-x ratio in PZN-PT crystals is increased, making PZN-PT shift toward the MPB composition, which produced higher Curie temperature in doped PZN-PT single crystals.

Fig. 22.

The electron spin resonance spectrum of (Mn,F) doped PZN-8%PT single crystal [278].

3.4.2 Fe-doped and Co-doped single crystals

The effects of Fe substitution in PZN-PT include: (i) lowering the field level required to obtain large strains, (ii) increased squareness in the strain-field response, indicative of “hard” piezoelectric properties, and (iii) enhanced linearity in the region where saturation is approached at high field levels [279]. In addition, the coercive field of Fe doped PZN-PT single crystals are significantly greater than that of the pure crystals [280]. In 2004, large-size and high-quality 0.2 mol% Fe-doped PMN-38%PT single crystals were grown by the modified Bridgman technique [281]. The doped single crystal showed a lower dielectric constant and dielectric loss compared with undoped crystal. Their excellent pyroelectric properties as well as being able to produce large-size and high-quality single crystals make this kind of single crystal very promising for high-performance infrared detectors and other pyroelectric applications. In 2003, Co-doped PZN-8%PT single crystals were grown by the modified flux technique [282]. Under high power drive, the mechanical quality factor Q_m and vibration velocity showed a considerable improvement. Co doping resulted in an increase of electric field level required for the rhombohedral to tetragonal phase transition, which indicates that Co imparts a hardening effect in the PZN-PT crystal [282].

4. Phase transitions and functional properties

4.1. Ferroelectric and dielectric properties

The coercive field and the polarization characteristics of PMN-xPT single crystals are strongly related to their compositions and crystal orientations. Generally speaking, the coercive field and remnant polarization increase with composition x. The largest coercive field and remnant polarization occurs in the spontaneous polarization direction. For example, the coercive fields of tetragonal PMN-38%PT single crystals are 8.25 kV/cm along [001]_c, 6.80 kV/cm along [011]_c, and 4.11 kV/cm along [111]_c, respectively. The remnant polarizations are 34.25, 22.64, and 18.87 µC/cm² in the [001]_c, [011]_c, and [111]_c directions, respectively [283]. In addition, triple-like polarization-electric field (P-E) hysteresis loops were found in PMN-PT single crystals [284]. Fig. 23 shows the P-E hysteresis loops of the [111]_c-oriented PMN-24%PT single crystal at different temperatures. The loop is evidently a ferroelectric-type loop from 25 to 70 °C. The remnant polarization and the spontaneous polarization have very little difference in this temperature range. When the temperature is between 80 and 85 °C, a triple-like loop appears; above 90 °C, the loop still presents, but the remnant polarization becomes much smaller. The triple-like loops originated from the transformation between the microdomain state and the metastable macrodomain state. In the [011]_c- and [001]_c-oriented PMN-24%PT single crystals, the trend is similar, but the triple-like loops were observed in a wider temperature range, between 80 °C and 90 °C. The triple-like loops also appear in PMN-PT single crystals with MPB composition, due to the field induced phase transitions between monoclinic/orthorhombic and tetragonal phases [285,286]. For example, an electric field applied along [011]_c of the tetragonal PMN-38%PT single crystal could induce an orthorhombic ferroelectric phase at lower temperature. The stability of the induced orthorhombic phase decreases with increasing temperature, and finally re-transforms back to the more stable tetragonal phase at higher temperature [287].

Fig. 23.

P-E hysteresis loops of the [111]_c-oriented PMN-24%PT single crystal at different temperatures: (a) 25 °C, (b) 70 °C, (c) 80 °C, and (d) 110 °C [284].

Fig. 24 shows the temperature and orientation dependence of the remnant polarization of PMN-24%PT single crystals. The PMN-24%PT single crystal has rhombohedral symmetry in the ferroelectric state, with spontaneous polarization along <111>_c. Thus, the amplitude of remnant polarizations in [011]_c and [001]_c are the corresponding polarization vector projections. As temperature increases, substantial decreases of the remnant polarization started at about 65°C, but the remnant polarization still had about 2 µC/cm² left over even at 130 °C, which is already above the Curie temperature of PMN-24%PT single crystals (~110 °C). This clearly shows the relaxor characteristic in the crystal. The relaxor behavior was observed in the PMN-xPT single crystals for x < 0.3. The degree of diffuseness in the dielectric maximum and the degree of relaxor characteristics decreases with increasing x. When x is larger than 0.35, PMN-PT single crystals behave like a normal ferroelectric material [288].

Fig. 24.

Temperature and orientation dependence of the remnant polarization of the PMN-24%PT single crystals [284].

Fig. 25(a) shows the dielectric constant ε_r of different compositions and crystal orientations. Poling along different crystal directions will induce different phase structures and domain states at room temperature. The dielectric constant in multidomain states is much larger than that of monodomain states. Fig. 25(c) shows the tunability of ε_r under the bias of 1 kV/mm and frequency of 10 kHz at room temperature. The tunability of ε_r was found to be 40.6% at the dc bias of 1 kV/mm in the [001]_c poled PMN-30%PT multidomain single crystal. The large dielectric tunability reflects the significant structure adaptivity of the engineered domain configurations, in which the applied electric field easily induces large distortions with compensating strain in each of the four equivalent domain states that remained after the crystal is poled along [001]_c. Under a very large field, there may be field induced phase transitions from the rhombohedral to the tetragonal phase and other metastable phases along the path for the spontaneous polarization to rotate from [111]_c to [001]_c. The presence of these metastable phases created by a dc field can also produce high structural responsiveness. In both cases, the relaxor nature plays an important role. The local random fields induced states are only metastably locked in under an applied electric field [289]. Thus, the relaxor nature contributes greatly to the sensitive engineered domain configurations and facilitates polarization rotation through metastable phases, and also contributes greatly to the structure adaptivity, piezoelectric enhancement and dielectric constant tunability.

Fig. 25.

(a) Dielectric constant ε_r (at 10 kHz), (b) piezoelectric constant d₃₃, and (c) dielectric constant tenability (at 1 kV/mm and 10 kHz) in poled PMN-xPT single crystals at room temperature [290].

For the [111]_c poled PMN-33%PT crystal, a very large ε_r tunability (73.4%) can be obtained under 1 kV mm⁻¹ bias [290]. Due to the compositional complexity near the MPB, the FE_r and FE_t phases may form a manifold of coexisting phases in the [111]_c poled PMN-33%PT crystal. Under a [111]_c-oriented electric field, the FE_t to FE_r phase transition, i.e., the induced polarization rotation from the [100]_c to the [111]_c direction, results in a large ε_r tunability. The large tunability of ε_r in PMN-PT crystals makes them one of the most promising candidates for potential applications in continuously adjustable capacitors and dielectric amplifiers. It should also be noted that, for poled crystals, multidomain states have much larger piezoelectric constants and dielectric tunability than the corresponding monodomain state.

4.2. Temperature induced phase transformations

The dielectric constants as functions of temperature and frequency (0.1, 1 and 10 kHz) for [001]_c, [011]_c, and [111]_c poled PMN-xPT single crystals with different compositions are presented in Fig. 26. For the poled PMN-24%PT single crystals with composition away from the MPB on the rhombohedral side, [001]_c, [011]_c or [111]_c poled crystals all show two phase transitions. The absence of frequency dispersion of relative permittivity between 25 °C and T_d (~85 °C) indicates a formation of a macrodomain ferroelectric state in poled crystals induced by the poling field. However, some frequency dispersion of the permittivity between T_d and T_m was observed, indicating the presence of refined microdomains. T_d is usually related to the decay of the macrodomain state into microdomain states in the heating process, and is similar to the characteristic temperature T_d in relaxor ferroelectrics, such as lead lanthanum zirconate titanate (PLZT) and PMN [291,292]. The ferroelectric tetragonal to paraelectric cubic phase transition takes place near the dielectric maximum temperature T_m (~110 °C, i.e. T_C). In the [001]_c poled PMN-30%PT single crystals, two small dielectric constant peaks were observed at T_RM and T_MT below the Curie temperature. The first small peak shows a phase transition from the rhombohedral to monoclinic phase, and the second small peak indicates the transition from the monoclinic to tetragonal phase. Similarly, for [011]_c poled PMN-30%PT single crystals, there are also two small permittivity peaks at T_RO and T_OT, respectively, but here the orthorhombic phase is the intermediate phase in between the rhombohedral and the tetragonal phases, similar to the result of [011]_c poled PMN-33%PT. In the [001]_c poled PMN-33%PT single crystal with the MPB composition, a stable monoclinic phase induced by the applied poling field exists at room temperature. This phase was used to interpret the origin of the ultra-high piezoelectric property of the multidomain single crystals. As the temperature increases, the monoclinic phase transforms into the higher temperature tetragonal phase near T_MT (~62 °C). However, for the [011]_c poled PMN-33%PT and tetragonal PMN-38%PT single crystals, poling along the non-polar [011]_c direction gives rise to a much smaller dielectric constant (ε₃₃ ~800) and piezoelectric constant d₃₃ of only ~300 pC/N, which coincide with the values in the induced orthorhombic phase. These facts indicate that the poling field along [011]_c may have induced a stable single-domain orthorhombic ferroelectric phase in crystals with the MPB composition. As the temperature further increases, the orthorhombic phase transforms into the higher temperature tetragonal phase. For the [111]_c poled PMN-30%PT and PMN-33%PT single crystals, only one phase transition between the rhombohedral and tetragonal phases has been observed at T_RT. For the [001]_c and [111]_c poled PMN-38%PT single crystals, no phase transition happened below the tetragonal-cubic phase transition temperature.

Fig. 26.

The composition and temperature dependence of the dielectric constant at 0.1, 1, and 10 kHz in (a) [001]_c, (b) [011]_c, and (c) [111]_c poled PMN-PT single crystals [290].

4.3. Electric-field-induced large strain

For rhombohedral phase PMN-PT and PZN-PT single crystals, high field induced strains (~ 0.6%) were found in the [001]_c poled single crystals without hysteresis. Fig. 27(a) schematically presents engineered domain states and their piezoelectric responses under a bias for [001]_c poled rhombohedral single crystals. When an E-field is applied along [001]_c, the polarization is expected to incline towards the E-field direction in each domain (step A in Fig. 27(a)), resulting in an increased lattice distortion. Domain reorientation does not occur during this process because neighboring domains must involve equal amounts of induced distortion with polarizations rotating in opposite directions, producing net longitudinal strain in [001]_c direction [293].

Fig. 27.

(a) Schematic diagram of domain configurations in [001]_c oriented rhombohedral single crystals under electric field (step A-piezoelectricity, step B-induced phase transition with sufficiently large field), (b) strain vs. electric field behavior for [001]_c oriented PZN-8%PT single crystal [293,294].

Ultrahigh strain level up to 1.7% could be achieved by an electric field level of ~120 kV/cm in [001]_c oriented PZN-8%PT single crystal with small hysteresis, as shown in Fig. 27(b). The sharp change of slope is associated with an electric field induced rhombohedral-tetragonal phase transformation, which has been verified by in situ x-ray diffraction measurements, in situ domain observations, and E-field dependence of dielectric and piezoelectric constants [295]. Increased polarization inclination towards [001]_c finally results in the collapse of all polarizations into the [001]_c direction (step B in Fig. 27(a)), which is a field induced rhombohedral to tetragonal phase transition. The piezoelectric coefficient d₃₃ ~480 pC/N calculated directly from the slope of strain versus E-field in the high field region (between 40 and 120 kV/cm in Fig. 27(b)) corresponded well to the d₃₃ value determined for the tetragonal phase (~500 pC/N).

5. Characterization of full matrix material constants

5.1. Elastic, dielectric, and piezoelectric constants

Full matrix material constants, i.e., a complete set of elastic, dielectric, and piezoelectric constants, are the basic physical parameters for a piezoelectric material and are very important for the design of electromechanical devices as well as for fundamental studies on these single crystals. Generally speaking, there are a maximum of 21 elastic constants, 18 piezoelectric constants, and 6 dielectric constants for an anisotropic material, but the actual numbers of independent constants are much less, depending on the macroscopic symmetries of the material under consideration.

If we choose the electric field and strain as independent variables, the linear piezoelectric constitutive equations are given as follows:

$$T=c^E·S-e·E$$ (3)

$$D=e·S+{\epsilon }^S·E$$ (4)

where T, S, E, and D are the stress, strain, electric field and electric displacement, respectively; c^E is the elastic stiffness constant (fourth-order tensor) under constant E, e is the piezoelectric stress constant (third-order tensor), ε^S is the clamped dielectric constant (second-order tensor) under constant S.

The piezoelectric constitutive equations can be described in other forms by choosing different independent variables, for example,

$$S=s^E·T+d·E$$ (5)

$$D=d·T+{\epsilon }^T·E$$ (6)

with the stress and electric field as independent variables. Here s^E is the elastic compliance constant (fourth-order tensor) under constant E, d is the piezoelectric strain constant (third-order tensor), ε^T is the dielectric constant (second-order tensor) under constant T.

If we use stress and electric displacement as the independent variables, the constitutive relations become

$$S=s^D·T+g·D$$ (7)

$$E=-g·T+{\beta }^T·D$$ (8)

where s^D is the elastic compliance constant (fourth-order tensor) under constant D, g is the piezoelectric voltage constant (third-order tensor), β^T is the dielectric stiffness constant (second-order tensor) under constant T.

One may also use strain and electric displacement as the independent variables, so that

$$T=c^D·S-h·D$$ (9)

$$E=-h·S+{\beta }^S·D$$ (10)

where c^D is the elastic stiffness constant (fourth-order tensor) under constant D, h is the piezoelectric stiffness constant (third-order tensor), β^s is the dielectric stiffness constant (second-order tensor) under constant S.

The relations between those coefficients in the four sets of constitutive equations can be written as follows [296]

$$c_{\mathit{\text{pr}}}^E{s}_{qr}^E=c_{\mathit{\text{pr}}}^D{s}_{qr}^D={\mathrm{\delta }}_{pq}$$ (11)

$${\beta }_{ik}^s{\epsilon }_{jk}^s={\beta }_{ik}^T{\epsilon }_{jk}^T={\mathrm{\delta }}_{ij}$$ (12)

$$c_{pq}^D=c_{pq}^E+e_{kp}{h}_{kq}$$ (13)

$$s_{pq}^D=s_{pq}^E-d_{kp}{g}_{kq}$$ (14)

$${\epsilon }_{ij}^T={\epsilon }_{ij}^s+d_{iq}{e}_{jq}$$ (15)

$${\beta }_{ij}^T={\beta }_{ij}^s-g_{iq}{h}_{jq}$$ (16)

$$d_{ip}={\epsilon }_{ik}^T{g}_{kp}$$ (17)

$$e_{ip}=d_{iq}{c}_{qp}^E$$ (18)

$$g_{ip}={\beta }_{ik}^T{d}_{kp}$$ (19)

$$h_{ip}=g_{iq}{c}_{qp}^D$$ (20)

where i, j, k = 1,2,3 and p, q, r = 1, 2, 3, 4, 5, 6, and δ_ij is the 3×3 unit matrix and δ_pq is the 6×6 unit matrix.

The numbers of independent tensor components will be reduced for high symmetry systems. In the case of PZT piezoelectric ceramics, the symmetry is isotropic before poling and conical (∞m) after poling, the independent property tensor components for poled PZT ceramics are the same as those of point group 6mm, i.e., there are a total of 10 independent material constants: 5 elastic, 3 piezoelectric, and 2 dielectric constants. PMN-PT and PZN-PT single crystals have different macroscopic symmetries when being poled in different crystallographic directions [297]. The [001]_c poling produces macroscopic tetragonal 4mm symmetry with 11 independent material constants: 6 elastic, 3 piezoelectric, and 2 dielectric constants. The [111]_c poling produces macroscopic rhombohedral 3m symmetry with 12 independent material constants: 6 elastic, 4 piezoelectric, and 2 dielectric constants. The [011]_c poling produces macroscopic orthorhombic mm2 symmetry with 17 independent material constants: 9 elastic, 5 piezoelectric, and 3 dielectric constants.

5.2. Resonance and anti-resonance method

Determination of the elastic, piezoelectric and dielectric constants of a piezoelectric material is a delicate task. Many methods, including static, quasi-static, optical, resonance and ultrasonic pulse-echo techniques have been developed to measure these constants. The resonance method is the most popular one, in which some specific resonance modes are excited by applying an ac electric signal to piezoelectric samples of specific geometry, aspect ratio and polarization orientation as detailed in the IEEE standard on piezoelectricity [296]. Resonance and antiresonance frequencies can be directly measured from the impedance spectra for the piezoelectric resonators.

The resonance method described by the IEEE standard has been used to measure PZT ceramics with the symmetry of ∞m, for which the number of independent material constants are the same as that of 6mm symmetry. The useful compositions of PMN-PT and PZN-PT systems have 3m rhombohedral crystal symmetry, but the engineered domain structures have macroscopic symmetry of 4mm after the crystals have been polarized along [001]_c. Usually, five samples are needed for the resonance technique: (i) [001]-plate; (ii) square plate with its major surface normal to [100]_c ([100]_c plate); (iii) k₃₃-bar; (iv) k₃₁-bar; and (v) bar with length rotated from [100]_c by 45° and electrode surface normal to [001]_c (45° k₃₁-bar). The resonance frequency f_r and anti-resonance frequency f_a are recorded from the frequency spectrum to calculate corresponding constants based on the dynamic equations for piezoelectric vibrators.

The most important thing in the resonance and anti-resonance method is the aspect ratio of the piezoelectric vibrator, especially for shear vibration mode. For example, the measurement of k₁₅ for PZT cannot be easily made with high accuracy due to the coupling between the thickness and shear modes, and with other unwanted modes [298]. The coupling effect is usually more pronounced for the antiresonant frequency. The lower frequency mode among the two types of shear motions associated with the same shear stain deformation has lower strength and its vibration amplitude continuously decreases as the long dimension of the vibrator increases. A nearly pure shear mode may be obtained with the aspect ratio greater than 20, but the influence of the other low frequency mode could not be totally eliminated even at such a large aspect ratio [298].

The most important parameter characterizing a piezoelectric material is the electromechanical coupling factor, whose square specifies the conversion efficiency between electrical and mechanical energies for a given vibration mode. For the resonance along the poling direction, there are two coupling factors defined, i.e., k_t and k₃₃, which are for resonators of the same mode but two extreme aspect ratios, and differ substantially. Standard resonance technique for measuring the k value is based on one-dimensional approximation, which needs to use samples with extreme geometries [299]. The coupling factor k is actually a function of the vibrator aspect ratio, and a unified formula for k has been derived by solving 2-D coupled vibration equations with explicit dependence on the aspect ratio. This allows us to get an idea about the electromechanical coupling factor of resonators of arbitrary aspect ratios [300,301,302,303]. The unified formula for this coupling coefficient as a function of the vibrator aspect ratio of PZT ceramics is given by

$$k=\frac{d_{z3}+\frac{2d_{z1}{s}_{13}^E}{(s_{11}^E+s_{12}^E)}[g^2(G)-1]}{\sqrt{(s_{33}^E+\frac{2{\left(s_{13}^E\right)}^2}{(s_{11}^E+s_{12}^E)}[g^2(G)-1])({\epsilon }_{zz}^T+\frac{2d_{z1}^2}{(s_{11}^E+s_{12}^E)}[g^2(G)-1])}}$$ (21)

When the aspect ratio G→0, g(G)→0, Eq. (21) recovers the expression for k_t:

$$\underset{G\to 0}{\text{lim}}k=\frac{d_{z3}-\frac{2d_{z1}{s}_{13}^E}{(s_{11}^E+s_{12}^E)}}{\sqrt{(s_{33}^E-\frac{2{\left(s_{13}^E\right)}^2}{(s_{11}^E+s_{12}^E)})({\epsilon }_{zz}^T-\frac{2d_{z1}^2}{(s_{11}^E+s_{12}^E)})}}=\sqrt{\frac{e_{z3}^2}{c_{33}^D{\epsilon }_{zz}^s}}=k_t$$ (22)

When the aspect ratio G→∞, g(G)→1, Eq. (21) becomes k₃₃:

$$\underset{G\to \infty }{\text{lim}}k=\frac{d_{z3}}{\sqrt{{\epsilon }_{zz}^T{s}_{33}^E}}=k_{33}$$ (23)

The unified formulae can provide a more accurate description of the effective coupling coefficient of resonators not satisfying the extreme aspect ratio requirements. Besides k_t and k₃₃, the aspect ratio dependence of electromechanical coupling coefficient k₃₁ of lateral-excitation piezoelectric vibrators was also analyzed using the theory of coupled-mode vibrations [304,305]. Fig. 28(a) shows the electromechanical coupling coefficient k^eff as a function of the aspect ratio G for PMN-30%PT single crystal and PZT-5 ceramics. Fig. 28(b) shows the frequency constant as a function of the aspect ratio G for a PMN-30%PT single crystal piezoelectric resonator based on the mode-coupling theory.

Fig. 28.

(a) Electromechanical coupling coefficient k^eff as a function of the aspect ratio G for PMN-30%PT single crystal and PZT-5 ceramics, and (b) frequency constant as a function of the aspect ratio G for a PMN-30%PT single crystal piezoelectric resonator based on the mode-coupling theory [303].

5.3. Combined resonance and ultrasonic method

Although the resonance technique has been widely used in the characterization of piezoelectric materials, it is difficult to implement for low symmetry systems. This is because several samples (piezoelectric vibrators) must be used in the measurements in order to obtain a complete set of elastic, piezoelectric and dielectric constants for piezoelectric materials with low symmetries. The property differences among these samples will produce large errors and destroy the self-consistency of the tensor properties [306,307]. In addition, the extraordinarily large piezoelectric constants d₃₃ and d₃₁ and the more than 90% coupling factors of these relaxor-based single crystals make some constitutive formulae unstable when deriving quantities that cannot be measured directly [308].

The ultrasonic pulse-echo technique is also frequently used to determine the elastic constants of solid materials, which does not have to be piezoelectric [309]. By sending longitudinal and shear waves into samples of specified orientations, all elastic constants can be measured. The ultrasonic method is more accurate than other methods because it is performed under non-resonance conditions (no mode interference effects) and can measure many constants from one same sample by sending longitudinal and shear waves along different crystallographic directions. For low symmetry systems, the ultrasonic pulse-echo technique can be problematic because some constants cannot be directly measured from the phase velocities of pure modes, which need to be derived by solving a complicated coupled Christoffel equation. In addition, this method is not accurate for measuring the piezoelectric and dielectric constants. The main reason is that the solution of the Christoffel equation for materials with low symmetries is usually coupled, involving many constants. Large errors will be generated while extracting these constants from such mixed solutions.

In 1998, a combined resonance and ultrasonic method was developed, which was proven to be the most reliable method to determine the full matrix material constants for piezoelectric PZT ceramics [310,311]. Therefore, the method was used to obtain the complete sets of material constants of PMN-PT and PZN-PT single crystals with different symmetries. In the combined resonance and ultrasonic method, the dielectric constants are determined by capacitance measurements, some simple piezoelectric modes are used to determine the piezoelectric constants, and some pure acoustic modes are used to determine the elastic constants. The number of samples is greatly reduced and the final results became much more accurate. Over determination from the combined method also makes cross checks possible to guarantee self-consistency of these tensor properties. To date, many complete sets of elastic, piezoelectric and dielectric constants have been measured for PMN-PT, PZN-PT, and PIN-PMN-PT single crystals using the combined resonance and ultrasonic method, including different compositions and [001]_c, [111]_c, and [011]_c poling cases. Relaxor-PT single crystals whose full matrix data obtained by the resonance and anti-resonance method (RAM), and combined resonance and ultrasonic method (CRUM) are listed in Table 6. These full sets of matrix data are useful for fundamental studies on relaxor-based ferroelectric single crystals and are also critically important for the design of electromechanical devices using these relaxor-PT single crystals. Currently available self-consistent full matrix data are presented in the Appendix.

Table 6.

Relaxor-PT single crystals whose complete sets of material constants are determined using the resonance and anti-resonance method, or combined resonance and ultrasonic method.

Single crystal	Poling direction	Macroscopic symmetry	Domain structure	Measuring method
PZN-4.5%PT	[001]c	4mm	multidomain	CRUM [312]
PZN-(6–7)%PT	[111]c	3m	single domain	RAM [313]
PZN-7%PT	[001]c	4mm	multidomain	CRUM [314]
	[011]c	mm2	multidomain	CRUM [315]
PZN-8%PT	[001]c	4mm	multidomain	CRUM [50]
PMN-28%PT	[001]c	4mm	multidomain	CRUM [316]
	[011]c	mm2	multidomain	RAM [317] CRUM [316]
	[111]c	3m	single domain	CRUM [316]
PMN-29%PT	[011]c	mm2	multidomain	CRUM [318]
PMN-30%PT	[001]c	4mm	multidomain	RAM [319]
	[011]c	mm2	multidomain	RAM [317]
PMN-32%PT	[011]c	mm2	single domain	RAM [317]
PMN-33%PT	[001]c	4mm	multidomain	CRUM [49]
	[111]c	3m	single domain	CRUM [320]
PMN-35%PT	[001]c	4mm	single domain	RAM [321]
PMN-38%PT	[001]c	4mm	single domain	RAM [322]
PMN-42%PT	[001]c	4mm	single domain	CRUM [323]
PIN-49%PMN-27%PT	[111]c	3m	single domain	CRUM [194]
PIN-46%PMN-28%PT	[011]c	mm2	multidomain	CRUM [324]
	[111]c	3m	single domain	CRUM [325]
PIN-38%PMN-29%PT	[001]c	4mm	multidomain	CRUM [326]
	[011]c	mm2	multidomain	CRUM [326]
PIN-47%PMN-29%PT	[001]c	4mm	multidomain	CRUM [327]
	[011]c	mm2	multidomain	CRUM [327]
PIN-46%PMN-30%PT	[011]c	mm2	multidomain	CRUM [328]
PIN-42%PMN-32%PT	[011]c	mm2	multidomain	CRUM [324]
PIN-40%PMN-33%PT	[001]c	4mm	multidomain	CRUM [329]
Mn:PIN-46%PMN-27%PT	[111]c	3m	single domain	CRUM [270]
Mn:PIN-47%PMN-29%PT	[001]c	4mm	multidomain	CRUM [327]
	[011]c	mm2	multidomain	CRUM [327]
Mn:PIN-PMN-PT	[011]c	mm2	multidomain, single domain	CRUM [268,269]

5.4. Error analysis and self-consistency of matrix data

In the complete set of material constant measurements, several samples are usually needed to obtain enough independent measurements for anisotropic materials. To ensure the self-consistency of the measured data sets, it is necessary to perform detailed error analysis.

Generally speaking, the errors mainly come from three sources: The first is property variation from sample to sample. This problem is always present but becomes more severe for PMN-PT and PZN-PT single crystals because there are large composition variations along the growth direction due to the Ti segregation and the extremely sensitive nature of their material properties to chemical composition [330]. It was found that 1% PT composition variation may cause up to 50% variation in some properties near the MPB composition. Property fluctuations from sample to sample make it extremely difficult to obtain a self-consistent data set. Thus, one should try to use samples with the same chemical composition and use the least number of samples possible.

The second error source comes from the domain structure variation due to different poling procedures. The macroscopic properties of PMN-PT and PZN-PT single crystals strongly depend on their domain structures. Each sample needs to be poled before measurements and the difference in the degree of poling will generate different domain configurations. In addition, the obtained domain structures also depend on the geometric boundary conditions. Domain pattern variation will produce large property differences even when the composition uniformity is guaranteed. All these factors will contribute to the accuracy and self-consistency of the full matrix data. Hence, it is very important to ensure that the properties of different samples are as consistent as possible. A simple method for checking the poling condition is to measure the piezoelectric constant using the Piezo d₃₃ meter after poling each sample.

The third error source comes from textbook formulas for the derived coefficients, as not all constants can be directly measured. The resonance method or the combined resonance and ultrasonic method can only measure some constants, while a few other constants must be calculated by constitutive formulas. Error amplification may occur if unstable formulas are used. Therefore, error analysis is an important step in the full matrix property characterization.

It is known that if a quantity q=f(x₁, x₂, ⋯) is a function of some other quantities x₁, x₂, ⋯, with errors Δx₁, Δx₂, ⋯, then the error of q can be expressed as Δq =∑_i|∂f/∂x_i|Δx_i [331]. This expression can be used to estimate the relative errors of derived constants. As an example, the relative error amplification factors of the derived e₃₁ and e₃₃ based on the formula of $e_{31}=d_{31}(c_{11}^E+c_{12}^E)+d_{33}{c}_{13}^E$and $e_{33}=2d_{31}{c}_{13}^E+d_{33}{c}_{33}^E$ for PZN-4.5%PT, PMN-33%PT, PZN-8%PT, and BaTiO₃ single crystals have been calculated and are listed in Table 7. One can see that the larger are the amplitudes of d₃₁ and d₃₃, the larger are the relative errors of e₃₁ and e₃₃. When these formulas are used for BaTiO₃ single crystals, there are problems because the relatively small piezoelectric constants do not introduce large error amplification. But, some of the formulas become unstable when they are used for PZN-PT and PMN-PT single crystals because both d₃₁ and d₃₃ are very large. The total error of a derived constant depends not only on the errors of measured quantities, but also on the absolute amplitude of quantities to be used in the calculations that affect the error propagation. Based on the error analysis, a complete set of self-consistent material constants for PMN-PT and PZN-PT single crystals can be determined with minimized errors.

Table 7.

Relative error amplification factors of derived piezoelectric coefficients e₃₁ and e₃₃ caused by variations of some elastic constants [331].

	PZN-8%PT d31=−1450 d33=2900	PMN-33%PT d31=−1334 d33=2820	PZN-4.5%PT d31=−970 d33=2000	BaTiO3 d31=−34.5 d33=85.6
$(\mathrm{\Delta }{e}_{31}/e_{31})/(\mathrm{\Delta }{c}_{12}^E/c_{12}^E)$	52.5	37.6	21.5	2.3
$(\mathrm{\Delta }{e}_{31}/e_{31})/(\mathrm{\Delta }{c}_{13}^E/c_{13}^E)$	109	78.9	43.8	4.9
$(\mathrm{\Delta }{e}_{33}/e_{33})/(\mathrm{\Delta }{c}_{33}^E/c_{33}^E)$	19.2	15.6	14.9	3.9
$(\mathrm{\Delta }{e}_{33}/e_{33})/(\mathrm{\Delta }{c}_{13}^E/c_{13}^E)$	36.6	31	28.7	7.2

There are also some fundamental physical principles which could be used to check if those obtained data are sound: (i). Energy conservation demands the electromechanical coupling factors to be always less than 100%. Thus, large piezoelectric constants demand large dielectric constants. After a full set of material constants are determined, the static electromechanical coupling factors for any vibration mode can be calculated. If any of these coupling factors is larger than 1, related data set are in question. (ii). When an elastic material deforms, the continuity requirement must be satisfied. For example, the Poison’s principle requires that all three dimensions cannot expand (or contract) at the same time under uniaxial force or field in these samples. This demands some elastic compliance constants to be negative. For example, for 4mm symmetry crystals, $s_{12}^E$ and $s_{13}^E$ must be negative and the compressibility must be positive, i.e., $2s_{11}^E+2s_{12}^E+4s_{13}^E+s_{33}^E>0$ [332]. For mm2 symmetry crystals, both $s_{12}^E$ and $s_{13}^E$ are generally negative. In special cases, one of $s_{12}^E$ and $s_{13}^E$ could be positive, then the other must be more negative. (iii). The elastic strain energy of a crystal should be positive. For example, for 4mm symmetry crystals, $c_{44}^E>0,c_{66}^E>0,c_{11}^E>\left|c_{12}^E\right|,(c_{11}^E+c_{12}^E)c_{33}^E>2{(c_{13}^E)}^2$, and $(s_{11}^E+s_{12}^E)s_{33}^E>2{(s_{13}^E)}^2$ must be satisfied. (iv). All types of piezoelectric constants d, e, h, and g should have the same signs. For example, for 4mm symmetry crystals, d₃₁ < 0 means that e₃₁, g₃₁ and h₃₁ should all be negative [333].

6. Acoustic properties

6.1. Bulk acoustic wave propagation in PMN-PT single crystal

Based on the measured full matrix of elastic, dielectric, and piezoelectric material constants, the orientation dependence of bulk sound velocity can be calculated by finding the eigenvalues and eigenvectors of Christoffel’s tensor for given wave propagation directions. For example, in the [001]_c poled PMN-33%PT single crystal, it was found that velocities of the longitudinal waves do not change as much as shear waves for different propagation directions [49]. In addition, the shear wave velocity in the [100]_c-[010]_c plane has a maximum (2882 m/s) in [100]_c and a minimum (880 m/s) in ${[\overline{11}0]}_{\mathrm{c}}$, respectively, which implies that a “soft shear acoustic mode” exists in this domain engineered single crystal. A similar situation was also found for the PZN-4.5%PT single crystal [312].

6.2. Guided wave propagation in PMN-PT single crystal

Some electromechanical devices use guided waves to achieve the conversion between mechanical energy and electrical energy. Such acoustic guided waves propagating in plates can be decoupled into two kinds of waves, namely, shear horizontal (SH) waves and Lamb waves, while Lamb waves can be further divided into symmetric and antisymmetric modes. The zero^th order symmetric mode (S₀) and antisymmetric mode (A₀) Lamb waves are the most useful ones [334,335]. Partial wave theory is the most commonly used method for analyzing harmonic wave propagation in anisotropic materials [336,337,338].

The guided waves propagating along [100]_c of a [001]_c poled PMN-33%PT crystal plate for short circuit case are shown in Fig. 29(a). The symmetric [S_i] and antisymmetric [A_i] modes exhibit multiple crossings as they approach the surface wave limits. Similar intercrossing dispersion relations were also found in nickel plates with free boundary conditions and a strongly orthotropic copper polycrystalline plate [339]. Note that as frequency increases, the velocities of the SH modes approach the bulk transversal wave velocity of 2880 m/s, which is coincident with the shear wave velocity in the [100]_c direction with displacement perpendicular to the poling direction. The dispersion relations of Lamb waves propagate along [110]_c direction of [001]_c poled PMN-33%PT crystal plate are shown in Fig. 29(b). In this direction, its Rayleigh wave velocity is about two times of that in the [100]_c direction, and the SH modes approach 880 m/s at high frequencies, which corresponds to the soft shear mode of bulk crystal observed in the [110]_c direction with displacement in the [11̄0]_c direction.

Fig. 29.

Guided waves propagating along (a) [100]_c and (b) [110]_c of [001]_c poled PMN-33%PT crystal plates for short circuit case [335].

Overall, the propagation of guided waves in free standing PMN-PT single crystals polarized along [001]_c, [011]_c and [111]_c of the cubic reference directions (so that the effective macroscopic symmetries are 4mm, mm2 and 3m, respectively) have been studied theoretically. Multiple mode couplings appear in the dispersion curves for both the symmetric and the antisymmetric Lamb mode and shear horizontal mode. The velocities of most guided waves decrease rapidly with frequency. The details of velocity dispersions can be found in Refs [340,341].

6.3. Surface acoustic wave propagation in PMN-PT single crystals

The power of surface acoustic wave (SAW) is concentrated near the surface of the device. SAW propagation velocity is much slower than that of electromagnetic waves, and signals can be accessed freely in the process of propagation. SAW devices have advantages of small size, low cost and broad compatibility. In recent years, SAW devices made of piezoelectric materials are widely used as radio frequency filters, delay line oscillators, resonators in communication systems, and sensors in chemical and biological industries [342, 343, 344, 345, 346]. The surface acoustic wave propagation characteristics of the piezoelectric single crystal can be obtained by solving the Christoffel equation with semi-infinite crystal boundary conditions [347].

When varying the propagation angle from 0° to 180°, the surface acoustic wave propagation in X-cut, Y-cut, and Z-cut relaxor-based PMN-33%PT ferroelectric single crystals poled along [001]_c has been analyzed theoretically. The corresponding phase velocity curves of free surface at the Y-cut and Z-cut are shown in Fig. 30. The PMN-33%PT single crystal with such a low SAW phase velocity compared with quartz and LGT is favorable for further miniaturization of SAW devices. The electromechanical coupling factor was found to be much higher than that of traditional piezoelectric materials. The power flow angle (PFA) can be zero in certain directions, which makes this crystal system a promising material for future SAW devices with much smaller size and enhanced performance [348,349,350,351].

Fig. 30.

The SAW phase velocity of [001]_c poled PMN-33%PT single crystal at (a) X-cut, (b) Y-cut, and (c) Z-cut [348].

6.4. Frequency dispersions of velocity and attenuation

6.4.1 Frequency dispersion of sound velocity

High-frequency broadband ultrasonic transducers can improve the axial and lateral resolution in medical imaging [352,353]. The design of high-frequency transducers requires better knowledge of material properties since ultrasonic dispersion becomes very important for frequencies above 50 MHz. The dispersions of velocity and attenuation may deform the acoustic pulse and cause inappropriate interpretation of ultrasonic signals. Hence, knowing the dispersions of velocity and attenuation of transducer materials at high frequencies is important for the design of high-frequency transducers, and for analyzing pulse signals in image processing. PZT piezoelectric ceramics have been the dominant ultrasonic transducer materials for the past 50 years. In 1999, the dispersions of velocity and attenuation of PZT-5H piezoelectric ceramics in the frequency range of 20–60 MHz were measured by using an ultrasonic spectroscopy method [354,355,356]. It was found that PZT ceramics exhibit high attenuation and large velocity dispersion at high frequencies due to the strong scattering of acoustic waves at the grain boundaries [357,358]. Therefore, LiNbO₃ and quartz crystals are usually used for making ultrasonic transducers for frequencies above 25 MHz [359,360]. Although they have negligible dispersion and attenuation at frequencies up to several hundred megahertz, their piezoelectric constants and electromechanical coupling factors are too low to produce broadband transducers with good sensitivity. This affects the penetration depth and consequently the imaging quality.

[001]_c poled PZN-PT and PMN-PT multidomain single crystals have much superior piezoelectric properties. The large d₃₃ and high k₃₃ are very attractive for making broadband ultrasonic transducers. High-frequency properties of these engineered domain single crystals have been investigated by using ultrasonic spectroscopy, and the results are very encouraging. Both the attenuation and velocity dispersions are very small in the frequency range of 50–110 MHz, making these crystals excellent piezoelectric materials for high frequency medical ultrasonic transducers [361]. Fig. 31 shows the frequency dispersion of the slowness of the longitudinal wave in the poling direction for [001]_c and [110]_c poled PMN-32%PT and [001]_c poled PMN-28%PT single crystals [362]. The dispersions of slowness in PZT-4 ceramic and LiNO₃ single crystal are also given for comparison.

Fig. 31.

The frequency dispersion of the slowness of the longitudinal wave in the poling direction for [001]_c and [110]_c poled PMN-32%PT and [001]_c poled PMN-28%PT single crystals. The dispersions of slowness in PZT-4 ceramic and LiNO₃ single crystal are also given for comparison [362].

6.4.2. Frequency dispersion of attenuation

The frequency dependence of ultrasonic attenuation of the longitudinal wave in the poling direction for [001]_c and [110]_c poled PMN-32%PT and [001]_c poled PMN-28%PT single crystals are shown in Fig. 32. The frequency dependence of ultrasonic attenuation in PZT-4 ceramic and LiNbO₃ single crystals are also provided for comparison. It was found that the dispersion and attenuation of PMN-PT single crystal are much smaller than that of PZT-4 ceramics, which has the lowest attenuation in the family of PZT ceramics. The frequency dispersion of the phase velocity of PMN-28%PT single crystals is comparable to that of LiNbO₃, whereas its attenuation is larger than that of LiNbO₃. In addition, the attenuation and velocity dispersion of PMN-32%PT single crystals poled along [110]_c are a little smaller than that of [001]_c poled PMN-32%PT single crystals. However, both crystals exhibit much higher attenuation and velocity dispersion than that of PMN-28%PT single crystals. This indicates that the domain pattern become more attenuative for high-frequency waves in the PMN-PT single crystals as its composition gets near the MPB. The ultrasonic attenuation in multidomain single crystals is mainly caused by the wave scattering from domain walls. Therefore, increasing domain-wall density will naturally cause more severe attenuation. This attenuation information is very critical for the practical application of the PMN-PT crystals since different electromechanical devices will have different requirements for the attenuation level. The actual sensitivity and bandwidth of an ultrasonic transducer are determined by the piezoelectric constants, electromechanical coupling factors as well as ultrasonic attenuation.

Fig. 32.

Frequency dependence of ultrasonic attenuation of the longitudinal wave in the poling direction for [001]_c and [110]_c poled PMN-32%PT and [001]_c poled PMN-28%PT single crystals. The dispersions of slowness in PZT-4 ceramic and LiNO₃ single crystals are also provided for comparison [362].

6.4.3. Kramers-Kronig relation and frequency dependence of elastic constants

It is known that the velocity dispersion for an acoustic wave propagating in an unbounded medium is mainly caused by the attenuation. In this case, the real and imaginary parts of the wave number, or phase velocity and attenuation, are correlated through the Kramers-Kronig relationship. Therefore, the phase velocity dispersion can be derived from the measured frequency-dependent attenuation and vice versa [363]. The approximate nearly local relationship is given by

$$v(\omega )=v({\omega }_0)+\frac{2v^2({\omega }_0)}{\pi }{\int }_{{\omega }_0}^{\omega }\frac{\alpha (\omega )}{{\omega }^2}d\omega$$ (24)

$$\alpha (\omega )=\frac{\pi {\omega }^2}{2v^2({\omega }_0)}\frac{dv(\omega )}{d\omega }$$ (25)

where ω₀ is the starting angular frequency, v(ω) and α(ω) are the sound velocity and attenuation coefficient at angular frequency ω, respectively.

The velocity and attenuation dispersion derived from the Kramers-Kronig relationship for [001]_c poled PIN-45%PMN-31%PT are shown in Fig. 33 together with the experimental data [364]. The small difference between the experimental data and the Kramers-Kronig relations is caused by the nonlinear nature of the material, because the Kramers-Kronig relations are valid only for a linear medium.

Fig. 33.

Frequency dispersion of the phase velocity and attenuation of the longitudinal wave in a [001]_c poled PIN-45%PMN-31%PT single crystal [364].

Based on the Christoffel wave equation, the phase velocity of longitudinal waves propagating along the poling direction [001]_c is connected with the elastic stiffness constant $c_{33}^D=\rho v^2$. When the attenuation is taken into account, the elastic stiffness constant becomes a complex number: $c_{33}^D=c\text{'}+jc"$. In general, we have |c"|<<|c'| for most known materials. The complex wave number can be expressed as

$$k^{*}=k-j\alpha$$ (26)

where k = ω/v is the wave number and α is the attenuation coefficient. Thus, the real and imaginary parts of the elastic stiffness constant are related to the measured phase velocity and attenuation by the following relations

$$c\text{'}=\rho v^2$$ (27)

$$c"=\frac{\rho v^3\alpha }{\pi f}$$ (28)

From the measured frequency dependence of phase velocity and attenuation, the real and imaginary parts of the elastic stiffened constant can be also calculated, as shown in Fig. 34.

Fig. 34.

Frequency dispersion of real and imaginary parts of elastic stiffness constant $c_{33}^D$ of a [001]_c poled PIN-45%PMN-31%PT single crystal [364].

7. Optical properties

7.1. Linear optical properties

Linear optical properties, such as refractive indices and their dispersions, optical transmittance as function of wavelength, and optical band gap characteristics, are necessary parameters for designing optical devices. For relaxor-based ferroelectrics, as-grown (unpoled) crystals at room temperature have many domain walls inside, and nanoregions of different orientations with respect to the optic axis. Domain boundaries cause multiple scattering and generate larger scattering losses [365,366]. Hence, relaxor-PT single crystals must be poled to eliminate these scattering centers for optical applications. It was found that after being poled along their spontaneous polarization directions, the crystals have much enhanced optical transmittance compared with their unpoled states [367]. Fig. 35 shows the PMN-38%PT single crystal before and after poling, revealing that the crystal is transparent to light with wavelength between 0.45µm and 5.5 µm and becomes completely absorbing below 0.4 µm in near the UV region and beyond 10 µm in the infrared region (optical absorption edges) [368,369]. Other relaxor-PT single crystals have similar transparent regions, such as PZN-PT and high-Curie temperature PIN-PT single crystals [370,371,372]. In addition, the wavelength cutoff in near UV is much sharper than the long wavelength cutoff, as shown in Fig. 35(c). Compared to crystals with rhombohedral and MPB compositions, tetragonal single crystals possess much superior transmission properties [373]. For example, the tetragonal PMN-38%PT single crystal has the spontaneous polarization along [001]_c. After being poled along [001]_c, the PMN-38%PT single crystal is in single domain state and the losses due to domain walls reduce substantially; hence the optical transmittance becomes much higher (~70%) with the reflection loss of 20%. It is believed that its optical transmittance may reach 90% after depositing antireflection coatings, indicating that tetragonal single crystals are promising for a wide range of optical and electro-optical applications [373].

Fig. 35.

(a) The PMN-38%PT as-grown crystal boules obtained by modified Bridgman technique. (b) After being poled and polished. (c) The transmission characteristics of [001]_c oriented PMN-38%PT single crystal before and after poling [368].

From optical transmission spectra, optical band gaps can be determined. It was found that as the PT content increases, the refractive index of PMN-PT single crystals increases, while the optical band gap energy decreases [374,375,376]. Similar phenomena have been found in relaxor-based ferroelectric PMN-PT thin films [377]. For PZN-PT single crystals, the optical absorption edges have a red-shift with increasing PT contents: it is 380 nm, 390 nm, 400 nm, and slightly more than 400 nm for x=0.45 [365], 0.07 [378], 0.09 [379], and 0.10 [380], respectively. For the PZN-xPT and PMN-xPT A(B₁B₂)O₃-type perovskite compounds, the common (B₁B₂)O₆ oxygen-octahedral structure determines the basic energy levels in the crystal. Therefore, we can anticipate that PZN-xPT and PMN-xPT single crystals with various compositions should have similar optical absorption edges with slight differences due to the different B-site (including B₁ and B₂) cations [365].

7.2. Electro-optic properties

Nowadays, electro-optic (EO) crystals have many applications, such as spatial light modulators [381], optical switches [382] and volume holographic memories [383]. Most of bulk electro-optic modulation devices operate on the basis of transverse and/or longitudinal electro-optic effects. In optical modulations, low operating voltage is preferred. Generally speaking, larger aspect ratio and higher EO coefficients are the two key factors for decreasing the half-wave voltage of the modulator. The EO effect describes the change Δn_ij in the refractive index due to an applied electric field E.

$$\mathrm{\Delta }{n}_{ij}=-\frac{1}{2}{n}_{ij}^3(\sum _{k=1}^3{r}_{ijk}{E}_k+\sum _{k,l=1}^3{g}_{ijkl}{E}_k{E}_l)$$ (29)

where n_ij is the refractive index, r_ijk and g_ijkl are linear and quadratic EO coefficients, respectively [384].

Early in 1973, the quadratic EO coefficients of PZN-PT single crystals have been characterized in the temperature region above the Curie temperature [385]. With the increase in PbTiO₃ content, the quadratic EO coefficient g increases. In 2000, the linear E-O coefficient r of PZN-PT was measured [384]. Later, the composition, orientation, and temperature dependences of linear E-O coefficients of PZN-PT and PMN-PT single crystals were investigated in more details [386]. Fig. 36, which shows the linear E-O coefficients r₁₃ and r₃₃ vs. compositions for PZN-PT single crystals, reveals several features. First, compared with r₃₃, r₁₃ is very small in both rhombohedral and tetragonal phase crystals. Second, the large EO coefficient r₃₃ was observed for compositions near the MPB, which is much higher than that of commonly used EO crystals, such as LiNbO₃ (r₃₃~30 pm/V) [387]. Third, for the PZN-0.08PT single crystal, the r₃₃ coefficient of the crystal poled in [001]_c (multidomain state) is much higher than that of the crystal poled in [111]_c (single domain state). More importantly, EO coefficients have much better temperature stability for crystals on the tetragonal side of the MPB [386].

Fig. 36.

Linear E-O coefficients r₁₃ and r₃₃ vs. compositions for PZN-PT single crystals [386].

PMN-PT single crystals have similar E-O properties as PZN-PT single crystals [388]. Fig. 37 shows the effective E-O coefficient r_c (usually used in optical intensity modulations) vs. composition for PMN-PT single crystals, r_c is expressed as [389]

$$r_c=r_{33}-{(\frac{n_{\mathrm{o}}}{n_{\mathrm{e}}})}^3{r}_{13}$$ (30)

Fig. 37.

Combined E-O coefficient r_c vs. compositions for PMN-PT single crystals [389].

Generally, E-O coefficients r₁₃ and r₃₃ can be measured by the Mach-Zender interferometer method [390], and the combined E-O coefficient r_c can be measured by the Sénarmont system [391,392].

Why do these relaxor-based ferroelectric single crystals have such large E-O coefficients? The reason is that the linear E-O coefficient r_ij is linked to the polarization-related quadratic E-O coefficients g_ij [388]. For single crystals in the rhombohedral phase, the E-O coefficients can be written as

$$r_{33}=\frac{2}{3}{\epsilon }_{33}{\epsilon }_0{P}_s(g_{11}+2g_{12}+2g_{44})$$ (31)

$$r_{13}=\frac{2}{3}{\epsilon }_{33}{\epsilon }_0{P}_s(g_{11}+2g_{12}-g_{44})$$ (32)

$$r_{51}=\frac{2}{3}{\epsilon }_{11}{\epsilon }_0{P}_s(g_{11}-g_{12}-\frac{1}{2}{g}_{44})$$ (33)

For single crystals in the tetragonal phase, the linear E-O coefficients can be related to polarization-related quadratic E-O coefficients g₁₁ and g₁₂, which can be determined in the prototype cubic phase at temperatures above the Curie temperature T_C ($\mathrm{\Delta }{n}_{ij}=-\frac{1}{2}{n}_{ij}^3\sum _{k,l=1}^3{r}_{ijkl}{p}_k{p}_l$, where P_k is the polarization component in the k direction),

$$r_{33}=2{\epsilon }_{33}{\epsilon }_0{P}_s{g}_{11}$$ (34)

$$r_{13}=2{\epsilon }_{33}{\epsilon }_0{P}_s{g}_{12}$$ (35)

where P_S and ε₃₃ are the spontaneous polarization and dielectric constant, respectively. Therefore, the observation of a negligibly small r₁₃ in comparison to r₃₃ implies a negligibly small g₁₂ in comparison to g₁₁. A large r₃₃ and a near-zero r₁₃ indicates that the applied electric field in the spontaneous polarization direction does not affect the overall polarization of the unit cell in directions perpendicular to it. Furthermore, the near-zero g₁₂ implies that the refractive index in these directions will not change with P_S as temperature changes, even at the FE-PE phase transition.

In addition, the influence of the converse piezoelectric effect on the electro-optic coefficients of the single domain PZN-0.07PT single crystal has been quantified under ambient conditions. It was found that the large piezoelectric constants d₃₁ and d₃₃ have a significant influence on the half-wave voltage of electro-optic modulators. Compared to commonly used electro-optic crystals LiNbO₃ and BaTiO₃, PZN-xPT single crystals are superior for optic phase modulation applications because they have much higher linear electro-optic coefficients and much lower half-wave voltages when the piezoelectric strain influence is considered [393]. For the single domain PZN-0.07PT crystal, the half-wave voltage $V_{\pi 13}^T$ is reduced by a factor of 8 and $V_{\pi 13}^L$ can be decreased by more than an order of magnitude due to the large piezoelectric effect.

More recently, linear E-O properties of PIN-PMN-PT single crystals, with compositions in the rhombohedral, MPB and tetragonal phases, have been investigated. A very large effective E-O coefficient r_c (204 pm/V) was observed in a PIN-PMN-PT single crystal with the MPB composition when it is poled along [001]_c. The half-wave voltage was calculated to be less than 1000V, which is much less than that of LiNbO₃ single crystal (2800V). Such superior properties make the ternary PIN-PMN-PT single crystals very promising for E-O modulation applications [394].

7.3. Acousto-optic properties

The acousto-optic (A-O) effect can also be used for optical modulations, called “acousto-optic modulation”. The A-O effect describes the change of the refractive index of a material due to applied stress or strain. The A-O coefficient π_ijkl relating the refractive index change Δn_ij and the applied mechanical stress T_ij is defined as [395].

$$\mathrm{\Delta }{n}_{ij}=-\frac{1}{2}{n}_{ij}^3\sum _{k,l=1}^3{\pi }_{ijkl}{T}_{kl}$$ (36)

Compared with widely used A-O materials, such as LiNbO₃ (π₃₃ = 0.2×10⁻¹² m²/N), PZN-PT single crystals possess very large A-O coefficients (π₃₃ =19.8×10⁻¹² m²/N) [396], and the large anisotropy exhibited in these coefficients allow designers more freedom to manipulate device performance. Because relaxor-PT single crystals also possess very high E-O and piezoelectric responses, it allows the development of a class of unique devices combining the high A-O [397], E-O, and piezoelectric effects, which could lead to significant advance in new devices with reduced size, enhanced performance, and minimized power consumption.

7.4. Photorefractive properties

In 2003, the photorefractive effect in the [111]_c poled PZN-9%PT single crystal was investigated by the two-wave mixing measurement [379], and the gain coefficient was similar to that of the undoped Sr_0.61Ba_0.39Nb₂O₆ single crystal [398]. The coupling constant of the two-wave mixing was 17 cm⁻¹, and the normalized time constant under 1 W·cm⁻² illumination was 12 s at the wavelength of 476 nm. The effective trap density is 5×10¹⁶ cm⁻³ and the dominant charge carriers were identified to be holes from the direction of two-wave mixing energy transfer. Later, the photorefractive effect in the Fe-doped PZN-9%PT single crystal was investigated. The maximum gain coefficient reached as high as 21 cm⁻¹, which is twice as large as that of undoped PZN-9%PT. It was also found that the grating formation rate decreased with the Fe concentration [399]. Recently, photorefractive properties of the [001]_c poled PMN-38%PT single crystal have been investigated by the two-wave mixing method [400]. The maximum gain coefficient was 5.4 cm⁻¹, the effective trap density was 1.2×10¹⁶ cm⁻³, and the normalized photorefractive response time under 1 W/cm² illumination was 1.5 s at the wavelength of 632.8 nm. The dominant charge carriers were again identified as holes from the direction of two-wave mixing energy transfer.

8. Device applications

The super-large piezoelectric strain constant d₃₃ (>2000 pC/N) and ultra-high electromechanical coupling factor k₃₃ (>90%) make [001]_c poled rhombohedral relaxor-based ferroelectric single crystals, including PMN-PT, PZN-PT, and PIN-PMN-PT, very attractive for electromechanical device applications, including medical ultrasonic transducers, actuators, vector sensors, accelerometers, hydrophones, and underwater acoustic transducers. Many electromechanical devices using these domain engineered single crystals show significant performance improvements compared to devices using PZT piezoelectric ceramics. In addition, relaxor-based ferroelectric single crystals were also used to make infrared (IR) detectors due to their extremely large pyroelectric effects. This section briefly reviews some recent progress in device applications using these relaxor-based ferroelectric single crystals.

8.1. Medical ultrasonic imaging transducers

Ultrasonic imaging is one of the most powerful tools in medical diagnosis for its excellent image resolution, deep penetration capability, free of harmful radiation and lower price compared to computed tomography (CT), magnetic resonance imaging (MRI), and X-ray imaging. The key component of an ultrasound imaging equipment is the ultrasonic transducer (or probe). High-frequency broadband ultrasonic transducers can offer better axial and lateral resolutions in medical ultrasonic imaging. As mentioned in Sec. 6, the relaxor-based ferroelectric single crystals have small attenuation and velocity dispersion in the frequency range of 20–100 MHz, making them good candidates for making high frequency medical ultrasonic transducers. Some high-performance medical ultrasonic imaging transducers had been designed using these relaxor-based ferroelectric single crystals [401,402].

In 1998, a 20 MHz single-element ultrasonic probe was successfully fabricated using the [001]_c poled PZN-9%PT single crystal [403]. The bandwidth of the probe was 13–26 MHz, which was 4 MHz broader than that of corresponding PZT-based ultrasonic probe. For higher sensitivity and broader bandwidth, a 96-channel phased array probe was fabricated in 1999 using a PZN-9%PT single-plate for echocardiography [404]. The bandwidth of the probe (center frequency at 3.5 MHz) almost equals to the combined bandwidths of two conventional PZT ceramic probes with center frequencies of 2.5 and 3.75 MHz. The echo amplitude of the probe was ~ 6 dB higher than that of the two PZT probes and the fractional bandwidths were 30% and 25% wider, respectively. The B-mode image quality of the PZN-9%PT probe was comparable to that of the two PZT probes, and the Doppler sensitivity was about the same as that of the 2.5 MHz PZT probe. This means that the PZN-9%PT probe matches the penetration of the 2.5 MHz PZT probe while having the resolution of the 3.75 MHz PZT probe. The structure of the 96-channel phased array probe is shown in Fig. 38. Later, a novel 128-channel phased array probe with center frequency of 3.7 MHz was fabricated using the PZN-9%PT single crystal, which had 5 dB higher sensitivity and 25% broader bandwidth than the corresponding PZT ceramic transducers [405]. In addition, it was found that the 40-channel phased array single-matching-layer probe with a center frequency of 3.5 MHz using the PZN-9%PT single crystal had a bandwidth broader than that of PZT probes with two-matching-layers [406]. In 2002, phased array probes were fabricated using the PZN-7%PT single crystal instead of the PZN-9%PT single crystal because the PZN-7%PT single crystal has better thermal stability [407]. The echo amplitudes and the bandwidths of those probes were almost the same as those of PZN-9%PT probes. Therefore, PZN-7%PT single crystal achieved the optimum balance between large piezoelectric properties and reasonable thermal stability; hence, it is more suitable for ultrasonic medical imaging transducers than other compositions of PZN-PT single crystals.

Fig. 38.

The construction of 96-channel phased array probe [404].

As mentioned above, phased array transducers using relaxor-PT single crystals instead of PZT ceramics as the active driving element were found to have 20–25% bandwidth and 3–5 dB sensitivity improvements, which allows these single-crystal transducers to produce significantly better quality images [408,409]. Theoretically, 130% bandwidth could be possible for PMN-PT based array transducers based on the KLM modeling. Experimentally, a measured bandwidth of up to 114% was reported for a PMN-PT array element [410]. In addition, finite element simulations were also performed to design single-crystal transducers using PZ-Flex based on measured full matrix electromechanical coefficients [411]. In 2002, a 64 channel 2.6 MHz phased array ultrasonic probe was fabricated using the PMN-33%PT single crystal [412]. The sensitivity of this PMN-PT probe was about 6 dB higher than that of corresponding PZT probe, and the −6 dB bandwidth was about 30% broader. The sensitivity variation of the PMN-PT probe was within ±2.0 dB. It was shown that the PMN-PT probe had higher sensitivity than that of PZT probe in the harmonic mode image. The color Doppler imaging of the PMN-PT probe, as shown in Fig. 39, was superior over that of the PZT probe. The color Doppler sensitivity of PMN-PT probe was about 5 dB higher than that of PZT probe. In 2003, a 128 channel 7.5 MHz linear array ultrasonic probe was fabricated using the PMN-33%PT single crystal. The sensitivity of the PMN-PT probe was about 3 dB higher than that of PZT probe, and the −6 dB bandwidth was about 30% broader. The sensitivity variation of PMN-PT probe was similar to that of the PZT probe [413]. Hence, phased array probes using relaxor-PT single crystals have triggered revolutionary changes in ultrasonic imaging quality due to their much higher sensitivity and broader bandwidth.

Fig. 39.

Color Doppler mode images of (a) PZT probe and (b) PMN-PT probe [412].

Piezoelectric materials are often incorporated into a polymer matrix to form 1–3 or 2-2 composites for improving the electromechanical coupling and decreasing the acoustic impedance of the piezoelectric resonator in ultrasound transducers [414]. In 2000, 3.5–4.5 MHz single element PZN-8%PT/polymer 1–3 composite transducers with −6 dB bandwidths of 75–141% were fabricated [415] and in 2003, a broadband single element Doppler transducer using 1–3 PMN-PT/epoxy composite was reported [416], as shown in Fig. 40. PiezoCad software was used to model several transducer designs to determine the best composite ratio and matching layer configurations for sub and second harmonic imaging. The transducer has a center frequency of 5.2 MHz with −6 dB bandwidth over 120%, ranging from 2.08 MHz to 8.32 MHz. Because the transducer response maintained at a high level even outside of the −6 dB band range, the actual useable bandwidth was estimated to be about 200%.

Fig. 40.

(a) Schematic of the transducer; (b) Picture of the broad band single element transducer [416].

In 2003, PMN-33%PT/epoxy 1–3 composites with different volume fractions of PMN-PT ranging from 0.4 to 0.8 were fabricated [417]. Their thickness electromechanical coupling factors can reach as high as 80%. A 2.4 MHz plane ultrasonic transducer, as shown in Fig. 41, was fabricated using a PMN-33%PT/epoxy 1–3 composite with 0.37 volume fraction of PMN-33%PT single crystal, which shows a −6 dB bandwidth of ~61% and an insertion loss of −14 dB. In 2010, a PMN-PT single crystal/epoxy 1–3 composite was fabricated by using a DRIE dry etching process with a 45% volume fraction of PMN-PT, which has an effective electromechanical coupling coefficient of 81%. A 35 MHz high-frequency ultrasonic flat transducer was fabricated using this composite, and the transducer has an insertion loss of 18 dB, and a −6 dB bandwidth as high as 100%. Tungsten wire phantom imaging shows that the transducer has an axial resolution of ~30 µm [418].

Fig. 41.

Photograph of the ultrasonic transducers and a drawing showing the structure of the transducer [417].

Philips started its single crystal investigation in 1997. The first broadband phased array transducer was released to the market in Nov. 2004 [419], which was named “PureWave” probe. The cardiac images obtained by a “PureWave” probe are shown in Fig. 42. In the tissue harmonic mode, the increased sensitivity and bandwidth of the single crystal transducer provide improved penetration depth, border delineation, and myocardial tissue assessment, even at deep depths on technically difficult to image patients. The resulting harmonic images have reduced clutter noises with enhanced structure details as seen in the endocardium and fine structures, such as valves and chordae tendinae. Color flow images also show excellent penetration and the ability to detect more detailed blood flows.

Fig. 42.

Apical 4 chamber view of cardiac harmonic (a) and color flow images (b) obtained using a single crystal transducer by Philips [419].

Phacoemulsification is a very common surgical procedure for treating cataracts. During the surgical operation, a surgeon makes a small incision about 3 mm wide on the cornea, and inserts a needle-thin probe with a diameter of around 1.2 mm into the cataract lens, hence combining a needle transducer with a phacoemulsification probe can facilitate real-time measurements of ultrasound attenuation during cataract surgery. Recently, a 46 MHz high-frequency needle transducer with a diameter of 0.9 mm was designed and fabricated using a 50-µm-thick PMN-33%PT single crystal, and was used to determine the acoustic properties of the lens [420,421]. A high-frequency needle ultrasound transducer with an aperture size of 0.4 mm was fabricated using a PMN-33%PT single crystal [422]. The center frequency and −6 dB bandwidth of the PMN-PT needle transducer were 44 MHz and 45%, respectively. The two-way insertion loss was approximately 15 dB. The transducers can be used for pulsed-wave Doppler and imaging applications. In 2008, a high-frequency angled needle ultrasound transducer with an aperture size of 0.4×0.56 mm² was fabricated using a PZN-7%PT single crystal. The angled needle probe configuration was achieved by dicing at 45° to the single crystal poling direction to satisfy a clinical request for blood flow measurement in the posterior portion of the eye, and wire phantom imaging was conducted using this transducer. The center frequency and the bandwidth at −6 dB of this transducer were 43 MHz and 45%, respectively and the two-way insertion loss was approximately 17 dB [423]. In 2009, a 40 MHz PMN-PT needle transducer with a beveled tip of 45° was used to image the posterior segment of the eye [424]. In 2010, a 45-MHz ultrasonic Doppler system with a PMN-PT needle transducer was developed to measure the blood flow velocity of rabbit retinal vessels [425]. In 2010, a novel high-frequency ultrasonic transducer structure was realized by using the PMNPT-on-silicon technology and silicon micromachining. The measured center frequency and −6 dB bandwidth were 35 MHz and 34%, respectively. Owing to the superior electromechanical coupling factor k_t and high piezoelectric constant d₃₃ of PMN-PT films, the transducer showed a good energy conversion efficiency with a very low insertion loss of 8.3 dB at the center frequency [426]. Recently, endoscopic ultrasound (EUS) radial arrays were fabricated with piezocrystal and piezocomposite, as shown in Fig. 43, which can be used in the endoscopic ultrasonic imaging [427,428]. The PMN-PT piezocrystal radial array transducer exhibits ~80% bandwidth and the PMNPT/Epoxy 1–3 piezocomposite radial array transducer exhibits ~100% bandwidth. Both bandwidths are broader than that of commercial PZT array transducers (< 70 %).

Fig. 43.

Photographs of the fabricated EUS transducers with (a) structure 1, and (b) structure 2 [427].

Ternary PIN-PMN-PT single crystals, due to their high coercivity and high depoling temperature, are promising materials for high-frequency ultrasound transducers for medical imaging applications. In 2008, a high-frequency ultrasonic transducer was fabricated using the PIN-44%PMN-32%PT single crystal. The center frequency and bandwidth were 35 MHz and 48 %, respectively, and the insertion loss was about 15 dB [429]. In 2009, two high-frequency PIN-PMN-PT single crystal ultrasound transducers at center frequencies of 35 MHz and 60 MHz were successfully fabricated using the PIN-50%PMN-27%PT single crystal, which showed similar performance but better thermal stability compared to the PMN-PT transducers [430]. The measured pulse-echo waveforms and spectra for the 35 and 60 MHz PIN-PMN-PT transducers are shown in Fig.44. In 2011, 1–3 composites based on PIN-45%PMN-31%PT single crystal and high-temperature epoxy were fabricated with volume fractions of PIN-PMN-PT ranging from 0.4 to 0.9. Ultrahigh electromechanical coupling factor (k_t=82%–93%) and low acoustic impedance (Z=17–19 MRayl) were obtained from room temperature up to 185 °C. Single element ultrasonic transducers using the PIN-PMN-PT 1–3 composite can still work normally at higher temperatures. Even at 165 °C, the transducer still has a bandwidth of 95% and the insertion loss of only −27 dB [431].

Fig. 44.

Measured pulse-echo waveforms and frequency spectra for the 35 and 60 MHz PIN-PMN-PT transducers [430].

Relaxor-xPT single crystals with composition near the MPB have the best piezoelectric properties but relatively poor thermal stability, while crystals with compositions far away from the MPB have good thermal stability but worse piezoelectric properties. Hence, people usually choose crystals with composition slightly away from the MPB for transducer applications to achieve the optimum balance between high piezoelectric performance and good thermal stability.

8.2. Acoustic sensors

In 2001, miniature (mesoscale) accelerometers were fabricated utilizing PMN-PT and PZN-PT single crystals as sensor elements [432]. In the frequency range from 100 Hz to 1000 Hz, the spectral noise of the crystal-based accelerometers was approximately one order of magnitude lower (20 dB down) than that of the PZT-based accelerometers with equal dynamic mass and physical dimensions. In addition, a novel method of strain amplification in flexural-type accelerometers, called platformed unimorph accelerometers (PUMA™), was used to create a new-type of accelerometers utilizing PZN-PT single crystals. The new accelerometer exhibited a 15 dB reduction in its noise floor [433]. A PUMA operating in the flexural mode and stress distribution in a PUMA accelerometer configuration employing a PZN-PT single crystal sensing element is shown in Fig. 45.

Fig. 45.

(a) PUMA operating in the flexural mode, and (b) the stress distribution in a PUMA accelerometer configuration employing a single crystal PZNT sensing element [433].

PMN-PT single crystals were also used to make electron acoustic signal detectors for the Electron Acoustic Imaging System (EAIS), which is a new nondestructive technology for microstructure analysis, defects testing beneath the surface and properties study in micro-regions [434]. The amplitude of electron acoustic signal detected by the PMN-PT detector was twice as high as that of a PZT-type detector. The resolution of the electron acoustic image was substantially improved.

In addition, PMN-PT single crystals had been used to make miniature vector sensors, as shown in Fig. 46, for towed array applications. This particular sensor has operational bandwidth from 5 Hz-7 kHz with a noise floor that crosses a sea state 0/shipping level 1 noise curve at approximately 1000 Hz for the accelerometers. The omni-directional hydrophone element (which uses conventional PZT) is quieter than the sea state curve across the entire frequency band. The excellent piezoelectric properties of the PMN-PT crystals allowed the vector sensor to meet underwater SONAR receiver required sensitivity and bandwidth [435,436].

Fig. 46.

Miniature vector sensor made by PMN-PT single crystal [435].

8.3. Actuators and related devices

In 2004, multilayer prototype actuators with 10 mm length were fabricated by a stack method using 55 pieces of 5×5×0.15 mm³ PMN-PT single crystals and PZT-5A ceramics. The stacking configuration of the monolithic multilayer piezoelectric actuator is shown in Fig. 47(a). The strain values for PMN-PT multilayer piezoelectric actuators are twice of those from PZT-5A multilayer actuators [437,438]. The side view of several single-crystal PMN-PT multilayer prototype actuators is shown in Fig. 47(b).

Fig. 47.

(a) Stacking configuration of a monolithic multilayer piezoelectric actuator, and (b) side view of single-crystal PMN-PT multilayer prototype actuators [437].

In 2005, a piezoelectric fluid ejector was fabricated using a PMN-35%PT single crystal ring [439], as shown in Fig 48. The ejector has a very high axial displacement and can be driven at a low voltage. The performance of the PMN-PT ejector was much better than that of a corresponding PZT ceramic ejector.

Fig. 48.

(a) Schematic diagram and (b) photograph of PMN-PT actuated ejector [439].

In 2007, two cylinder-shaped ultrasonic motors with 4.8 mm in diameter were developed. The motor was driven by four pieces of piezoelectric materials, which were used to excite the first-bending mode, as shown in Fig. 49 [440]. PMN-PT single crystals and PZT ceramics were used as the drive elements in the two motors. The one based on PMN-PT single crystal could operate at a low voltage of 25 V_p-p (peak to peak). When driven at a 100 V_p-p voltage, the motor could run at frequencies ranging from 26 to 68 kHz, the revolution speed can reach 450 rpm at 42.25 kHz. The motor based on PZT ceramics performed much worse than the PMN-PT motor. In general, the motors had the largest revolution speed when excited at their resonant frequencies. In 2010, cylinder-shaped ultrasonic motors based on PMN-PT single crystals were fabricated, which had wider exciting frequencies, lower exciting voltages and much larger mechanical output power than conventional PZT ceramics based motors. The largest revolution speed of the PMN-PT motor is 780 rpm and a maximum load reached ~0.008 Nm [441].

Fig. 49.

(a) Structure of the piezoelectric composite stator and (b) operating principle of the motor. The symbol P indicates the polarization direction [440].

Ternary PIN-PMN-PT single crystals were used to fabricate a double-mode piezoelectric ultrasonic micro-actuator. The longitudinal displacement of the actuator is ~0.11 µm with an applied voltage of 5 V, which is comparable to that of a multilayer piezoelectric-ceramic actuator of the same size. This crystal micro-actuator was successfully used to drive a slider moving linearly [442]. In 2013, a face-shear mode ultrasonic motor (USM) made of a [011]_c poled Zt±45° cut PIN-PMN-PT single crystal was developed as shown in Fig. 50, which took the advantage of the extremely large d₃₆=2368 pC/N [443]. This motor has a maximum no-load linear velocity of 182.5 mm/s and a maximum output force of 1.03 N under the drive of V_p=50 V at the frequency of f=72 kHz. Compared with the k₃₁ mode USM made of PZT, the k₃₆ mode USM has simpler structure, lower driving frequency, much higher electromechanical coupling factor, and more than twice power density. This USM may be used for low frequency operations as well as cryogenic actuations with a large torque.

Fig. 50.

Face-shear PIN-PMN-PT single crystal ultrasonic motor: (a) motor configuration; (b) mode shape of the stator; (c) motion trajectory of the driving tip [443].

8.4. Other electromechanical devices

PMN-PT and PZN-PT single crystals were also used to make sound projectors (underwater SONAR transducers) using the k₃₁-mode [444], k₃₂-mode [445] and k₃₃-mode [446,447,448,449]. In most SONAR projectors, the piezoelectric element is driven in the k₃₃-length extensional mode by a large electric field ~0.4 MV/m under compressive mechanical stress ranging from 7 MPa to 63 MPa. The purpose of this pre-stress is to prevent the piezoelectric elements from going into tension state during operation. It was found that an elastic instability of the rhombohedral crystal happened near 30 MPa compression. This instability was attributed to the ferroelectric rhombohedral (F_R) to orthorhombic (O_R) phase transition with the polarization rotated from [111]_c to [011]_c. A dc bias field of ~0.60 MV/m could stabilize the F_R state for up to 40 MPa compressive stresses for PMN-30%PT single crystals [450]. Therefore, a stable operation of SONAR projectors fabricated using PMN-PT and PZN-PT single crystals requires the use of a bias electric field [451]. For this reason, crystals with improved thermal stability and higher coercive field, such as PMN-PZT [452] and PIN-PMN-PT [453] single crystals, would be more suitable for sound projectors than PMN-PT single crystals.

In 2006, PMN-PT single crystals and PZT ceramics were used to construct ultrasonic transducers for non-destructive evaluation (NDE) applications [454]. The PMN-PT single crystal showed more uniform large surface displacements than that of the PZT disc, as shown in Fig. 51. In 2011, angle beam two-element prototype ultrasonic transducers for NDE applications using PMN-PT single crystals and PMN-PT/epoxy 1–3 composites were fabricated [455]. Both the PMN-PT single crystal and commercial PZT-based 1–3 composite transducers show similar performance in sensitivity and bandwidth, while the PMN-PT/epoxy 1–3 composite transducer gave the best performance. The two-way insertion loss and bandwidth of the PMN-PT/epoxy 1–3 composite transducer at −6 dB are −21.3 dB and 94.5%, respectively.

Fig. 51.

Displacement amplitudes across the top surfaces of the: (a) PMN-PT and (b) PZT discs measured by a laser vibrometer (Vertical scale: 50 nm/V) [454].

In 2008, a multilayer Rosen-type piezoelectric transformer 20 mm long, 4 mm wide and 2.8 mm thick was fabricated using a PMN-29%PT single crystal [456]. The efficiency of this transformer can reach 92% and the voltage step-up ratio under open circuit condition exceeded 100. Furthermore, the transformer can successfully drive a 0.5 W LCD backlight under a lower input voltage than for a PZT transformer without an obvious temperature rise. In 2010, a longitudinal piezoelectric transformer 16 mm long, 2 mm wide and 2 mm thick was designed and fabricated using a PMN-29%PT single crystal [457]. Compared to the Rosen-type transformer, this transformer has advantages of smaller-size, simpler structure, no spurious vibrations and no acoustic mismatch between the input and output parts. At the resonance frequency of 114 kHz, a step-up voltage of about 30 can be achieved under a 10 MΩ load resistance.

PMN-PT single crystals were also used to fabricate energy-harvesting devices, which can be used in low-power portable electronics and wireless sensors [458,459]. The energy-harvesting devices based on PMN-29%PT single crystals showed a high output power of 4.94 mW and a peak voltage of 3.14 V under a cyclic force of 4 N at 1.4 kHz with a matching load resistance of 1.0 kΩ [460], as shown in Fig 52. Under a cyclic force of 0.05 N, a peak voltage of 91.23 V and a maximum power of 4.16 mW were obtained at 60 Hz with a proof mass of 0.5 g [461].

Fig. 52.

(a) The side view of the layer and the electrodes; (b) the plan form of the layer and the electrodes; (c) the schematic diagram of the multilayer structure device [460].

In 2010, a high frequency ultrasonic needle transducer for microfluidic analysis system was fabricated using a PMN-PT single crystal. The center frequency and −6 dB bandwidth of the PMN-PT needle transducer were 60 MHz and 36%, respectively. The two-way insertion loss was −15.8 dB. Such devices had been successfully built into a microfluidic channel for measuring the acoustic velocity and attenuation of the medium flowing into the channel [462]. A shear-mode PMN-PT single crystal-based piezoelectric resonator was integrated in a microfluidic system for cell detection [463], as shown in Fig 53.

Fig. 53.

Cross sectional schematic (a), top view configuration (b), and photograph (c) of the microfluidic acoustic device integrated with a shear mode PMN-PT piezoelectric single crystal resonator. [463].

8.5. Pyroelectric devices

Pyroelectric devices are widely used for thermal radiation energy detections and thermal radiation configuration imaging based on continuous wave, pulse or modulated signals [464]. Pyroelectric detectors have faster response and higher detection sensitivity than other thermal detectors. They also have broader and more uniform spectral responsivity with lower cost than other infrared (IR) detectors based on photon detection mechanisms. Pyroelectric devices could be operated at relatively wide temperature range, which makes them applicable for uncooled IR detection and imaging applications. Traditional pyroelectric materials for pyroelectric devices include LiTaO₃ (LT), triglycine sulfate (TGS), barium strontium titanate (BST) and lead scandium tantalite (PST). They have been utilized to fabricate portable uncooled infrared focal plane arrays (UFPA) for military, paramilitary, and commercial imaging applications [465,466].

However, LT and TGS have very low dielectric constants, which is unfavorable for UFPA devices. On the other hand, BST and PST must be operated under electrical bias and require temperature stabilization. Recent investigations on relaxor-based ferroelectric single crystals revealed that they possess excellent pyroelectric characteristics, including very high pyroelectric coefficients, low thermal diffusivity and high figures of merit. At room temperature, the [111]_c-oriented PMN-29%PT single crystal has a pyroelectric coefficient p (12.8×10⁻⁴ C/m² K), a low thermal diffusivity D (~3.7×10⁻⁷ m²/s), and a high detectivity figure of merit F_d (> 9.8×10⁻⁵ Pa^−1/2), which make PMN-PT single crystals excellent materials for uncooled infrared detectors and other IR imaging applications. Fig. 54 shows the pyroelectric coefficients of PMN-PT single crystals as a function of composition and crystal orientation at room temperature [467,468,469,470,471,472]. The pyroelectric coefficients of PMN-xPT single crystals decrease with increasing the PT content x. The pyroelectric coefficients of the [111]_c oriented PMN-xPT single crystals (x ≤ 0.3) with a rhombohedral crystal structure are larger than those of [011]_c and [001]_c oriented single crystals, whose polarization directions are 35.3° and 54.7°, respectively, from the polar direction [111]_c. The results indicate that the pyroelectric coefficients oriented along the spontaneous polarization direction are larger than those poled in other crystallographic directions.

Fig. 54.

Pyroelectric coefficients as a function of the composition and the crystal orientation at room temperature for PMN-xPT single crystals [467].

There are other attempts at making pyroelectric devices using PMN-PT single crystals. Fig. 55 shows the single element pyroelectric detector and its interior view [473,474]. The PMN-26%PT single crystal element size is Φ= 2 mm with a metal back layer. The thickness of the PMN-PT single crystal is 60 µm and the electrodes are NiCr. When the detector was irradiated by chopped infrared radiation from a blackbody furnace at 500 K at the frequency of 12.5 Hz, the voltage responsivity was 211 V/W and the detectivity D*=1.06×10⁸ cm·Hz^1/2·W⁻¹. The performance already met the requirements of practical devices. It is expected that the prototype can be further improved through optimizing the device structure design, improving the processing of single crystals and decreasing the thickness of the elements.

Fig. 55.

The pyroelectric detectors based on PMN-PT single crystals [473].

In 2011, the applicability of PIN-PMN-PT single crystal in pyroelectric detectors was evaluated and compared with high-quality Mn-doped PMN-28%PT and standard LTO. Pyroelectric and dielectric measurements confirmed an increased operating temperature range due to higher phase transition temperatures of PIN-PMN-PT. Pyroelectric coefficients of 705–770 µC/m²K were obtained in PIN-PMN-PT single crystals, which is about 70% to 80% of that of PMN-PT single crystals but still four times higher than that of LTO. Manganese doping has proven a good solution to decrease the dielectric loss of PMN-PT and PIN-PMN-PT single crystals. An outstanding specific detectivity D* of about 1·10⁹ cm·Hz^1/2/W was achieved at the frequency of 3 Hz for Mn-doped PMN-PT and PIN-PMN-PT detectors [475]. The fabricated pyroelectric PMN-PT detector and the circuit diagram are shown in Fig. 56 [476].

Fig. 56.

(a) Pyroelectric PMN-PT detector and (b) circuit diagram [476].

9. Summary and expectations

This article provides an up to date review on the development of relaxor-based ferroelectric single crystals and their applications, including binary PMN-PT and PZN-PT, ternary PIN-PMN-PT, as well Mn-doped PMN-PT and Mn-doped PIN-PMN-PT single crystals. Topics covered in this article include hystorical development, crystal growth methods, accurate full matrix property characterization, fundamental mechanism studies and practical device innovations. The correlation between functional properties and the morphotropic phase boundaries are discussed, and phase diagrams of these single crystals were summarized. Specific attention was given to the domain engineering concept, which can be realized by poling the rhombohedral phase crystals along [001]_c, [011]_c and [111]_c pseudo-cubic directions. Domain pattern symmetries are created through domain engineering process, which lead to the enhancement of particular functional properties, giant piezoelectric properties and pyroelectric properties. It was confirmed that the large electric field induced strains in these crystals mainly come from polarization rotation effect.

Relaxor-PT ferroelectric single crystals were successfully grown by the high temperature flux technique, top seeded solution growth technique and solid state growth technique, but only the modified Bridgman method could produce high quality crystals that are large enough for commercial device applications. Many complete sets of elastic, piezoelectric and dielectric constants of PMN-PT, PZN-PT, and PIN-PMN-PT single crystals with different symmetries were measured using the combined resonance and ultrasonic method to guarantee self-consistency. These data are very useful for device designs and fundamental studies. Hence, we have compiled them in the Appendix for interested researchers conducting fundamental research on these crystals or using them for device simulations. The attenuations and velocity dispersions of these crystals are small, so that they can be used for high frequency medical ultrasonic transducers.

We also summarized device innovations utilizing the super-large piezoelectric and pyroelectric properties, as well as the ultra-high electromechanical coupling factors of these relaxor-based ferroelectric single crystals. The new piezoelectric materials have triggered the birth of many new generation electromechanical devices, including ultrasonic transducers, sensors and actuators with greatly improved performance. In particular, the [001]_c poled PMN-PT single crystals have brought a revolutionary improvement in medial ultrasonic imaging.

With the much improved mechanical Q-values and the substantially increased temperature stability, Mn-doped PIN-PMN-PT single crystals, which has been called the 4^th generation of relaxor-PT single crystals, are expected to bring revolutionary changes to underwater SONAR systems and other high-power piezoelectric devices. Looking ahead, as the crystal quality becomes more uniform and the cost of production becomes lower, one could expect many new innovative devices being created in the near future utilizing the superior and tunable piezoelectric, pyroelectric, and dielectric properties of these amazing relaxor-PT single crystals.

Of course, at the moment, there are still some open questions, such as Ti segregation during growth, optimization of domain patterns for specified applications, better thermal stability and the high cost to grow these crystals. Some possible solutions to resolve these issues are already emerging, for example, continuous-feeding growth technique is under development to counter the Ti segregation problem, which could increase the useful portion of the crystal boules to help improve the uniformity and lower the cost. People are also trying to find new ways to manipulate the size and configurations of domains, which could further enhance piezoelectric effects. With many researchers still actively involved in this field, we can optimistically expect that these issues be successfully resolved within the next few years.

Nomenclature

A₀

Zero^th order antisymmetric mode

ABO₃

Perovskite structure

C

Capacitance

c^D

Elastic stiffness constant under constant electric displacement

c^E

Elastic stiffness constant under constant electric field

D

Electric displacement

d_ij

Piezoelectric strain constant

E

Electric field

E_C

Coercive field

e_ij

Piezoelectric stress constant

F

Free energy

f

Frequency

f_a

Anti-resonance frequency

f_r

Resonance frequency

g_ij

Piezoelectric voltage constant

h_ij

Piezoelectric stiffness constant

k

Wave number

k_ij

Electromechanical coupling factor

Q_m

Mechanical quality factor

P_r

Remnant polarization

P_s

Spontaneous polarization

S

Strain

S₀

Zero^th order symmetric mode

s^D

Elastic compliance constant under constant electric displacement

s^E

Elastic compliance constant under constant electric field

T

Stress

tanδ

Dielectric loss tangent

T_C

Curie temperature

T_m

Temperature of dielectric maximum

T_RT

Rhombohedral-tetragonal phase transition temperature

U

Internal energy

v

Sound velocity

v_l

Longitudinal wave velocity

v_s

Shear wave velocity

Z

Acoustic impedance

α

Attenuation coefficient

β^S

Dielectric stiffness constant under constant strain

β^T

Dielectric stiffness constant under constant stress

ε^S

Dielectric constant under constant strain

ε^T

Dielectric constant under constant stress

ε^r

Relative permittivity

ε_max

Dielectric permittivity maximum

ρ

Density

(φ,θ,ψ)

Euler’s angles

2D

Two dimensional

CT

Computed tomography

DFT

Diffuse phase transition

EAIS

Electron acoustic imaging system

E-O

Electro-optic

ESR

Electron spin resonance

LAPW

Linearized augmented plane wave

LDA

Local density-functional approximation

M-phase

Monoclinic phase

MPB

Morphotropic phase boundary

MRI

Magnetic resonance imaging

NDE

Non-destructive evaluation

O-phase

Orthorhombic phase

PFA

Power flow angle

PIN-PT

(1-x)Pb(In_1/2Nb_1/2)O₃-xPbTiO₃

PIN-PMN-PT

(1-x-y)Pb(In_1/2Nb_1/2)O₃-yPb(Mg_1/3Nb_2/3)O₃-xPbTiO₃

PLZT

Pb_1-xLa_x(Zr_1-yTi_y)_1-x/4O₃

PMN

Pb(Mg_1/3Nb_2/3)O₃

PMN-PT

(1-x)Pb(Mg_1/3Nb_2/3)O₃-xPbTiO₃

PMRs

Polar micro-regions

PNRs

Polar nano-regions

PSN-PT

(1-x)Pb(Sc_1/2Nb_1/2)O₃-xPbTiO₃

PT

PbTiO₃

PVDF

Polyvinylidene fluoride

PYN-PT

(1-x)Pb(Yb_1/2Nb_1/2)O₃-xPbTiO₃

PZ

PbZrO₃

PZN

Pb(Zn_1/3Nb_2/3)O₃

PZN-PT

(1-x)Pb(Zn_1/3Nb_2/3)O₃-xPbTiO₃

PZT

PbZr_1-xTi_xO₃

R-phase

Rhombohedral phase

SAW

Surface acoustic wave

SH

Shear horizontal

SSCG

Solid-state crystal growth

Subscript “c”

Cubic coordinates

T-phase

Tetragonal phase

TDGL

Time-dependent Ginzburg Landau

TSSG

Top seeded solution growth

Appendix

Independent full matrix data of relaxor-PT single crystals are given in the following format:

$$\left(\begin{array}{cccccccccccc}\hfill c_{11}^E\hfill & \hfill c_{12}^E\hfill & \hfill c_{13}^E\hfill & \hfill c_{14}^E\hfill & \hfill c_{15}^E\hfill & \hfill c_{16}^E\hfill & \hfill d_{11}\hfill & \hfill d_{12}\hfill & \hfill d_{13}\hfill & \hfill d_{14}\hfill & \hfill d_{15}\hfill & \hfill d_{16}\hfill \\ \hfill c_{21}^E\hfill & \hfill c_{22}^E\hfill & \hfill c_{23}^E\hfill & \hfill c_{24}^E\hfill & \hfill c_{25}^E\hfill & \hfill c_{26}^E\hfill & \hfill d_{21}\hfill & \hfill d_{22}\hfill & \hfill d_{23}\hfill & \hfill d_{24}\hfill & \hfill d_{25}\hfill & \hfill d_{26}\hfill \\ \hfill c_{31}^E\hfill & \hfill c_{32}^E\hfill & \hfill c_{33}^E\hfill & \hfill c_{34}^E\hfill & \hfill c_{35}^E\hfill & \hfill c_{36}^E\hfill & \hfill d_{31}\hfill & \hfill d_{32}\hfill & \hfill d_{33}\hfill & \hfill d_{34}\hfill & \hfill d_{35}\hfill & \hfill d_{36}\hfill \\ \hfill c_{41}^E\hfill & \hfill c_{42}^E\hfill & \hfill c_{43}^E\hfill & \hfill c_{44}^E\hfill & \hfill c_{45}^E\hfill & \hfill c_{46}^E\hfill & \hfill {\epsilon }_{11}^T\hfill & \hfill {\epsilon }_{12}^T\hfill & \hfill {\epsilon }_{13}^T\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill c_{51}^E\hfill & \hfill c_{52}^E\hfill & \hfill c_{53}^E\hfill & \hfill c_{54}^E\hfill & \hfill c_{55}^E\hfill & \hfill c_{56}^E\hfill & \hfill {\epsilon }_{21}^T\hfill & \hfill {\epsilon }_{22}^T\hfill & \hfill {\epsilon }_{23}^T\hfill & \hfill \hfill & \hfill \rho \hfill & \hfill \hfill \\ \hfill c_{61}^E\hfill & \hfill c_{62}^E\hfill & \hfill c_{63}^E\hfill & \hfill c_{64}^E\hfill & \hfill c_{65}^E\hfill & \hfill c_{66}^E\hfill & \hfill {\epsilon }_{31}^T\hfill & \hfill {\epsilon }_{32}^T\hfill & \hfill {\epsilon }_{33}^T\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$

where $c_{ij}^E$ (10¹⁰ N/m²) is the elastic stiffness constant under constant E, d_ij (10⁻¹² C/N) is the piezoelectric strain constant, ε^T (ε₀) is the dielectric constant under zero stress and ρ (kg/m³) is the mass density. Other constants can be calculated by the following constitutive equations:

$$c_{\mathit{\text{pr}}}^E{s}_{qr}^E=c_{\mathit{\text{pr}}}^D{s}_{qr}^D={\mathrm{\delta }}_{pq}$$

$${\beta }_{ik}^s{\epsilon }_{jk}^s={\beta }_{ik}^T{\epsilon }_{jk}^T={\mathrm{\delta }}_{ij}$$

$$c_{pq}^D=c_{pq}^E+e_{kp}{h}_{kq}$$

$$s_{pq}^D=s_{pq}^E-d_{kp}{g}_{kq}$$

$${\epsilon }_{ij}^T={\epsilon }_{ij}^s+d_{iq}{e}_{jq}$$

$${\beta }_{ij}^T={\beta }_{ij}^s-g_{iq}{h}_{jq}$$

$$d_{ip}={\epsilon }_{ik}^T{g}_{kp}$$

$$e_{ip}=d_{iq}{c}_{qp}^E$$

$$g_{ip}={\beta }_{ik}^T{d}_{kp}$$

$$h_{ip}=g_{iq}{c}_{qp}^D$$

where i, j, k = 1,2,3 and p, q, r = 1, 2, 3, 4, 5, 6; δ_ij is the 3×3 unit matrix and δ_pq is the 6×6 unit matrix [296].

1. PZN-4.5%PT single crystal poled along [001]_c [312]

   $$\left(\begin{array}{cccccccccccc}\hfill 11.1\hfill & \hfill 10.2\hfill & \hfill 10.1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 140\hfill & \hfill 0\hfill \\ \hfill 10.2\hfill & \hfill 11.1\hfill & \hfill 10.1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 140\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 10.1\hfill & \hfill 10.1\hfill & \hfill 10.5\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -970\hfill & \hfill -970\hfill & \hfill 2000\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.4\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 3100\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.4\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 3100\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8310\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.3\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 5200\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
2. PZN-(6–7)%PT single crystal poled along [111]_c [313]

   $$\left(\begin{array}{cccccccccccc}\hfill 18.0\hfill & \hfill 8.0\hfill & \hfill 4.8\hfill & \hfill -2.6\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6000\hfill & \hfill 2560\hfill \\ \hfill 8.0\hfill & \hfill 18.0\hfill & \hfill 4.8\hfill & \hfill 2.6\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1280\hfill & \hfill -1280\hfill & \hfill 0\hfill & \hfill 6000\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 4.8\hfill & \hfill 4.8\hfill & \hfill 17.1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -35\hfill & \hfill -35\hfill & \hfill 93\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -2.6\hfill & \hfill 2.6\hfill & \hfill 0\hfill & \hfill 1.6\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 11000\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1.6\hfill & \hfill -2.6\hfill & \hfill 0\hfill & \hfill 11000\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8207\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -2.6\hfill & \hfill 5.0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 700\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
3. PZN-7%PT single crystal poled along [001]_c [314]

   $$\left(\begin{array}{cccccccccccc}\hfill 11.3\hfill & \hfill 10.3\hfill & \hfill 10.5\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 176\hfill & \hfill 0\hfill \\ \hfill 10.3\hfill & \hfill 11.3\hfill & \hfill 10.5\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 176\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 10.5\hfill & \hfill 10.5\hfill & \hfill 10.91\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -1204\hfill & \hfill -1204\hfill & \hfill 2455\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.3\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 3000\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.3\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 3000\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8350\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 7.1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 5622\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
4. PZN-7%PT single crystal poled along [011]_c [315]

   $$\left(\begin{array}{cccccccccccc}\hfill 14.50\hfill & \hfill 15.32\hfill & \hfill 12.67\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1823\hfill & \hfill 0\hfill \\ \hfill 15.32\hfill & \hfill 18.02\hfill & \hfill 15.00\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 50\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 12.67\hfill & \hfill 15.00\hfill & \hfill 14.10\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 478\hfill & \hfill -1460\hfill & \hfill 1150\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.47\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 8240\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0.34\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1865\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8038\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 7.10\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 3180\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
5. PZN-8%PT single crystal poled along [001]_c [50]

   $$\left(\begin{array}{cccccccccccc}\hfill 11.5\hfill & \hfill 10.5\hfill & \hfill 10.9\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 159\hfill & \hfill 0\hfill \\ \hfill 10.5\hfill & \hfill 11.5\hfill & \hfill 10.9\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 159\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 10.9\hfill & \hfill 10.9\hfill & \hfill 11.51\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -1455\hfill & \hfill -1455\hfill & \hfill 2890\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.34\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 2900\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.34\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 2900\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8315\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.50\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 7700\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
6. PMN-28%PT single crystal poled along [001]_c [316]

   $$\left(\begin{array}{cccccccccccc}\hfill 12.04\hfill & \hfill 10.68\hfill & \hfill 9.19\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 122\hfill & \hfill 0\hfill \\ \hfill 10.68\hfill & \hfill 12.04\hfill & \hfill 9.19\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 122\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 9.19\hfill & \hfill 9.19\hfill & \hfill 10.35\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -569\hfill & \hfill -569\hfill & \hfill 1182\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.57\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1672\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.57\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1672\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8092\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.12\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 5479\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
7. PMN-28%PT single crystal poled along [011]_c [316]

   $$\left(\begin{array}{cccccccccccc}\hfill 19.53\hfill & \hfill 8.30\hfill & \hfill 1.12\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 2162\hfill & \hfill 0\hfill \\ \hfill 8.30\hfill & \hfill 19.53\hfill & \hfill 8.97\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 160\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1.12\hfill & \hfill 8.97\hfill & \hfill 13.82\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 447\hfill & \hfill -1150\hfill & \hfill 860\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.57\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 4235\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0.48\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1081\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8095\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 4.45\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 3873\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
8. PMN-28%PT single crystal poled along [111]_c [316]

   $$\left(\begin{array}{cccccccccccc}\hfill 19.10\hfill & \hfill 8.66\hfill & \hfill 4.08\hfill & \hfill -1.27\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 2382\hfill & \hfill 624\hfill \\ \hfill 8.66\hfill & \hfill 19.10\hfill & \hfill 4.08\hfill & \hfill 1.27\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 312\hfill & \hfill -312\hfill & \hfill 0\hfill & \hfill 2382\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 4.08\hfill & \hfill 4.08\hfill & \hfill 17.02\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -43\hfill & \hfill -43\hfill & \hfill 97\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -1.27\hfill & \hfill 1.27\hfill & \hfill 0\hfill & \hfill 1.03\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 4983\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1.03\hfill & \hfill -1.27\hfill & \hfill 0\hfill & \hfill 4983\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8095\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -1.27\hfill & \hfill 5.22\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 593\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
9. PMN-29%PT single crystal poled along [011]_c [318]

   $$\left(\begin{array}{cccccccccccc}\hfill 22.9\hfill & \hfill 13.56\hfill & \hfill 13.03\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1188\hfill & \hfill 0\hfill \\ \hfill 13.56\hfill & \hfill 10.9\hfill & \hfill 11.3\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 167\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 13.03\hfill & \hfill 11.3\hfill & \hfill 13.9\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 610\hfill & \hfill -1883\hfill & \hfill 1020\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.7\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 3564\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1.44\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1127\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8090\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 7.67\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 4033\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
10. PMN-30%PT single crystal poled along [001]_c [319]

    $$\left(\begin{array}{cccccccccccc}\hfill 16.04\hfill & \hfill 14.96\hfill & \hfill 7.51\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 592\hfill & \hfill 0\hfill \\ \hfill 14.96\hfill & \hfill 16.04\hfill & \hfill 7.51\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 592\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 7.51\hfill & \hfill 7.51\hfill & \hfill 12.0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -1395\hfill & \hfill -1395\hfill & \hfill 2000\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 5.38\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 7093\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 5.38\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 7093\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8093\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 2.87\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6610\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
11. PMN-33%PT single crystal poled along [001]_c [49]

    $$\left(\begin{array}{cccccccccccc}\hfill 11.5\hfill & \hfill 10.3\hfill & \hfill 10.2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 146\hfill & \hfill 0\hfill \\ \hfill 10.3\hfill & \hfill 11.5\hfill & \hfill 10.2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 146\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 10.2\hfill & \hfill 10.2\hfill & \hfill 10.3\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -1330\hfill & \hfill -1330\hfill & \hfill 2820\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.9\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1600\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.9\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1600\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8060\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.6\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 8200\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
12. PMN-33%PT single crystal poled along [111]_c [320]

    $$\left(\begin{array}{cccccccccccc}\hfill 20.12\hfill & \hfill 7.36\hfill & \hfill 11.5\hfill & \hfill -4.15\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 4100\hfill & \hfill 2680\hfill \\ \hfill 7.36\hfill & \hfill 20.12\hfill & \hfill 11.5\hfill & \hfill 4.15\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1340\hfill & \hfill -1340\hfill & \hfill 0\hfill & \hfill 4100\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 11.5\hfill & \hfill 11.5\hfill & \hfill 17.12\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -90\hfill & \hfill -90\hfill & \hfill 190\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -4.15\hfill & \hfill 4.15\hfill & \hfill 0\hfill & \hfill 2.90\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 3950\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 2.90\hfill & \hfill -4.15\hfill & \hfill 0\hfill & \hfill 3950\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8060\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -4.15\hfill & \hfill 6.38\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 640\hfill \end{array}\right)$$
13. PMN-35%PT single crystal poled along [001]_c [321]

    $$\left(\begin{array}{cccccccccccc}\hfill 14.5\hfill & \hfill 15.1\hfill & \hfill 7.5\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 703\hfill & \hfill 0\hfill \\ \hfill 15.1\hfill & \hfill 14.5\hfill & \hfill 7.5\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 703\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 7.5\hfill & \hfill 7.5\hfill & \hfill 11.2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -152\hfill & \hfill -152\hfill & \hfill 250\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 3.6\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 4102\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 3.6\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 4102\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8080\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 3.6\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 3141\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
14. PMN-38%PT single crystal poled along [001]_c [322]

    $$\left(\begin{array}{cccccccccccc}\hfill 21.25\hfill & \hfill 14.33\hfill & \hfill 13.51\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 380\hfill & \hfill 0\hfill \\ \hfill 14.33\hfill & \hfill 21.25\hfill & \hfill 13.51\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 380\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 13.51\hfill & \hfill 13.51\hfill & \hfill 9.92\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -123\hfill & \hfill -123\hfill & \hfill 300\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 5.56\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 4301\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 5.56\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 4301\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8093\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.95\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 734\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
15. PMN-42%PT single crystal poled along [001]_c [323]

    $$\left(\begin{array}{cccccccccccc}\hfill 17.51\hfill & \hfill 8.51\hfill & \hfill 8.3\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 131\hfill & \hfill 0\hfill \\ \hfill 8.51\hfill & \hfill 17.51\hfill & \hfill 8.3\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 131\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 8.3\hfill & \hfill 8.3\hfill & \hfill 10.5\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -91\hfill & \hfill -91\hfill & \hfill 260\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 2.85\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 8627\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 2.85\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 8627\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8100\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 8.0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 660\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
16. PIN-49%PMN-27%PT single crystal poled along [111]_c [194]

    $$\left(\begin{array}{cccccccccccc}\hfill 20.26\hfill & \hfill 9.02\hfill & \hfill 5.32\hfill & \hfill -2.67\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 2015\hfill & \hfill 980\hfill \\ \hfill 9.02\hfill & \hfill 20.26\hfill & \hfill 5.32\hfill & \hfill 2.67\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 490\hfill & \hfill -490\hfill & \hfill 0\hfill & \hfill 2015\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 5.32\hfill & \hfill 5.32\hfill & \hfill 18.47\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -21\hfill & \hfill -21\hfill & \hfill 75\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -2.67\hfill & \hfill 2.67\hfill & \hfill 0\hfill & \hfill 2.34\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 3950\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 2.34\hfill & \hfill -2.67\hfill & \hfill 0\hfill & \hfill 3950\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8095\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -2.67\hfill & \hfill 5.62\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 640\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
17. PIN-46%PMN-28%PT single crystal poled along [011]_c [324]

    $$\left(\begin{array}{cccccccccccc}\hfill 19.96\hfill & \hfill 12.51\hfill & \hfill 7.19\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 2203\hfill & \hfill 0\hfill \\ \hfill 12.51\hfill & \hfill 13.54\hfill & \hfill 11.89\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 114\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 7.19\hfill & \hfill 11.89\hfill & \hfill 15.36\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 460\hfill & \hfill -1156\hfill & \hfill 782\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.49\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 5000\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0.76\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1030\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8102\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 5.33\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 2920\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
18. PIN-46%PMN-28%PT single crystal poled along [111]_c [325]

    $$\left(\begin{array}{cccccccccccc}\hfill 20.96\hfill & \hfill 8.29\hfill & \hfill 6.46\hfill & \hfill -2.66\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 2190\hfill & \hfill 1022\hfill \\ \hfill 8.29\hfill & \hfill 20.96\hfill & \hfill 6.46\hfill & \hfill 2.66\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 511\hfill & \hfill -511\hfill & \hfill 0\hfill & \hfill 2190\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 6.46\hfill & \hfill 6.46\hfill & \hfill 17.65\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -34\hfill & \hfill -34\hfill & \hfill 74\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -2.66\hfill & \hfill 2.66\hfill & \hfill 0\hfill & \hfill 2.10\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6286\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 2.10\hfill & \hfill -2.66\hfill & \hfill 0\hfill & \hfill 6286\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8102\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -2.66\hfill & \hfill 6.33\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 702\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
19. PIN-38%PMN-29%PT single crystal poled along [001]_c [326]

    $$\left(\begin{array}{cccccccccccc}\hfill 11.57\hfill & \hfill 10.03\hfill & \hfill 10.15\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 147\hfill & \hfill 0\hfill \\ \hfill 10.03\hfill & \hfill 11.57\hfill & \hfill 10.15\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 147\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 10.15\hfill & \hfill 10.15\hfill & \hfill 11.32\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -651\hfill & \hfill -651\hfill & \hfill 1338\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.45\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1666\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.45\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1666\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8141\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 5.44\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 4532\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
20. PIN-38%PMN-29%PT single crystal poled along [011]_c [326]

    $$\left(\begin{array}{cccccccccccc}\hfill 20.41\hfill & \hfill 14.01\hfill & \hfill 8.55\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 2288\hfill & \hfill 0\hfill \\ \hfill 14.01\hfill & \hfill 16.21\hfill & \hfill 13.61\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 94\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 8.55\hfill & \hfill 13.61\hfill & \hfill 15.07\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 496\hfill & \hfill -1268\hfill & \hfill 972\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.79\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 5000\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0.71\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1201\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8141\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 4.88\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 3384\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
21. PIN-47%PMN-29%PT single crystal poled along [001]_c [327]

    $$\left(\begin{array}{cccccccccccc}\hfill 12.43\hfill & \hfill 10.90\hfill & \hfill 11.02\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 122\hfill & \hfill 0\hfill \\ \hfill 10.90\hfill & \hfill 12.43\hfill & \hfill 11.02\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 122\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 11.02\hfill & \hfill 11.02\hfill & \hfill 12.45\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -646\hfill & \hfill -646\hfill & \hfill 1285\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.98\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1728\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.98\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1728\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8122\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.21\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 4753\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
22. PIN-47%PMN-29%PT single crystal poled along [011]_c [327]

    $$\left(\begin{array}{cccccccccccc}\hfill 20.85\hfill & \hfill 12.77\hfill & \hfill 6.07\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 2373\hfill & \hfill 0\hfill \\ \hfill 12.77\hfill & \hfill 15.74\hfill & \hfill 12.93\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 106\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 6.07\hfill & \hfill 12.93\hfill & \hfill 15.39\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 488\hfill & \hfill -1196\hfill & \hfill 922\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.78\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 5028\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0.67\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1273\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8122\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 4.87\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 3613\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
23. PIN-46%PMN-30%PT single crystal poled along [011]_c [328]

    $$\left(\begin{array}{cccccccccccc}\hfill 20.86\hfill & \hfill 12.59\hfill & \hfill 7.04\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 3122\hfill & \hfill 0\hfill \\ \hfill 12.59\hfill & \hfill 12.96\hfill & \hfill 11.70\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 142\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 7.04\hfill & \hfill 11.70\hfill & \hfill 15.54\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 675\hfill & \hfill -1693\hfill & \hfill 1068\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.50\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 7459\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0.59\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1596\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8161\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 4.51\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 4574\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
24. PIN-42%PMN-32%PT single crystal poled along [011]_c [324]

    $$\left(\begin{array}{cccccccccccc}\hfill 21.45\hfill & \hfill 15.01\hfill & \hfill 8.01\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 3354\hfill & \hfill 0\hfill \\ \hfill 15.01\hfill & \hfill 17.37\hfill & \hfill 14.10\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 162\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 8.01\hfill & \hfill 14.10\hfill & \hfill 15.26\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 744\hfill & \hfill -1781\hfill & \hfill 1363\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.37\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6814\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0.48\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1483\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8185\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 4.56\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 4361\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
25. PIN-40%PMN-33%PT single crystal poled along [001]_c [329]

    $$\left(\begin{array}{cccccccccccc}\hfill 12.2\hfill & \hfill 11.3\hfill & \hfill 10.8\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 232\hfill & \hfill 0\hfill \\ \hfill 11.3\hfill & \hfill 12.2\hfill & \hfill 10.8\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 232\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 10.8\hfill & \hfill 10.8\hfill & \hfill 11.2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -1337\hfill & \hfill -1337\hfill & \hfill 2742\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.9\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 10081\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.9\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 10081\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8198\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 7244\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
26. Mn:PIN-47%PMN-29%PT single crystal poled along [001]_c [327]

    $$\left(\begin{array}{cccccccccccc}\hfill 12.52\hfill & \hfill 10.14\hfill & \hfill 10.33\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 101\hfill & \hfill 0\hfill \\ \hfill 10.14\hfill & \hfill 12.52\hfill & \hfill 10.33\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 101\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 10.33\hfill & \hfill 10.33\hfill & \hfill 11.74\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -408\hfill & \hfill -408\hfill & \hfill 855\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.90\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1240\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.90\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1240\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8173\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.41\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 2599\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
27. Mn:PIN-47%PMN-29%PT single crystal poled along [011]_c [327]

    $$\left(\begin{array}{cccccccccccc}\hfill 22.02\hfill & \hfill 13.05\hfill & \hfill 6.46\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1959\hfill & \hfill 0\hfill \\ \hfill 13.05\hfill & \hfill 13.05\hfill & \hfill 10.61\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 82\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 6.46\hfill & \hfill 10.61\hfill & \hfill 15.85\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 330\hfill & \hfill -776\hfill & \hfill 473\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.92\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 4010\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0.77\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1020\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8173\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 5.87\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 2046\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
28. Mn:PIN-PMN-PT single crystal (part A in rhombohedral phase) poled along [011]_c [268]

    $$\left(\begin{array}{cccccccccccc}\hfill 19.1\hfill & \hfill 12.2\hfill & \hfill 7.43\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 2030\hfill & \hfill 0\hfill \\ \hfill 12.2\hfill & \hfill 13.3\hfill & \hfill 11.9\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 125\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 7.43\hfill & \hfill 11.9\hfill & \hfill 15.2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 455\hfill & \hfill -1200\hfill & \hfill 810\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.44\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 4916\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0.86\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1084\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8166\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 5.00\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 3213\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
29. Mn:PIN-PMN-PT single crystal (part B in rhombohedral phase) poled along [011]_c [268]

    $$\left(\begin{array}{cccccccccccc}\hfill 19.5\hfill & \hfill 13.6\hfill & \hfill 8.32\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 2986\hfill & \hfill 0\hfill \\ \hfill 13.6\hfill & \hfill 15.1\hfill & \hfill 13.0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 160\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 8.32\hfill & \hfill 13.0\hfill & \hfill 15.1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 608\hfill & \hfill -1508\hfill & \hfill 1053\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6.16\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6274\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0.53\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1499\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8180\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 4.67\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 3523\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right)$$
30. Mn:PIN-42%PMN-32%PT single crystal poled along [011]_c [269]

    $$(\begin{array}{cccccccccccc}\hfill 20.0\hfill & \hfill 10.6\hfill & \hfill 4.64\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 3100\hfill & \hfill 0\hfill \\ \hfill 10.6\hfill & \hfill 14.9\hfill & \hfill 10.2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 2435\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 4.64\hfill & \hfill 10.2\hfill & \hfill 15.0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 110\hfill & \hfill -302\hfill & \hfill 267\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1.84\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 6000\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0.49\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 17000\hfill & \hfill 0\hfill & \hfill \hfill & \hfill 8190\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 7.14\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1240\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array})$$