Skip to main content
PMC home page
Nature Portfolio logoLink to Nature Portfolio
. 2014 Jul 11;5:4144. doi: 10.1038/ncomms5144

Turning a band insulator into an exotic superconductor

Xiangang Wan 1,a, Sergey Y Savrasov 2
PMCID: PMC4104436  PMID: 25014912

Abstract

Understanding exotic, non-s-wave-like states of Cooper pairs is important and may lead to new superconductors with higher critical temperatures and novel properties. Their existence is known to be possible but has always been thought to be associated with non-traditional mechanisms of superconductivity where electronic correlations play an important role. Here we use a first principles linear response calculation to show that in doped Bi2Se3 an unconventional p-wave-like state can be favoured via a conventional phonon-mediated mechanism, as driven by an unusual, almost singular behaviour of the electron–phonon interaction at long wavelengths. This may provide a new platform for our understanding of superconductivity phenomena in doped band insulators.

Inline graphicMost superconductors that exhibit exotic pairing symmetries are derived from host materials that are Mott insulators. Xiangang Wan and Sergey Savrasov show that it may be possible to realize an exotic p-wave superconductor in doped Bi2Se3, which is a topological band insulator.

Since Bardeen, Cooper and Schrieffer’s (BCS) seminal discovery of their microscopic theory of superconductivity in 1957 (ref. 1), there has been more than a half-century work to understand how the Cooper pairs can condense into the states with the angular momentum greater than spherically symmetric s-state of the BCS theory. Such possibilities in much celebrated heavy fermion2 and high-Tc (critical temperature ) cuprate superconductors3, Sr2RuO4 (ref. 4) and superfluid He3 (ref. 5) are widely known but have nothing to do with the original BCS idea that elementary excitations of the lattice, phonons, are responsible for the formation of the Cooper pairs, and, despite a great amount of discussion6,7,8,9,10,11,12, there is no well-accepted example that the phonon-mediated unconventional pairing is indeed realized in nature. A recently triggered search for novel topological superconductors13,14,15,16 has, however, raised this issue to a completely new level with some revolutionary promising applications for fault-tolerant quantum computing17.

Here we demonstrate that some doped band insulators with layered structures and strong spin–orbit coupling where time reversal and inversion symmetries are unbroken can be good candidate materials in realizing an unconventional state of the fermions pair that are attracted via conventional phonon-mediated mechanism. We address this problem by performing first principle density-functional linear response calculations18 of full wave–vector-dependent electron–phonon interaction (EPI) in doped band insulator Bi2Se3 and argue that a highly unusual case of a singular coupling is realized for this material. We discuss the consequences of such singular behaviours and uncover which peculiar details of the electrons interacting with lattice can provide a novel platform for unconventional superconductivity phenomena. Our numerical results are presented for the archetypal topological insulator Bi2Se3 (ref. 19), but the characteristic features of its bulk spectrum of electrons as well as their interactions with lattice are expected to be generic for other systems, not related to their topological aspect. Our findings include: (1) very large electron–phonon matrix elements in the long-wavelength limit for those vibrational modes that break the inversion symmetry and lift the band degeneracy of strongly spin–orbit-coupled Fermi electrons; (2) a very large contribution to the electron–phonon coupling constant λ from the acoustic phonons due to their low vibrational frequencies; (3) a strong Fermi surface (FS) nesting at small wavevectors q along the z-direction due to layered nature of the lattice that enhances λ. Our calculated coupling constants for all s, p and d pairing channels are found to be very close to each other. By further considering the effects of the Coulomb pseudopotential μ* and some spin–fluctuation-induced interaction, we propose that pairs with higher angular momentum are favoured in doped Bi2Se3 and it may be the first phonon-mediated unconventional superconductor with the A2u symmetry (pz-like nodal pseudospin triplet) of its order parameter.

Results

Singular EPI model

A solution for the superconducting critical temperature Tc in a given α-pairing channel is described by the BCS formula Tc,α=1.14ωDexp[−1/λα] where ωD is the Debye frequency and the electron–phonon coupling constant λα is given by the FS average of the EPI W(k, k′):

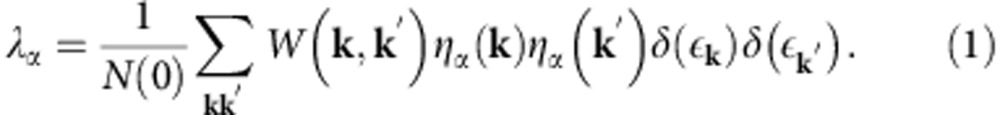graphic file with name ncomms5144-m1.jpg

Here ɛk and N(0) are the energies and density of states of the electrons with respect to the Fermi level, while ηα(k) represents a set of orthogonal FS polynomials, ∑kηα(k)ηβ(k)δ(ɛk)/N(0)=δαβ, such as crystal20 or FS21 harmonics introduced as generalizations of spherical harmonics for arbitrary surfaces. In the original BCS limit, W(k, k′) is just a constant that automatically produces λα=0 for all α>s due to the orthogonality of ηα(k). In reality, W(k, k′) is a slow-varying function of k and k′, which makes the coupling constant λ with α=s largest among all possible pairing channels and results in a largest energy gain by forming the pairs of the s-wave symmetry for practically all known electron–phonon superconductors.

Instead of a weakly momentum-dependent EPI, let us imagine an extreme case of a singular coupling at only certain wavevector q0 (together with its symmetry-related partners). Namely, assume that W(k, k′)≃W0δ(k−k′−q0)=W0∑αηα(k)ηα(k′+q0). Then λα=W0∑kηα(k)ηα(k+q0)δ(ɛk). It is then clear that the overlap between any two α>s polynomials separated by q0 is always smaller than the one for ηs(k)≡1 and the s-wave pairing still wins. This is unless q0→0, or if the original FS and the one shifted by q0 are indistinguishable, in which cases all pairing channels become degenerate and compete with each other. This provides us with a general idea where to find unconventional superconductors with conventional electron–phonon mechanism. In particular, we argue by our first principles linear response calculation18 that this exact case of a singular EPI with strongly nested FS at long wavelengths is realized for CuxBi2Se3.

Relevance to topological superconductivity

Our study has a direct relevance to the search of novel topological superconductors requiring an odd parity fully gapped state of Cooper pairs22 that have recently attracted a great interest due to the existence of Majorana modes that appear inside a superconducting energy gap13. Such exotic states are traditionally thought to be associated with an electronic mechanism of superconductivity, but the proposed candidate materials, such as CuxBi2Se3 (ref. 23), TlBiTe2 (ref. 24) and Sn1−xInxTe (ref. 25), are systems with weakly correlated sp electrons23,24,25, and it is likely that the conventional phonon-mediated mechanism plays a major role.

There are currently hot debates in the literature about the pairing symmetry in CuxBi2Se3 (refs 22, 23, 26, 27, 28, 29, 30): based on a two-orbital model, Fu and Berg22 proposed that it is a topological superconductor with a fully gapped state of odd parity pairing. Using tunnelling experiments, two groups have observed zero-bias conductance peak, which may be a signature of topological surface states associated with non-trivial pairing27,28. The absence of the Pauli limit and the comparison of critical field Bc2(T) to a polar-state function indicates a spin–triplet superconductivity29. However, contrary to these viewpoints, a recent scanning tunnelling microscopy measurement suggests that Cu0.2Bi2Se3 is a classical s-wave superconductor with a momentum-independent order parameter30. At the absence of any other examples in nature that phonons can trigger a pairing state other than s, does this experiment provide a most plausible scenario for this highly interesting phenomenon? Since CuxBi2Se3 crystals are intrinsically inhomogeneous, it may be difficult to elucidate the features of the mechanism as mentioned above. And very recently, it was found that under high pressure, Bi2Se3 displays anomalous superconducting behaviour indicating the unconventional pairing31.

Linear response calculations of phonons and their linewidths

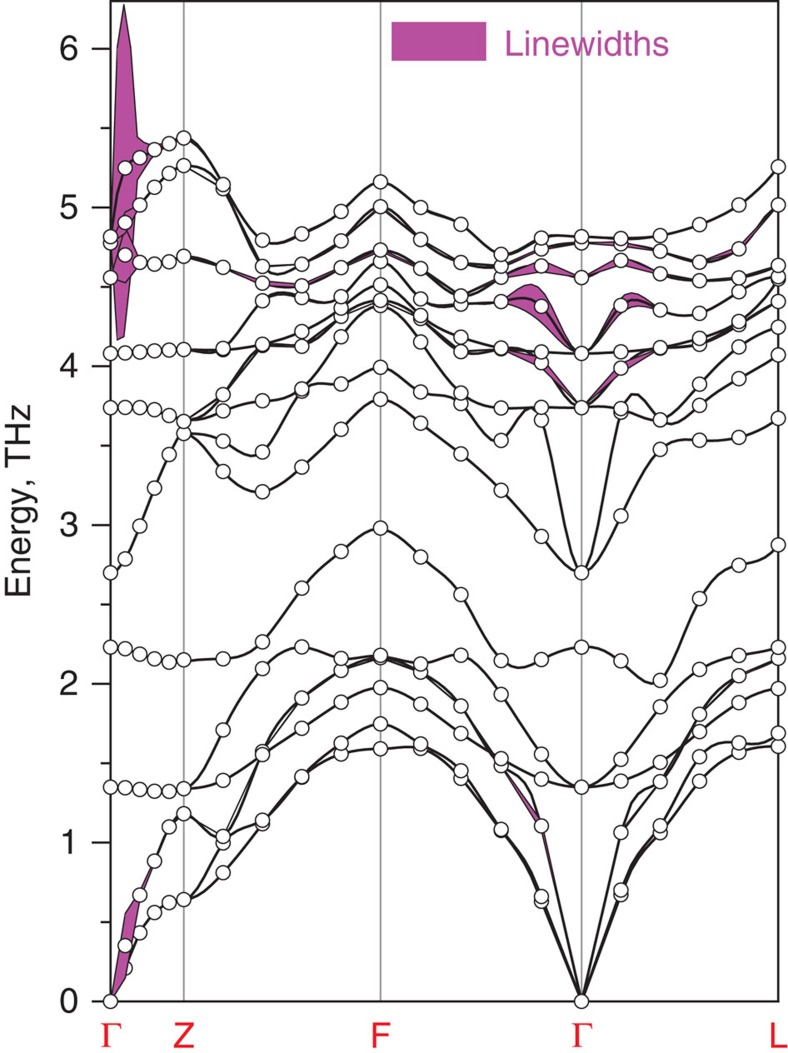
Here we apply density functional linear response method to study the problem of doped Bi2Se3. Our numerical electronic structures are in accord with previous theoretical results19. Our calculated phonon dispersions for Bi2Se3 along several high-symmetry directions of the Brillouin zone (BZ) are shown in Fig. 1, where similar to prior work32, we see that the phonon frequencies of Bi2Se3 span up to 5.5 THz, and all vibrational modes are found to be quite dispersive despite its two-dimensional-like layered structure. There are two basic panels in the phonon spectrum: the top nine branches above 2.5 THz are mainly contributed by vibrations of Se atoms, while the six low branches come from the Bi modes. Our calculated phonon frequencies at Γ agree with the experimental33,34 and previous numerical results32 very well.

Figure 1. Description of lattice dynamical properties.

Figure 1

Open in a new tab

Calculated phonon dispersions (points) of Bi2Se3 using density-functional linear response approach. The widening shows our caclulated phonon linewidth arising from the EPI in CuxBi2O3 (x=0.16).

It is found that superconducting CuxBi2Se3 has the maximum Tc of 3.8 K at x~0.12 (ref. 23) and on further doping the Tc gradually decreases, but superconductivity remains till x~0.6 (ref. 26). The copper atoms populate into the interlayer gaps23 and have a small effect on the structural properties34,35. To simulate the doping, we perform virtual crystal approximation calculation with adding x electrons into the unit cell as a uniform background and calculate wavevector (q)- and vibrational mode (ν)-dependent phonon linewidths γqν from which the electron–phonon coupling constant can be deduced36.

Our calculated phonon linewidths γqγ for a representative doping x=0.16 are shown in Fig. 1 by widening the phonon dispersion curves ωqν proportionally to γqγ. A striking feature is that only the phonons along ΓZ line of the BZ, especially one optical mode with the vector q=(0,0,0.04)(2π)/(c) has a very large linewidth. We also note a considerable linewidth for a longitudinal acoustic mode at the same q. This is in principle detectable via neutron-scattering experiment. Interestingly, as the contribution to λ from each mode is proportional to γqν divided by 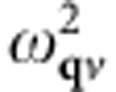Inline graphic, it is the acoustic mode that would provide a dominant contribution to total λ rather than the optical one.

Origin of large EPI

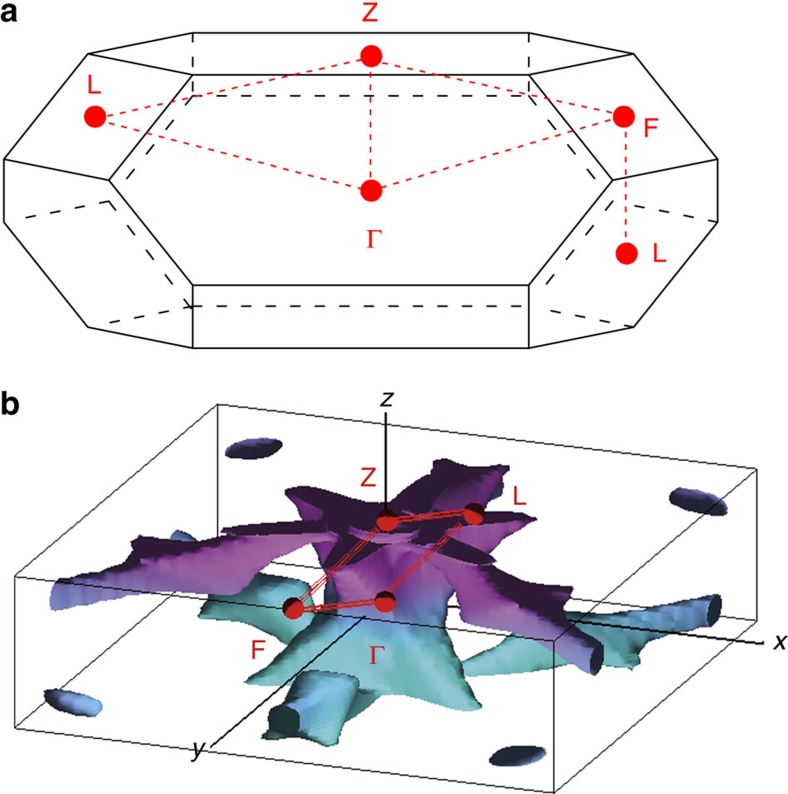
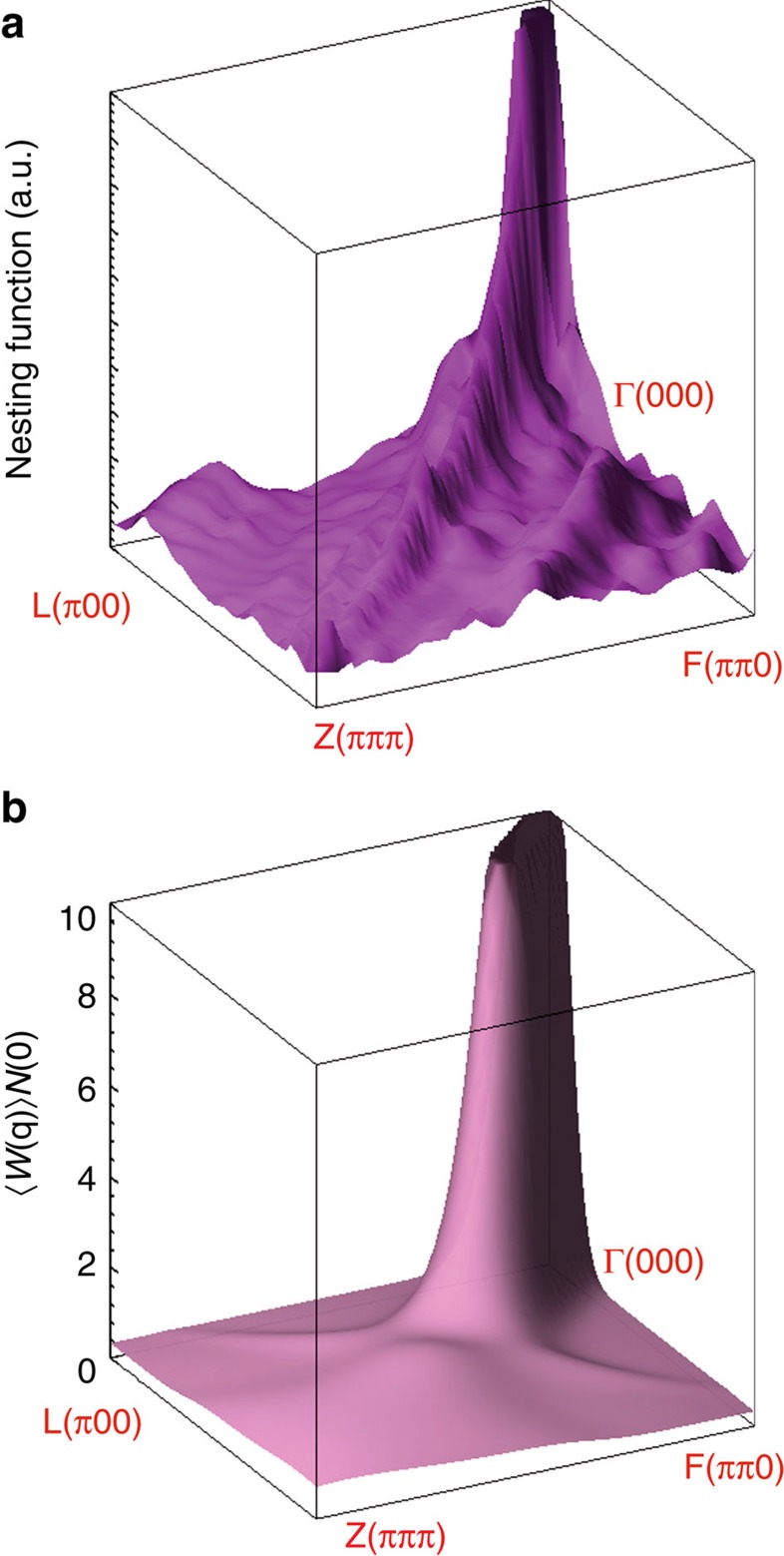
We first look at possible nesting like features of the FS. We mark time reversal invariant momenta (Γ(000), L(π,0,0), F(π,π,0) and Z(π,π,π)) of the first BZ in Fig. 2a, and show our calculated FS for x=0.16 in Fig. 2b that is open, in agreement with recent ARPES and dHvA measurements37. Although the FS has strong three-dimensional features, there is a prism-like electron pocket around the Γ point that indicates a nesting for the wavevectors along the ΓZ line. To confirm this result, Fig. 3a shows our calculated nesting function X(q)=∑kδ(ɛk)δ(ɛk+q) within the plane that contains ΓFZL points of the BZ. One can see clearly that X(q) exhibits a ridge along the ΓZ line, where the nesting function reaches its largest values as q approaches zero along ΓZ. This is despite a general tendency for X(q) to diverge as q→0, that is connected to a commonly used linearization of imaginary electronic susceptibility Im χ(q,ω) with respect to ω when it is within the range of the phonon frequencies; the approximation that breaks down for small wave vectors but is irrelevant for estimating any types of three-dimensional integrals over q due to the appearance of the q2 prefactor.

Figure 2. Calculation for the FS.

Figure 2

Open in a new tab

(a) BZ of hexagonal Bi2Se3 where we mark the time reversal invariant momenta Γ(000), L(π,0,0), F(π,π,0) and Z(π,π,π). (b) FS of CuxBi2Se3 for doping x=0.16. A colour (magenta positive, cyan negative) corresponds to a proposed p-wave solution for the superconducting energy gap of the A2u symmetry discussed in text.

Figure 3. Behaviour of the electron–phonon pairing interaction.

Figure 3

Open in a new tab

(a) Calculated nesting function for CuxBi2Se3 corresponding to x=0.16. Notice that the basal area given by ΓFZL points of the momentum space is in fact rhombus as seen from the BZ plot shown in Fig. 2a. (b) Calculated average electron–phonon pairing interaction ‹W(q)›N(0) as a function of momentum within the basal area ΓFZL.

A strong enhancement of the electron–phonon coupling due to nesting is an interesting but not an uncommon effect in metals. In particular, nesting alone will not result in any type of unconventional pairing, as the latter is the property of the peculiar behaviour of the pairing interaction W(k, k′) appeared in equation (1). To analyse it, we introduce the following average

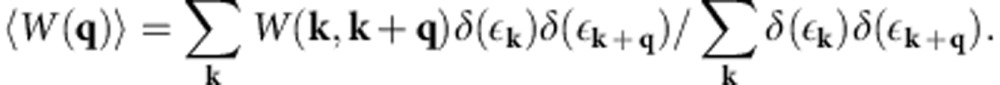graphic file with name ncomms5144-m3.jpg

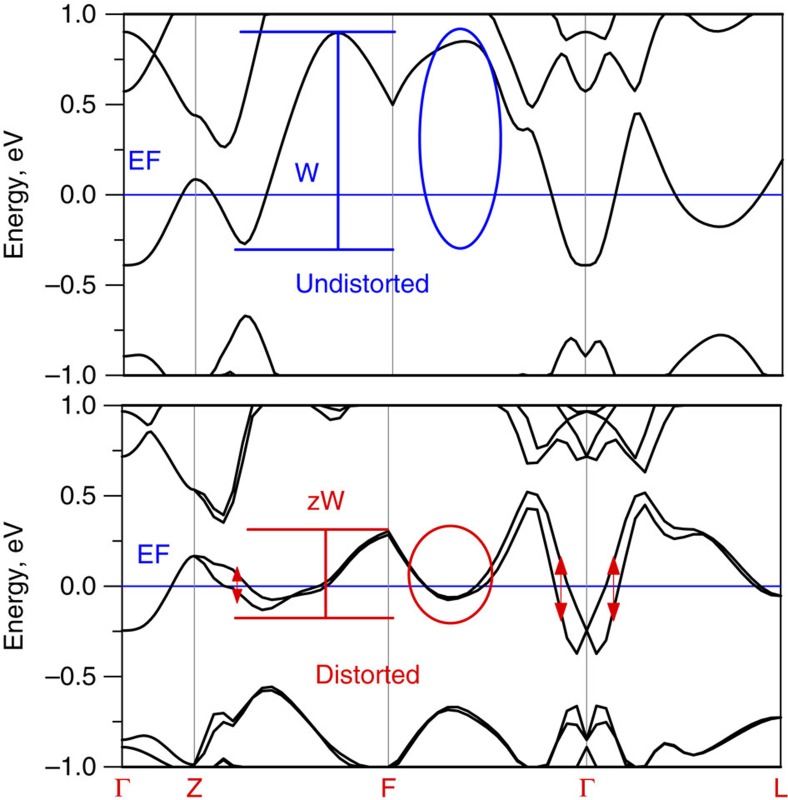
The plot of ‹W(q)›N(0)) within the ΓFZL plane is shown in Fig. 3b. Remarkably, we again find a strongly enhanced function that is peaked at small values of q once it approaches zero along ΓZ. As all nesting features have been eliminated, it is interesting to understand the nature of this highly non-trivial behaviour that originated from the acoustic and the optical modes. Both essentially correspond to the motion of the Bi atoms along z-direction. By ignoring the smallness of the wave vector, we performed the calculation for q=0 by moving the atoms according to the eigenvectors of the optical mode. Such deformation potential calculation is shown in Fig. 4 where the band structures for the undistorted (Fig. 4a), and the distorted (Fig. 4b) lattices are plotted in the vicinity of the Fermi level to illustrate the crucial change in the electronic structure. Bi2Se3 has both time-reversal symmetry and the inversion symmetry, and despite the presence of spin–orbit coupling, this results in every energy band to be at least double degenerate for the undistorted structure. The discussed phonon displacement breaks the inversion symmetry and lifts the double degeneracy, resulting in a large EPI. It is worth to mention that this effect only exists for the system with both inversion symmetry and strong spin–orbit coupling, and the spin–orbit coupling is essential here but in its very unusual role to generate a large EPI. In addition to this effect, there is a considerable renormalization of the bandwidth as well as other noticeable features as illustrated in Fig. 4 that result in the strongly enhanced EPI at long wavelengths.

Figure 4. Illustration of large coupling by deformation potentials.

Figure 4

Open in a new tab

Calcuated energy bands for the undistorted (a) and distorted (b) structures of Bi2Se3, corresponding to the Γ point optical mode associated with the inversion breaking dispacement of Bi atom along z-axis. Illustrated are the splitting of double degenerate bands as well as renormalization of their width that result in a large EPI.

Results for electron–phonon coupling constants

We now discuss our calculated total values of the electron–phonon λα for various pairing channels that are classified according to the D3d point group of Bi2Se3. Since here the single-particle states are affected by spin–orbit coupling, the Cooper pairs are no longer pure spin singlets or triplets but should be composed from superpositions of spinor states. However, the presence of time reversal and inversion symmetries ensures the twofold degeneracy of the Fermi electrons (conveniently labelled via the use of a pseudospin index) from which the Cooper pairs of even/odd parity and of zero momentum are composed38. We use crystal harmonics for the FS polynomials after ref. 20. For a representative doping with x=0.16 we obtain 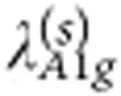Inline graphic=0.45 (s-like) for the even parity pseudospin singlet, and 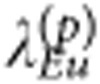Inline graphic=0.21 (px/y-like), 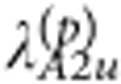Inline graphic=0.39 (pz-like) for the odd parity pseudospin triplets. We also evaluated the coupling constants with d-wave-like symmetries and obtained the values of λ around 0.2 for the two Eg symmetries and 0.37 for the A1g (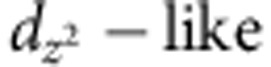Inline graphic) one. Consistent with the discussion of our singular electron–phonon model, one can see a remarkable proximity of all pairing constants, and especially of 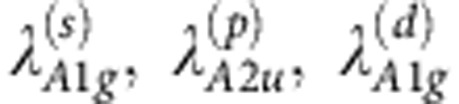Inline graphic. Very similar trends hold for slightly smaller and larger values of x where we find that all couplings constants change monotonically with doping.

Finally, we note that the effective coupling should include the effect of the Coulomb pseudopotential μ* and other possible renormalizations such as, for example, spin fluctuations. It is well known that the values of μs* range between 0.10 and 0.15 for most s-wave electron–phonon superconductors. We also expect that 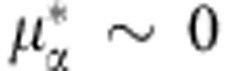Inline graphic for the pairings with higher angular momentum11. While we do not expect that spin fluctuations are essential for the sp electron material like doped Bi2Se3, we have also evaluated spin fluctuational λs using a single-band fluctuation exchange approximation39. 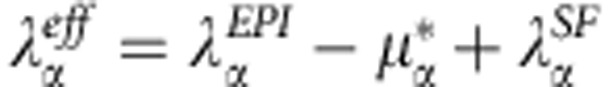Using a representative value of U=0.5 eV (which approximately constitutes 0.4 of the electronic bandwidth) we have obtained for x=0.16: Inline graphic, which produces slightly negative (repulsive) contributions for the s- and d-wave and slightly positive (attractive) ones for the p-wave pairings. Overall, combining these data in the effective coupling Inline graphic, we see that it favours the pseudotriplet pairing of A2u symmetry in doped topological superconductor Bi2Se3, and is capable of producing the values of Tc=3~5 K. The behaviour of the superconducting energy gap for this symmetry is shown by colouring the FS in Fig. 2b, where the nodal plane corresponds to kz=0.

Calculations for other systems

In addition to doped Bi2Se3, we also performed similar studies for TlBiTe2 (ref. 24) and Sn1−xInxTe (ref. 25). For both compounds, in a wide range of carrier concentration, we cannot find any singular behaviour of EPI, and our results show that the coupling in s-wave pairing channel is considerably larger than that in all other channels. Thus we believe that TlBiTe2 and Sn1−xInxTe are conventional s-wave superconductors.

Discussion

In perspective, we think that our discussed effects could be present in several other layered band insulators where strong spin–orbit coupling as well as unbroken time reversal and inversion symmetries could interplay with certain lattice distortions and create exotic superconducting states upon doping. Synthesizing such systems with isolating their thin flakes using a famous graphene’s scotch tape method should not be too difficult to make. This may provide a new platform for realizing unconventional superconductivity in general. Although our proposed solution for Bi2Se3 is gapless pseudospin triplet, an odd-parity fully gapped pairing state thought in a topological superconductor can also in principle be realized in other systems using the above-discussed singular EPI. Finally, a gate tuning was recently used to introduce a carrier doping in monolayered MoS2 and turned on superconductivity40, which may be a good way to overcome the inhomogenuity in CuxBi2Se3 and experimentally clarify the nature of its pairing state.

Methods

The results reported here were obtained from density functional linear response approach, which has been proven to be very successful in the past to describe EPIs and superconductivity in metals41, including its applications to plutonium42, MgB2 (ref. 43), lithium-deposited graphene44 and many other systems45. The full potential all-electron linear–muffin–tin–orbital method18 had been used, and an effective (40,40,40) grid in k-space (total 10,682 irreducible k points) has been used to generate γqγ on (6,6,6), (8,8,8) and (10,10,10) grids of the phonon wavevector to ensure the convergence of the calculated results.

Author contributions

X.W. came up with the idea of checking the mechanism of electron–phonon coupling in doped topological insulators. S.Y.S. developed the method and computer codes for computations of phonons and EPIs for general pairing. X.W. performed the computations of lattice dynamics and coupling constants for Bi2Se3. S.Y.S. ellaborated the idea of singular EPI model. Both authors discussed the results of the calculations and wrote the paper.

Additional information

How to cite this article: Wan, X. & Savrasov, S. Y. Turning a band insulator into an exotic superconductor. Nat. Commun. 5:4144 doi: 10.1038/ncomms5144 (2014).

Acknowledgments

We acknowledge the useful discussions with J. Bauer, X. Dai, G. Kotliar, I. Mazin, J.-X. Li, and W. Pickett. X.W. acknowledges support by the National Key Project for Basic Research of China (Grant Nos. 2011CB922101 and 2010CB923404), NSFC (Grant Nos. 11374137, 91122035 and 11174124) and PAPD. S.Y.S acknowledges support by the DOE Computational Material Science Network (CMSN) Grant No. DESC0005468.

References

  1. Bardeen J., Cooper L. N. & Schrieffer J. R. Microscopic theory of superconductivity. Phys. Rev. 106, 162–164 (1957). [Google Scholar]
  2. Steglich F. et al. Superconductivity in the presence of strong Pauli paramagnetism: CeCu2Si2. Phys. Rev. Lett. 43, 1892–1896 (1979). [Google Scholar]
  3. Bednorz J. G. & Müller K. A. Possible high Tc superconductivity in the Ba-La-Cu-O system. Z. Physik B 64, 189–193 (1986). [Google Scholar]
  4. Maeno Y. et al. Superconductivity in a layered perovskite without copper. Nature 372, 532–534 (1994). [Google Scholar]
  5. Lee D. M. The extraordinary phases of liquid. 3He. Rev. Mod. Phys. 69, 645–665 (1997). [Google Scholar]
  6. Abrikosov A. A. Parity of the order parameter in high-temperature superconductors with respect to a π/2 rotation. Phys. Rev. B 52, 15738–15740 (1995). [DOI] [PubMed] [Google Scholar]
  7. Shen Z. X., Lanzara A., Ishihara S. & Nagaosa N. Role of the electron-phonon interaction in the strongly correlated cuprate superconductors. Philos. Mag. B 82, 1349–1368 (2002). [Google Scholar]
  8. Varelogiannis G. Small-q phonon-mediated superconductivity in organic k-BEDT-TTF compounds. Phys. Rev. Lett. 88, 117005 (2002). [DOI] [PubMed] [Google Scholar]
  9. Klironomos F. D. & Tsai S. W. Phonon-mediated tuning of instabilities in the Hubbard model at half-filling. Phys. Rev. B 74, 205109 (2006). [Google Scholar]
  10. Schnell I., Mazin I. I. & Liu A. Y. Unconventional superconducting pairing symmetry induced by phonons. Phys. Rev. B 74, 184503 (2006). [Google Scholar]
  11. Alexandrov A. S. Unconventional pairing symmetry of layered superconductors caused by acoustic phonons. Phys. Rev. B 77, 094502 (2008). [Google Scholar]
  12. Ye X. S., Yao Z. J. & Li J. X. Phonon-mediated unconventional superconductivity in NaxCoO2yH2O compounds. J. Phys. Condens. Matter 20, 045227 (2008). [Google Scholar]
  13. Qi X.-L. & Zhang S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011). [Google Scholar]
  14. Schnyder A. P., Ryu S., Furusaki A. & Ludwig A. W. W. Classification of topological insulators and superconductors in three spatial dimensions. Phys. Rev. B 78, 195125 (2008). [Google Scholar]
  15. Qi X.-L., Hughes T. L., Raghu S. & Zhang S.-C. Time-reversal-invariant topological superconductors and superfluids in two and three dimensions. Phys. Rev. Lett. 102, 187001 (2009). [DOI] [PubMed] [Google Scholar]
  16. Roy R. Topological superfluids with time reversal symmetry. Preprint at http://arxiv.org/abs/0803.2868 (2008).
  17. Alicea J. New directions in the pursuit of Majorana fermions in solid state systems. Rep. Prog. Phys. 75, 076501 (2012). [DOI] [PubMed] [Google Scholar]
  18. Savrasov S. Y. Linear-response theory and lattice dynamics: a muffin-tin-orbital approach. Phys. Rev. B 54, 16470–16486 (1996). [DOI] [PubMed] [Google Scholar]
  19. Zhang H. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 5, 438–442 (2009). [Google Scholar]
  20. Putikka W. & Joynt R. Stability of anisotropic superconducting phases in UPt3. Phys. Rev. B 37, 2372–2375 (1988). [DOI] [PubMed] [Google Scholar]
  21. Allen P. B. Fermi-surface harmonics: a general method for nonspherical problems. Application to Boltzmann and Eliashberg equations. Phys. Rev. B 13, 1416–1427 (1976). [Google Scholar]
  22. Fu L. & Berg E. Odd-parity topological superconductors: theory and application to CuxBi2Se3. Phys. Rev. Lett. 105, 097001 (2010). [DOI] [PubMed] [Google Scholar]
  23. Hor Y. S. et al. Superconductivity in CuxBi2Se3 and its implications for pairing in the undoped topological insulator. Phys. Rev. Lett. 104, 057001 (2010). [DOI] [PubMed] [Google Scholar]
  24. Chen Y. L. et al. Single dirac cone topological surface state and unusual thermoelectric property of compounds from a new topological insulator family. Phys. Rev. Lett. 105, 266401 (2010). [DOI] [PubMed] [Google Scholar]
  25. Sasaki S. et al. Odd-parity pairing and topological superconductivity in a strongly spin-orbit coupled semiconductor. Phys. Rev. Lett. 109, 217004 (2012). [DOI] [PubMed] [Google Scholar]
  26. Kriener M. et al. Electrochemical synthesis and superconducting phase diagram of CuxBi2Se3. Phys. Rev. B 84, 054513 (2011). [Google Scholar]
  27. Sasaki S. et al. Topological superconductivity in CuxBi2Se3. Phys. Rev. Lett. 107, 217001 (2011). [DOI] [PubMed] [Google Scholar]
  28. Kirzhner T., Lahoud E., Chaska K. B., Salman Z. & Kanigel A. Point-contact spectroscopy of Cu0.2Bi2Se3 single crystals. Phys. Rev. B 86, 064517 (2012). [Google Scholar]
  29. Bay T. V. et al. de Superconductivity in the doped topological insulator CuxBi2Se3 under high pressure. Phys. Rev. Lett. 108, 057001 (2012). [DOI] [PubMed] [Google Scholar]
  30. Levy N. et al. Experimental evidence for s-wave pairing symmetry in superconducting CuxBi2Se3 single crystals using a scanning tunneling microscope. Phys. Rev. Lett. 110, 117001 (2013). [DOI] [PubMed] [Google Scholar]
  31. Kirshenbaum K. et al. Pressure-induced unconventional superconducting phase in the topological insulator Bi2Se3. Phys. Rev. Lett. 111, 087001 (2013). [DOI] [PubMed] [Google Scholar]
  32. Cheng W. & Ren S.-F. Phonons of single quintuple Bi2Te3 and Bi2Se3 films and bulk materials. Phys. Rev. B 83, 094301 (2011). [Google Scholar]
  33. Richter W., Kohler H. & Becker C. R. A Raman and far-infrared investigation of phonons in the rhombohedral V2-VI3 compounds Bi2Te3, Bi2Se3, Sb2Te3 and Bi2(Te1−xSex)3 (0<x<1), (Bi1−ySby)2Te3 (0<y<1). Phys. Stat. Sol. B 84, 619–628 (1977). [Google Scholar]
  34. Gnezdilov V. et al. Helical fluctuations in the Raman response of the topological insulator Bi2Se3. Phys. Rev. B 84, 195118 (2011). [Google Scholar]
  35. Chen H.-J. et al. Phonon dynamics in CuxBi2Se3 (x=0, 0.1, 0.125) and Bi2Se2 crystals studied using femtosecond spectroscopy. Appl. Phys. Lett. 101, 121912 (2012). [Google Scholar]
  36. Allen P. B. Neutron spectroscopy of superconductors. Phys. Rev. B 6, 2577–2579 (1972). [Google Scholar]
  37. Lahoud E. et al. Evolution of the Fermi surface of a doped topological insulator with carrier concentration. Phys. Rev. B 88, 195107 (2013). [Google Scholar]
  38. Sigrist M. & Ueda K. Phenomenological theory of unconventional superconductivity. Rev. Mod. Phys. 63, 239–311 (1991). [Google Scholar]
  39. Bickers N. E. & Scalapino D. J. Conserving approximations for strongly fluctuating electron systems I. Formalism and calculational approach. Ann. Phys. 193, 206–251 (1989). [Google Scholar]
  40. Ye J. T. et al. Superconducting dome in a gate-tuned band insulator. Science 338, 1193–1196 (2012). [DOI] [PubMed] [Google Scholar]
  41. Savrasov S. Y. & Savrasov D. Y. Electron-phonon interactions and related physical properties of metals from linear-response theory. Phys. Rev. B 54, 16487–16501 (1996). [DOI] [PubMed] [Google Scholar]
  42. Dai X. et al. Calculated phonon spectra of plutonium at high temperatures. Science 300, 953–955 (2003). [DOI] [PubMed] [Google Scholar]
  43. Kong Y., Dolgov O. V., Jepsen O. & Andersen O. K. Electron-phonon interaction in the normal and superconducting states of MgB2. Phys. Rev. B 64, 020501 (2001). [Google Scholar]
  44. Profeta G., Calandra M. & Mauri F. Phonon-mediated superconductivity in graphene by lithium deposition. Nat. Phys. 8, 131–134 (2012). [Google Scholar]
  45. Li Y. L. et al. Pressure-induced superconductivity in CaC2. PNAS 110, 9289–9294 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Nature Communications are provided here courtesy of Nature Publishing Group

RESOURCES