Inverse computational analysis of in vivo corneal elastic modulus change after collagen crosslinking for keratoconus

Abstract

Corneal collagen crosslinking with riboflavin photosensitization and ultraviolet irradiation is a novel approach to limiting the progression of keratoconus in patients by increasing the elastic modulus of the degenerate cornea. Beneficial reductions in corneal steepness and aberrations after crosslinking also frequently occur. In a previous study, we described a computational modeling approach to simulating topographic progression in keratoconus and regression of disease with corneal collagen crosslinking. In the current study, this model has been expanded and applied to the inverse problem of estimating longitudinal time-dependent changes in the corneal elastic modulus after crosslinking using in vivo measurements from 16 human eyes. Topography measured before crosslinking was used to construct a patient-specific finite element model with assumed hyperelastic properties. Then the properties of the cornea were altered using an inverse optimization method to minimize the difference between the model-predicted and in vivo corneal shape after crosslinking. Effects of assumptions regarding sclera-to-cornea elastic modulus ratio and spatial attenuation of treatment effect due to ultraviolet beam characteristics on the predicted change in elastic modulus were also investigated. Corneal property changes computed by inverse finite element analysis provided excellent geometric agreement with clinical topography measurements in patient eyes post-crosslinking. Over all post-treatment time points, the estimated increase in corneal elastic modulus was 110.8±48.1%, and slightly less stiffening was required to produce the same amount of corneal topographic regression of disease when the sclera-to-cornea modulus ratio was increased. Including the effect of beam attenuation resulted in greater estimates of stiffening in the anterior cornea. Corneal shape responses to crosslinking varied considerably and emphasize the importance of a patient-specific approach.

1 Introduction

The normal cornea exhibits remarkable topographic stability throughout a wide range of intraocular pressures (McMonnies and Boneham, 2007). Keratoconus (KC) is a degenerative corneal disease where the normal composite structure of the cornea is drastically modified in end-stage disease (Meek et al., 2005; Hayes et al., 2012; Ruberti et al., 2011). Clinical signs of KC such as corneal topographic distortion, corneal stress lines, and rupture of Descemet membrane suggest biomechanical failure as a central feature of the disease. The keratoconic cornea exhibits increased topographic compliance in vivo in response to elevated intraocular pressure (IOP) (McMonnies and Boneham, 2010) and significant reductions in elastic modulus ex vivo relative to non-keratoconic corneal samples (Andreassen et al., 1980; Nash et al., 1982). Current clinical treatment protocols such as rigid contact lenses, intra-corneal rings do not limit the progression of the disease, and in later stages of the disease, corneal transplant is often necessary to restore vision to the affected eye.

Ultraviolet (UV-A) induced corneal collagen crosslinking (CXL) is a minimally invasive clinical technique that aims primarily to increase the biomechanical stability of the keratoconic cornea and inhibit the progression of corneal steepening (Wollensak et al., 2003a; Spoerl et al., 1998). In its current clinical form, CXL is achieved by irradiating the cornea with UV-A light after saturation with riboflavin solution and results in significant increases in Young's modulus by ex vivo testing (Wollensak et al., 2003b, 2009). Several clinical studies have also noted corneal topographic flattening and reductions in corneal aberrations (Wollensak et al, 2003a; Koller et al., 2011; Greenstein et al., 2011; Wittig-Silva et al., 2008). A small number of FEM studies have investigated the biomechanical behavior of model corneas in which either material properties, corneal thickness or both were reduced to simulate the corneal steepening that is the clinical hallmark of KC (Pandolfi and Manganiello, 2006; Gefen et al., 2009; Carvalho et al., 2009). We recently described a corneo-scleral FE model of KC that was able to replicate the topographic features of progressing KC while incorporating clinical patient-specific corneal tomographic measurements as model input (Sinha Roy and Dupps, 2011). We further applied the model to simulations of standard CXL technique and novel CXL technique modifications in patient-specific KC models and compared the effects on corneal topographic characteristics such as the magnitude of corneal flattening, movement of the location of steepest point, and reductions in corneal first-surface aberrations to those reported in the clinical literature (Sinha Roy and Dupps, 2011). This study showed that simulation of the post-photopolymerization effects of CXL as a regional zone of increased elastic modulus provides reasonable in silica replication of key clinical responses, including visually favorable reductions in corneal steepness and aberrations. It also established the dependence of these effects on the magnitude of increase in elastic modulus, the effective depth of CXL, and the spatial distribution of CXL effect relative to cone location.

While this work established mechanistic links between corneal stiffening and topographic improvement of the disease, clinical measurements of actual material property changes after crosslinking are elusive (Sedaghat et al., 2010; Spoerl et al., 2011; Gikka et al., 2012). In vivo measurement of the material property changes associated with various permutations of CXL is of significant basic interest for understanding the biomechanical underpinnings of crosslinking therapy and its many variables. Quantitative assessment of material property changes in living tissue is critical to the long-term goal of applying patient-specific models to the prediction and optimization of treatment outcomes. The aim of this study was to develop an inverse FE modeling method to estimate the magnitude of elastic modulus change of the cornea relative to pre-CXL state. The inverse model was built using the pre-CXL patient topography and clinical intraocular pressure (IOP) measurements as the loading force. The simulated CXL procedure in the models was designed to approximate standard clinical treatment parameters. To estimate the change in modulus, the material properties of the anterior stroma were perturbed and optimized to minimize the difference between the computed FE and measured in vivo anterior surface curvature of the cornea.

2 Methods

2.1 Clinical Protocol

Patients with progressive keratoconus or post-refractive surgery corneal ectasia were enrolled in a prospective, randomized, single-site clinical trial to determine the safety and effectiveness of a clinical system for corneal collagen cross-linking. The study was a physician-sponsored IND performed under the guidelines of the FDA and approved by the Emory investigational review board (Clinical Trials.gov identifier # NCT00567671). A signed written informed consent was obtained from all participants. After an initial ocular, medical history and ophthalmologic screening exam, the eyes that met the inclusion criteria were randomized to either the treatment or control group. Only KC eyes in the treatment group were evaluated in this study.

Crosslinking procedures were performed by 2 surgeons (JBR and RDS) in 16 eyes. IOP was measured before surgery with Goldman applanation tonometry. After instillation of topical anesthetic drops, the central 9 mm of the corneal epithelium was removed using a blunt blade to facilitate riboflavin diffusion into the cornea. Rotating Scheimpflug imaging of the cornea (Pentacam Oculus Optikgeräte GmbH, Germany, software v 1.61) was performed at the screening visit (pre-CXL) and at follow-up visits ranging from 3 to 15 months after the CXL treatment. The imaging device was capable of recording both the shape of the anterior and posterior surface combined with the thickness at different locations of the cornea. Corneal thickness measurements were reviewed before and after the epithelium removal to assure a residual corneal thickness of at least 350 microns. The riboflavin solution used was an isotonic (0.9%) sodium chloride solution containing 0.1% riboflavin and 20% Dextran T500, adjusted to a pH of 7.0, and packaged in 3 mL sterile dropper bottles for topical ophthalmic use. After epithelial removal, 1 drop of riboflavin solution was instilled topically on the eye every 2 minutes for 30 minutes. At the end of the 30 minute riboflavin pre-treatment period, each eye was examined with cobalt blue illumination for the presence of a yellow flare in the anterior chamber, indicating adequate riboflavin saturation of the corneal tissue. Ultrasound pachymetry (DGH-550 Pachette 2, DGH Technology Inc., Exton, PA) was performed at the thinnest point, and if the corneal thickness was < 400 microns, 2 drops of hypotonic riboflavin 0.1% were instilled every 10 to 15 seconds until the corneal thickness increased to at least 400 microns to minimize the risk of UV damage of the corneal endothelium (Spoerl et al., 2007). A lid speculum was placed and the eye was aligned under the UV-X™ System (IROC, Zurich, Switzerland). The UV-A irradiation was applied at a 50 mm working distance for 30 minutes using an average 3 mW/cm² irradiance on the anterior surface of the cornea. One drop of riboflavin was applied every 2 minutes during UV exposure. A bandage contact lens was placed just after the treatment and was removed in 4 to 7 days. In an ex vivo setting, the stiffening effect of CXL has been detected as early as the first few hours after treatment (Wollensak et al., 2003a; Kling et al., 2010). However, same-day corneal tomography before onset of epithelial healing was not part of the clinical protocol, and corneal geometries obtained in the immediate postoperative period would likely be confounded by corneal edema related to loss of the hydrophobic epithelial barrier.

2.2 Geometry and Meshing

The geometries of the anterior and posterior corneal surfaces of individual corneas were derived from the 3-D elevation output of the Scheimpflug tomographer. We have previously described in detail our approach to re-constructing the 3-D geometry of the cornea in a computer-aided design software package (Sinha Roy and Dupps, 2011). To simulate an unconstrained limbus (Sinha Roy and Dupps, 2009), the sclera for each eye was modeled as a layer of tissue with an external diameter of 23 mm, an axial eye length of 22 mm and a uniform thickness of 850 um connected to the corneal 3-D structure at the limbus (Sinha Roy and Dupps, 2011). The internal surface of the cornea and sclera was loaded with the measured IOP in each eye. The posterior region of the sclera (at the site of optic nerve head) was constrained in 3 dimensions, i.e., x, y and z displacements were set to zero. We assumed that mild apparent increases in corneal applanation pressures after CXL are due to increases in corneal bending resistance (Dupps et al., 2007; Gikka et al., 2011; Kymionis et al., 2010) and that true IOP after CXL is effectively unchanged (Sinha Roy and Dupps, 2011). Meshing of the corneo-sceral whole eye model was performed in TrueGrid (XYZ Scientific Applications, Inc., USA) using 8-noded linear, hexahedral elements adapted for an incompressible material (Fig. 1A). The number of elements in the FE mesh was varied to evaluate the dependency of computed stress and strain on it. Mesh independency was confirmed when less than 0.5% change in strain and displacement values was obtained. The number of elements and nodes were 38955 and 44864, respectively.

Figure 1.

(a) and (b) Whole-eye FE model showing the cornea and sclera; (c) A schematic representation of the model showing the weaker keratoconic zone and the crosslinked zone in a standard 9mm-diameter simulated treatment.

2.3 Material Properties of Pre-CXL and Post-CXL state

Corneal buttons with advanced KC have been shown to lack the preferred collagen orientation and fiber packing density of normal corneas (Meek et al., 2005; Hayes et al., 2010). Given this evidence for a lack of preferred orientation in KC corneas, we adopted a material model for the KC cornea that is fiber direction-independent and locally isotropic (Sinha Roy and Dupps, 2011). Stress vs. strain data derived from ex vivo testing of normal corneas (Wollensak et al., 2003a) was fitted to a reduced polynomial material model for an incompressible material,

$$\mathrm{W̅}={\mathrm{C}}_{10}\times ({\mathrm{Ī}}_1-3)+{\mathrm{C}}_{20}\times {({\mathrm{Ī}}_1-3)}^2$$ (1)

$${\mathrm{W̅}}_{\text{total}}=\mathrm{W̅}+\frac{{(\mathrm{J}-1)}^2}{\mathrm{D}}$$ (2)

where W̅ is the strain energy density function, C₁₀ and C₂₀ are constants (Sinha Roy and Dupps, 2011), Ī₁(= trC̅) is the strain invariant and is the trace of C̅(= J^{−2 / 3}C). C is the modified right Cauchy-Green deformation tensor. J is determinant of the deformation gradient, F. C₁₀ and C₂₀ are coefficients that relate the strain energy density of the tissue to the strain invariant and can be determined from stress vs. strain data obtained from mechanical testing of corneal tissue. The Cauchy stress tensor (σ) is given by:

$$\mathrm{\sigma }=\frac{2}{\mathrm{J}}\text{dev}\left[\mathrm{F̄}\frac{\partial \mathrm{W̅}}{\partial \mathrm{C̅}}{\mathrm{F̄}}^{\mathrm{T}}\right]+\frac{2(\mathrm{J}-1)}{\mathrm{D}}$$ (3)

where F̅(= J^{−1 / 3}F) is the modified deformation gradient, and dev is an operator given by $\text{dev}[.]=[.]-\frac{1}{3}([.]:\mathrm{I})\mathrm{I}$ where I is the 2^nd order unit tensor D was set at 10⁻⁶ and is the incompressibility constraint. The elasticity tensor needed for Newton iterations was computed numerically (Sun et al., 2008). In finite-strain hyperelastic theory, the elasticity tensor is comprised of the tangent modulus. In this paper, we refer to this tangent modulus as the elastic modulus. From eq. 1 and 3, it is clear that there is a linear relationship between elastic modulus and, C₁₀ and C₂₀, e.g., increasing both C₁₀ and C₂₀ by 50% will also increase the elastic or tangent modulus by 50% at any strain. The KC model also incorporates a cylindrical zone of reduced elastic modulus (Fig. 1C) (Sinha Roy and Dupps, 2011). Henceforth, we refer to this zone as the “weak zone”. Since the cornea is weaker in this zone, the constants C₁₀ and C₂₀ for normal cornea were reduced, as a function of radius and independent of corneal thickness, by:

$$\mathrm{\alpha }={\mathrm{m}}_1+\frac{{\mathrm{m}}_2}{1+{\mathrm{e}}^{(\mathrm{r}-{\mathrm{r}}_0)/\mathrm{d}\mathrm{r}}}$$ (4)

where m₁ and m₂ are regressed constants, r is the local radius measured from center of the weak zone such that in the weak zone, 0 < α ≤ 1. Thus in pre-CXL models, the decrease in elastic modulus in the weak zone was modeled as an exponential decay from the edge to the center of the circular weak zone and, in the region outside the weak zone, α = 1. Within the weak zone, W̅ was modified as:

$$\mathrm{W̅}=\mathrm{\alpha }\times ({\mathrm{C}}_{10}\times ({\mathrm{Ī}}_1-3)+{\mathrm{C}}_{20}\times {({\mathrm{Ī}}_1-3)}^2)$$ (5)

The values of m₁, m₂, r₀, dr and the diameter of the weak zone have been discussed previously (Sinha Roy and Dupps, 2011). With these conditions, the volume−averaged reduction in elastic modulus (1 − ᾱ) in the weak zone was ~0.5 for each eye model, similar to ex vivo measurements of elastic modulus of KC corneal tissue (Andreassen et al., 1980; Nash et al., 1982). We also assumed the center of the weak zone to be the location of the steepest point of the cornea; that is, the location of the minimum radius of curvature on the anterior corneal surface (Sinha Roy and Dupps, 2011). The location of the weak zone is therefore determined on a patient-specific basis.

To simulate CXL, W̅ was altered within the central 9 mm CXL zone (Figure 1C) by modifying α to α'. Note that the CXL zone also includes the weak cylindrical zone of the KC cornea. Standard clinical UV-A sources for CXL exhibit an intensity drop off of 10% from the center to edge of the beam (Sinha Roy and Dupps, 2011). Further, attenuation of UV intensity with increasing depth within the cornea has been experimentally demonstrated to follow the Beer-Lambert law (Spoerl et al., 2007; Speorl et al., 2010, Schumacher et al., 2012). Thus, incident UV intensity at any zone within the cornea is a function of radius and depth assuming that the beam intensity is radially symmetric (independent of meridian) and the beam was centered at the geometric center of the cornea. To model CXL, we assumed that the magnitude of increase in elastic modulus is linearly proportional to the beam intensity and peak magnitude of elastic modulus increase is at the geometric center of the cornea. In this study, we also assumed that the CXL effect was independent of riboflavin concentration through the depth of the anterior cornea up to 300 microns as the most commonly described clinical CXL protocol has been designed to achieve nearly uniform riboflavin concentration up to a depth of 300 microns (Spoerl et al., 2007; Speorl et al., 2010). Therefore in each eye model for post-CXL state, α was modified to α' given by:

$$\mathrm{\alpha }\text{'}=\mathrm{\alpha }\times (\mathrm{f}\times \mathrm{g}+1)$$ (6)

where f (f > 1) was the magnitude of increase in elastic modulus due to CXL of the anterior-most crosslinked layers of the cornea, and (1 – g) was the decrease in the magnitude of elastic modulus increase f due to beam attenuation in deeper layers of the cornea. Since attenuation of UV-A results in deeper layers of the cornea, it is hypothesized that the anterior most layers of the corneal stiffen the most and magnitude of stiffening decreases in deeper layers of the cornea (Spoerl et al., 2010; Schumacher et al., 2012). These phenomena can be described by a mathematical function, e.g., g can be a linear function such that g = 1 in the anterior most layer of the cornea and g = 0 at the 300 um stromal depth.

As described in the preceding paragraph and in this study, f was varied as a linear function of radius from the geometric center of the cornea such that its maximum value (f_max) is at the geometric center and its minimum value (f_min = 0.9×f_max) is at the edge of CXL zone. We kept g as 1 as the stiffening was assumed to be independent of depth since in vivo estimate of depth variation in the magnitude of stiffening is lacking and only theoretical estimates exist. Additionally, in the inverse model of one eye in which CXL led to topographic flattening, we investigated the theoretical effect of varying g proportional to the intensity decrease caused by beam attenuation as an exponential decay. This can be expressed as:

$$\mathrm{g}=\mathrm{f}\times {\mathrm{e}}^{-\mathrm{\beta }\mathrm{t}}$$ (7)

where β is the attenuation coefficient and t is the depth measured from the anterior surface of the cornea. Two different magnitudes, 60 cm⁻¹ (Spoerl et al., 2010) and 120 cm⁻¹, were used in the analyses. This simulated CXL procedure in each eye was similar to the “standard broad-beam” CXL protocol described previously (Sinha Roy and Dupps, 2011). The scleral material properties were modeled by eq. [5] with a constant α > 1 as the sclera is stiffer than the cornea (Woo et al., 1972; Thorton et al., 2009). To quantify the effect of sclera-to-cornea modulus (S/C) ratio on the inverse model results, the inverse model for each eye was solved for three different values of α (α= 3, 4 and 5).

2.4 Calculation of Corneal Curvature Outcomes

The x, y and z coordinates of the anterior surface of the cornea were fitted to 12^th order Zernike polynomials with a normalization radius of 5.75 mm. For the all the corneas evaluated with Zernike polynomials, the root mean square error of the anterior corneal surface elevation was less than 0.28 micron. The local radius of curvature of the anterior surface of cornea along meridia from 0° to 355° at 2° intervals and along the radius at 0.05 mm intervals was calculated using the 1^st and 2^nd order derivatives of Zernike polynomials. In clinical terminology, the local radius of curvature is also known as the tangential radius of curvature. Tangential curvature (K_t) was calculated as the ratio of (n – 1) to R_t, where R_t was the tangential radius of curvature in meters and n (= 1.3375) was the keratometric refractive index of the cornea. Maximum tangential curvature was referred to as K_t,max. We also calculated the simulated keratometry or SimK at the central 3 mm diameter. SimK provided two curvatures (K₁, K₂) and the meridian or axis at which K₁ is obtained. In clinical terminology, SimK is written as K₂/K₁ @ axis. The wavefront aberrations of the anterior surface of the cornea with a pupil diameter of 6 mm were also calculated using Zernike polynomials. The lower order root mean square (RMS) was calculated using the 2^nd order Zernike coefficients (3 in number). The higher order root mean square (RMS) was calculated using the 3^rd to 12^th order Zernike coefficients (85 in number). Using single index notation starting from 0, the RMS in terms of Zernike coefficients (Z_n) were as follows:

$$\text{Lower Order}\mathrm{R}\mathrm{M}\mathrm{S}=\sqrt{\frac{{\mathrm{Z}}_3^2+{\mathrm{Z}}_4^2+{\mathrm{Z}}_5^2}{3}}$$ (8)

$$\text{Higher Order}\mathrm{R}\mathrm{M}\mathrm{S}=\sqrt{\frac{{\mathrm{Z}}_6^2+{\mathrm{Z}}_7^2+\dots \mathrm{..}+{\mathrm{Z}}_{89}^2+{\mathrm{Z}}_{90}^2}{85}}$$ (9)

2.5 Inverse FE Optimization

Since the magnitude of change in elastic modulus post-CXL is unknown, it was estimated using an inverse FE approach. From eq. [6], it can be seen that f is the variable that provides the magnitude of increase in the elastic modulus as a function of radius with a maximum value of f_max at the geometric center of the cornea. Since f varied linearly with radius such that f at the edge of the CXL zone was 90% of f_max, it is evident that f_max was the optimized variable. Fig. 2 illustrates the inverse modeling approach described below:

• Step 1: Build Pre-CXL FE model of the eye.

• Step 2: Solve for the no-load (zero IOP) configuration of the FE structure. In this step, the pre-stressed configuration of the pre-CXL cornea-sclera model is determined. Since pre-CXL geometries were measured under physiological loading at in vivo IOP, the no-load configuration is determined to allow application of the simulated CXL procedure prior to model loading. The mathematical formulation to compute the no-load geometry has been described in detail in other studies (Pandolfi and Holzapfel, 2008; Sinha Roy and Dupps, 2011).

• Step 3: In this step, the optimization process begins. We update α to α' in the no-load FE model using initial estimate for f_max. This will change the material properties of the cornea within CXL zone. The factor, g, will be updated depending upon whether the effect of beam attenuation on the stiffness change in deeper regions of the stroma up to a depth of 300 microns was also being considered.

• Step 4: In this step, the post-CXL FE structure of the eye is computed by solving the no-load FE model stressed to in vivo IOP with perturbed properties α'

• Step 5: From the computed FE result in step 4, the difference between the post-CXL in vivo and FE results is obtained. This difference is quantified by an objective function, φ(K_t). Since 80% of the optical power of the cornea is determined by its anterior surface, φ(K_t) is also defined as a function of its tangential curvature. This function is evaluated at each optimization iteration in a 1 mm diameter zone around the pre-CXL location of the cone.

  $$\mathrm{\phi }({\mathrm{K}}_{\mathrm{t}})=\sum _{\mathrm{i}=1}^{\mathrm{n}}{({\mathrm{K}}_{\mathrm{t},\mathrm{i}}^{\text{invivo}}-{\mathrm{K}}_{\mathrm{t},\mathrm{i}}^{\mathrm{F}\mathrm{E}})}^2$$ (10)

  where ${\mathrm{K}}_{\mathrm{t}}^{\text{invivo}}$ and ${\mathrm{K}}_{\mathrm{t}}^{\mathrm{F}\mathrm{E}}$ are the in vivo and FE computed tangential curvature, respectively. The summation in Eq. 10 is performed over n sampled points on the anterior surface. Convergence of the optimization procedure is defined by computing the relative change (ε) in the magnitude of φ(K_t). The RMS of the error function (φ(K_t)) and the convergence criteria (ε) for the optimization procedure is defined as:

  $$\mathrm{R}\mathrm{M}\mathrm{S}={\left(\frac{\mathrm{\phi }({\mathrm{K}}_{\mathrm{t}})}{\mathrm{n}}\right)}^{1/2}$$ (11)

  $$\mathrm{\epsilon }=\frac{{\mathrm{\phi }}_{\mathrm{j}+1}-{\mathrm{\phi }}_{\mathrm{j}}}{{\mathrm{\phi }}_{\mathrm{j}}}\times 100$$ (12)

  where j+1 and j are the current and preceding iteration number, respectively. If ε ≤ 0.5%, then the optimization is accepted as converged and the optimized value of f_max or the magnitude of change in the elastic modulus is obtained. If ε > 0.5%, then f_max is updated using the Levenberg–Marquardt algorithm for the following optimization iteration, j + 2. Then, steps 4 and 5 are repeated again until ε ≤ 0.5% was achieved. To ensure that the global minimum is reached, the optimization was performed for each eye with different initial estimates of f_max. Only the result that gave the minimum error is reported in this paper. The FE simulations were solved in the analysis package ABAQUS (Simulia Inc., Waltham, MA, USA). The optimization process along with the Levenberg–Marquardt algorithm was coded in Python scripting language. Linear regression analyses between the in vivo and iFE values of K_t,max, SimK and anterior surface aberrations were performed to determine the amount of variance in these in vivo metrics that was predicted by the iFE model.

Figure 2.

The inverse FE optimization approach.

3 Results

A total of 16 eyes were analyzed. Table 1 summarizes the pre– and post–CXL in vivo curvature data. The iFE results for different S/C ratios of 3, 4 and 5 are also listed in Table 1. The in vivo measurements indicate flattening of the cornea (reduction in K_t,max, K_flat, K_steep) and reduction in aberrations (LORMS, HORMS) in response to collagen crosslinking. The same trend was seen from iFE computed values with similar means and standard deviations (Table 1). Table 2 lists the mean±standard deviation of f_max for different S/C ratios and different ranges of follow-up months. For all values of S/C ratio, f_max increased after CXL though the increase was not linear with time. The S/C cornea ratio impacted the range of f_max from 2.11 ± 1.48 to 1.96 ± 1.23 (a small difference of 7.1%) for S/C ratio of 3 and 5, respectively. The relatively large standard deviations indicate that the value of f_max, an estimate of the elastic modulus increase produced by CXL, varied considerably from patient to patient. To evaluate the patient-specific performance of the iFE approach, comparisons between in vivo and iFE results were performed. Figures 3a–c show linear regression of in vivo measurements and iFE modeling results (K_max, K₁, K₂). All the regressions produced high R² values with a slope approximately equal to 1. Figures 4a–c show linear regression of in vivo measurements and iFE modeling results (LORMS, HORMS). Once again the slope approaching unity could be obtained. However, the R² obtained for LORMS was significantly lower compared to other optical indices.

Table 1.

Summary of curvature and aberrometry before and after CXL for all eyes. Both in vivo and computed inverse FE (iFE) values are listed here as mean ± standard deviation. The colored rows list the in vivo data. The remaining rows list the iFE estimates. The variables listed are: 1) K_t,max - Maximum tangential power, 2) K₁ and K₁ - SimK curvature along the steepest and flattest meridian evaluated at 3 mm diameter, 3) LORMS - Root mean square of lower order aberration Zernike coefficients, 4) HORMS - Root mean square of higher order aberration Zernike coefficients, 5) RMS error - Root mean square of difference between in vivo and iFE results (see Eq. 11).

	Pre-CXL	S/C = 3	S/C = 4	S/C = 5
Kt,max (D)	60.27 ± 16.64	63.24 ± 6.53
iFE Kt,max (D)		63.12 ± 6.39	63.09 ± 6.39	63.07 ± 6.39
K2 (D)	45.56 ± 12.39		48.38 ± 3.71
iFE K2 (D)		48.53 ± 3.67	48.52 ± 3.67	48.59 ± 3.63
K1 (D)	50.14 ± 13.76	53.08 ± 3.65
iFE K1 (D)		53.15 ± 3.28	53.13 ± 3.29	52.97 ± 3.57
LORMS (µm)	5.80 ± 2.53	5.54 ± 2.28
iFE LORMS (µm)		5.24 ± 2.35	5.24 ± 2.34	5.24 ± 2.33
HORMS (µm)	4.52 ± 1.87	4.55 ± 1.71
iFE HORMS (µm)		4.60 ± 1.66	4.60 ± 1.65	4.60±1.65
RMS Error (µm)		0.84 ± 0.87	0.85±0.86	0.83±0.87

Table 2.

Mean values of f_max computed by inverse FE for different sclera-to-cornea modulus ratios (S/C). Group average indicates the mean f_max for all time points for a particular S/C. A trend toward progressive corneal stiffening in the follow-up months is present. As S/C ratio increased from 3 to 5, the inverse estimate of stiffening decreased.

Follow-up interval:	S/C = 3	S/C = 4	S/C = 5
3 ≤ month < 6	1.83 ± 0.98	1.77 ± 0.98	1.73 ± 0.91
6 ≤ month < 9	2.27 ± 1.55	2.10 ± 1.55	2.07 ± 1.36
9 ≤ month < 12	2.45 ± 1.60	2.34 ± 1.60	2.25 ± 1.47
Group average	2.11 ± 1.48	2.00 ± 1.36	1.96 ± 1.23

Figure 3.

Comparison of in vivo and inverse FE (iFE) estimated optical parameters of the anterior surface of the analyzed eyes. Data from all 16 eyes is shown for different sclera-tocornea modulus ratio (S/C RMS for higher order aberrations): a) S/C = 3; b) S/C = 4; c) S/C = 5. Regressions suggest strong agreement between in vivo and iFE results.

Figure 4.

Comparison of in vivo and inverse FE estimated wavefront aberration of the anterior surface of the analyzed eyes. Data from all 16 eyes is shown for different sclera-to-cornea modulus ratio (S/C): a) S/C = 3; b) S/C = 4; c) S/C = 5. Better correlation between in vivo and iFE RMS for higher order aberrations (HORMS) was seen than for RMS for lower order aberrations (LORMS).

Figure 5 shows the longitudinal (time) change in f_max in the follow-up months after CXL computed with the iFE approach for a S/C ratio of 3. Crosslinked eyes were evaluated over 3 to 15 months depending on the follow-up visits. Wide fluctuations in f_max were demonstrated over initial follow-up visits, though most eyes stabilized a year after CXL. A linear regression of f_max vs. time in months after CXL was performed for all the eyes for each S/C ratio. These results are plotted in black. The linear regression clearly shows a stiffening effect that tends to increase as time progresses. In Figure 5, one of the eyes exhibited significant progressive weakening of the cornea within six months after CXL.

Figure 5.

Change in f_max [(f_max - 1) × 100 = % increase in modulus of the cornea at the geometric apex in the follow-up months after CXL estimated by the inverse FE. The effect of different sclera-to-cornea modulus ratios (S/C) were illustrated by the linear regression lines. There was considerable variability both intra-patient as well as inter-patient in the follow-up months. As S/C increased, iFE predicted that slightly less stiffening would occur to produce the same corneal curvature change with crosslinking.

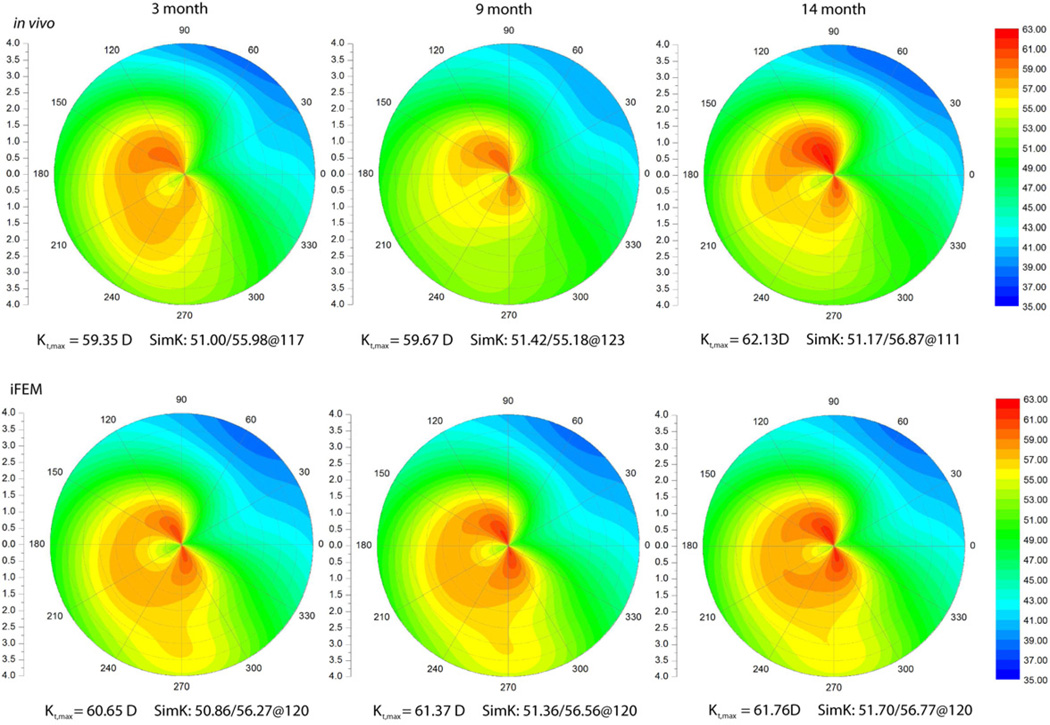
We now examine two cases which demonstrate the variability of clinical responses to CXL. Figure 6 shows the in vivo and iFE results of an eye that underwent CXL. The in vivo data shows progressive flattening up to the 15 month follow-up (characterized by a decrease in K_t,max and SimK). Similarly, the iFE result shows progressive flattening and the curvature result (K_t,max) is within 0.5D of the in vivo data. At the 15 month follow-up, the difference is greater than 1D. Figure 7 shows the in vivo and iFE result of another eye that underwent CXL. The in vivo data shows moderate steepening up to the 14 month follow-up (increase in K_t,max and SimK) that probably indicates disease progression despite corneal CXL. In contrast to the first case, the iFE result shows progressive steepening with a curvature result within 1D of the in vivo data. The contrasting responses of these two cases are evident in a plot of the magnitude of f_max at different time points (Figure 8). The case that responded more favorably to CXL demonstrated an increasing value of f_max over time, whereas the case that responded less favorably demonstrated a progressive decrease in f_max over a similar follow-up period. Figure 8 also demonstrates that the material property estimates were only minimally dependent on the S/C ratio.

Figure 6.

A comparison of in vivo and inverse FE (iFE) estimate of tangential curvature (in Diopters) of one of the eyes showing progressive flattening (regression of keratoconic steepening) in the months following crosslinking. Vertical and horizontal axis units are in millimeters.

Figure 7.

A comparison of in vivo and inverse FE estimate of tangential curvature (Diopters) of one of the three eyes showing progressive steepening (keratoconic progression) at least 6 months after crosslinking. Vertical and horizontal axis units are in millimeters.

Figure 8.

A comparison of change in f_max [(f_max - 1) × 100 = % increase in modulus of the cornea at the geometric apex) and sensitivity to sclera-to-cornea elastic modulus ratio using the data from the two cases described in Figure 6 and 7. Note that the case that with an estimated loss of stiffening effect over time and possible progression of keratoconus showed no sensitivity to the assumed sclera-to-cornea elastic modulus ratio (overlapping data points). At 14 month, the eye with disease progression showed a stiffening of ~10% whereas the other eye had stiffened by over 200%.

The CXL effect is theoretically dependent on incident beam intensity at a local point within the stroma. Depth-dependent beam attenuation reduces the overall beam intensity and thus, possibly the extent of tissue stiffening. Figure 9 illustrates the effect of beam attenuation on the inverse optimization if a depth-dependent CXL effect was assumed [eq. 7]. In this inverse model, the factor g imparts a progressive reduction in the magnitude of the modulus change in deeper layers of the stroma. The case described in Figure 6 served as the substrate for this analysis. The results for β = 60 and 120 cm⁻¹ are presented in Figure 9. For the same amount of pre- to post-treatment decrease in curvature, β = 120 cm⁻¹ shows a more concentrated increase in tissue stiffness in the anterior-most regions of stroma compared to β = 60 cm⁻¹. Further, the effect of varying S/C ratio can be clearly distinguished in the anterior layers but not near the edge of the CXL zone at 300 micron depth.

Figure 9.

Variation in f_max [(f_max - 1) × 100 = % increase in modulus of the cornea at the geometric apex] though the depth of the cornea using a depth-dependent inverse FE method. Data from the eye presented in Figure 6 were used in these analyses. Two different coefficients, β = 60 and 120 cm⁻¹ [see Eq. 6] were used to simulate depth-dependent stiffening effect for all sclera-to-cornea modulus ratios (S/C). With β = 120 cm⁻¹, the stiffening in the anterior stroma was significantly higher than with β = 60 cm⁻¹.

4 Discussion

We have presented a computationally efficient inverse FE analysis approach for estimating the stiffness change in the cornea after CXL using clinical tomography and traditional clinical efficacy endpoints for optimization. A strength of this approach is that it is built on patient-specific geometry and loading conditions. The models also incorporated simulations of the physical effects of UV attenuation and radial variation in incident UV intensity. The inverse method was sufficiently sensitive to changes in curvature and corneal anterior surface aberrations to produce meaningful differences in inverse estimates of corneal hyperelastic property changes. A tool based on classical mechanics principles for quantifying the mechanical effect of a treatment has not been previously reported in an ophthalmic application.

To assess the validity of the method and compare elastic modulus change estimates to the available literature, we used clinical data from a series of 16 consecutive eyes that underwent CXL. The inverse FE results showed that localized flattening of the cornea can be explained by an increase in regional tissue elastic modulus. Ex vivo extensiometric measurements have suggested increases in Young's modulus of 80% and 350% in porcine and human corneal tissue after CXL (Wollensak et al., 2003a). Supersonic shear imaging in crosslinked porcine corneas ex vivo yielded an increase in the Young's modulus by 360% (Tanter et al., 2009). Another ex vivo study using Scheimpflug imaging of whole-globe inflational tests on crosslinked porcine corneas yielded an increase in the Young's modulus of 58% (Kling et al., 2010). Our previous FE study involving computational simulation of keratoconus and CXL in 2 patient-specific geometries predicted that increases in modulus of 200–300% would be required to produce 2 to 3D of flattening of the steepest corneal point (Sinha Roy and Dupps, 2011), a curvature response that is at upper end of the spectrum reported in most clinical series. The present study revealed similar increases in modulus. Our inverse model also incorporated assumptions about the depth-dependent stiffening effects of crosslinking. Further ex vivo and in vivo study with emerging techniques such as supersonic shear imaging (Nguyen et al. 2012), optical coherence elastography (Ford et al. 2011) and Brillouin microscopy (Scarcelli et al., 2013) will be important for further refinement of these assumptions, which are dependent upon the irradiation source (Koller et al. 2013) and other treatment variables such as the method of delivery and composition of riboflavin solution (Armstrong et al, 2013).

Estimates of modulus change varied considerably as a function of time over the postoperative course and between cases and punctuate the importance of a patient-specific approach. Changes in f_max with time could reflect influences beyond pure stromal modulus change such as redistribution of stress within the stroma due to collagen remodeling and postoperative changes in epithelial thickness profile that affect surface topography and estimated property changes. The unusual case illustrated in Figure 5 involving a reduction in computed modulus during follow-up was not noted to have any treatment protocol anomalies and could represent progression of disease due to ineffective CXL or unusually aggressive disease.

The accuracy and repeatability of the tomographic measurement technique used to generate the models are expected to influence the results of the inverse FE approach. The optimization objective function was designed to depend on the tangential curvature rather than axial curvature since the former provides more accurate representations of the magnitude and location of irregular corneal shape features away from the corneal center (Roberts, 1994; Dupps, 2006). Our ongoing studies in a different series of CXL patients have demonstrated that using multiple post-operative images acquired after CXL reduces variability in the estimation of f_max at different follow-up intervals (Sinha Roy et al., 2012). Corneal anterior surface aberrations could also be included in the objective function, but aberrometry in KC may suffer from poor repeatability depending on the imaging technology and stage of disease (Shanker et al., 2008). Anterior segment imaging technology is improving rapidly in speed and resolution, and related improvements in repeatability and accuracy will increasingly support more accurate model solutions.

Another potential source of error in the estimation of material property changes is an implicit assumption that the epithelial thickness profile of the post-CXL cornea is the same as in the pre-CXL epithelium in each eye and that this thickness distribution is constant across all studied time points. Changes in epithelial thickness profiles have been shown in some post-LASIK ectatic eyes treated with CXL (Reinstein et al., 2011). Although the epithelium does not contribute substantially to the mechanical behavior of the cornea and is a very thin layer relative to the stroma, it’s thickness profile does influence surface topography and thus the optimization variables. Since our objective function depends on curvature, future studies will include the the patient-specific 3D structure of the epithelium in the FE model. Optical coherence tomography provides the means for generating this data, along with reflectance-based estimates of the depth of CXL effect (Doors et al., 2009).

Continuum mechanics models of normal cornea have been used to investigate the interaction between fiber lamellae and cellular matrix (Pandolfi and Manganiello, 2006; Pandolfi and Holzapfel, 2008). Measurements in excised KC corneal buttons have shown the absence of preferred fiber orientation in the affected zone with some evidence of normal preferred fiber orientation in the peripheral cornea (Meek et al. 2005). However, patient-specific fiber-matrix distributions are not currently available in vivo from KC patients and we have limited our continuum approach to a locally fiber-independent model with spatially varying elastic moduli to approximate similar material inhomogeneity in KC corneas. These approximations can be improved upon as more is learned about the in vivo composite structure of the normal and keratoconic cornea across a range of disease severity.

Significant improvements in the fidelity of these models and of simulation-based studies of ectatic disease and therapy in general might be realized by incorporating patient-specific pretreatment material properties of the cornea. Based on ex vivo tissue tensile testing data, our iFE models assumed the same initial material properties (C₁₀ and C₂₀) for all the analyzed eyes. Techniques for elasticity quantification in the stroma are in development (Tanter et al., 2009; Ford et al., 2011) and may eventually allow for the patient-specific determination of pre-CXL spatially distributed material properties (C₁₀, C₂₀ variables in Eq. 4 and fiber directions). Successful integration of this data into forward FE model implementations can potentially be used for personalized medicine and optimization of corneal optics with customized treatment approaches (Sinha Roy and Dupps 2011).

Highlights.

1. We present the first report of a continuum modeling approach for evaluating in vivo corneal elastic modulus changes after collagen crosslinking for keratoconus.

2. The method employs patient-specific inverse finite element modeling of clinical pre- and post-crosslinking geometry over multiple postoperative examinations.

3. High-fidelity finite element representations of clinical corneal topography were obtained with low RMS error and high correlations to clinical shape metrics.

4. Inverse optimizations suggested a mean doubling of corneal elastic modulus within the treatment zone, phenomenologically consistent with in vitro studies.

5. Individual variation in crosslinking-mediated material property change was high and varied significantly over the follow-up period.