Graphene, a material for high temperature devices – intrinsic carrier density, carrier drift velocity, and lattice energy

Abstract

Heat has always been a killing matter for traditional semiconductor machines. The underlining physical reason is that the intrinsic carrier density of a device made from a traditional semiconductor material increases very fast with a rising temperature. Once reaching a temperature, the density surpasses the chemical doping or gating effect, any p-n junction or transistor made from the semiconductor will fail to function. Here, we measure the intrinsic Fermi level (|E_F| = 2.93 k_BT) or intrinsic carrier density (n_in = 3.87 × 10⁶ cm⁻²K⁻²·T²), carrier drift velocity, and G mode phonon energy of graphene devices and their temperature dependencies up to 2400 K. Our results show intrinsic carrier density of graphene is an order of magnitude less sensitive to temperature than those of Si or Ge, and reveal the great potentials of graphene as a material for high temperature devices. We also observe a linear decline of saturation drift velocity with increasing temperature, and identify the temperature coefficients of the intrinsic G mode phonon energy. Above knowledge is vital in understanding the physical phenomena of graphene under high power or high temperature.

Since the discoveries of carbon nanotube and graphene¹,², a significant amount of attention has been directed toward the room temperature and low temperature measurements in pursuing a high carrier mobility³,⁴,⁵. As people seek device applications for graphene, high field and high current measurements start to appear⁶,⁷,⁸,⁹,¹⁰. The importance of electron-phonon coupling is well recognized¹¹,¹²,¹³. However, little attention has been made to the role of intrinsic carriers in graphene, because the great ability of graphene to tolerate the impact of temperature masks the existence of its intrinsic carriers. Thus, the importance of graphene as a material for high temperature devices is not noticed. Here we use a Raman method to measure the level of intrinsic carriers in a voltage biased graphene device up to 2400 K. We find the level of intrinsic carriers in graphene is an order of magnitude less sensitive to the temperature than that of traditional semiconductors, silicon and Germanium. The result tells us that a properly fabricated graphene p-n junction or transistor can operate well above 1500 K and will not fail until other parts melt. Working together with silicon carbide (SiC), graphene might be one of the building materials for coming high temperature devices. We also observe a linear decline of saturation drift velocity in graphene with increasing temperature in contrast to a constant saturation drift velocity in traditional semiconductors, as the result of the degeneracy of carriers and the Pauli exclusion principle. At the same time, we identify the temperature coefficients of the intrinsic G mode lattice vibration energy up to 2400 K. Above information highlights the great application potentials for graphene in high temperature devices, suggests a new exploring direction for graphene research, and is critical in the physics of graphene under high field, high current or high temperature conditions.

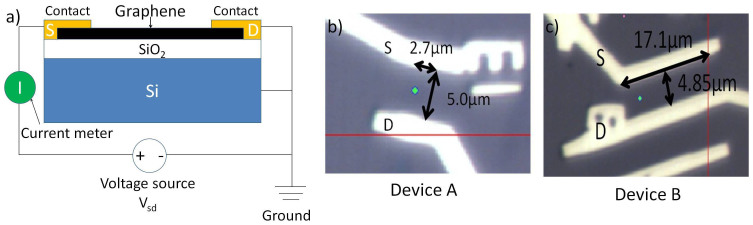
The graphene devices were fabricated by mechanical exfoliation from graphite. Figure 1a shows a sketch of the layout of graphene devices and electrical measurement. Contacts were formed on top of the graphene after steps of E-beam lithography, metal evaporation and liftoff. The contacts are 100 nm Au with 5 nm Cr between Au and graphene. The substrate is doped Si with 300 nm SiO₂ isolation layer on top. When an electrical bias is applied to a device, the drain electrode and Si substrate are grounded. A Kethley 2400 is used both as a voltage source and a current meter. During the measurements, the devices were kept in a flowing nitrogen gas environment in order to prevent the oxidization of the sample. A Horiba Raman microscope was used to measure the Raman spectra of the sample from the top. The excitation laser is a He-Ne 633 nm (1.96 eV) laser. The focusing objective is a long working distance 50× objective lens. Two graphene devices are measured; the optical pictures of these graphene devices are showing in Fig. 1b and 1c. Device A is 5 μm in length and 2.7 μm in width, and device B is 4.85 μm in length and 17.1 μm in width. For example, we measured the device A from V_sd = 0 V to V_sd = 21 V with an increasing step of 1 V, then a downward scan (with a step size of −1 V) back to V_sd = 0. For each different V_sd, a Raman spectrum from the center of the device was recorded; the currents of the device before and after each Raman measurement were recorded as well.

Figure 1. Graphene device information.

(a), The sketch of the stacking structure of the devices and the electrical measurement layout. (b), Optical picture of the graphene device A. (c), Optical picture of the graphene device B. The widths and lengths of the devices are marked in the pictures. The blue dots are the optical focus positions during the measurements of the devices. The letters D and S indicate the drain electrodes and source electrodes.

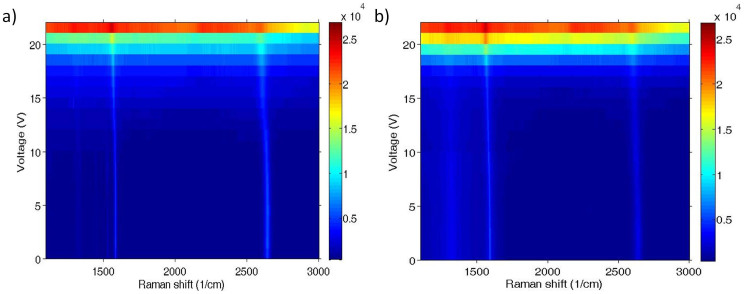
Our measurement result reveals the dominating impact of intrinsic carrier due to increasing temperature in the devices under high bias conditions. In Figure 2, we plot the measurement results of Raman spectra as a function of V_sd for device A. We can see two main Raman peaks, G mode around 1600 cm⁻¹ and 2D mode¹⁴ around 2600 cm⁻¹. In both subfigures, G mode intensity increases with a larger V_sd. At the same time, a dramatic increasing of the background signal appears with a high V_sd voltage and this background will drop back down with the decreasing V_sd during the downward scan. In an earlier report¹⁵, C.-F. Chen et al. presented that the G mode intensity has resonant behavior when the twice of the Femi level in graphene matches the excitation photon energy or the photon energy minus a G mode phonon energy. They also reported an increasing background in the spectra near the resonant condition, and they attributed this high background signal to hot luminescence in graphene. Our data's resonant behaviors in the G mode intensity and background are very similar to those reported behaviors, therefore we believe that the G mode intensity change is due to a changing Femi level in the graphene device. The Femi level (E_F) in graphene is directly linked to the carrier density (n) with 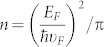, where ν_F is the graphene Fermi velocity, 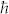is the reduced Planck constant. A higher Fermi level will have a higher carrier density, and vice versa. There are four possible reasons may change the device carrier density. They are intrinsic carrier density increasing due to rising temperature, permanent defects in graphene, back gating effect due to increasing V_sd, and the desorbing of the surface molecules. In comparison with Fig. 3a in C.-F. Chen et al.'s paper¹⁵ after shifting the resonant peak due to different excitation photon energies (785 nm to 633 nm, 1.58 eV to 1.96 eV), we use the relative intensity of the G mode at V_sd = 21 V over base intensity at V_sd = 0–5 V, and determine that |E_F| ≈ 0.8 eV or n ≈ 4 × 10¹³ cm⁻² when V_sd = 21 V. First of all, this high carrier density clearly is not the result of permanent defects in the device, because the V_sd downward scan shows this carrier density will go down with a lower voltage. For unintentional residual and surface adsorbate doping, the carrier density is normally at the scale of 10¹¹–10¹² cm⁻², and this doping should only decrease with an increasing temperature. The back gating effect of the V_sd can be estimated after calculating the back gating capacitance. For a 300 nm SiO₂ layer (permittivity ε = 4), the typical back gating capacitance C_bg = 1.2 × 10⁻⁸ F·cm⁻²; for V_sd = 20 V, back gating carrier density at the middle of the device n_bg ≈ C_bgV_sd/2 = 7.5 × 10¹¹ cm⁻². This value is two orders of magnitude smaller than what we have (n ≈ 4 × 10¹³ cm⁻²). The only reasonable explanation for this high rising carrier density is the increasing intrinsic carrier density due to rising temperature within the device. Also, the scales of other effects, back gating and desorption of surface adsorbate, are a couple orders of magnitude smaller than the intrinsic carrier density under the high bias condition in our sample. We determine that the thermally generated intrinsic carrier is the dominating factor for those short samples under high bias voltage conditions.

Figure 2. Raman spectra of device A plotted in color maps for different source drain voltages (V_sd).

(a), The spectra during the V_sd upward scan. (b), The spectra during the V_sd downward scan.

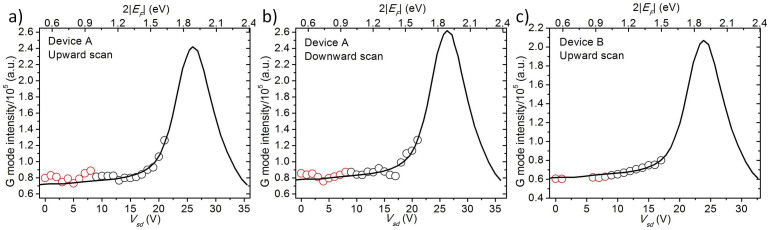
Figure 3. Measurement and fitting results for G mode intensities as a function of the V_sd.

(a), Device A during V_sd upward scan. (b), Device A during V_sd downward scan. (c), Device B during V_sd upward scan. The data points are fitted with the curve from Fig. 3a in C.-F. Chen et al.'s paper¹⁵ after shifting 0.38 eV (the difference between excitation photon energies, 785 nm to 633 nm or 1.58 eV to 1.96 eV). We only use the V_sd ≥ 9 V data points for the fitting in order to give a better fitting weight for the high bias data points.

First, we will use the G mode intensity to determine the Fermi level in the devices. The Fermi level in the graphene device is changed with V_sd, but not directly tuned by V_sd. The V_sd drives the graphene device to generate heat; the heat generated carrier density rises in the device with an increasing temperature; with the help of external field from V_sd, heat generated carriers break balance between electron carriers and hole carriers, and the major carrier winning out raises the Fermi level in the graphene device. For graphene with Fermi level at the Dirac point and no external field, Tian Fang et al. calculated thermally generated carrier density¹⁶, 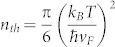, where k_B is the Boltzmann constant, T is the temperature. Their result gives out a n_th for both the electrons and the holes, the electrons and holes cancel each other so the Fermi level is still zero. Clearly, our graphene devices under high field don't fit into their calculation's pre-condition, and their calculation result probably is numerically invalid for our case as well. In a connected real device with a certain electric voltage level, the Fermi level can go well above zero. For our devices, we assume the Fermi level due to rising intrinsic carrier density at the measurement point of a device,

where α is a device and location dependent constant, E₀ is a constant Fermi level when V_sd = 0. The reasons behind this assumption are: it is reasonable to guess |E_F|∝k_BT, and we notice that device temperature T has a linear relationship with V_sd. (This will be discussed later when we discuss transport data, and in supplementary information.) Equation (1) works much better for V_sd downward scan than V_sd upward scan. During V_sd upward scan, the graphene device goes through desorption of surface adsorbate and increasing of permanent defects due to rising temperature¹⁷, so the E₀ is not a constant. During V_sd downward scan, the surface adsorbate was fully released at the upward scan step, and the permanent defects should be the same because the device is cooling, so the E₀ is about a constant during downward scan. This argument is supported by Figure 4a, which shows that the downward scan data for G mode positions shows a much better smoothness and data continuity than the upward scan data. In addition, Figure 4a shows that the G mode peak position, Ω_G = 1590.44 cm⁻¹, for V_sd = 0 after the downward scan. I. Calizo et al. reported that the graphene G mode energy linear coefficient with temperature is −0.016 cm⁻¹/K for a temperature range 83 K–373 K, and Ω_G = 1584 cm⁻¹ for T = 0 K¹⁸, so Ω_G = 1579.2 cm⁻¹ for T = 298.15 K (room temperature) if the Fermi level in graphene is zero. The blue shifted 11.24 cm⁻¹, in G mode energy at V_sd = 0 after downward scan, is due to the Fermi level E₀ in graphene. Because¹⁵ ΔΩ_G = |E_F| × 42 cm⁻¹eV⁻¹, we will have E₀ = 0.2676 eV for device A during downward scan. Figure 3 shows our measured G mode intensities as a function of the V_sd. The fitting curves are the curve retrieved from C.-F. Chen et al.'s paper¹⁵ Fig. 3a for I_G vs. 2|E_F|, after blue shifted 0.38 eV. (They use a 785 nm–1.58 eV excitation laser and we use a 633 nm–1.96 eV excitation laser.) Our experimental data are fitted to the curve with two fitting parameters, α in equation (1) with constant E₀ = 0.2676 eV and a linear scaling factor between our G mode intensity and I_G in C.-F. Chen et al.'s paper. The fitting is most accurate for device A during downward scan, because the E₀ value is measured for it. We do the same fitting for device A upward scan anyway, just to show a comparison. We only use the V_sd ≥ 9 V data points for the fitting in order to give a better fitting weight for the high bias data points, which matter the most in this fitting. The G mode intensities at the high bias voltages already rise significantly above the random error range, especially for the data from device A. Therefore, our data have enough signal-to-noise ratios to make this fitting method valid, although our data doesn't cover the full resonant peak. For device A, the upward scan data fitting gives α = 0.0520 eV/V; the downward scan data fitting gives α = 0.0513 eV/V; these two values are close and we take the downward scan α = 0.0513 eV/V as the value for device A. Data from device B has lower quality than the data from device A, however we use device B for the verification purpose only. Because device B broke down after the measurement at V_sd = 17 V during the upward scan, no data is available for device B V_sd downward scan and we can't accurately determine the E₀. In Fig. 4a, the high bias (V_sd ≥ 6 V) data points' behaviors are similar between the upward scan and downward scan for device A, this might suggest that the average E₀ value for high bias conditions in upward scan is close to the E₀ value in downward scan. We also consider device B has a similar length and goes through similar processes as device A, it is likely that device B has a similar defect level as device A. So, we use E₀ = 0.2676 eV from device A, as an approximation value, for the fitting of device B high bias data in Fig. 3c. The fitting gives α ≈ 0.0566 eV/V for device B.

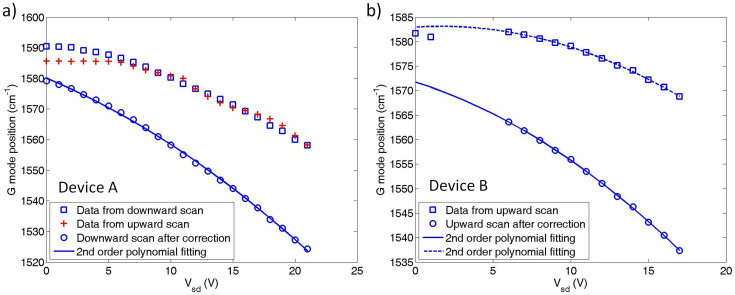
Figure 4. The G mode peak positions as a function of the V_sd.

(a), Device A. The blue square, red cross, and blue circle data points are the experimental data points for V_sd downward scan, V_sd upward scan, and the G mode position for downward scan after taking out the effect of carrier density, respectively. The blue curve is the fitting result for the corrected G mode position with a 2^nd order polynomial function. (b), Device B. The blue square and blue circle data points are the experimental data points for V_sd upward scan and the G mode position after taking out the effect of carrier density. The blue solid curve and dash curve are the fitting results for the corrected G mode position and the original data points, respectively, with a 2^nd order polynomial function. Only the data points of V_sd ≥ 6 V are used for the fittings of device B.

Next, we will find out the temperatures at the measurement point for difference V_sd situations using G mode peak position information. The key information we used to determine temperature is: the value of room temperature, the intrinsic G mode peak position shift (after correcting the doping effect) as a result of temperature change, the reported G mode energy temperature coefficient for temperature range 83 K to 373 K from Ref. 18, and a 2^nd order polynomial fitting of our G mode peak position. The 2^nd order fitting gives the relationship between the first and second temperature coefficients; our device temperature range overlaps with Ref. 18, so the reported the linear temperature coefficient from Ref. 18 sets another condition for the first and second temperature coefficients. Combining both conditions, we can have the values of the first and second temperature coefficients for G mode energy. With the value of room temperature and G mode Raman shift of each data point, we can have the device temperature of each data point. Figure 4 shows the G mode peak positions as a function of the V_sd for device A and device B. In comparison between upward scan and downward scan G mode positions for device A, the downward scan data shows a much better smoothness and data continuity. The surface adsorbate was fully released during upward scan, so no chemical doping changes during downward scan. The device goes through cooling during downward scan, the permanent defects have a constant amount, and only shift the downward scan data a constant amount in G mode energy. Therefore, we use the downward scan data for further data analyzing. During V_sd downward scan, the G mode peak position, Ω_G, satisfies Ω_G = Ω_{G_T} + ΔΩ_{G_in} + ΔΩ_{G_defect}, where Ω_{G_T} is the intrinsic G mode energy as a function of the temperature, ΔΩ_{G_in} is the G mode energy shift due to rising Fermi level (intrinsic carrier density) as a function of V_sd, ΔΩ_{G_defect} is a constant from the permanent defects level in the graphene. We know that ΔΩ_{G_in} + ΔΩ_{G_defect} = |E_F| × 42 cm⁻¹eV⁻¹ and 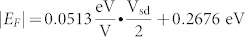for device A, then we can have a corrected G mode energy, Ω_{G_T} = Ω_G − (ΔΩ_{G_in} + ΔΩ_{G_defect}), and we plot the new values in Fig. 4a as blue circle points. The new, after correction, G mode energies are fitted very well with a 2^nd order polynomial function,

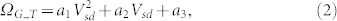where a₁, a₂ and a₃ are fitting parameters. For device A, we get a₁ = −0.0474 cm⁻¹V⁻², a₂ = −1.6901 cm⁻¹V⁻¹, and a₃ = 1580 cm⁻¹. We have not found any report about the coefficients of the graphene G mode energy as a function of the temperature for a temperature range up to 2500 K. H. Herchen and M. Cappelli reported that a first order Raman mode energy of diamond has a 2^nd order polynomial dependence on temperature up to 2000 K¹⁹. So, it is reasonable to assume, for G mode in graphene, that

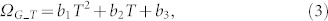where b₁, b₂ and b₃ are graphene dependent only constants. The temperature of the device appears a linear relationship with V_sd, and we define

where β is a device and location dependent constant and T_RT is the room temperature, 298.15 K. Combining equations (2), (3) and (4), we will have

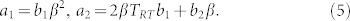I. Calizo et al. reported that the graphene G mode energy linear coefficient with temperature is −0.016 cm⁻¹/K for a temperature range 83 K–373 K, and Ω_{G_T} = 1584 cm⁻¹ for T = 0 K¹⁸. Because b₁, b₂ and b₃ are graphene dependent only constants, we have

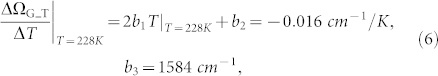in which 228 K is the average of 83 K and 373 K. Combining equations (5) and (6) with knowing values for a₁ and a₂ from fitting of device A, we can solve b₁ = −4.596 × 10⁻⁶ cm⁻¹K⁻², b₂ = −0.0139 cm⁻¹K⁻¹, b₃ = 1584 cm⁻¹, and β = 101.5 K/V for the measurement point in device A. Finally, we combine equation (1) and (4), and have |E_F| = γT to describe a graphene device intrinsic Fermi level as a function of the temperature, where γ = α/2β. From device A, our measurement gives out a graphene device intrinsic Fermi level, |E_F| = 2.53 × 10⁻⁴ eVK⁻¹·T or |E_F| = 2.93 k_BT. Using graphene 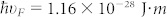, we have a graphene device intrinsic carrier density, n_in = 3.87 × 10⁶ cm⁻²K⁻²·T².

In Fig. 4b, the square points are the measured G mode positions of device B as a function of V_sd. The circle points are the corrected G mode energies using the same correction method for device A, but with 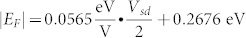. For the β value, it is invalid to process the limited data from device B with the same method for device A. Luckily, a₁ is a fitting parameter independent from the values of α and E₀. In order to prove this point, we did the 2nd order polynomial fittings for both measured G mode positions and corrected G mode energies, and plotted the fitting curves as a dash line and a solid line, respectively, in Fig 4b. Both fittings give a₁ = −0.0603 cm⁻¹V⁻². Because b₁ is a graphene dependent only constant and should be same for all graphene, we can use the b₁ = −4.596 × 10⁻⁶ cm⁻¹K⁻² value from device A, for device B. Using equation (5), a₁ = b₁β², we can get β = 114.5 K/V for device B. Together with α ≈ 0.0566 eV/V for device B, we get γ = 2.47 × 10⁻⁴ eV/K from device B. This γ value of device B is consistent with the γ value from device A. Such an agreement between device A and device B supports the validity of our method.

Graphene shows a great potential as a material for high temperature devices, compared to traditional semiconductors. High temperature devices are demanded for military, astronautic, and heavy industry applications, where high power density is required or high temperature environment can't be avoided. In order to make a nonlinear semiconductor device (p-n junction or transistor) functioning, the chemically doped carriers or the gating generated carriers have to be the controlling factor within the semiconductor material. However, when the device temperature increases, the semiconductor's intrinsic carrier density will increase. Once the temperature reaches a certain point that, the semiconductor's intrinsic carrier surpasses the chemical doping or gating effect and dominates the device's response, the nonlinear device will simply fail its function. For instance, a Si device's intrinsic carrier density will double if temperature increases 8 K from room temperature, the maximum operation temperature for a Si device is 250°C; a Ge device's intrinsic carrier density will double if temperature increases 12 K from room temperature, the maximum operation temperature for a Ge device is 100 °C²⁰. Normally for a semiconductor, a larger band gap gives a higher operation temperature; however, a larger band gap also increases the difficulty of carrier density tuning. Graphene is semi-metallic, not a semiconductor. By a doping or field effect, graphene can be made into a p-n junction or a transistor as well. Running our numbers for graphene, we find that it will take 125 K for graphene intrinsic carriers to double from room temperature. At 1500 K, graphene intrinsic carrier density is 8.7 × 10¹² cm⁻². Multiple research reports¹⁵,²¹,²² have demonstrated that a top gating method or a chemical doping can tune the graphene carrier density to a level above ±3 × 10¹³ cm⁻². Therefore, we foresee that a well-fabricated top gated graphene transistor or a chemical doped graphene p-n junction will be still well functioning at a temperature above 1500 K. A lot of things melt at 1500 K, for example gold melting temperature is about 1340 K. So, such a graphene transistor or graphene p-n junction will never fail due to rising intrinsic carrier density before other parts start to melt. Above analyses reveal the great potential of graphene as the material for high temperature devices and point out a new research direction for graphene applications.

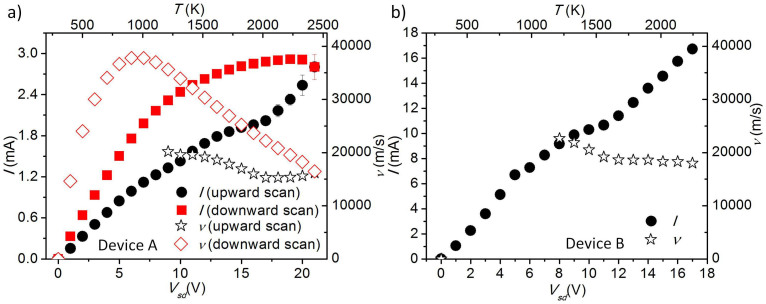
Finally, we will show and discuss carrier drift velocity in graphene up to 2400 K. Fig. 5 shows the device I–V curves, temperatures and carrier drift velocities of device A and device B. Carrier drift velocity, ν, equates to I/(qWn), where I is the current, q is the electron charge, W is the device width, n is the carrier density. The device B broke down after V_sd > 17 V and the device A was also on the brink of breakdown at V_sd = 21 V and showed clear runaway effect, in which the current keeps increasing and feeds itself with a constant driving V_sd. The maximum temperature is about 2400 K for device A and 2200 K for device B, those temperatures are consistent with the theoretically calculated graphene breakdown temperature, 2230 ± 700 K, in vaccum⁸. The drift velocities from device A, V_sd downward have the best accuracy compared to the values from upward scans, and map out a very nice three stage behavior under high field. In the first stage, the drift velocity increases linearly with the field, Ohm's law holds perfectly. Then with a further increased field, lattice scattering dominates, the drift velocity still increases but with a reducing rate, Ohm's law still works but with a reducing conductivity. In the last stage, after the field reaches a certain level, intrinsic carrier dominates, the drift velocity stops to increase. Traditionally, the drift velocity at this point is called the saturation drift velocity, and this saturation drift velocity stays the same for traditional semiconductors if the field increases further. For example, for Si, it is about 1 × 10⁵ m/s. Our graphene sample shows a linear drop of “saturation” drift velocity with the increasing temperature. This reducing saturation drift velocity of graphene has been predicted by theoretical calculation considering the degeneracy of carriers and the Pauli exclusion principle²³. The same calculation gives a saturation drift velocity value, 2 × 10⁵ m/s, for an ideal graphene with a doping level 10¹³ cm⁻² at 300 K. The maximum drift velocity of our graphene with a defect level of 4 × 10¹² cm⁻² is about 4 × 10⁴ m/s at 1000 K. Our value is not far from the calculation value after considering the temperature difference and the scattering from the defects. The declining saturation drift velocity in graphene helps delay the current runaway point, where the current keeps increasing on its own with a constant driving voltage, to an even higher temperature; but it also limits the ability of graphene in delivering large current. Another thing we want to point out is that Ohm's law fails totally in the intrinsic carrier dominated third stage. The electrons and the lattice are in a non-equilibrium state, in which the energy electrons taking from the field is not fully dumped to the lattice. This is why the device temperature has a linear relationship with V, not the IV. The difference in drift velocity for a same V_sd between downward and upward scan is due to different effective electron temperatures, despite a similar lattice temperature. During downward scan a graphene device appears a smaller contact resistant (or barrier) than the upward scan²⁴, therefore, downward scan data has a larger current, electrons carrying more energy and moving faster, or a higher effective electron temperature than the upward scan data.

Figure 5. Device I–V curves, temperatures, and carrier drift velocities.

(a), Device A, the defect level is 4 × 10¹² cm⁻². (b), Device B. Red solid square points and black solid round points are the I–V data during V_sd downward and upward scan, respectively, using left y axis. The current values are the averages of the currents before and after the Raman measurements, the differences of the two are plotted as error bars. Red hollow diamond points and black hollow star points are calculated carrier drift velocities during V_sd downward and upward scan, respectively, using right y axis. Only the data points with carrier density n ≥ 1.4 × 10¹⁷ m⁻² during the upward scan are plotted in order to control the error in drift velocities due to the uncertainty in E₀. The top axis plots the device temperature, which is calculated from V_sd using equation (4).

In summary, we use Raman method to quantitatively measure the graphene intrinsic carrier density, drift velocity and G mode phonon energy as functions of temperature up to 2500 K. We find that the intrinsic carrier density of graphene is an order of magnitude less sensitive to temperature than that of traditional semiconductor materials. We foresee graphene becomes the material for high temperature devices and a properly fabricated graphene transistor or p-n junction will not fail at all before other parts melt. We map out the three stage behavior of carrier drift velocity as a function of the field or temperature, and graphene shows a linear decline in “saturation” drift velocity in contrast to a constant saturation drift velocity in traditional semiconductor materials. We also find the G mode phonon intrinsic energy coefficients with temperature, Ω_G = −4.596 × 10⁻⁶ cm⁻¹K⁻²T² + −0.0139 cm⁻¹K⁻¹T + 1584 cm⁻¹. All of above reveal the great potential of graphene as a foundational material for high temperature devices, identify a new research direction for graphene applications, and are vital in understanding the physics of graphene under high field or high temperature.

Author Contributions

Y.Y. designed the experiments, carried out the measurements, performed the data analyses and drafted the initial manuscript; Z.C. contributed to sample fabrication; L.W. and K.J. provided the instruments for transport measurements and funding support, W.W. provided the Raman instrument. All authors discussed the results and wrote the paper together.

Supplementary Material

Supplementary Information

SUPPLEMENTARY INFO