Skip to main content
PMC home page
Mathematical Medicine and Biology logoLink to Mathematical Medicine and Biology
. 2011 Jan 25;29(1):85–94. doi: 10.1093/imammb/dqq025

Computational models of VEGF-associated angiogenic processes in cancer

Marianne O Stefanini 1, Amina A Qutub 2, Feilim Mac Gabhann 3, Aleksander S Popel 4,*
PMCID: PMC4104688  PMID: 21266494

Abstract

Tumour angiogenesis allows a growing mass of cancer cells to overcome oxygen diffusion limitation and to increase cell survival. The growth of capillaries from pre-existing blood vessels is the result of numerous signalling cascades involving different molecules and of cellular events involving multiple cell and tissue types. Computational models offer insight into the mechanisms governing angiogenesis and provide quantitative information on parameters difficult to assess by experiments alone. In this article, we summarize results from computational models of tumour angiogenic processes with a focus on the molecular-detailed vascular endothelial growth factor-associated models that have been developed in our laboratory, spanning multiple scales from the molecular to whole body.

Keywords: computational biology, systems biology, angiogenesis

1. Introduction

When diffusion is not sufficient to sustain oxygen delivery to a tumour, new capillaries may arise from nearby pre-existing blood vessels. This phenomenon, known as tumour angiogenesis, has its origin within the cancer cells where transcription factors stimulate secretion of growth factors into the extracellular space. The binding of these growth factors to their receptors on the endothelial cells lining the blood vessels induce signalling cascades which initiate the growth of the new vasculature from the existing vessels.

Several research groups have modelled tumour angiogenesis by focusing on the structural or mechanistic aspects of the newly formed blood vessels, while grouping the growth factors into a generic ‘tumour angiogenic factor’ (Chaplain et al., 2006). However, each molecule plays a specific role in this process and ideally these molecular details would be maintained in tumour angiogenic models (Mantzaris et al., 2004). In particular, multiscale models of tumour angiogenesis are of high interest as they provide insights into tissue and organ level effects while keeping the molecular level detail.

General recent reviews on the mathematical modelling of angiogenesis are available (Anderson & Quaranta, 2008; Byrne, 2010; Peirce, 2008). In this article, we specifically focus on the effects of vascular endothelial growth factor (VEGF) in tumour angiogenesis. We refer to the models formulated by our laboratory and other researchers, spanning multiple levels, from transcription factor to whole body, and summarize their main results. This includes the intracellular, cellular, tissue and whole-body levels. At the tissue level, we consider both spatial and non-spatial models.

2. Models of transcription factor HIF1α pathways

As tumours grow beyond ∼1 mm, they no longer can rely purely on diffusion to provide them with a sufficient oxygen supply. Hypoxia is a major stimulus for the recruitment of local host vasculature and the growth of capillaries within tumours. As such, some of the key molecules involved in tumour angiogenesis are transcription factors mediated by intracellular oxygen levels.

While numerous transcription factors and growth factors are involved in angiogenesis and cellular hypoxic response (e.g. protein 53, nuclear factorκB, phosphoinositide 3-kinase, insuline-like growth factor, fibroblast growth factor), for the purposes of this article, we focus on one key transcription factor hypoxia-inducible factor (HIF1) and one key HIF-activated growth factor—VEGF.

HIF1α is a transcription factor that has been called both an ‘angiogenic switch’ (Semenza, 2000) and a requirement for sustained angiogenesis (Dewhirst et al., 2007). HIF1α is omnipresent—a factor all nucleated cells in the human body are thought to be capable of expressing. However, in a basal normoxic state, HIF1α is rarely detected. This is the result of HIF1α’s very rapid hydroxylation and subsequent degradation in the presence of oxygen. Conversely, when oxygen levels drop, HIF1α cannot be hydroxylated. Instead, it enters the cell’s nucleus, where it binds to its constitutively expressed partner, HIF1β/aryl hydrocarbon receptor nuclear translocator. This α-β dimer then activates genes through their hypoxic response element. The large number of genes that HIF1 regulates makes its pathway a prime target for both pro- and anti-angiogenic therapies.

To help characterize such a complex network, computational modelling has emerged as a prominent tool (Dayan et al., 2009; Kohn et al., 2004; Qutub & Popel 2006, 2007, 2008; Yu et al. 2007; Yucel & Kurnaz 2007). All the models have focused on characterizing the dynamics of HIF1’s intracellular signalling pathway. One of the first computational models of the HIF1 pathway tested therapeutic strategies to enhance hydroxylation—a potential mechanism to lower HIF1α levels in cancer cells (Qutub & Popel, 2006). Enzymes called the prolyl hydroxlyase domain-containing proteins (PHDs) require the cofactors iron, deoxoglutarate and oxygen, prior to binding and hydroxylating HIF1α. The model predicted the degree to which supplementing with ascorbate (vitamin C) could rescue iron from its ferric form, freeing it to bind to the PHDs, and increase HIF1α hydroxylation. Subsequent experiments have shown ascorbate can shrink tumours in mice (Gao et al., 2007), and the PHD pathway is a target of anti-angiogenic drug development. Another HIF1-related model predicted how factor-inhibiting HIF1 can lead to the differential regulation of genes over a gradient of oxygen levels (Dayan et al., 2009).

Along with hypoxia being a stimulus for tumour angiogenesis, the ability of some cancer cells to adjust—even thrive—in a hypoxic microenvironment is an equally intriguing driving force behind computational models of the HIF1 pathway. High expression of HIF1α has been linked to a tumour’s resistance to radiation and chemotherapy (Moeller et al., 2004; Zhou et al., 2006). One hypothesized mechanism is through the generation of reactive oxygen species. An intracellular computational model predicted the effects of reactive oxygen species on HIF1α expression levels, and showed quantitatively how hydrogen peroxide and moderate HIF1α levels in cancer cells could allow for sustained cell growth (Qutub & Popel, 2008). The hypoxic microenvironment may also provide a fertile niche for ‘cancer stem cells’—self-renewing cells that are not yet fully differentiated and that are prone to become cancerous.

Understanding the crosstalk between cancer cells and their microenvironment as well as cancer cells and endothelial cells in the presence of hypoxia requires going beyond intracellular models of HIF1. Extending these models to the tissue level and combining them with mechanistically detailed models of upstream regulators and downstream growth factors will further advance anti-angiogenic therapeutic development.

3. Single-compartment tissue models describing VEGF ligand–receptor interactions

Homeostatic regulation of VEGF is vital for physiological angiogenesis and dysregulation can result in disease (Ferrara, 2005; Folkman, 1990) and has been studied in computational modelling (Mac Gabhann & Popel, 2008; Qutub et al., 2009). Thus another method to limit oxygen delivery to the vascularized tumour is to diminish or abrogate VEGF signalling, which results in reduction or even regression of neovascularization. To determine optimal strategies for vascular endothelial growth factor inhibition, we developed a computational model of VEGF distribution in tissue applicable to many diseases and used the model to compare multiple methods of targeting neuropilin-1 (NRP1), a VEGF co-receptor, in breast tumours (Mac Gabhann & Popel, 2006). The model describes kinetic ligand– receptor interactions between VEGF isoforms (VEGF121, VEGF165) and endothelial cell surface receptors (VEGFR1, VEGFR2 and NRP1), as well as extracellular matrix (ECM) binding sites for VEGF165. VEGFR1 binding to NRP1 and forming VEGFR2–VEGF165–NRP1 triplets are considered. This model does not describe 3D tissue geometry explicitly; instead, it comprises spatially integrated components (e.g. capillaries, endothelial cells, interstitial space and basement membranes) and within its components, concentrations of molecular species are defined. Several of our observations from this model are generalizable to other ligand–receptor systems.

First, we noted that direct interference with the binding of a ligand to one receptor, e.g. a decrease in receptor expression or blockade of the ligand-binding site on the receptor, does not impact the steady-state receptor activation unless there is an alternative receptor competing for the ligand to bind. Due to the constant production of new ligand by the parenchymal cells, the ligand will passively overcome a barrier such as this by increasing its concentration (due to reduction in internalization) unless it is diverted to a different internalization route. This also introduces a characteristic time—some therapies reduce signalling for longer than others.

Second, as a consequence of the first observation, the outcome of therapeutic interventions depends not only on the expression of the target molecule but also on other ligands and receptors within the same family. Thus, efficacy varies based on differences in both tumour and host (e.g. receptor expression on normal vs. pathological blood vessels and on tumour vs. parenchymal cells).

Third, one effective method for the reduction in efficacy of a ligand is the conversion of a cell surface receptor to a ‘dummy’ receptor, i.e. a receptor that binds the ligand and internalizes it, without initiating a signal. The example from our study is an antibody that binds to NRP1, allowing VEGF to bind but sterically preventing the subsequent presentation of VEGF to the signalling VEGFR2 receptor. By providing a novel pathway for the removal of ligand from the interstitial space, this takes advantage of the competing ligand–receptor system to simultaneously reduce VEGF concentration and signalling efficiency.

In our study, inhibition of VEGFR2 signalling was effected by blocking NRP1 binding only when VEGFR1 was also present; whereas the conversion of NRP1 to a dummy receptor was shown to be effective in both VEGFR1-expressing and non-expressing tissues. Thus, the model predicts the efficacy of therapies and also suggests tests that should be carried out to determine those characteristics of the tissues that will most determine which approaches should be used.

More generally, the models revealed the importance of the competition between multiple pathways for VEGF binding and internalization in assessing therapeutic potential. This becomes even more important in understanding the impact of new broad- and narrow-spectrum tyrosine kinase inhibitors that can target some or all the signal-initiation complexes that receptors form due to homo- and heterodimerization (Mac Gabhann & Popel, 2007).

4. Multi-compartment models of VGEF distribution

In current therapeutic anti-angiogenic strategies targeting VEGF, an anti-VEGF agent (e.g. bevacizumab—a humanized monoclonal antibody, or aflibercept [VEGF Trap]—a fusion protein [Gaur et al., 2009]) is administered into the blood that subsequently binds and neutralizes VEGF. To investigate the distribution and transport of VEGF and potentially exogenous therapeutic agents between the normal tissue, blood and tumour, we have developed a three-compartment model (Fig. 1).

Fig. 1.

Fig. 1.

Open in a new tab

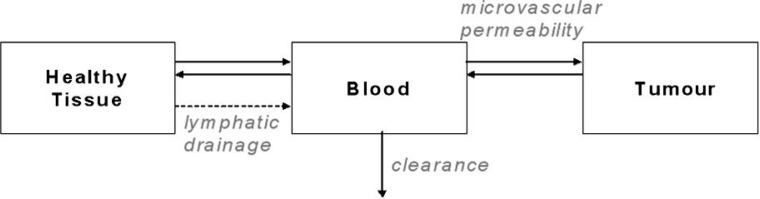
Schematic of a tumour angiogenesis compartment model.

The model was motivated by our meta-analysis of elevated free (unbound) plasma VEGF in cancer patients compared to healthy subjects (Kut et al., 2007). One of the aims of the model was to understand the underlying mechanisms that could explain this increase in VEGF when the cancer develops (Stefanini et al., 2008). Molecular interactions in each compartment included predominant VEGF isoforms (VEGF121 and VEGF165), VEGF receptors (VEGFR1 and VEGFR2) and co-receptor NRP1.

The system is described by non-linear ordinary differential equations (ODEs) that include VEGF secretion and binding to its receptors, VEGF isoform binding to the ECM and basement membranes, receptor insertion and internalization and VEGF microvascular permeability and plasma clearance. The full system of equations can be found in Stefanini et al. (2008, 2009). As a sample, the VEGF165 isoform variations in time in the available interstitial fluid and the blood are given by the following equations. The subscripts/superscripts N, B and T represent the normal tissue, the blood and the tumour, respectively. The definition of each term can be found in Table 1:

d[V165]Ndt=qV165N−kon,V165,MEBM[V165]N[MEBM]N+koff,V165,MEBM[V165MEBM]N                       −kon,V165,MECM[V165]N[MECM]N+koff,V165,MECM[V165MECM]N                       −kon,V165,MPBM[V165]N[MPBM]N+koff,V165,MPBM[V165MPBM]N                       −kon,V165,R1[V165]N[R1]N+koff,V165R1[V165R1]N−kon,V165,R2[V165]N[R2]N                      +koff,V165R2[V165R2]N−kon,V165,N1[V165]N[N1]N+koff,V165N1[V165N1]N                      −(kL+kpVNBSNBUN)[V165]NKAV,N+kpVBNSNBUNUBUp[V165]B, (4.1)
d[V165]Bdt=cV165[V165]B−kon,V165,R1[V165]B[R1]B                       +koff,V165R1[V165R1]B−kon,V165,R2[V165]B[R2]B                       +koff,V165R2[V165R2]B−kon,V165,N1[V165]B[N1]B+koff,V165N1[V165N1]B                       −kpVBNSNBUp[V165]B+(kL+kpVNBSNBUB)[V165]NKAV,N                      −kpVBTSTBUp[V165]B+kpVTBSTBUB[V165]TKAV,T. (4.2)

Table 1.

Glossary of terms used in (4.1) and (4.2)

Concentrations and densities
[MECM] Density of VEGF binding sites in the ECM,
[MEBM] in the endothelial basement membrane (EBM) and
[MPBM] in the parenchymal basement membrane (PBM)
[V165] Concentration of unbound VEGF165 in the available interstitial fluid
[R1], [R2] Density of the unoccupied receptor tyrosine kinases VEGFR1 and VEGFR2
[N1] Density of the unoccupied co-receptor NRP1
[R1 N1] Density of the VEGFR1-NRP1 complex
[V165 Rj] Concentration of VEGF165 bound to VEGF receptor j
[V165 N1] Concentration of VEGF165 bound to co-receptor NRP1
Kinetic parameters
qV 165 Secretion rate of VEGF165
sR Rate at which the receptors are inserted into the cell membrane
k on Kinetic rate for binding
k off Kinetic rate for unbinding
k int Internalization rate of the receptors
kpVij Microvascular permeability kp for VEGF (denoted as V) from compartment i to j (N = tissue; B = blood; T = tumour)
kL Lymph flow rate
cV 165 Clearance of VEGF165 in the blood
Geometric parameters
Ui Volume of the compartment i (N = tissue, B = blood, T = tumour; p = plasma)
Si B Total surface of the microvessels at the interface of the tissue (i) and the blood (B)
K AV, i Available volume fraction in the tissue i, i.e., ratio of available fluid volume to total tissue volume Ui
Open in a new tab

A sensitivity analysis was performed and we found that an increase in tumour VEGF secretion and/or an increase in microvascular permeability in the tumour could not explain a 4–5 fold increase of VEGF concentration in plasma seen in breast cancer patients. Thus, additional mechanisms need to be incorporated into the design. Such a model allows testing of biological hypotheses and also provides insights into the VEGF distribution and the VEGF receptors and co-receptor occupancy.

These computational models can also serve to predict the system behaviour in response to pro- or anti-angiogenic treatments. For example, (1) a compartmental model was used to examine how soluble VEGF receptor-1 can trap VEGF (Wu et al., 2009) and (2) the increase of plasma VEGF observed after intravenous administration of bevacizumab was reproduced by a pharmacokinetic model (Stefanini et al., 2010).

5. Multi-scale 3D spatial models of angiogenesis

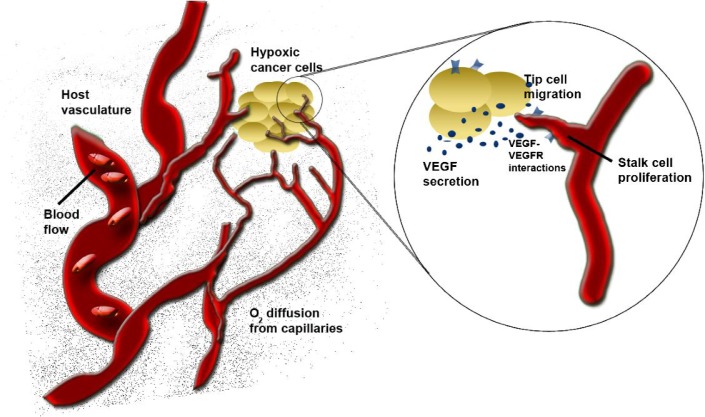
The designs discussed above (intracellular transcription factor pathways, growth factor receptor–ligand binding interactions and compartment models) are described by ODEs as they do not include explicit spatial representation. However, the process of tumour angiogenesis is highly dependent on spatial cues. In vivo, an endothelial cell on a quiescent microvessel can be activated by VEGF secreted by a tumour. Once activated, the leading cell (or tip cell) can start to migrate through the surrounding ECM in a heterogeneous, 3D microenvironment. This migration requires degrading the matrix as the cell migrates. The degree of endothelial cell migration and proliferation in a growing capillary sprout is a function of chemical and mechanical stimuli.

To characterize angiogenesis both in a quantitative and in a spatial way, 2D and 3D models have evolved addressing different parts of the process: microvascular blood flow with vessel growth (McDougall et al., 2006) or oxygen transport to tissue (Ji et al., 2006); effects of fibronectin in the ECM (Levine et al., 2002); VEGF spatial gradients (Ji et al., 2007; Mac Gabhann et al., 2007; Mac Gabhann & Popel, 2006); tip cell migration and cell–matrix interactions via matrix metalloproteinases (Karagiannis & Popel, 2006); the sequence of cell elongation, migration and proliferation during capillary sprout formation (Qutub & Popel, 2009) and capillary anastomosis Milde et al. (2008). Two methods used to represent 3D spatial models include partial differential equations (PDEs) and agent-based models (ABMs). PDEs are frequently employed at the molecular level to describe time-dependent or steady-state diffusion and convection of molecular species, while ABMs have been applied to heuristically describe both molecular and cellular components. These methods and related models were recently reviewed in detail (Peirce, 2008; Qutub et al., 2009; Sefcik et al., 2010). 3D spatial models of angiogenesis have wide applications. As examples, they have been employed to study capillary sprout formation accounting for key proteins involved in angiogenesis (Bentley et al., 2008, 2009; Peirce, 2008; Qutub & Popel, 2009) and tumour angiogenesis (Bearer et al., 2009; Billy et al., 2009; Owen et al., 2009) (Fig. 2).

Fig. 2.

Fig. 2.

Open in a new tab

Representation of the angiogenic processes by 3D models. These have included blood flow, O2 diffusion, VEGF–VEGFR interactions, endothelial cell activation, migration and proliferation, capillary sprout and vascular network formation.

One 3D agent-based spatial model describes endothelial cell sprouting at the onset of angiogenesis (Qutub & Popel, 2009). Agents are computational datastructures that can respond to and be modified by their environment (Bonabeau, 2002). In turn, agents can modify each other and their surroundings. Logical rules determine how agents respond, and what events occur in a model. The rules that govern agents can be articulated as equations, Boolean queries, or probabilities, as well as numerous other computational methods. In building the model, we relied on experimental work compiled from extensive literature research and formulated the logical rules to represent biological processes consistent with experiments.

We first applied the model to conditions that might occur in a 3D in vitro setting. Physiological changes are represented at the cell level. These include endothelial cell activation, migration, elongation, proliferation and branching. We then tested cell-level behaviour in response to different stimuli, first a threshold change in VEGF and then changes in delta-like ligand 4 (Dll4). From the combined, combinatorially complex interactions of single cells, a new capillary network emerges. This capillary network can then be characterized phenotypically and spatially—by branching, multiple sprouting, anastomosing, looping and regression. We used this model to evaluate the hypothesis that the characteristics of a growing capillary network are dependent on a set sequence of cellular events: a combination of elongation, migration and proliferation between the leading tip cell and its adjacent stalk cell. Additionally, we produced in silico knockouts of the Dll4 ligand, and cell-level knockouts of individual cellular processes, and observed the resulting vascular network in each case—with the goal of eventually guiding therapy aimed at particular processes.

The ABM we described here can be used as a framework for integration of angiogenesis models in our laboratory (e.g. HIF1α, VEGF, matrix metalloproteinase), and also could include contributions from multiple laboratories; the models spanning multiple scales, from molecular, to cellular, tissue, organ and organ system or whole body (Qutub et al., 2009). The development involves creation of a computational framework that enables the computer simulation of multiple models with different mathematical representations (e.g. ODEs, PDEs and ABMs). A key point is that each model—spatial or non-spatial—plays a unique role (e.g. focuses on a unique molecule; new receptor–ligand interaction, different spatial scale or cellular process). Through this means, each model individually helps elucidate the mechanisms underlying proteins and other molecular factors in angiogenesis, while the simulation resulting from the integration of the models is one step closer to being used for clinical and therapeutic applications.

6. Conclusions

In this article, we have shown that computational models of angiogenesis can provide useful insights, whether it is at the nano- to microscopic level (molecules/cells), at the mesoscopic level (microvascular/tissue) or at the macroscopic level (organ and organ system). The focus of our approach is to analyse complex processes in tumour angiogenesis while preserving the molecular details. This systems biology approach is complementary to other approaches, experimental and theoretical, used to study tumour angiogenesis.

References

  1. Anderson AR, Quaranta V. Integrative mathematical oncology. Nat Rev Cancer. 2008;8:227–234. doi: 10.1038/nrc2329. [DOI] [PubMed] [Google Scholar]
  2. Bearer EL, Lowengrub JS, Frieboes HB, Chuang YL, Jin F, Wise SM, Ferrari M, Agus DB, Cristini V. Multiparameter computational modeling of tumor invasion. Cancer Res. 2009;69:4493–4501. doi: 10.1158/0008-5472.CAN-08-3834. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bentley K, Gerhardt H, Bates PA. Agent-based simulation of notch-mediated tip cell selection in angiogenic sprout initialisation. J Theor Biol. 2008;250:25–36. doi: 10.1016/j.jtbi.2007.09.015. [DOI] [PubMed] [Google Scholar]
  4. Bentley K, Mariggi G, Gerhardt H, Bates PA. Tipping the balance: robustness of tip cell selection, migration and fusion in angiogenesis. PLoS Comput Biol. 2009;5:e1000549. doi: 10.1371/journal.pcbi.1000549. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Billy F, Ribba B, Saut O, Morre-Trouilhet H, Colin T, Bresch D, Boissel JP, Grenier E, Flandrois JP. A pharmacologically based multiscale mathematical model of angiogenesis and its use in investigating the efficacy of a new cancer treatment strategy. J Theor Biol. 2009;260:545–562. doi: 10.1016/j.jtbi.2009.06.026. [DOI] [PubMed] [Google Scholar]
  6. Bonabeau E. Agent-based modeling: methods and techniques for simulating human systems. Proc Natl Acad Sci USA. 2002;99(Suppl 3):7280–7287. doi: 10.1073/pnas.082080899. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Byrne HM. Dissecting cancer through mathematics: from the cell to the animal model. Nat Rev Cancer. 2010;10:221–230. doi: 10.1038/nrc2808. [DOI] [PubMed] [Google Scholar]
  8. Chaplain MA, Mcdougall SR, Anderson AR. Mathematical modeling of tumor-induced angiogenesis. Annu Rev Biomed Eng. 2006;8:233–257. doi: 10.1146/annurev.bioeng.8.061505.095807. [DOI] [PubMed] [Google Scholar]
  9. Dayan F, Monticelli M, Pouyssegur J, Pecou E. Gene regulation in response to graded hypoxia: the non-redundant roles of the oxygen sensors PHD and FIH in the HIF pathway. J Theor Biol. 2009;259:304–316. doi: 10.1016/j.jtbi.2009.03.009. [DOI] [PubMed] [Google Scholar]
  10. Dewhirst MW, Cao Y, Li CY, Moeller B. Exploring the role of HIF-1 in early angiogenesis and response to radiotherapy. Radiother Oncol. 2007;83:249–255. doi: 10.1016/j.radonc.2007.05.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Ferrara N. The role of VEGF in the regulation of physiological and pathological angiogenesis. Exs. 2005:209–231. doi: 10.1007/3-7643-7311-3_15. Available at: http://www.ncbi.nlm.nih.gov/pubmed/15617481. [DOI] [PubMed] [Google Scholar]
  12. Folkman J. What is the evidence that tumors are angiogenesis dependent? J Natl Cancer Inst. 1990;82:4–6. doi: 10.1093/jnci/82.1.4. [DOI] [PubMed] [Google Scholar]
  13. Gao P, Zhang H, Dinavahi R, Li F, Xiang Y, Raman V, Bhujwalla ZM, Felsher DW, Cheng L, Pevsner J, Lee LA, Semenza GL, Dang CV. HIF-dependent antitumori-genic effect of antioxidants in vivo. Cancer Cell. 2007;12:230–238. doi: 10.1016/j.ccr.2007.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Gaur P, Bose D, Samuel S, Ellis LM. Targeting tumor angiogenesis. Semin Oncol. 2009;36:S12–S19. doi: 10.1053/j.seminoncol.2009.02.002. [DOI] [PubMed] [Google Scholar]
  15. Ji JW, Mac Gabhann F, Popel AS. Skeletal muscle VEGF gradients in peripheral arterial disease: simulations of rest and exercise. Am J Physiol Heart Circ Physiol. 2007;293:H3740–H37409. doi: 10.1152/ajpheart.00009.2007. [DOI] [PubMed] [Google Scholar]
  16. Ji JW, Tsoukias NM, Goldman D, Popel AS. A computational model of oxygen transport in skeletal muscle for sprouting and splitting modes of angiogenesis. J Theor Biol. 2006;241:94–108. doi: 10.1016/j.jtbi.2005.11.019. [DOI] [PubMed] [Google Scholar]
  17. Karagiannis ED, Popel AS. Distinct modes of collagen type I proteolysis by matrix metallo-proteinase (MMP) 2 and membrane type I MMP during the migration of a tip endothelial cell: insights from a computational model. J Theor Biol. 2006;238:124–145. doi: 10.1016/j.jtbi.2005.05.020. [DOI] [PubMed] [Google Scholar]
  18. Kohn KW, Riss J, Aprelikova O, Weinstein JN, Pommier Y, Barrett JC. Properties of switch-like bioregulatory networks studied by simulation of the hypoxia response control system. Mol Biol Cell. 2004;15:3042–3052. doi: 10.1091/mbc.E03-12-0897. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Kut C, Mac Gabhann F, Popel AS. Where is VEGF in the body? A meta-analysis of VEGF distribution in cancer. Br J Cancer. 2007;97:978–985. doi: 10.1038/sj.bjc.6603923. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Levine HA, Pamuk S, Sleeman BD, Nilsen-Hamilton M. Mathematical modelling of tumour angiogenesis and the action of angiostating as a protease inhibitor. J Theor Med. 2002;4:133–145. [Google Scholar]
  21. Mac Gabhann F, Ji JW, Popel AS. VEGF gradients, receptor activation, and sprout guidance in resting and exercising skeletal muscle. J Appl Physiol. 2007;102:722–734. doi: 10.1152/japplphysiol.00800.2006. [DOI] [PubMed] [Google Scholar]
  22. Mac Gabhann F, Popel AS. Targeting neuropilin-1 to inhibit VEGF signaling in cancer: comparison of therapeutic approaches. PLoS Comput Biol. 2006;2:e180. doi: 10.1371/journal.pcbi.0020180. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Mac Gabhann F, Popel AS. Dimerization of VEGF receptors and implications for signal trans-duction: a computational study. Biophys Chem. 2007;128:125–139. doi: 10.1016/j.bpc.2007.03.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Mac Gabhann F, Popel AS. Systems biology of vascular endothelial growth factors. Microcircu-lation. 2008;15:715–738. doi: 10.1080/10739680802095964. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Mantzaris NV, Webb S, Othmer HG. Mathematical modeling of tumor-induced angiogenesis. J Math Biol. 2004;49:111–187. doi: 10.1007/s00285-003-0262-2. [DOI] [PubMed] [Google Scholar]
  26. McDougall SR, Anderson AR, Chaplain MA. Mathematical modelling of dynamic adaptive tumour-induced angiogenesis: clinical implications and therapeutic targeting strategies. J Theor Biol. 2006;241:564–589. doi: 10.1016/j.jtbi.2005.12.022. [DOI] [PubMed] [Google Scholar]
  27. Milde F, Bergdorf M, Koumoutsakos P. A hybrid model for three-dimensional simulations of sprouting angiogenesis. Biophys J. 2008;95:3146–3160. doi: 10.1529/biophysj.107.124511. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Moeller BJ, Cao Y, Li CY, Dewhirst MW. Radiation activates HIF-1 to regulate vascular radiosensitivity in tumors: role of reoxygenation, free radicals, and stress granules. Cancer Cell. 2004;5:429–441. doi: 10.1016/s1535-6108(04)00115-1. [DOI] [PubMed] [Google Scholar]
  29. Owen MR, Alarcon T, Maini PK, Byrne HM. Angiogenesis and vascular remodelling in normal and cancerous tissues. J Math Biol. 2009;58:689–721. doi: 10.1007/s00285-008-0213-z. [DOI] [PubMed] [Google Scholar]
  30. Peirce SM. Computational and mathematical modeling of angiogenesis. Microcirculation. 2008;15:739–751. doi: 10.1080/10739680802220331. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Qutub AA, Mac Gabhann F, Karagiannis ED, Vempati P, Popel AS. Multiscale models of angiogenesis. IEEE Eng Med Biol Mag. 2009;28:14–31. doi: 10.1109/MEMB.2009.931791. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Qutub AA, Popel AS. A computational model of intracellular oxygen sensing by hypoxia-inducible factor HIF1 alpha. J Cell Sci. 2006;119:3467–3480. doi: 10.1242/jcs.03087. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Qutub AA, Popel AS. Three autocrine feedback loops determine HIF1 alpha expression in chronic hypoxia. Biochim Biophys Acta. 2007;1773:1511–1525. doi: 10.1016/j.bbamcr.2007.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Qutub AA, Popel AS. Reactive oxygen species regulate hypoxia-inducible factor 1alpha differentially in cancer and ischemia. Mol Cell Biol. 2008;28:5106–5119. doi: 10.1128/MCB.00060-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Qutub AA, Popel AS. Elongation, proliferation & migration differentiate endothelial cell phenotypes and determine capillary sprouting. BMC Syst Biol. 2009;3:13. doi: 10.1186/1752-0509-3-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Sefcik LS, Wilson JL, Papin JA, Botchwey EA. Harnessing systems biology approaches to engineer functional microvascular networks. Tissue Eng Part B Rev. 2010;16:361–370. doi: 10.1089/ten.teb.2009.0611. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Semenza GL. HIF-1: using two hands to flip the angiogenic switch. Cancer Metastasis Rev. 2000;19:59–65. doi: 10.1023/a:1026544214667. [DOI] [PubMed] [Google Scholar]
  38. Stefanini MO, Wu FT, Mac Gabhann F, Popel AS. A compartment model of VEGF distribution in blood, healthy and diseased tissues. BMC Syst Biol. 2008;2:77. doi: 10.1186/1752-0509-2-77. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Stefanini MO, Wu FT, Mac Gabhann F, Popel AS. The presence of VEGF receptors on the luminal surface of endothelial cells affects VEGF distribution and VEGF signaling. PLoS Comput Biol. 2009;5:e1000622. doi: 10.1371/journal.pcbi.1000622. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Stefanini MO, Wu FT, Mac Gabhann F, Popel AS. Increase of plasma VEGF after intravenous administration of bevacizumab is predicted by a pharmacokinetic model. Cancer Res. 2010;70:1–9. doi: 10.1158/0008-5472.CAN-10-1419. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Wu FT, Stefanini MO, Mac Gabhann F, Popel AS. A compartment model of VEGF distribution in humans in the presence of soluble VEGF receptor-1 acting as a ligand trap. PLoS One. 2009;4:e5108. doi: 10.1371/journal.pone.0005108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Yu Y, Wang G, Simha R, Peng W, Turano F, Zeng C. Pathway switching explains the sharp response characteristic of hypoxia response network. PLoS Comput Biol. 2007;3:e171. doi: 10.1371/journal.pcbi.0030171. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Yucel MA, Kurnaz IA. An in silico model for HIF-alpha regulation and hypoxia response in tumor cells. Biotechnol Bioeng. 2007;97:588–600. doi: 10.1002/bit.21247. [DOI] [PubMed] [Google Scholar]
  44. Zhou J, Schmid T, Schnitzer S, Brune B. Tumor hypoxia and cancer progression. Cancer Lett. 2006;237:10–21. doi: 10.1016/j.canlet.2005.05.028. [DOI] [PubMed] [Google Scholar]

Articles from Mathematical Medicine and Biology are provided here courtesy of Oxford University Press

RESOURCES