Automated detection of cross-frequency coupling in the electrocorticogram for clinical inspection

Abstract

We developed a toolbox for detecting high-frequency oscillations and evaluating cross-frequency phase-amplitude coupling in electrocorticographic (ECoG) data with optimal parameters. Here we demonstrate use of the toolbox using simulated and realistic ECoG data. The results confirmed its potential usefulness for clinical research or practice. The tools have been released as a Phase-Amplitude Coupling Toolbox (PACT) plug-in for EEGLAB, an open software environment for electrophysiological data analysis (sccn.ucsd.edu/eeglab).

I. Introduction

It is sometimes necessary to record intracranial EEG in pre-surgical evaluations of patients with medically uncontrolled epilepsy to determine where the epileptic seizures arise and plan surgery for adequate seizure control [1]. Previous studies reported that high-frequency oscillations (HFOs) above 80 Hz are intermittently emitted during interictal periods of slow wave sleep (periods between epileptic seizure events), and that surgical removal of the cortical sites exhibiting such HFOs is associated with a larger chance of post-surgical seizure control [2]. Conversely, it has been shown that not all HFOs during slow-wave sleep are epileptogenic. HFOs with similar spectral character are frequently and spontaneously generated in healthy cortical areas including sensorimotor and visual cortex [3]. Thus, development of a well-defined and easy-to-apply method for differentiating epileptogenic from non-pathological HFOs is highly desirable for further research toward clinical application of HFO measurements in planning surgery for epilepsy.

In a recent report, HFOs in non-pathological cortex were reported to be significantly phase-locked to slow-wave activity near 1 Hz, a strong background frequency in healthy visual cortex during slow-wave sleep [3]. On the other hand, HFOs generated at the same time in the seizure onset zone were phase locked to slightly higher frequency slow-wave activity at 3-4 Hz [3]. A plausible hypothesis, therefore, is that the strength of coupling between slow-wave phase and HFO amplitude (i.e., their phase-amplitude coupling or PAC) could serve as a better biomarker of epileptogenicity than HFO amplitude alone.

Here, we demonstrate the Phase-Amplitude Coupling Toolbox (PACT), a plug-in for EEGLAB [4]. PACT searches for relevant combinations of parameters while automatically detecting HFO events in each input channel, then calculates circular phase statistics and computes a measure of cross-frequency phase-amplitude coupling. We apply the toolbox to two types of data for evaluation: simulated data and intracranial ECoG data recorded from an epileptic patient.

II. Materials and Methods

A. Simulated Data

Pink noise (540 s, sampled at 1000 Hz, variance 0.0385) was generated to serve as simulated noise-only data. Thirty-six 1.5-s events, each a 6-cycle 4-Hz low-frequency oscillatory burst (LFO) (peak-to-peak amplitude, 1.00), were added to the noise-only data at random latencies to serve as the signal-plus-noise condition (variance 0.0189) (Figure 1, top right). To introduce cross-frequency phase-amplitude coupling, 120-Hz, 8-cycle, sinusoidal high-frequency oscillatory bursts (HFOs) (peak-to-peak amplitude, 0.34) were nested in the trough of LFO bursts and Hann-windowed. The HFO and LFO amplitudes were selected to follow a 1/f power law. SNR was −3.09 dB.

Figure 1.

Simulated cross-frequency phase-amplitude coupling data: signal-plus-noise (left column) and noise-only (right column). Top left: A simulated signal event. Top right: The same event embedded in the noise. Second row: PAC Modulation Index (gray) comparison with 99% confidence interval (CI, no face color). Asterisk shows p < 0.05. Third row: phase/amplitude histograms. Mean resultant vectors are superimposed in red; the vector length scales are noted (in the 60-90 deg segments). Bottom: phase-sorted amplitude histogram comparison. LFO phase is shown in red.

B. Electrocorticographic data

Electrocorticographic (ECoG) data were recorded from the exposed cortical surface of a patient (age 9, female) who became seizure-free following surgical resection. The multichannel ECoG data, 540-s in duration, were sampled at 1000 Hz. Offline visual inspection by a neurologist identified HFOs above 80 Hz independently arising in the seizure onset zone (which was subsequently removed surgically) and from a non-pathological cortical area (preserved in the surgery).

C. Signal processing

Simulated and actual data were imported into EEGLAB 12.0.0.0 running on MATLAB R2012b (The Mathworks, Inc., Natick MA) to apply PACT tools. Data were first separated into LFO phase and HFO amplitude using band-pass filters followed by Hilbert transformation. To construct the band-pass filter, the EEGLAB plug-in pop_eegfiltnew() was used [7]. This function designs a Hamming-windowed FIR filter with optimized filter order.

The LFO frequency range of the ECoG data was determined by scanning the parameter space using PACT function pac_scanLfoPhaseFreq(). To estimate the LFO frequency range relevant for the PAC analysis, the function performs a brute-force computation on combinations of two independent variables: LFO frequency band and the percentage of highest absolute value points in the high-pass filtered data to sample. Since neurological interest here is more in the precise LFO frequency range than the HFO, the HFO frequency range is fixed. There are two output measures: Mean Resultant Vector Length (described below) and Canolty’s PAC Modulation Index [5][6], a measure of cross-frequency phase-amplitude coupling. The former is naturally normalized to [0 1] while the latter has no fixed range since it takes amplitudes into account. Because of the large amplitude difference between the two channels in the actual ECoG data we used Mean Resultant Vector Length to select parameters from the parameter space (described below).

For the simulated data, we applied band-pass filter with the same frequency ranges used in the simulate data: 4.0-to-4.1 Hz for the LFO band (transition bandwidth 1 Hz, filter order 1651), and a 120-to-121 Hz band-pass filter for the HFO band (transition band width 15 Hz, filter order 111).

For the actual data, we consulted the results of pac_scanLfoPhaseFreq()(Figure 2 top) to design 1.3-Hz to 2.3-Hz band-pass filter for the LFO band (transition bandwidth 1.3 Hz, filter order 2541). The band-pass filter for the HFO included frequencies between 80 and 300 Hz (transition bandwidth 20 Hz, filter order 167) to cover high frequencies broadly.

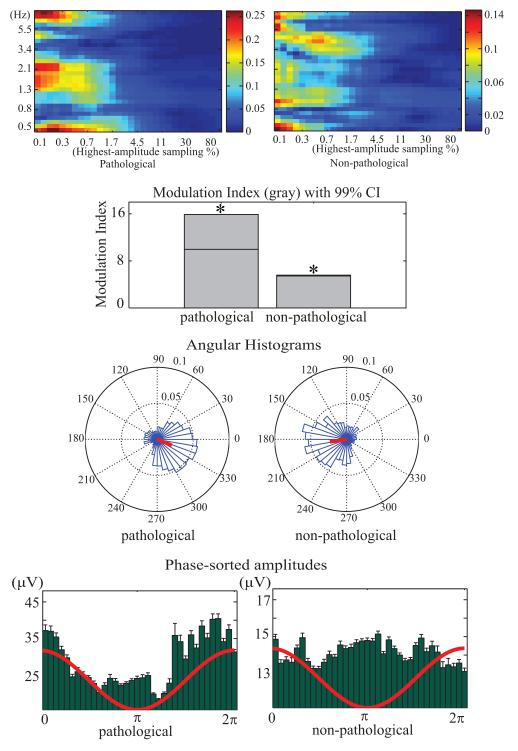
Figure 2.

Pathological (left column) and healthy (right column) ECoG data channels from the same subject. Top: results of brute-force computation on combinations of LFO frequencies (Hz) and highest-amplitude window sampling rate (%). Note the difference between conditions in the 1.3 Hz to 2.1 Hz LFO band and 0.1% to 1.7% data sampling frequency range. These parameter values were then used to compute and test PAC values. Other panels as in Figure 1.

For both datasets, the HFO data were sorted from high to low values, and the 2% of data points with highest absolute values were used in the PAC computation (as determined by consulting Figure 2, top). HFO and LFO measures for these windows were combined to construct complex-valued phasors

$$z\left[n\right]={\alpha }_{HFO}\left[n\right]\exp \left(i{\varphi }_{LFO}\right[n\left]\right)$$ (1)

where α_HFO represents HFO amplitude and φ_LFO LFO phase. From these phasors, the mean resultant vector length, angular histogram of φ_LFO, phase-sorted amplitude, and the PAC Modulation Index were computed. Mean Resultant Vector Length, R, reflecting phase consistency across the highest-amplitude windows, was computed as:

$$R=\mid \mid \frac{1}{N}\sum _{n=1}^{N}r\left[n\right]\mid \mid$$ (2)

where r[n] = exp(iφ_LFO) and N is the total number of observations. The PAC Modulation Index, M, was calculated as:

$$M=\mid \mid \frac{1}{N}\sum _{n=1}^{N}z\left[n\right]\mid \mid$$ (3)

D. Statistics

To test the null hypothesis that LFO phase and HFO amplitude are decoupled in the data, either surrogate data or analytic methods may be used [6][8]. For estimating the significance of the PAC Modulation Index, we used the surrogate data method proposed in [5]. We randomly paired the amplitude and phase of z[n] by circularly permuting the phase time-series φ_LFO[n] relative to the amplitude series and computed the PAC Modulation Index for the resulting surrogate time series. We repeated this process 1,000 times to produce distributions of values of M for data sets in which the null hypothesis should hold (i.e., that phase/amplitude coincidence is only by chance). Values of these variables for the original (non-permuted) data were then compared to the quantiles of this distribution to obtain uncorrected p-values for violation of the null hypothesis. The number of phase bins was set to 36. The significance threshold to p<0.05.

A histogram of Mean Resultant Vector Lengths, R, was computed, and its deviation from a uniform circular distribution was tested using the Rayleigh test, Omnibus test, and Rao’s test as provided in CircStat, a MATLAB toolbox for circular statistics [8]. Here we report the Rayleigh test results.

Mean HFO amplitude values sorted by LFO phase angle was computed, and their deviation from a uniform distribution was tested (Figure 1 third row). Circular statistics were not useable here because the measure is not phase but mean amplitude of each phase bin. We used Kolmogorov-Smirnov and Chi-square tests using standard MATLAB functions. Here, we report the Kolmogorov-Smirnov test results.

The above measures and statistics were computed for single data channels of interest. Results were corrected for multiple comparisons (e.g., likelihood of occurrence by chance in at least one of the recorded channels) using Bonferroni, Bonferroni-Holm [9] and False Discovery Rate [10] corrections. Here we report Bonferroni-corrected results.

III. Results

A. Simulated Data Results

The PAC Modulation Index M was considerably larger in the signal-plus-noise data than in the noise-only (0.036 vs. 0.0028). In the signal-plus-noise data, M reached significance (p < 0.05) whereas in the noise-only data it did not (Figure 1, second row). This test confirmed that PACT detected the presence of relatively weak, rarely occurring (about p=0.1) cross-frequency phase-amplitude coupling events embedded in the noise background.

The angular histogram of the signal-plus-noise data (Figure 1 third row) deviated significantly from a uniform distribution (p<0.001) detecting that the vector length maxima were placed at π radians (troughs of the LFO). The noise-only data did not show it.

Mean Resultant Vector Length, R, for the signal-plus-noise data was 0.35 (with a phase angle of −3.11), that was significantly longer than for the phase-randomized surrogate data (p < 0.05) whereas Mean Resultant Vector Length of the noise-only data was 0.04 (with a phase angle of −2.69), not longer than chance.

As expected, maximal HFO amplitudes appeared near π radians. The distribution of phase-sorted HFO amplitudes was significantly different from a uniform distribution (p < 0.001), whereas this pattern was not present in the noise-only data (Figure 1, bottom).

For exploratory purposes, we estimated the sensitivity of PACT by increasing the noise level in the simulated data. When the SNR of the simulated HFOs was −10 dB or less, the PACT function failed to detect the embedded PAC.

B. Electrocorticographic Data Results

The PACT LFO frequency-range search produces color maps representing the distribution of Mean Resultant Vector Length values in the plane of LFO frequencies (from 0.5 Hz to 8 Hz, log spaced) and highest-absolute value sampling densities (from 0.1% to 100%, log spaced) (Figure 2, top). These maps indicate that the observed Mean Resultant Vector Length value was larger in the pathological channel than in the non-pathological channel, with a peak for the LFO frequency range 1.3 Hz to 2.3 Hz, and highest-amplitude data sampling percentages from 0.1% to 1.7%. PAC successfully identified spikes and relatively sustained HFOs in the pathological channels.

The PAC Modulation Index also was larger in the pathological channel than in the non-pathological channel (15.9 vs. 5.57), though both values were statistically above chance (p < 0.01).

Mean Resultant Vector Length was 0.387 (with a phase angle of −0.38) for the pathological channel and 0.376 (with a phase angle of −3.00) for the non-pathological channel; again, both reached statistical significance (p < 0.01).

Maxima of the phase-sorted HFO amplitudes for the pathological channel contained a non-significant peak near 0 radians (Figure 2, bottom). These results suggest that PAC occurred in both the pathological and non-pathological channels, but with different characteristics. Further studies are warranted to differentiate pathological from non-pathological PAC patterns. Figure 3 shows an example of a 3-s data period in which HFOs (highlighted in red) were identified by PACT at the pathological and non-pathological recording sites.

Figure 3.

High-frequency oscillation marked in red by the PACT data scrolling tool on the unfiltered electrocorticogram. The automated high-frequency oscillation detection successfully captures both transient spikes and frequent bursts of high-frequency oscillation (HFO).

Computation times were as follows: A 37-channel, 275-s, data set with a sampling rate of 1000 Hz was processed using a 3.2-GHz, 12-GB RAM Linux computer in 20 s (using 200 surrogate data sets) or in 150 s (using 2,000 surrogates). Computational time is proportional to data length, number of channels, and inversely proportional to the LFO frequency range. These times do not include the time required for the LFO frequency-band scan, which was much slower because of the repeated application of high-pass filtering. Also, the lower the high-pass filter frequency band, the slower the computations.

IV. Limitation

First, both healthy and pathological cortical channel recordings showed PAC, suggesting a significantly large Modulation Index does not guarantee that an observed PAC is pathological. PAC characteristics in pathological and non-pathological channel data need to be fully investigated. Second, the highest-amplitude data sampling method treats a selected data percentage regardless of the presence or absence of true HFO events. Finally, there may be better inferential statistics for phase-sorted amplitude.

V. Conclusion

Here we demonstrated the application of PACT tools to simulated and actual ECoG data, and confirmed the potential usefulness of the tools for clinical research possibly leading to clinical application. The toolbox provides research neurologists and neuroscientists a tool for exploring cross-frequency phase-amplitude coupling which has recently been posited to be an important form of cortical dynamics [5]. Use of PACT methods in clinical practice might lower the burden on neurologists to visually inspect and evaluate large amounts of recorded ECoG data from each monitored patient. However, the clinical usefulness of PACT requires further clarification of differences between pathological and normal PAC in epileptic and non-epileptic tissue. We hope that the development and release of PACT may contribute to further research in this direction.

Recently, we have demonstrated that single channels in standard ECoG data are not independent of each other but, like scalp EEG channels (though to a lesser extent) each sum activities arising in more than one effective cortical source area [11]. It should be of interest, therefore, to apply PAC measures to independent components [12] of ECoG data to explore whether PAC phenomena show up more clearly in ICA-decomposed data [13][14].

The use of PACT is not limited to clinical research; it can also be applied more general scientific EEG (or MEG) research. PACT is freely available from the EEGLAB website of the Swartz Center for Computational Neuroscience at UCSD (http://sccn.ucsd.edu/wiki/PACT).