From Complex B₁ Mapping to Local SAR Estimation for Human Brain MR Imaging Using Multi-channel Transceiver Coil at 7T

Abstract

Elevated Specific Absorption Rate (SAR) associated with increased main magnetic field strength remains as a major safety concern in ultra-high-field (UHF) Magnetic Resonance Imaging (MRI) applications. The calculation of local SAR requires the knowledge of the electric field induced by radiofrequency (RF) excitation, and the local electrical properties of tissues. Since electric field distribution cannot be directly mapped in conventional MR measurements, SAR estimation is usually performed using numerical model-based electromagnetic simulations which, however, are highly time consuming and cannot account for the specific anatomy and tissue properties of the subject undergoing a scan. In the present study, starting from the measurable RF magnetic fields (B₁) in MRI, we conducted a series of mathematical deduction to estimate the local, voxel-wise and subject-specific SAR for each single coil element using a multi-channel transceiver array coil. We first evaluated the feasibility of this approach in numerical simulations including two different human head models. We further conducted experimental study in a physical phantom and in two human subjects at 7T using a multi-channel transceiver head coil. Accuracy of the results is discussed in the context of predicting local SAR in the human brain at UHF MRI using multi-channel RF transmission.

I. INTRODUCTION

Ultra-high-field (UHF) Magnetic Resonance Imaging (MRI) systems (7T and higher) have been pursued with increasing interest [1]. Their main advantages include higher signal-to-noise ratio (SNR), higher spatial resolution, and increased sensitivity for intrinsic contrast mechanisms such as blood oxygenation level-dependent (BOLD) contrast. However, the magnitude of electric fields generated for a given strength of the transmit magnetic field increases with the operating radio frequency (RF) (proportional to the main magnetic field strength). The electric fields induce eddy currents and hence dissipate heat into the human body, resulting in elevated energy deposition as the frequency increases [2],[3]. Possible local overheating due to the latter poses a serious safety concern at UHF. Consequently, when using a multiple element transmit coil which has been recognized as a powerful tool for B₁ inhomogeneity compensation and has been widely utilized at UHF [4–6], energy deposition in the body must be carefully controlled and kept under international safety guidelines. Although attempts to address this overheating concern have been made by constraining B₁ shimming or parallel transmission RF pulse design solutions with worst-case conditions derived from electromagnetic (EM) simulations [7–9], in some situations this may excessively limit the achievable SNR and contrast at UHF.

Although various approaches have been proposed for the assessment of RF heating at UHF [10–12], current guidelines (International Standard IEC 60601-2-33 2010) impose upper limits on global specific absorption rate (SAR) as well as on local SAR averaged through 10 gram of tissue. In practice, local averaged SAR often reaches maximum upper limits before global SAR at UHF [11]. While global SAR estimation can be estimated by real-time measurement of forward and reflected RF power at the coil ports [13], the estimation of local SAR for human MR experiments typically relies on highly time-consuming computational electromagnetic simulations. Such extensive computations have been conducted using a variety of commercial software, based on the numerical models of EM properties of the human body [14–19]. However, beside the time-consuming constraint of these simulation approaches, it remains to be shown whether such findings based on a very limited number of different individuals' anatomy could reliably provide a quantitative prediction of local SAR characteristics of a given specific subject undergoing a scan. As such, real-time and subject-specific local SAR estimation is highly desired in UHF MRI applications.

Recently, B₁-mapping based electric field and SAR estimation approaches have been developed by post-processing the measured complex B₁ fields (rotating RF field induced by MRI RF coils, consisting of transmit B₁ and receive B₁ [20]) through a series of mathematical deduction, which involves the retrieval of complex B₁ information and the reconstruction of electrical properties (EPs) of the subject (known as Electrical Properties Tomography, EPT) [21–24]. This approach overcomes the limitation of conventional simulation methods relying on a generic human body model, and allows for real-time calculation [23],[25]. Most previous EPT studies were typically restricted to conventional quadrature birdcage coils, relying only on the spatial transmit B₁ phase which was approximated as one half of the measured total phase in a single transmit and receive (transceiver) element [22]. However, for multiple-element coils (e.g. transceiver coil array) at UHF, the shorter operating RF wavelength yields significant spatial phase and magnitude discrepancies between transmit and receive B₁ fields for each coil element, hindering the use of this simplification. Complex information for both transmit and receive B₁ is, however, essential for a reliable estimation of the electric field distributions that will subsequently be used for SAR calculation. In order to address this need at UHF with multi-channel RF coils, a new approach has recently been introduced to measure transmit and receive complex B₁ fields that includes the retrieval of absolute B₁ phases from measured relative B₁ phases between coil elements [26],[27]. In addition, most existing EPT inverse methods utilize the Helmholtz equation by assuming negligible local spatial gradients of the electrical properties [21],[22],[25],[27]. It can be anticipated that, when using this assumption in biological tissues with complex anatomical structures, artifacts may arise in the vicinity of tissue boundaries in reconstructed EPs maps, resulting in an inaccurate SAR estimation. Nevertheless, the Dual-Excitation EPT algorithm, that has been previously proposed [24], takes the spatial variation of EPs distribution into account and produced reasonable simulation results for head tissues, indicating that this method could improve EPs reconstruction accuracy.

As described in our recent studies [24],[26],[27], three assumptions have been proposed and employed throughout the mathematical deduction and data analysis, from complex B₁-mapping to EPs reconstruction: (1) a fairly left-right symmetric structure of the human brain about coronal plane through the brain center, (2) the 16-fold elliptical symmetric head coil structure about the long axis, and (3) negligible spatial variations of the z-axis component of induced RF magnetic fields. Besides quantitatively and separately evaluating the performance of above assumptions in the calculated intermediate quantities (e.g., reconstructed EPs in [24], and extracted proton density in [27]), it is necessary to rigorously investigate the resulted error propagation altogether along the whole data post-processing towards the ultimate local SAR estimation.

In the present study, subject-specific local SAR estimation is demonstrated for human brain imaging, at 7T, for individual coil element in a 16-channel transceiver coil, based on complex transmit and receive B₁ maps acquired from MR data acquisition. For this purpose, EPs reconstruction was obtained with a modified, B₁-based Dual-Excitation inverse algorithm. The performance of the proposed method is assessed and evaluated by computer simulations using two human head models, and with experiments in a physical phantom and on two human subjects.

II. THEORY

A. Complex B₁ Mapping for Individual Coil Element

Using a N-channel microstrip transceiver array coil [28–30] and a hybrid B₁-mapping technique [5],[31],[32], the magnitude of transmit B₁ field (labeled $\left|{\mathrm{B̃}}_{1,k}^{+}\right|$ with “~” denoting complex quantity), the magnitude of receive B₁ field biased by proton density (PD) (labeled $P{D}_{\mathit{\text{ratio}}}\times \left|{\mathrm{B̃}}_{1,j}^{-}\right|$), and the relative phase distributions between coil elements can be measured for each coil element, where k ∈[1,2,…N] and j ∈[1,2,…N] refer to the transmit and receive components of each coil element, respectively. Based on the approximately elliptical symmetry of the human brain in a transverse plane, the PD distribution and the magnitude of receive B₁ field for each coil element are extracted and estimated separately. Then, knowing the relative phase information between coil elements for both transmit and receive B₁ fields, assuming negligible spatial variation of RF-coil-induced B̃_z component along z-axis direction, as |∂B̃_z / ∂z|<< |∂B̃_x / ∂x| & |∂B̃_y / ∂y|, the absolute transmit and receive B₁ phases of each coil element can be calculated by applying Gauss’s Law for magnetism [26],[27].

B. Modified Dual-excitation Algorithm – the Inverse Problem

Considering the magnetic permeability inside biological tissues to be equal to that in a vacuum, assuming isotropic EPs distribution, the previously proposed dual-excitation algorithm reads [24]

$$\{\begin{array}{c}-{\nabla }^2{\mathrm{B̃}}_x\approx {\omega }^2{\mu }_0{\mathrm{B̃}}_x{\mathrm{\epsilon ̃}}_c-(\partial {\mathrm{B̃}}_x/\partial Z)[(\partial {\mathrm{\epsilon ̃}}_c/\partial Z)/{\mathrm{\epsilon ̃}}_c]+(\partial {\mathrm{B̃}}_y/\partial x-\partial {\mathrm{B̃}}_x/\partial y)[(\partial {\mathrm{\epsilon ̃}}_c/\partial y)/{\mathrm{\epsilon ̃}}_c]\hfill \\ -{\nabla }^2{B}_y\approx {\omega }^2{\mu }_0{\mathrm{B̃}}_y{\mathrm{\epsilon ̃}}_c-(\partial {\mathrm{B̃}}_y/\partial Z)[(\partial {\mathrm{\epsilon ̃}}_c/\partial Z)/{\mathrm{\epsilon ̃}}_c]-(\partial {\mathrm{B̃}}_y/\partial x-\partial {\mathrm{B̃}}_x/\partial y)[(\partial {\mathrm{\epsilon ̃}}_c/\partial x)/{\mathrm{\epsilon ̃}}_c]\hfill \end{array}$$ (1)

in which B̃_x and B̃_y are induced RF magnetic field components in Cartesian frame, μ₀ the free space permeability, ω the operating angular frequency, ε̃_c the complex permittivity ε̃c = ε_rε₀ − iσ / ω with ε_r as the relative permittivity and ε₀ as the free space permittivity. Negligible spatial variations of RF coil induced B̃_z are assumed as |∂B̃_z / ∂x| << |∂B̃_x / ∂z|, |∂B̃_z / ∂y| << |∂B̃_y / ∂z| and |∂B̃_z / ∂z| << |∂B̃_x / ∂x| or |∂B̃_y / ∂y|.

The principle of reciprocity [20] links magnetic field components in Cartesian and rotating frames via

$$\{\begin{array}{c}{\mathrm{B̃}}_1^{+}=({\mathrm{B̃}}_x+i{\mathrm{B̃}}_y)/2\hfill \\ {\mathrm{B̃}}_1^{-}={({\mathrm{B̃}}_x-i{\mathrm{B̃}}_y)}^{*}/2\hfill \end{array}$$ (2)

where * denotes complex conjugation. Based on Gauss’s Law for magnetism (Eq. 3), due to much smaller magnitude of the z-component of Cartesian magnetic field B̃_z when compared with that of B̃_x and B̃_y within RF head coil [24],[27], by ignoring the B̃_z gradient term in Eq.(3)

$$\partial {\mathrm{B̃}}_x/\partial x+\partial {\mathrm{B̃}}_y/\partial y+\partial {\mathrm{B̃}}_z/\partial z=0$$ (3)

Eq. (4) is derived as follows

$$2(\partial {\mathrm{B̃}}_1^{+}/\partial x-i\partial {\mathrm{B̃}}_1^{+}/\partial y)=\partial {\mathrm{B̃}}_x/\partial x+\partial {\mathrm{B̃}}_y/\partial y+i(\partial {\mathrm{B̃}}_y/\partial x-\partial {\mathrm{B̃}}_x/\partial y)\approx i(\partial {\mathrm{B̃}}_y/\partial x-\partial {\mathrm{B̃}}_x/\partial y)$$ (4)

By combining the two expressions in Eq. (1) with Eq. (4), the following equation is re-written in the form of ${\mathrm{B̃}}_1^{+}$

$$-{\nabla }^2{\mathrm{B̃}}_1^{+}={\omega }^2{\mu }_0{\mathrm{B̃}}_1^{+}{\mathrm{\epsilon ̃}}_c-(\partial {\mathrm{B̃}}_1^{+}/\partial z)[(\partial {\mathrm{\epsilon ̃}}_c/\partial z)/{\mathrm{\epsilon ̃}}_c]-(\partial {\mathrm{B̃}}_1^{+}/\partial x-i\partial {\mathrm{B̃}}_1^{+}/\partial y)[(\partial {\mathrm{\epsilon ̃}}_c/\partial x-i\partial {\mathrm{\epsilon ̃}}_c/\partial y)/{\mathrm{\epsilon ̃}}_c]$$ (5)

Eq. (5) is the central equation of the modified dual-excitation algorithm, in which ε̃_c, (∂ε̃_c / ∂z) / ε̃_c and (∂ε̃_c / ∂x + i∂ε̃_c / ∂y) / ε̃_c are unknowns. Thus, at least three sets of ${\mathrm{B̃}}_1^{+}$ data are needed to solve ε_c. In the present study, three datasets were arbitrarily formed via the summation of the retrieved complex ${\mathrm{B̃}}_1^{+}$ of individual coil element in the following three groups of channels: {1,4,7,10,13}, {2,5,8,11,14} and {3,6,9,12,15}. (Note that, similar to Eq. (5), an equation can also be written in the form of ${\mathrm{B̃}}_1^{-}$). Here, compared to the original dual-excitation algorithm, the calculations are directly performed over the B₁ field, avoiding excessive calculations of the Cartesian transverse magnetic components of the induced RF field.

C. Local SAR Estimation

Local SAR is defined by [14]:

$$\mathrm{S}\mathrm{A}\mathrm{R}=\sigma ({\left|{Ẽ}_x\right|}^2+{\left|{Ẽ}_y\right|}^2+{\left|{Ẽ}_z\right|}^2)/2\rho$$ (6)

where Ẽ_x, Ẽ_y and Ẽ_z are Cartesian components of the induced electric field, and ρ is material mass density. Under the assumption that |Ẽ_z| dominates the electric field [33],[34], only the |Ẽ_z| component is considered in local SAR estimation, as shown in Eq. (9) (this issue will be further investigated in the following sections).

$$\mathrm{S}\mathrm{A}\mathrm{R}\approx \sigma {\left|{Ẽ}_z\right|}^2/2\rho$$ (7)

The Ampere’s Law is

$$(\partial {\mathrm{B̃}}_y/\partial x-\partial {\mathrm{B̃}}_x/\partial y)/(i\omega {\mu }_0{\mathrm{\epsilon ̃}}_c)={Ẽ}_z$$ (8)

From Eq. (8) and Eq. (2), the following can be derived:

$$-i(\partial {\mathrm{B̃}}_1^{+}/\partial x-i\partial {\mathrm{B̃}}_1^{+}/\partial y-\partial {\mathrm{B̃}}_1^{-*}/\partial x-i\partial {\mathrm{B̃}}_1^{-*}/\partial y)/(i\omega {\mu }_0{\mathrm{\epsilon ̃}}_c)=(\partial {\mathrm{B̃}}_y/\partial x-\partial {\mathrm{B̃}}_x/\partial y)/(i\omega {\mu }_0{\mathrm{\epsilon ̃}}_c)={Ẽ}_z$$ (9)

Therefore, through measuring and estimating the complex B₁ distribution which involves receive B₁ magnitude estimation and absolute phase retrieval as described in [27], EPs values can be reconstructed based on Eq. (5), allowing for computing |Ẽ_z| via Eq. (9); and local SAR can then be estimated via Eq. (7).

It has been shown in previous simulation studies [14],[19] that, some local SAR hot spots as well as local temperature rise can be localized in the skin. However, in experimental conditions, weak MRI signals observed in bone tissues are expected to significantly deteriorate B₁-mapping results and the subsequent EPs reconstructions within scalp and skull regions [27]. For this reason, the anatomical targets of the present study, including B₁ mapping, EPs reconstruction and local SAR estimation, were spatially confined within brain tissues. Addressing the local SAR estimation in the scalp is an important concern, which will require additional acquisition and reconstruction strategies that are beyond the scope of the present work.

RF safety standards as defined by the International Electrotechnical Commission (IEC) rely on SAR averaged over 10 grams of tissues. In practice, several computing difficulties arise for averaged SAR calculation that include the type of meshing approaches used to spatially distribute the Ẽ field, B̃ field and EPs, as well as the type of averaging algorithm used to produce 10g averaged SAR in certain locations (e.g. edge voxels at air/tissue interface). As a result, in the current study, non-averaged, voxel-wise SAR distribution is investigated in order to facilitate direct result comparison, avoiding possible interference or misleading interpretation that may arise due to the non-linear relationship between voxel-wise and 10g averaged local SAR.

III. MATERIALS AND METHODS

A. Simulations

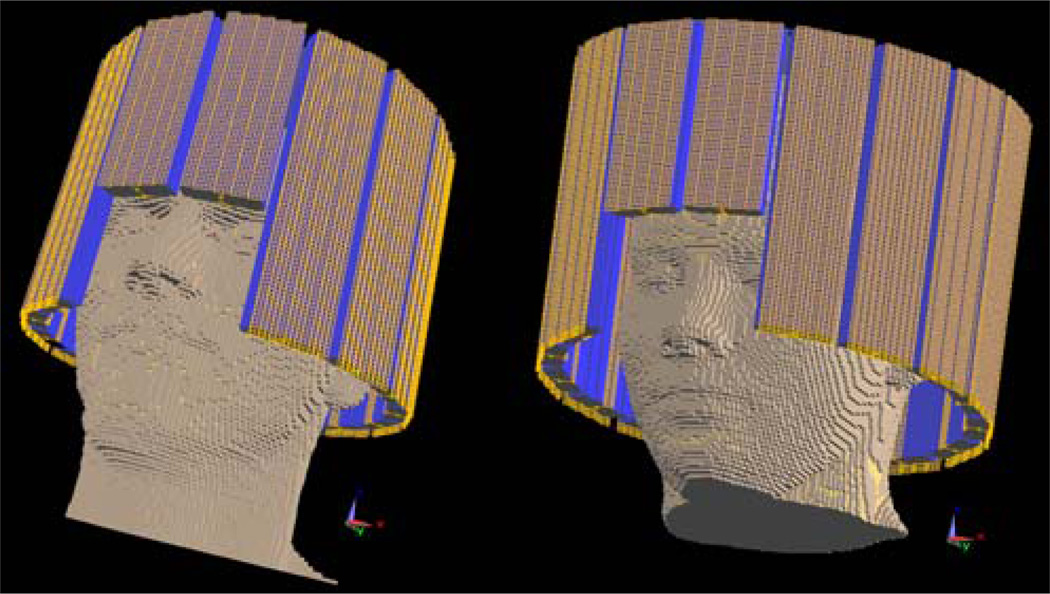
Simulation data were utilized to test the above methods. Finite-Difference Time-Domain (FDTD) based electromagnetic (EM) simulation software SEMCAD (Speag, Switzerland) was used to perform the simulation of B₁ distributions in the human head. The coil model design reproduced the elliptical 16-channel RF microstrip transceiver coil that was utilized in experiments [30]. The heads and necks of Duke and Ella models from Virtual Family (25.6cm for Duke model and 22.4cm for Ella model in length along the z-axis direction), with 2×2×2mm³ resolution, were utilized to load the RF coil in EM simulations as illustrated in Fig. 1. The coil was tuned to 300MHz (7T) when loaded.

Fig. 1.

The reproduced 16-channel elliptical microstrip transceiver head coil loaded with SEMCAD Duke (left) and Ella (right) head models.

Electromagnetic fields were calculated with the same RF power applied to a single coil element at a time, assuming that all RF coil elements were ideally decoupled. The final sixteen simulated complex ${\mathrm{B̃}}_{1,k}^{+}$ and ${\mathrm{B̃}}_{1,j}^{-}$ maps were derived from the simulated complex Cartesian magnetic field components by Eq. (2). Each individual ${\mathrm{B̃}}_{1,j}^{-}$ magnitude image was then multiplied by typical proton density values, i.e. PD_CSF:PD_GM:PD_WM = 1:0.8:0.65 for CSF, gray matter and white matter, respectively [35], in order to mimic the experimentally measured PD-biased receive B₁ magnitude maps [27]. In the following, according to the parametric maps effectively measured in experimental conditions, the magnitude of the sixteen ${\mathrm{B̃}}_{1,k}^{+}$ fields, the sixteen PD-biased ${\mathrm{B̃}}_{1,j}^{-}$ fields, and the relative phase maps of complex B₁ field (transmit and receive) between each coil element will be the only simulation results utilized as known variables to subsequently generate simulation-based EPs and SAR maps. First-order derivatives were computed over adjacent voxels, while the Laplacian operator was applied over a 3×3×3 kernel. Note that known mass density values reported in the literature for different head tissues [14] were utilized in the local SAR calculation in this simulation study.

In addition, using the Ella head model, an offset of 6mm, 10mm and 20mm along x-, y- and z- axis, respectively, was introduced to the model position at one time, to evaluate the differences of local SAR distributions with respect of the head position within the coil.

For a reconstructed quantity q (e.g. EPs, SAR, etc.) in a specific region of interest, the relative error (RE) and correlation coefficient (CC) are defined to evaluate the performance of the present method as follows:

$$\mathrm{R}{\mathrm{E}}_q=\sum _{i=1}^N(q_i-q_{i,\mathit{\text{tar}}})/(N·q_{i,\mathit{\text{tar}}})\mathrm{C}{\mathrm{C}}_q=\frac{[N·\sum _{i=1}^N(q_i·q_{i,\mathit{\text{tar}}})-\sum _{i=1}^N{q}_i·\sum _{i=1}^N{q}_{i,\mathit{\text{tar}}}]}{\sqrt{[N·\sum _{i=1}^N{(q_i)}^2-{(\sum _{i=1}^N{q}_i)}^2][N·\sum _{i=1}^N{(q_{i,\mathit{\text{tar}}})}^2-{(\sum _{i=1}^N{q}_{i,\mathit{\text{tar}}})}^2]}}$$ (10)

where q_i,tar is the target (simulated) value in the ith voxel, qi the estimated (reconstructed) value in the ith voxel, and N the total number of voxels within the specified region of interest.

Electromagnetic fields and the following reconstructions were computed in a similar manner using the numerical design of a cylindrical phantom which will be described in the following section.

B. Experimental Studies

Imaging experiments were performed on a 7T magnet (Magnex Scientific, UK) driven by a Siemens console (Erlangen, Germany). The 16-channel transceiver head coil, as described above, was used for both RF transmit and receive operations, with the transmit channels powered by 16×1kW amplifiers (CPC, Hauppauge, NY) interfaced with a remotely controlled phase/amplitude gain unit. A single-compartment phantom, made of an acrylic cylinder with a diameter of 8.7cm and a length of 20cm, built for the validation purpose, was filled with a gel composed of distilled water, NaCl, Gelatin and CuSO₄·5H2O (mass ratios 100:0.12:3:0.025) with a conductivity of 0.34 S/m and a relative permittivity of 77. For MR measurements, the phantom was placed in the head coil with its long axis parallel to B₀.

In vivo data were acquired in two healthy human volunteers who had signed a consent form approved by the University of Minnesota Institutional Review Board, and laid in supine position with the head centered in the head coil.

A similar imaging protocol was used in both phantom and in vivo human experiments as follows (acquisition parameters are detailed in [27]). A series of 16 small flip angle 2D gradient-recalled echo (GRE) images were acquired with only one channel transmitting at a time while receiving signal on 16 independent channels. Relative phase maps between coil elements were calculated for the transmit $({\mathrm{B̃}}_{1,k}^{+})$ and receive $({\mathrm{B̃}}_{1,j}^{-})$ fields for each coil elements, with k=1,2,…,16 and j=1,2,…,16, as described in [5]. A 3D map of the excitation flip angle was obtained with the Actual Flip Angle (AFI) technique [36], by all channels transmitting together, to be merged with previously acquired small flip angle GRE images in order to calculate the magnitude map of $({\mathrm{B̃}}_{1,k}^{+})$ for each of the sixteen coil elements as indicated in [31]. Finally, a 2D GRE image was acquired, by all channels transmitting together, using a large flip angle (high SNR), a long TR (longitudinal magnetization approximately at equilibrium) and a short TE (negligible T2* relaxation); each of the sixteen images (one per receive channel) of this data set was normalized by the sinus of the excitation flip angle to produce sixteen PD-biased ${\mathrm{B̃}}_{1,j}^{-}$ magnitude maps [30].

Data were acquired in axial views at a spatial resolution of 1.5×1.5×1.5 mm³ in phantoms and of 1.5×1.5×5 mm³ in humans with, in both cases, an in-plane FOV of 288×189 mm². B₁ data (axial slices) were filtered in plane with a 2D Hanning window, 7×7 in size, to reduce Gibbs ringing artifact and thermal noise. First-order derivatives were computed over adjacent voxels, while the Laplacian was calculated within a kernel of 3×3×3.

For SAR estimation in the human experiments, average values for brain conductivity and relative permittivity [37] were assigned for those regions where negative or very large values occurred in the reconstructed EPs maps [27]; meanwhile, the mass density was assumed to be constant through the whole head region.

Experimental results for phantom and in vivo studies were compared against simulations results. For the human brains, the axial slices exhibiting the largest structural similarities between the simulation model and experimental anatomical images were chosen for this comparison. Computations were performed using MATLAB 2011b (Mathworks Inc., MA, USA) with its Parallel Computing Toolbox. The computation time on a single axial slice for each individual simulation or experiment subject was within 5 minutes.

IV. RESULTS

A. Simulations

With channel #13 arbitrarily chosen as a reference for all relative B₁ maps, Fig. 2 depicts, on the axial slice of interest as indicated in (a1) and (b1) (slice #33 of 65 total slices for the Duke model, and slice #33 of 60 total slices for the Ella model), for coil element #13, the target and reconstructed distributions of: (a2)&(b2) absolute phase of transmit B₁, (a3)&(b3) the absolute phase of receive B₁, (a4)&(b4) the relative phase between transmit and receive B₁, and (a5)&(b5) conductivity and (a6)&(b6) relative permittivity for both head models, respectively. The retrieved phase exhibits a CC of 0.990 on both models when compared with the target distribution, while reconstructed EPs for CSF, GM and WM showed −32.3%, −3.3%, +5.9% (Duke) / −28.1%, −2.6%, +10.7% (Ella) REs for conductivity, and −16.6%, −8.2%, +4.5% (Duke) / −15.9%, −7.4%, +2.0% (Ella) REs for relative permittivity, respectively. Note that the present approach is able to retrieve the relative phase distribution between transmit and receive B₁ for each coil element, which is essential for Ẽ_z calculation using the closed-form Eq. (9).

Fig. 2.

Simulation results. (a1) Sagittal view of the Duke head model (colors represent different tissue types) with the axial slice of interest indicated; (a2)–(a4) absolute phase of transmit B₁, absolute phase of receive B₁, and relative phase between transmit and receive B₁ for coil element #13 (the reference channel), (a5) conductivity map, and (a6) relative permittivity map; 1st row: target (simulated) results, 2nd row: estimated (reconstructed) results. (b1) Sagittal view of the Ella head model with the axial slice of interest indicated; (b2)–(b4) absolute phase of transmit B₁, absolute phase of receive B₁, and relative phase between transmit and receive B₁ for coil element #13, (b5) conductivity map, and (b6) relative permittivity map; 3rd row: target results, 4th row: estimated results.

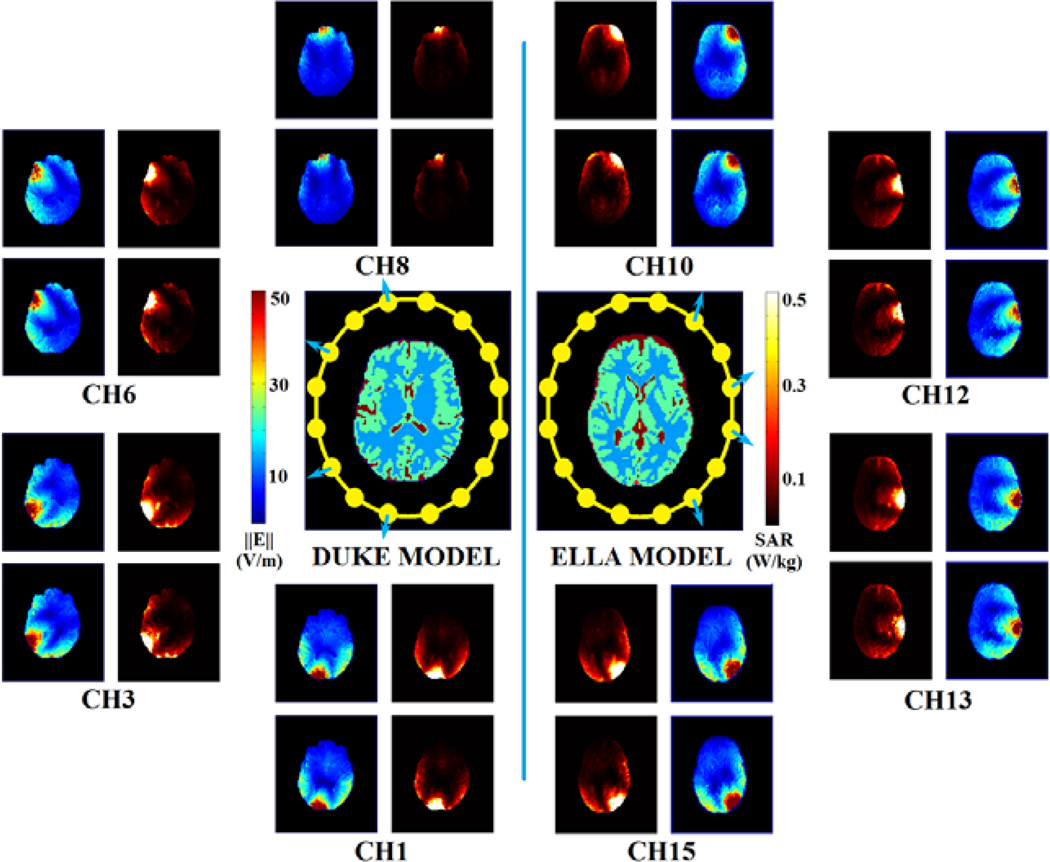
Fig. 3 shows in pairs: for both head models, on the aforementioned axial slice of interest (shown in the central maps), the target and estimated electric field and voxel-wise SAR results for selected channels, in which the target electric field intensity ‖Ẽ_total‖ includes all three components (Ẽ_x, Ẽ_y and Ẽ_z), while only z component electric field intensity |Ẽ_z| was estimated. The estimated |Ẽ_z| and SAR show reasonably similar distributions with the target distribution: exhibiting CCs of 0.922±0.030 (electric field) / 0.951±0.023 (SAR) for Duke model, and 0.931±0.018 (electric field) / 0.962±0.013 (SAR) for Ella model.

Fig. 3.

Simulation results. In the center: the axial view of the Duke (left) and Ella (right) head models (colors represent different tissue types) on the slice of interest with the arrangement of all coil elements. Surrounding inset maps: electric field intensity (colormaps range from blue to red) and voxel-wise SAR (colormaps range from black to white) distributions for selected coil element. In each inset map, top row: target (simulated) results, and bottom row: estimated (reconstructed) results.

Fig. 4 (a1)&(b1) show, on the slice of interest for each head model, the distribution of voxel-wise relative errors of estimated |Ẽ_z| compared with the target full electric field intensity (considering all three components). In addition, diagrams (a2)&(b2) show the relative error of the estimated voxel-wise local SAR compared with the target local SAR, all in blue bars, respectively (REs were calculated by summarizing the results for each individual coil element used for transmission at a time). Since hot spots with relatively higher SAR values draw more attention in terms of safety concern at UHF MRI, a threshold of 0.5 W/kg was arbitrarily chosen to further summarize local SAR results, restricted to SAR values above the threshold, for both models in (a3)&(b3). As it was empirically observed that these histograms consistently exhibited a Gaussian-like shape, they were fitted with a Gaussian distribution (red line) in order to facilitate their comparisons. Each Gaussian curve shows a mean relative error ${\overline{\mathrm{R}\mathrm{E}}}_{\mathit{\text{Gaussian}}}$ and a standard deviation of 6.43%±26.68% (electric field), −13.31±40.01% (SAR) −8.06±29.27% (SAR with threshold) for Duke model, and 1.75%±26.76% (electric field), −5.27±37.40% (SAR) −4.12±31.27% (SAR with threshold) for Ella model. The quadratic dependency of SAR upon |Ẽ_z| (see Eq. (7)) explains the wider distribution for local SAR estimation seen in Fig. 4(a2)(b2), whereas omitting |Ẽ_x| and |Ẽ_y| components may explain the fact that, in Fig. 4(b), the corresponding Gaussian distributions of RE for local SAR are now shifted towards larger, negative mean values.

Fig. 4.

Simulation results. Top row: using Duke head model, bottom row: using Ella head model. The number of voxels versus the relative error of estimated (a1)&(b1) electric field intensity, (a2)&(b2) local SAR, and (a3)&(b3) local SAR (above 0.5 W/kg) on the axial slice of interest, respectively. The original distributions (plotted in blue bars) are fitted against with a Gaussian distribution (in red lines). This is a summarization of all the results while each of sixteen coil elements were used for transmission.

For each axial slice (slices numbered along head→foot direction), RE distributions of estimated |Ẽ_z| and of local SAR (with and without threshold) were calculated and fitted against by Gaussian curves (data not shown). The corresponding ${\overline{\mathrm{R}\mathrm{E}}}_{\mathit{\text{Gaussian}}}$ and its standard deviation of the latter are plotted in Fig. 5(a1)–(a3)&(b1)–(b3), respectively, for both head models. An illustration of the total number of voxels with the target SAR value above threshold is summarized on each axial slice for both models, when each individual coil element used for transmission at a time, as in Fig. 5 (a4)&(b4), implying a larger SAR distribution within central transverse slices. Another direct illustration of local SAR spatial pattern is also provided for channel #16 with a comparison, in a sagittal view (on the central sagittal slice), between target and estimated SAR maps in Fig. 5 (a5)&(b5), respectively, with estimated SAR results exhibiting CCs of 0.9513 (Duke) and 0.9443 (Ella). The estimated SAR distributions reproduced the main pattern characteristics observed in the target maps, including, for a particular position along y-axis, faster spatial variation of SAR along the z-axis at the top and bottom of the head compared with the coil center. It can also be seen that, as the slice position along the z-axis moves away from the coil center and reaches the physical extremities of the RF coil, reconstructed SAR values are more and more underestimated compared with target values. This can easily be appreciated in Fig. 5(a2)&(b2), where ${\overline{\mathrm{R}\mathrm{E}}}_{\mathit{\text{Gaussian}}}$ reaches around −80% for the top slices. It is speculated that, as slice position gets closer to the upper end of the coil element along z, Ẽ_z magnitude becomes comparable to, or smaller than that of the transverse components of the electric field in those regions; in this situation, the dominant |Ẽ_z| approximation utilized in Eq. (7) does not hold anymore.

Fig. 5.

Simulation results. Top row: using Duke head model, bottom row: using Ella head model. The mean relative error (in red dots) and its standard deviation (in blue lines) of the fitted Gaussian distribution for (a1)&(b1) the electric field intensity, (a2)&(b2) local SAR, and (a3)&(b3) local SAR (above 0.5 W/kg) for each brain axial slice (along z-axis, from head to foot), respectively. (a4)&(b4) Summarized total number of voxels with the target SAR value above 0.5 W/kg for each axial slice when each individual coil element used for transmission at a time. (a5)&(b5) Target (upper) and estimated (lower) voxel-wise SAR on the central sagittal slice of interest when coil element #16 as the transmitter.

In Fig. 6, on an axial slice of interest, for channel #1 (a1) and #10 (a2), the previously demonstrated target (simulated) local SAR distributions (upper row) are plotted against the simulated local SAR distributions considering the aforementioned position offset (lower row). Notable differences are observed: the position offset has introduced an overall under-estimation with an average RE of −70.1% for channel #1, and an over-estimation with an average RE of +150.7% for channel #10. Selected SAR profiles along two vertical axes as denoted in (a1) and (a2) are shown in (b) as a comparison.

Fig. 6.

Simulated voxel-wise target SAR on an axial slice of interest of Ella head model. For channel #1 (a1) and #10 (a2), target SAR distribution (in dB, 0 dB = 1.6 W/kg) without (upper row) and with (lower row) a head model position offset within the coil, respectively. Selected SAR profiles (in W/kg) along vertical axes denoted in (a1) and (a2) are plotted in (b).

B. Phantom Experiment

Channel #5 was arbitrarily chosen as the reference for absolute phase retrieval. The values of the reconstructed EPs are 0.32±0.21 S/m for conductivity and 78±15 for permittivity; these mean values were used for subsequent SAR calculation. Simulated SAR distributions and estimated experiment results are shown for five channels (#2, #3, #4, #11 and #12) on an axial slice in Fig. 7, in which an agreement (including the localization of two hot spots) between simulated and experiment results are observed. The small shift of hot spots localization observed in Fig. 7 between experimental and simulation results may be due to some residual errors when assigning the experimental phantom position within the RF coil during FDTD modeling.

Fig. 7.

Phantom results. (a) Estimated axial proton density image of the phantom within the 16-channel microstrip head coil. (b) The simulated voxel-wise SAR (top row) and estimated voxel-wise SAR of experiment results (bottom row).

C. Human Experiment

Fig. 8 shows, for two human subjects, normalized T1-weighted images on the slice of interest [38], extracted proton density images, and, for two selected coil elements in each case, voxel-wise SAR as calculated based on simulated and experiment results. The two axial slices taken from the Ella head model, used as a comparison reference for SAR distribution, exhibit structure patterns with overall reasonable similarity with those observed in the T1-weighted images of the two human experiments. Note that, with RF wavelengths equivalent or shorter than the size of the human head at UHF, B₁ distribution is more sensitive to head geometry, head position within the coil, as well as actual current distribution along coil conductors. Noticeable differences can be observed in Fig. 8, which may result from such factors in numerical modeling.

Fig. 8.

Human results. Subject I: (a1) The reference axial slice from Ella head model (colors represent different tissue types) with coil elements arrangement, (a2) simulated voxel-wise local SAR for coil element #4, and (a3) for coil element #11; (b1) normalized T1-weighted image of the slice of interest, (b2) extracted proton density image, (b3) estimated voxel-wise local SAR for coil element #4, and (b4) for coil element #11. Subject II: (c1) The reference axial slice from Ella head model with coil elements arrangement, (c2) simulated voxel-wise local SAR for coil element #5, and (c3) for coil element #12; (d1) normalized T1-weighted image of the slice of interest, (d2) extracted proton density image, (d3) estimated voxel-wise local SAR for coil element #5, and (d4) for coil element #12.

V. DISCUSSION

Unlike external model-based SAR simulation methods that are based on a few human models (i.e. not derived on a per-subject basis) and are highly time-consuming, EPs mapping methods derived from measured B₁ maps may allow for fast, subject specific SAR calculation. Our present simulation and experimental results are encouraging, which suggest that real-time local SAR prediction for a specific human subject may be eventually feasible, relying only on measurable B₁ information (i.e. magnitude and relative phase). Indeed, simulation studies conducted with electromagnetic numerical models of a 16 channel transceiver coil, loaded with a phantom and human heads at 7T, were in general consistent with experimental results; further development of EPT methods would result in acceptable accuracy of SAR estimation based on complex transmit B₁ and/or receive B₁ distributions. The present method can be applied to any MRI system equipped with a multi-channel transceiver coil; furthermore, B₁ measurements using as few as five coil elements are sufficient to retrieve the necessary information for subsequent computation [27].

Recently, several EPs reconstruction methods have been proposed with multi-element coil arrays [39],[40], utilizing the homogeneous Helmholtz equation as the fundamental equation. Differing from these approaches, the phase retrieval of the proposed method originates from the Gauss’s Law for magnetism, utilizing the continuously differentiable nature of the magnetic field vector in space. Furthermore, the present modified Dual-Excitation algorithm, which also offers a more convenient implementation than in a previously introduced formalism [24], takes into account the spatial variation of EPs distribution as Eq.(5) indicates. Therefore, the proposed approach is theoretically capable of dealing with objects with inhomogeneous EPs distribution, and further work will be dedicated to demonstrate that this can indeed provide a practical way to study complex anatomical structures, such as the human brain. Note that, in a recent simulation study, it has been shown that simplifying the head model into a more homogeneous object produces a more uniform local SAR pattern, leading to lower SAR peaks [41], which suggests that an elevated safety concern exists at transitions between dielectrics due to increased local SAR values, which necessitates a more accurate EPs reconstruction in the vicinity of tissue boundaries. Another property, specific to the proposed method, is a phase retrieval approach capable of deriving the relative phase between transmit and receive B₁ for each channel directly, without direct knowledge of transceive phase which requires redundant phase removal (e.g. ΔB₀ and eddy currents phases) from the raw MRI image phase [25]. Retrieving this relative phase information, however, is necessary for accurate closed-form Ẽ_z calculation as Eq. (9) indicates.

In the current stage of this study, the proposed approach still relies on two assumptions. First, a fairly left-right symmetric structure of the human brain about the coronal plane through the brain center and the 16-fold elliptical symmetric head coil structure about the long axis were both utilized to estimate receive B₁ magnitude for each coil element. As previous studies suggested [32],[27], even considering the residual coupling between coil elements, by examining the extracted proton density distribution of human subjects, the mirroring symmetry between coupled transmit and receive B₁ along the vertical axis still preserves. While such an approximate symmetry nature is expected to exhibit in healthy human brains, however, further investigations are needed to overcome this limitation in order to extend its application to human anatomical structures where such symmetry does not apply, either because of pathological processes, or simply because of anatomical variations. Secondly, B₁-mapping techniques have been well established to measure the transverse RF magnetic field components that contribute to MR signal; however, there is currently no standard MR method to measure the longitudinal RF magnetic field B̃_z. Thus, the spatial variations of B̃_z were neglected throughout the whole approach, from absolute phase retrieval, via EPs reconstruction, up to SAR calculation. Specifically, B̃_z is essential for the calculation of transverse induced electric field components Ẽ_x and Ẽ_y, as the Ampere's Law indicates. As a result, in ours and others' related studies [23],[25],[33],[34],[39], SAR computation has been dictated to only considering Ẽ_z component (Eq. (7)), thus restricted to spatial regions where Ẽ_z is assumed to be dominant. Consistent with this observation, on both head models, the present simulated SAR-estimation results were judged satisfactory (${\overline{\mathrm{R}\mathrm{E}}}_{\mathit{\text{Gaussian}}}$ around −10%) when examining slices at the level of the coil center, exhibiting spatial patterns similar to those derived from experiments in locations where induced currents are anticipated to flow mostly along z-axis direction. This assumption, however, does not stand in regions close to the upper end of the coil elements (close to the apex) where Ẽ_x and Ẽ_y are not anymore minor components of the electric field: by observing simulation data, |Ẽ_z| usually 7~20 times higher than |Ẽ_x| and |Ẽ_y| on central brain slices, but 1~3 times less than |Ẽ_x| and |Ẽ_y| close to coil upper end. This rationale provides a direct explanation to the apparent drop in calculated SAR close to the upper end of the coil elements, as shown in Fig. 5 (a5)&(b5). Considering the whole brain for all coil elements, the relative error increases rapidly as a function of the distance of a given transverse slice upper to the central slice along z-axis, as seen in Fig. 5, with about −60% (Duke model) and −50% (Ella model) in |Ẽ_z| estimation close to the top of the brain, and with corresponding drop of about −90% (Duke and Ella models) in estimated SAR value. When examining voxels with target SAR value above 0.5 W/kg (taken as an arbitrary threshold), a flatter ${\overline{\mathrm{R}\mathrm{E}}}_{\mathit{\text{Gaussian}}}$ curve is seen for both head models as in Fig. 5(a3)&(b3), with ${\overline{\mathrm{R}\mathrm{E}}}_{\mathit{\text{Gaussian}}}$ of −40%~−80% on the uppermost slices, while within −40%~0% for the other slices; on the twenty central slices, nevertheless, ${\overline{\mathrm{R}\mathrm{E}}}_{\mathit{\text{Gaussian}}}$ was within −20%~0%. Moreover, as is depicted in Fig. 5 (a4)&(b4), a larger target SAR distribution is observed on central transverse slices, within which a dominant |Ẽ_z| is expected and an accuracy of 40%~0% of SAR estimation can be reached. Thus, on one hand, it will be worth investigating when using similar microstrip head coils, whether a stronger energy deposition pervades in such a region, in which a more reliable SAR estimation can be attained due to a dominant |Ẽ_z|. On the other hand, further work remains to be pursued to amend the absence of Ẽ_x and Ẽ_y in SAR computation via any possible B̃_z measurement or estimation techniques, aiming for a more accurate SAR prediction as well as an extensive application by using various multi-channel RF coils designs.

In addition, computational EM simulation, which has been regarded as one of the standard tools for SAR prediction in current UHF MRI applications, computes SAR distribution each time for a specific position the model is placed at. However, despite accurate subject modeling, position offset would occur because it is less straightforward to capture the exact position of the subject with respect to the RF coil. As documented in Fig. 6 and in agreement with [41], significant SAR estimation discrepancies can be introduced with a trivial position offset. Therefore, it is believed that the B₁ based approach, which does not require or rely heavily on accurate 3D modeling (in terms of model structure and position), preserves certain merits in subject-specific local SAR quantification. Also note that an acquisition time of more than 1 hour was needed to obtain the B₁ maps with satisfactory SNR; further efforts should be mainly dedicated to improving the B₁-mapping technique with a much shorter acquisition time, enabling the proposed B₁ based approach to be a substantially real-time local SAR prediction scenario.

Although differences in mass densities through different human tissues have been reported [14], e.g. ρ_CSF = 1000 kg/m³, ρ_GM = 1036 kg/m³ and ρ_WM = 1027 kg/m³, reflecting negligible ≈3% differences, it is assumed, for simplicity, a homogeneous mass density in SAR calculation in the present human experiment. Note that the resulting SAR inaccuracies do not impact the conclusions with regards to electric field mapping, EPs mapping or SAR result comparisons, considering that mass density is only utilized at the last SAR computational step and has no role in electric field or EPs mapping.

Also note that, while there are other approaches being pursued for the estimation of EPs of biological tissues, including Electrical Impedance Tomography (EIT) [42],[43], Magnetic Resonance Electrical Impedance Tomography (MREIT) [44–46], and Magnetoacoustic Tomography with Magnetic Induction (MAT-MI) [47–49], these approaches are operated at much lower frequency so not able to estimate EPs during frequency range of MRI.

In summary, the ultimate goal of this work is to rapidly estimate local SAR, during an in vivo scanning session, based on B1-mapping technique. The present results suggest that electric fields for each coil element and electric properties for each voxel of tissue can be derived from measured complex B₁ maps for individual coil element. The present approach holds promises for enabling the use of subject-specific local SAR computation which in turn can be used as explicit constraint in B₁ shimming calculation and parallel transmission RF pulse design.