3D Through-Time Radial GRAPPA for Renal Magnetic Resonance Angiography

Abstract

Purpose

To achieve high temporal and spatial resolution for contrast-enhanced time-resolved MR angiography exams (trMRAs), fast imaging techniques such as non-Cartesian parallel imaging must be employed. In this study, the 3D through-time radial GRAPPA method is used to reconstruct highly accelerated stack-of-stars data for time-resolved renal MRAs.

Theory and Methods

Through-time radial GRAPPA has been recently introduced as a method for non-Cartesian GRAPPA weight calibration, and a similar concept can also be utilized in 3D acquisitions. By combining different sources of calibration information, acquisition time can be reduced. Here, different GRAPPA weight calibration schemes are explored in simulation, and the results are applied to reconstruct undersampled stack-of-stars data.

Results

Simulations demonstrate that an accurate and efficient approach to 3D calibration is to combine a small number of central partitions with as many temporal repetitions as exam time permits. These findings were used to reconstruct renal trMRA data with an in-plane acceleration factor as high as 12.6 with respect to the Nyquist sampling criterion, where the lowest RMSE value of 16.4% was achieved when using a calibration scheme with 8 partitions, 16 repetitions, and a 4 projection x 8 read point segment size.

Conclusion

3D through-time radial GRAPPA can be used to successfully reconstruct highly accelerated non-Cartesian data. By using in-plane radial undersampling, a trMRA can be acquired with a temporal footprint less than 4s/frame with a spatial resolution of approximately 1.5mm × 1.5mm × 3mm.

INTRODUCTION

Accelerated image acquisition and reconstruction techniques are frequently employed in MRI, and are particularly important for time-resolved, 3-dimensional (3D) acquisitions, in which volumetric coverage and temporal and spatial resolution requirements cannot be met without the use of fast imaging methods. One such application is contrast enhanced, time-resolved MR Angiography (trMRA), where a high spatial resolution is required to assess small arteries and characterize stenoses, and a high temporal resolution is needed to capture the arterial phase of enhancement without venous contamination. Several acceleration methods which have been employed include view-sharing (1–7), parallel imaging (8–11), non-Cartesian trajectories (12–18), compressed sensing (19–21), and various combinations of these methods (for example, (22–24)).

This work focuses on combining parallel imaging methods with non-Cartesian trajectories for rapid 3D data acquisition. Alone, parallel imaging reconstructions can be used for acceleration in both phase and partition encoding directions (25–29), and have been shown to provide reduction factors of up to eight for these 3D acquisitions (28). Similarly, used on their own, non-Cartesian k-space trajectories such as radial have many benefits, including robustness to deleterious effects from motion and less detrimental undersampling artifacts in comparison to Cartesian sampling (30,31). The combination of non-Cartesian acquisitions and parallel imaging techniques has been shown to provide high spatial and/or temporal resolution images (32–40) from highly accelerated datasets. In addition to the aforementioned benefits of each of these techniques, non-Cartesian parallel imaging could allow higher acceleration factors than either non-Cartesian trajectories or parallel imaging alone. Unlike when using view-sharing, or even some compressed sensing methods, the resulting images have well-defined, short temporal footprints, and the techniques are easy to implement. However, non-Cartesian data acquisitions necessitate the use of modified parallel imaging techniques (32,33,35–44). For example, special formulations of the GRAPPA reconstruction method must be used when working with undersampled non-Cartesian trajectories (33,37,39,40,42–44). In the case of a radial acquisition, GRAPPA weights are applied to the acquired radial projections to estimate missing projections. The challenge in performing radial GRAPPA reconstructions is the calibration of the GRAPPA weights, which can be calculated using through-k-space information as in Cartesian scans (33), or using through-time information as shown in (39,40). The aim of this study is to explore methods for the calibration of 3D through-time radial GRAPPA for a stack-of-stars trajectory.

THEORY

The principles of radial GRAPPA reconstruction are similar to those used when performing GRAPPA on Cartesian data, and have been previously described in detail in (40). In a radial acquisition, the calibration of GRAPPA weights must be adapted for the radial trajectory, since the kernel geometry is dependent on both its location along a projection and its angular orientation. However, one can take advantage of the fact that the change in geometry is small throughout k-space, and multiple similar kernel replicas can be extracted by moving the kernel through a segment of k-space, as shown in Figure 1A (33,40). For example, in a segment size of 1 projection x 4 read points, the kernel is shifted along the projection to four different readout points such that there are a total of four kernel occurrences per receiver coil. It is important to note that this method on its own has an inherent tradeoff between the improvement in weight accuracy by increasing the number of kernel occurrences by using a large segment and the degradation of accuracy when kernel geometries are too dissimilar within that large segment.

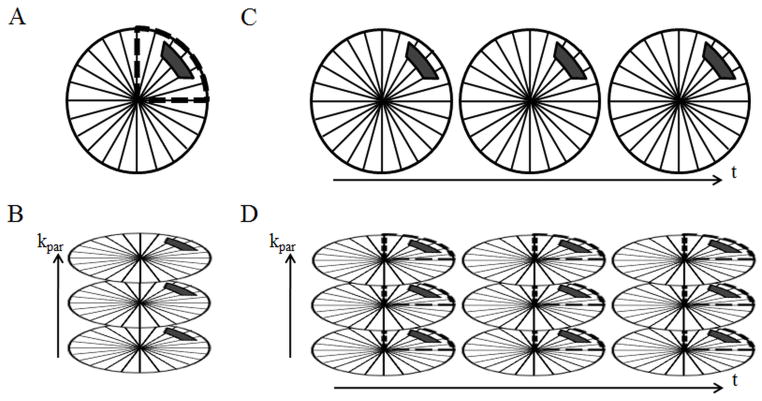
Figure 1.

Three different 3D non-Cartesian GRAPPA weight calibration methods are shown separately (A–C) and in combination for an example 3D through-time radial GRAPPA calibration (D). Figure 1A depicts through-k-space calibration using segmentation, where kernel occurrences are accumulated by shifting a small kernel (solid block) through a segment of a radial trajectory (indicated by the dashed line). Figure 1B demonstrates through-partition calibration, where kernel occurrences are accumulated by shifting the kernel along the partition dimension. Figure 1C depicts through-time calibration, where kernel occurrences are accumulated by shifting the kernel through temporal repetitions of the trajectory. Because these methods are independent of each other, these can be combined for 3D through-time radial GRAPPA calibration, and a simple example of this is shown in Figure 1D.

In a 3D stack-of-stars acquisition, the data are acquired using a radial trajectory in the k_x-k_y plane and with Cartesian encoding steps in the k_z direction. The rectilinear Cartesian encoding steps will be referred to as partitions in this work. As depicted in Figure 1B, the 2D GRAPPA kernel can be replicated in each partition to increase the number of kernel occurrences for calibration. Unlike through-k-space calibration using segmentation, through-partition calibration allows for exact replication of kernel geometries, but partitions located far away from the k-space center suffer from decreased SNR, especially in the outer portions of the radial trajectory, and may not provide the full benefit compared to the time spent collecting this data.

Instead of acquiring a single, fully-sampled dataset for calibration, multiple time frames can be acquired for through-time calibration, as shown in Figure 1C. This method creates exact replications of kernel geometries in each temporal repetition, which has been shown to provide excellent image quality (40). During the through-time calibration acquisition, patient motion can occur, leading to differences in calibration information in identical partitions acquired at different times. The motion is negligible during acquisition of neighboring projections, so points within a single GRAPPA calibration kernel are unaffected. However, one drawback to through-time calibration is that it requires additional calibration time, and thus there is always interest in minimizing this calibration time while preserving the highest image quality.

In order to minimize the total time needed for calibration, each of these three different calibration options (through-k-space with segmentation, through-k-space through-partition, and through-time) must be combined in an efficient way, as shown schematically in Figure 1D. Here, several fully-sampled partitions are acquired over multiple time points (all projections are acquired in each partition and at each time point), and all radial data are segmented for through-k-space calibration. However, this is not necessarily the most efficient way to acquire calibration data. For example, the use of several different partitions may provide more unique calibration information than using multiple repetitions of the same partition, as partition encoding provides additional variety beyond relying on image differences through-time. However, despite being a potential source of unique information for calibration, using many outer, lower signal partitions may also decrease accuracy of GRAPPA weights. In this study, the trade-off between through-k-space, through-partition, and through-time calibration and the overall accuracy of these GRAPPA weight calibration methods will be explored, and the results applied to undersampled in vivo renal MRA data.

METHODS

Simulations

The goal of the simulations was to assess the effect of using different amounts of through-time and partition calibration data for the 3D through-time radial GRAPPA reconstruction. Optimization of this calibration scheme for 3D renal trMRA cannot be explored directly due to the limitations of in vivo acquisitions, so a simulation-based approach was implemented (similar to that used in (40)), and the reconstruction results were used to select the GRAPPA calibration scheme for in vivo acquisitions/reconstructions. The simulations also explored calibration efficiency; the acquisition of each partition and repetition for calibration adds to the total scan time equally, so the simulations were designed to evaluate which calibration scheme provides lower reconstruction error for a given amount of calibration acquisition time. A modified 3D Shepp-Logan phantom with random, continuous motion similar to that designed in (40) was used to generate calibration and undersampled data. This phantom was sampled in-plane to have 144 projections and 256 oversampled read points with a base matrix size of 128². The phantom had a total of 64 partitions, different numbers of which were used in the calibration process to explore the effects of this parameter.

For the undersampled data, a similarly constructed randomly moving 3D Shepp-Logan phantom with 16 partitions and an in-plane matrix size of 128² was generated. The object was varied to mimic in vivo data such that object information changed continuously for each time frame and each partition. A total of 64 different frames were generated for the calibration data and 5 frames for the undersampled data, and the contrast for those five undersampled frames was altered in comparison to the calibration data. Finally, coil sensitivities obtained from the combination of a 6-channel Siemens body array and 6 channels of a spine array were applied to the data to simulate a multi-coil acquisition similar to that used for the renal MRA. As the undersampling only occurs in-plane in the angular direction (no undersampling is performed in the partition direction), all reconstructions used a 2D kernel with 2 × 3 points (projection x read) as in (40), and the calibration segment size was set at 1 projection x 4 read points and 4 projection x 8 read points (where the kernel is shifted along the read direction such that there are a total of four kernel occurrences and thirty-two occurrences, respectively). The calibration data was varied by adjusting the number of partitions and repetitions used for calibration; each ranged between 1 and 64. For calibration schemes using fewer than the maximum number of partitions, the central k-space partitions were used for calibration. Only simulations that had a fully-determined system of equations for GRAPPA weight estimation were performed, meaning that at least 72 kernel occurrences (6 source kernel points × 12 coils) must be present in the calibration data for each point in the reconstruction. Data were undersampled such that 24 projections were used, which is a radial acceleration factor of 6 and an acceleration of 8.4 with respect to Nyquist sampling criterion. 3D through-time GRAPPA reconstructions were performed where the weights were determined with these different calibration possibilities, and the resulting root mean squared error (RMSE) values were computed in comparison to the fully-sampled dataset.

in vivo Imaging

In this IRB approved, HIPAA compliant study, contrast-enhanced data were acquired in five asymptomatic volunteers (mean age: 23, age range: 19–31, 1 female/4 males) after obtaining informed consent. Imaging was performed at 3T (Magnetom Verio, Siemens Healthcare, Erlangen, Germany) with a standard 6-channel body matrix receive coil and spinal array coil (using between 9 and 12 channels), similar to that used in the simulations but with additional spine coils. All data were collected using a FLASH sequence with a stack-of-stars trajectory in order to acquire a time-resolved angiography exam after injection of a single dose (0.1 mmol/kg) of gadobenate dimeglumine (Multihance, Bracco Diagnostics Inc., Princeton, NJ).

A dataset was acquired for one subject to confirm the effects of using different calibration schemes tested in simulations for the reconstructions of in vivo data with 3D through-time radial GRAPPA. Calibration data were acquired during free breathing after contrast injection (more than 2 minutes after injection), and a single, breath-held, fully-sampled volume was acquired and retrospectively undersampled for reconstruction. These axial data were acquired with the scanning parameters shown in Table 1 for Figure 3. These data were retrospectively undersampled to 40 projections/partition, and were reconstructed with 3D through-time radial GRAPPA using a segment size of 1 projection x 4 read points, and varying numbers of partitions and repetitions. Note that various amounts of calibration data were used to simulate different calibration acquisition times. The calibration acquisition time was 22 seconds when the product of partitions and repetitions was 32 (i.e. partitions x repetitions = 32), 43 seconds when partitions x repetitions = 64, and 87 seconds when partitions x repetitions = 128. The fully-sampled and retrospectively undersampled data were also reconstructed for a comparison of image quality, and RMSE values were calculated using the fully-sampled data as the reference.

Table 1.

Parameters for in vivo experiments performed throughout the study

	Figure 3	Figure 4	Figure 5	Figures 6–7	Figure 8–9
Fully-sampled Projections	240	224	224	224	224
Undersampled Projections	40	28	28	28	28
Partitions	32	36	36	40	36
Partition Oversampling	25%	22.2%	22.2%	10%	25%
Acceleration Factor (with respect to Nyquist)	8.8	12.6	12.6	12.6	12.6
Partial Fourier (Partition)	None	6/8	6/8	6/8	6/8
Matrix Size	224 × 224	224 × 224	224 × 224	224 × 224	224 × 224
TR (ms)	2.82	3.91	3.69	3.71	3.68
TE (ms)	1.26	1.58	1.5	1.49	1.49
Flip Angle	8°	20°	20°	20°	20°
BW (Hz/pixel)	890	600	740	720	740
FoV (mm3)	380×380×64	335×335×108	325×325×108	340×340×120	330×330×108
Spatial Resolution (mm3)	1.7×1.7×4	1.5×1.5×3	1.5×1.5×3	1.5×1.5×3	1.5×1.5×3
Temporal Resolution (s)	13.5	3.8	3.6	3.5	3.5
Segment Size (proj x read)	1 × 4	4 × 8	4 × 8	4 × 8	4 × 8
Calibration Repetitions	Varied (Max: 32)	16	16	(Max: 20)	16
Calibration Partitions	Varied (Max: 32)	8	8	8	8

Figure 3.

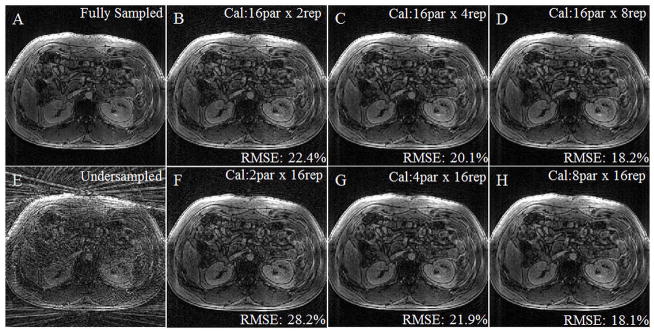
A contrast-enhanced, breath-held dataset was acquired fully sampled, retrospectively undersampled to have a radial in-plane acceleration factor of 6, and reconstructed with different calibration schemes. Figure 3A shows the fully-sampled image, and Figure 4E shows an image after retrospective undersampling. Figures 3B–D and 3F–H were reconstructed with 3D through-time radial GRAPPA with calibration parameters noted in the upper right hand corner (partitions x repetitions). RMSE was calculated using the fully-sampled image as the comparison and was noted for each reconstruction in the lower right hand corner. Calibration time increases from left to right along both rows and is the same for each column. The lowest RMSE is found when 8 partitions are used with 16 repetitions (3H), although calibration schemes with similar parameters (3C, D, and G) also yield good results.

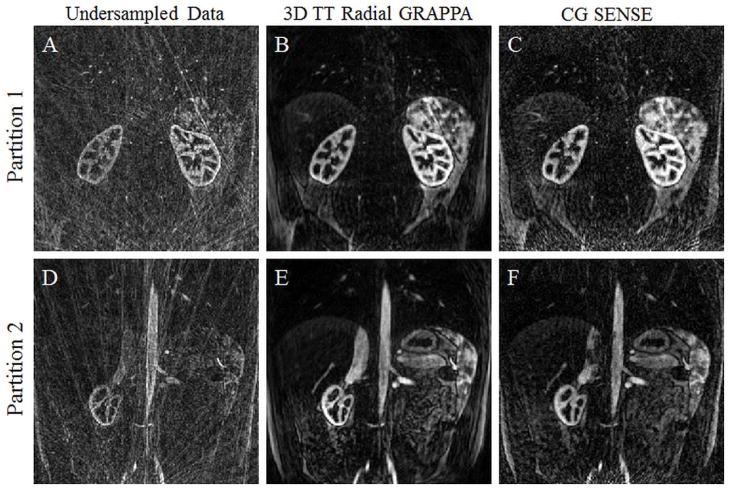
In order to compare the performance of 3D through-time radial GRAPPA with existing techniques, a dataset was acquired using the parameters listed under Figure 4 in Table 1, and reconstructed using both the CG SENSE algorithm (32) (2x oversampling, four iterations, Tikhonov regularization with a regularization parameter of 0.1) and 3D through-time radial GRAPPA. Density compensation weights using the Voronoi method (45) were used for preconditioning of the CG algorithm and to preserve image resolution. The coil maps were calculated using the adaptive combination method (46) by averaging over the 16 fully-sampled calibration frames.

Figure 4.

Two example partitions from a contrast-enhanced, breath-held dataset acquired with a radial in-plane acceleration factor of 8 reconstructed with NUFFT (4A, D), 3D through-time radial GRAPPA (4B, E), and CG SENSE (4C, F). Note the improved image quality of both the parallel imaging reconstructions in comparison to the undersampled data, and the reduced streaking artifacts and noise level in the 3D through-time radial GRAPPA reconstruction.

Two additional datasets were acquired to demonstrate the use of 3D through-time radial GRAPPA to reconstruct highly accelerated data in vivo. Renal contrast-enhanced trMRAs were acquired coronally with volumetric coverage of the kidneys, renal arteries, and aorta. These were performed in two different subjects (2 males, age: 20) with similar protocols (described in Table 1 for Figures 5 through 7), where changes were made to achieve similar spatial and temporal resolution for the specific anatomy of the volunteer. Free-breathing calibration scans were performed with the calibration parameters determined using the simulations studies prior to contrast injection.

Figure 5.

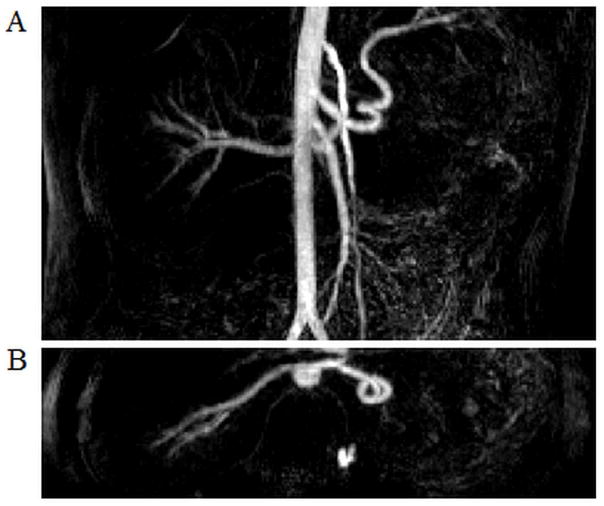
A time resolved, contrast-enhanced, breath-held renal MRA exam was reconstructed using 3D through-time radial GRAPPA with a calibration time of 1.8 min. This data was accelerated in-plane with a factor of 12.6 with respect to Nyquist, and a partial Fourier acquisition was used along the partition direction. A single frame is shown here with a sub-volume, coronal (5A) and axial (5B) MIP image with a temporal resolution of 3.6 s/frame. The axial MIP was zero-padded to display at an isotropic resolution of 1.5 mm × 1.5 mm × 1.5 mm.

Figure 7.

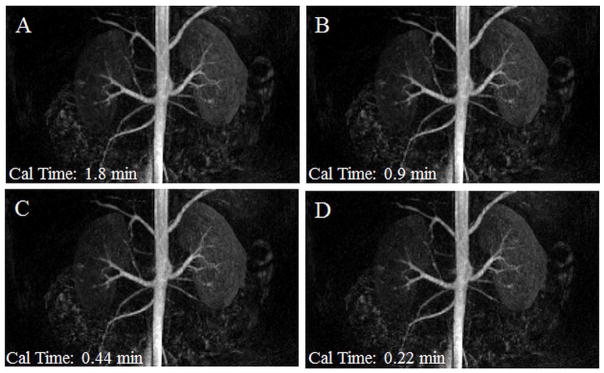
A time resolved, contrast-enhanced, breath-held renal MRA exam was reconstructed using 3D through-time radial GRAPPA. This data was accelerated in-plane with a factor of 12.6 with respect to Nyquist, and a partial Fourier acquisition was used along the partition direction. The same coronal frame is shown here as MIPs for four different GRAPPA weight calibration schemes: 8 calibration partitions with 16, 8, 4, and 2 calibration repetitions (A, B, C, and D). Calibration acquisition times are noted in the lower left corner (Cal time). These images have a spatial resolution of 1.5mm × 1.5mm × 3mm and a temporal resolution of 3.5 s/frame.

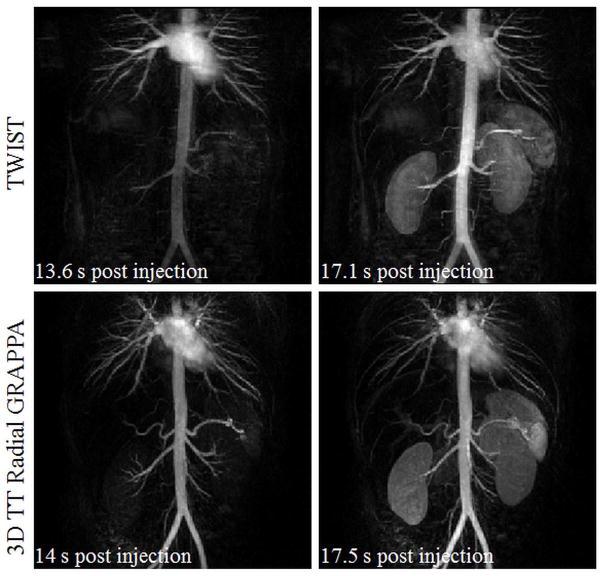
Finally, 3D through-time radial GRAPPA was compared to a commercially-available trMRA technique known as TWIST (time-resolved imaging with stochastic trajectories) (6,7). The same volunteer was scanned on two different dates spaced one week apart on a 3T scanner using an 18-channel body array and 20 channels of the spine array (Magnetom Skyra, Siemens Healthcare, Erlangen Germany). Data for the first exam were acquired with the undersampled stack-of-stars trajectory, and reconstructed with 3D through-time radial GRAPPA (acquisition and reconstruction parameters shown in Table 1 for Figure 8). The second exam utilized the TWIST acquisition and reconstruction. Where possible, the TWIST acquisition matched the acquisition parameters in the 3D through-time radial GRAPPA scan (including FoV, temporal and spatial resolution, bandwidth/pixel, repetition time, echo time, and flip angle). However, to achieve the desired frame rate of 3.5 s, acceleration in the TWIST scan was achieved by using a combination of view-sharing (pA=0.16, pB=0.2), a Cartesian GRAPPA undersampling factor of 3, and partial Fourier of 6/8 in the slice direction. With this acquisition, the TWIST reconstruction used data from four neighboring frames, yielding a temporal footprint of 17.5 s/frame. The TWIST acquisition does not use view-sharing in the first time point, resulting in a longer acquisition time of 10.1 seconds.

Figure 8.

A time resolved, contrast-enhanced renal MRA exam. Images in the top row were acquired with a commercially available Cartesian TWIST sequence that utilizes Cartesian GRAPPA, view-sharing, and partial Fourier. Images in the bottom row were acquired with an undersampled stack-of-stars trajectory with an in-plane acceleration of 12.6 with respect to Nyquist, and reconstructed using a 3D through-time radial GRAPPA. Coronal subtracted MIP images for two neighboring time frames are shown for each of these acquisition/reconstruction methods. The spatial and temporal resolution of both datasets is nominally the same (3.5 s/frame, 1.5×1.5×3mm³). Note that the TWIST dataset has a temporal footprint of 17.5s, while the 3D through-time radial GRAPPA has a temporal footprint of 3.5s.

Undersampled radial data were reconstructed offline in MATLAB (MathWorks, Natick, MA) with 3D through-time radial GRAPPA using a calibration segment size of 4 projections x 8 read out points, 16 calibration repetitions, and 8 calibration partitions for data shown in Figures 4, 5, 8, and 9 as suggested by the results of the simulation studies. The images shown in Figures 6 and 7 were reconstructed using the same parameters except for the calibration repetitions, which were varied (20, 16, 8, 4, and 2 repetitions were used) to demonstrate the robustness of the reconstruction even when using fewer repetitions in order to decrease the calibration time. Data were reconstructed to compensate for the partial Fourier acquisition using projection onto convex sets (POCS) prior to applying the Fourier transform along the partition direction. Density compensation and NUFFT (47) were then applied to in-plane radial data to generate the reconstructed images.

Figure 9.

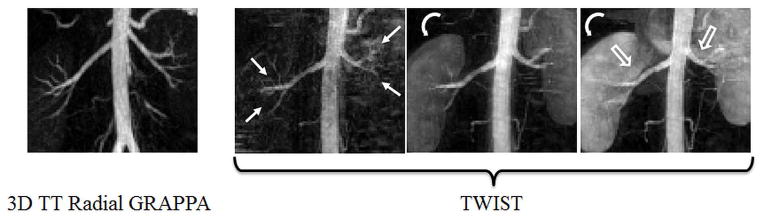
Zoomed sub-volume MIP images of the time resolved contrast-enhanced renal MRA exams for the same subject using through-time radial GRAPPA acceleration (left) and TWIST acceleration (right 3 frames). The leftmost image shows the renal arteries and aorta at peak aortic/arterial enhancement for the radial GRAPPA exam. The corresponding TWIST image obtained from a near-identical timepoint is shown to the right of the first image. The aorta and arteries continue to enhance further into the subsequent two frames, reaching peak enhancement in the rightmost image, an effect caused by the view-sharing reconstruction. The first and second order branches of the renal arteries (solid, straight arrows in TWIST images) are better depicted in the single, peak enhancement frame of the radial GRAPPA exam. As the view-shared TWIST exam reaches peak aortic enhancement in the two rightmost frames, parenchymal enhancement (curved arrows) and venous enhancement (open arrows) complicate visualization of the small branch vessels.

Figure 6.

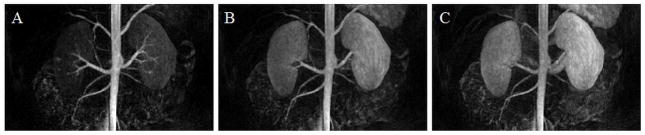
A time resolved, contrast-enhanced, breath-held renal MRA exam was reconstructed using 3D through-time radial GRAPPA with a calibration time of 2.2 min. This data was accelerated in-plane with a factor of 12.6 with respect to Nyquist, and a partial Fourier acquisition was used along the partitions direction. Three time-resolved, coronal frames are shown here as MIPs. These images have spatial resolution of 1.5mm × 1.5mm × 3mm and a temporal resolution of 3.5 s/frame.

Subtracted maximum intensity projection (MIP) images were generated for a single time frame at peak arterial enhancement for the renal MRA exams in the dataset for Figure 5, and images were cropped to display the renal arteries. The true resolution of the axial MIPs was non-isotropic, so data were displayed at approximately isotropic resolution by reconstructing with zero-padding. Coronal MIPs were shown for the dataset used in Figure 6 and 8 at multiple time points during contrast enhancement.

RESULTS

Simulations were performed to evaluate the effect of adding through-time calibration information when performing 3D through-time radial GRAPPA. This simulation showed that increasing the number of calibration repetitions from 1 to 16 decreased the RMSE (as expected from the 2D through-time calibration results (40)). Once the amount of calibration data becomes large (in this example, beyond 8 repetitions), additional temporal repetitions have a diminishing improvement on reconstruction errors.

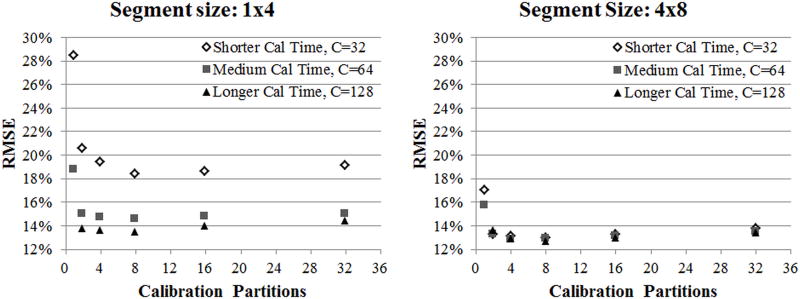
Figure 2 explores in simulation how to efficiently acquire calibration data to achieve low RMSE by varying the number of partitions or repetitions within a constant calibration time. The plots show RMSE values for two segment sizes (1×4 and 4×8) when using different numbers of partitions to perform the calibration, and each data point represents a different number of repetitions to maintain a constant calibration time (large number of calibration partitions indicates that a small number of calibration repetitions were used and vice versa). In the plot showing the 1×4 segment size reconstructions, these results show that for a set amount of calibration time, the use of more calibration partitions decreases the error until approximately 8 partitions are used. At this point, error begins to increase for a higher number of partitions and fewer repetitions. These results also show that by increasing the total calibration time, reconstruction error decreases (this can be seen by looking at the triangles, with a high RMSE and short calibration time, vs. the diamonds, with a low RMSE and a long calibration time). In the plot showing the 4×8 segment size reconstructions, the general trends in RMSE are similar to those in the 1×4 segment size, but there is an overall decrease in RMSE.

Figure 2.

This figure shows root mean squared error (RMSE) values for simulations with a radial undersampling factor of 6. These reconstructions were calibrated using a segment size of 1 projection x 4 read (on left) and 4 projections x 8 read (on right), a varied number of partitions, and a varied number of repetitions. The calibration acquisition time for each curve was held constant, meaning that at a low number of partitions, a high number of repetitions are acquired, and vice versa. Calibration time is noted in the legend, where the total acquisition time is equal to 144 projections x TR x C. The RMSE is high at low number of partitions, reaches a minimum at 8 partitions, and begins to gradually increase at high number of partitions.

To confirm the effects of the calibration scheme on the reconstruction results using in vivo renal trMRA data, Figure 3 shows the results when varying the number of partitions and repetitions for a late contrast-enhanced renal scan. Figure 3A shows an example partition generated using the fully-sampled data and Figure 3E shows the same undersampled partition for comparison. Figures 3B–D were reconstructed using 3D through-time radial GRAPPA with a segment sizes of 1 projection x 4 read points, 16 calibration partitions, and a varied number of repetitions. As the number of repetitions increases from 2 to 8, the image quality improves, and the RMSE decreases. Figures 3F–H were calibrated with a segment size of 1 projection x 4 read points, 16 repetitions, and a varied number of partitions. Increasing the amount of calibration data by increasing the number of partitions also improves image quality and decreases RMSE. Additionally, each column is reconstructed with the same amount of calibration data. Similar to the simulation results, very few calibration partitions and a large number of repetitions results in the highest error, and the minimum RMSE is found when using 8 calibration partitions, although visually the image quality is very similar in Figures 3C–D and G–H. The same behavior is observed when a segment size of 4 projections x 8 read points is used for the in vivo reconstructions, although as in the simulations, the RMSE values and thus visual appearance are similar with different numbers of repetitions and partitions. As in the simulation data, the lowest RMSE value was found when using a calibration scheme with 8 partitions, 16 repetitions, and a 4 projection x 8 read point segment size (RMSE = 16.4%).

Figure 4 demonstrates reconstruction results of two sets of source images from single partitions using different reconstruction algorithms. The same undersampled data are shown after applying density compensation and the NUFFT (left column), after reconstruction using the 3D through-time radial GRAPPA algorithm (middle column) (with a 4×8 segment size and a total of eight partitions and 16 repetitions for calibration, as suggested by the simulations and in vivo data) and after the CG SENSE algorithm (right column). The gridded images demonstrate that these data are highly undersampled with a high level of residual streaking artifacts, which are reduced in both the 3D through-time radial GRAPPA and CG SENSE reconstructions. By visual inspection, the radial GRAPPA method offers a better overall image quality.

Figure 5 depicts reconstruction results from contrast-enhanced, time-resolved MRA (trMRA) exams of the kidneys, where the data were undersampled in-plane by a factor of 12.6 with respect to Nyquist (see Table 1 for acquisition parameters). This figure depicts a single frame of a sub-volume, subtracted MIP in both a coronal and axial view, where 16 calibration repetitions and 8 partitions, along with a segment size of 4×8, were used for the reconstruction. Here, the residual streaking artifacts that would result from undersampling are largely removed, and the image quality allows for clear visualization of the renal arteries as well as first and second order branches. Note in Figure 5, the trMRA shows a variant anatomy where the subject only had a single kidney.

Figures 6 and 7 depict reconstruction results from a contrast-enhanced trMRA exam acquired with an undersampling factor of 12.6 with respect to Nyquist sampling criterion. Figure 6 displays three frames of sub-volume, subtracted MIPs in the coronal view, where 20 calibration repetitions and 8 partitions, along with a segment size of 4×8, were used for the reconstruction. These data demonstrate various stages of contrast enhancement that can be imaged with this high temporal resolution. Figure 7 shows reconstruction results for a single frame of a sub-volume, subtracted MIP in the coronal view for four different calibration schemes. Most calibration parameters were held constant (calibration segment size of 4 projections x 8 read points and 8 calibration partitions), while the number of calibration repetitions was set to 16, 8, 4, and 2. These correspond to a decreasing calibration acquisition time of 1.8 min, 0.9 min, 0.44 min, and 0.22 min, respectively. This figure shows the stability in the reconstruction quality despite the use of significantly less calibration data (and thus a much faster calibration acquisition time).

Figure 8 shows full volume subtracted MIP reconstructions from successive frames for the renal trMRA using TWIST (Figure 8 top row) and 3D through-time radial GRAPPA (Figure 8 bottom row), for the same subject. The depicted volumes were acquired at nearly identical time points after contrast injection. The spatial and nominal temporal resolutions of both datasets are identical (3.5 s/frame, 1.5×1.5×3mm³). The TWIST dataset has a temporal footprint of 17.5s, while the 3D through-time radial GRAPPA has a temporal footprint of 3.5s. Cropped and zoomed images from sub-volume MIP reconstructions centered on the renal arteries are shown in Figure 9. The maximally enhanced renal arteries seen at the peak of aortic enhancement in the through time radial GRAPPA exam are shown in the leftmost image. To the right of this image is the TWIST frame taken with near identical timing after contrast administration. Successive frames after this point as the peak of arterial enhancement is reached in the TWIST exam are shown in the next two images. The peak of aortic enhancement is reached in the third TWIST frame shown (rightmost image). The arrows in Figure 9 point to some problematic features of the TWIST exam. The straight solid arrows point to second and third order branches of the renal arteries that are not as clear visualized with TWIST. The curved arrows point to parenchymal enhancement, and the open arrows show locations of venous contamination.

DISCUSSION

In this study, simulations and in vivo experiments were performed to explore through-partition and through-time calibration for 3D through-time radial GRAPPA. Similar to the previously reported results for 2D imaging (40), through-time calibration can improve reconstruction results in 3D data. However, this alone is not the best way to allocate calibration time since different partitions and different time points do not provide equivalent information quality to the GRAPPA weight solution. In fact, our simulations and acquired data show that the lowest RMSE was reported for 8 partitions. At a higher number of partitions, the reconstruction error levels off, and even begins to increase. This is likely due to the low signal content in the outer regions of k-space; these outer partitions do not provide as much information as partitions closer to the center of k-space. At lower a number of partitions (≤2), the reconstruction error increases. This is most likely due to the fact that the central partition appears similar at different points in time (as it is simply the projection of the 3D volume, which appears similar despite motion), and adding additional repetitions of just the center partition do not provide significant new information for the calibration. By encoding more partitions, more different calibration data is available than when simply performing through-time calibration using one or two central partitions. As expected, increasing the calibration time reduces the overall error at all partition/repetition combinations. Additionally, these simulations describe results for two segment sizes for through-k-space calibration. As mentioned in the theory section and in previously published results for 2D reconstructions (40), there is a trade-off in segment size selection, and a large segment size can introduce inaccuracies in the GRAPPA weights. Therefore, both segment sizes were selected to be relatively small, and the 4×8 segment size has a lower RMSE, which is due to the larger number of kernel occurrences.

In summary, simulations show that multiple low spatial resolution partitions with as many calibration repetitions as can be performed within a given exam time offer the lowest RMSE for a given calibration time. For this particular simulation set-up, which was meant to mimic the in vivo renal trMRA acquisition, eight partitions resulted in the lowest RMSE. It is important to note that these recommendations are based on the kernel size, the acceleration factor, the coil array, and the object used in these simulations, and therefore may be different in other applications. However, an examination of the in vivo data reconstructed with different parameters shows good agreement of the results obtained from the simulations despite these differences.

In order to compare the 3D through-time radial GRAPPA reconstruction to existing non-Cartesian parallel imaging techniques, CG SENSE was also used to reconstruct this highly accelerated data. While both reconstructions show improved results over the undersampled data, the GRAPPA reconstruction produces fewer residual aliasing artifacts and lower noise than the CG SENSE reconstruction. It is hypothesized that this difference in image quality is due to potential mismatches between the coil sensitivity maps used and the actual undersampled images, which can lead to errors in the CG SENSE reconstruction that would not be found in the 3D through-time radial GRAPPA reconstructions. Thus, in such dynamic studies, the use of a technique that does not require coil sensitivity maps, such as through-time radial GRAPPA, may be beneficial. It is important to note that the regularization used in the CG SENSE reconstruction was not optimized in this study, and different regularization methods or parameters result in improved reconstructions.

The 3D through-time radial GRAPPA method was also compared to a trMRA that was acquired with a commercially available Cartesian TWIST acquisition. These images illustrate how the short temporal footprint of 3D through-time radial GRAPPA can lead to improved image quality. While the spatial and temporal resolutions of the two scans were nominally similar, the overall temporal footprint for the TWIST dataset is 17.5s, while that of the 3D through-time radial GRAPPA data set is 3.5 s. The absence of view-sharing and short temporal footprint in the radial GRAPPA examination reduces edge blurring. Edges and fine details in the second and third order branches of the renal arteries can be better visualized in the first frame of the 3D through-time radial GRAPPA images in comparison with the view-shared TWIST exam. The hepatic and splenic branches of the celiac artery are better depicted in the 3D through-time radial GRAPPA exam in the same frame. Similarly small branches of the superior mesenteric artery were better visualized in the 3D through-time radial GRAPPA exam. While a single optimal frame depicts the arterial enhancement for the 3D through-time radial GRAPPA exam, the small vessels difficult to see in the corresponding TWIST frame. Subsequent TWIST frames at peak aortic/arterial enhancement start to show parenchymal enhancement and venous enhancement, thus also precluding optimal evaluation of the small arteries.

As mentioned above, motion or changes in signal are expected to occur during the through-time calibration. This motion will provide different calibration data for repetitions of the same partition. If the motion experienced is correlated with the calibration acquisition time or the motion is minimal, this may potentially limit the amount of different calibration data provided by through-time calibration. A potential solution could be to randomize the partition encoding order and spacing, which may improve the uniqueness of the calibration data by randomizing the timing of each repetition of the same partition. While this was not likely (or experienced) in renal trMRA exams, it may be an additional calibration methodology to be considered in some applications such as cardiac imaging.

The primary drawback of this method is the additional scan time needed for GRAPPA weight calibration. However, it can be seen here that with a hybrid approach of combining through-k-space (within plane and through-partition) and through-time calibration, good reconstruction quality can be achieved at clinically acceptable scan times. Furthermore, the improvement in image quality of highly accelerated data may justify an increase in overall scan time for many applications, especially when the additional scans place no additional burden on a patient. A period of less than two minutes of free-breathing scan time is a minimal addition to the overall study, especially when this time is used to produce robust, high quality, high spatio-temporal resolution imaging for the contrast-enhanced exam. Additionally, when performing multiple scans with the same coverage but different contrast, the same calibration data can be employed, allowing for the acceleration of several different scans during a single examination. If a reduced calibration time is desired, the simulations show that for this application, only eight calibration partitions should be acquired with a reduced number of calibration repetitions. While this will increase the reconstruction error, our results demonstrate the robustness of the 3D through-time radial GRAPPA reconstruction when smaller amounts of calibration data are used. When calibration time decreased to below 15 seconds, image quality in these subtracted MIP images is affected by an increase in noise, but remains clinically acceptable.

This implementation of 3D through-time radial GRAPPA has been demonstrated with in-plane, radial undersampling and partial Fourier applied in the partition direction. Further acceleration could be explored in future works by implementing parallel imaging along the partition direction (48,49), applying a CAIPIRINHA-type acquisition where undersampling in each partition is rotated with respect to neighboring partitions (48), using an asymmetric field-of-view (50), or by using more efficient trajectories as was shown with 2D through-time spiral GRAPPA (39).

In conclusion, 3D through-time radial GRAPPA can be used to successfully reconstruct highly accelerated non-Cartesian data. In simulation, the hybrid calibration scheme with the lowest reconstruction error was found to be a moderate number of high signal central partitions combined with as many temporal repetitions as exam time permits. These findings were then applied by acquiring in vivo calibration data with eight partitions and 16–20 repetitions to reconstruct data with an in-plane acceleration factor as high as 12.6 with respect to Nyquist criterion in addition to partial Fourier along the partition direction to achieve a time-resolved, renal MRA with a temporal resolution of less than 4 s/frame and a spatial resolution of approximately 1.5 mm × 1.5 mm × 3 mm.