Genomic imprinting and the units of adaptation

Abstract

Two guiding principles identify which biological entities are able to evolve adaptations. Williams' principle holds that, in order for an entity to evolve adaptations, there must be selection between such entities. Maynard Smith's principle holds that, in order for an entity to evolve adaptations, selection within such entities must be absent or negligible. However, although the kinship theory of genomic imprinting suggests that parent-of-origin-specific gene expression evolves as a consequence of natural selection acting between—rather than within—individuals, it evades adaptive interpretation at the individual level and is instead viewed as an outcome of an intragenomic conflict of interest between an individual's genes. Here, I formalize the idea that natural selection drives intragenomic conflicts of interest between genes originating from different parents. Specifically, I establish mathematical links between the dynamics of natural selection and the idea of the gene as an intentional, inclusive-fitness-maximizing agent, and I clarify the role that information about parent of origin plays in mediating conflicts of interest between genes residing in the same genome. These results highlight that the suppression of divisive information may be as important as the suppression of lower levels of selection in maintaining the integrity of units of adaptation.

Is nayne in warld at scaithis ma do mar Than weile trastyt in borne familiar Hary, The Wallace

Introduction

Natural selection gives rise to biological adaptation: the appearance of design in the living world (Gardner, 2009). Usually, adaptive design is recognized at the level of the individual organism (Darwin, 1859), where it functions to maximize the individual's inclusive fitness (Hamilton, 1964). And, indeed, the individual-level adaptationist programme has been extraordinarily successful, for example, in the field of behavioural ecology (Davies et al., 2012). However, adaptation may also manifest at other levels of biological organization, giving rise to ideas of ‘selfish genes' (Hamilton, 1972; Dawkins, 1976, 1978; Burt and Trivers, 2006; Gardner and Welch, 2011) and ‘superorganisms' (Wheeler, 1911; Wilson and Sober, 1989; Gardner and Grafen, 2009; Hölldobler and Wilson, 2009).

Two guiding principles identify which biological entities are able to evolve adaptations, and under which circumstances. Williams' principle holds that, in order for an entity to evolve adaptations, there must be selection between such entities (Williams, 1966; Sober and Wilson, 2011; Gardner, 2013). For example, group-level adaptation requires the operation of selection between groups. Maynard Smith's principle holds that, in order for an entity to evolve adaptations, selection within such entities must be absent or negligible (Maynard Smith, 1987, 1988; Gardner, 2013). For example, group-level adaptation requires that within-group selection be abolished. Formal justification for both of these principles is provided by Gardner and Grafen (2009).

However, these guiding principles do not appear to provide a complete account of the units of adaptation. According to the kinship theory of genomic imprinting (Haig, 2002), parent-of-origin-specific gene expression evolves as a consequence of natural selection acting between—rather than within—organisms. Yet, it evades adaptive interpretation at the level of the individual organism, and is instead viewed as an outcome of intragenomic conflict between the individual's maternally and paternally derived genes. The kinship theory has been empirically successful, correctly predicting the direction of imprint for genes that are of medical importance (Haig, 2002; Burt and Trivers, 2006). However, the idea that selection operating on such genes acts according to a design objective of fitness maximization at the gene level, and not at the individual level, remains to be formalized.

Here, I formalize the idea that natural selection may drive intragenomic conflicts of interest between genes originating from different parents. Specifically, I establish mathematical links between the dynamics of natural selection, captured by Price's (1970, 1972) equation, and the idea of the gene as an inclusive-fitness-maximizing agent, captured by an optimization program (Gardner and Welch, 2011), in the context of a population in which half of all genes are maternal in origin and half are paternal in origin. I then consider whether genes residing in the same individual but differing in their parent of origin may also differ in their maximands, yielding scope for intragenomic conflict of interest. In particular, I investigate the importance of a gene having information about its parent of origin in mediating this conflict of interest. My goal for this analysis is not to offer strikingly novel insights about genomic imprinting, but rather to formalize existing ideas and to illuminate more general principles of Darwinian adaptation.

Genes as inclusive-fitness maximizers

Overview

This section of the paper is concerned with justifying the view that genes maximize their inclusive fitness, and clarifying the meaning of this quantity. I build upon the analysis of Gardner and Welch (2011), who considered a simple model in which all genes are equivalent aside from the alleles carried by themselves and by those with whom they interact socially (that is, absence of class structure) that disallowed parent-of-origin specific phenotypes. Here, I extend that model to consider that there are two classes of gene: those deriving from the individual's mother and those deriving from the individual's father. First, I describe a population model of genes, their phenotypes and their fitnesses. Second, I use this population model to derive a statement about the action of natural selection, within the framework of Price's equation. Third, I use the population model to formalize statements about genes as inclusive-fitness maximizers, within the framework of the optimization program. Fourth, I derive mathematical connections between dynamics and optimization to justify the view that genes maximize their inclusive fitness. This sets the stage for a formal analysis of intragenomic conflict in the next section of the paper.

Population model

I consider a very large, but finite, population of diploid, sexual, hermaphrodite individuals, each assigned a unique index i∈I. For ease of exposition, I consider unicellular individuals (although this is not strictly necessary, as the mathematical analysis does allow for undifferentiated unicells to be grouped into multicellular assemblages). For simplicity, I assume that individuals have only one genetic locus and, within each individual, I assign each of the two genes a class k∈K={m,p} according to whether it is maternal or paternal in origin (each individual having one maternally derived gene and one paternally derived gene at the locus of interest). Accordingly, every gene in the population is uniquely identifiable by its carrier's index i and its own class k. For simplicity, I assume discrete generations. In addition, for ease of exposition, I assume that generations are non-overlapping (although the mathematical analysis does allow for overlapping generations, with a gene's survival to the next generation being exactly equivalent to it producing an extra replica). For simplicity, I assume the total number of genes is the same in every generation.

Every gene is assigned an allelic type a∈A, according to its nucleic acid sequence. Thus, the allele associated with the class-k gene in individual i is denoted a_ik. Every allele is associated with a genic value, given by g=(a), where is the genotype function. Thus, the genic value associated with the class-k gene in individual i is denoted g_ik. The assignment of genic values to alleles is completely arbitrary. For example, g=1 might be assigned to a particular allele and g=0 to all the others, so that the population average genic value E(g) will represent the frequency of the allele in the population. Alternatively, the genic value might reflect the average effect of the allele with respect to a phenotype of interest (Fisher, 1941).

I will consider two versions of the population model. In the first version, phenotypes may be mediated by class as well as allele, so that every allele is associated with two (potentially, though not necessarily, different) phenotypes, one for when the gene is maternal in origin and one for when the gene is paternal in origin. Thus, the class-k phenotype is given by π_k=(a;k)∈P, where is the phenotype function and P is the set of possible phenotypes. Note that I have assumed that both maternally and paternally derived genes may adopt any phenotype from the same set, P. In addition, I assume that there is at least one allele that encodes any given pair of phenotypes (cf, Haig, 2000a). In the second version of the model, phenotypes are mediated only by allele and not by class. Thus, the class-k phenotype is given by π_k=(a)∈P. In both versions of the model, the phenotype associated with the class-k gene in individual i is denoted π_ik. All phenotypes are defined sufficiently proximately (for example, as a level of gene expression) that they may reasonably be considered under the sole control of a single gene.

Finally, a gene's fitness is given by the expected number of (mutated as well as non-mutated) replicas it leaves to the next generation. This expectation is taken over future uncertainty, which is not explicitly handled here (see Gardner and Welch, 2011 for details), and is jointly determined by a term 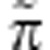that describes the phenotypic composition of the gene's social partners (including itself) and a term Π that describes the phenotypic composition of the entire population. The 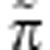term may vary from gene to gene, as different genes may have different social partners, but the Π term is common to all genes in any given generation. This allows a formal separation of social versus global frequency-dependence effects (Gardner and Welch, 2011). Specifically, fitness is given by w=(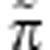;Π), where is the fitness function. Thus, the fitness of the class-k gene in individual i is denoted w_ik. I assume that, owing to fair meiosis, the expected fitness of a maternally derived gene is constrained to be equal to that of its paternally derived counterpart, that is, w_im=w_ip. This rules out the possibility of selection within individuals (for example, meiotic drive).

Dynamics of selection

Natural selection is defined as the population genetic change that is driven by systematic differences in individual fitness. This change may be captured using Price's (1970, 1972) equation:

In words, the change in the average genic value that is ascribable to natural selection (left hand side) is equal to the covariance of fitness and genic value, taken over all genes in the population (right hand side). The idea that personal fitness (also termed ‘neighbour-modulated fitness' Hamilton, 1964) is a crucial covariate of genic value in the Price equation has led to it being termed a ‘target of selection' (Grafen, 2002).

Importantly, I have not assumed that nonselective evolutionary change, owing to differences between parent and offspring genic values (that is, transmission effects), and/or deviations of realized fitness from its expected value (that is, random drift) are absent. Rather, I have simply set them aside as not of interest for the purpose of the present analysis. Briefly, this is because only selection—and not non-Darwinian factors such as mutation and random drift—is expected to give rise to a design rationale recognizable as biological adaptation. Gardner and Welch (2011) provide further details and discussion.

Maximization of inclusive fitness

I now turn from the dynamics of selection to the idea of the gene as a fitness-maximizing agent. This requires a stronger notion of fitness than simply ‘target of selection'. Specifically, although the gene's personal fitness functions as an adequate covariate in the dynamical Equation (1), it does not follow that genes will act to maximize this quantity. This is because they do not have sole control of their personal fitness, insofar as this is also mediated by their social partners. Put another way, correlations between genic value and personal fitness may arise for reasons other than direct causation, and those genes that are favoured by natural selection are not necessarily those that causally increase their personal fitness. What is needed is a reformulation of fitness that puts the focal gene in complete causal control. This is achieved by inclusive fitness (Hamilton, 1964; Gardner and Welch, 2011).

First, following the approach of Gardner and Welch (2011), I decompose a gene's personal fitness into baseline (B), additive (A) and non-additive (N) components:

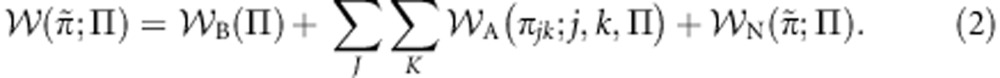Here, the quantity _A(π_jk;j,k,Π) is the additive contribution to a focal gene's personal fitness that is ascribed to the phenotype π_jk adopted by the class-k gene in its role-j social partner, in the context of a population with composition Π (Gardner and Welch, 2011). Note that the focal gene's own class does not appear in this calculation, as the personal fitness of a maternally derived gene is constrained to be the same as that of the paternally derived gene residing at the same locus in the same individual, and hence this quantity is independent of the gene's class.

Second, following the instructions of Hamilton (1964), I construct the gene's inclusive fitness by adding to baseline fitness the additive effects that the focal gene has upon the personal fitness of its social partners, weighting each increment or decrement by the appropriate coefficient of relatedness. This yields:

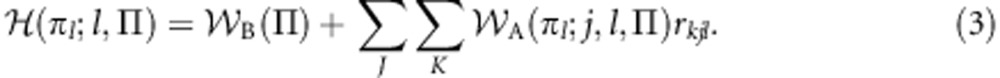where r_kjl is the genetic relatedness between a class-k recipient gene and the class-l gene acting in its role-j social partner, calculated from the perspective of the actor gene (Gardner and Welch, 2011).

Note that although I have defined inclusive fitness in terms of additive effects, I have not assumed that nonadditive fitness effects are absent from the model. Rather, they simply do not contribute to the computation of inclusive fitness. Later in this section, I will show that, despite this neglect of nonadditive effects, the inclusive fitness approach does provide a full account of the action of natural selection (see also Gardner and Welch, 2011). Also note that the maternally and paternally derived genes residing in the same individual are constrained to have the same fitness, and this is reflected in the absence of an argument k describing the recipient's class in the additive fitness effect _A.

Defining r_jl=½ r_mjl+½ r_pjl as the relatedness between a recipient gene of unknown class and the class-l gene acting in its role-j social partner, Equation (3) may be rewritten as:

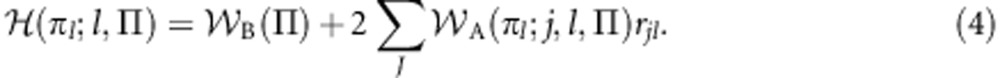That inclusive fitness is under the sole control of the focal gene is made explicit in the fact that it takes as its argument only that gene's phenotype (plus the gene's class and the population context shared in common with all genes; Gardner and Welch, 2011) and not the whole list of phenotypes expressed by the gene's social partners. Accordingly, it is logically possible to regard the gene as striving to maximize its inclusive fitness (although so far, I have provided no further justification for doing so). Indeed, the idea that a class-l gene employs its phenotype π_l∈P as a strategy in pursuit of the objective of inclusive-fitness maximization may be formally captured as an optimization program:

The optimization program (5) not only provides a formal statement of the idea that a gene strives to maximize its inclusive fitness, but also permits formal definitions of phenotypic optimality and suboptimality. Specifically, an optimal phenotype π_l* is one that maximizes the gene's inclusive fitness within the constraints imposed by the strategy set, that is, π_l*∈P: (π_l*l,Π)⩾(π_l;l,Π)∀π_l∈P. And a suboptimal phenotype π_l° is one that fails to maximize inclusive fitness within the constraints imposed by the strategy set, that is, π_l°∈P:∃π∈P: (πl,Π)>(π_l°l,Π).

The inclusive fitness function (4) and corresponding optimization program (5) are appropriate if the focal gene knows its own class, and this is reflected in the presence of an argument l describing its class in the inclusive fitness function . However, if the gene is ignorant of its own class, then the appropriate inclusive fitness will be given by:

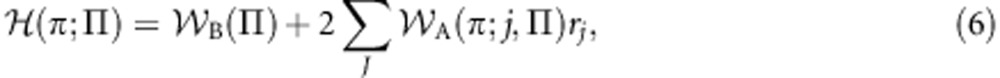where r_j=½ r_jm+½ r_jp is the relatedness between a recipient gene of unknown class and an actor gene of unknown class in its role-j social partner. The corresponding idea that the gene employs its phenotype π∈P as a strategy in pursuit of the objective of inclusive-fitness maximization may also be formally captured as an optimization program:

Again, the optimization program (7) permits formal definitions of phenotypic optimality and suboptimality: an optimal phenotype π* is one that maximizes inclusive fitness within the constraints imposed by the strategy set, that is, π*∈P: (π*Π)⩾(πΠ)∀π∈P; and a suboptimal phenotype π° is one that fails to maximize inclusive fitness within the constraints imposed by the strategy set, that is, π°∈P:∃π∈P: (πΠ)>(π°Π). More generally, the distinction between optimization programs (5) and (7) formally captures the idea that a gene's intention may depend on the information that it has at its disposal (in this case, concerning its parent of origin).

Inclusive fitness as target of selection and maximand

I derived an expression (1) for the dynamics of natural selection, in which personal fitness is given as a target of selection. I then showed that inclusive fitness, rather than personal fitness, is logically of the correct form to be considered a maximand of an intentional gene. I now show that inclusive fitness also functions as a target of selection, and I derive mathematical connections between the dynamics of selection and the maximization of inclusive fitness to provide formal justification for the idea that natural selection acts according to a design objective of inclusive-fitness maximization at the gene level.

Considering the version of the population model in which a gene's phenotype is determined both by its allele and its class, I am able to derive a link between the dynamical Equation (1) and the optimization program (5), such that the target of selection is the inclusive-fitness maximand appropriate for when the gene is privy to information about its parent of origin:

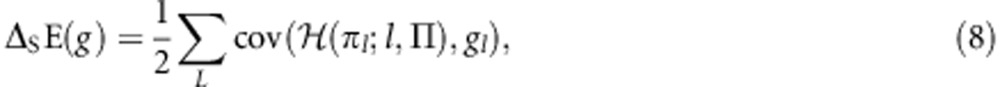(see Appendix for derivation). More generally, I derive six mathematical correspondences between the dynamical Equation (1) and the optimization program (5), equivalent to those derived by Gardner and Welch (2011) for a nonclass-structured population (Table 1; derivations in Appendix). These correspondences provide formal justification for the idea that natural selection acts according to a design objective of inclusive-fitness maximization at the gene level, and specifically for the idea that a gene's intentions may depend on its parent of origin when it has the option of employing different phenotypes according to whether it is of maternal or paternal origin.

Table 1. Correspondences between dynamical and purposeful accounts of gene-level adaptation.

Numeral	Correspondence
I	If all agents are optimal, there is no scope for selection (no expected change in the average of any genic value)
II	If all agents are optimal, there is no potential for positive selection (no introduced allele can increase from rarity due to selection)
III	If all agents are suboptimal, but equally so, there is no scope for selection
IV	If all agents are suboptimal, but equally so, there is potential for positive selection (there exists an allele that, if introduced, can increase from rarity due to selection)
V	If agents vary in their optimality, there is scope for selection, and change in the average of all genic values is given by their average within-class covariance with attained maximand
VI	If there is neither scope for selection nor potential for positive selection, all agents are optimal

Formal justification for the ‘gene as fitness-maximizing agent' view rests upon the ability to translate this way of thinking into formal population genetics, and vice versa. Derivations are provided in Appendix.

Considering the version of the population model in which a gene's phenotype is determined solely by its allele and is not mediated by its class, I am able to derive a link between the dynamical Equation (1) and the optimization program (7), such that the target of selection is the inclusive-fitness maximand appropriate for when the gene is ignorant of its parent of origin:

(see Appendix for derivation). More generally, I derive six mathematical correspondences between the dynamical Equation (1) and the optimization program (5), equivalent to those described above and by Gardner and Welch (2011) for a nonclass-structured population (Table 1; derivations in Appendix). These correspondences provide formal justification for the idea that natural selection acts according to a design objective of inclusive-fitness maximization at the gene level, and specifically for the idea that a gene's intentions do not depend on its parent of origin when it does not have the option of employing different phenotypes according to whether it is of maternal or paternal origin.

Intragenomic conflict

In the previous section, I provided formal justification for the idea that genes maximize their inclusive fitness in the context of a population structured into genes of maternal origin and genes of paternal origin. Moreover, I showed that if a gene's phenotype may be mediated by its parent of origin and not only by its allele, then the gene's inclusive-fitness agenda will be such that it appears to have information about its parent of origin. Having formalized the intentionality of genes, I now consider how their agendas give rise to intragenomic conflicts of interest.

First, I consider the scenario where a gene's phenotype is not mediated by its parent of origin, but determined solely by its allele. Accordingly, genes optimize as if they are ignorant as to their parent of origin, that is, according to optimization program (7). That is, they strive to maximize the inclusive fitness function (6). How does this inclusive fitness function differ for different genes? If the two genes are in two different individuals, then they potentially interact with different social partners when acting within any particular role, j. Importantly, they may share individual social partners (including each other), but as they interact with them in potentially different roles (different j's), they are liable to value these same social partners with different coefficients of relatedness (different r_j's)—and this gives potential for a conflict of interests. However, if the two genes are in the same individual—specifically, the maternally and the paternally derived gene at the locus of interest—then they interact with exactly the same set of social partners, and always in the same roles (same j), and hence they will always value these social partners with the same coefficients of relatedness (same r_j's)—and this yields no potential for a conflict of interests.

Second, I consider the scenario where a gene's phenotype is mediated by its parent of origin as well as its allele. Accordingly, genes optimize as if they are privy to information about their parent of origin, that is, according to optimization program (5). That is, they strive to maximize the inclusive fitness function (4). How does this inclusive fitness function differ for different genes? If the two genes are in two different individuals, then—once again—they potentially interact with the same social partners but in the context of different roles, j, and this gives potential for a conflict of interests. However, if the two genes are in the same individual—specifically, the maternally and the paternally derived genes at the locus of interest—then, although they interact with exactly the same set of social partners and always in the same roles (same j), they need not always value these same social partners with the same coefficients of relatedness, because relatedness also depends on the gene's class, and this is different for genes of maternal versus paternal origin (different r_jl's, that is, r_jm versus r_jp). Accordingly, if individuals may be differentially related to their social partners via their two parents, then their maternally derived genes may disagree with their paternally derived genes about the valuation of those social partners, leading to intragenomic conflicts of interest.

The formal separation of selective dynamics from inclusive-fitness agenda also helps to clarify the distinction between the conflict of interest between an individual's maternally paternally derived genes versus what has been termed ‘parental antagonism' (Haig, 1997). A parentally antagonistic allele is one that enjoys a selective advantage when inherited via one parent and suffers a selective disadvantage when inherited via the other parent; a scenario that is captured in the dynamical Equation (8) whenever the covariance of relative fitness and the genic value associated with this allele is positive among genes originating from one parent, and negative among genes originating from the other parent. The resulting interference in the overall genetic change is properly viewed as a constraint to adaptation rather than a true intragenomic conflict. The very existence of alleles with parent-of-origin-specific expression means that it is possible for there to be intragenomic conflict between maternally and paternally derived genes (that is, different inclusive fitness agendas) without there being parental antagonism (that is, selection covariance of each class having opposite sign). In addition, one may imagine scenarios in which there would be parental antagonism without intragenomic conflict; for example, if there were a cooperative division of labour between the maternally and paternally derived genomes, with certain alleles being good at fulfilling the adaptive role of one class but not the other.

Discussion

Application of Williams' and Maynard Smith's principles of adaptation suggests that any biological entity may evolve adaptations so long as there is selection between, and not within, such entities. However, parent-of-origin-specific gene expression poses a problem for this simplistic view of adaptation. The kinship of genomic imprinting suggests that such a pattern of gene expression is not optimized according to the interests of the individual, despite being driven by selection acting between rather than within individuals, and must instead be interpreted as a gene-level adaptation. Here, I have provided formal support for the suggestion that natural selection acting between individuals may drive intragenomic conflicts of interest between genes that differ in their parent of origin. I have explicitly connected an optimization program that formally captures the idea of the gene as an inclusive-fitness maximizer with Price's equation of selection dynamics, and shown that information about parent of origin may lead different genes in the same individual to have different social agendas—owing to their differential valuation of maternal versus paternal relations—despite the absence of selection within the individual. This understanding about the source of intragenomic conflicts between genes with different parent of origin is, of course, not new (Haig, 2000a provides an excellent overview). However, the present analysis is the first to explicitly examine the divergent agendas of maternally versus paternally derived genes that formally emerge from the dynamics of natural selection.

Limitations of the model

For the purpose of simplicity and clarity, my analysis has been deliberately limited in a number of respects. First, my focus has been on uncovering the existence of conflicts of interest between genes and not the details of the resolution of this conflict. Accordingly, I have investigated how genes with different parents of origin may prefer to adopt divergent phenotypes in pursuit of the maximization of their inclusive fitness, which is a prerequisite for genomic imprinting, without considering the interplay of potentially multiple genes—including imprinters as well as imprinteds (Burt and Trivers, 1998; Haig, 2000a)—that is required to actually bring about parent-of-origin differences in gene expression levels. Second, in order to avoid class structure beyond the designation of genes as maternal versus paternal in origin, I have assumed a population of hermaphrodites. Separation of sexes would require four classes of genes, designated according to their carrier's sex as well as parent of origin (cf, Haig, 1997). This simplification rules out some of the demographic factors that have been suggested to drive the evolution of genomic imprinting. For example, sex-biased dispersal provides a means of making an individual more related to her neighbours through her parent of the less-dispersing sex (Haig, 2000b; Úbeda and Gardner, 2010, 2011, 2012; Úbeda et al., 2014). However, a difference in the dispersal rates of female versus male gametes in hermaphrodite broadcast spawners could yield a similar result.

Tokens versus types

I have followed the approach of Gardner and Welch (2011) in identifying the genic agent as a scrap of nucleic acid (that is, a physical object or ‘token') rather than as an allelic variant (that is, an abstract category or ‘type'). Genes are often described as being ‘selfish' (Dawkins, 1976), but genic tokens, as maximizers of inclusive fitness, may equally be altruistic or spiteful. There is a sense in which allelic types may be informally considered as ‘selfish', in that the alleles that are evolutionarily successful are (trivially) those that increase their representation in the population. However, this is true of alleles that predominate by mutation pressure or random drift, and not just by natural selection, so this idea of the selfish allele has a distinctly non-Darwinian flavour. Moreover, it is tokens rather than types that directly manifest adaptation, as they are real-world objects rather than residents of a Platonic realm of abstractions. Furthermore, the idea that an “offspring's paternally derived genes have different interests from the offspring's maternally derived genes” (Haig, 2002) can only make sense if genes are tokens rather than types, because it is the genic tokens rather than the allelic types that have parents of origin. In any case, if the allele-as-maximizing-agent analogy can be mathematically formalized, this remains to be done.

Haig (2012) suggests that this genic token approach may only be valid owing to the artificial assumption of no class structure in the model of Gardner and Welch (2011) that “collapses everything a gene might do into a single token that can be considered the recipient of its own effects” (Haig, 2012). This is incorrect, and here I have shown that the approach extends to a model in which genes are separated into nonequivalent maternal-origin versus paternal-origin classes. As an alternative, Haig (2012) suggests that the ‘strategic gene' is better viewed as a collective of identical-by-descent tokens. This has some validity if we consider a collective that is guaranteed to be identical by descent, according to the information that is available to every member of the collective; for example, all the maternally derived genes residing at a particular locus within the body of an individual organism. Indeed, the formal justification for the view that a genetically uniform collective may be viewed as an adaptive agent is provided by Gardner and Grafen (2009).

However, Haig (2012) intends the strategic gene to encompass all the identical-by-descent copies in all the focal individual's social partners (which collapses everything a gene might do into a single token that can be considered the recipient of its own effects). This is problematic, because a focal genic token does not necessarily know which other genic tokens are identical by descent. Rather, from the perspective of any given gene, there will generally be a wide collection of genic social partners to which it has a nonzero probability of identity by descent. Consequently, the genes in this diffuse cloud will not be selectively favoured to consider each other as ‘self', but rather to value each other according to their probability of identity by descent—just as individual organisms who engage in social interaction with nonidentical relatives do not consider them as ‘self' but rather value them according to probabilities of sharing alleles in common (Hamilton, 1964; Grafen, 2006). Moreover, Haig's notion of the strategic gene is also incompatible with describing a gene as being maternal or paternal in origin as, within any collective of identical-by-descent tokens stretching across multiple individuals, different tokens are liable to have different parents of origin.

Principles of adaptation

More generally, the present analysis clarifies that, as a general principle of adaptation, the suppression of divisive information may be just as important as the suppression of lower levels of selection (Maynard Smith's principle) in sustaining the integrity of a unit of adaptation (Bourke, 2011; Gardner, 2013). This principle was overlooked in the analysis of Gardner and Grafen (2009) that examined conditions under which social groups may be considered adaptive units in their own right, owing to their crucial assumption that all social interaction takes place within and not between social groups. Thus, in the ‘repression of competition' model of Gardner and Grafen (2009), in which group mates are genetically heterogeneous but constrained to have the same expected fitness (for example, genes in a genome under fair meiosis; Leigh, 1977), the only way for the lower-level units to increase their inclusive fitness is to increase the fitness of their social group. However, if social interactions also extend between groups, then inclusive fitness may be increased at the expense of one's group if it provides benefits to one's relatives in other groups—who might not be relatives of one's group mates. This highlights that altruistic behaviour, although often conceived as a step along the road to a major transition in individuality, may actually reignite conflicts of interest between lower-level units that erode the integrity of existing units of adaptation (Gardner, 2013).

These insights also clarify the error in the application of William's principle by Sober and Wilson (2011) that led them to conclude that individuals in clonal groups are not units of adaptation on the basis that there is no selection at the individual level in such scenarios. The same reasoning would suggest that imprinted genes are not adaptive agents, and that the adaptive rationale for genomic imprinting must be sought at the individual level, because there is no selection at the gene level—a suggestion that the present analysis has formally refuted. Sober and Wilson's (2011) error is to confuse ‘individual selection' with ‘within-group selection' (and, accordingly, ‘gene selection' with ‘within-individual selection'), so that the absence of within-group selection in the context of clonal groups appears to preclude adaptation at the individual level. However, the formal analysis of Gardner and Grafen (2009) clarifies that the proper notion of ‘individual selection' is selection among all the individuals in the population, and not just those within a particular group. Consequently, there is selection between individuals even in populations with clonal groups, because an individual in one group may be genetically distinct (and fitter) than an individual in a different group (Gardner, 2014). Thus, it is possible to simultaneously view the group and the individual as units of adaptation, just as a honeybee retains her adaptive, inclusive-fitness-maximizing integrity even though her colony may qualify as a superorganism in its own right. Moreover, this clarifies the importance of mathematical (rather than just verbal) theories of adaptation (contra Sober and Wilson, 2011), as words are slippery and may confuse more than they clarify.

Appendix

Phenotype mediated by allele and class

Noting that g=½∑_Lg_l, the action of natural selection can be written as:

Substituting Equation (2) into Equation (A1) obtains:

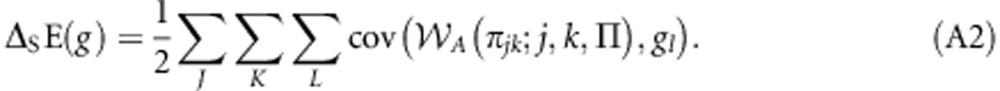Using the fact that cov(x,y)=β(y,x)cov(x,x), where β(y,x) is the least-squares linear regression of y against x, Equation (A2) can be rewritten as:

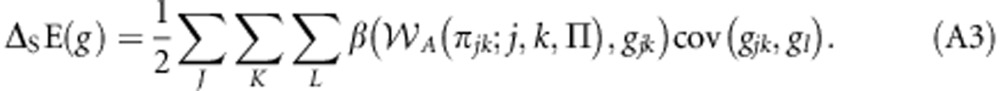Noting that K=L={m,p}, Equation (A3) can be rewritten as:

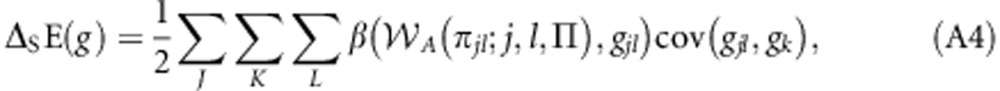or:

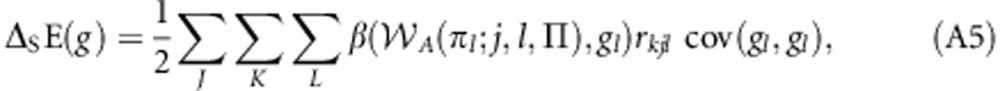where r_kjl=cov(g_k,g_jl)/cov(g_l,g_l). Finally, some rearrangement gives:

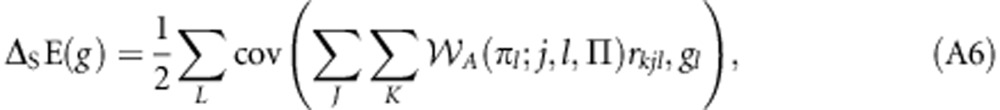which is equivalent to Equation (8) of the main text. This result allows the derivation of the following correspondences:

I. If all agents are optimal, there is no scope for selection

If all agents behave optimally according to optimization program (5), then (π_l;l,Π)=(π_l*l,Π)∀i∈I and ∀l∈L. Hence, from Equation (8), the action of selection is Δ_SE(g)=(1/2)∑_Lcov((π_l;l,Π),g_l)=(1/2)∑_Lcov((π_l*l,Π),g_l)=0.

II. If all agents are optimal, there is no potential for positive selection

Choose a population composition in the vicinity of Π such that a new allele a′∈A is present at vanishingly low frequency and with negligible impact upon the genetic relatedness of social partners. Carriers of the allele a′ have phenotype π_l′=(a′;l), according to their class; and all other genes, being optimal according to optimization program (5), have phenotype π_m* or π_p*, according to their class. Assigning carriers of allele a′ a genic value g=1 and carriers of all other alleles a genic value g=0 then, from Equation (8), the action of selection is Δ_SE(g)=(1/2)∑_Lcov((π_l;l,Π),g_l)=(1/2)∑_LE(g_l)(1−E(g_l)) ((π_l′l,Π)−(π_l*l,Π)). As (π_l′l,Π)⩽(π_l*l,Π) for all π′∈P, then Δ_SE(g)⩽0.

III. If all agents are suboptimal, but equally so, there is no scope for selection

If all agents behave suboptimally but equally so according to optimization program (5), then (π_l;l,Π)=(π_l°l,Π)∀i∈I and ∀l∈L. Hence, from Equation (8), the action of selection is Δ_SE(g)=(1/2)∑_Lcov((π_l°l,Π),g_l)=(1/2)∑_Lcov((π_il;l,Π),g_l)=0.

IV. If all agents are suboptimal, but equally so, there is potential for positive selection

Choose a population composition in the vicinity of Π such that the allele a* corresponding to the optimal pair of phenotypes π_m* and π_p*, according to optimization program (5), is present at vanishingly low frequency and with negligible impact upon the genetic relatedness of social partners. All other genes, being suboptimal according to optimization program (5), have phenotypes π_m° or π_p°, according to their class. Assigning carriers of the allele a* a genic value g=1 and carriers of the other alleles a genic value g=0 then, from Equation (8), the action of selection is Δ_SE(g)=(1/2)∑_Lcov((π_l;l,Π),g_l)=(1/2)∑_LE(g_l)(1−E(g_l)) ((π_l*l,Π)−H(π_l°l,Π)). As (π_l*l,Π)>(π_l°l,Π), then Δ_SE(g)>0.

V. If agents vary in their optimality, there is scope for selection, and the change in the average of all genic values is given by their average within-class covariance with attained maximand

From Equation (8), Δ_SE(g)=(1/2)∑_L cov((π_l;l,Π),g_l).

VI. If there is neither scope for selection nor potential for positive selection, all agents are optimal

If all agents are optimal, there is neither scope for selection (I) nor potential for positive selection (II); if all agents are suboptimal but equally so, then there is no scope for selection (III) but there is potential for positive selection (IV); and if agents vary in their optimality, there is scope for selection (V). These exhaust the possibilities in the optimization view; hence, if there is neither scope for selection nor potential for positive selection, all agents must be optimal.

Phenotype mediated by allele but not class

Substituting Equation (2) into Equation (1) obtains:

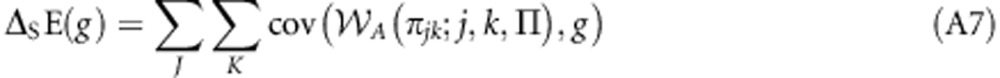which, as _A(π_jk;j,k,Π)=_A(π_j;j,Π) for all k∈K, is equivalent to:

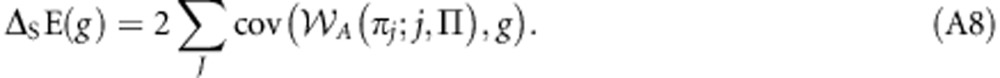This may be written as:

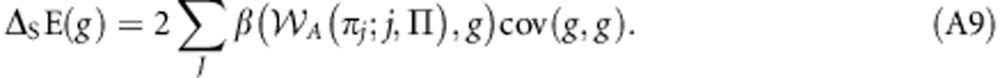Note that β(_A(π_j;j,Π),g)=β(_A(π_j;j,Π),g_j) × β(g_j,g), β(_A(π_j;j,Π),g_j)=β(_A(πj,Π),g) and β(g_j,g)=r_j. Making these substitutions yields:

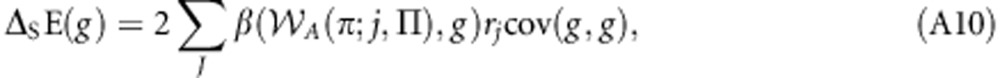which may be written as:

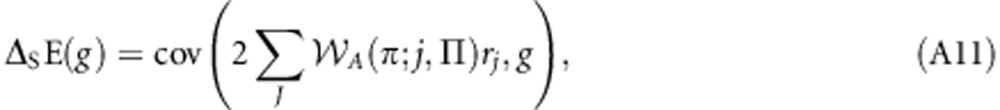which is equal to Equation (9) of the main text. This result allows the derivation of the following correspondences:

I. If all agents are optimal, there is no scope for selection

If all agents behave optimally according to optimization program (7), then (πΠ)=(π*Π)∀i∈I. Hence, from Equation (9), the action of selection is Δ_SE(g)=cov((πΠ),g)=cov((π*Π),g)=0.

II. If all agents are optimal, there is no potential for positive selection

Choose a population composition in the vicinity of Π such that a new allele a′∈A is present at vanishingly low frequency and with negligible impact upon the genetic relatedness of social partners. Carriers of the allele a′ have phenotype π′=(a′) and all other genes, being optimal according to optimization program (7), have phenotype π*. Assigning carriers of allele a′ a genic value g=1 and carriers of all other alleles a genic value g=0 then, from Equation (9), the action of selection is Δ_SE(g)=cov((πΠ),g)=E(g)(1−E(g)) ((π′Π)−(π*Π)). As (π′Π)⩽(π*Π) for all π′∈P, then Δ_SE(g)⩽0.

III. If all agents are suboptimal, but equally so, there is no scope for selection

If all agents behave suboptimally but equally so according to optimization program (7), then (πΠ)=(π°Π)∀i∈I. Hence, from Equation (9), the action of selection is Δ_SE(g)=cov((π°Π),g)=cov((πΠ),g)=0.

IV. If all agents are suboptimal, but equally so, there is potential for positive selection

Choose a population composition in the vicinity of Π such that the allele a* corresponding to the optimal phenotypes π*, according to optimization program (7), is present at vanishingly low frequency and with negligible impact upon the genetic relatedness of social partners. All other genes, being suboptimal according to optimization program (7), have phenotype π°. Assigning carriers of the allele a* a genic value g=1 and carriers of the other alleles a genic value g=0 then, from Equation (9), the action of selection is Δ_SE(g)=cov((πΠ),g)=E(g)(1−E(g)) ((π*Π)−(π°Π)). As (π*Π)>(π°Π), then Δ_SE(g)>0.

V. If agents vary in their optimality, there is scope for selection, and the change in the average of all genic values is given by their average within-class covariance with attained maximand

From Equation (9), Δ_SE(g)=cov((πΠ),g). Note that as there is effectively only one class of genes here—that is, genes that are unaware of their parent of origin—then the average within-class covariance is equal to the total covariance within that single class.

VI. If there is neither scope for selection nor potential for positive selection, all agents are optimal

If all agents are optimal, there is neither scope for selection (I) nor potential for positive selection (II); if all agents are suboptimal but equally so, then there is no scope for selection (III) but there is potential for positive selection (IV); and if agents vary in their optimality, there is scope for selection (V). These exhaust the possibilities in the optimization view; hence, if there is neither scope for selection nor potential for positive selection, all agents must be optimal.

The author declares no conflict of interest.