Moving Beyond the Hazard Ratio in Quantifying the Between-Group Difference in Survival Analysis

Abstract

In a longitudinal clinical study to compare two groups, the primary end point is often the time to a specific event (eg, disease progression, death). The hazard ratio estimate is routinely used to empirically quantify the between-group difference under the assumption that the ratio of the two hazard functions is approximately constant over time. When this assumption is plausible, such a ratio estimate may capture the relative difference between two survival curves. However, the clinical meaning of such a ratio estimate is difficult, if not impossible, to interpret when the underlying proportional hazards assumption is violated (ie, the hazard ratio is not constant over time). Although this issue has been studied extensively and various alternatives to the hazard ratio estimator have been discussed in the statistical literature, such crucial information does not seem to have reached the broader community of health science researchers. In this article, we summarize several critical concerns regarding this conventional practice and discuss various well-known alternatives for quantifying the underlying differences between groups with respect to a time-to-event end point. The data from three recent cancer clinical trials, which reflect a variety of scenarios, are used throughout to illustrate our discussions. When there is not sufficient information about the profile of the between-group difference at the design stage of the study, we encourage practitioners to consider a prespecified, clinically meaningful, model-free measure for quantifying the difference and to use robust estimation procedures to draw primary inferences.

INTRODUCTION

To quantify the burden or progression of disease via the occurrence of a specific clinical event relating to morbidity or mortality, the time to the event for each study patient is frequently used as a primary end point for a clinical study. The underlying survival or hazard function provides a profile for the temporal behavior of the event times.^1,2 At any specific time point, the value of the survival function is simply the probability of a patient remaining event free. The corresponding hazard function is approximately the ratio of the probability that an event-free patient would experience the event in the next small time period to the length of such a time span (eg, a month). Unlike the survival function, the absolute values of the hazard function may be difficult to interpret clinically.

When comparing two groups, a common practice is to make the assumption that the ratio of the two hazard functions is constant over time and to use such a constant ratio as a parameter to quantify the between-group difference. The Cox procedure is then used to estimate this unknown constant hazard ratio parameter.³ In fact, CONSORT guidelines⁴ and the Cochrane handbook⁵ advise reporting a hazard ratio estimate to quantify the group difference. When the proportional hazards (PH) assumption is plausible, this parameter would partially capture the relative difference between two survival curves but is not entirely satisfactory. This is because this summary ratio, without appropriate background information about the absolute hazard, lacks the context to allow study investigators to translate the hazard ratio into a more transparent clinical benefit, such as the prolonged survival time. Moreover, like the relative risk (or odds) ratio for a binary outcome, the precision of the hazard ratio estimator depends primarily on the observed number of events, not the sample size or duration of the study. When the event rates are low for both groups, as is common in the safety evaluation of drugs and devices, the resulting CI for the hazard ratio estimate can be quite large, ostensibly suggesting that there is not enough information to properly assess the between-group difference. However, when the two groups are identical and the study has a large number of patients and a long follow-up time, such a conclusion can be misleading. The patients' exposure times, if properly used, also provide valuable information for evaluating the between-group difference, especially for an equivalence or noninferiority study. Alternative approaches discussed in this article may be more appropriate for handling this situation.

When the PH assumption is violated (ie, the true hazard ratio is changing over time), the parameter actually being estimated by the Cox procedure may not be a meaningful measure of the between-group difference; it is not, for example, simply an average of the true hazard ratio over time.⁶ Furthermore, this parameter generally depends on the study-specific follow-up times. As a result, two studies enrolling patients from the same population could produce different hazard ratio estimates, no matter how large the sample sizes may be, because of the choice of follow-up time used in each study. Furthermore, because of misspecification of how the difference between groups varies over time, the PH estimation procedure may not be able to effectively detect a true difference between groups. These undesirable features^6–9 render the PH estimation procedure a nonrobust measure of the difference between two survival curves.

Note that for any comparison of two survival curves, there is no single metric or parameter that can capture the entire profile of their difference. However, a population summary measure for the between-group difference is crucial for the purposes of study design and planning as well as for the overall evaluation of a particular intervention. In this article, we present several well-known alternative, model-free summary measures. A model-free measure for the group difference does not rely on a specific assumption to generate each of the survival functions or to express the contrast between the two survival curves. When there is not sufficient information about the profile of the between-group difference at the design stage of the study, we encourage practitioners to consider a prespecified, clinically meaningful, model-free measure for quantifying the difference and to use robust estimation procedures to draw primary inferences. The survival data from three recent cancer clinical trials representing different scenarios are used to illustrate the issues previously described as well as various model-free alternative approaches. The computer code (surv2sampleComp) for implementing the estimation procedures discussed in this article is available from the CRAN (http://cran.r-project.org).

EXAMPLES FROM CANCER CLINICAL TRIALS WITH SURVIVAL TIME END POINT

The first example is from a recent study conducted by the Eastern Cooperative Oncology Group (ECOG) for comparing two groups of patients treated by low- and high-dose dexamethasone for newly diagnosed multiple myeloma.¹⁰ For this trial, there were 445 enrolled patients: 222 were assigned to the low-dose and 223 to the high-dose group. Figure 1A shows the Kaplan-Meier (KM) curves of overall survival based on the data collected by November 2008.¹⁰ The survival curve for the low-dose group (blue) is always above the one for the high-dose group (gold), except at the end of the follow-up. With such a differential pattern of survival, the patients in the low-dose group visually appear to survive longer than those in the high-dose group. The hazard ratio (low dose over high dose) estimate is 0.87 (95% CI, 0.60 to 1.27) with a P value of .47. The wide CI suggests that either there is not enough information to assess the between-group difference or that the constant hazard ratio assumption cannot adequately describe the difference.

Fig 1.

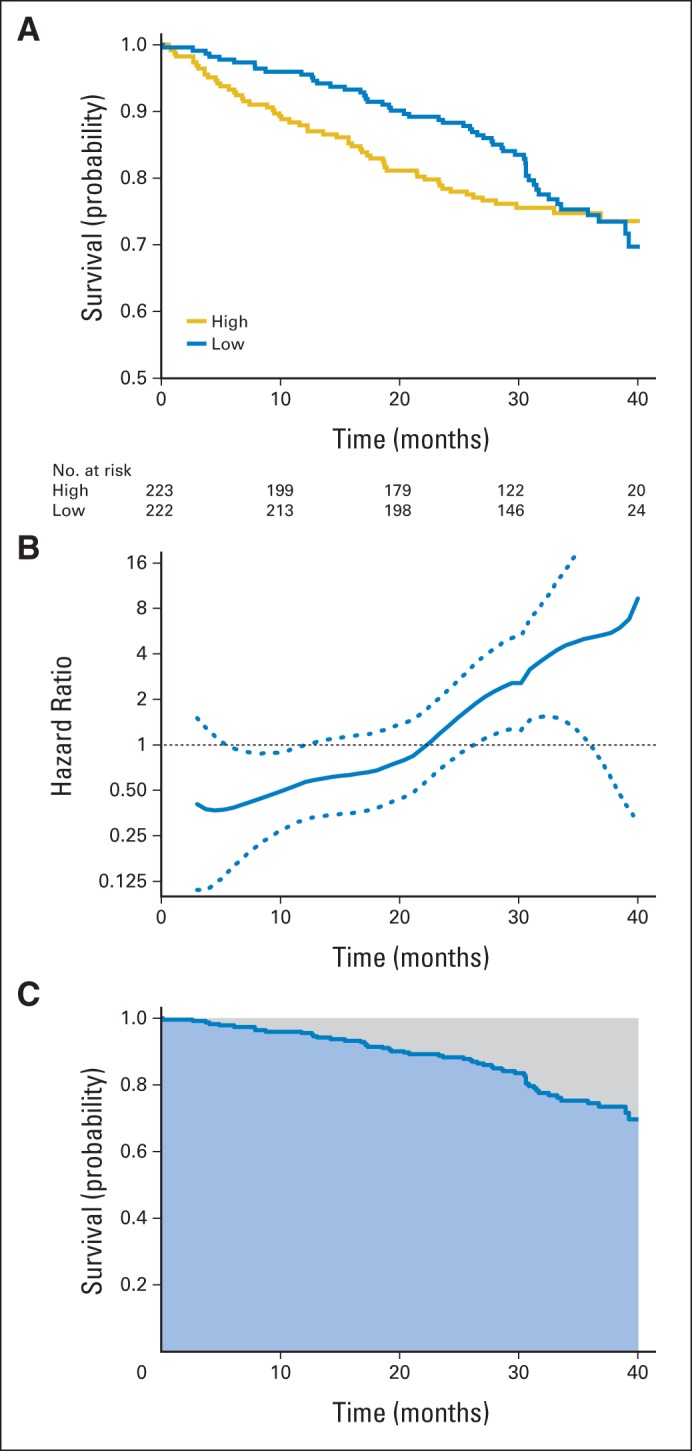
Estimated survival curves, hazard ratio, and restricted mean survival times with data from the Eastern Cooperative Oncology Group E4A03 study. (A) Kaplan-Meier curves for low-dose (blue) and high-dose (gold) groups. (B) Estimate of the ratio of hazard functions (low dose over high dose) over time and corresponding 0.95 point-wise confidence band. (C) Estimate of restricted mean survival time (blue area) and the restricted mean time lost (gray area) up to 40 months for the low-dose group.

To explore the data further, Figure 1B shows a nonparametric estimate of the hazard ratio (low dose over high dose) as a function of time with 95% confidence band,¹¹ indicating that the hazard rate is initially lower in the low-dose group than in the high-dose group, with the ratio gradually increasing over time. The hazard ratio curve crosses one in the middle of the study, suggesting that there is a qualitative interaction between the hazard ratio and time. Note that the overall hazard ratio estimate of 0.87 does not mean that the hazard rate of the patients in the low-dose group is reduced by 13% uniformly throughout the study. Such an empirical summary of the group difference can be misleading in this case.

In practice, it can be rather difficult to justify the validity of a model such as the PH model. For instance, a conventional approach to examining the adequacy of the PH assumption is based on lack-of-fit tests.^12–14 However, such tests would generally not provide much comfort for the assessment of model adequacy, because they may not have adequate power to detect model misspecifications with small or moderate numbers of observed events in the study. Conversely, for a study with a large number of events, it is likely that one would reject a PH model, even with only minor departures from true proportionality. For this cancer example, the PH assumption appears to be invalid on visual inspection. This is supported by the standard lack-of-fit tests for the PH model based on Schoenfeld residuals¹² and cumulative martingale residuals.¹⁴ The resulting P values are .002 and .001, respectively. Now, in such circumstances in which the PH assumption is violated, the question is what other measures could be used to summarize the difference between two groups.

For the second example, we used the data from a study published in the Journal of Clinical Oncology (JCO)¹⁵ with a seemingly quantitative interaction between the hazard ratio and time in contrast to the qualitative interaction observed in the ECOG trial. This study was a randomized trial to compare the overall survival time distributions between single-agent pemetrexed (P) and the combination of carboplatin and pemetrexed (CP) in patients with advanced non–small-cell lung cancer with an ECOG performance status of 2. The trial enrolled 205 eligible patients who were observed for a median of 27.5 months. The median survival times of the CP arm and the P arm were 9.3 and 5.3 months, respectively, and the hazard ratio was 0.62 (95% CI, 0.46 to 0.83; P = .001).¹⁵ Note that the individual survival time observations from the study are not available to the public. For illustration purposes, we use the algorithm proposed by Guyot et al¹⁶ to reconstruct the individual-level survival times from the information presented in the article.¹⁵ Specifically, the software DigitizeIt was used to scan the KM curves. The scanned data and the numbers of patients at risk for various time points were used with the algorithm. With such reconstructed survival times, the resulting KM curves are reported in Figure 2A, which appear to be identical with their counterparts presented in the article. Moreover, with the reconstructed data, the hazard ratio and the corresponding 95% CI estimates are 0.63 (95% CI, 0.47 to 0.84), which are practically identical to those published in Zukin et al.¹⁵ Figure 2B provides the nonparametrically estimated hazard ratio (CP over P). The hazard ratio varies over time, visually in favor of CP early in the study but then approaching one at the end of the study. It is interesting to note that the P value for testing the adequacy of the PH assumption is .43 on the basis of the Scheofeld residuals. This is a typical case in which a global lack-of-fit test is not informative. Because it is not clear that the PH assumption is valid, the reported 37% hazard reduction may be difficult to interpret. The assessment of the treatment effect based on the estimated hazard ratio is further complicated by the lack of absolute hazard experienced in the P arm as a reference.

Fig 2.

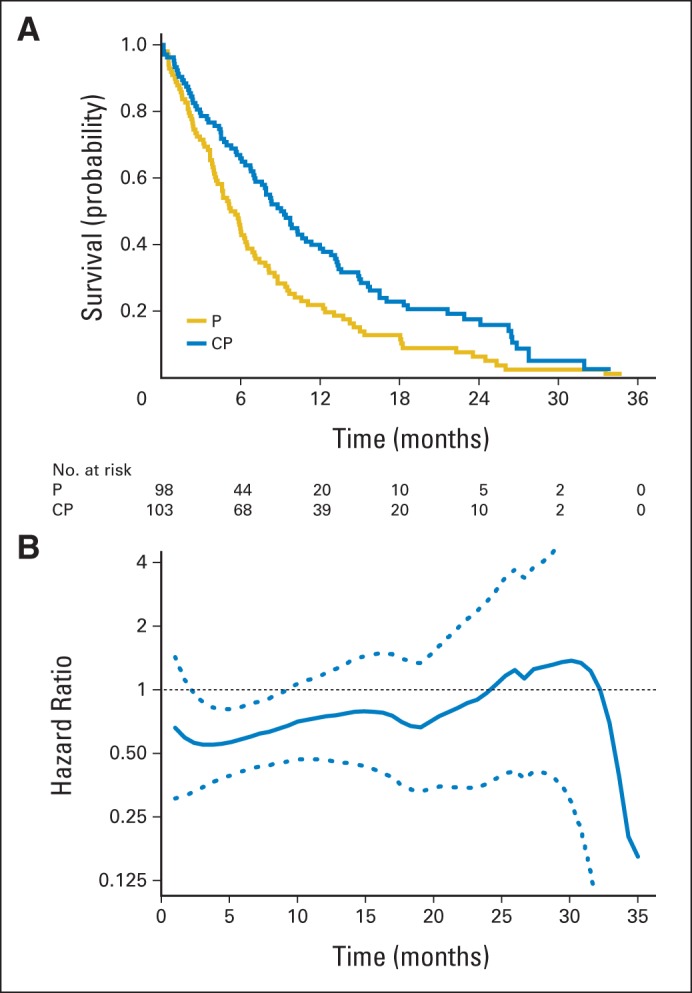
Estimated survival curves and the hazard ratio with reconstructed data for comparing single-agent pemetrexed (P) with carboplatin plus pemetrexed (CP) in patients with advanced non–small-cell lung cancer. (A) Kaplan-Meier curves for CP (blue) and P (gold). (B) Estimate of the ratio of hazard functions (CP over P) over time and the corresponding 0.95 point-wise confidence band.

For the third example, we used the data from the study reported by Allegra et al¹⁷ published in JCO, which was a randomized trial to assess efficacy and safety of the combination of bevacizumab and FOLFOX6 as the adjuvant therapy in patients with stage II to III colon cancer. A total of 2,678 patients were observed for overall survival after being randomly assigned to either modified FOLFOX6 (mFF6) or mFF6 plus bevacizumab. The median follow-up time was 4.9 years. Again, because the data are not available to the public, we used the algorithm proposed by Guyot et al¹⁶ to reconstruct the patients' survival times. Figure 3A and B show the resulting KM curves for the survival time end point and the hazard ratio estimates over time. It appears that the hazard ratio is approximately constant throughout the study period. The hazard ratio estimate is 0.95 (95% CI, 0.79 to 1.13) with P = .56.¹⁷ Despite a large study size (n = 2,678) with a relatively long study follow-up time, the interval estimate for the hazard ratio is rather wide because of low observed event rates, suggesting that there may be lack of information to make a clinical comparison of these two treatments. Such a conclusion may be misleading.

Fig 3.

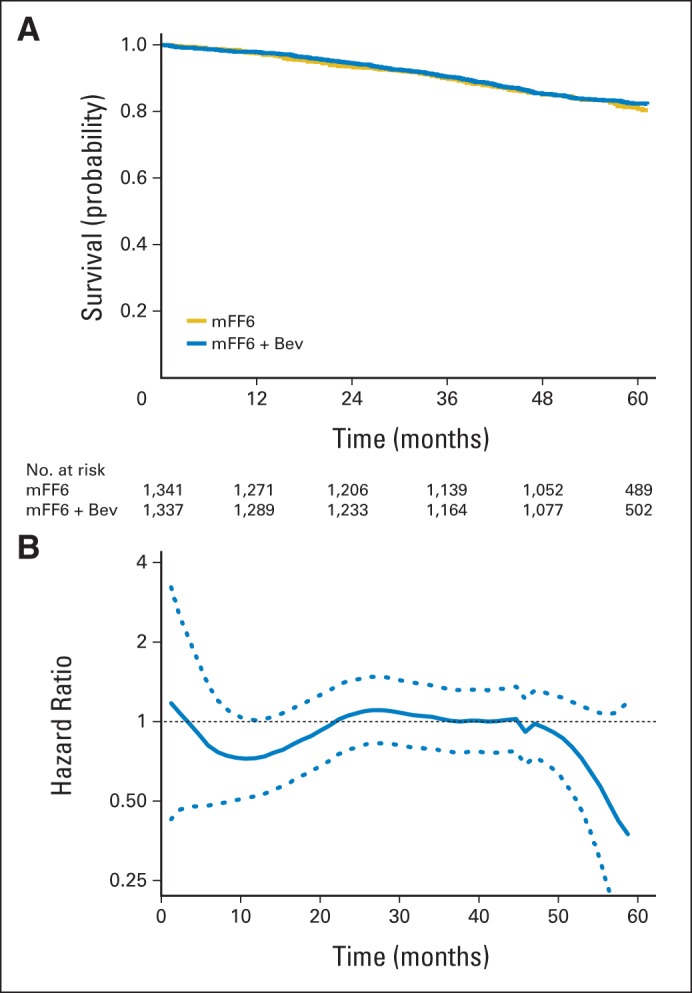
Estimated survival curves and the hazard ratio with reconstructed data for comparing modified FOLFOX6 (mFF6) plus bevacizumab (Bev) with mFF6 in patients with stage II to III colon cancer. (A) Estimated survival curves for mFF6 + Bev (blue) and mFF6 (gold). (B) Estimate of the ratio of hazard functions (mFF6 + Bev over mFF6) and the corresponding 0.95 point-wise confidence band.

ALTERNATIVE ROBUST MEASURES FOR THE DIFFERENCE BETWEEN TWO SURVIVAL CURVES

There are various model-based summary measures for the between-group difference, for example, the incidence rate ratio obtained from the Poisson model ¹⁸ or the scale-change parameter, assuming that the ratio of survival times for the two groups is constant stochastically.¹⁹ Like the hazard ratio estimate, the corresponding estimate of such model-based summary measures can be difficult to interpret when the modeling assumption is violated. Here, we present several model-free summaries for the two survival curves and illustrate them by using the data from the ECOG multiple myeloma study. We report the resulting model-free summary estimates in Table 1 with the data from the other two examples.

Table 1.

Summary of Various Estimates for the Between-Group Difference and Corresponding 95% CIs

Group Contrast Measure	Study
	Rajkumar et al10 (myeloma)		Zukin et al15 (NSCLC)		Allegra et al17 (colon cancer)
	Estimate	95% CI	Estimate	95% CI	Estimate	95% CI
Hazard ratio (PH model)	0.87	0.60 to 1.27	0.62	0.46 to 0.83	0.95	0.79 to 1.13
t-year survival	Month 40		Month 24		Month 60
Difference	−0.04	−0.15 to 0.06	0.11	0.02 to 0.21	0.02	−0.02 to 0.05
Ratio	0.95	0.82 to 1.10	2.74	1.09 to 6.93	1.02	0.98 to 1.06
Percentiles	10th		50th		10th
Difference (months)	10.9	2.6 to 19.1	3.7	1.3 to 6.0	1.5	−3.9 to 7.0
Ratio	2.15	1.17 to 3.96	1.66	1.21 to 2.27	1.04	0.90 to 1.21
Restricted mean survival time	Month 40		Month 35		Month 60
Difference (months)	2.2	0.1 to 4.2	3.9	1.5 to 6.3	0.3	−0.7 to 1.3
Ratio	1.06	1.00 to 1.13	1.49	1.17 to 1.91	1.00	0.99 to 1.02
Ratio of restricted mean time lost	0.68	0.47 to 0.98	0.86	0.77 to 0.94	0.95	0.78 to 1.16

Abbreviations: NSCLC, non–small-cell lung cancer; PH, proportional hazards.

Ratio (or difference) of t-Year Survival Rates

If we are interested in, for example, a relatively long-term survival benefit, a simple comparison of the survival probabilities at a given time (eg, the survival rate ratio or difference) is a sensible choice for quantifying the group difference. Such measures can be easily estimated via the KM curves. For the multiple myeloma example, if we are interested in survival at 40 months, the two observed survival rates are 0.697 for low-dose and 0.735 for high-dose therapy. The ratio of the two survival rates (low dose over high dose) is 0.95 (95% CI, 0.82 to 1.10). Numerically, although not statistically significant, the low dose appears slightly worse than the high dose at this time point. Conversely, for a short-term survival comparison, say, at month 24, the observed survival rates are 0.882 for low-dose and 0.784 for high-dose therapy. The estimated ratio is 1.13 (95% CI, 1.03 to 1.23), indicating that the low dose is significantly better at this time point.

Ratio (or difference) of Percentiles of Survival Functions

Another commonly used model-free contrast in practice is the ratio (or difference) of two median survival times. The estimate can be easily obtained via the KM curves, and the CI estimate for such a group contrast measure can be constructed via a simple resampling method such as bootstrapping.²⁰ However, if the event rate is relatively low or the follow-up time is short, the median failure time may not be estimable from the observed data. In this case, one may estimate the ratio of lower percentiles of the survival curves.²¹ For the multiple myeloma example, the estimated tenth and twentieth percentiles are 20.3 and 30.8 months for the low-dose group and 9.5 and 22.1 months for the high-dose group, respectively, based on the KM curves. The ratios of the survival times (low dose over high dose) based on the tenth and twentieth percentiles are 2.15 (95% CI, 1.17 to 3.96) and 1.39 (95% CI, 0.87 to 2.23), respectively.

Ratio (or difference) of Restricted Mean Survival Times or Restricted Mean Time Lost

As an alternative to the median, the mean survival time would be a good summary of the survival time distribution, but it typically cannot be estimated well because of censoring. Conversely, unlike the median, one can slightly modify the concept by using the restricted mean survival time (RMST) as a summary to accommodate the study follow-up time.^22–26 For the multiple myeloma example, the study follow-up time was about 40 months. The RMST is simply the population average of the amount of event-free survival time experienced during this initial 40 months of follow-up. This quantity can be easily estimated by the area under the KM curve up to 40 months. The area under the low-dose KM curve (light blue area in Fig 1C) is 35.4 months; that is, one expects a typical patient treated with the low-dose therapy to be alive for 35.4 months of the 40 months of follow-up. The corresponding area under the high-dose curve is 33.3 months. Then the ratio, 1.06 (95% CI, 1.00 to 1.13), of the two estimated RMSTs would be a clinically meaningful global summary of the group difference. The choice of 40 months to define the RMST is crucial, and a rule for choosing this value may be prespecified at the study design stage with respect to the clinical relevance and feasibility of conducting the study. If we are interested in the so-called restricted mean time lost or “months of life lost up to 40 months,” whose empirical counterpart is the area above the KM curve (light gray area in Fig 1C), the estimates for the low and high doses are 4.6 (40 − 35.4 months) and 6.7 (40 − 33.3 months), respectively. The ratio of these two (low dose over high dose) is 0.68 (95% CI, 0.47 to 0.98). This ratio also has a meaningful clinical interpretation: on average, the low-dose patients experienced 32% less loss of lifetime than the high-dose patients during the 40 months of follow-up. With these contrast measures using the RMST, the low-dose group appears to have an overall survival benefit compared with the high-dose group. Moreover, unlike the hazard ratio estimate, we can obtain an interpretable background summary for the high-dose group, 33.3 months of survival (or 6.7 months lost) of a 40-month window, which may provide valuable information for assessing the relative difference between two groups clinically.

For the second lung cancer example discussed in “Examples From Cancer Clinical Trials With Survival Time End Point,” in which the hazard ratio potentially interacts quantitatively with time, the estimated RMST up to 35 months for the P arm is 7.9 months and for the CP arm is 11.8 months. Therefore, the estimated difference of two RMSTs (CP minus P) is 3.9 months (95% CI, 1.5 to 6.3; P = .001) and the estimated ratio of two RMSTs (CP over P) is 1.49 (95% CI, 1.17 to 1.91; P = .001). With these between-group contrast measures, the difference between the two treatment groups is highly statistically significant, just as with the conventional test. Moreover, with the estimated RMSTs from both arms, we are able to make better assessments of the treatment difference from a clinical perspective than those based on the conventional hazard ratio estimate.

For the third colon cancer example, in which the hazard ratio remains relatively close to one, the estimated difference of two RMSTs up to 60 months (mFF6 plus bevacizumab minus mFF6) is 0.3 months (95% CI, −0.7 to 1.2; P = .61). The CI includes zero and thus the two RMSTs are not statistically different. Moreover, the CI appears to be rather tight in comparison with the estimated background RMST of 55.2 months in the mFF6 plus bevacizumab arm and 54.9 months in the mFF6 arm, suggesting that at least with respect to the RMST, the study provided strong evidence on the clinical similarity of these two treatments. The estimated ratio of RMSTs, 1.00 (95% CI, 0.99 to 1.02), further confirms this observation. This is in contrast to the inconclusive interpretation that uses the hazard ratio estimate, possibly because of the low observed event rates.

DISCUSSION

If it has a strong justification clinically, biologically, or empirically from previous studies, a model-based population measure such as a constant hazard ratio or scale-change parameter (ie, under a two-sample accelerated failure time model) can be a good choice as a prespecified summary for the between-group difference. Otherwise, we highly recommend using a model-free parameter, with clinical and analytic interpretability, as the summary contrast measure. The choice of such a primary parameter should match the aim of the study. For example, if we are interested in the relative time for a specific percentile or the ratio of the survival rates at a fixed time point, the corresponding population measure introduced in “Alternative Robust Measures for the Difference Between Two Survival Curves” can be the primary target. Conversely, to capture a global profile of the between-group difference with a single summary measure, the ratio (difference) based on the RMSTs, with an appropriate prespecified follow-up time, is a good choice. All the model-free measures discussed here can be estimated well nonparametrically, and their corresponding inference procedures such as the CI estimation can be constructed analytically or via a simple resampling method.

In this article, we were mainly interested in quantifying the between-group difference rather than hypothesis-testing procedures; a P value does not have any inherent clinical meaning. The conventional log-rank test for testing the equality of two survival distributions is model free. However, its close connection to the PH model means that it may lack the power to detect differences such as that in the multiple myeloma example in which the PH assumption is clearly violated. Moreover, for the last colon cancer example in which the event rate was low, a large P value from the log-rank test cannot differentiate between “no clinically meaningful group difference” and “not enough information for estimating the group difference.” The CI estimate for an appropriate summary measure would be more appropriate for the purpose of clinically assessing a treatment difference.

AUTHORS' DISCLOSURES OF POTENTIAL CONFLICTS OF INTEREST

The author(s) indicated no potential conflicts of interest.

AUTHOR CONTRIBUTIONS

Manuscript writing: All authors

Final approval of manuscript: All authors