Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Jul 22;4:5695. doi: 10.1038/srep05695

The impact of hot charge carrier mobility on photocurrent losses in polymer-based solar cells

Bronson Philippa 1, Martin Stolterfoht 2, Paul L Burn 2, Gytis Juška 3, Paul Meredith 2, Ronald D White 1, Almantas Pivrikas 2,a
PMCID: PMC4105785  PMID: 25047086

Abstract

A typical signature of charge extraction in disordered organic systems is dispersive transport, which implies a distribution of charge carrier mobilities that negatively impact on device performance. Dispersive transport has been commonly understood to originate from a time-dependent mobility of hot charge carriers that reduces as excess energy is lost during relaxation in the density of states. In contrast, we show via photon energy, electric field and film thickness independence of carrier mobilities that the dispersive photocurrent in organic solar cells originates not from the loss of excess energy during hot carrier thermalization, but rather from the loss of carrier density to trap states during transport. Our results emphasize that further efforts should be directed to minimizing the density of trap states, rather than controlling energetic relaxation of hot carriers within the density of states.

While natural photosynthesis transfers electrons through a cascade of energy states, artificial photovoltaic systems must extract photogenerated charges to the electrodes, and despite recent performance gains1, fundamental questions about this charge extraction still remain unanswered. There has been intense scrutiny of the mechanisms of charge generation and the impact of above-bandgap photon energy2,3,4, however, this level of attention has not extended to studies of the extraction of such ‘hot' charge carriers, despite the fact that efficient charge extraction is crucial for device performance5.

The most characteristic feature of charge transport in disordered systems is the dispersion of the charge carrier movement velocities6. Dispersive transport harms device performance because the slowest carriers bring down the average mobility7, and consequently, the vast majority of novel organic semiconductors remain inapplicable for efficient devices. Moreover, the detrimental effects of dispersion are exacerbated by the inhomogeneities in film thicknesses caused by the targeted low cost deposition methodologies, because the transit time distributions become dramatically longer and more dispersed in regions of increased thickness.

Dispersive transport in organic semiconductors is usually thought to be caused by the energetic relaxation of hot charge carriers within their density of states8. Spectroscopic measurements and Monte Carlo simulations have revealed energetic relaxation extending even to the microsecond timescales, where it could be relevant to bulk charge transport9,10. Even if the bulk of the energetic relaxation were to occur on very fast timescales, there is still the question of whether residual thermalization might continue to long, microsecond timescales. This energetic relaxation is often understood to cause a time-dependent mobility and therefore explain dispersive current transients11,12, yet we will show here that this commonly-used model is inconsistent with our observations in high efficiency organic solar cell materials. Instead, there is an alternative mechanism for the creation of a distribution of carrier velocities, namely, via trapping. This observation has a very direct impact on the numerous models, theories and experimental results describing dispersive charge transport in disordered organic semiconductors. Furthermore, it points to a new strategy for improving charge transport “management” in devices such as organic solar cells.

The classic signature of dispersive transport is a time-of-flight photocurrent signal that decays with time even before the carriers have transited through the film13. This decay in photocurrent can occur due to two mechanisms, a reduction in carrier mobility, and/or a reduction in the number (or concentration) of moving carriers. The former, a time-dependent hot carrier mobility, is presently commonly believed to be the cause of dispersion in organic semiconductors8,11,12 and it is usually understood to originate from a loss of energy as carriers thermalize within their density of states14,15,16. Higher energy carriers are expected to have a higher hopping probability, and hence a higher velocity17,18,19, so the thermalization within the density of states causes the carrier mobility to decline. Recent studies9,10 have reported mobility thermalization times on the order of microseconds. However, an alternative explanation for the decaying transient photocurrent, which is less commonly accepted in organic semiconductors, is a time dependent concentration that can arise if carriers are gradually lost to traps20,21,22. The photocurrent signal will continue to reduce as long as the net concentration of moving carriers continues to decrease. If that physical process prevails, there can be decaying photocurrent despite the moving carriers having a constant drift velocity. Additionally, if the cause of dispersion is trapping, then it will influence all devices, even those which operate in the dark23,24.

In this article, we demonstrate that a time-dependent hot carrier mobility cannot explain the dispersive transport in our studied bulk heterojunction solar cells. We address this issue by performing transient photoconductivity experiments in which we vary the transit time by changing the electric field and/or device thickness. The expectation is that if the dominant cause of dispersive transport is mobility relaxation, then the average mobility and the amount of dispersion should vary with the electric field and/or film thickness, because longer transit times will allow for more relaxation to occur. Conversely, if the dominant effect is trapping, then it is the concentration of carriers which is changing in time rather than their mobility, and consequently, the average mobility and the dispersion range should not vary with film thickness or electric field. This transit time dependence allows these two dispersive mechanisms to be experimentally distinguished.

Results

Numerical Simulations of Resistance dependent PhotoVoltage (RPV) measurements

Our experiments were made possible by the development of a new transient photoconductivity technique that we call Resistance dependent PhotoVoltage (RPV), which is described here and in the Methods section. The experimental measurement circuit for RPV is shown in Figure 1. This setup is similar to time-of-flight, where charge carriers are photogenerated by a short low-intensity laser pulse. A low light intensity is necessary so that the electric field inside the device is undisturbed. The transient photosignal is determined by the competition between two simultaneous processes: the transport of charge carriers inside the film, and the response of the external RC circuit. Unique to the RPV approach, and in contrast with time-of-flight, the entire measurement is repeated at many different load resistances spanning the range from differential mode (small R) to integral mode (large R). The resistance is varied for two reasons: firstly, to visualize the transit times, as will be shown below; and secondly, to reveal the slower carrier mobility by amplifying the slower carrier's conduction current. The slower carriers produce a much smaller current than the faster carriers, and their transit would be buried in the noise at resistances that are optimized for the faster carriers. Slower carriers have much longer transit times, allowing the use of larger resistances, and consequently allowing for their weaker electrical signal to be amplified. In this way, RPV bridges the gap between differential mode and integral mode time-of-flight, and allows measurement of the transport of both types of charge carriers.

Figure 1. Resistance dependent PhotoVoltage (RPV) measurement circuit (top) and timing diagram (bottom).

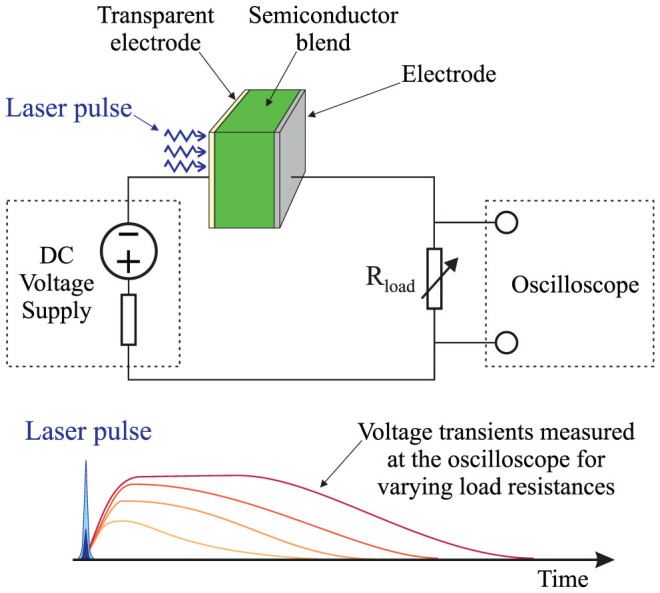
Figure 1

Open in a new tab

A low light intensity nanosecond laser pulse is used to photogenerate charge carriers inside (for example) the semiconductor junction of an organic solar cell. Low light intensity is critical in the RPV experiment to ensure operation within the “small charge extraction mode” where the internal electric field distribution in the film is not altered by transported charges. After photogeneration, the charge carrier transport through the film is driven by the built-in or the applied external electric field, and the resulting transient photosignal is recorded by an oscilloscope. The transient photosignals are measured at various load resistances Rload.

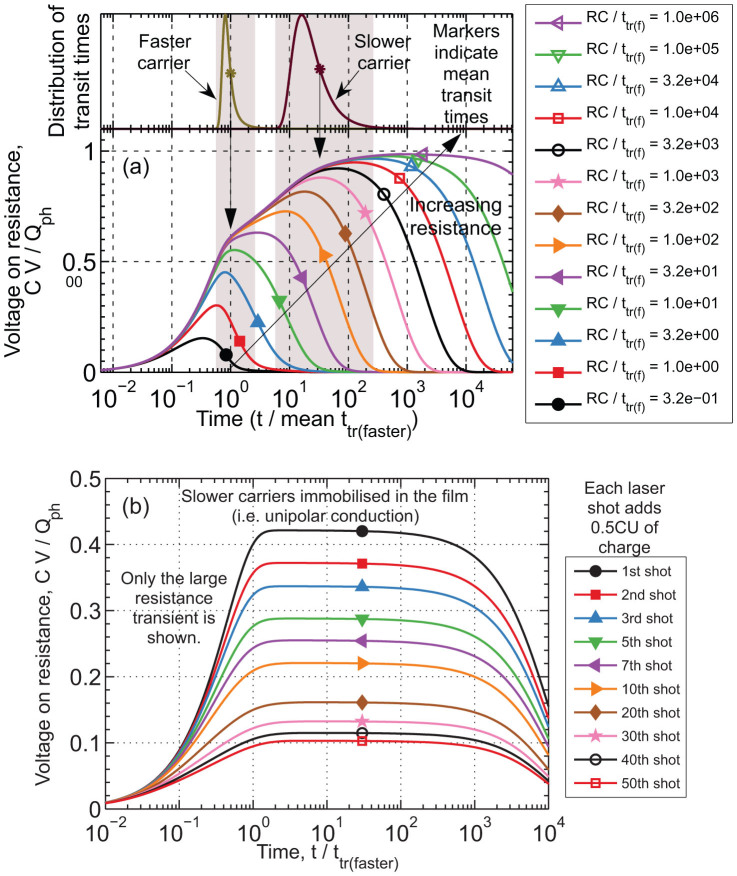
The combination of the RC circuit dynamics, dispersive transport, and optical interference effects prevent analytic analysis of the transients. To study highly dispersive systems, such as organic solar cells, the simultaneous impact of all these effects must be understood. We applied numerical simulations to develop this understanding. The simulations are described in the Methods section and in the Supplementary Information. Typical simulated transients for an organic solar cell with dispersive transport are shown in Figure 2 (a). The transients show two distinct extraction “shoulders,” as indicated by the arrows. The transients at different resistances assist in visually identifying the location of these “shoulders.” The positions of these arrows correspond to the mean transit times required for the faster and slower carriers to cross the entire thickness of the film. In this simulation, carriers are repeatedly trapped and de-trapped, creating dispersion because the total time spent in traps is different for different carriers. The resulting distribution of transit times is shown at the top of Figure 2 (a), and its approximate width is indicated by the shaded background. It can be seen that the RPV technique allows the mean charge carrier mobility to be obtained even in the presence of strong dispersion.

Figure 2. Numerically simulated RPV transients in the case of (a) dispersive transport caused by shallow traps, and (b) film charging caused by deep traps.

Figure 2

Open in a new tab

(a) In the case of dispersive transport, the extraction “shoulders” approximately correspond to the mean charge carrier mobility. (b) In the case of deep traps, the film becomes charged and the magnitude of the RPV transient is reduced in subsequent shots of the laser, but the transit “shoulder” remains unhindered which allows for reliable charge carrier mobility estimation.

In addition to shallow traps that cause dispersion, we also considered deep traps that immobilize carriers for times much longer than the transit time of either carrier. Long lived trapping is typical in disordered organic semiconductors22,25, because many organic materials behave as unipolar conductors, and solar cells often have strongly imbalanced mobilities26. In these cases, repeated photogeneration adds more trapped charge in the form of the immobilized charge carriers, which might accumulate with every repetitive laser shot, redistributing the electric field and distorting the measurement. Figure 2 (b) shows simulations of this film charging for the case of fast Langevin-type recombination under repeated laser shots, as would arise from the presence of deep trap states far inside the forbidden energy gap27. These are large resistance transients, in other words, the measurement circuit has integrated the photocurrent such that the peak voltage is proportional to the extracted charge. If the extracted charge is decreasing and the extraction time remains constant, then carriers must be lost to recombination and not due to field screening, and hence we conclude that the trapped charges act as recombination sites for the mobile carriers. However, the mobility of the charge carriers can be determined independently of the trapping effects, because the rapid Langevin recombination prevents the build-up of large amounts of trapped charge that would disturb the transit time.

Experimental measurements

We chose to study the well-known photovoltaic blend28 of poly[N-9″-hepta-decanyl-2,7-carbazole-alt-5,5-(4′,7′-di-2-thienyl-2′,1′,3′-benzothiadiazole)] (PCDTBT) and [6,6]-phenyl-C70-butyric acid methyl ester (PC71BM) in an optimized blend ratio of 1:4 by weight29. This blend is ideally suited to this study because its amorphous nature allows the elimination of any film thickness dependent morphology30. In order to see the generality of observed effects, we have also done the same experiments on poly[[4,8-bis[(2-ethylhexyl)oxy]benzo[1,2-b:4,5-b′]dithiophene-2,6-diyl] [3-fluoro-2-[(2-ethylhexyl)carbonyl] thieno[3,4-b]thiophenediyl]] (PTB7):PC71BM blends, the results of which are shown in the Supplementary Information. The thin film (active layer thickness of 75 nm) PCDTBT:PC71BM solar cell exhibited a power conversion efficiency of 6.3% under standard AM1.5G illumination, while the PTB7:PC71BM blends reached 7.7%. Current-voltage curves for both devices are shown in Supplementary Figure 5. None of the optimized PCDTBT or PTB7 based devices demonstrated any significant film morphology inconsistencies in the range of studied film thickness. (See the Methods section for the details of the fabrication and the Supplementary Information for characterization of photovoltaic performance). The presence of dispersive transport was confirmed by time-of-flight experiments on thick films (Supplementary Figure 6). No photocurrent plateaus were observed; the transients decrease with time as is typical of dispersive systems.

Figure 3 shows the recorded RPV transient signals for a PCDTBT:PC71BM solar cell. All transients were recorded at near to short-circuit conditions. This remains true even at large resistances, because the maximum photovoltage occurring during the transient is substantially less than the built-in voltage. The first shoulder marks the arrival time of faster carriers (27 ns), which is attributed to electron transport since the time scale is similar to that measured for PC71BM (please refer to the Supplementary Information for measurements on PC71BM). The second shoulder is less well defined due to the strongly dispersive nature of hole transport in this system, but marks the arrival of the slower carriers (2.59 μs). Mean electron and hole mobilities were determined from the shoulders in the transients, as indicated by arrows in Figure 3, with the approximate spread of arrival times indicated by the shaded boxes (corresponding to the regions where the transients deviate from the dotted lines). The edges of these shaded boxes give the “fastest” and “slowest” case transit times, from which we obtained the dispersion range in the mobilities for each species. This range is an essential feature of the dispersive transport exhibited by this system, because a single mobility value does not correctly quantify the transport when the system is dispersive. We measured the mean electron mobility to be 2.9 × 10−3 cm2 V−1 s−1 with a dispersion range from 1.1 × 10−3 cm2 V−1 s−1 to 4.5 × 10−3 cm2 V−1 s−1 and the mean hole mobility to be 3 × 10−5 cm2 V−1 s−1 with a dispersion range from 9.2 × 10−6 cm2 V−1 s−1 to 7.4× 10−5 cm2 V−1 s−1. Despite the high level of dispersion observed here (the hole dispersion range covers nearly an order of magnitude), the OPV device still maintains good performance. However, further work is necessary to identify the impact of the dispersion range on the performance of solar cells.

Figure 3. Experimentally measured RPV transient photo-signals in an optimized PCDTBT:PC71BM solar cell.

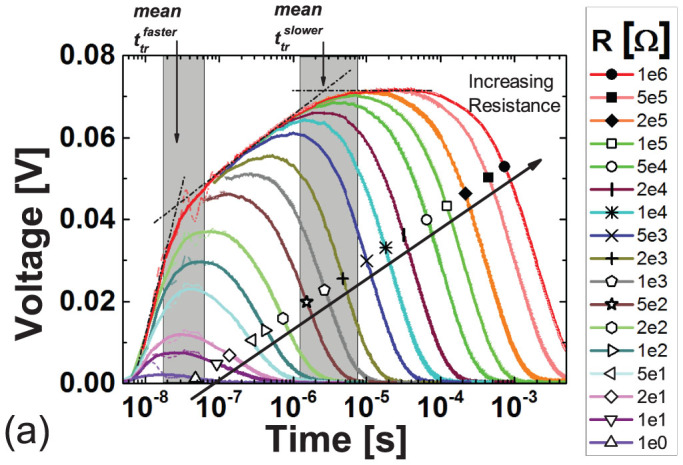
Figure 3

Open in a new tab

Mean electron (faster) and hole (slower) transit times are marked, from which the respective mean mobilities are estimated. The dispersive nature of charge transport in the studied solar cells is highlighted by shaded boxes marking the range of carrier arrival times. Thin curves show recorded data, while bold lines show data smoothed by adjacent averaging. The short timescales for large resistances were omitted for clarity.

Next, we studied the impact of photon energy on the hot charge carrier transport, because any relaxation effects are likely to be dependent upon the initial energy. This is important because of recent suggestions that excess above-bandgap energy may assist excitonic dissociation4, although the methodology of that observation has been challenged31. We note that quantum yields have been shown to be independent of the energy level of the excited state, suggesting that hot excitons are indeed not beneficial for exciton separation32. Nevertheless, hot charge carriers – rather than excitons – might also possess excess energy and shape the internal quantum efficiency spectra; therefore, it is important to clarify these effects, aiming for improvement in the charge extraction of typical low mobility organic materials. In the past the absence of hot charge carrier effects has been observed indirectly33. Numerical simulations predict that RPV is independent of optical interference effects (Supplementary Figures 2 and 3), allowing direct and unambiguous measurement of any hot charge carrier effects that may be present. RPV transients were measured at two different photon energies, 3.49 eV (355 nm) and 2.33 eV (532 nm). The results are plotted in Figure 4, showing nearly identical transients resulting from laser excitation at the two different wavelengths. The photon energy independent mobility suggests that excess energy plays a minimal role in dispersive transport, since carrier thermalization (if it is present) must happen in time scales much shorter than the transit time.

Figure 4. RPV transients measured on a 75 nm PCDTBT:PC71BM solar cell using two different laser wavelengths: 355 nm (3.49 eV) and 532 nm (2.33 eV).

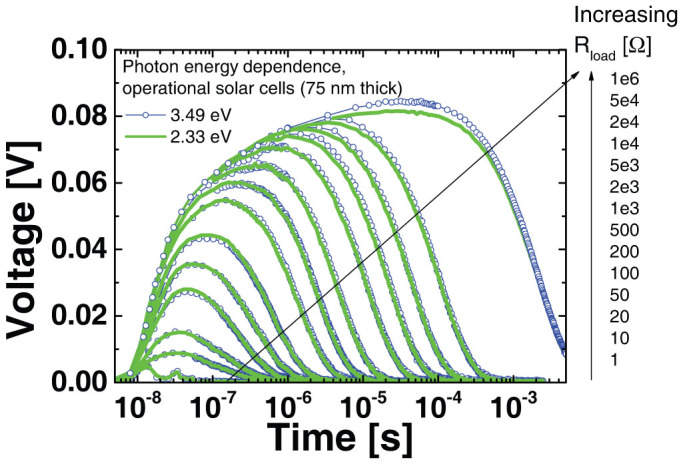
Figure 4

Open in a new tab

The nearly identical transient responses directly demonstrate the absence of hot carrier effects in this system.

To further confirm that the dispersion in hot carrier mobilities is not caused by the thermalization of carriers, we studied the electric field and film thickness dependence. Longer transit times should allow more time for thermalization, thus influencing the result if the dispersion is due to carrier relaxation. The results are shown in Figure 5; the Supplementary Information includes a selection of the transients from which these mobilities were estimated. The mobilities and dispersion ranges are completely independent of electric field and photon energy [Figure 5 (a)], suggesting that trapping mechanisms are more significant than relaxation mechanisms. The lack of electric field dependence is in contrast with the Poole-Frenkel dependence reported in pristine PCDTBT34. This is an unexpected result, because in disordered organic systems significant electric field dependence is typically observed, even at relatively low values of electric fields34, which is thought to originate from hopping-type charge transport. Further studies of the temperature dependence, and measurements on other systems, have to be performed in order to clarify the origin of this observation. Additionally, we observe that the mean mobilities and dispersion ranges are nearly independent of the film thickness [Figure 5 (b)]. We attribute the small changes in mobility to device-to-device variations that result from the fabrication process. The thickness independence of the mean mobilities and dispersion ranges further support the claim that the dispersion is caused by traps instead of relaxation. A charge carrier density dependence in the mobility even at low concentrations has been observed in P3HT:PCBM blends24, and we note that a concentration dependence might cause dispersion as carriers gradually become trapped and the density decreases. We do not exclude the possibility of a density dependence here. However, in our measurements, increasing thickness corresponds to lower densities because the amount of photogenerated charge was always less than CU, which is inversely proportional to thickness. Consequently, the thickness independence in the mobility implies that there is negligible density dependence at the concentrations probed here.

Figure 5. Electron and hole mobilities measured in PCDTBT:PC71BM solar cells.

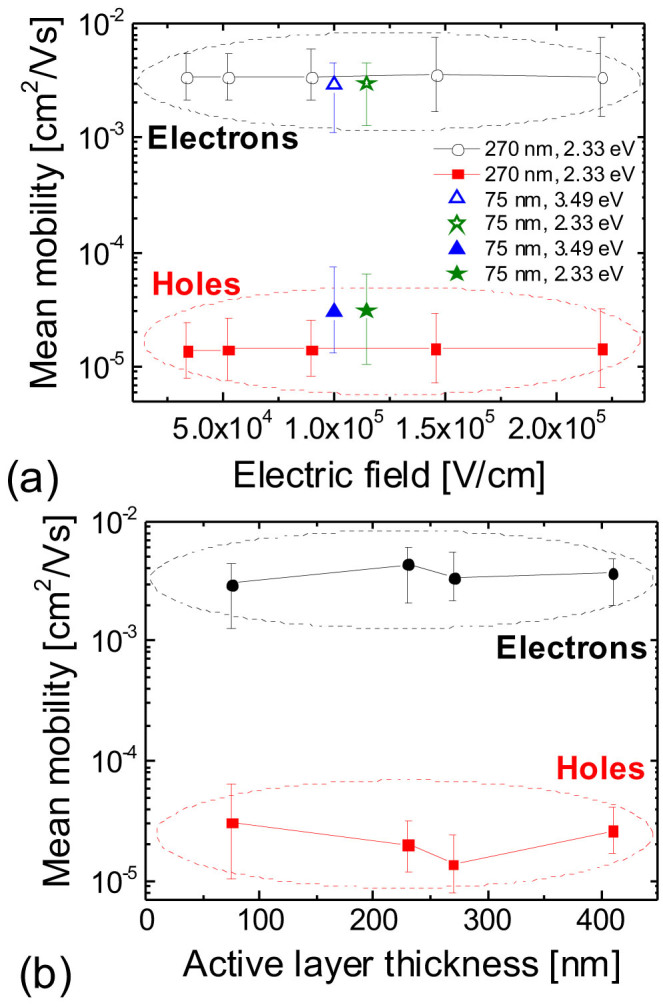
Figure 5

Open in a new tab

The error bars show the dispersion ranges. Carrier mobilities and dispersion ranges are independent of electric field and photon energy [panel (a)], and nearly independent of film thickness [panel (b)], demonstrating that carrier thermalization cannot account for the dispersive transport in this system. Consequently, dispersion is caused by trapping.

Further measurements were also performed on solar cells made with PTB7 blends. The results show the same conclusions as the PCDTBT blends: the mean mobility and dispersion ranges are independent of film thickness, applied electric field, and photon energy (Supplementary Figures 8, 10, and 11). The results reported here appear to be generally applicable and are certainly not specific to PCDTBT blends.

Discussion

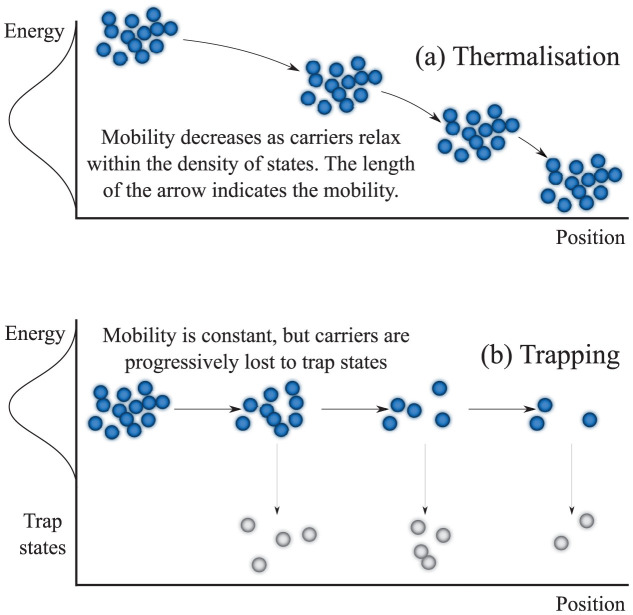
Charge transport in the studied operational OPV blends is strongly dispersive, as demonstrated by the decaying time-of-flight photocurrent transients in thick devices (Supplementary Figure 6). These time-of-flight transients were recorded in a regime where drift dominates over diffusion, so the current density is described by j = eE (nμn + pμn), where e is the charge of an electron, μn and μp are the electron and hole mobilities, n and p are the carrier concentrations, and E is the electric field. The observation of a decaying photocurrent density j can be explained by two mechanisms: thermalization (a time dependent mobility, μ), and/or trapping (a time dependent concentration of moving charge carriers, n). These mechanisms are schematically illustrated in Figure 6, from which it can be seen that either model would result in dispersive photocurrent transients. We found no evidence of thermalization-type effects on the timescales comparable with those involved in charge transport. Figure 4 directly demonstrates that that excess energy of hot carriers has essentially no contribution to mobility or dispersion. In Figure 5, we demonstrate that the dispersion range is independent of the applied electric field and changes very little with thickness. If thermalization on transport time scales16 were the cause of the dispersion, then modifications to the transit time should change the mean mobility and/or dispersion range by varying the time available for relaxation. Such a variation was not observed, and hence we exclude thermalization as the mechanism of the dispersive transport. Any relaxation processes must be much faster than charge transport, so that the distance covered by charges as they relax is insignificant compared with the film thickness, and hence the relaxation has negligible contribution to the overall dispersion. With relaxation excluded, the only remaining mechanism is a reduction in the concentration of moving carriers, therefore, we conclude that trapping is the primary cause of the dispersion in these systems. This challenges the widely-used model of hot carrier relaxation within the density of states. Consequently, dispersive transport potentially impacts on the many different devices that employ films made from disordered semiconductors, including those that operate in the dark or at steady-state conditions.

Figure 6. Schematic illustration of the two pathways to dispersive transport.

Figure 6

Open in a new tab

(a) Thermalisation causes the mobility to decrease with time, whereas (b) trapping causes the loss of carrier density. We have shown here that the latter case (trapping) is the dominant effect in the studied solar cells.

In conclusion, electron and hole mobilities and their dispersion ranges were measured simultaneously using the RPV technique in a high efficiency narrow optical gap polymer/fullerene system (PCDTBT:PC71BM). We found that the transport of electrons and holes are both strongly dispersive in these thin, efficient solar cells. We introduced the dispersion range as a parameter to quantify charge transport, since a single mobility value is insufficient to properly characterize a dispersive material. We directly observed the absence of “hot carrier” effects on time scales relevant to charge extraction, and furthermore found that the dispersion is caused by trapping rather than thermal relaxation. We have found that the widely-used model of hot carrier relaxation within a density of states is not the dominant process causing the dispersion in the studied solar cells. Furthermore, in contrast with the Poole-Frenkel dependence previously reported in pristine PCDTBT and other disordered systems, the studied solar cell blends exhibit an unexpected negligible electric field dependence. While further work is needed to clarify this observation, electric field independence may assist in maintaining a good fill factor by keeping the mobility higher near the maximum power point. The absence of hot carrier effects and an electric field independent mobility were also observed in PTB7:PC71BM solar cells, suggesting that these conclusions may be more generally applicable. This work signifies the importance of localized trap states as opposed to thermalization and hot carrier effects in efficient polymer-based solar cells. Since dispersion arises from trapping, it is also important for other types of devices, such as organic field effect transistors and diodes. Trap states are relevant whether the carriers were injected or photogenerated, and whether the device is in transient or equilibrium conditions. Our results suggest that further scientific research should be directed towards reducing the density of trap states rather that utilizing above-bandgap energy for improving electronic device performance.

Methods

Numerical simulations

The simulations are based on a standard one-dimensional drift-diffusion-recombination solver35,36 assuming a negligible amount of equilibrium carriers, which is typically the case in organic semiconductors37 as well as in the studied devices. For simulations of dispersive transport, we implemented a multiple trapping and release model20,21,38 with an exponential density of localized states. The full list of equations are given in the Supplementary Information.

Solar cell fabrication

15 Ω/sq. Indium tin oxide (80 nm thick, purchased from Kintec) coated glass substrates were cleaned in a 100°C water bath with alconox (detergent), followed by sonicating in sequence with de-ionized water, acetone and 2-propanol for 6 minutes each. Next, a 30 nm layer of poly(3,4-ethylenedioxythiophene):poly(styrenesulfonate) (PEDOT:PSS) was spin-coated at 5000 rpm for 60 sec onto the cleaned substrates, which were then annealed at 170°C for a few minutes in air. For PCDTBT devices, a solution of PCDTBT (purchased from SJPC Group) and PC71BM (purchased from Nano-C) was prepared by using a 1:4 blend ratio by weight and a total concentration of 25 mg/cm3 in 1,2-dichlorobenzene (DCB). Solar cells with four active layer thicknesses, 75 nm, 230 nm, 270 nm and 410 nm (measured by a DekTek profilometer), were fabricated by spin coating. For PTB7 devices, the active layer of PTB7 (1-Material, Mw = 97.5 kDa, PDI = 2.1) and PC71BM (ADS) was prepared as previously described1 resulting in 100 nm, 150 nm, 230 nm, and 700 nm thick films. To complete the solar cells 1.2 nm of samarium and 75 nm of aluminium were deposited under a 10−6 mbar vacuum by thermal evaporation. The device areas were 0.2 cm2 for current density versus voltage (J-V) measurements and 3.5 mm2 for charge transport measurements. J-V characteristics were obtained in a 4-wire source sense configuration and an illumination mask was used to prevent photocurrent collection from outside of the active area. An Abet solar simulator was used as the illumination source and provided ~100 mW/cm2 AM1.5G light.

RPV measurements

A delay/trigger generator (Stanford Research Systems DG535) was used to trigger the laser and function generator (Agilent 33250 A) pulses for timing control. A pulsed Nd:Yag laser (Brio Quantel) with a pulse length of 5 ns was used to generate the carriers. Optical filters were used to reduce the laser intensity for the RPV measurements. A function generator was used to apply external voltage pulses for electric field dependent mobility measurements. RPV photovoltage signals were recorded with an oscilloscope (WaveRunner 6200 A) at various external load resistances. RPV transients were smoothed with an adjacent averaging function to neutralize the electromagnetic wave oscillations in the measurement circuit. In agreement with previous studies done by Clarke et al.39, dark-CELIV transient responses showed no equilibrium carrier extraction, justifying the application of RPV to the studied devices. Optical interference simulations were performed using the transfer matrix approach40 with typical optical constants of PCDTBT/PCBM blends41.

Author Contributions

B.P. and A.P. wrote the manuscript and interpreted the results. B.P. wrote the software and performed the simulations. M.S. fabricated the devices and performed the measurements. P.L.B. and P.M. supervised the experimental study. R.D.W. supervised the theoretical study and assisted with developing the software and simulations. G.J. contributed to the experimental design. A.P. conceptualized the experiment.

Supplementary Material

Supplementary Information

SUPPLEMENTARY INFO

srep05695-s1.pdf (2.2MB, pdf)

Acknowledgments

We thank Jao van de Lagemaat for providing the software for the transfer matrix optical interference simulations, and Ardalan Armin for assistance with the optical simulations. Computational resources were provided by the James Cook University High Performance Computing Centre. AP is the recipient of an Australian Research Council Discovery Early Career Researcher Award (Projects: ARC DECRA DE120102271, UQ ECR59-2011002311 and UQ NSRSF-2011002734). PM and PLB are UQ Vice Chancellor's Senior Research Fellows. Research at Vilnius University was funded by the European Social Fund under the Global Grant measure. We acknowledge funding from the University of Queensland (Strategic Initiative – Centre for Organic Photonics & Electronics), the Queensland Government (National and International Research Alliances Program). This work was performed in part at the Queensland node of the Australian National Fabrication Facility (ANFF) - a company established under the National Collaborative Research Infrastructure Strategy to provide nano and microfabrication facilities for Australia's researchers.

References

  1. He Z. et al. Enhanced power-conversion efficiency in polymer solar cells using an inverted device structure. Nat. Photonics 6, 593–597 (2012). [Google Scholar]
  2. Bakulin A. A. et al. The role of driving energy and delocalized states for charge separation in organic semiconductors. Science. 335, 1340–4 (2012). [DOI] [PubMed] [Google Scholar]
  3. Jailaubekov A. E. et al. Hot charge-transfer excitons set the time limit for charge separation at donor/acceptor interfaces in organic photovoltaics. Nat. Mater. 12, 66–73 (2013). [DOI] [PubMed] [Google Scholar]
  4. Grancini G. et al. Hot exciton dissociation in polymer solar cells. Nat. Mater. 12, 29–33 (2013). [DOI] [PubMed] [Google Scholar]
  5. Heeger A. J. 25th Anniversary Article: Bulk Heterojunction Solar Cells: Understanding the Mechanism of Operation. Adv. Mater. 26, 10–27 (2014). 10.1002/adma.201304373. [DOI] [PubMed] [Google Scholar]
  6. Tessler N., Preezant Y., Rappaport N. & Roichman Y. Charge Transport in Disordered Organic Materials and Its Relevance to Thin-Film Devices: A Tutorial Review. Adv. Mater. 21, 2741–2761 (2009). [Google Scholar]
  7. Blom P. W. M. & Vissenberg M. C. J. M. Charge transport in poly(p-phenylene vinylene) light-emitting diodes. Mater. Sci. Eng. R Reports 27, 53–94 (2000). [Google Scholar]
  8. Bässler H. Charge Transport in Disordered Organic Photoconductors a Monte Carlo Simulation Study. Phys. Status Solidi 175, 15–56 (1993). [Google Scholar]
  9. Melianas A. et al. Dispersion-Dominated Photocurrent in Polymer:Fullerene Solar Cells. Adv. Funct. Mater. (2014). 10.1002/adfm.201400404. [Google Scholar]
  10. Howard I. A., Etzold F., Laquai F. & Kemerink M. Nonequilibrium Charge Dynamics in Organic Solar Cells. Adv. Energy Mater. (2014). 10.1002/aenm.201301743. [Google Scholar]
  11. Street R., Song K., Northrup J. & Cowan S. Photoconductivity measurements of the electronic structure of organic solar cells. Phys. Rev. B 83, 1–13 (2011). [Google Scholar]
  12. Seifter J., Sun Y. & Heeger A. J. Transient Photocurrent Response of Small-Molecule Bulk Heterojunction Solar Cells. Adv. Mater. 26, 2486 (2014) 10.1002/adma.201305160. [DOI] [PubMed] [Google Scholar]
  13. Scher H. & Montroll E. Anomalous transit-time dispersion in amorphous solids. Phys. Rev. B 12, 2455–2477 (1975). [Google Scholar]
  14. Baranovskii S., Cordes H., Hensel F. & Leising G. Charge-carrier transport in disordered organic solids. Phys. Rev. B 62, 7934–7938 (2000). [Google Scholar]
  15. Schönherr G., Bässler H. & Silver M. Dispersive hopping transport via sites having a Gaussian distribution of energies. Philos. Mag. Part B 44, 47–61 (1981). [Google Scholar]
  16. Österbacka R. et al. Mobility and density relaxation of photogenerated charge carriers in organic materials. Curr. Appl. Phys. 4, 534–538 (2004). [Google Scholar]
  17. Novikov S., Dunlap D., Kenkre V., Parris P. & Vannikov A. Essential role of correlations in governing charge transport in disordered organic materials. Phys. Rev. Lett. 81, 4472–4475 (1998). [Google Scholar]
  18. Pasveer W. F. et al. Unified description of charge-carrier mobilities in disordered semiconducting polymers. Phys. Rev. Lett. 94, 1–4 (2005). [DOI] [PubMed] [Google Scholar]
  19. Fishchuk I. I. et al. Unified description for hopping transport in organic semiconductors including both energetic disorder and polaronic contributions. Phys. Rev. B 88, 125202 (2013). [Google Scholar]
  20. Tiedje T. & Rose A. A physical interpretation of dispersive transport in disordered semiconductors. Solid State Commun. 37, 49–52 (1980). [Google Scholar]
  21. Jakobs A. & Kehr K. W. Theory and simulation of multiple-trapping transport through a finite slab. Phys. Rev. B 48, 8780–8789 (1993). [DOI] [PubMed] [Google Scholar]
  22. Schubert M. et al. Mobility relaxation and electron trapping in a donor/acceptor copolymer. Phys. Rev. B 87, 024203 (2013). [Google Scholar]
  23. Street R. A., Krakaris A. & Cowan S. R. Recombination through different types of localized states in organic solar cells. Adv. Funct. Mater. 22, 4608–4619 (2012). [Google Scholar]
  24. Shuttle C. G., Hamilton R., Nelson J., O'Regan B. C. & Durrant J. R. Measurement of charge-density dependence of carrier mobility in an organic semiconductor blend. Adv. Funct. Mater. 20, 698–702 (2010). [Google Scholar]
  25. Nicolai H. T. et al. Unification of trap-limited electron transport in semiconducting polymers. Nat. Mater. 11, 882–887 (2012). [DOI] [PubMed] [Google Scholar]
  26. Armin A. et al. Balanced carrier mobilities: not a necessary condition for high-efficiency thin organic solar cells as determined by MIS-CELIV. Adv. Energy Mater. (2013). 10.1002/aenm.201300954. [Google Scholar]
  27. Lampert M. A. & Mark P. Current injection in solids. (Academic Press, 1970). [Google Scholar]
  28. Park S. H. et al. Bulk heterojunction solar cells with internal quantum efficiency approaching 100%. Nat. Photonics 3, 297–302 (2009). [Google Scholar]
  29. Baumann A., Lorrmann J., Rauh D., Deibel C. & Dyakonov V. A new approach for probing the mobility and lifetime of photogenerated charge carriers in organic solar cells under real operating conditions. Adv. Mater. 24, 4381 (2012). [DOI] [PubMed] [Google Scholar]
  30. Staniec P. A. et al. The Nanoscale Morphology of a PCDTBT:PCBM Photovoltaic Blend. Adv. Energy Mater. 1, 499–504 (2011). [Google Scholar]
  31. Armin A., Zhang Y., Burn P. L., Meredith P. & Pivrikas A. Measuring internal quantum efficiency to demonstrate hot exciton dissociation. Nat. Mater. 12, 593–593 (2013). [DOI] [PubMed] [Google Scholar]
  32. Vandewal K. et al. Efficient charge generation by relaxed charge-transfer states at organic interfaces. Nat. Mater. 13, 63–68 (2013). [DOI] [PubMed] [Google Scholar]
  33. Cunningham P. D. & Hayden L. M. Carrier Dynamics Resulting from Above and Below Gap Excitation of P3HT and P3HT/PCBM Investigated by Optical-Pump Terahertz-Probe Spectroscopy. J. Phys. Chem. C 112, 7928–7935 (2008). [DOI] [PubMed] [Google Scholar]
  34. Chan K. K. H., Tsang S. W., Lee H. K. H., So F. & So S. K. Charge injection and transport studies of poly(2,7-carbazole) copolymer PCDTBT and their relationship to solar cell performance. Org. Electron. 13, 850–855 (2012). [Google Scholar]
  35. Koster L., Smits E., Mihailetchi V. & Blom P. Device model for the operation of polymer/fullerene bulk heterojunction solar cells. Phys. Rev. B 72, 085205 (2005). [Google Scholar]
  36. Neukom M. T., Reinke N. A. & Ruhstaller B. Charge extraction with linearly increasing voltage: A numerical model for parameter extraction. Sol. Energy 85, 1250–1256 (2011). [Google Scholar]
  37. Armin A. et al. Doping-induced screening of the built-in-field in organic solar cells: effect on charge transport and recombination. Adv. Energy Mater. 3, 321–327 (2013). [Google Scholar]
  38. Orenstein J. & Kastner M. Photocurrent Transient Spectroscopy: Measurement of the Density of Localized States in a-As2Se3. Phys. Rev. Lett. 46, 1421–1424 (1981). [Google Scholar]
  39. Clarke T. M. et al. Charge carrier mobility, bimolecular recombination and trapping in polycarbazole copolymer:fullerene (PCDTBT:PCBM) bulk heterojunction solar cells. Org. Electron. 13, 2639–2646 (2012). [Google Scholar]
  40. Pettersson L. A. A., Roman L. S. & Inganäs O. Modeling photocurrent action spectra of photovoltaic devices based on organic thin films. J. Appl. Phys. 86, 487 (1999). [Google Scholar]
  41. Sun Y. et al. Efficient, air-stable bulk heterojunction polymer solar cells using MoO(x) as the anode interfacial layer. Adv. Mater. 23, 2226 (2011). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

SUPPLEMENTARY INFO

srep05695-s1.pdf (2.2MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES