A new and fast image feature selection method for developing an optimal mammographic mass detection scheme

Abstract

Purpose:

Selecting optimal features from a large image feature pool remains a major challenge in developing computer-aided detection (CAD) schemes of medical images. The objective of this study is to investigate a new approach to significantly improve efficacy of image feature selection and classifier optimization in developing a CAD scheme of mammographic masses.

Methods:

An image dataset including 1600 regions of interest (ROIs) in which 800 are positive (depicting malignant masses) and 800 are negative (depicting CAD-generated false positive regions) was used in this study. After segmentation of each suspicious lesion by a multilayer topographic region growth algorithm, 271 features were computed in different feature categories including shape, texture, contrast, isodensity, spiculation, local topological features, as well as the features related to the presence and location of fat and calcifications. Besides computing features from the original images, the authors also computed new texture features from the dilated lesion segments. In order to select optimal features from this initial feature pool and build a highly performing classifier, the authors examined and compared four feature selection methods to optimize an artificial neural network (ANN) based classifier, namely: (1) Phased Searching with NEAT in a Time-Scaled Framework, (2) A sequential floating forward selection (SFFS) method, (3) A genetic algorithm (GA), and (4) A sequential forward selection (SFS) method. Performances of the four approaches were assessed using a tenfold cross validation method.

Results:

Among these four methods, SFFS has highest efficacy, which takes 3%–5% of computational time as compared to GA approach, and yields the highest performance level with the area under a receiver operating characteristic curve (AUC) = 0.864 ± 0.034. The results also demonstrated that except using GA, including the new texture features computed from the dilated mass segments improved the AUC results of the ANNs optimized using other three feature selection methods. In addition, among 271 features, the shape, local morphological features, fat and calcification based features were the most frequently selected features to build ANNs.

Conclusions:

Although conventional GA is a powerful tool in optimizing classifiers used in CAD schemes of medical images, it is very computationally intensive. This study demonstrated that using a new SFFS based approach enabled to significantly improve efficacy of image feature selection for developing CAD schemes.

I. INTRODUCTION

Breast cancer is the second most prevalent cancer in women and ranks second as a cause of cancer death in women after lung cancer.¹ Scientific evidence has shown that early detection of breast cancer combined with improved treatment strategies significantly reduced patients’ mortality and morbidity rates over the last four decades.^2,3 However, due to the large variability of breast abnormalities, overlapping dense fibro-glandular tissues, and the low cancer detection rate in the screening environment,⁴ interpreting mammograms remains a difficult task, which results in high false positive (FP) recall rates and substantially reduces efficacy of screening mammography.

In the last two decades, many computer-aided detection (CAD) schemes have been developed aiming to assist radiologists in reading mammograms.^5–11 In CAD development, many different image features have been proposed for detection and/or classification of suspicious lesions.^5,6,8,12,13 Among them, the popular features include (1) shape features that are frequently computed to identify malignant masses based on their morphological/geometrical appearance,^5,14–18 (2) intensity based features that compute contrast and gray level based descriptors,^15,19–22 and (3) texture based features that are computed from gray-level co-occurrence matrix, spatial gray-level dependence matrix, run length statistics, and wavelet coefficients.^17,23–28 The majority of studies computed texture features from the whole lesion,^23,24,26,28 while some only used segmented locations within the lesion or its surrounding background.^17,27

Hence, from different feature categories, a large number of diverse features have been proposed and computed. Due to difference between human vision and computer vision, it is difficult to visually select the relevant features that are beneficial to CAD schemes and remove the redundant or irrelevant features. To do this, many computerized feature selection methods have been presented in the literature; they can be generally divided into genetic algorithm (GA) and stepwise feature selection based approaches. GA is popular optimization tool incorporating search heuristics that emulate Darwinian evolution (“survival of the fittest”) and has been applied to select optimal features for mass detection.^29–32 An advantage of GA is that it performs a global search (using crossover, mutation and parent selection operators), which does not often get stuck in local optimal solutions. However, GA is very computationally expensive. Another popular approach is stepwise feature selection.^26,28,31,33 With this approach, the algorithm first starts with an empty feature pool. Then, at each following step, an available feature is added or removed from the feature pool based on an analyzed selection criterion. The stepwise feature selection is more computationally efficient than GA, however, it is often trapped in local optimal solutions and yields lower performance.

In developing CAD schemes, feature selection is also not an independent process and it combines with a specific feature classifier to distinguish between true and FP lesions. The reported classifiers include linear discriminant analysis (LDA),^24,34 artificial neural networks (ANNs),^{19,21,35–37} Bayesian networks,³² binary decision trees,^12,38 and others. Among them, ANN is the most popular classifier used in the CAD field. In the majority of ANN based classifiers, the ANN topology (number of hidden nodes and connections) was determined by trial-and-error experiments.^{5,19,21,31,36,39} However, the addition of each connection adds an extra dimension to the search space and requires additional parameter tuning. Furthermore, having redundant structure can cause “overfitting” of the ANN leading to poorer generalization on the independent testing sets. Thus, studies to design optimal ANN architectures have been examined for computer-aided breast cancer diagnosis.^40–47 They can be generally divided into rule based or GA based solutions.

In early work, Setiono⁴¹ proposed a pruning algorithm for three-layer feedforward ANNs. The algorithm extracted rules from a pruned network by considering finite numbers of hidden unit activation values. Using this pruning strategy, a simpler network enabled to yield the accuracy that was approximately equivalent with the unpruned network. In Ref. 42, Gurcan et al. analyzed three automated methods, namely, steepest descent, simulated annealing, and GAs to determine the optimal structure of a neural network for microcalcification detection. They concluded that simulated annealing using a Boltzman cooling schedule was the most efficient approach for their task. In Ref. 45, the authors demonstrated that a GA-optimized ANN yielded higher sensitivity than the ANN optimized using manually selected image features in detecting microcalcification clusters.

However, using GAs to determine an optimal ANN architecture faces a major obstacle of the Competing Conventions Problem.⁴⁸ This problem occurs when a solution (or ANN) can be encoded in more than one way. During crossover, two unidentical genomes that represent the same solution is likely to produce damaged offspring. The NeuroEvolution of Augmenting Topologies (NEAT) method proposed by Stanley and Miikkulainen,^47,49 has been shown to successfully solve this problem,⁴⁷ and performed well in many diverse problem settings, particularly in the reinforcement learning domain.^47,50 Recently, a NEAT variant, called Phased Searching with NEAT in a Time-Scaled Framework was shown to outperform NEAT on developing a CAD scheme for lung nodules.⁵¹

Despite the great efforts in CAD development, there is no agreement on how to identify optimal features used in CAD schemes to date. Hence, selecting optimal image features remains technically challenging. It is also a computationally inefficient process. The purpose of this study aims to improve efficacy of image feature selection in developing CAD schemes by investigating and identifying a new more effective and computationally efficient image feature selection method to analyze a large feature pool including novel and multiple texture, shape, isodensity, fat, spiculation, and contrast based features for developing a CAD scheme for breast masses. Specifically, we analyzed and compared the performances of two conventional and two new feature selection methods to optimize an ANN classifier. Two conventional methods are (1) a standard stepwise feature selection, namely, sequential forward selection (SFS), and (2) a conventional genetic algorithm (GA). Two new methods are (1) a Phased Searching with NEAT in a Time-Scaled Framework classifier and (2) a modified sequential floating forward selection (SFFS) algorithm proposed by Ververidis and Kotropoulos.^52,53 These four feature selection methods were tested using the same image dataset and a tenfold cross validation method. The classification performance was evaluated using the area under a receiver operating characteristic (ROC) curve (AUC). Through the comparison, we investigated whether using a new method can significantly improve the efficacy of feature selection and ANN optimization for developing CAD schemes.

II. MATERIALS

In this study, our dataset involves 1600 regions of interest (ROIs). Among them, 800 are positive, in which each ROI comprises of one mass region detected by radiologists during original mammogram reading and later pathologically verified by biopsy, and 800 are negative but involve FP mass regions detected by our CAD scheme.^54–56 The 1600 ROIs originated from a large database of digitized screen-film based mammograms. The detail descriptions of the image database and its characteristics have been reported in previous studies.^54–56 Each ROI has a fixed size of 512 × 512 pixels, which was extracted from the center of each identified suspicious mass lesion. Each ROI image was reduced (subsampled) by a pixel averaging method using a kernel of 8 × 8 pixels in both the x and y directions. In this way, the pixel size is increased from 50 × 50μm in the original digitized image to 400 × 400 μm in the subsampled image, which is a common practice used in the CAD of breast mass detection in order to increase the computational efficiency and reduce the noise in the computed image features.^6,57

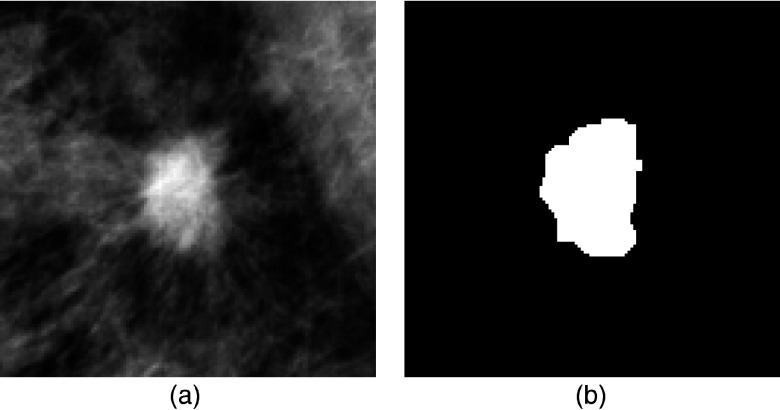
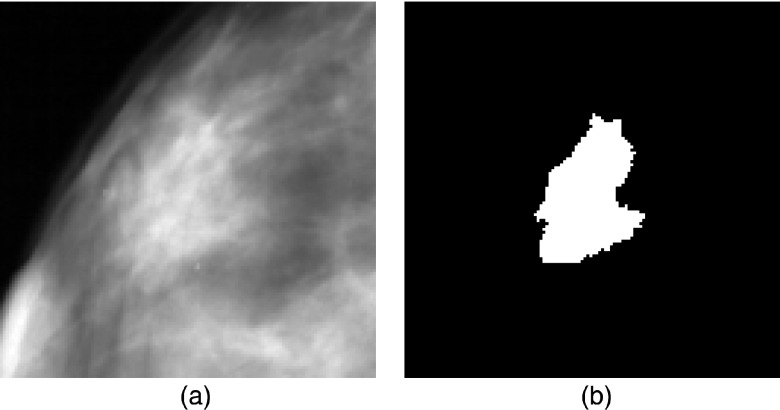
Using the ROI center as the seed for a region growing algorithm, the mass region was segmented by a multilayer topographic region growth algorithm.^22,58 For each ROI, automated segmentation result was visually examined. If there was noticeable segmentation error, the mass boundary was manually corrected (redrawn). This correction step is required as an accurate segmentation result of the mass is crucial for assessing feature relevance. In Figs. 1 and 2, examples of a malignant mass and a FP detection from our image database are displayed, along with the automated segmentation results.

FIG. 1.

(a) and (b) Example of a malignant mass ROI and its corresponding segmentation mask.

FIG. 2.

(a) and (b) Example of a FP detection ROI and its corresponding segmentation mask.

III. METHODS

III.A. Feature computation

From each ROI, a total of 271 image features were computed, which combine various features based on lesion shape, spiculation, texture, contrast, isodensity, presence, and location of fat (necrosis) and/or calcifications. Among them, 90 are new features that we introduced in this study (which will be discussed later in this section), and 181 are selected from previous CAD literature. A summary of the computed features according to their feature grouping/type and number is provided in Table I.

TABLE I.

Summary of computed image features according to feature subgroup, number, and description.

Feature grouping/type	Feature number	Description
Shape	1–11	Eccentricity, equivalent diameter, extent, convex area, major axis length, minor axis length, orientation, solidity, shape factor ratio, ratio of major to minor axis length, modified compactness
Fat	12–15	Size (pixel number), size factor ratio (size/mass area), region number, average distance to the mass center (average distance/mean radial length of mass region)
Calcifications	16–18	Size (pixel number), size factor ratio (size/mass area), region number
Texture (lesion segment only)	19–44	4 gray level co-occurrence matrix based features, 22 average and maximum values of gray level run length based texture features
Texture (dilated lesion segments)	45–134	24 average and maximum values of gray level co-occurrence matrix based features, 66 average and maximum values of gray level run length based texture features, computed on dilated lesion segments
Spiculation	135–154	Features computed on the maxima points and on the whole image of the DNG and the CNG of the segmented lesion regions
Contrast	155–214	Contrast based features (previously defined in Refs. 19 and 20, and 22) computed for different-sized regions and locations of the lesion segments and background
Isodensity	215–244	Isodensity based features (previously defined in Ref. 19) computed for different-sized regions and locations of the lesion segments and background
Other features	245–271	Local morphological based features computed and used in our previous CAD scheme (reported in Refs. 22 and 54, and 59)

First, we computed 11 shape based features previously described in Ref. 60 on all the pixels within the segmented lesions. They consist of a mixture of common and uncommon features for the mass detection task. Of these, the shape factor ratio^5,14,15 and the modified compactness^18,61 features are the most frequently used in the literature.

Second, based on our observation that the presence of fat (necrosis) within a mass is a good indicator used by radiologists in predicting the likelihood of a mass being malignant. However, this feature has rarely been computed and analyzed in CAD schemes for mass detection and/or classification. We hereby chose to analyze four features that were originally proposed and shown to be effective for mass classification in Refs. ⁶⁰ and ⁶². In addition, we also computed three features to quantify the presence of calcifications within the lesion segments.

Third, various groups have analyzed different texture features for mass detection and/or classification.^{5,17,20,27,63,64} In this study, we computed the gray level run length based features^65–68 and gray level co-occurrence matrix (GCM) based features.⁶⁹

Fourth, although the divergence of the normalized gradient (DNG) and the curl of the normalized gradient (CNG) are popular methods aiming to detect lesion spiculation, our previous study indicated that CNG and DNG features were not very useful for classification between benign and malignant masses possibly due to tissue superposition within the mass regions on 2D projection images.⁶⁰ Hence, in this study, we proposed and investigated a new method to compute texture features that more sensitively correlates to mass spiculation.

To generate the dilated lesion segments, an image dilation procedure with a “disc” structuring element (SE) was performed on the original (undilated) lesion segments. On the dilated segments, the computation of the texture features is performed in the region of the smallest rectangular bounding box encompassing the dilated lesion segment. Our purpose of computing the texture features on the dilated regions of the lesion segments is to enable to detect and quantify the spicules/radiating lines that are frequently observed in malignant masses, as a differentiating feature between malignant masses and FP detections/normal tissue. A clearer description/depiction of the computation procedure of the novel texture based features is demonstrated in Fig. 3, in which we can observe that the radiating lines in the malignant mass frequently extend beyond the smallest bounding box of the mass (lower-left column of Fig. 3). Thus, in our experiments, we used a “disc” SE of three different sizes to perform image dilation of the original lesion segments, namely, mean radial length, 1/2 mean radial length and 1/4 mean radial length. The definition of the mean radial length is given in Ref. 14, and it is the average value of the Euclidean distance from the lesion center to each of the lesion boundary coordinates.

FIG. 3.

Computation of texture (gray level run length and gray level co-occurrence matrix based) features on a malignant mass. The conventional approach is to compute the features only on the lesion ROI (bottom-left column). We propose the computation of the features on the lesion segments dilated by three different sizes of a “disc” SE, namely 1/4 mean radial length, 1/2 mean radial length and mean radial length, and in four directions.

Fifth, we computed four contrast measures previously proposed in Refs. 15 and 19, and ²⁰ and computed them over different regions of the mass and background. The detailed description of the contrast features and their computation method has been described in Refs. ⁶⁰ and ⁶².

Sixth, we computed isodensity features (presented by te Brake et al.¹⁹) to discriminate structures that are similar in appearance to mass regions. In Ref. 19, these features were applied to detect low-intensity regions (holes) within the mass segments. One limitation is that the location and numbers of “holes” within the mass regions cannot be easily and correctly identified. To overcome this limitation, we presented a new approach of computing 30 isodensity features on differently predefined inner and outer regions on the lesion segments as reported previously.^60,62

Seventh, our feature pool includes 27 local morphological features that have been applied in our previous CAD scheme. The detail description and computational methods have been reported previously.^22,54,59

III.B. Feature selection and classification

In order to build a highly performing and robust classification scheme, a feature selection step is required to reduce the redundancy and dimensionality of the initial input feature set. In our study, the ratio of the number of features (271) to the number of the images in our database (1600) is quite high. Thus, it is appropriate to apply a feature selection algorithm due to the curse of dimensionality,⁷⁰ and to avoid the risk of “overfitting” on the training set. If the feature selection algorithm analyzes the value of the feature set without regard to the classifier, it is known as a filter. On the other hand, feature selection techniques that maximize the correct classification rate (CCR) of the classifier are known as wrappers. After the relevant features are selected by the feature selection algorithm, they are applied to a classifier to classify the input data as FP detection or malignant. This section explains four different feature selection and classification approaches that are analyzed in this study. They are: (1) Phased Searching with NEAT in a Time-Scaled Framework⁵¹ using the maximization of AUC as the fitness function; (2) A fast and accurate SFFS based method^52,53 combined with fixed-topology ANNs; (3) Feature selection and optimization of ANNs using a GA algorithm and trained by backpropagation;^35,71–73 and (4) SFS combined with fixed-topology ANNs.

In the literature, many methods have been proposed and tested to build ANN based classifiers with trial-and-error experiments to determine the ANN topologies/structure.^5,19,21,36 However, each extra input feature or connection in the ANN adds an extra dimension to the search space, and slows down the search for optimal solutions. Thus, in this study, we chose to analyze and compare four different feature selection and classification approaches to train and optimize the ANN classifier. The first approach, Phased Searching with NEAT in a Time-Scaled Framework combines feature selection with the classification/learning task, and relies entirely on a GA to train and optimize the weights, topologies, and features used in the ANN. The second approach decouples the feature selection stage from the classification stage, and uses a fast and accurate SFFS based feature selection algorithm combined with fixed-topology ANNs trained by backpropagation at the classification stage. The third approach combines GAs with ANNs trained by backpropagation, and uses a GA scheme to select relevant features and to find the optimal number of hidden nodes to be used in the hidden layer of the ANNs. Finally, the fourth approach is a standard SFS algorithm combined with ANNs trained by backpropagation.

Optimization of all parameters in the four approaches and the feature selection procedure was performed on the training subsets, which were kept completely separated from the testing subsets. The details of the parameters used in the four approaches are given in Appendixes A–C. To enable adequate performance comparisons to be made between the four different approaches, some of the parameters were fixed between the approaches; e.g., the number of iterations for the ANN training by backpropagation for the first, third, and fourth approaches, and the number of runs (repetitions) for the two GA based methods. Also, for all four approaches, we performed linear normalization of the input features (normalize the input values between 0 and 1).

III.B.1. Phased Searching with NEAT in a Time-Scaled Framework

The task of determining optimal topology of an ANN is not trivial. The addition of each feature or connection to the ANN requires additional parameter tuning and adds another dimension to the search space. In Ref. 51, a novel classifier called Phased Searching with NEAT in a Time-Scaled Framework was presented, which automatically determines the optimal topologies, weights, and features of ANN classifiers by evolving them in a GA based framework. It is based on the NEAT algorithm proposed by Stanley and Miikkulainen,^47,49 and on the threshold based Phased Searching method originally proposed by Green.^74,75 Phased Searching outperforms the original NEAT method in that it removes redundant structure in the ANNs evolved by NEAT, and finds optimal solutions faster than NEAT. NEAT is distinct from other neuroevolution methods (methods that evolve ANNs using GAs where the networks are the phenotype being evaluated⁴⁷) in three ways: (1) crossover of different topologies is performed using innovation numbers as historical markings; (2) structural innovation is protected by speciation; (3) incremental growth is performed from almost minimal structure.

One of the pitfalls of NEAT is that it does not perform feature selection. Phased Searching improves on NEAT in that it performs feature selection implicitly, by allowing input connections (features) that are beneficial for the classification task to be retained through the course of evolution, and vice versa. Furthermore, with Phased Searching, the search for useful network topologies is evolved in alternating complexification/simplification phases; during the complexification phase(s), useful structure (features, nodes, and connections) is added to the networks, whereas during the simplification phase(s), redundant and irrelevant structure is discarded. Through the process of discarding redundant and irrelevant features and topologies, the search for optimal structure proceeds faster, as less parameter tuning is required. For a detailed description of this new approach, the reader is referred to Ref. 51.

In Ref. 51, Phased Searching with NEAT in a Time-Scaled Framework was shown to perform comparably well with a SVM classifier and with fixed-topology ANNs in experiments performed on 360 lung CT scans for a lung nodule detection task. In the previous study,⁵¹ the minimization of the absolute error on the validation set was used as the fitness function for assessing ANN performance, namely, if the absolute error on the validation set was minimized, the ANN had a higher chance of being selected by the GA scheme to generate a new chromosome in the next generation. In this study, we modified the original program [SharpNEAT ver.2.2.0 (Ref. ⁷⁵)] by using a new fitness function that analyzes the maximization of the AUC on the training dataset. We compared classification performance of the new fitness function with the original fitness function of the minimization of the absolute error.

Furthermore, in Ref. 51, the complexification and simplification phases of Phased Searching with NEAT in a Time-Scaled Framework were implemented with equal values, e.g., 200 generations of complexification followed by 200 generations of simplification, in alternating cycles. In this study, we analyzed the networks’ performance for different values of the complexification and simplification phases, such as 50 generations of complexification/150 generations of simplification, 20 generations of complexification/180 generations of simplification, and 35 generations of complexification/165 generations of simplification, over an 800 generation time scale. To decide on the best classification scheme to use on the testing subsets, we performed an analysis on the evolution of the mean best fitness and the mean network complexity over the training subsets; the final parameter values that were used for the Phased Searching experiments are provided in Appendix A.

III.B.2. A new SFFS based method combined with fixed-topology ANNs

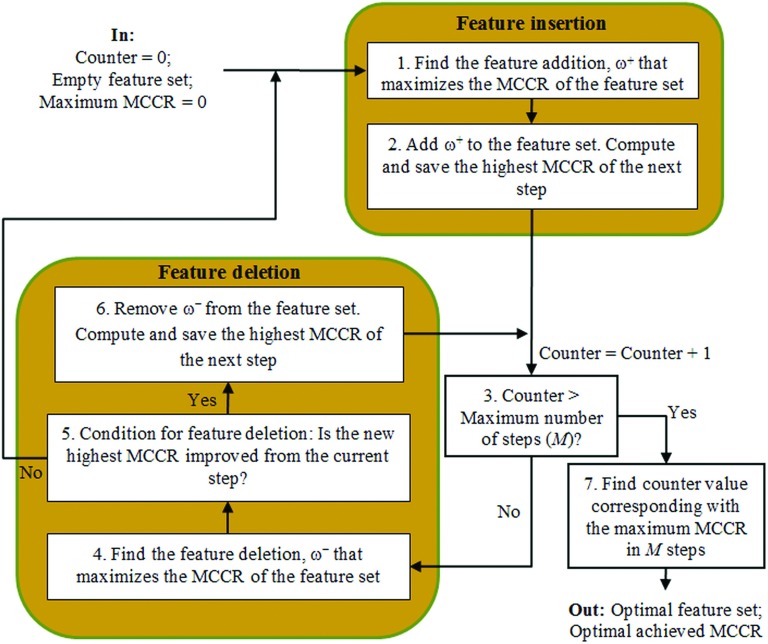
We analyzed the value of decoupling the feature selection and classification stages, namely to separate the two stages into two distinct and separate steps. At the feature selection stage of this approach, we analyzed a faster and more accurate version of the SFFS feature selection algorithm,^52,53 originally proposed by Pudil et al. in Ref. 76. In Refs. ⁵² and ⁵³, Ververidis and Kotropoulos presented an efficient SFFS based algorithm that reduced the computation time and produced better results measured by a CCR, compared to the original SFFS method. We had previously analyzed this novel SFFS based approach and obtained good results on our mass benign/malignant classification system in Ref. 60. A flowchart of the SFFS algorithm (modified from Ref. 52) is displayed in Fig. 4.

FIG. 4.

Flowchart of the fast and accurate SFFS algorithm (modified from Ref. 52).

The proposed SFFS based method^52,53 uses the CCR of the Bayes classifier as the criterion employed in SFFS in a wrapper based framework. The CCR can be estimated by using N-fold cross-validation. Each training dataset was split into N parts. In our experiments, we used N = 10. N-1 parts were used to train the Bayes classifier, and the Nth part was used to compute CCR during testing. Finally, the resulting CCRs on the ten testing subsets were averaged to compute the mean CCR (MCCR). Repeated N-fold cross-validation, which is simply N-fold cross-validation repeated many times⁷⁷ was implemented by the authors in Refs. ⁵² and ⁵³. The variance of the MCCR estimated by repeated N-fold cross-validation varies less than that measured by N-fold cross-validation. Using their proposed method,⁵² the authors showed that SFFS computational time was reduced, and the CCR for the selected feature set varied less than the CCR obtained by standard SFFS.

In our experiments, we reused the Bayes classifier for the SFFS algorithm,^52,53 due to its speed in training and validation. We also used all the standard parameters recommended in Ref. 52 except the total number of feature insertions and exclusions, M and the difference between the cross-validated CCR required to add another feature, γ. In Ref. 52, the authors recommended a typical value of M = 25. However, we had observed that the peak in the MCCR curve indicating selection of the best feature set, frequently occurred between M = 25–35 in our experiments; thus, we chose to use M = 35 and selected γ = 0.0075 as a trade-off between computational load and consistency of features selected in the final feature set (a lower value of γ means a higher consistency of features selected, but a higher computation time requirement).

The selection of relevant features by the SFFS based approach is just the first step of the classification stage; in the next step, the selected features are given to a fixed-topology ANN classifier trained by backpropagation using the Matlab^® Neural Network Toolbox. The details of the parameters used in the ANN training are given in Appendix B.

III.B.3. A genetic algorithm based feature selection and ANN optimization

We have previously applied a publicly available GA software package [Genesis (Ref. ⁷⁸)] to evolve ANNs trained by backpropagation as reported in our previous studies.^35,71–73 With this approach, the relevant features and the optimal number of hidden nodes of the ANNs are evolved and determined by the GA. In this approach, the evolved ANNs were trained by backpropagation and the fitness function of the GA was the maximization of the AUC computed on the training sets, namely, the networks that produced higher AUC values on the training sets were more likely to survive in the evolutionary run. To enable similar and comparable performance comparisons with the Phased Searching experiments, we selected the best network that produced the highest AUC result on the training subsets over five runs, to be validated on the testing subsets. To also enable similar and comparable performance comparisons with the SFFS based method combined with fixed-topology ANNs, we limited the number of ANN training iterations by backpropagation of both approaches to 500. Other parameters of the Genesis software, and of the parameters related to the ANN training using this approach are given in Appendix C.

III.B.4. SFS combined with fixed-topology ANNs

Finally, we selected a SFS using a quadratic discriminant analysis classifier that utilizes CCR as a loss measure in a tenfold cross-validation framework. At the classification stage of the SFS, we also used a fixed-topology ANN with the same training parameters as used in the SFFS based approach (described in Appendix B). We compared both classification performance levels and training efficiency (computational time) between SFS and the other three feature selection and classifier optimization methods tested in this study.

III.C. Experimental setup and classification methodology

We applied a tenfold cross-validation scheme to train and test the ROIs in our database. In this scheme, the 800 true positive (TP) ROIs and 800 FP ROIs were randomly segmented into ten exclusive subsets. Nine TP and nine FP subsets were used to train the ANN classifier in each training and testing cycle. Then, after training, the ANN was applied to each ROI in the remaining one TP and one FP subset to generate a likelihood score of the ROI being malignant. We iteratively executed this procedure ten times, using the different combinations of data subsets each time. Thus, each ROI was tested once with an ANN-generated probability score.

In each of tenfold tests, the ANN-generated probability scores were used to compute a ROC curve and the area under the ROC curve (an AUC value). After all tenfold testing, ten AUC values were computed. We then computed the average and standard deviation of the AUC values as well as the average computation time per fold for each feature selection approach. The statistical significance was tested at the 5% significance level using the Wilcoxon signed rank test. The confusion matrix of the approach with the highest AUC result was also tabulated. To assess which feature groups/types are really relevant for mass detection, we performed an analysis of the features selected by SFFS, GA-ANN, and SFS based on the feature grouping/type and frequency of feature selection. In addition, to assess the relevance of the new texture features computed on the dilated regions of the lesion segments (discussed in Sec. III A), we also compared the AUC values with and without inclusion of these new texture features for all four feature selection methods.

IV. RESULTS

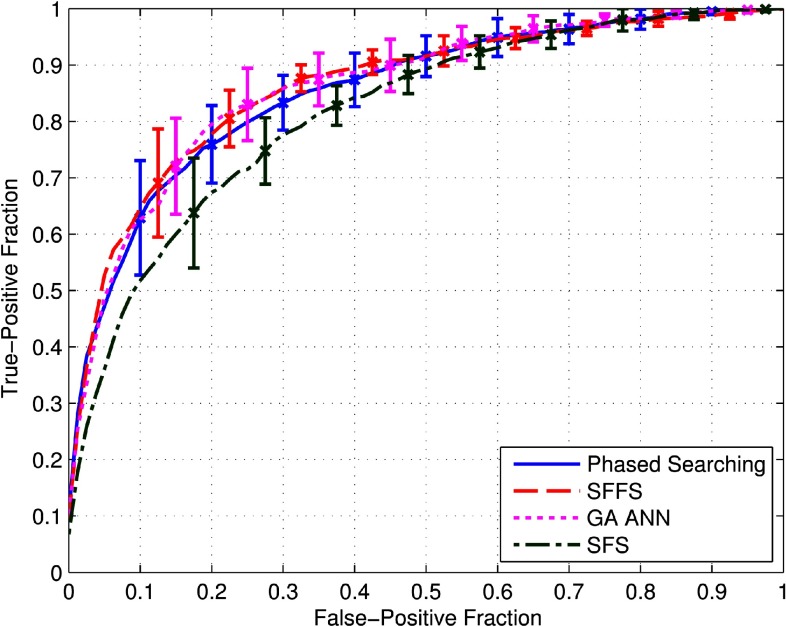
Figure 5 demonstrates four ROC curves computed using four different approaches including (1) Phased Searching with NEAT in a Time-Scaled Framework using AUC as the fitness function, (2) the SFFS based method combined with fixed-topology ANNs, (3) optimization of ANNs using a GA algorithm and trained by backpropagation, and (4) SFS combined with fixed-topology ANNs. The error bars on the plots are symmetric and represent two standard deviation units in length. The computed average and standard deviation results of the AUC of each approach, over ten folds, are summarized in Table II. It shows that the SFFS-based approach yielded the highest AUC value.

FIG. 5.

ROC curves of the four compared feature selection and classification approaches computed over the tenfold cross-validation experiments-–(1) Phased Searching with NEAT in a Time-Scaled Framework using the maximization of AUC as the fitness function, (2) A fast and accurate SFFS based method combined with fixed-topology ANNs, (3) Optimization of ANNs using a GA algorithm and trained by backpropagation, and (4) SFS combined with fixed-topology ANNs. The error bars are symmetric and are two standard deviation units in length.

TABLE II.

Average AUC results and computation times per fold and corresponding standard deviation intervals for the four compared feature selection and classification approaches computed over the tenfold cross-validation experiments.

			Average computation time
No.	Method	AUC	per fold (min)
1	Phased Searching	0.856 ± 0.029	134.6 ± 3.6
2	SFFS	0.864 ± 0.034	34.6 ± 1.2
3	GA-ANN	0.863 ± 0.036	1009 ± 12.4
4	SFS	0.835 ± 0.020	13.3 ± 1.6

Although the difference between the three AUC values of SFFS, GA-ANN and Phased Searching shown in Table II is very comparable (p > 0.05), the SFFS based approach is much more computationally efficient than GA-ANN and Phased Searching whereby it required around 6 h of computation time to complete one run of the tenfold cross-validation experiments; Phased Searching required around 22 h of computing/processing time, followed by GA-ANN, which required around one week of processing time in this specific optimization task using a regular Dell precision T3600 workstation. The total computation time for GA-ANN and Phased Searching was significantly different from SFFS (p = 0.002) for both GA-ANN and Phased Searching. SFS was the fastest method, but it was outperformed by the other three methods, namely: SFFS (p = 0.010), GA-ANN (p = 0.037), and Phased Searching (p = 0.13).

For the Phased Searching experiments, we compared the performances using two different fitness functions optimized on the training subsets, namely (1) minimization of the absolute error and (2) maximization of the AUC. All other parameters were maintained between the two methods except the implementation of the fitness function. The result in Fig. 5 was obtained with the second fitness function, namely, the maximization of the AUC. Its corresponding result on the testing subsets is AUC = 0.856 ± 0.029, which is significantly different (p = 0.004) from the result obtained with the minimization of the absolute error (AUC = 0.774 ± 0.036).

Table III shows a confusion matrix generated using SFFS. Using the classifier prediction score of 0.5 as a threshold, the confusion matrix in Table III shows that 80.1% (1281/1600) of ROIs were correctly predicted by the SFFS based method, whereas 19.9% (319/1600) of ROIs were misclassified, at this prediction threshold. The TP fraction was 77.4% (619/800), whereas the true negative (TN) fraction was 82.8% (662/800).

TABLE III.

Confusion matrix of the classification results using an ANN optimized by SFFS based method when applying a threshold of 0.5 on the ANN generated classification scores.

Prediction ->	Negative images	Positive images
Negative images	662	138
Positive images	181	619

The results of the analysis performed on the features selected by SFFS. GA-ANN and SFS are displayed in Table IV. In the far-left column of Table IV, the feature type is shown. In the middle column of Table IV, the fraction of that feature group out of all available features (271) is displayed; e.g., in the first row of Table IV, there are 11 shape features out of the total of 271 features. The far-right columns show the percentage of features that were selected by SFFS, GA-ANN, and SFS in each group, namely, the average percentage value of selected features within a group, and the standard deviation intervals computed over the tenfold cross-validation experiment. For example, in the first row, an average of 30.0% of 11 shape features (30.0% × 11 = 3.3 features) were selected by SFFS with standard deviation intervals of 16.6% or 1.83 features. A similar feature analysis for Phased Searching was performed in Ref. 79.

TABLE IV.

Features selected by the SFFS, GA-ANN, and SFS methods. The feature pool of 271 features is divided into 9 groups listed in the far-left column. The fraction of the features represented in each group is shown in the middle column. The average percentages of the features selected by the three methods along with their standard deviation intervals are displayed in the far-right columns.

Feature		SFFS	GA-ANN	SFS
group/type	Fraction	(%)	(%)	(%)
Shape	11/271	30.0 ± 16.6	54.5 ± 10.5	9.1 ± 8.6
Fat	4/271	7.5 ± 12.1	55.0 ± 19.7	2.5 ± 7.9
Calcifications	3/271	10.0 ± 16.1	80.0 ± 28.1	0
Texture (mass segment only)	26/271	7.3 ± 3.4	46.5 ± 9.3	3.5 ± 2.2
Texture (dilated mass segments)	90/271	2.3 ± 1.0	47.2 ± 6.5	1.7 ± 0.8
Spiculation	20/271	1.5 ± 3.4	44.5 ± 8.6	0.50 ± 1.6
Contrast	60/271	2.3 ± 1.4	48.5 ± 7.8	0.83 ± 0.88
Previously computed morphological features	27/271	11.1 ± 4.3	57.0 ± 9.1	11.5 ± 4.4
Isodensity	30/271	11.0 ± 6.1	20.0 ± 3.8	3.0 ± 3.1

In addition, Table V displays the AUC results obtained with and without the inclusion of the new texture features for all four approaches using the same training and testing case indices. The results show that the inclusion of the new texture features improved the overall performance of three feature selection and classification approaches of Phased Searching, SFFS, and SFS.

TABLE V.

Average AUC values and corresponding standard deviations computed for four feature selection methods with and without inclusion of the new texture features.

		AUC (with new	AUC (without new
No.	Method	texture features)	texture features)
1	Phased Searching	0.856 ± 0.029	0.841 ± 0.028
2	SFFS	0.864 ± 0.034	0.857 ± 0.023
3	GA-ANN	0.863 ± 0.036	0.864 ± 0.030
4	SFS	0.835 ± 0.020	0.826 ± 0.028

V. DISCUSSION

Computerized quantitative image analysis methods enable to extract and compute a large number of image features. However, many of these features are redundant and/or irrelevant to the targeted classification tasks. How to effectively identify a set of small number of effective (nonredundant) features is an important and challenging task in developing CAD schemes. In this study, we assembled an initially large feature pool of 271 features. The majority of these features have been proposed and/or used in previously different CAD studies. In order to automatically and effectively select a small set of relevant features to optimize a classifier used in CAD schemes, we compared four image feature selection and classifier optimization methods for developing a CAD scheme of breast masses. The AUC values in Fig. 5 and Table II show that the ANNs optimized using SFFS and GA achieved very comparable performance levels, which are slightly better than the ANN optimized by Phased Searching with NEAT in a Time-Scaled Framework. All of these three analyzed approaches also outperformed a standard SFS based method. The study results indicate that the SFFS based method is robust and can work well for the task of CAD scheme of breast masses. The results also show that there are advantages in decoupling the feature selection and classification stages, using the SFFS based algorithm combined with fixed-topology ANNs, and it outperforms Phased Searching, which combines feature selection with the classification/learning task. Therefore, the most encouraging result of this study is that we demonstrated that using a new SFFS method enabled to significantly improve computational efficiency of image feature selection and ANN optimization process as compared to the conventional GA without decreasing the classification performance of the ANN. The ANN optimized by SFFS also involves a much smaller number of features as compared to that optimized using a GA approach, which may be another advantage of the SFFS method to be more robust in future testing.

The results also reiterate/reconfirm the good performance of our GA algorithm combined with ANNs trained by backpropagation, which has been previously examined for various tasks.^35,71–73 An advantage of this approach might be that it combines a global search for good solutions (using GAs) with a local refinement of the search (through training by backpropagation), compared with a purely GA based approach like Phased Searching. Although Phased Searching is a very flexible method that does not require the network topology/structure to be specified beforehand, it conducts the entire search for good solutions (namely, evolving the network weights, features, and connections) using GAs. The results indicate that the GA algorithm combined with ANNs trained by backpropagation might have a slight advantage over Phased Searching, and that a refinement of the global search for good solutions initiated by the GA evolution might be useful for finding better solutions.

The feature analysis results in Table IV show that the shape features were selected most frequently by the SFFS based algorithm. This was followed by our previously computed local morphological features,^22,54,59 and the new location based isodensity features. These results differ slightly from the results of a similar feature analysis procedure that we had performed on our mass benign/malignant classification scheme recently.⁶⁰ In Ref. 60, we obtained the result that the shape features, features to detect the presence of fat and the isodensity based features were the most frequently selected features (in that order). The different features selected for the classification and detection tasks indicate that the structure and appearance of benign masses differ from FP detections/normal tissue, and that different features and thus, differently trained classifiers are required to discriminate benign/malignant masses and malignant masses/normal tissue. This finding is important as it indicates that the classifiers have to be individualized and trained separately for malignant mass/normal tissue detection, and mass benign/malignant classification in CAD schemes, respectively.

We also observed from Table IV that SFFS selects a much smaller average number of features (16) compared to GA-ANN (125), at the same time, producing slightly better AUC results. In this way, the feature computation, and training and validation time for the features selected by SFFS will be a fraction of the features selected by GA-ANN. The small set of features may increase the robustness of the classifier in future applications. We also observe that the calcification-related features, previously computed local morphological features, and the fat based features were selected most frequently by GA-ANN. For Phased Searching, the calcification and fat based features were selected most frequently, followed by the shape based features. The similarities of feature selection frequency observed in the feature types selected by the different methods tested in this study indicate that our training or optimization process using these feature selection methods is robust or not biased.

In this study, we also investigated a new approach to compute texture features to detect mass spiculation. The results in Table V shows that the inclusion of the new texture features improved the final AUC results. This result was consistent for three of the four examined approaches. The results of the frequency of selection of the new texture features in Table IV for SFFS was only 2.3%, however, this is probably due to the reasoning that there were many texture features (gray level co-occurrence and run-length based) that were computed for each ROI (90 features altogether), on three sizes of SE dilations and in four directions. It is also important to note that the feature selection algorithm could still select relevant features out of the 90 computed new texture features, as demonstrated by the improvement of the AUC results with the inclusion of the new texture features in Table V.

In addition, the method of Phased Searching with NEAT in a Time-Scaled Framework is also an interesting approach that automatically determines the network weights, topologies, and features. Although it requires more computational time compared to the SFFS method, it is much faster computationally than the GA based approach. We also compared the performance of Phased Searching using two fitness functions computed as the maximization of AUC on the training set and the minimization of the absolute error initially proposed in Ref. 51. The difference between the AUC results obtained using the two fitness functions was statistically significant (p = 0.004), which indicates that selecting fitness functions could also play an important role in specific applications.

We recognize that this preliminary study has some limitations. For example, first, we did not conduct an observer evaluation study. Thus, some empirically determined thresholds or parameters, including the fixed threshold of 2600 to detect fat inside the mass region may not be optimal. To overcome these limitations, adaptive thresholds and other image processing methods need to be examined and tested with feedback from observers (e.g., radiologists) in our future studies. Second, in this study we only compared four feature selection methods in optimizing ANNs with fixed topology. Whether using the nonfixed (or adaptive) topology based ANNs will generate different results has not been investigated. Third, although we used a relatively large and diverse image dataset, as well as a tenfold cross-validation method, the robustness of this study's conclusions also needs to be further validated using new independent testing databases in the future.

APPENDIX A: PHASED SEARCHING PARAMETERS

In this study, we used the parameters recommended by SharpNEAT ver2.2.0 (Ref. ⁷⁵) as listed in Table VI.

TABLE VI.

Parameters that remained constant throughout the evolutionary run.

Parameter	Value
Population number	200
Species number	10
Number of generations (per run)	800
Connection weight range (gets or sets the connection weight range to use in the genomes; e.g., a value of 5 defines a weight range of −5 to 5. The weight range is strictly enforced, i.e., when creating new connections and mutating existing ones)	{−0.05, 0.05}
Probability that all excess and disjoint genes were copied into an offspring genome during sexual reproduction	0
Interspecies mating rate	0.01
Elitism proportion	0.2
Selection proportion	0.2

We also applied the following alternation scheme for network evolution: 50 generations complexification/150 generations simplification, over an 800 generation evolutionary time scale (initial experiments on the training subsets indicated that 800 generations was sufficient for our application). We obtained the parameters of the alternation scheme by observing the evolution of the mean best fitness and the mean network population complexity over the training subsets. The hyperbolic tangent activation function was used at the hidden nodes, and a modified sigmoidal activation function⁴⁷ was used at the output node. The parameters used during the complexification and simplification phases are listed in Table VII. These parameters were found experimentally and follow a logical pattern, namely, links need to be added more often than nodes.

TABLE VII.

Parameters that varied according to the complexification/simplification phases.

Parameter	Complexification	Simplification
Add node probability	0.15	0
Add connection probability	0.35	0
Connection weight mutation probability	0.5	0.6
Probability that a genome mutation was a “delete connection” mutation	0.001	0.4
Proportion of offspring from asexual reproduction (mutation)	0.8	1
Proportion of offspring from sexual reproduction (crossover)	0.2	0

APPENDIX B: FIXED-TOPOLOGY ANN BACKPROPAGATION TRAINING PARAMETERS—SFFS AND SFS APPROACHES

To find the optimal number of hidden nodes of ANN, we analyzed the networks’ performance using 2–40 nodes in the hidden layer, which was initialized with random weights. We trained 150 different ANNs on the training subsets, and found the network that maximized the AUC on the training subsets. The network with the highest AUC optimized on the training subset was applied to the testing subset; this was repeated ten times for the ten different testing subsets (folds). The hyperbolic tangent activation function was used at the hidden nodes, and a linear activation function at the output node, which are the default settings in the Matlab^® Neural Network Toolbox. Other parameters related to the ANN training by backpropagation are listed in Table VIII.

TABLE VIII.

Parameters for fixed-topology ANN backpropagation training.

Parameter	Value
Number of training iterations	500
Training momentum	0.9
Learning rate	0.01

APPENDIX C: OPTIMIZATION OF ANN USING GAs AND TRAINED BY BACKPROPAGATION TRAINING

The parameters of the Genesis (Ref. ⁷⁸) software, optimized on the training subsets are as follows: Chromosome strings containing 271 genes (one for each feature), and four extra genes for the representation of the hidden nodes in the ANNs were used. Initial experiments on the training subsets indicated that the population size and the number of generations (per run) were sufficient for the task. The search seeds were assigned randomly. For ANN training on the features selected by the Genesis algorithm, we used the hyperbolic tangent activation function at the hidden nodes, and the sigmoidal function at the output node. All other parameters related to the Genesis software and the ANN training are given in Table IX.

TABLE IX.

Parameters for Genesis software and fixed-topology ANN backpropagation training.

Parameter	Value
Population number	100
Number of generations (per run)	100
Crossover rate	0.6
Mutation rate	0.01
Generation gap (one indicates that the entire population of chromosomes was replaced in each generation)	1
Selection ranking [the ranking selection algorithm is a linear mapping under which the worst structure is assigned selection_ranking offspring and the best is assigned (2—selection_ranking)]	0.75
Scaling window [allows the user to control how often the baseline performance is updated. If this parameter value is set > 0, the baseline performance is updated after the scaling_window (number of generations) specified]	5
Number of training iterations	500
Training momentum	0.6
Learning rate	0.01